Abstract
The evolutionary response to selection depends on the distribution of genetic variation in traits under selection within populations, as defined by the additive genetic variance-covariance matrix (G). The structure and evolutionary stability of G will thus influence the course of phenotypic evolution. However, there are few studies assessing the stability of G and its relationship with population divergence within foundation tree species. We compared the G-matrices of Mainland and Island population groups of the forest tree Eucalyptus globulus, and determined the extent to which population divergence aligned with within-population genetic (co)variation. Four key wood property traits exhibiting signals of divergent selection were studied—wood density, extractive content, and lignin content and composition. The comparison of G-matrices of the mainland and island populations indicated that the G-eigenstructure was relatively well preserved at an intra-specific level. Population divergence tended to occur along a major direction of genetic variation in G. The observed conservatism of G, the moderate evolutionary timescale, and close relationship between genetic architecture and population trajectories suggest that genetic constraints may have influenced the evolution and diversification of the E. globulus populations for the traits studied. However, alternative scenarios, including selection aligning genetic architecture and population divergence, are discussed.
1. Introduction
Understanding the potential of populations to respond to selection requires a multiple-trait perspective, an issue that has become increasingly important in the face of ongoing and future global environmental change [1]. For a set of quantitative traits, the additive genetic variance-covariance matrix (G) within populations has a crucial importance in predicting multivariate responses to selection [2], and plays a central role in facilitating or constraining the course of adaptive evolution [3,4]. Evolutionary change is determined by the availability of genetic variation in the multivariate direction of selection, which will reflect the patterns of genetic constraint represented by the G matrix [5,6]. One of the first indications that adaptive diversification may be constrained by the amount and structure of genetic variation within populations was provided by Schluter [7]. Working with three-spine stickleback, Schluter [7] suggested that, during the early stages of adaptive radiation, trait means of conspecific populations under natural selection may not evolve in the direction of the greatest improvement in fitness on the adaptive landscape, but instead tend to evolve closely to the direction of the leading eigenvector of G (gmax) in the ancestral population. This will cause the orientation of the matrix of divergence among population trait means (D) to be biased toward gmax—the direction in a multivariate trait space that has the most genetic variance—which Schluter [7] has called the “genetic line of least resistance”. However, the distribution of genetic variation in the G matrix will determine how a population will respond to selection, implying that, besides gmax, other multivariate axes of higher than average genetic variance can also influence the direction of evolutionary change [6,8,9]. Thus, genetic constraints due to the distribution of multivariate genetic variance in G can affect adaptive evolution by biasing responses to selection (and hence evolutionary trends) toward directions of trait combinations with more available genetic variance. In particular, such constraints may reflect high G-matrix eccentricity [10,11,12], in which case genetic variation is concentrated in fewer directions of the multi-dimensional trait space, and thus genetic variance could be insufficient for a population to evolve in the direction of selection [13]. In contrast, a uniform distribution of genetic variation across the eigenvectors of G may be indicative that the amount and structure of genetic (co)variances will not limit adaptation, hence supporting rapid adaptive divergence among populations under directional selection [3,4]. Subsequently to Schluter’s [7] work, several empirical studies have indicated the potential for the G-eigenstructure to directionally constrain the course of phenotypic evolution of closely-related species or conspecific populations [6,8,9,13,14,15,16,17,18]. The role of G in influencing the direction and rate of phenotypic differentiation among populations under natural selection is expected to decay over evolutionary time [7]. Yet, a close association between genetic architecture and population divergence can persist over long-time scales of millions of years, whether occurring along genetic lines of least resistance (e.g., [7,18]) or along other multivariate axes of high genetic variance besides gmax (e.g., [6,16]).
Ultimately, the predictive significance of genetic constraints in causing deviations from the optimal response to selection may depend on whether G remains relatively stable or changes in a predictable fashion over the evolutionary time scale of interest [7,19]. Genetic (co)variances are determined by allele frequencies and the distribution of their effect sizes [20,21,22], and thus are liable to change over time and/or space owing to the effects of natural selection, genetic drift, mutation, and migration, as well as due to the interaction among these evolutionary forces [23,24,25]. Simulation-based studies exploring the impact of interactions among these forces on the dynamics of G have indicated that this matrix may be stable under certain conditions and unstable in others, although a general trend emerging from these studies suggests that G-stability (evaluated from the effects produced on the three features—size, shape, and orientation—describing the G-eigenstructure) over evolutionary time may reflect some compromise between multivariate patterns imposed by natural selection and mutation, coupled with large effective population size [10,26,27,28,29,30]. Thus, the long-term stability of G becomes eventually an empirical question and, in this sense, comparisons among closely-related species or conspecific populations have found relatively stable G-matrices (e.g., conserved eigenvectors, although eigenvalues may vary; [14,24,25,31,32,33]), while other empirical studies have shown evidence for divergent (unstable) G-matrices [34,35,36,37]. In addition, stability of G-matrices may depend on the traits considered (e.g., [38]), with unstable G-matrices being expected for traits under mainly directional selection and stable G-matrices being more likely for traits under correlational (and stabilizing) selection [10,23]. The genetic basis of the traits will also determine the extent to which selection may alter G [21]; for traits affected by many loci and alleles per locus, with a multivariate normal distribution of effects, changes in allele frequencies in response to selection are likely to be slow [22], which may facilitate genetic (co)variances to be sustained [20].
Changing genetic architecture within diversifying populations over evolutionary time may potentially alter or conserve the relationship between major axes of genetic variation and population divergence [24]. Schluter [7] assumed that populations evolve under continuous directional selection that is random with respect to gmax (hence, the bias to the direction of divergence may be interpreted as an expectation over all possible directions of selection). However, natural selection within populations is expected to directly affect G-matrix evolution and stability, as an alignment of G with the adaptive landscape may be promoted by the landscape’s curvature and the movement of the selective optimum [23,25]. Thus, as previously noted by Schluter [7], selection rather than genetic (co)variances may underlie the relationship between genetic architecture and evolutionary trajectories. Theoretical work suggests that an alignment of G with the adaptive landscape can be produced when traits are under stabilizing and correlational selection [10]. Additionally, when a population evolves in response to an adaptive landscape with a steadily moving optimum (inducing directional selection driven by temporal changes in the environment, for example), the direction of peak movement may affect the evolution and stability of G [26]. In particular, selection can cause orientation stability of G over evolutionary time when the adaptive landscape has a persistent configuration producing strong correlational selection (i.e., a ridge-shaped landscape), and a multivariate population mean tracks its moving adaptive peak along the landscape’s leading eigenvector (ωmax) [25,26]. This direction of peak movement may be visualized as a ridge on the adaptive landscape, which has been called the “selective line of least resistance” by Arnold et al. [23]. Selection can also have an indirect impact on G-matrix evolution and stability via the influence on the (co)variance matrix of mutational effects (M), as M evolves to become aligned with the adaptive landscape [27,28].
Together with large effective population size, evolutionary persistent and coordinated patterns of correlational selection, pleiotropic mutation, and peak movement can contribute to eventually stabilizing the G-eigenstructure within diverging populations, as G will tend to conform its orientation to the adaptive landscape and M over both intermediate and long time scales [25]. Under these circumstances, populations will tend to evolve gmax axes that are oriented toward ωmax (and thus facilitating evolution along both genetic and selective lines of least resistance; [26]), and additionally both of these directions will be aligned with the leading eigenvector of D (dmax) [23,39], hence resulting in orientation similarity between G and D. Yet, without knowing the actual direction of selection operating on traits through evolutionary time, and particularly over long timeframes, it may be difficult to verify whether an observed relationship between genetic architecture and population divergence is due to constraints imposed by genetic (co)variance patterns or to the influence of natural selection in potentially shaping both G and D [13,40].
The present study uses wood property data from populations of the Australian forest tree Eucalyptus globulus Labill. to address the following objectives: (1) assess the extent to which the G-eigenstructure has been conserved at an intra-specific level, through the comparison of G matrices between two distantly-related population groups (Mainland and Island); and (2) evaluate the influence of within-population genetic (co)variation on the evolutionary divergence among populations. While these evolutionary issues have been addressed in several empirical studies with plants (e.g., [15,17,37]), studies with forest tree populations are scarce and have dealt mainly with phenological traits (e.g., [41]). Trees account for about 90% of the Earth’s biomass and, while independently evolved in many plant families, share functional features such as large size, long life span, and a self-supporting perennial woody trunk [42]. We here considered four traits commonly used to characterize their trunk wood—basic density, extractives content, lignin content, and lignin composition—which likely exhibit varying degrees and types of integration (sensu [43]). Basic density is a complex trait, which in angiosperms is influenced by the properties of the xylem vessels and the matrix of fibers and other cells [44]. It is often negatively associated with drought-induced mortality/damage or home-site drought conditions [45,46,47]. This association reflects an influence of underlying anatomical traits, such as vessel wall thickness and lumen area, on the vulnerability of the xylem water column to cavitation/embolism under water stress [48,49,50]. Wood extractives are a mix of non-structural compounds soluble in organic solvents or water that are mainly deposited in heartwood [51] and, as a total extract, have been positively associated with heartwood durability and decay resistance [52,53,54]. Lignin is the major structural component of the cell walls of vascular plants and is constructed from three monolignol monomers: p-hydroxyphenyl (H), guaiacyl (G), and syringyl (S) [55]. It contributes to many of the mechanical and physical characteristics of wood. Specifically, lignin confers mechanical strength, contributes to the maintenance of the water transport system within the plant (including prevention of embolism), and can act as a defensive barrier against pathogens and herbivores [55,56]. In woody angiosperms, the lignin is mainly constructed from the syringyl and guaiacyl monomers, and their ratio (S/G) varies between cell types, populations, and species [57]. Lignin rich in guaiacyl, for example, is preferentially deposited in xylem vessels, and is a more rigid and hydrophobic monomer than syringyl, although the greater elasticity of the syringyl monomer is thought to give the xylem cell walls flexibility to avoid fracture under negative pressure [56]. The lignin monomers also vary in their resistance to fungal decay, with guaiacyl being more resistant to white rot fungi than syringyl [58,59]. These fungi are one of the most common causes of wood decay in native eucalypts, entering the stem through the roots, stem damage, branch stubs, and insect galleries [59]. Lignin deposition in plant cell walls is one of the main factors that allowed the terrestrial radiation of plants [55]. Together, these four wood properties represent key functional traits in woody angiosperms impacting mechanical support, water relations, and susceptibility to pathogens and herbivores. All four traits exhibit significant genetic-based variation within and among populations of E. globulus, with S/G increasing, but extractives and basic density decreasing, with home-site latitude [60]. While there is evidence that divergent selection is implicated in this population differentiation [60], the extent to which the genetic architecture of the populations has influenced their evolutionary trajectories is unknown.
2. Materials and Methods
2.1. Study System and Measured Traits
E. globulus is native to south-eastern Australia, including the southern islands of Tasmania, where it occurs over a latitudinal range from 38.4° to 43.5° S, and altitudinal range from sea-level to 830 m [61,62]. It is one of the major eucalypts grown in industrial plantations in temperate regions of the world, including Australia [63]. During its domestication, large common-garden, base-population trials were established using open-pollinated (OP) seed collected from wild mother trees sampled in natural populations across the geographic range of E. globulus [64]. These field trials have shown extensive population differentiation in numerous quantitative traits, which Dutkowski and Potts [61] summarized by classifying the species into 13 geographic races and 20 subraces (the subraces are, hereafter, referred to as “populations”). The mainland and island populations are separated along a latitudinal gradient and by the major disjunction of Bass Strait, which has formed on multiple occasions following rising sea-levels during the warming phases of the Pleistocene glacial cycles [65]. The mainland populations (hereafter referred to as the “Mainland” group of populations) are broadly grouped on nuclear microsatellites, as are the eastern Tasmanian and adjacent Furneaux Island populations (hereafter referred to as the “Island” group of populations) [66,67].
We used wood property data collected from one of the largest base-population field trials of E. globulus, as detailed in Stackpole et al. [60,68]. In brief, the trial was established in northern Tasmania with 570 native OP families. The experimental layout of the trial was a resolvable incomplete block design with five replicates, each divided into 24 incomplete blocks of 24 families planted in two-tree plots. At age 16 years from planting, a subset of 467 families was assessed for wood properties, with one tree per family-plot sampled in most replicates, omitting minor populations. Bark-to-bark wood cores were taken at 1.1 m from each tree to estimate basic density (BD) and to provide near-infrared predictions of the percentage of Klason lignin (KL) and methanol-derived extractives (EX) on a dry weight basis, as well as the S/G ratio. Klason lignin is the conventional way lignin content is quantified by the pulp industry, it is highly correlated with total lignin (r > 0.9; [54]) and widely reported in plants [56]. The current study used a subset of the field-tested populations with a representation of families that are typical of the widespread distribution of the species in either the Mainland or the Island regions. In total, 10 populations, 408 families, and 1857 trees were used; the Mainland group included 4 populations, 203 families, and 929 observations; and the Island group comprised 6 populations, 205 families, and 928 observations (Table S1; Supplementary Materials).
2.2. Data Analysis
The following data analyses were undertaken using ASReml [69], SAS [70], and R [71].
2.2.1. Estimation and Comparison of G Matrices for the Mainland and Island Population Groups
Evaluating whether the G-eigenstructure has been conserved is the first step to explore the prospect of long-term genetic constraints on phenotypic evolution. Ideally, this evaluation would be pursued within a phylogenetic framework in empirical studies, such that contemporary populations used to compare G matrices are sampled on a phylogeny to assess whether there is a phylogenetically-structured pattern of variation in genetic architecture [14,24]. In any case, inferences about the stability of G over time based on studies comparing G-estimates from contemporary populations assume that these populations have a common ancestral population, as well as that their genetic architectures reflect the original G-matrix and changes in it through time [72]. Although the phylogeny of the studied 10 populations was estimated (Methods S1 and Figure S1; Supplementary Materials), the number of families sampled per population (Table S1) would have resulted in limited precision for some G-estimates, which precluded to compare G matrices of individual populations in a phylogenetic context. Thus, to evaluate whether the G-eigenstructure was conserved through the evolutionary divergence of the E. globulus populations, G matrices were compared between the Mainland and Island groups, where populations in the Island group tended to be phylogenetically distant from those in the Mainland group (Figure S1). In this sense, data for each group were combined to estimate the respective G as a single matrix for the populations represented within the group.
Prior to analyses, the traits were mean standardized for each group (i.e., the raw data for a trait were divided by the corresponding mean within a group) to put them on a comparable scale, and thus to avoid interpretation problems due to the effects of different trait measurement scales. All measures of the focal traits are continuous, positive real numbers for which scaling in relation to the mean is both permissible and meaningful [73]. Mean-standardized G matrices are also suitable for the estimation, interpretation, and comparison of measures that capture the potential for evolution ([6]; see below). Variance-component modeling was then undertaken for each group by using a multivariate linear mixed model defined as
where, for the four traits denoted as 1 to 4 in subscripts, is a vector of mean-scaled observations; is a vector of fixed effects; is a vector of random OP-family effects within populations; is a vector of random incomplete block effects; is a vector of random residual effects; , and are incidence matrices linking a tree phenotype to the fixed and random effects; the superscript ’ denotes the transpose operation. The vector b included a mean term, as well as terms for the fixed effects of populations and replicates as required for each trait. Under the model specified in Equation (1), the joint distribution of the random terms was assumed to be multivariate normal with a zero-mean vector and a block-diagonal variance matrix, specified as a direct sum of variance-covariance matrices related to the effects in , and . The variance-covariance matrix was defined for the effects in as
where the diagonal and off-diagonal elements refer to trait variances and covariances, respectively; is an identity matrix of dimension ( = number of OP families); denotes the Kronecker product operation. For the effects in and , the variance-covariance matrices were defined as in Equation (2), with the dimension of being specified by the number of incomplete blocks and observations, respectively. Restricted maximum likelihood (REML) estimates of (co)variance parameters were obtained by using the average information REML algorithm implemented in the ASReml software [69].
E. globulus has a mixed mating system, resulting in the OP-seed to be a mixture of selfed and outcrossed progeny [74]. Assuming an average outcrossing rate of 70% in native forests of E. globulus, a coefficient of relationship between OP-sibs of 0.4 has been used to get estimates of additive genetic (co)variances based on OP-progeny [63,64], instead of 0.25 as expected for pure half-sibs [75]. Estimates of additive genetic (co)variances comprising the G matrix were thus obtained by multiplying the REML estimates of OP-family (co)variances by 2.5 (i.e., rather than 4 as for pure half-sibs). For a given trait, the mean-standardized additive genetic variance equals the expected proportional change per generation to directional selection of unit strength (assuming selection on the trait to be as strong as on fitness itself), and thus can be interpreted as a univariate mean-scaled evolvability (hereafter denoted as ; [6]). Standard errors of the additive genetic (co)variances were obtained from the inverse of the Average Information matrix (i.e., after multiplying by 2.52 its diagonal elements corresponding to the OP-family effects), and the Delta method was used to calculate approximate standard errors for genetic correlations estimated between the traits. Statistical significance was assessed for variance estimates via one-tailed likelihood-ratio (LR) tests [76], and for covariance and correlation estimates via two-tailed LR tests. Two-tailed LR tests were also used to assess whether parameter estimates differed significantly between the two groups, following the approach described by Shaw [77]. Although allowing evaluation of whether G matrices differ in regard to the particular REML estimates of (co)variances, this approach does not enable examination of matrix differences in terms of the influence of G-eigenstructure on the response to selection. In this sense, we used the following measures to compare the mean-standardized G matrices of the two groups.
Hansen and Houle [6] developed multivariate measures that capture the potential for evolution, and showed how they can be used to interpret and compare G matrices. In this context, we evaluated the unconditional evolvability (), the conditional evolvability () and the autonomy (), defined for a vector of selection gradients and a G matrix. We also evaluated the evolutionary “flexibility” measure proposed by Marroig et al. [78]. Given that they are calculated as functions of a specified selection gradient , these measures may vary in different directions of the phenotypic space. In the absence of knowledge about the actual vector acting on the traits, we computed average measures over random selection gradients distributed within a wide range of directions, as suggested by Hansen and Houle [6]. Mean values of unconditional evolvability (), conditional evolvability (), autonomy (), and flexibility () were calculated over 5000 random selection gradients uniformly distributed in the q-dimensional space (in our case, q = 4). For , , and , this approach led to results similar to those based on analytic approximations provided by Hansen and Houle [6]. In particular, for a mean-standardized G matrix, can alternatively be calculated by the average of the eigenvalues of G or by the average of the trait values. Further details on the estimation and interpretation of these measures are given in Table 1, and Methods S2 (Supplementary Materials).

Table 1.
Multivariate measures capturing the potential for evolution that were evaluated to compare the Mainland and Island G-matrices.
To evaluate the difference between the Mainland and Island G-matrices in the direction of the response to selection, we quantified the average similarity between the matrices in their response to a set of random selection gradients (i.e., “random skewers”; [79]). Each of the two mean-standardized G matrices was thus subjected to the same set of 5000 unit-length random selection vectors (generated as described in Table 1), and multivariate similarity in the directions of the response to selection was evaluated by
where is the mean value of the angle (converted from radians to degrees by the factor ) between response vectors over a set (n = 5000) of random selection gradients; is the angle (in radians) between response vectors for G matrices subjected to the jth selection gradient; atan, sin, and cos denote the four-quadrant inverse tangent, sine, and cosine functions, respectively. The value of reflects matrix differences in eigenvectors, and thus will be indicative of the extent to which the compared G-matrices share a common orientation (with decreasing as similarity in matrix orientation increases). Further details on this method are given in Methods S3 (Supplementary Materials).
Although not having an interpretation in line with the effects of G-eigenstructure on response to selection, the Krzanowski geometric approach [80,81] was applied as an additional method to compare the Mainland and Island G-matrices in terms of orientation. By finding the closest alignment between two matrix subspaces, each defined by a subset of k eigenvectors within a q-dimensional trait space (and subject to the condition that k ≤ q/2; [80]), Krzanowski’s approach gives a bounded index of overall similarity in orientation (hereafter denoted as ) between the matrix subspaces being compared. This index varies from 0 to k, with 0 indicating that the two subspaces are dissimilar (no shared structure), whereas a value close to k indicates that the two subspaces are coincident (share a similar structure) (for further details on this method, see Methods S4; Supplementary Materials).
2.2.2. Evolutionary Divergence among Populations
The influence of intra-specific genetic (co)variation on the evolutionary trajectory of a population and its divergence from other populations was assessed through the estimation of evolvability in the direction of evolutionary change of a population. As a complementary approach, we also did a comparison of G and D matrices in terms of size, shape, and orientation. The procedures used in this matrix comparison are described in Methods S5 (Supplementary Materials), including the estimation of phylogenetic-corrected among-population (co)variances in the D-matrix.
Hansen and Houle [6] suggested to evaluate the influence of genetic architecture on the direction and extent of population differentiation based on the amount of mean-scaled genetic variance available along the direction of divergence of a population. Specifically, considering the vector z that defines the direction of divergence of a population, observed unconditional (), and conditional () evolvabilities in this direction are compared to the expected evolvabilities in a random direction ( and ). If populations tend to diversify in directions where evolvability is much higher than expected (i.e., and greater than and , respectively), then G may have shaped the direction of population differentiation (conversely, it is also possible that G has evolved to reflect past selection, in which case the direction of population divergence could shape G, and thus cause high evolvability [6]). In addition, a positive association between either or and the amount of divergence in the z-direction may indicate that G could also have affected the extent of population differentiation [9].
Table 2 provides details on the estimation of z as a direction of divergence of a population from the inferred ancestral states (i.e., phylogenetically-weighted trait means), as well as on the estimation of evolvabilities and the amount of divergence along a z-direction. The calculation of and was based on a G matrix that was estimated by combining all data, and thus to obtain a G-matrix common to all populations across the Mainland and Island groups. This followed from the G-matrix comparison between these groups, which indicated that the G-eigenstructure was reasonably well conserved at an intra-specific level (see Results). Thus, similar to other studies (e.g., [14,15]), we assumed the pooled within-population genetic (co)variances to be an approximation for describing the average of G over evolutionary time for each population. This pooled G-matrix was estimated under the model described in Equation (1), and it was mean-standardized by using estimates of phylogenetically-weighted trait means (so that z and G were on a comparable scale; Table 2). Populations were fitted as fixed effects in this model (akin to the data analyses within groups), and least-squares (phenotypic) means were estimated for each trait and population; Wald F-tests were used to assess the statistical significance of differences among populations for the traits, with the denominator degrees of freedom calculated as defined by Kenward and Roger [82].

Table 2.
Measures used to assess the influence of intra-specific genetic (co)variation on the evolutionary trajectory of a population and its divergence from other populations.
2.2.3. Estimation of Sampling Error for the Measures Used to Compare Matrices
Variance-covariance matrices have an estimation error and so do functions of them, such as the measures described above for matrix comparison. Assessing uncertainty in these measures followed the restricted maximum-likelihood multivariate normal (REML-MVN) sampling approach suggested by Houle and Meyer [85]. This approach samples a variance-covariance matrix that had been estimated by REML, and the matrix samples are then used to assess the sampling variability and to obtain confidence intervals for measures based on the estimated matrix. We applied REML-MVN sampling to construct 100,000 samples of either G or D matrix estimates, calculated the target measures for each sample, and generated the sampling distribution for each measure across samples. Lower and upper limits of the 95% confidence intervals for the measures of interest were approximated from the 2.5th and 97.5th percentiles, respectively, of the generated sampling distributions. Further details on the REML-MVN approach and on its application in the present study (e.g., sampling on the L-scale) are given in Methods S6 (Supplementary Materials).
2.2.4. Evaluating the Statistical Support for Similarity of Two Estimated (Co)Variance Matrices
Evaluating the statistical support for similarity of two estimated variance-covariance matrices being compared depended on whether [19]:
- .
- measures were computed separately for each matrix and then compared between matrices (i.e., measures that capture the potential for evolution; measures of matrix size and shape), where we generated the sampling distribution for the difference between matrices in a measure, based on 100,000 REML-MVN matrix samples drawn from either estimated matrix; or
- .
- measures were directly calculated from a between-matrix comparison (i.e., , and the angle between gmax and dmax), where we computed the statistic —for a measure m, evaluates whether differences within matrices due to sampling error are similar to differences between matrices (Equation (9) in [86])—and drew 100,000 pairs of REML-MVN matrix samples from either estimated matrix to generate the sampling distribution of .
Statistical support for similarity between estimated matrices in the evaluated measures was examined through the 95% confidence intervals approximated from the generated sampling distributions (i.e., matrix similarity was indicated by a 95% confidence interval overlapping with zero). Methods S7 (Supplementary Materials) gives further details on the procedures described above.
3. Results
3.1. Comparison of G Matrices for the Mainland and Island Population Groups
Table 3 presents the mean-standardized additive genetic (co)variances estimated for the G matrices of the Mainland and Island groups, with the variances being equivalent to the evolvabilities. Estimates of trait means, phenotypic standard deviations, and narrow-sense heritabilities are also given in Table S2 (Supplementary Materials). The estimates were highly significant (p < 0.001) for all traits and ranked similarly in both population groups, with the levels of being the highest for EX and the lowest for KL (Table 3). Under a model ignoring trait covariances, two-tailed LR tests conducted within a group to assess whether the estimates differed between a pair of traits indicated that either EX or KL was significantly (p < 0.05) different from the other three traits, whereas the difference between S/G and WD was not statistically significant (not show). Both G matrices tended to have negative covariances between S/G and either BD or EX, and a similar pattern of covariances of EX with the other two traits (i.e., positive with KL; low and not significant with BD) (Table 3).

Table 3.
Additive genetic (G) variance-covariance matrices estimated for wood traits (S/G, KL, BD, and EX) within the Mainland and Island population groups of E. globulus. Parameter estimates are given together with their standard errors for variances (diagonal), covariances (below diagonal), and correlations (above diagonal).
In analyses jointly modeling data from both groups under Equation (1), three null hypotheses were tested to evaluate whether the G matrices differed in (co)variance estimates. As shown in Table 4, reduced models where both G matrices were constrained to have the same estimates for each of the 10 parameters, the 4 variances or the 6 covariances did not lead to a significantly worse fit (at the 5% level) than a full model where all parameters were estimated independently for each matrix. This was also observed when testing a single parameter per se, except for the genetic covariance between S/G and KL which differed significantly (p < 0.05) between matrices (not shown). In general, these results suggest a weak differentiation between the (co)variance patterns of the two G-matrices.

Table 4.
Results from two-tailed likelihood-ratio (LR) tests that were applied to test whether estimates of additive genetic (co)variances differed significantly between the additive genetic (G) variance-covariance matrices, estimated within the Mainland and Island population groups of E. globulus.
The results obtained for the measures reflecting the influence of G-eigenstructure on response to selection are given in Table 5. The Mainland-G had lower levels of mean evolvability ( = 0.41% and = 0.09%) when compared to the Island-G ( = 0.58% and = 0.12%), indicating that, on average, more genetic variation was available in the Island group for response to a wide range of selection gradients (Table 5). Yet, the expected ability of a multivariate phenotype to respond to any random selection vector did not appear to significantly differ between the G matrices. The 95% confidence interval (CI) for the difference between matrices in (Figure S2a; Supplementary Materials) or (Figure S2b) included zero, hence providing statistical support for matrix similarity in these measures (note that, alternatively to using evolvability differences, 95% CIs generated for ratios of or values overlapped with one, and thus also indicated matrix similarity). In particular, the results for also suggested that the G matrices did not significantly differ in the degree to which evolvability was (on average) affected by genetic covariances between traits. This is better elucidated by the mean evolutionary autonomy over random directions (), as shown in Table 5. The G matrices had similar magnitudes of (see also Figure S2c) indicating that, on average, conditional evolvabilities were 29% of the unconditional evolvabilities, which may be translated into a reasonably high level of mean evolutionary integration (sensu [43]) over random directions (i.e., 1 − = 0.71) in both groups. This relative reduction in the overall level of independent evolutionary potential suggests that genetic covariances could have been important in constraining the number of directions of the phenotypic space (trait combinations) along which the focal traits would be highly evolvable. As also reflected in the magnitude of , the two G-matrices had an uneven distribution of the eigenvalues, with 86% of the total genetic variation being accounted for by the first eigenvector (Table S3; Supplementary Materials), indicating that both matrices had a similar ellipsoid shape (i.e., large eccentricity). Consistent with these results, the G matrices had similar mean flexibility () values (Table 5; Figure S2d). The moderate magnitude of 0.6 for indicates that, on average, a multivariate phenotype would have a limited ability to respond to (or to track with) a wide range of selection pressures, hence suggesting that genetic architecture could be important in deviating the direction of evolutionary response from the direction of selection. The evolvability, autonomy, or flexibility measures along different random directions were reasonably well correlated between the two G-matrices (Table S4; Supplementary Materials), providing an additional indication of matrix similarity in these measures.

Table 5.
Comparison of the additive genetic (G) variance-covariance matrices, estimated within the Mainland and Island population groups of E. globulus, based on measures reflecting the influence of G-eigenstructure on response to selection (with 95% confidence intervals within parentheses).
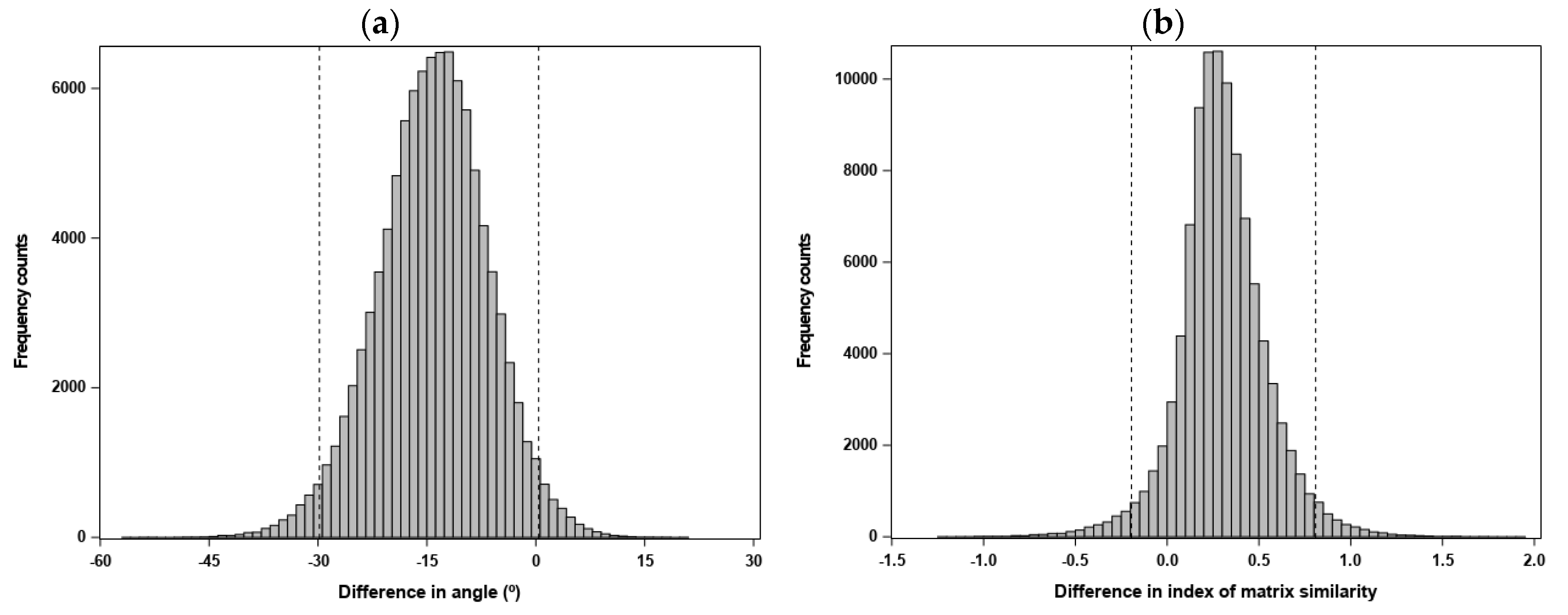
The mean angle between response vectors predicted by subjecting the G matrices to the same selection gradients (“random skewers”) was relatively small ( = 17°; Table 5), indicating that genetic variance was similarly structured in the two matrices. This shared matrix orientation was statistically supported by the 95% CI of the statistic (which, for a measure m, compares estimates from samples of the same matrix to estimates from samples of different matrices), as shown in Figure 1a. The CI for included zero (albeit marginally), indicating that the dissimilarity between matrices in was not larger than that expected from sampling error. Under the Krzanowski method, the first two eigenvectors (accounting for 96% of the total genetic variation; Table S3) of the G matrices defined the subspaces to be used in a two-dimensional matrix comparison. Krzanowski’s index () of overall similarity was 1.78 (95% CI: 1.32, 1.94) of a possible 2, indicating substantial trait information shared between eigenvectors of the two matrices, and thus similarity in matrix orientation. This was also supported by the 95% CI of , which overlapped with zero (Figure 1b). Overall, the results obtained from the comparison of the Mainland and Island G-matrices indicated that the G-eigenstructure was reasonably well conserved at an intra-specific level.
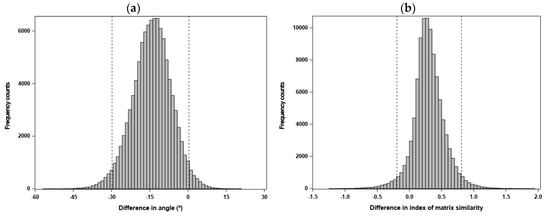
Figure 1.
Simulated sampling distributions and 95% confidence intervals (depicted by the dashed vertical lines), obtained by the REML-MVN sampling approach [85], for the statistic used to assess whether the mean-standardized G-matrices estimated for the Mainland and Island population groups shared a similar orientation, based on the following measures directly computed from a between-matrix comparison: (a) mean angle between vectors of response to a set of randomly-generated selection gradients (i.e., "random skewers"); and (b) Krzanowski’s index of overall similarity in orientation between matrix subspaces. For a given measure, the statistic evaluates whether differences within matrices due to sampling error are similar to differences between matrices (Equation (9) in [86]; see Methods S7). When overlapping with zero, a 95% confidence interval for indicates statistical support for similarity in orientation between the two matrices being compared.
3.2. Evolutionary Divergence among Populations
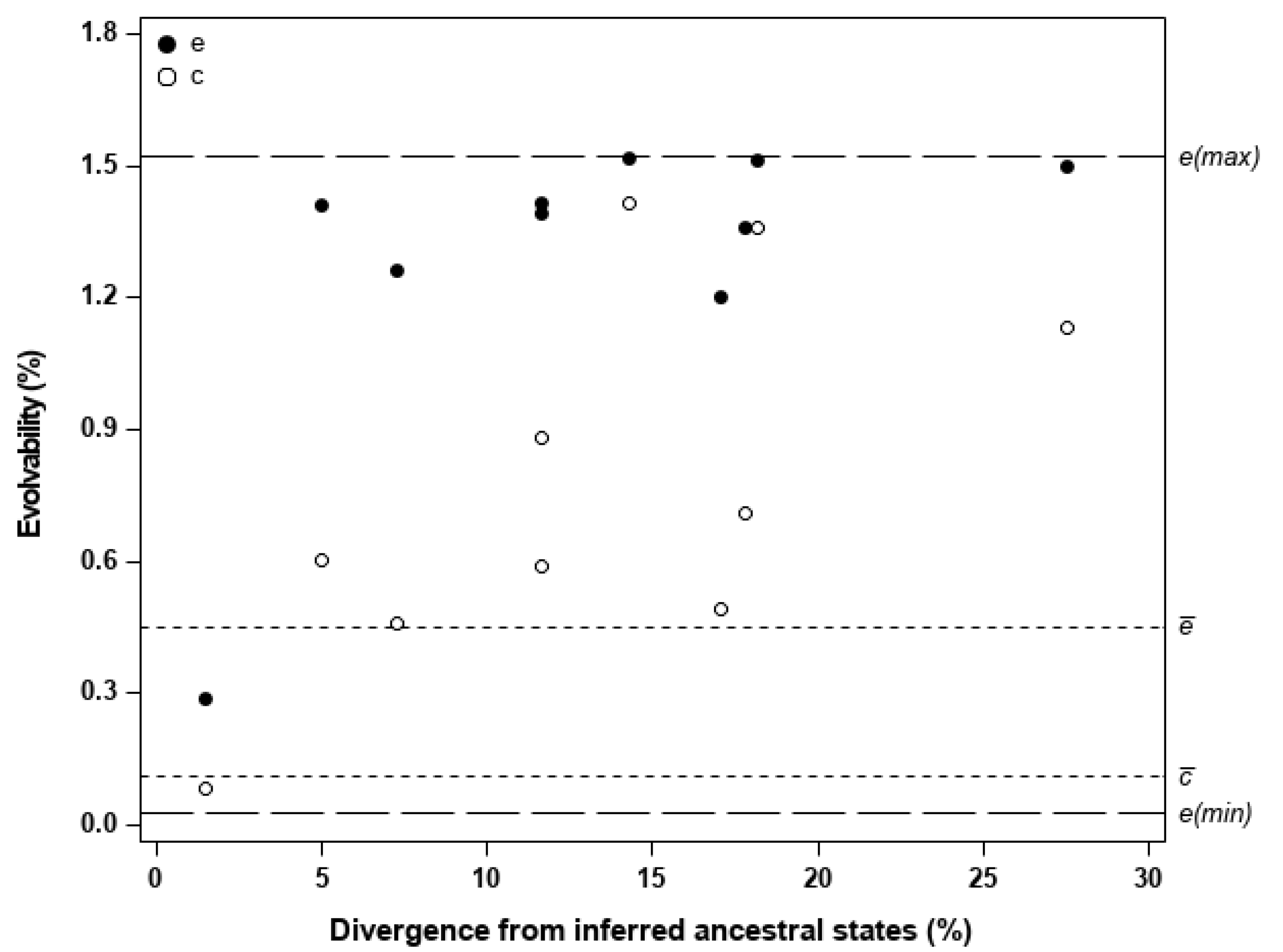
Figure 2 shows the observed unconditional () and conditional () evolvabilities in the direction of divergence (z) of a population from the inferred ancestral states, and plotted against the amount of its divergence in this direction. The observed and were also compared to the and , as well as to the maximum (e(max)) and minimum (e(min)) possible evolvability values, based on the mean-standardized G matrix common to all populations. This matrix is presented in Table S5 (Supplementary Materials); when compared to the corresponding estimates given in Table 5, the pooled G-matrix provided intermediate values in or , and similar values in or (Table S6; Supplementary Materials). The estimated population means, used to define the z-vectors of evolutionary change, differed significantly (p < 0.001) for every trait, indicating strong population differentiation. The inferred ancestral states for the traits were: S/G = 1.94 ± 0.04; KL = 20.67% ± 0.30; BD = 546.72 kg/m3 ± 8.18; EX = 5.06% ± 0.36.
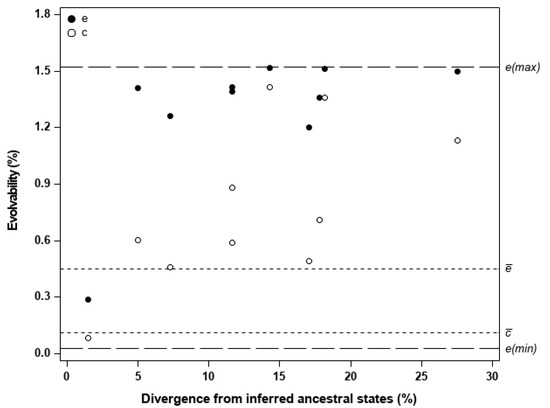
Figure 2.
Observed mean-scaled unconditional evolvabilities (e; black dots) and conditional evolvabilities (c; white dots) for each E. globulus population in the direction of its divergence from the inferred ancestral states, plotted against the amount of divergence in that direction. For comparison with the observed evolvabilities along the direction of population divergence, the dashed horizontal lines indicate (after [6,9]): the expected unconditional and conditional evolvabilites in a random direction, denoted as and , respectively; the maximum and minimum possible values for either unconditional or conditional evolvability, denoted as e(max) and e(min), respectively. All the evolvability estimates were based on the mean-standardized G-matrix common to all populations, and further details are provided in Table 2.
When the direction of population divergence is not random in regard to evolvability, the observed and will tend to deviate from and , respectively. This was the case for the studied populations, as most of them have diversified in directions where the available mean-scaled genetic variance was substantially higher than expected in random directions. Figure 2 shows that most populations have diverged in directions where the observed were closer to e(max) (i.e., the evolvability along gmax) than to , and also in directions where the observed were well above . The averages of the observed and were 1.287% and 0.773%, being almost three and seven times the evolvabilities expected in random directions (i.e., = 0.452%, and = 0.111%), respectively. This trend for populations to diversify in directions of high evolvability suggests that genetic architecture may have affected the direction of population divergence (i.e., evolutionary trajectories being biased toward the directions of major multivariate axes of genetic variation). Besides influencing the range of directions along which populations evolve, genetic architecture may also affect the extent of population divergence. The amount of population divergence along z tended to be positively related to , with a significant linear association (r = 0.65, p = 0.041) being detected, but this trend was not evident with (Figure 2). This provides some indication that populations changing further from the inferred ancestral states had also a propensity to diverge in directions of higher evolvability, particularly when mean-scaled genetic variance along z was independent of trait genetic covariances in directions other than z (assumed to be under stabilizing selection), as reflected in .
In general, the studied populations have diverged in directions closely aligned with the direction of the first eigenvector (gmax) of the pooled G-matrix, as most of the angles between gmax and each of the z-vectors were relatively small and less than the critical value (i.e., 28.6° at the 5% level) from a null distribution, generated by simulating 100,000 pairs of random vectors uniformly distributed in a four-dimensional space (Table S7; Supplementary Materials). The mean angle between gmax and the z-vectors was 20.3°, being considerably less than expected by chance (i.e., the mean angle of 63.5° between the generated pairs of random vectors; note that these mean angles were calculated as in Equation (3)). Directions of divergence with high evolvability can be different from gmax, since G may include other multivariate axes of higher than average genetic variance beyond gmax. This was not the case here, as genetic variance was concentrated (i.e., 84% of the total) along the first eigenvector of the pooled G-matrix (Tables S8 and S9; Supplementary Materials), which thus may underlie the observed close alignment between z and gmax in most of the populations.
The main results obtained by comparing the G matrix common to all populations with the phylogenetically-corrected D matrix are summarized here, and further details are given in Supplementary Materials (Results S1). The descriptor of matrix shape provided 94% and 84% for the percentage of the total variance being accounted for by the first eigenvector of D and G, respectively (Table S9). Similarity in matrix shape was not statistically supported, as the 95% CI for the difference between matrices in this measure did not include zero (Figure S3b; Supplementary Materials), and thus indicated that G and D were not proportional. This suggests that genetic drift may not have played an important role in generating population differentiation, as G and D are expected to be proportional under neutral divergence (see Discussion). A high level of shared orientation between G and D was indicated by Krzanowski’s index of overall similarity (), and by the angle between gmax and dmax (i.e., the leading axis of divergence among populations). Under a two-dimensional matrix comparison, the index was 1.91 (95% CI: 1.66, 1.98) of a possible 2 (Table S9). The gmax and dmax directions were closely aligned, with an angle of 5.9° (95% CI: 2.6°, 11.8°) between them. Statistical support for similarity in matrix orientation could not be rejected for either of these two measures (Figure S3c,d). These results suggest that axes of greatest within-population genetic (co)variance may have determined trajectories of evolutionary change, with the observed population divergence occurring mainly close to the direction of a genetic line of least resistance.
4. Discussion
We aimed to assess the extent to which the G-eigenstructure for four wood properties was conserved among populations of E. globulus, and evaluate its influence on the evolutionary divergence among populations. Given the radiation of related eucalypts in southern Australia, this population divergence would have occurred within the last 2–3 M years, when accelerated radiation of the southern clades of eucalypts occurred with the onset of increasing aridity in Australia (Figure S8 in [87]). Genome-wide phylogenetic studies indicate that E. pseudoglobulus is the sister species to E. globulus (Figure 9 in [88]). The Mainland populations of E. globulus have closer affinities to this sister species than do the Tasmanian populations [62], suggesting more recent divergence of the Island populations. This divergence most likely occurred over the last 0.5 M years, over a period when the cycle of glaciations would have produced multiple opportunities for migration between the mainland and the islands of Tasmania due to lowered sea levels in glacial periods creating a land-bridge, followed by interglacial isolation with the formation of Bass Strait [65,89]. The eastern side of the land-bridge is more persistent due to shallower seas, where the Furneaux islands and Tasmania (which comprise the Island group in the present study) would have been the last connection to be severed as sea-levels rose [90]. While the main contemporary distribution of E. globulus is in eastern and south-eastern Tasmania, studies of the maternally inherited chloroplast DNA suggest that E. globulus colonized Tasmania not via the eastern land-bridge but via a wetter western route from the Otways region, where the species now only occurs as a series of small disjunct remnants [91]. While the timing of the colonization is unknown, there have been four major glacial periods over the last 0.5 M years [89] when this would have been possible, the longest ca. 405 to 330 K years ago, and the most recent during the Last Glacial Maximum (22–18 K years ago) with the land-bridge flooded ca. 12 K years ago [92]. Given that tall forest eucalypts in Tasmania may reach 500 years of age [93], with generation times of between 200 and 500 years, the Mainland and Island populations would have been most recently spatially isolated for anywhere between 24 to 60 generations. Regardless of the timing of colonization and extent of isolation, the observed population differentiation would have been associated with latitudinal variation in climate superimposed on dramatic temporal changes through the glacial transition(s) [92].
For conspecific populations derived from a common ancestor and experiencing similar genetic constraints, Schluter’s [7] hypothesis predicts that divergence in multivariate mean phenotype among evolving populations will be biased (i.e., relative to the direction of selection) toward directions of greatest genetic variance of the G matrix in the ancestral population. For a set of traits, the predictive importance of this hypothesis will depend on whether recent selection mirrors historical selection, and on patterns of genetic (co)variance remaining fairly stable over evolutionary time (and thus be reflected in measured G-matrices of each of the diverging populations). These assumptions could be plausible over moderate time frames as adaptation may take a while following the introduction of populations into new habitats [40]. Empirical studies often find that axes of genetic variance are well preserved across conspecific populations or closely-related species [24,25], even in face of differences in natural selection [32], and after 20–40 millions of years of divergence [18]. Thus, even under an evolving G, the structure of genetic (co)variances within populations may remain (at least partly) conserved over evolutionary time. In the present case, given the tree life cycle, population divergence times (potentially less than 500 K years) of the E. globulus populations would be moderate. For the focal wood properties, there appears to have been a weak differentiation in G-eigenstructure following the colonization of Tasmania, as the G-matrices of the Mainland and Island groups showed similarity in average measures that capture the expected potential for evolution over a wide range of selection gradients on the traits. The weak differentiation observed in G-eigenstructure could suggest that the genetic architecture for the studied traits may have been relatively well kept through time. However, it could also reflect that G may have evolved in a consistent manner to become aligned with the adaptive landscape, so that natural selection has shaped similarly genetic (co)variation within populations ([25]; see discussion below). Yet, while it may be the result of various interacting mechanisms (see the Introduction for references of simulation studies), the observed G-conservatism justified the pooling of G-matrices across the population groups to approach an estimate of the average of G over time, which could then be used in evolutionary inference for the timescale of interest (e.g., [11,12,14,15,94]).
The observed G-conservatism may also support a putative enduring influence of genetic constraints in causing deviations of populations from optimal response to selection over evolutionary time [19]. Consistent with this possibility, the present study found that most populations diverged in directions of high evolvability, and also that populations diverging in directions of higher conditional evolvability tended to change further from the inferred ancestral states. A strong relationship between G and divergence is likely for traits with a high degree of evolutionary integration [17], as also indicated by the relatively low value of the average autonomy (i.e., ≈ 0.3) obtained for the wood properties. The distribution of the additive genetic variance was uneven in the estimated G for the studied traits, with an expected limited ability for response to a broad range of selection gradients (i.e., ≈ 0.6) reflecting the large percentage (i.e., >80% of the total) of the variance concentrated on the gmax direction, and thus indicating a possible role of genetic constraints on population differentiation (e.g., [11,12,13,14]). Indeed, nearly all populations diverged from the inferred ancestral states in a direction that was not significantly different from the genetic line of least resistance (Table S7), a trend that was supported by the strong alignment (i.e., 5.9°; Table S9) between the first eigenvectors of the G matrix common to all populations and the phylogenetically-corrected D matrix. This suggests that population trajectories may have been biased toward a direction determined by genetic (co)variation in wood extractives (EX) (which was the trait with the greatest evolvability), lignin content (KL) and S/G (Tables S5 and S8). There is an indication that the focal traits may be genetically integrated to some degree, based on the co-location of quantitative-trait loci (QTL) detected within four E. globulus full sib-families [95]. However, as suggested in empirical studies [17,18], the effects on standing genetic (co)variation patterns produced by the per-generation input of new mutations are likely to have an important contribution to long-term genetic constraints imposed on phenotypic evolution. In particular, Houle et al. [96] demonstrated a strong positive relationship between variation produced by mutation, standing genetic variation, and the rate of evolution over a period of 40 million years in Drosophila melanogaster. Nevertheless, mechanisms other than persistent genetic constraints may also have contributed to the association we have observed between genetic architecture and population divergence, as discussed below.
As indicated in two recent empirical studies [18,37], and noted earlier [7], the relationship between genetic architecture and population divergence may arise because both are shaped by the same natural selection pressures. This entails that G evolves to become aligned with the adaptive landscape, so that natural selection shapes both G and D in a similar direction [25]. Such a scenario could be plausible for functionally integrated traits with strong adaptive correlations, where correlational selection within populations would lead to a tendency for selective differences among populations to occur along an adaptive ridge in the phenotypic space (i.e., directions of population divergence in close alignment with ωmax; [23]). Correlational selection for co-adaptation may be a possibility for the studied traits, given the relationship between their functions (as outlined in the Introduction) and also as suggested by the pattern of strong correlated evolution among populations (described by the covariances in the D-matrix; Table S5). In particular, correlational selection for resistance to wood decay could be one possibility, as: (i) there are likely local topographic (gully versus slopes [97]) and broad-scale [98] gradients in disease risk across the range of E. globulus; and (ii) the trait relationships on the first eigenvector of the G and D matrices (Table S8) are consistent with evolutionary changes expected to increase resistance to wood decay (i.e., increasing EX, KL and, depending upon the type of decay, decreasing S/G; see Introduction). Theoretical work developed by Jones et al. [10,26] indicated that conditions inducing high orientation stability of G—i.e., the alignment of an adaptive landscape producing strong correlational selection and a M-matrix describing strong mutational covariance, coupled with large population size—did also promote the evolution of an eccentric G-matrix (see also [29]), as may have occurred in the present case. Directional selection can confer greater orientation stability on G relative to stabilizing selection alone and, in combination with an alignment of the adaptive landscape and M, a steady movement of the selective optimum along ωmax facilitates orientation stability of G by reinforcing the evolution of an eccentric G-matrix [25,26]. An evolving M-matrix was also found to further enhance orientation stability of G relative to a static mutational architecture, especially as M evolves toward alignment with the adaptive landscape [27,28]. This triple alignment of G, M, and the adaptive landscape could be produced by a landscape configuration that supports persistent correlational (and stabilizing) selection within populations over evolutionary time [25], and such a coordinated pattern of genetic variation, mutation and selection could have contributed to the observed similarity of G matrices, as well as to the observed alignment of G and D matrices.
Migration is another factor which could lead to the observed alignment between genetic architecture and population divergence [7]. Using a mainland-island migration model, Guillaume and Whitlock [30] indicated that continuous high levels of gene flow from the mainland population could affect all features (size, shape, and orientation) describing an island G-eigenstructure, and lead to an increase in genetic variance along the direction of population divergence. However, the changes caused by migration were found to be slow and to increase over time, and tended to be reduced with increased correlational selection and/or mutation correlation [30]. In the present case, the contribution of gene flow cannot be completely dismissed, considering: (i) E. globulus to be pollinated by animals, including a key bird pollinator which annually migrates between the Mainland and Island populations [67,99]; and (ii) the demonstrated potential for post-dispersal selection favoring the products of long-distance dispersal due to a release from inbreeding depression [100]. While the effective pollen dispersal curve has been shown to be fat-tailed, the average dispersal distance has been estimated as only between 69 m and 833 m, depending on the studied population [74]. Nevertheless, gene flow would be expected between more-or-less continuous populations within either region, but it is unlikely to be strong between Mainland and Island groups which are separated by a disjunction of over 130 km. While the influence of inter-population migration cannot be completely discounted, it is unlikely in the present case as a continuous high level of gene flow is required to have a major effect on the G-eigenstructure, as well as in inducing an alignment between genetic (co)variation and population divergence [30].
Another important issue is whether the observed alignment of genetic architecture and population divergence is caused by genetic drift. Phillips et al. [101] showed that genetic drift can cause among-population variation in G by influencing all features describing the G-eigenstructure within individual populations but, on average, it will lead to proportionality of G and D. Thus, when population differentiation is due to genetic drift alone, G and D will have a similar expectation in terms of shape, but also in orientation so that population means will diverge along directions of greatest genetic variance [2,39,101,102]. In this sense, proportionality of G and D matrices reflecting matrix similarity in both shape and orientation could be indicative of genetic architecture biasing population divergence that is generated by drift [39]. However, in the present case, we would argue against an over-riding role of drift in generating population differentiation on the basis of: (i) while G and D did not differ significantly in size and orientation, they did in shape (i.e., they were not proportional; Table S9, Figure S3); and (ii) evidence for divergent selection acting on all of the studied wood properties (i.e., statistically significant QST > FST [60]). While drift can alter the course of evolution via its continuing effects on G, it is unlikely to have played a major role in the evolutionary history of populations when comparative studies indicate that G has remained relatively stable over long periods of time [103], as suggested from the Mainland-Island comparison in the present case. Certainly with a minimum of 24 to 60 generations since the spatial isolation of the Mainland and Island population groups, the role of genetic drift is unlikely, especially with the populations sampled coming from large, more-or-less continuous, regional distributions of the species, and molecular studies revealing no signs of inbreeding or loss of genetic diversity which would signal sustained population bottlenecks [62,66].
Finally, the studied populations were evaluated in a common-garden experiment and not in their natural habitats. Environmentally-induced variation in G has been found to be on the same order of magnitude as observed differences in G among species (e.g., [104]) or conspecific populations (e.g., [36]). Therefore, it is possible that deviations of the common-garden conditions from the natural environments of the populations may have affected trait (co)variation at both the within- and among-population levels, as a result of genotype-by-environment interaction. However, multiple common-garden experiments of E. globulus have shown that wood properties exhibit relatively low genotype-by-environment interaction, particularly when compared to growth traits [95,105,106].
5. Conclusions
The present study indicated that population divergence for the set of wood properties occurred along a genetic line of least resistance. While we did not have sufficient statistical power to warrant testing G-matrix variation among individual populations within the Mainland and Island groups, there was no evidence for a systematic difference in the G matrices of the two groups as would be expected if natural selection, gene flow or genetic drift during the Island colonization differentially impacted G-matrix evolution. In general, the unconditional evolvability estimates suggested that standing additive genetic variance would not substantially limit the traits to respond to directional selection (but see lignin). However, as indicated by the estimated average level of autonomy of this genetic variance, the reasonably high degree of evolutionary integration of the focal traits may have been important in underlying the observed close relationship between genetic architecture and population trajectories. It is not possible to ascertain whether these results reflect genetic constraints, or an association between evolutionary forces that may have shaped genetic variation and those that have led to population diversification. The latter scenario could arise from genetic (co)variance patterns that may have consistently evolved to become aligned with natural selection, since genetic drift and/or migration may not have played an important role in generating divergence among the studied populations. Yet, as the G-eigenstructure appeared to be relatively well preserved at an intra-specific level, and given the moderate evolutionary timescale involved, the potential effects of genetic constraints in influencing the evolution and diversification of the E. globulus populations for the set of focal traits may not be discounted.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4425/11/9/1095/s1, Methods S1: Reconstruction of the phylogeny of the E. globulus populations. Methods S2: Measures that capture the potential for evolution. Methods S3: Matrix comparison using the “random skewers” method. Methods S4: Krzanowski’s geometric approach. Methods S5: Comparison of G and D matrices. Methods S6: REML-MVN sampling approach. Methods S7: Statistical support for similarity of two estimated (co)variance matrices. Results S1: Comparison of G and D matrices. Figure S1: The phylogenetic tree generated for the ten studied populations of E. globulus. Figure S2: Differences between the Mainland and Island G-matrices in measures that capture the potential for evolution. Figure S3: Differences between a G matrix common to all populations and a phylogenetically-corrected D matrix in measures of matrix size, shape and orientation. Table S1: Identification of the studied populations within the Mainland and Island groups, and number of families and trees measured per population. Table S2: Means, phenotypic standard deviations, mean-scaled within-family variance, and narrow-sense heritabilities for the measured wood property traits. Table S3: Principal component analysis of the G matrices estimated within the Mainland and Island groups. Table S4: Pearson correlations between the estimated G-matrices of the Mainland and Island groups for measures that capture the potential for evolution along different random directions. Table S5: G and D matrices estimated across all the studied populations. Table S6: Mean values of unconditional evolvability, conditional evolvability, autonomy and flexibility based on the estimated G-matrix common to all populations. Table S7: Amount of divergence from the inferred ancestral states, unconditional and conditional evolvabilities along the direction of divergence (z), and angle between z and gmax, for the studied populations. Table S8: Principal component analysis of the G and D matrices estimated across all the studied populations. Table S9: Comparison of the G and D matrices estimated across all the studied populations in measures of matrix size, shape, and orientation.
Author Contributions
J.C.eS. conceived the reported study. B.M.P. provided the field trial design and trait data. J.C.eS. undertook data analyses, with contributions from B.M.P. and P.A.H. to the analysis of the phylogeny reconstruction of the studied populations. The manuscript was primarily written by J.C.eS. but with contributions from B.M.P. and reviewed by all the authors. All authors have read and agreed to the published version of the manuscript.
Funding
The contribution of João Costa e Silva to this work was supported by Fundação para a Ciência e a Tecnologia I.P. (FCT), Portugal, through the Norma Transitória DL 57/2016/CP1382/CT0008 and UID/AGR/00239/2019. This work was also supported by the Centro de Estudos Florestais, a research unit that is funded by FCT (Unit Project Reference: UIDB/00239/2020). The contribution of Brad M. Potts to this work was part of the Australian Research Discovery (ARC) grant DP190102053, and that of Peter A. Harrison as part of the ARC Training Centre for Forest Value (IC150100004). We are thus grateful to all of these institutions for their financial support, which provided the opportunity to complete this study.
Acknowledgments
We thank Greg Jordan (University of Tasmania) and Jacob Butler (University of Tasmania) for discussion on the phylogenetic analysis. Molecular data for the phylogenetic analysis was generated by Josquin Tibbits (AgriBioc) and Hossein Kahrood (University of Melbourne), and the distance matrix generated by Jacob Butler (University of Tasmania). Lignin composition data was measured by José Rodrigues and Ana Alves (Centro de Estudos Florestais), and other wood property data by Desmond Stackpole (University of Tasmania).
Conflicts of Interest
All the authors declare no conflicts of interest.
References
- Hoffmann, A.A.; Sgro, C.M. Climate change and evolutionary adaptation. Nature 2011, 470, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Lande, R. Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 1979, 33, 402–416. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.F.; Stinchcombe, J.R. How much do genetic covariances alter the rate of adaptation? Proc. R. Soc. B Biol. Sci. 2009, 276, 1183–1191. [Google Scholar] [CrossRef] [PubMed]
- Walsh, B.; Blows, M.W. Abundant genetic variation + strong selection = multivariate genetic constraints: A geometric view of adaptation. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 41–59. [Google Scholar] [CrossRef]
- Blows, M.W.; Hoffmann, A.A. A reassessment of genetic limits to evolutionary change. Ecology 2005, 86, 1371–1384. [Google Scholar] [CrossRef]
- Hansen, T.F.; Houle, D. Measuring and comparing evolvability and constraint in multivariate characters. J. Evol. Biol. 2008, 21, 1201–1219. [Google Scholar] [CrossRef]
- Schluter, D. Adaptive radiation along genetic lines of least resistance. Evolution 1996, 50, 1766–1774. [Google Scholar] [CrossRef]
- Blows, M.W.; Higgie, M. Genetic constraints on the evolution of mate recognition under natural selection. Am. Nat. 2003, 161, 240–253. [Google Scholar] [CrossRef][Green Version]
- Hansen, T.F.; Voje, K.L. Deviation from the line of least resistance does not exclude genetic constraints: A comment on Berner et al. (2010). Evolution 2011, 65, 1821–1822. [Google Scholar] [CrossRef][Green Version]
- Jones, A.G.; Arnold, S.J.; Bürger, R. Stability of the G-matrix in a population experiencing pleiotropic mutation, stabilizing selection, and genetic drift. Evolution 2003, 57, 1747–1760. [Google Scholar] [CrossRef]
- Haber, A. Phenotypic covariation and morphological diversification in the ruminant skull. Am. Nat. 2016, 187, 576–591. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, M.J.; Haber, A.; Thurman, C.L. Constraints on geographic variation in fiddler crabs (Ocypodidae: Uca) from the western Atlantic. J. Evol. Biol. 2016, 29, 1553–1568. [Google Scholar] [CrossRef] [PubMed]
- Chenoweth, S.F.; Rundle, H.D.; Blows, M.W. The contribution of selection and genetic constraints to phenotypic divergence. Am. Nat. 2010, 175, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Bégin, M.; Roff, D.A. From micro- to macroevolution through quantitative genetic variation: Positive evidence from field crickets. Evolution 2004, 58, 2287–2304. [Google Scholar] [CrossRef] [PubMed]
- Colautti, R.I.; Barrett, S.C.H. Population divergence along lines of genetic variance and covariance in the invasive plant Lythrum salicaria in eastern North America. Evolution 2011, 65, 2514–2529. [Google Scholar] [CrossRef]
- Innocenti, P.; Chenoweth, S.F. Interspecific divergence of transcription networks along lines of genetic variance in Drosophila: Dimensionality, evolvability, and constraint. Mol. Biol. Evol. 2013, 30, 1358–1367. [Google Scholar] [CrossRef]
- Bolstad, G.H.; Hansen, T.F.; Pélabon, C.; Falahati-Anbaran, M.; Pérez-Barrales, R.; Armbruster, W.S. Genetic constraints predict evolutionary divergence in Dalechampia blossoms. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130255. [Google Scholar] [CrossRef]
- McGlothlin, J.W.; Kobiela, M.E.; Wright, H.V.; Mahler, D.L.; Kolbe, J.J.; Losos, J.B.; Brodie III, E.D. Adaptive radiation along a deeply conserved genetic line of least resistance in Anolis lizards. Evol. Lett. 2018, 2, 310–322. [Google Scholar] [CrossRef]
- Teplitsky, C.; Robinson, M.R.; Merilä, J. Evolutionary potential and constraints in wild populations. In Quantitative Genetics in the Wild; Charmantier, A., Garant, D., Kruuk, L., Eds.; Oxford University Press: Oxford, UK, 2014; pp. 190–208. [Google Scholar]
- Lande, R. The genetic covariance between characters maintained by pleiotropic mutations. Genetics 1980, 94, 203–215. [Google Scholar]
- Turelli, M. Phenotypic evolution, constant covariances, and the maintenance of additive variance. Evolution 1988, 42, 1342–1347. [Google Scholar] [CrossRef]
- Barton, N.H.; Turelli, M. Evolutionary quantitative genetics—How little do we know. Annu. Rev. Genet. 1989, 23, 337–370. [Google Scholar] [CrossRef] [PubMed]
- Arnold, S.J.; Pfrender, M.E.; Jones, A.G. The adaptive landscape as a conceptual bridge between micro- and macroevolution. Genetica 2001, 112, 9–32. [Google Scholar] [CrossRef] [PubMed]
- Steppan, S.J.; Phillips, P.C.; Houle, D. Comparative quantitative genetics: Evolution of the G matrix. Trends Ecol. Evol. 2002, 17, 320–327. [Google Scholar] [CrossRef]
- Arnold, S.J.; Bürger, R.; Hohenlohe, P.A.; Ajie, B.C.; Jones, A.G. Understanding the evolution and stability of the G-matrix. Evolution 2008, 62, 2451–2461. [Google Scholar] [CrossRef]
- Jones, A.G.; Arnold, S.J.; Burger, R. Evolution and stability of the G-matrix on a landscape with a moving optimum. Evolution 2004, 58, 1639–1654. [Google Scholar] [CrossRef]
- Jones, A.G.; Arnold, S.J.; Bürger, R. The mutation matrix and the evolution of evolvability. Evolution 2007, 61, 727–745. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.G.; Bürger, R.; Arnold, S.J. Epistasis and natural selection shape the mutational architecture of complex traits. Nat. Commun. 2014, 5, 3709. [Google Scholar] [CrossRef]
- Revell, L.J. The G matrix under fluctuating correlational mutation and selection. Evolution 2007, 61, 1857–1872. [Google Scholar] [CrossRef]
- Guillaume, F.; Whitlock, M.C. Effects of migration on the genetic covariance matrix. Evolution 2007, 61, 2398–2409. [Google Scholar] [CrossRef]
- Arnold, S.J.; Phillips, P.C. Hierarchical comparison of genetic variance-covariance matrices. II Coastal-inland divergence in the garter snake, Thamnophis elegans. Evolution 1999, 53, 1516–1527. [Google Scholar]
- Delahaie, B.; Charmantier, A.; Chantepie, S.; Garant, D.; Porlier, M.; Teplitsky, C. Conserved G-matrices of morphological and life-history traits among continental and island blue tit populations. Heredity 2017, 119, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Hangartner, S.; Lasne, C.; Sgrò, C.M.; Connallon, T.; Monro, K. Genetic covariances promote climatic adaptation in Australian Drosophila. Evolution 2020, 74, 326–337. [Google Scholar] [CrossRef] [PubMed]
- Roff, D.A.; Mousseau, T.; Møller, A.P.; de Lope, F.; Saino, N. Geographic variation in the G matrices of wild populations of the barn swallow. Heredity 2004, 93, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Eroukhmanoff, F.; Svensson, E.I. Evolution and stability of the G-matrix during the colonization of a novel environment. J. Evol. Biol. 2011, 24, 1363–1373. [Google Scholar] [CrossRef]
- Wood, C.W.; Brodie III, E.D. Environmental effects on the structure of the G-matrix. Evolution 2015, 69, 2927–2940. [Google Scholar] [CrossRef]
- Walter, G.M.; Aguirre, J.D.; Blows, M.W.; Ortiz-Barrientos, D. Evolution of genetic variance during adaptive radiation. Am. Nat. 2018, 191, E108–E128. [Google Scholar] [CrossRef]
- Teplitsky, C.; Mouawad, N.G.; Balbontin, J.; De Lope, F.; Møller, A.P. Quantitative genetics of migration syndromes: A study of two barn swallow populations. J. Evol. Biol. 2011, 24, 2025–2039. [Google Scholar] [CrossRef]
- Hohenlohe, P.A.; Arnold, S.J. MIPoD: A hypothesis-testing framework for microevolutionary inference from patterns of divergence. Am. Nat. 2008, 171, 366–385. [Google Scholar] [CrossRef]
- Hendry, A.P. Eco-Evolutionary Dynamics; Princeton University Press: Oxford, UK, 2017. [Google Scholar]
- Firmat, C.; Delzon, S.; Louvet, J.M.; Parmentier, J.; Kremer, A. Evolutionary dynamics of the leaf phenological cycle in an oak metapopulation along an elevation gradient. J. Evol. Biol. 2017, 30, 2116–2131. [Google Scholar] [CrossRef]
- Petit, R.J.; Hampe, A. Some evolutionary consequences of being a tree. Annu. Rev. Ecol. Evol. Syst. 2006, 37, 187–214. [Google Scholar] [CrossRef]
- Armbruster, W.S.; Pélabon, C.; Bolstad, G.H.; Hansen, T.F. Integrated phenotypes: Understanding trait covariation in plants and animals. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130245. [Google Scholar] [CrossRef] [PubMed]
- Preston, K.A.; Cornwell, W.K.; DeNoyer, J.L. Wood density and vessel traits as distinct correlates of ecological strategy in 51 California coast range angiosperms. New Phytol. 2006, 170, 807–818. [Google Scholar] [CrossRef] [PubMed]
- Dutkowski, G.; Potts, B. Drought tolerant Eucalyptus globulus provenances have thick bark, high basic density and grow poorly on wet sites. In Joining Silvicultural and Genetic Strategies to Minimize Eucalyptus Environmental Stresses: From Research to Practice, Proceedings of IUFRO Group 2.08.03 Conference, Porto Seguro, Brazil, 16–18 November 2011; The Luiz de Queiroz College of Agriculture (ESALQ): Piracicaba, São Paulo, Brazil, 2011; pp. 143–148. [Google Scholar]
- O’Brien, M.J.; Engelbrecht, B.M.J.; Joswig, J.; Pereyra, G.; Schuldt, B.; Jansen, S.; Kattge, J.; Landhäusser, S.M.; Levick, S.R.; Preisler, Y.; et al. A synthesis of tree functional traits related to drought-induced mortality in forests across climatic zones. J. Appl. Ecol. 2017, 54, 1669–1686. [Google Scholar] [CrossRef]
- Nabais, C.; Hansen, J.K.; David-Schwartz, R.; Klisz, M.; López, R.; Rozenberg, P. The effect of climate on wood density: What provenance trials tell us? For. Ecol. Manag. 2018, 408, 148–156. [Google Scholar] [CrossRef]
- Hacke, U.G.; Sperry, J.S.; Pockman, W.T.; Davis, S.D.; McCulloh, K.A. Trends in wood density and structure are linked to prevention of xylem implosion by negative pressure. Oecologia 2001, 126, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of tree mortality under drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef]
- Poke, F.S.; Wright, J.K.; Raymond, C.A. Predicting extractives and lignin contents in Eucalyptus globulus using near infrared reflectance analysis. J. Wood Chem. Technol. 2004, 24, 55–67. [Google Scholar] [CrossRef]
- Wong, A.H.H.; Wilkes, J.; Heather, W.A. Influence of wood density and extractives content on the decay resistance of the heartwood of Eucalyptus delegatensis R. T. Baker. J. Inst. Wood Sci. 1983, 9, 261–263. [Google Scholar]
- Bush, D.; McCarthy, K.; Meder, R. Genetic variation of natural durability traits in Eucalyptus cladocalyx (sugar gum). Ann. For. Sci. 2011, 68, 1057. [Google Scholar] [CrossRef]
- Poke, F.S.; Potts, B.M.; Vaillancourt, R.E.; Raymond, C.A. Genetic parameters for lignin, extractives and decay in Eucalyptus globulus. Ann. For. Sci. 2006, 63, 812–821. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Handa, N.; Sharma, R.; Kaur, H.; Kohli, S.; Kumar, V.; Kaur, P. Lignins and abiotic stress: An overview. In Physiological Mechanisms and Adaptation Strategies in Plants Under Changing Environment; Ahmad, P., Wani, M., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Pereira, L.; Domingues-Junior, A.P.; Jansen, S.; Choat, B.; Mazzafera, P. Is embolism resistance in plant xylem associated with quantity and characteristics of lignin? Trees 2018, 32, 349–358. [Google Scholar] [CrossRef]
- Anterola, A.M.; Lewis, N.G. Trends in lignin modification: A comprehensive analysis of the effects of genetic manipulations/mutations on lignification and vascular integrity. Phytochemistry 2002, 61, 221–294. [Google Scholar] [CrossRef]
- Faix, O.; Mozuch, M.D.; Kirk, T.K. Degradation of gymnosperm (guaiacyl) vs. angiosperm (syringyl/guaiacyl) lignins by Phanerochaete chrysosporium. Holzforschung 1985, 39, 203–208. [Google Scholar] [CrossRef]
- Wardlaw, T.; Grove, S.; Hopkins, A.; Yee, M.; Harrison, K.; Mohammed, C. The uniqueness of habitats in old eucalypts: Contrasting wood-decay fungi and saproxylic beetles of young and old eucalypts. Tasforests 2009, 18, 17–32. [Google Scholar]
- Stackpole, D.J.; Vaillancourt, R.E.; Alves, A.; Rodrigues, J.; Potts, B.M. Genetic variation in the chemical components of Eucalyptus globulus wood. G3 GenesGenomesGenet 2011, 1, 151–159. [Google Scholar] [CrossRef]
- Dutkowski, G.W.; Potts, B.M. Geographic patterns of genetic variation in Eucalyptus globulus ssp. globulus and a revised racial classification. Aust. J. Bot. 1999, 47, 237–263. [Google Scholar] [CrossRef]
- Jones, R.C.; Steane, D.A.; Lavery, M.; Vaillancourt, R.E.; Potts, B.M. Multiple evolutionary processes drive the patterns of genetic differentiation in a forest tree species complex. Ecol. Evol. 2013, 3, 1–17. [Google Scholar] [CrossRef]
- Potts, B.M.; Vaillancourt, R.E.; Jordan, G.J.; Dutkowski, G.W.; Costa e Silva, J.; McKinnon, G.E.; Steane, D.A.; Volker, P.W.; Lopez, G.A.; Apiolaza, L.A.; et al. Exploration of the Eucalyptus globulus gene pool. In Eucalyptus in a Changing World, Proceedings of the IUFRO Conference; Aveiro, Portugal, 11–15 October 2004, RAIZ, Instituto de Investigação da Floresta e Papel: Aveiro, Portugal, 2004; pp. 46–61. [Google Scholar]
- Costa e Silva, J.; Potts, B.M.; Dutkowski, G. Genotype by environment interaction for growth of Eucalyptus globulus in Australia. Tree Genet. Genomes 2006, 2, 61–75. [Google Scholar] [CrossRef]
- McKinnon, G.E.; Jordan, G.J.; Vaillancourt, R.E.; Steane, D.A.; Potts, B.M. Glacial refugia and reticulate evolution: The case of the Tasmanian eucalypts. Philos. Trans. R. Soc. Lond.-Ser. B Biol. Sci. 2004, 359, 275–284. [Google Scholar] [CrossRef]
- Steane, D.A.; Conod, N.; Jones, R.C.; Vaillancourt, R.E.; Potts, B.M. A comparative analysis of population structure of a forest tree, Eucalyptus globulus (Myrtaceae), using microsatellite markers and quantitative traits. Tree Genet. Genomes 2006, 2, 30–38. [Google Scholar] [CrossRef]
- Yeoh, S.H.; Bell, J.C.; Foley, W.J.; Wallis, I.R.; Moran, G.F. Estimating population boundaries using regional and local-scale spatial genetic structure: An example in Eucalyptus globulus. Tree Genet. Genomes 2012, 8, 695–708. [Google Scholar] [CrossRef]
- Stackpole, D.J.; Vaillancourt, R.E.; Aguigar, M.; Potts, B.M. Age trends in genetic parameters for growth and wood density in Eucalyptus globulus. Tree Genet. Genomes 2010, 6, 179–193. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Welham, S.J.; Thompson, R. ASReml User Guide Release 4.1; VSN International Ltd.: Hemel Hempstead, UK, 2015. [Google Scholar]
- SAS. SAS/STAT® 14.1. User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2015. [Google Scholar]
- R-Core-Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Podolsky, R.H.; Shaw, R.G.; Shaw, F.H. Population structure of morphological traits in Clarkia dudleyana. II. constancy of within-population genetic variance. Evolution 1997, 51, 1785–1796. [Google Scholar]
- Houle, D.; Pélabon, C.; Wagner, G.P.; Hansen, T.F. Measurement and meaning in biology. Q. Rev. Biol. 2011, 86, 3–34. [Google Scholar] [CrossRef]
- Mimura, M.; Barbour, R.C.; Potts, B.M.; Vaillancourt, R.E.; Watanabe, K.N. Comparison of contemporary mating patterns in continuous and fragmented Eucalyptus globulus native forests. Mol. Ecol. 2009, 18, 4180–4192. [Google Scholar] [CrossRef]
- Lynch, M.; Walsh, B. Genetics and Analysis of Quantitative Traits; Sinauer Associates Inc.: Sunderland, MA, USA, 1998. [Google Scholar]
- Stram, D.O.; Lee, J.W. Variance components testing in the longitudinal mixed effects model. Biometrics 1994, 50, 1171–1177. [Google Scholar] [CrossRef]
- Shaw, R.G. The comparison of quantitative genetic parameters between populations. Evolution 1991, 45, 143–151. [Google Scholar] [CrossRef]
- Marroig, G.; Shirai, L.T.; Porto, A.; de Oliveira, F.B.; De Conto, V. The evolution of modularity in the mammalian skull II: Evolutionary consequences. Evol. Biol. 2009, 36, 136–148. [Google Scholar] [CrossRef]
- Cheverud, J.M. Quantitative genetic analysis of cranial morphology in the cotton-top (Saguinus oedipus) and saddle-back (S. fuscicollis) tamarins. J. Evol. Biol. 1996, 9, 5–42. [Google Scholar] [CrossRef]
- Krzanowski, W. Principles of Multivariate Analysis: A User’s Perspective; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Blows, M.W.; Chenoweth, S.F.; Hine, E. Orientation of the genetic variance-covariance matrix and the fitness surface for multiple male sexually selected traits. Am. Nat. 2004, 163, 329–340. [Google Scholar] [CrossRef] [PubMed]
- Kenward, M.G.; Roger, J.H. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics 1997, 53, 983–997. [Google Scholar] [CrossRef] [PubMed]
- Revell, L.J. phytools: An R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2012, 3, 217–223. [Google Scholar] [CrossRef]
- Revell, L.J. Size-correction and principal components for interspecific comparative studies. Evolution 2009, 63, 3258–3268. [Google Scholar] [CrossRef]
- Houle, D.; Meyer, K. Estimating sampling error of evolutionary statistics based on genetic covariance matrices using maximum likelihood. J. Evol. Biol. 2015, 28, 1542–1549. [Google Scholar] [CrossRef]
- Robinson, M.R.; Beckerman, A.P. Quantifying multivariate plasticity: Genetic variation in resource acquisition drives plasticity in resource allocation to components of life history. Ecol. Lett. 2013, 16, 281–290. [Google Scholar] [CrossRef]
- Thornhill, A.H.; Crisp, M.D.; Külheim, C.; Lam, K.E.; Nelson, L.A.; Yeates, D.K.; Miller, J.T. A dated molecular perspective of eucalypt taxonomy, evolution and diversification. Aust. Syst. Bot. 2019, 32, 29–48. [Google Scholar] [CrossRef]
- Jones, R.C.; Nicolle, D.; Steane, D.A.; Vaillancourt, R.E.; Potts, B.M. High density, genome-wide markers and intra-specific replication yield an unprecedented phylogenetic reconstruction of a globally significant, speciose lineage of Eucalyptus. Mol. Phylogenet. Evol. 2016, 105, 63–85. [Google Scholar] [CrossRef]
- De Deckker, P.; van der Kaars, S.; Macphail, M.K.; Hope, G.S. Land-sea correlations in the Australian region: 460 ka of changes recorded in a deep-sea core offshore Tasmania. Part 1: The pollen record. Aust. J. Earth Sci. 2019, 66, 1–15. [Google Scholar] [CrossRef]
- Lambeck, K.; Chappell, J. Sea Level Change through the Last Glacial Cycle. Science 2001, 292, 679–686. [Google Scholar] [CrossRef]
- Freeman, J.S.; Jackson, H.D.; Steane, D.A.; McKinnon, G.E.; Dutkowski, G.W.; Potts, B.M.; Vaillancourt, R.E. Chloroplast DNA phylogeography of Eucalyptus globulus. Aust. J. Bot. 2001, 49, 585–596. [Google Scholar] [CrossRef]
- Petherick, L.; Bostock, H.; Cohen, T.J.; Fitzsimmons, K.; Tibby, J.; Fletcher, M.S.; Moss, P.; Reeves, J.; Mooney, S.; Barrows, T.; et al. Climatic records over the past 30 ka from temperate Australia—A synthesis from the Oz-INTIMATE workgroup. Quat. Sci. Rev. 2013, 74, 58–77. [Google Scholar] [CrossRef]
- Wood, S.W.; Hua, Q.; Allen, K.J.; Bowman, D.M.J.S. Age and growth of a fire prone Tasmanian temperate old-growth forest stand dominated by Eucalyptus regnans, the world’s tallest angiosperm. For. Ecol. Manag. 2010, 260, 438–447. [Google Scholar] [CrossRef]
- Revell, L.J.; Harmon, L.J.; Langerhans, R.B.; Kolbe, J.J. A phylogenetic approach to determining the importance of constraint on phenotypic evolution in the neotropical lizard Anolis cristatellus. Evol. Ecol. Res. 2007, 9, 261–282. [Google Scholar]
- Freeman, J.S.; Potts, B.M.; Downes, G.M.; Pilbeam, D.; Thavamanikumar, S.; Vaillancourt, R.E. Stability of QTL for growth and wood properties across multiple pedigrees and environments in Eucalyptus globulus. New Phytol. 2013, 198, 1121–1134. [Google Scholar] [CrossRef]
- Houle, D.; Bolstad, G.H.; van der Linde, K.; Hansen, T.F. Mutation predicts 40 million years of fly wing evolution. Nature 2017, 548, 447–450. [Google Scholar] [CrossRef]
- Wilkinson, G.R. Population differentiation within Eucalyptus obliqua: Implications for regeneration success and genetic conservation in production forests. Aust. For. 2008, 71, 4–15. [Google Scholar] [CrossRef]
- Hamilton, M.G.; Williams, D.R.; Tilyard, P.A.; Pinkard, E.A.; Wardlaw, T.J.; Glen, M.; Vaillancourt, R.E.; Potts, B.M. A latitudinal cline in disease resistance of a host tree. Heredity 2013, 110, 372–379. [Google Scholar] [CrossRef]
- Hingston, A.B.; Gartrell, B.D.; Pinchbeck, G. How specialized is the plant-pollinator association between Eucalyptus globulus ssp. globulus and the swift parrot Lathamus discolor? Austral Ecol. 2004, 29, 624–630. [Google Scholar]
- Costa e Silva, J.; Potts, B.M.; Lopez, G.A. Heterosis may result in selection favouring the products of long-distance pollen dispersal in Eucalyptus. PLoS ONE 2014, 9, e93811. [Google Scholar] [CrossRef]
- Phillips, P.C.; Whitlock, M.C.; Fowler, K. Inbreeding changes the shape of the genetic covariance matrix in Drosophila melanogaster. Genetics 2001, 158, 1137–1145. [Google Scholar] [PubMed]
- McGuigan, K.; Chenoweth, S.F.; Blows, M.W. Phenotypic divergence along lines of genetic variance. Am. Nat. 2005, 165, 32–43. [Google Scholar] [CrossRef] [PubMed]
- Whitlock, M.C.; Phillips, P.C.; Fowler, K. Persistence of changes in the genetic covariance matrix after a bottleneck. Evolution 2002, 56, 1968–1975. [Google Scholar] [CrossRef] [PubMed]
- Bégin, M.; Roff, D.A.; Debat, V. The effect of temperature and wing morphology on quantitative genetic variation in the cricket Gryllus firmus, with an appendix examining the statistical properties of the Jackknife–manova method of matrix comparison. J. Evol. Biol. 2004, 17, 1255–1267. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Borralho, N.M.G.; Araujo, J.A.; Vaillancourt, R.E.; Potts, B.M. Genetic parameters for growth, wood density and pulp yield in Eucalyptus globulus. Tree Genet. Genomes 2009, 5, 291–305. [Google Scholar] [CrossRef]
- Nickolas, H.; Williams, D.; Downes, G.; Tilyard, P.; Harrison, P.A.; Vaillancourt, R.E.; Potts, B. Genetic correlations among pulpwood and solid-wood selection traits in Eucalyptus globulus. New For. 2020, 51, 137–158. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).