Modeling within and between Sub-Genomes Epistasis of Synthetic Hexaploid Wheat for Genome-Enabled Prediction of Diseases
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phenotypic Evaluations
2.2. Genotyping
2.3. Phenotypic Model for Disease Traits TS, SNB and SB
2.4. Genomic Prediction Models
2.4.1. Whole Genome Models
2.4.2. Sub-Genome Models
2.5. Cross-Validation Schemes
2.6. Software
3. Results
3.1. Estimated Variance Components for the Different Traits and Statistical Models
3.2. Genomic Prediction
4. Discussion
4.1. Activation of Genes from Sub-Genome D with Those of Sub-Genome A and B
4.2. Study of Epistasis of Sub-Genome A, B, and D Genes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santantonio, N.; Jannink, J.L.; Sorrells, M. Prediction of subgenome additive and interaction effects in allohexaploid wheat. G3 Genes Genomes Genet. 2019, 9, 685–698. [Google Scholar] [CrossRef]
- Zohary, D.; Hopf, M.; Weiss, E. Domestication of Plants in the Old World: The Origin and Spread of Domesticated Plants in Southwest Asia, Europe, and the Mediterranean Basin; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Villareal, R.L.; Mujeeb-Kazi, A.; Fuentes-Davila, G.; Rajaram, S.; Del Toro, E. Resistance to Karnal Bunt (Tilletia indica Mitra) in Synthetic Hexaploid Wheats Derived from Triticum turgidum × T. tauschii. Plant Breed. 1994, 112, 63–69. [Google Scholar] [CrossRef]
- Mujeeb-Kazi, A.; Hettel, G. (Eds.) Utilizing Wild Grass Biodiversity in Wheat Improvement: 15 Years of Wide Cross Research at CIMMYT; CIMMYT: Mexcio City, Mexcio, 1995. [Google Scholar]
- Mujeeb-Kazi, A.; Rosas, V.; Roldán, S. Conservation of the genetic variation of Triticum tauschii (Coss.) Schmalh. (Aegilops squarrosa auct. non L.) in synthetic hexaploid wheats (T. turgidum L. s. lat. 9 T. tauschii; 2n = 6x = 42, AABBDD) and its potential utilization for wheat improvement. Genet Resour. Crop. Evol. 1996, 43, 129–134. [Google Scholar] [CrossRef]
- Mujeeb-Kazi, A.; Cano, S.; Rosas, V.; Cortes, A.; Delgado, R. Registration of five synthetic hexaploid wheat and seven bread wheat germplasm lines resistant to wheat spot blotch. Crop Sci. 2001, 41, 1653–1654. [Google Scholar] [CrossRef]
- Mujeeb-Kazi, A.; Gul, A.; Ahmad, F.; Farooq, M.; Rizwan, S.; Bux, H.; Iftikhar, S.; Asad, S.; Delgado, R. Aegilops tauschii, as spot blotch (Cochliobolus sativus) resistance source for bread wheat improvement. Pak. J. Bot. 2007, 39, 1207–1216. [Google Scholar]
- Dreisigacker, S.; Kishii, M.; Lage, J.; Warburton, M. Use of synthetic hexaploid wheat to increase diversity for CIMMYT bread wheat improvement. Aust. J. Agric. Res. 2008, 59, 413–420. [Google Scholar] [CrossRef]
- Rosyara, U.; Kishii, M.; Payne, T.; Sansaloni, C.P.; Singh, R.P.; Braun, H.-J.; Dreisigacker, S. Genetic Contribution of Synthetic Hexaploid Wheat to CIMMYT’s Spring Bread Wheat Breeding Germplasm. Sci. Rep. 2019, 9, 12355. [Google Scholar] [CrossRef]
- Aberkane, H.; Payne, T.; Kishi, M.; Smale, M.; Amri, A.; Jamora, N. Transferring diversity of goat grass to farmers’ fields through the development of synthetic hexaploid wheat. Food Secur. 2020, 12, 1017–1033. [Google Scholar] [CrossRef]
- Yu, J.; Pressoir, G.; Briggs, W.H.; Vroh Bi, I.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef]
- Yang, J.; Zaitlen, N.A.; Goddard, M.E.; Visscher, P.M.; Price, A.L. Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 2014, 46, 100–106. [Google Scholar] [CrossRef]
- Gianola, D.; Fariello, M.I.; Naya, H.; Schön, C.C. Genome-wide association studies with a genomic relationship matrix: A case study with wheat and Arabidopsis. G3 Genes Genomes Genet. 2016, 6, 3241–3256. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; De Los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic selection in plant breeding: Methods, models, and perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef] [PubMed]
- Gholami, M.; Wimmer, V.; Sansaloni, C.; Petroli, C.; Hearne, S.J.; Covarrubias-Pazaran, G.; Rensing, S.; Heise, J.; Pérez-Rodríguez, P.; Dreisigacker, S.; et al. A comparison of the adoption of genomic selection across different breeding institutions. Front. Plant Sci. 2021, 12, 728567. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Bonnett, D.; Li, Y.; Crossa, J.; Dreisigacker, S.; Basnet, B.; Pérez-Rodríguez, P.; Alvarado, G.; Jannink, J.L.; Poland, J.; Sorrells, M. Response to Early Generation Genomic Selection for Yield in Wheat. Front. Plant Sci. 2022, 12, 718611. [Google Scholar] [CrossRef]
- Dreisigacker, S.; Martini, J.W.R.; Cuevas, J.; Pérez-Rodríguez, P.; Lozano-Ramírez, N.; Huerta, J.; Singh, P.K.; Crespo-Herrera, L.; Bentley, A.R.; Crossa, J. Genomic prediction of Synthetic Hexaploid Wheat upon tetraploid durum and diploid Aegilops parental pools. Plant Genome 2023, submitted.
- Crossa, J.; de los Campos, G.D.L.; Pérez, P.; Gianola, D.; Burgueño, J.; Araus, J.L.; Makumbi, D.; Singh, R.P.; Dreisigacker, S.; Yan, J.; et al. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 2010, 186, 713–724. [Google Scholar] [CrossRef]
- Jiang, Y.; Reif, J.C. Modeling epistasis in genomic selection. Genetics 2015, 201, 759–768. [Google Scholar] [CrossRef]
- Martini, J.W.R.; Wimmer, V.; Erbe, M.; Simianer, H. Epistasis and covariance: How gene interaction translates into genomic relationship. Theor. Appl. Genet. 2016, 129, 963–976. [Google Scholar] [CrossRef]
- Martini, J.W.R.; Toledo, F.H.; Crossa, J. On the approximation of interaction effect models by Hadamard powers of the additive genomic relationship. Theor. Popul. Biol. 2020, 132, 16–23. [Google Scholar] [CrossRef]
- Jiang, Y.; Reif, J.C. Efficient algorithms for calculating epistatic genomic relationship matrices. Genetics 2020, 216, 651–669. [Google Scholar] [CrossRef] [PubMed]
- Lozano-Ramírez, N.; Dreisigacker, S.; Sansaloni, C.P.; He, X.; Sandoval-Islas, J.S.; Pérez-Rodríguez, P.; Carballo, A.C.; Nava-Díaz, C.; Kishii, M.; Singh, P.K. Genome-Wide Association Study for Resistance to Tan Spot in Synthetic Hexaploid Wheat. Plants 2022, 11, 433. [Google Scholar] [CrossRef] [PubMed]
- Lozano-Ramirez, N.; Dreisigacker, S.; Sansaloni, C.P.; He, X.; Sandoval-Islas, J.S.; Pérez-Rodríguez, P.; Carballo, A.C.; Diaz, C.N.; Kishii, M.; Singh, P.K. Genome-Wide Association Study for Spot Blotch Resistance in Synthetic Hexaploid Wheat. Genes 2022, 13, 1387. [Google Scholar] [CrossRef]
- Lamari, L.; Bernier, C.C. Evaluation of wheat lines and cultivars to tan spot [Pyrenophora tritici-repentis] based on lesion type. Can. J. Plant Pathol. 1989, 11, 49–56. [Google Scholar] [CrossRef]
- Dreisigacker, S.; Sehgal, D.; Jaimez, A.R.; Garrido, B.L.; Savala, S.M.; Núñez-Ríos, C.; Mollins, J.; Mall, S. CIMMYT Wheat Molecular Genetics: Laboratory Protocols and Applications to Wheat Breeding; Mollins, J., Mall, S., Eds.; CIMMYT: Mexico City, Mexico, 2016. [Google Scholar]
- Sansaloni, C.; Petroli, C.; Jaccoud, D.; Carling, J.; Detering, F.; Grattapaglia, D.; Kilian, A. Diversity Arrays Technology (DArT) and next-generation sequencing combined: Genome-wide, high throughput, highly informative genotyping for molecular breeding of Eucalyptus. BMC Proc. 2011, 5, P54. [Google Scholar] [CrossRef]
- The International Wheat Genome Sequencing Consortium (IWGSC); Appels, R.; Eversole, K.; Feuillet, C.; Keller, B.; Rogers, J.; Stein, N.; Pozniak, C.J.; Stein, N.; Choulet, F.; et al. Shifting the limits in wheat research and breeding using a fully annotated reference genome. Science 2018, 361, eaar7191. [Google Scholar] [CrossRef]
- Maccaferri, M.; Sanguineti, M.C.; Mantovani, P.; Demontis, A.; Massi, A.; Ammar, K.; Kolmer, J.A.; Czembor, J.H.; Ezrati, S.; Tuberosa, R. Association mapping of leaf rust response in durum wheat. Mol. Breed. 2019, 26, 189–228. [Google Scholar] [CrossRef]
- Luo, M.-C.; Gu, Y.Q.; Puiu, D.; Wang, H.; Twardziok, S.O.; Deal, K.R.; Huo, N.; Zhu, T.; Wang, L.; Wang, Y.; et al. Genome sequence of the progenitor of the wheat D genome Aegilops tauschii. Nature 2017, 551, 498–502. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D. Theory and Analysiss of the Threshold Characters. J. Anim. Sci. 1982, 54, 1079–1096. [Google Scholar] [CrossRef]
- Lopez-Cruz, M.; Crossa, J.; Bonnett, D.; Dreisigacker, S.; Poland, J.; Jannink, J.L.; Singh, R.P.; Autrique, E.; de los Campos, G. Increased prediction accuracy in wheat breeding trials using a marker × environment interaction genomic selection model. G3 2015, 5, 569–582. [Google Scholar] [CrossRef] [PubMed]
- Basnet, B.R.; Crossa, J.; Dreisigacker, S.; Perez-Rodriguez, P.; Manes, Y.; Singh, R.P.; Royara, U.R.; Camarillo-Castillo, F.; Murua, M. Hybrid Wheat prediction using genomic, pedigree and environmental covariables interaction models. Plant Genome 2019, 12, 180051. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Rodríguez, P.; de los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Chu, C.G.; Friesen, T.L.; Xu, S.S.; Faris, J.D. Identification of novel tan spot resistance loci beyond the known host- selective toxin insensitivity genes in wheat. Theor. Appl. Genet. 2008, 117, 873–881. [Google Scholar] [CrossRef]
- Akdemir, D.; Jannink, J.L. Locally epistatic genomic relationship matrices for genomic association and prediction. Genetics 2015, 199, 857–871. [Google Scholar] [CrossRef]
- Vitezica, Z.; Legarra, A.; Toro, M.A.; Varona, L. Orthogonal estimates of variances for additive, dominance, and epistatic effects in population. Genetics 2017, 206, 1297–1307. [Google Scholar] [CrossRef]
- González-Diéguez, D.; Crossa, J.; Rivera-Amado, C.; Pinera-Chavez, F.; Pinto, F.; Pierre, C.S.; Pérez-Rodríguez, P.; Dreisigacker, S.; Reynolds, M. Genome-based predictions of sub-genome genetic interactions effects in wheat populations. In Proceedings of the XVIIIth Eucarpia Biometrics in Plant Breeding Conference, Paris, France, 21–23 September 2022. [Google Scholar]
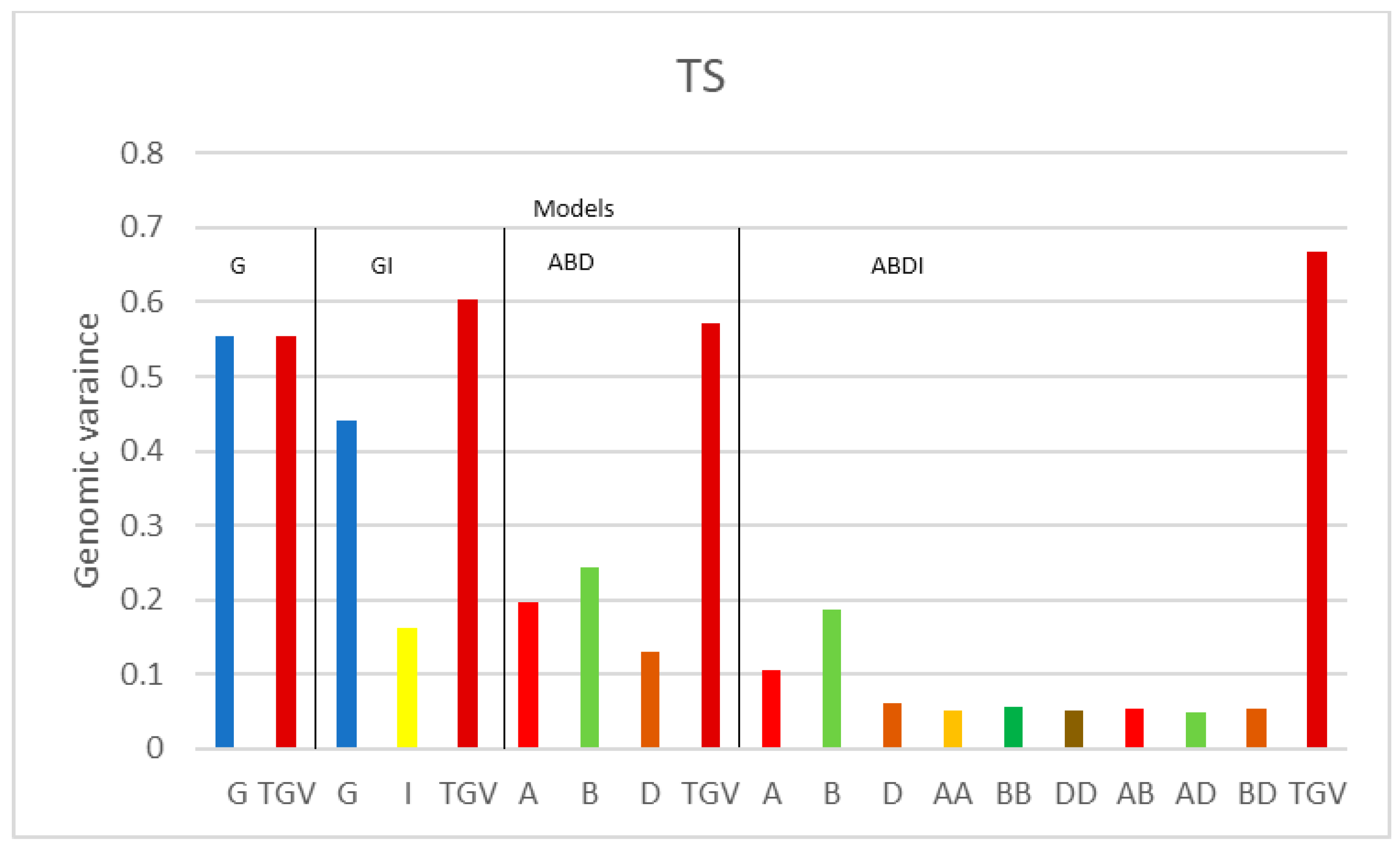
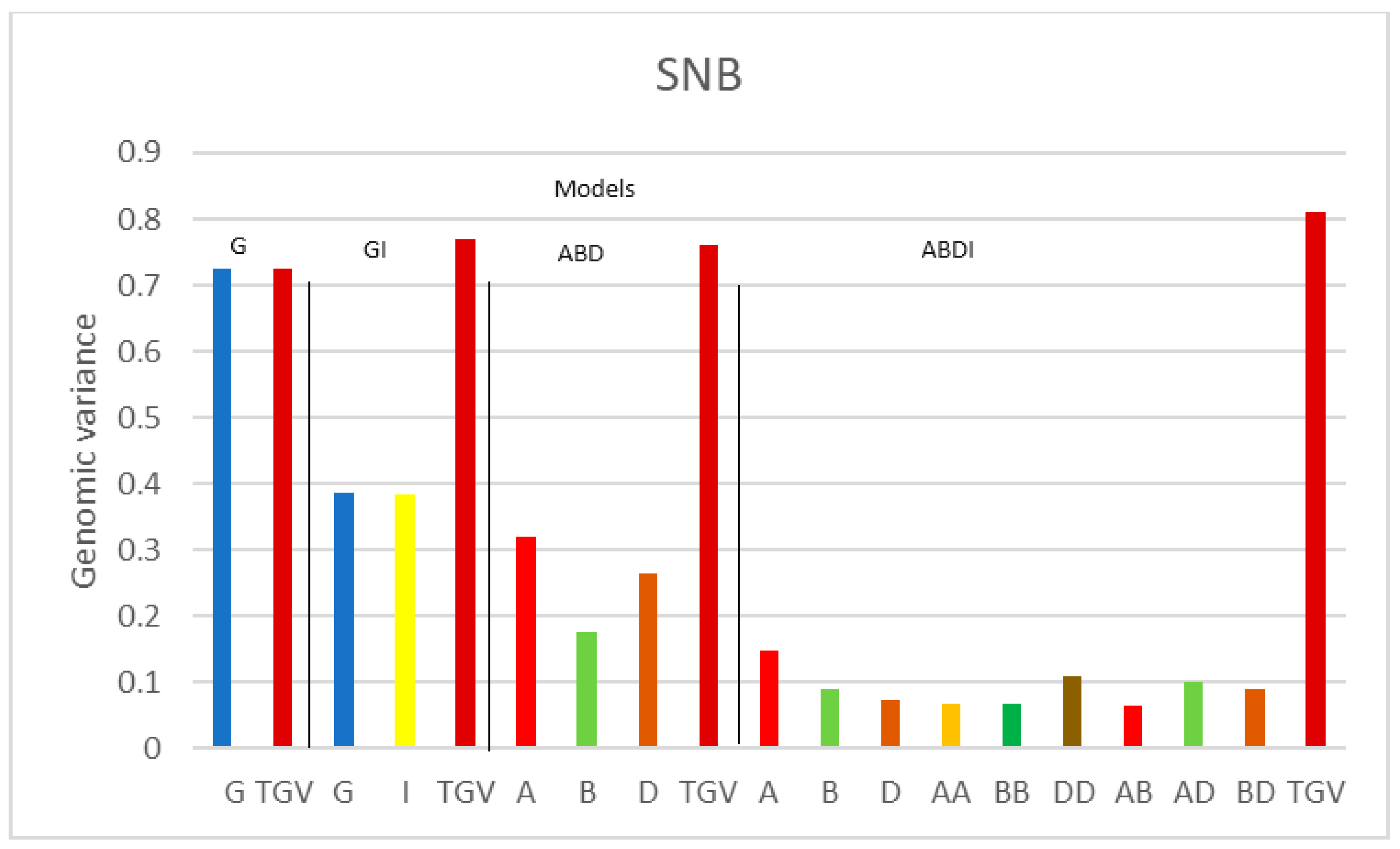



| Variance Components | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TRAIT | Model | Res | |||||||||||
| TS | G | 0.555 | 0.330 | ||||||||||
| GI | 0.440 | 0.163 | 0.261 | ||||||||||
| ABD | 0.196 | 0.244 | 0.131 | 0.326 | |||||||||
| ABDI | 0.105 | 0.187 | 0.061 | 0.052 | 0.056 | 0.052 | 0.053 | 0.048 | 0.054 | 0.234 | |||
| SNB | G | 0.724 | 0.403 | ||||||||||
| GI | 0.386 | 0.383 | 0.259 | ||||||||||
| ABD | 0.321 | 0.176 | 0.265 | 0.396 | |||||||||
| ABDI | 0.148 | 0.091 | 0.072 | 0.067 | 0.068 | 0.109 | 0.065 | 0.100 | 0.091 | 0.235 | |||
| SB | G | 0.608 | 0.535 | ||||||||||
| GI | 0.339 | 0.337 | 0.416 | ||||||||||
| ABD | 0.179 | 0.205 | 0.343 | 0.503 | |||||||||
| ABDI | 0.081 | 0.090 | 0.100 | 0.072 | 0.069 | 0.146 | 0.075 | 0.092 | 0.077 | 0.353 | |||
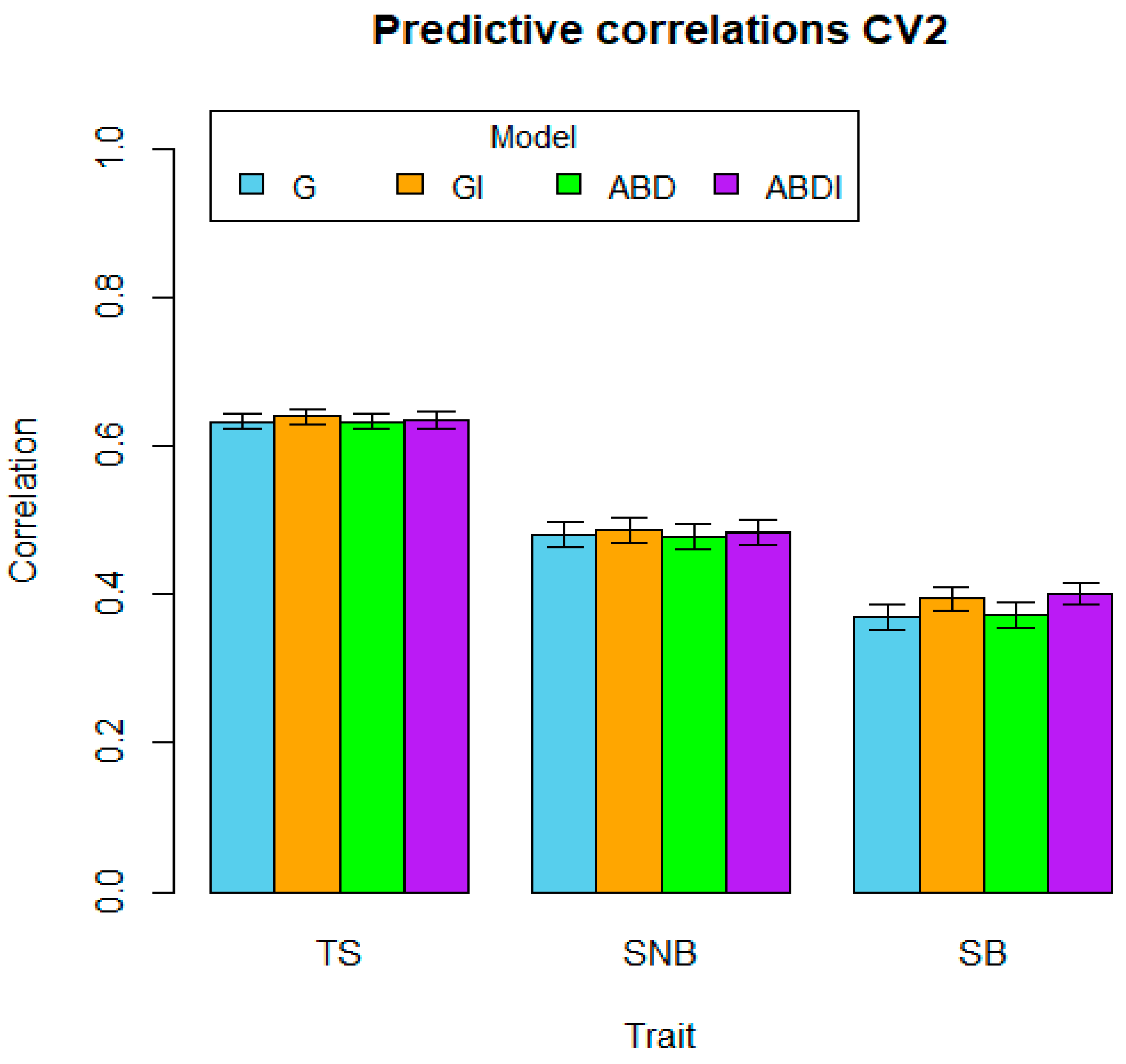
| Traits | CV1 | CV2 | CV3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G | GI | ABD | ABDI | G | GI | ABD | ABDI | G | GI | ABD | ABDI | ||
| TS | Mean | 0.702 | 0.724 | 0.702 | 0.724 | 0.632 | 0.639 | 0.632 | 0.635 | 0.691 | 0.714 | 0.691 | 0.715 |
| SE | 0.007 | 0.007 | 0.007 | 0.007 | 0.010 | 0.011 | 0.010 | 0.011 | 0.009 | 0.009 | 0.009 | 0.009 | |
| SNB | Mean | 0.597 | 0.647 | 0.596 | 0.650 | 0.481 | 0.487 | 0.479 | 0.484 | 0.587 | 0.641 | 0.587 | 0.644 |
| SE | 0.010 | 0.009 | 0.009 | 0.009 | 0.017 | 0.017 | 0.017 | 0.017 | 0.008 | 0.008 | 0.009 | 0.008 | |
| SB | Mean | 0.482 | 0.500 | 0.486 | 0.506 | 0.370 | 0.394 | 0.371 | 0.401 | 0.475 | 0.495 | 0.476 | 0.500 |
| SE | 0.011 | 0.011 | 0.011 | 0.010 | 0.017 | 0.015 | 0.017 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuevas, J.; González-Diéguez, D.; Dreisigacker, S.; Martini, J.W.R.; Crespo-Herrera, L.; Lozano-Ramirez, N.; Singh, P.K.; He, X.; Huerta, J.; Crossa, J. Modeling within and between Sub-Genomes Epistasis of Synthetic Hexaploid Wheat for Genome-Enabled Prediction of Diseases. Genes 2024, 15, 262. https://doi.org/10.3390/genes15030262
Cuevas J, González-Diéguez D, Dreisigacker S, Martini JWR, Crespo-Herrera L, Lozano-Ramirez N, Singh PK, He X, Huerta J, Crossa J. Modeling within and between Sub-Genomes Epistasis of Synthetic Hexaploid Wheat for Genome-Enabled Prediction of Diseases. Genes. 2024; 15(3):262. https://doi.org/10.3390/genes15030262
Chicago/Turabian StyleCuevas, Jaime, David González-Diéguez, Susanne Dreisigacker, Johannes W. R. Martini, Leo Crespo-Herrera, Nerida Lozano-Ramirez, Pawan K. Singh, Xinyao He, Julio Huerta, and Jose Crossa. 2024. "Modeling within and between Sub-Genomes Epistasis of Synthetic Hexaploid Wheat for Genome-Enabled Prediction of Diseases" Genes 15, no. 3: 262. https://doi.org/10.3390/genes15030262
APA StyleCuevas, J., González-Diéguez, D., Dreisigacker, S., Martini, J. W. R., Crespo-Herrera, L., Lozano-Ramirez, N., Singh, P. K., He, X., Huerta, J., & Crossa, J. (2024). Modeling within and between Sub-Genomes Epistasis of Synthetic Hexaploid Wheat for Genome-Enabled Prediction of Diseases. Genes, 15(3), 262. https://doi.org/10.3390/genes15030262







