GRE: A Framework for Significant SNP Identification Associated with Wheat Yield Leveraging GWAS–Random Forest Joint Feature Selection and Explainable Machine Learning Genomic Selection Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources and Preprocessing
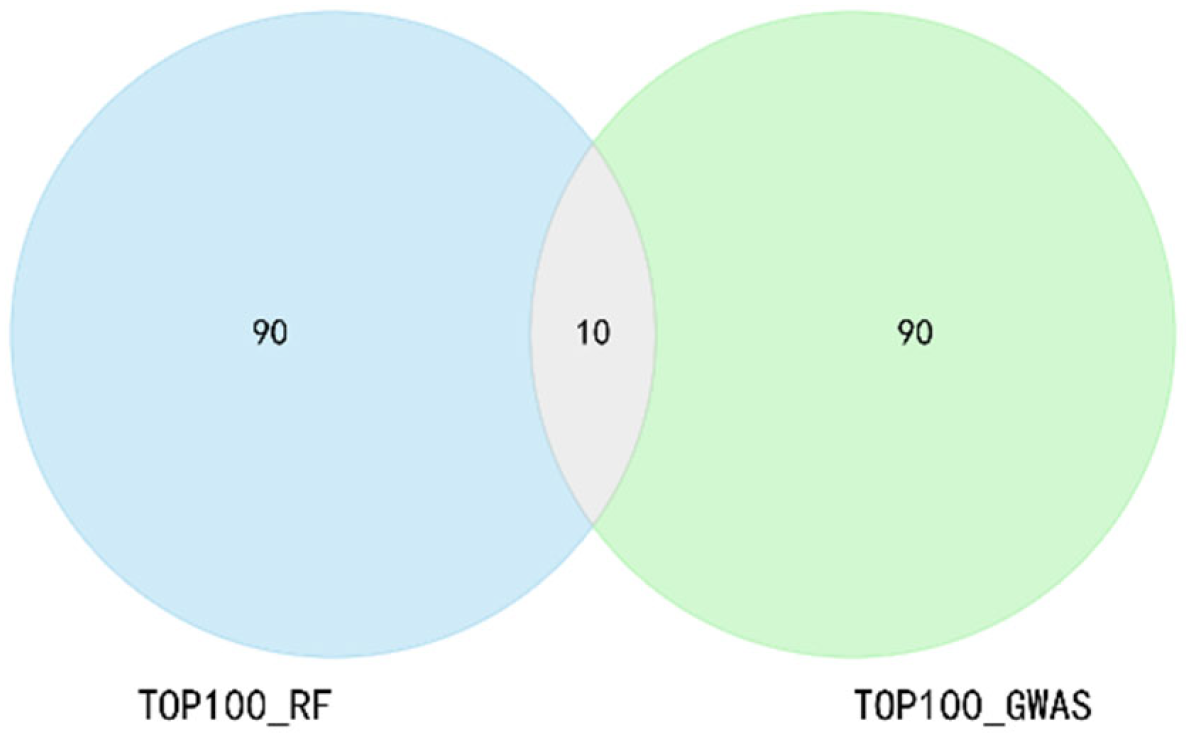
2.2. Feature Selection Strategy of GRE
2.3. Prediction Model and Hyperparameter Settings
2.4. Model Training and Validation
2.5. Comparison of Random SNP Selection with Feature Selection Using GRE
2.6. GRE’s Explainability Leveraging SHAP Techniques
2.7. Computing Platform
3. Results
3.1. The Dimension of the Feature Subset and the Label Distribution
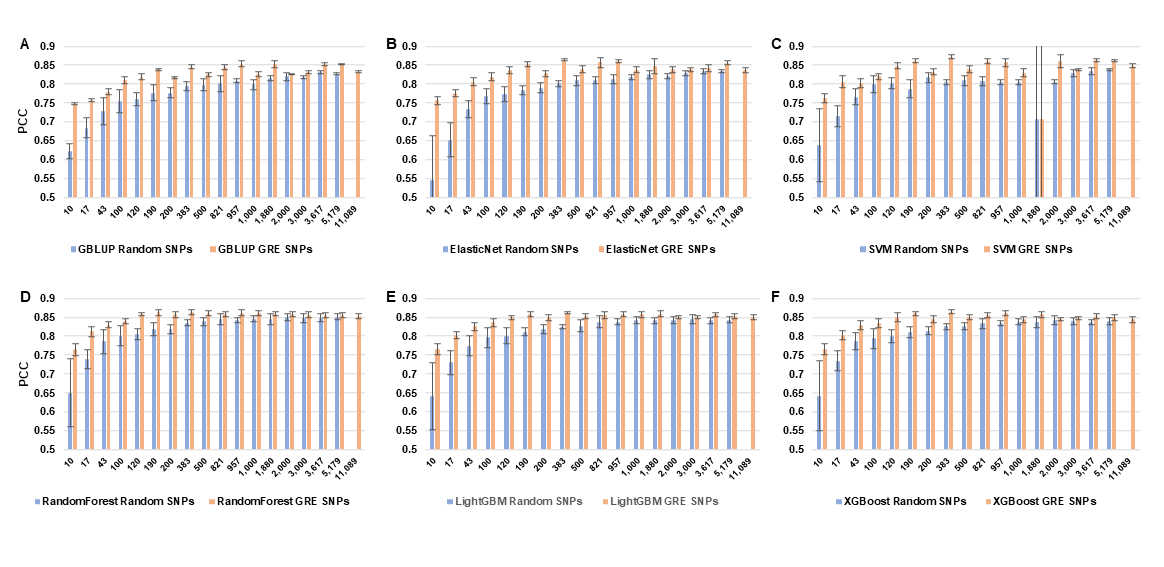
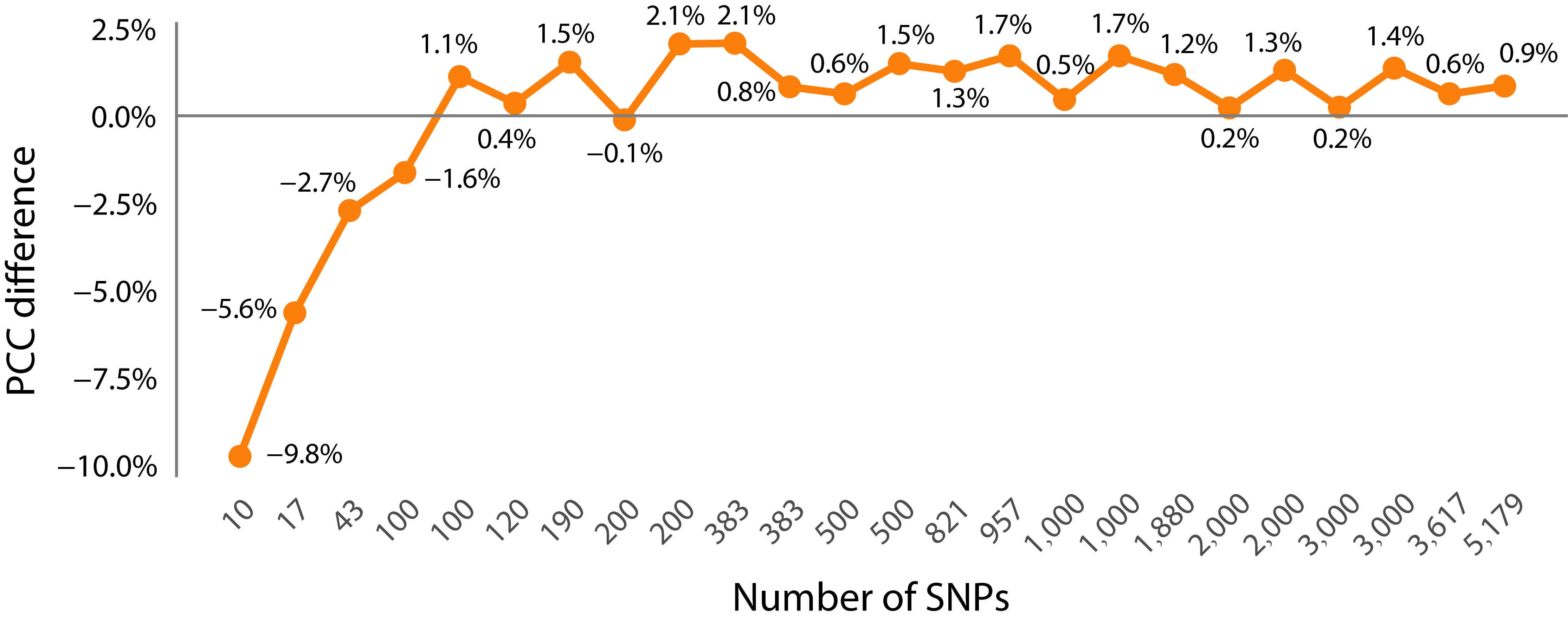
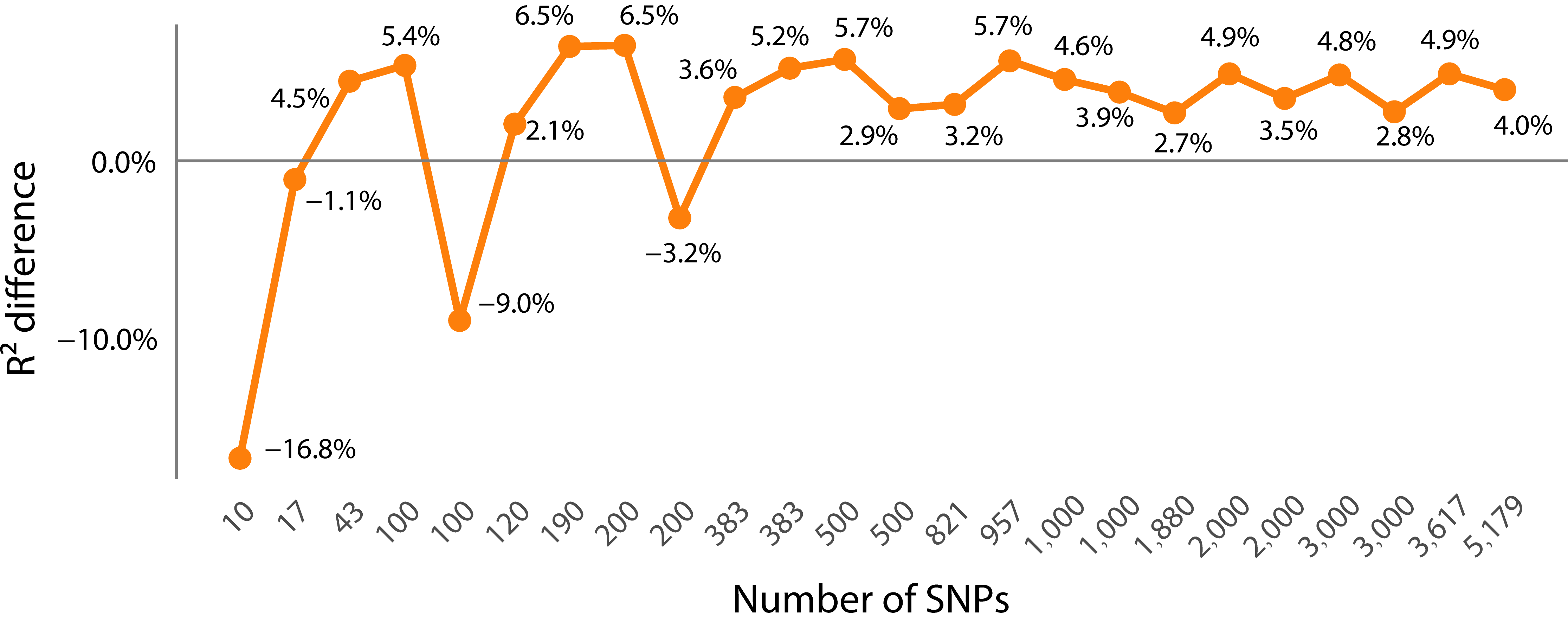
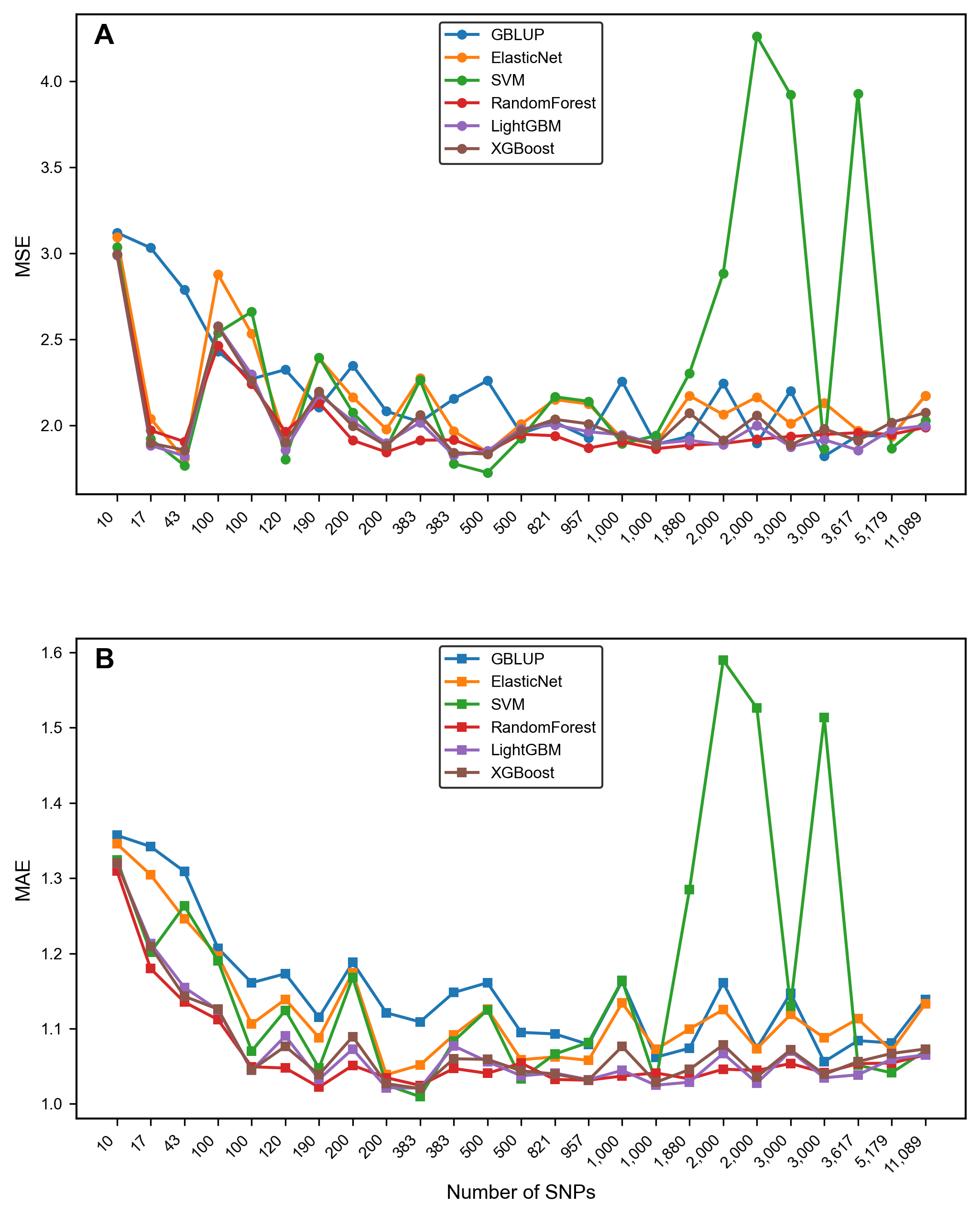
3.2. The Impact of Feature Selection Strategy on Prediction Accuracy
- (1).
- Comparison of the effects of random SNP selection and GRE in predicting GEBV
- (2).
- Comparison of PCC prediction results between the dimensionality-reduced subset and the whole SNP set
- (3).
- Comparison of the error metrics
3.3. Comparison of Model Performance
3.4. Identification of the Optimal Combination
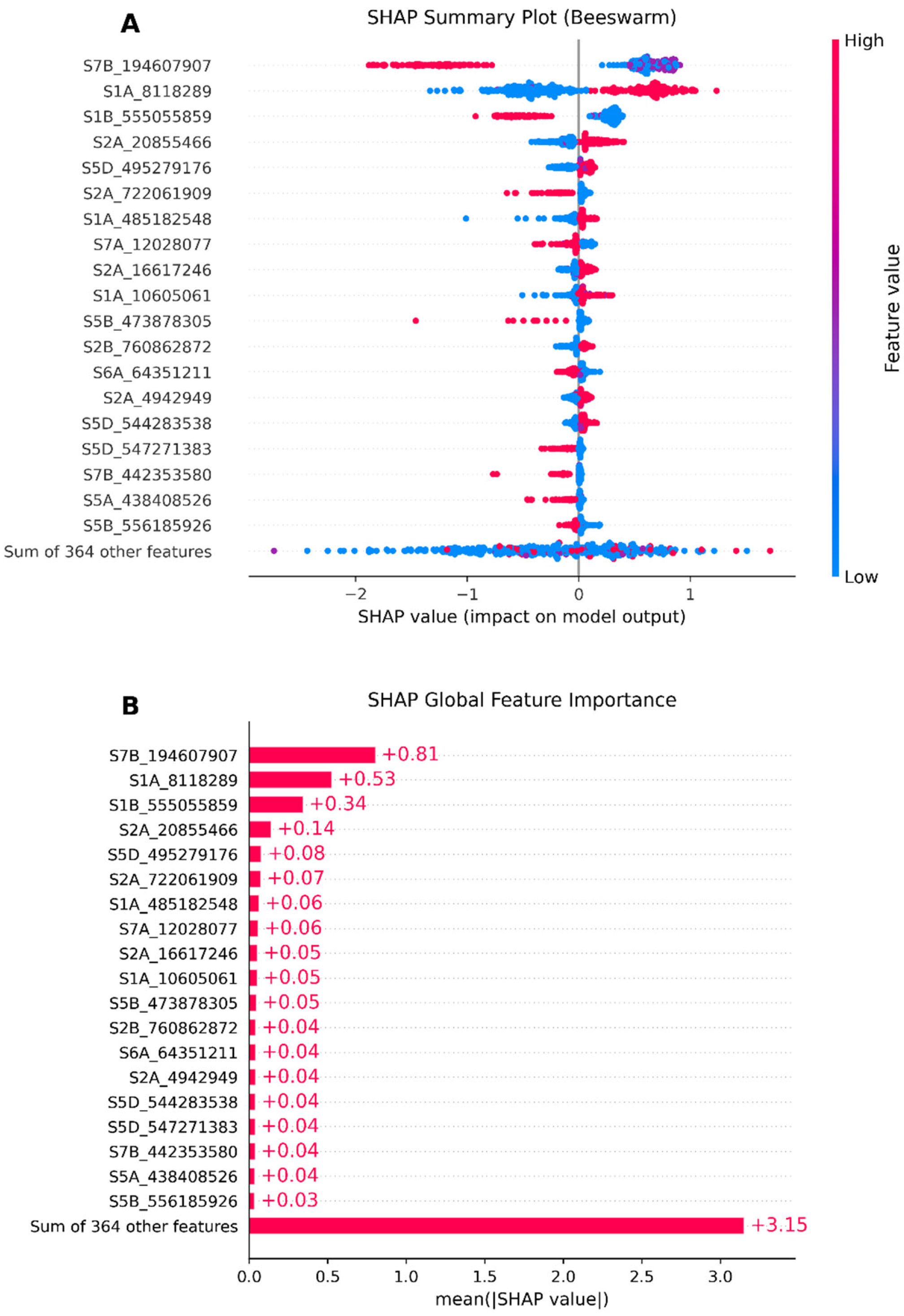
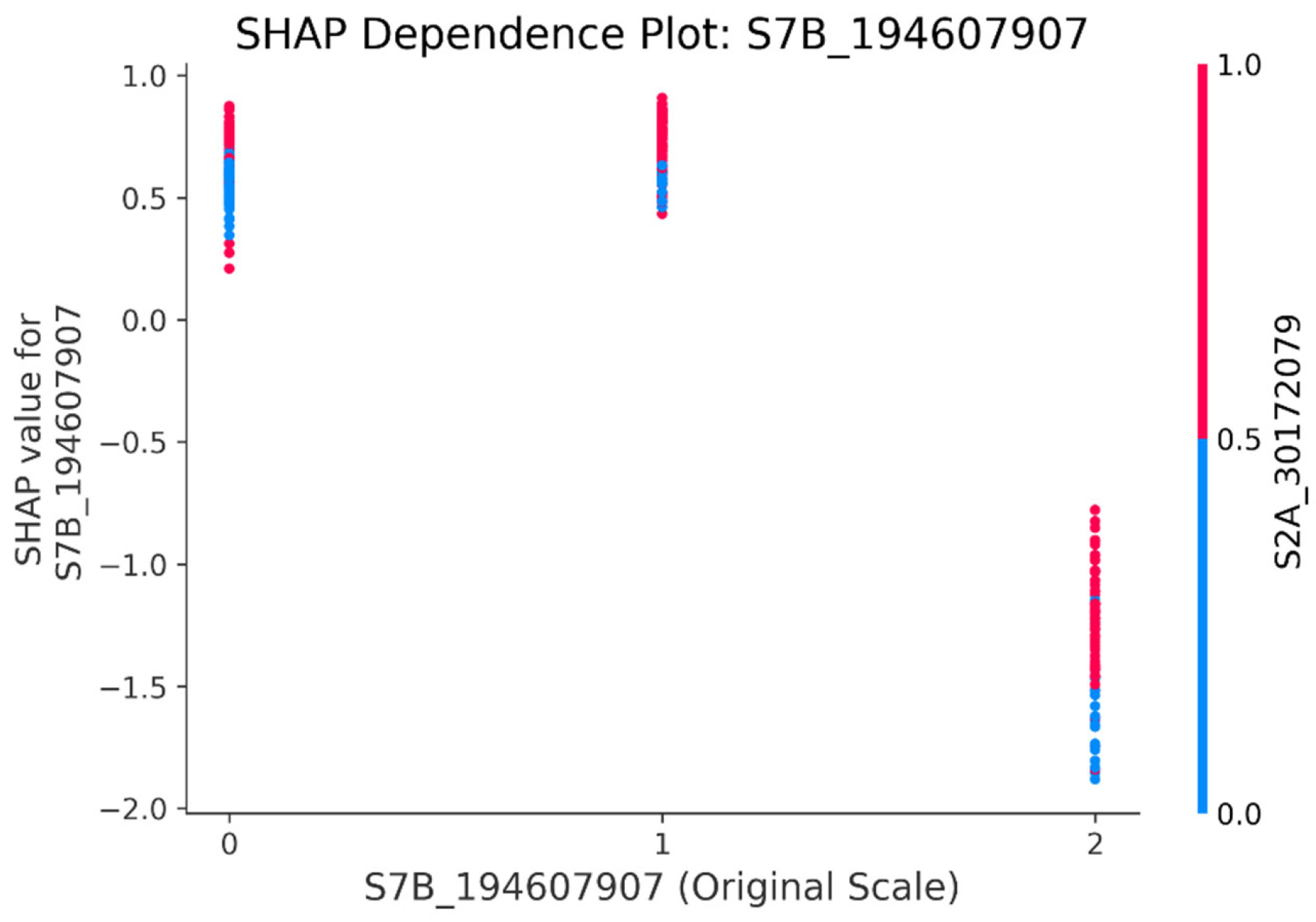
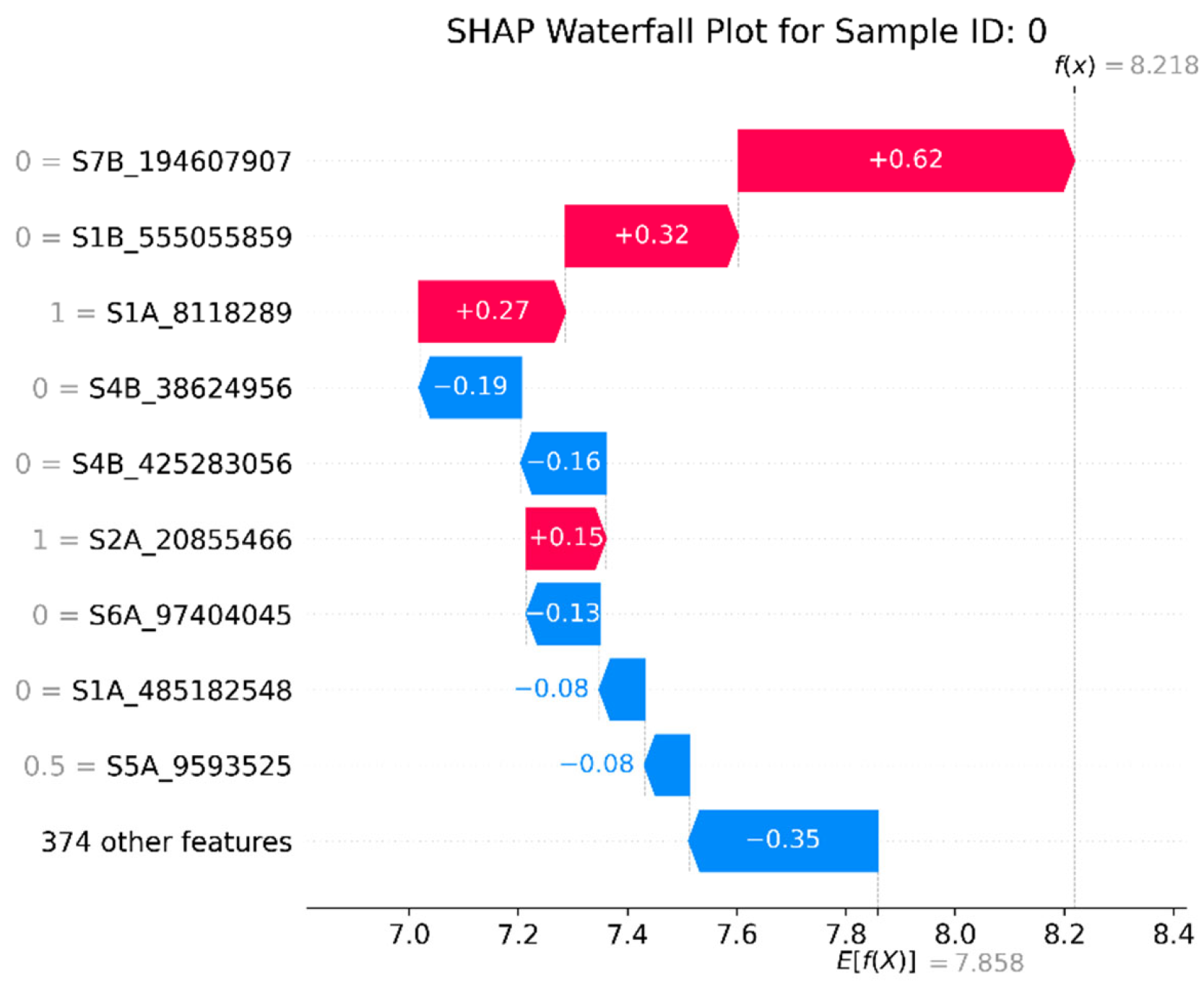
3.5. Model Interpretability Based on SHAP
4. Discussion
4.1. GRE Helps Simplify the Data Structure and Improve the Prediction Accuracy of GS
4.2. Leveraging the Complementary Performance Advantages of the GS Model Can Enhance Prediction Capabilities
4.3. An Optimal Value for the Number of Significant SNPs in Wheat Yields Traits
4.4. GRE’s SHAP Techniques Help Identify Significant SNPs in Wheat Yield Traits
4.5. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Alemu, A.; Åstrand, J.; Montesinos-López, O.A.; Isidro, Y.S.J.; Fernández-Gónzalez, J.; Tadesse, W.; Vetukuri, R.R.; Carlsson, A.S.; Ceplitis, A.; Crossa, J.; et al. Genomic selection in plant breeding: Key factors shaping two decades of progress. Mol. Plant 2024, 17, 552–578. [Google Scholar] [CrossRef]
- Zhao, H.; Xie, X.; Ma, H.; Zhou, P.; Xu, B.; Zhang, Y.; Xu, L.; Gao, H.; Li, J.; Wang, Z.; et al. Enhancing Genomic Prediction Accuracy in Beef Cattle Using WMGBLUP and SNP Pre-Selection. Agriculture 2025, 15, 1094. [Google Scholar] [CrossRef]
- Crossa, J.; Campos Gde, L.; Pérez, P.; Gianola, D.; Burgueño, J.; Araus, J.L.; Makumbi, D.; Singh, R.P.; Dreisigacker, S.; Yan, J.; et al. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 2010, 186, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Dreisigacker, S.; Pérez-Rodríguez, P.; Crespo-Herrera, L.; Bentley, A.R.; Crossa, J. Results from rapid-cycle recurrent genomic selection in spring bread wheat. G3 2023, 13, jkad025. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; Martini, J.W.R.; Vitale, P.; Pérez-Rodríguez, P.; Costa-Neto, G.; Fritsche-Neto, R.; Runcie, D.; Cuevas, J.; Toledo, F.; Li, H.; et al. Expanding genomic prediction in plant breeding: Harnessing big data, machine learning, and advanced software. Trends Plant Sci. 2025, 30, 756–774. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Dong, Z.; Zhao, L.; Ren, Y.; Zhang, N.; Chen, F. The Wheat 660K SNP array demonstrates great potential for marker-assisted selection in polyploid wheat. Plant Biotechnol. J. 2020, 18, 1354–1360. [Google Scholar] [CrossRef]
- Manthena, V.; Jarquín, D.; Varshney, R.K.; Roorkiwal, M.; Dixit, G.P.; Bharadwaj, C.; Howard, R. Evaluating dimensionality reduction for genomic prediction. Front. Genet. 2022, 13, 958780. [Google Scholar] [CrossRef]
- Gill, H.S.; Halder, J.; Zhang, J.; Brar, N.K.; Rai, T.S.; Hall, C.; Bernardo, A.; Amand, P.S.; Bai, G.; Olson, E.; et al. Multi-Trait Multi-Environment Genomic Prediction of Agronomic Traits in Advanced Breeding Lines of Winter Wheat. Front. Plant Sci. 2021, 12, 709545. [Google Scholar] [CrossRef]
- Tahmasebi, S.; Heidari, B.; Pakniyat, H.; McIntyre, C.L. Mapping QTLs associated with agronomic and physiological traits under terminal drought and heat stress conditions in wheat (Triticum aestivum L.). Genome 2017, 60, 26–45. [Google Scholar] [CrossRef]
- Juliana, P.; He, X.; Marza, F.; Islam, R.; Anwar, B.; Poland, J.; Shrestha, S.; Singh, G.P.; Chawade, A.; Joshi, A.K.; et al. Genomic Selection for Wheat Blast in a Diversity Panel, Breeding Panel and Full-Sibs Panel. Front. Plant Sci. 2021, 12, 745379. [Google Scholar] [CrossRef]
- Juliana, P.; Poland, J.; Huerta-Espino, J.; Shrestha, S.; Crossa, J.; Crespo-Herrera, L.; Toledo, F.H.; Govindan, V.; Mondal, S.; Kumar, U.; et al. Improving grain yield, stress resilience and quality of bread wheat using large-scale genomics. Nat. Genet. 2019, 51, 1530–1539. [Google Scholar] [CrossRef]
- Zhang, F.; Kang, J.; Long, R.; Li, M.; Sun, Y.; He, F.; Jiang, X.; Yang, C.; Yang, X.; Kong, J.; et al. Application of machine learning to explore the genomic prediction accuracy of fall dormancy in autotetraploid alfalfa. Hortic. Res. 2023, 10, uhac225. [Google Scholar] [CrossRef]
- Shi, A.; Bhattarai, G.; Xiong, H.; Avila, C.A.; Feng, C.; Liu, B.; Joshi, V.; Stein, L.; Mou, B.; du Toit, L.J.; et al. Genome-wide association study and genomic prediction of white rust resistance in USDA GRIN spinach germplasm. Hortic. Res. 2022, 9, uhac069. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Zeng, X.; Xu, M.; Li, M.; Zhang, F.; He, F.; Yang, T.; Wang, C.; Gao, T.; Long, R.; et al. The whole-genome dissection of root system architecture provides new insights for the genetic improvement of alfalfa (Medicago sativa L.). Hortic. Res. 2025, 12, uhae271. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; Kim, J.Y.; Kim, N. GMStool: GWAS-based marker selection tool for genomic prediction from genomic data. Sci. Rep. 2020, 10, 19653. [Google Scholar] [CrossRef] [PubMed]
- Andersen, C.M.; Bro, R. Variable selection in regression-a tutorial. J. Chemometr. 2010, 24, 728–737. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 2018, 58, 267–288. [Google Scholar] [CrossRef]
- Shahsavari, M.; Mohammadi, V.; Alizadeh, B.; Alizadeh, H. Application of machine learning algorithms and feature selection in rapeseed (Brassica napus L.) breeding for seed yield. Plant Methods 2023, 19, 57. [Google Scholar] [CrossRef]
- Bermingham, M.L.; Pong-Wong, R.; Spiliopoulou, A.; Hayward, C.; Rudan, I.; Campbell, H.; Wright, A.F.; Wilson, J.F.; Agakov, F.; Navarro, P.; et al. Application of high-dimensional feature selection: Evaluation for genomic prediction in man. Sci. Rep. 2015, 5, 10312. [Google Scholar] [CrossRef]
- Heinrich, F.; Lange, T.M.; Kircher, M.; Ramzan, F.; Schmitt, A.O.; Gültas, M. Exploring the potential of incremental feature selection to improve genomic prediction accuracy. Genet. Sel. Evol. 2023, 55, 78. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genom. 2021, 22, 19. [Google Scholar] [CrossRef] [PubMed]
- Chachar, Z.; Fan, L.N.; Chachar, S.; Ahmed, N.; Narejo, M.U.N.; Ahmed, N.; Lai, R.Q.; Qi, Y.W. Genetic and Genomic Pathways to Improved Wheat (Triticum aestivum L.) Yields: A Review. Agronomy 2024, 14, 1201. [Google Scholar] [CrossRef]
- Alam, M.; Baenziger, P.S.; Frels, K. Frels, Emerging Trends in Wheat (Triticum spp.) Breeding: Implications for the Future. Front Biosci Elite Ed. 2024, 16, 2. [Google Scholar]
- Wang, K.; Abid, M.A.; Rasheed, A.; Crossa, J.; Hearne, S.; Li, H. DNNGP, a deep neural network-based method for genomic prediction using multi-omics data in plants. Mol. Plant 2023, 16, 279–293. [Google Scholar] [CrossRef]
- Yang, Z.; Song, M.; Huang, X.; Rao, Q.; Zhang, S.; Zhang, Z.; Wang, C.; Li, W.; Qin, R.; Zhao, C.; et al. AdaptiveGS: An explainable genomic selection framework based on adaptive stacking ensemble machine learning. Theor. Appl. Genet. 2025, 138, 204. [Google Scholar] [CrossRef]
- Lozada, D.N.; Ward, B.P.; Carter, A.H. Gains through selection for grain yield in a winter wheat breeding program. PLoS ONE 2020, 15, e0221603. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z. GAPIT Version 3: Boosting Power and Accuracy for Genomic Association and Prediction. Genom. Proteom. Bioinform. 2021, 19, 629–640. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Charmet, G.; Tran, L.G.; Auzanneau, J.; Rincent, R.; Bouchet, S. BWGS: A R package for genomic selection and its application to a wheat breeding programme. PLoS ONE 2020, 15, e0222733. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Ning, C.; Ouyang, H.; Xiao, J.; Wu, D.; Sun, Z.; Liu, B.; Shen, D.; Hong, X.; Lin, C.; Li, J.; et al. Development and validation of an explainable machine learning model for mortality prediction among patients with infected pancreatic necrosis. eClinicalMedicine 2025, 80, 103074. [Google Scholar] [CrossRef]
- Shahi, D.; Guo, J.; Pradhan, S.; Khan, J.; Avci, M.; Khan, N.; McBreen, J.; Bai, G.; Reynolds, M.; Foulkes, J.; et al. Multi-trait genomic prediction using in-season physiological parameters increases prediction accuracy of complex traits in US wheat. BMC Genom. 2022, 23, 298. [Google Scholar] [CrossRef]
- Lell, M.; Gogna, A.; Kloesgen, V.; Avenhaus, U.; Dörnte, J.; Eckhoff, W.M.; Eschholz, T.; Gils, M.; Kirchhoff, M.; Koch, M.; et al. Breaking down data silos across companies to train genome-wide predictions: A feasibility study in wheat. Plant Biotechnol. J. 2025, 23, 2704–2719. [Google Scholar] [CrossRef] [PubMed]
- Meyenberg, C.; Thorwarth, P.; Spiller, M.; Kollers, S.; Reif, J.C.; Longin, C.F.H. Insights into a genomics-based pre-breeding program in wheat. Crop Sci. 2025, 65, e70125. [Google Scholar] [CrossRef]
- Vitale, P.; Montesinos-López, O.; Gerard, G.; Velu, G.; Tadesse, Z.; Montesinos-López, A.; Dreisigacker, S.; Pacheco, A.; Toledo, F.; Saint Pierre, C.; et al. Improving wheat grain yield genomic prediction accuracy using historical data. G3 2025, 15., e70125. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, P.; Wright, E.M.; Cichy, K. GWAS-assisted and multitrait genomic prediction for improvement of seed yield and canning quality traits in a black bean breeding panel. G3 2025, 15, jkaf007. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Zhang, S.; Qiu, S.; Qin, R.; Zhao, C.; Wu, Y.; Sun, H.; Liu, G.; Cui, F. GRE: A Framework for Significant SNP Identification Associated with Wheat Yield Leveraging GWAS–Random Forest Joint Feature Selection and Explainable Machine Learning Genomic Selection Algorithm. Genes 2025, 16, 1125. https://doi.org/10.3390/genes16101125
Song M, Zhang S, Qiu S, Qin R, Zhao C, Wu Y, Sun H, Liu G, Cui F. GRE: A Framework for Significant SNP Identification Associated with Wheat Yield Leveraging GWAS–Random Forest Joint Feature Selection and Explainable Machine Learning Genomic Selection Algorithm. Genes. 2025; 16(10):1125. https://doi.org/10.3390/genes16101125
Chicago/Turabian StyleSong, Mei, Shanghui Zhang, Shijie Qiu, Ran Qin, Chunhua Zhao, Yongzhen Wu, Han Sun, Guangchen Liu, and Fa Cui. 2025. "GRE: A Framework for Significant SNP Identification Associated with Wheat Yield Leveraging GWAS–Random Forest Joint Feature Selection and Explainable Machine Learning Genomic Selection Algorithm" Genes 16, no. 10: 1125. https://doi.org/10.3390/genes16101125
APA StyleSong, M., Zhang, S., Qiu, S., Qin, R., Zhao, C., Wu, Y., Sun, H., Liu, G., & Cui, F. (2025). GRE: A Framework for Significant SNP Identification Associated with Wheat Yield Leveraging GWAS–Random Forest Joint Feature Selection and Explainable Machine Learning Genomic Selection Algorithm. Genes, 16(10), 1125. https://doi.org/10.3390/genes16101125





