Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis
Abstract
:1. Introduction
2. Materials and Methods
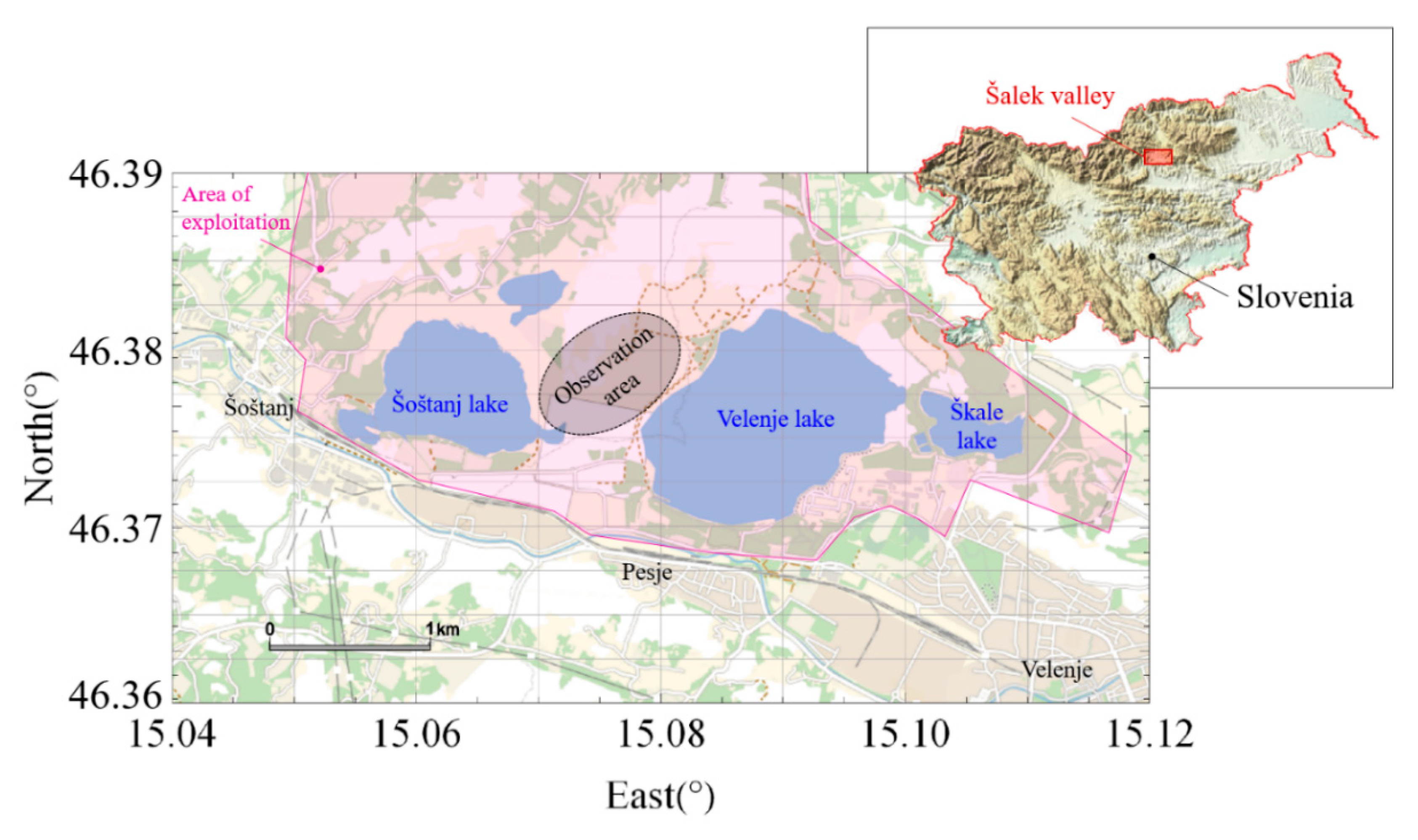
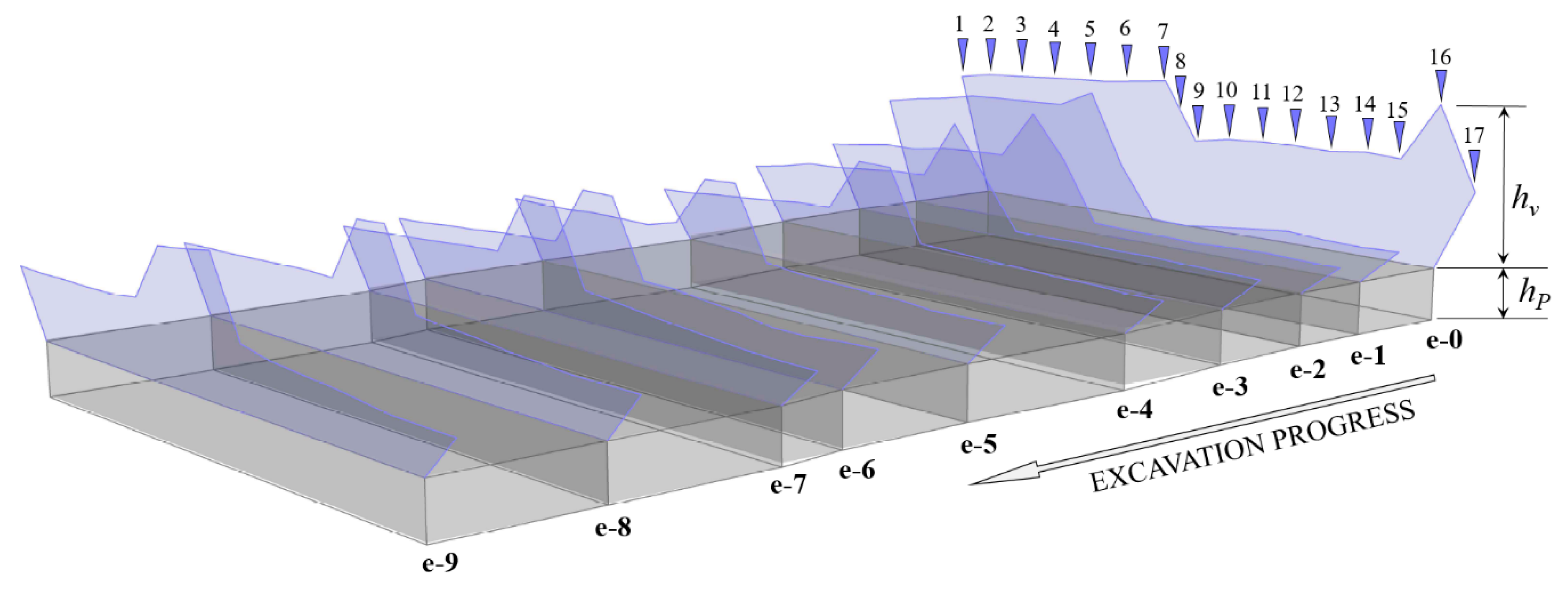
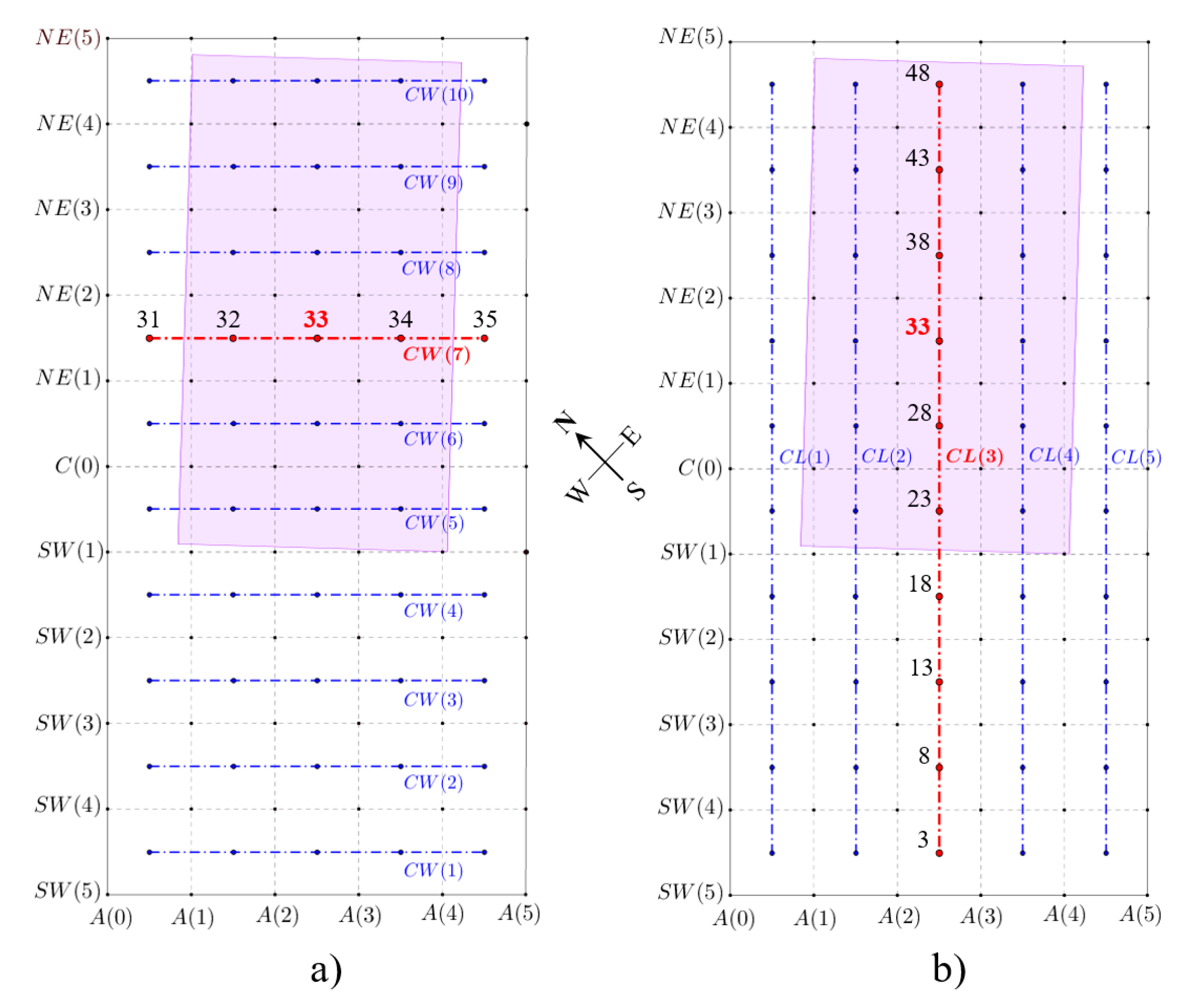
2.1. Observation Area and Monitoring Data
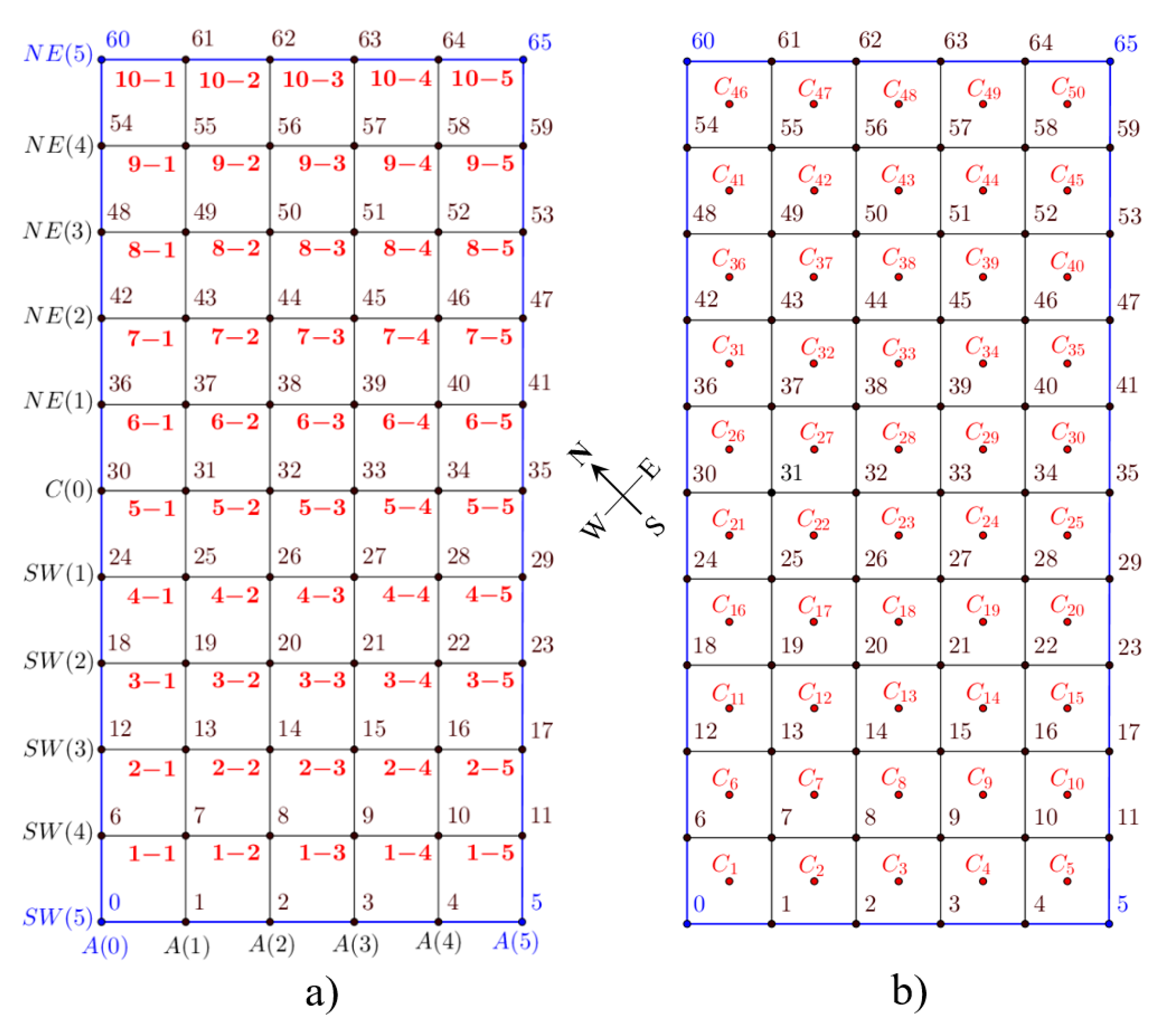
2.2. Sectors Layout and Plane Fitting
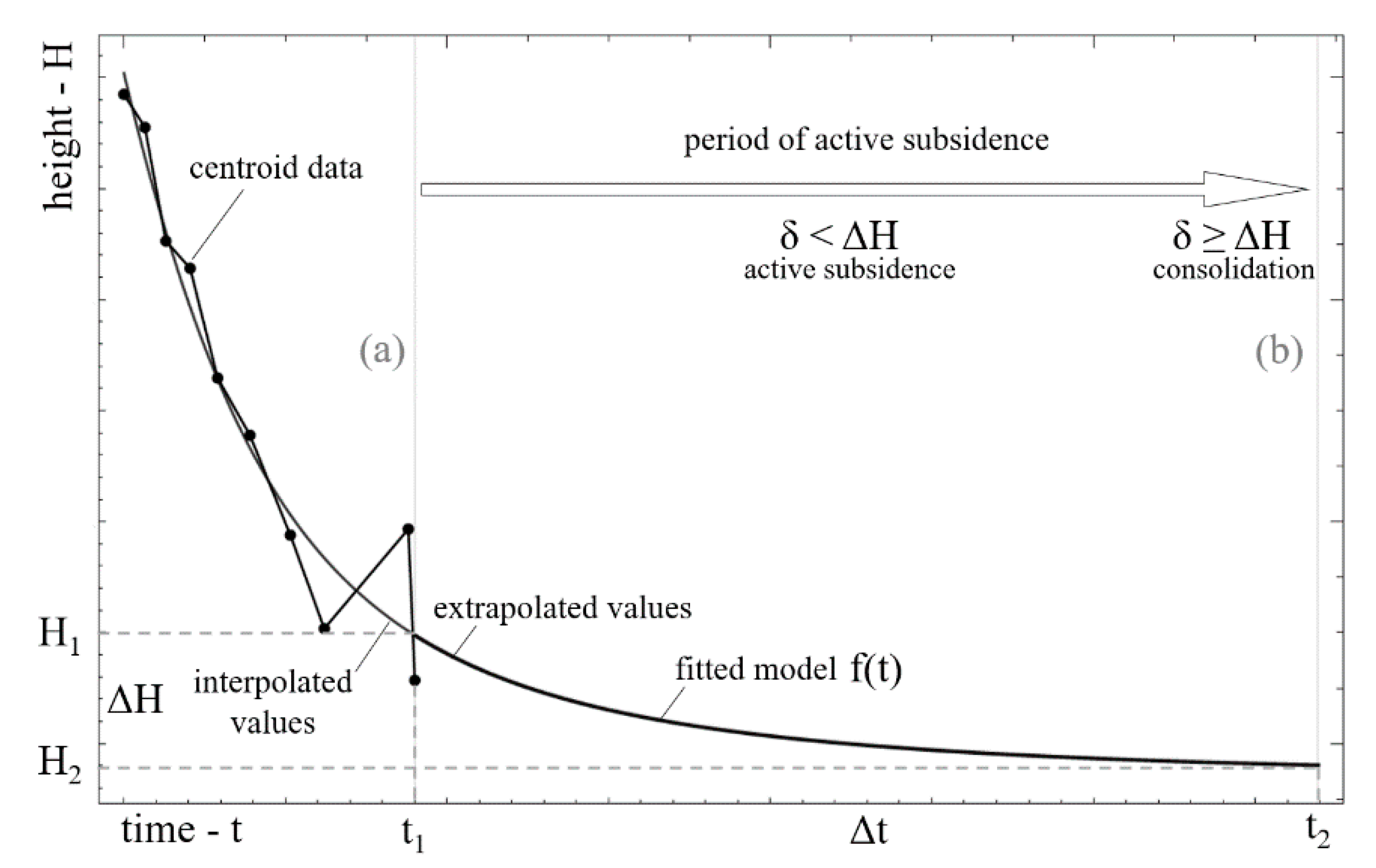
2.3. Overview of the FNSE Theory (Consolidation Prognosis)
2.4. Categorization Method
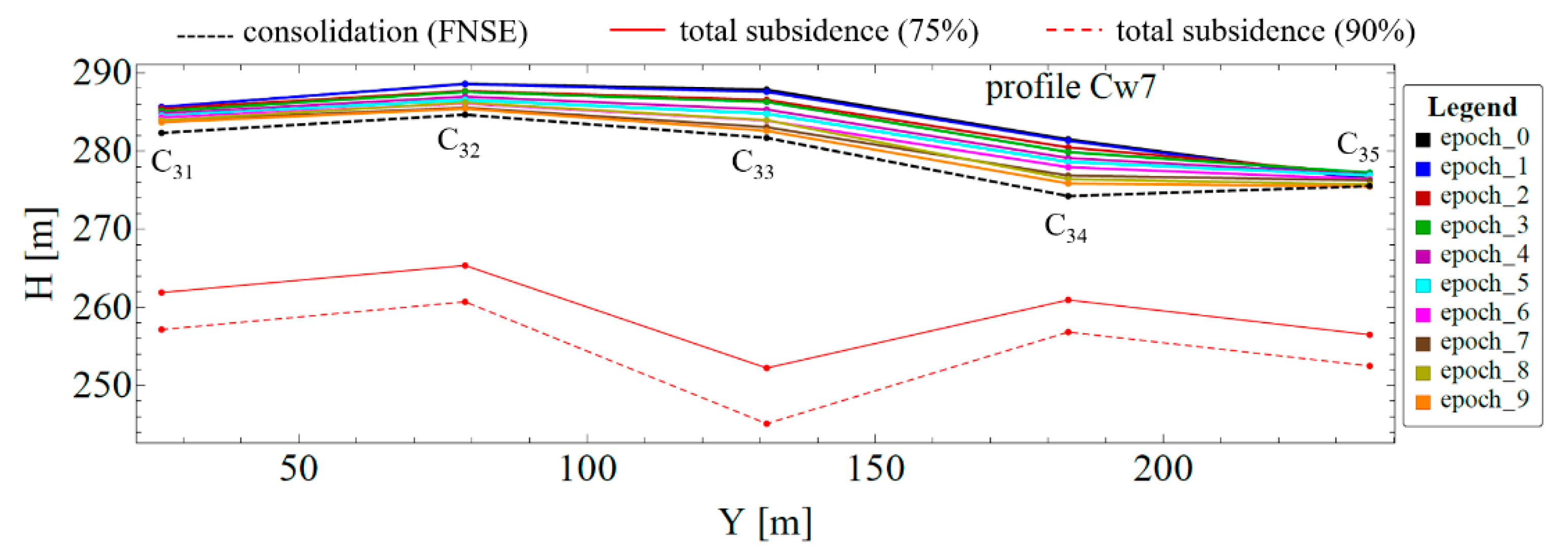
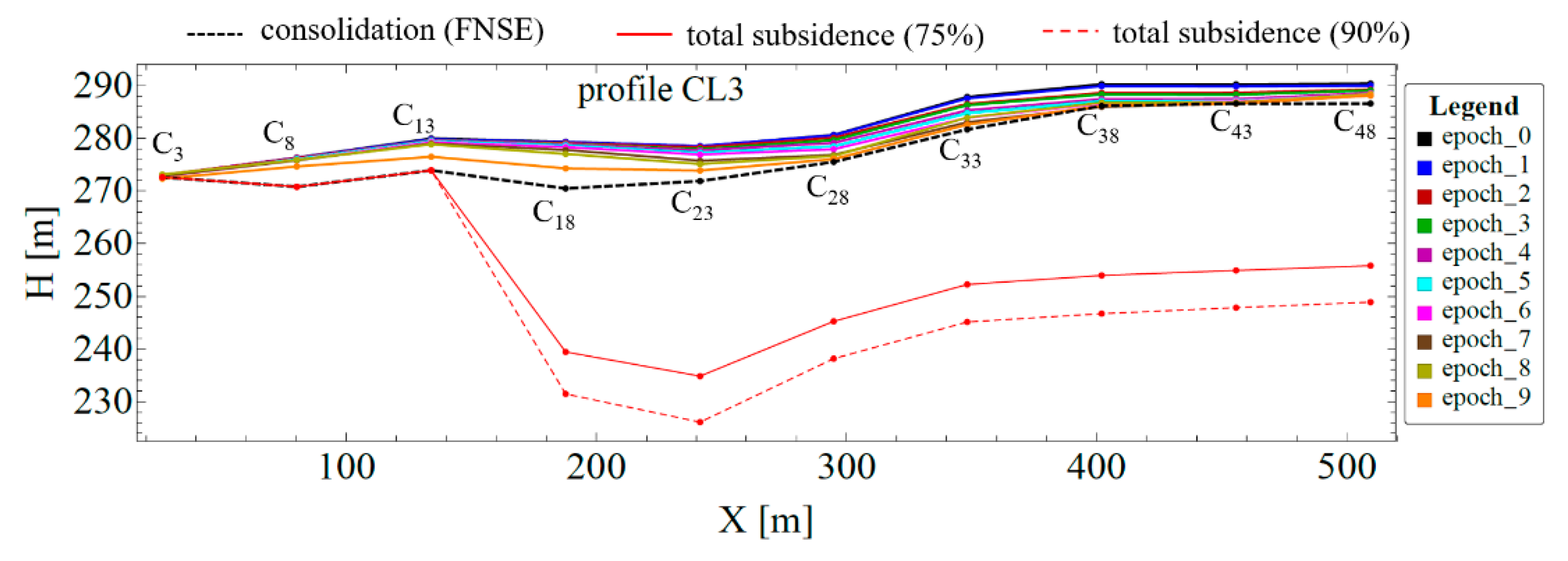
2.5. Final Subsidence Prognosis
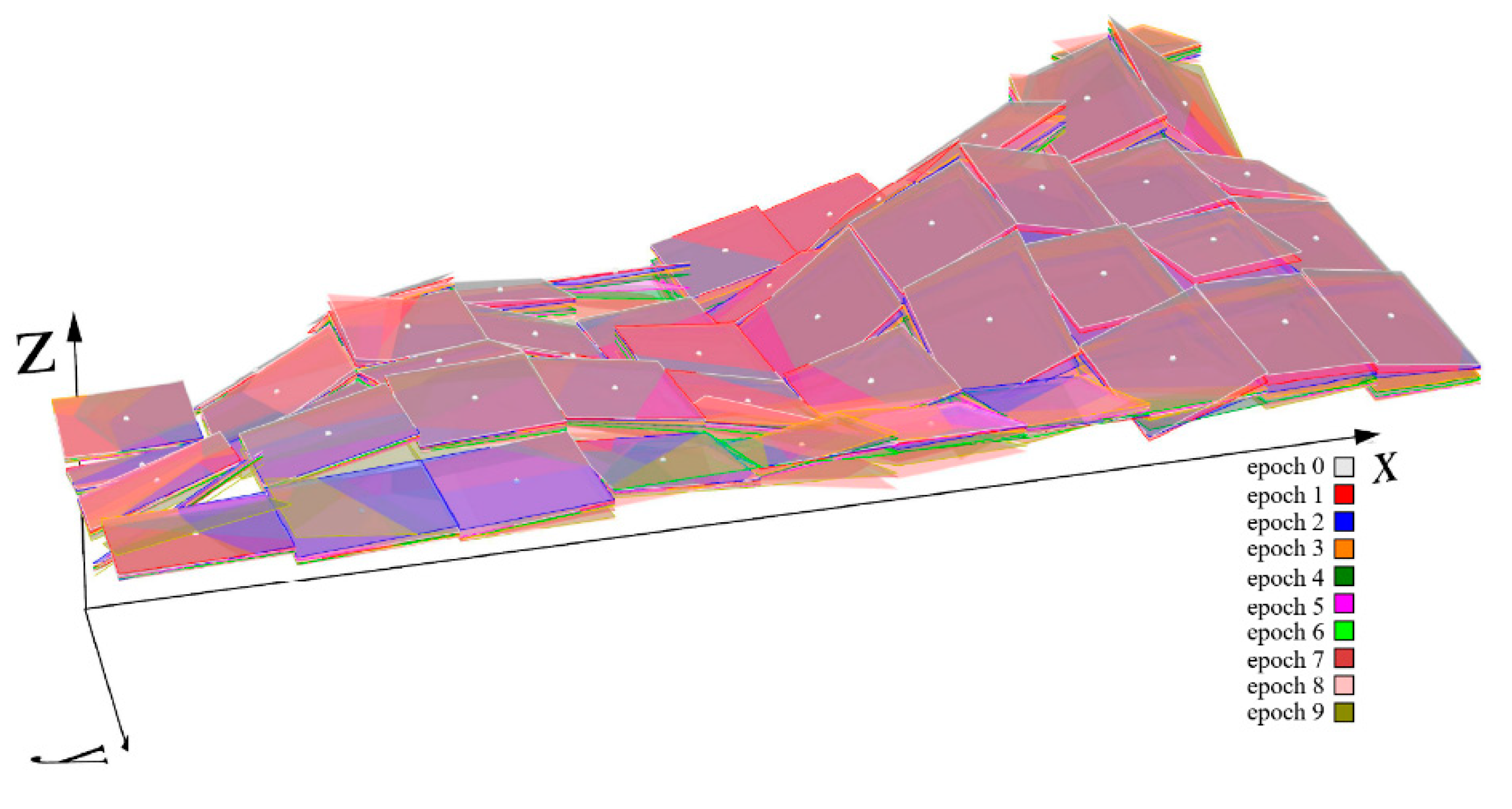
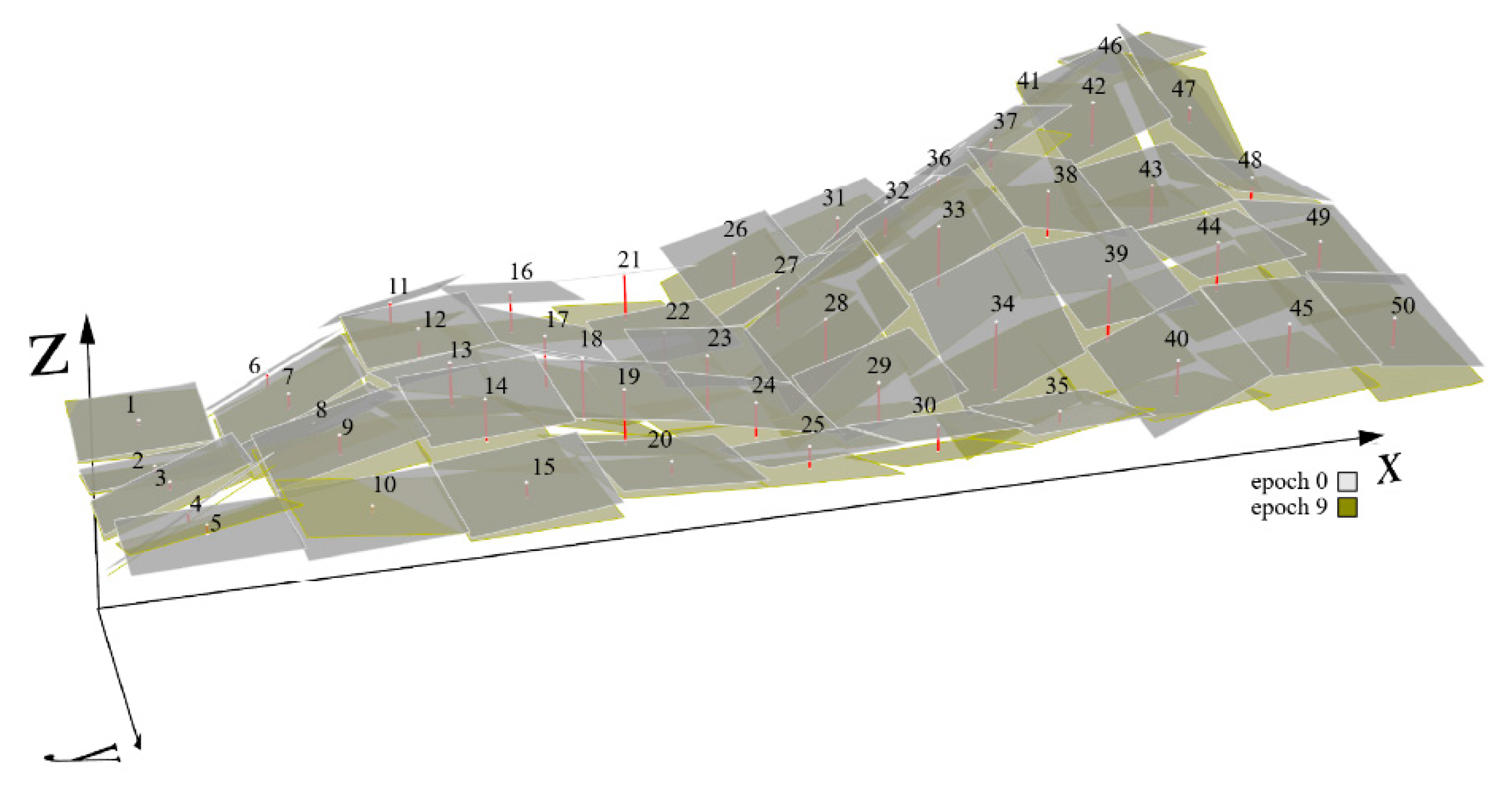
2.6. 3D Point Cloud Analysis
3. Results
3.1. Plane-Fitting Results
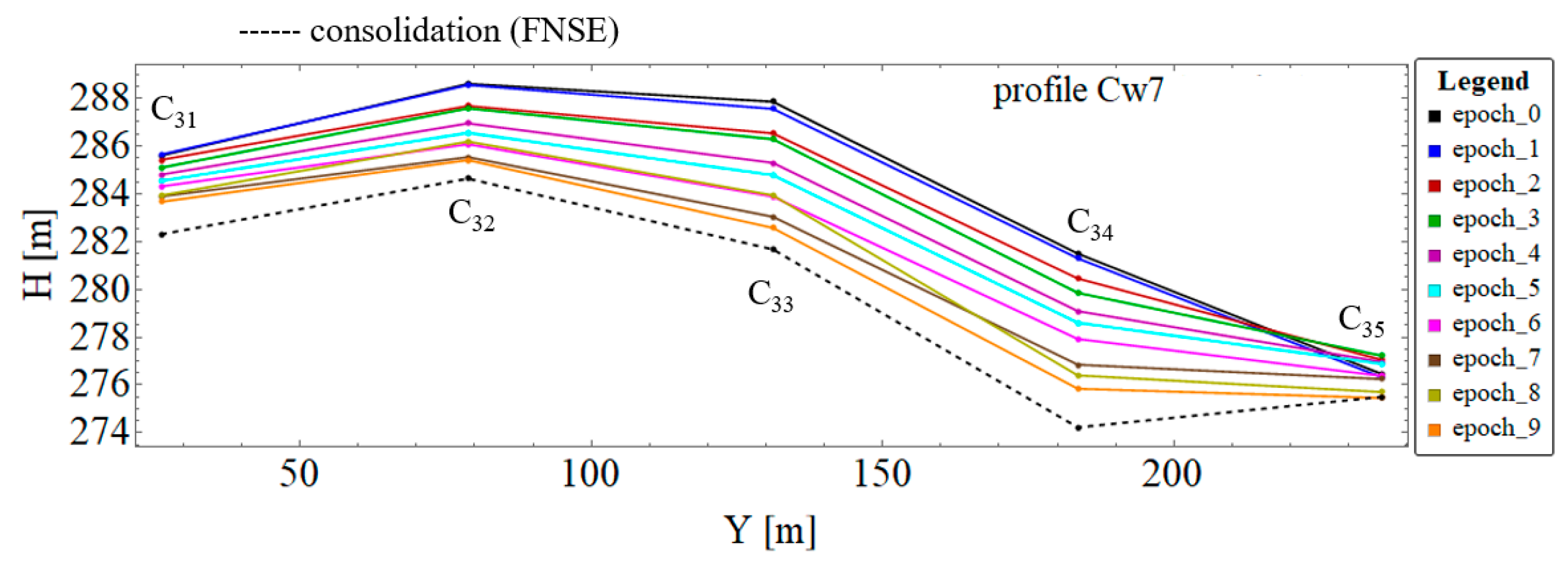
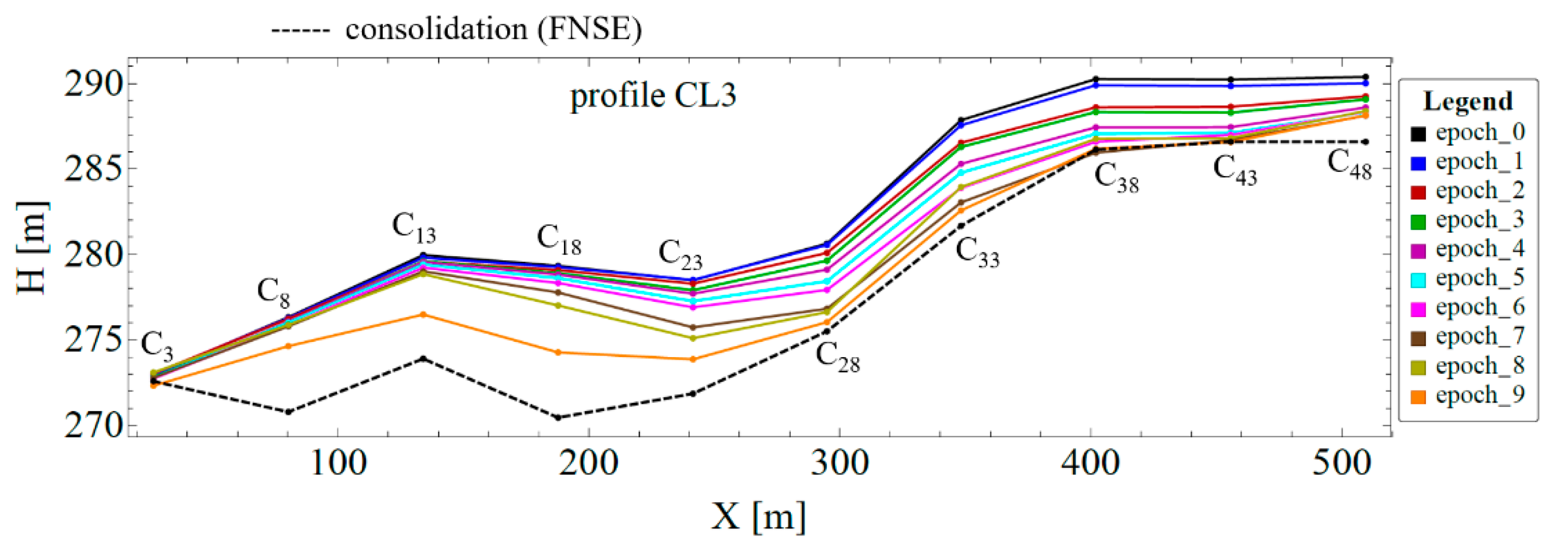
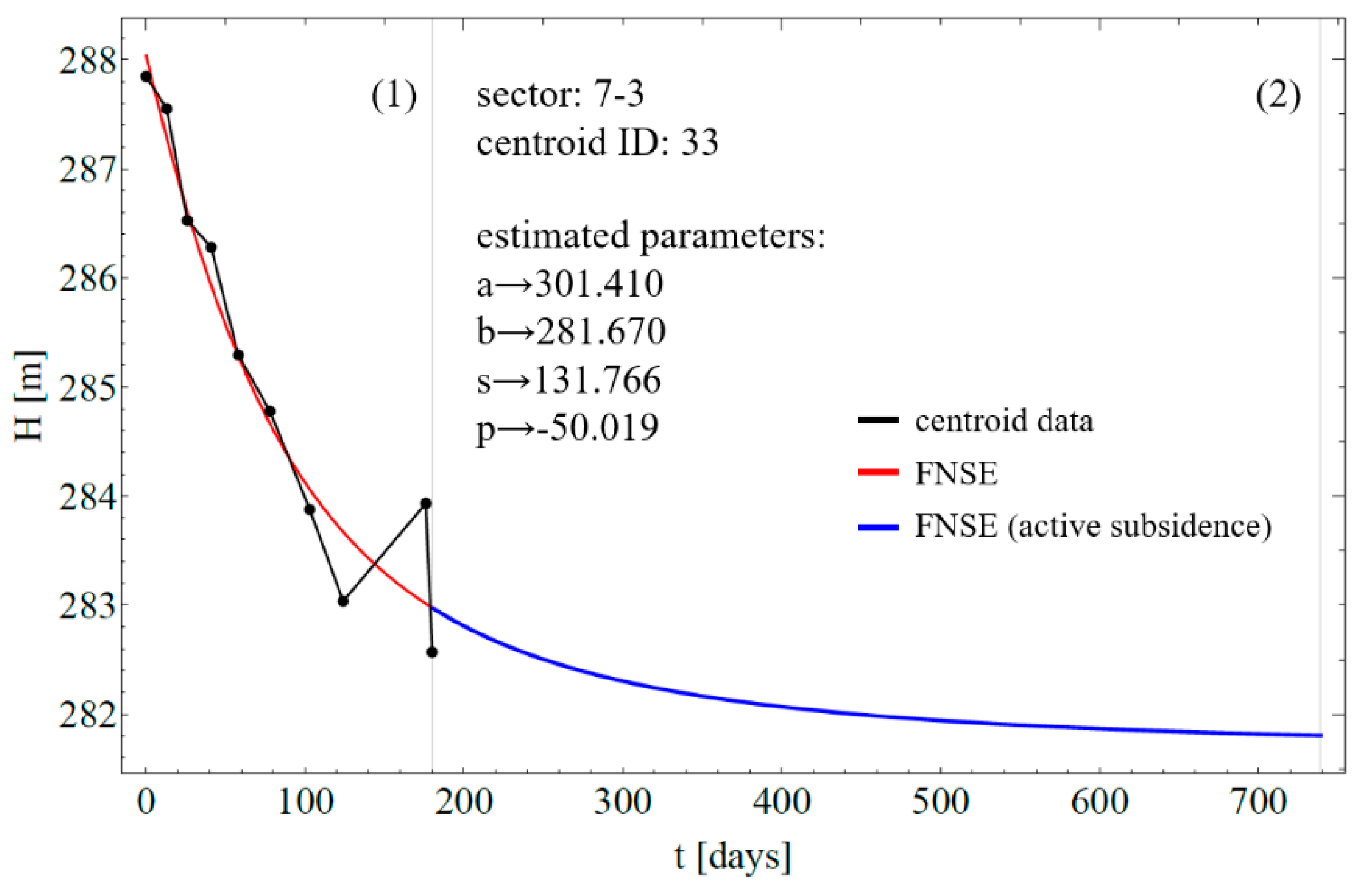
3.2. Prognosis by Profiles
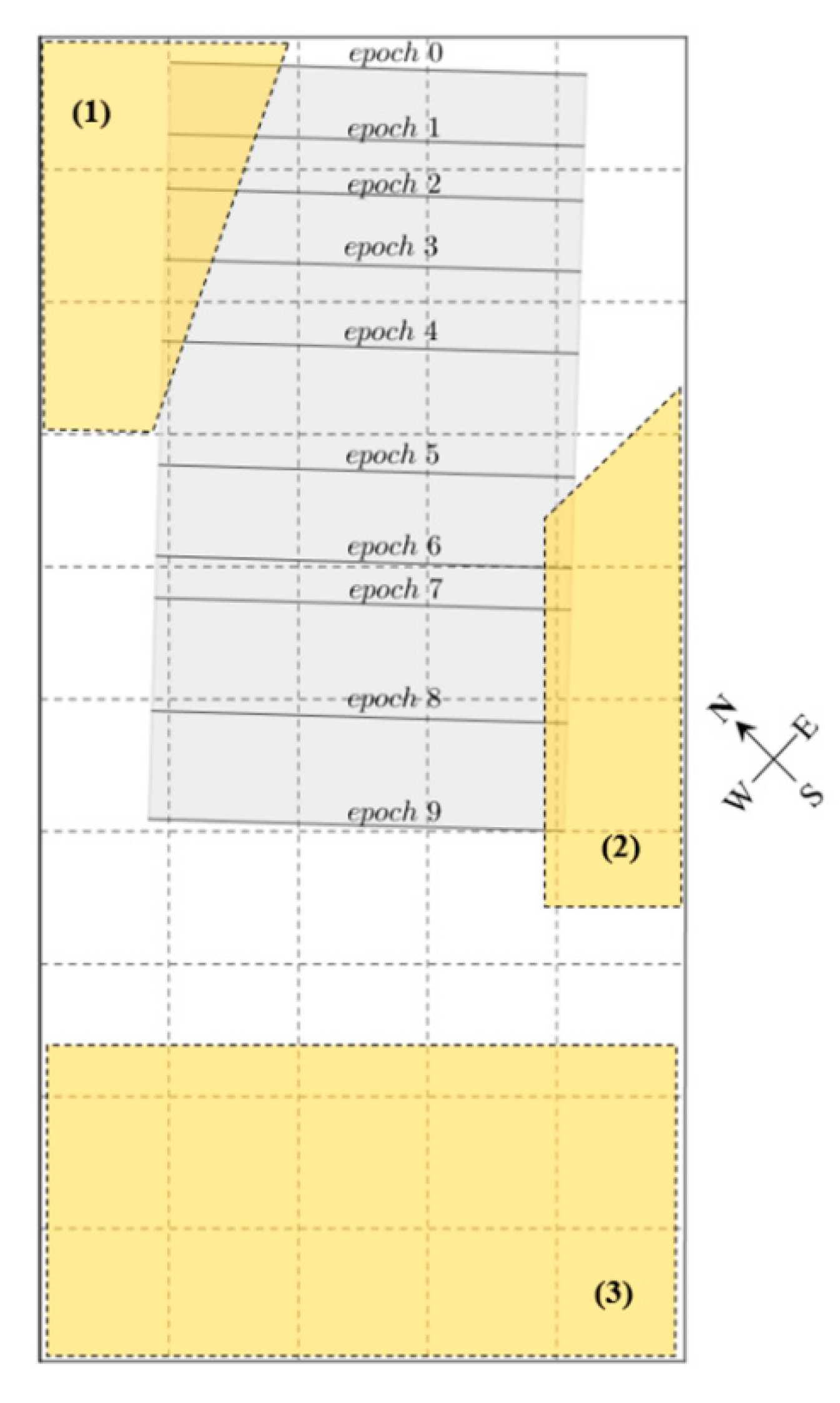
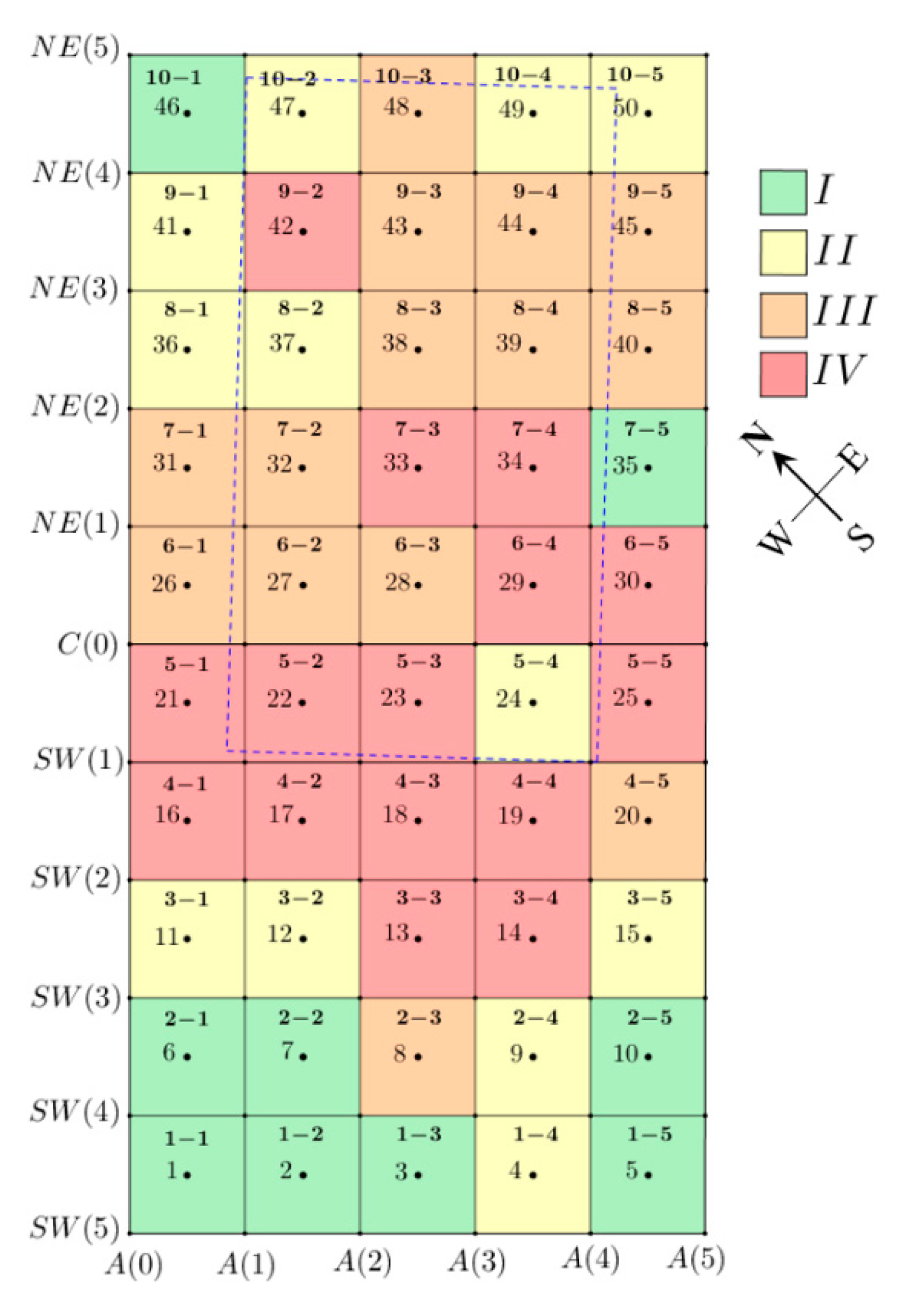
3.3. Terrain Categorization
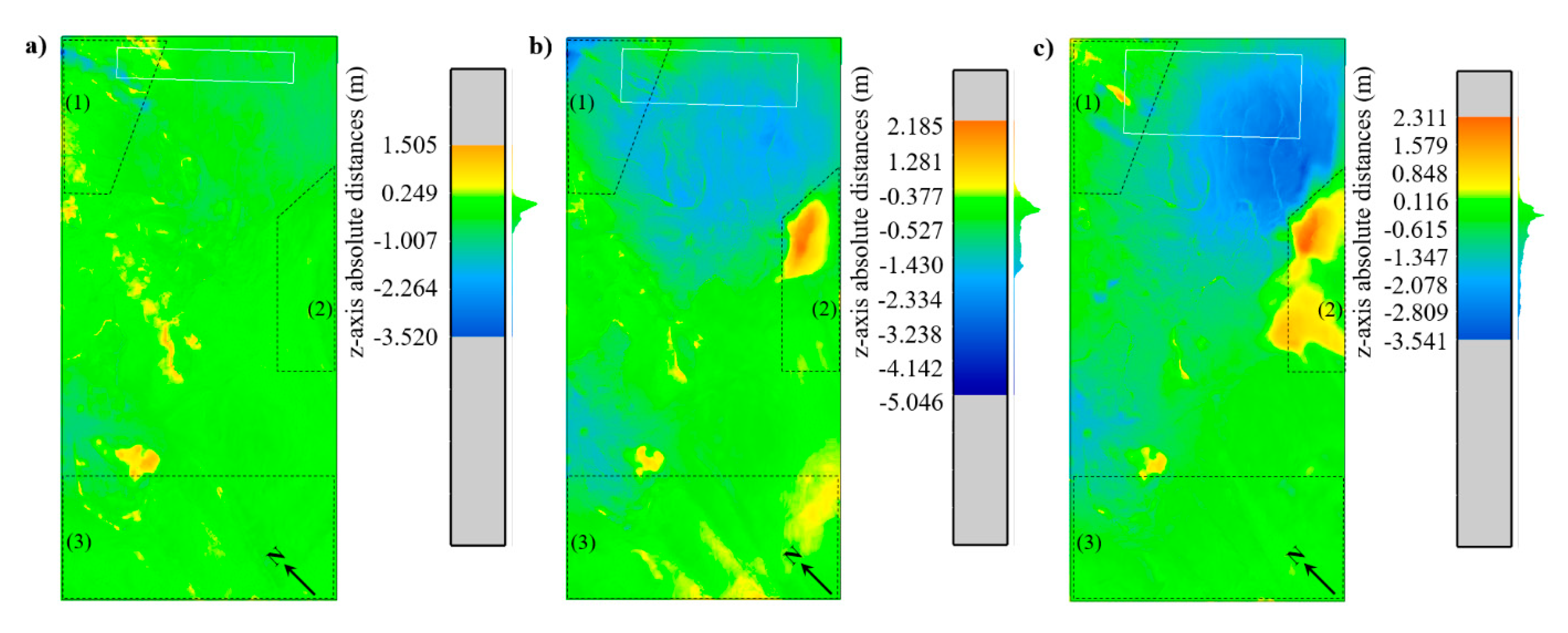
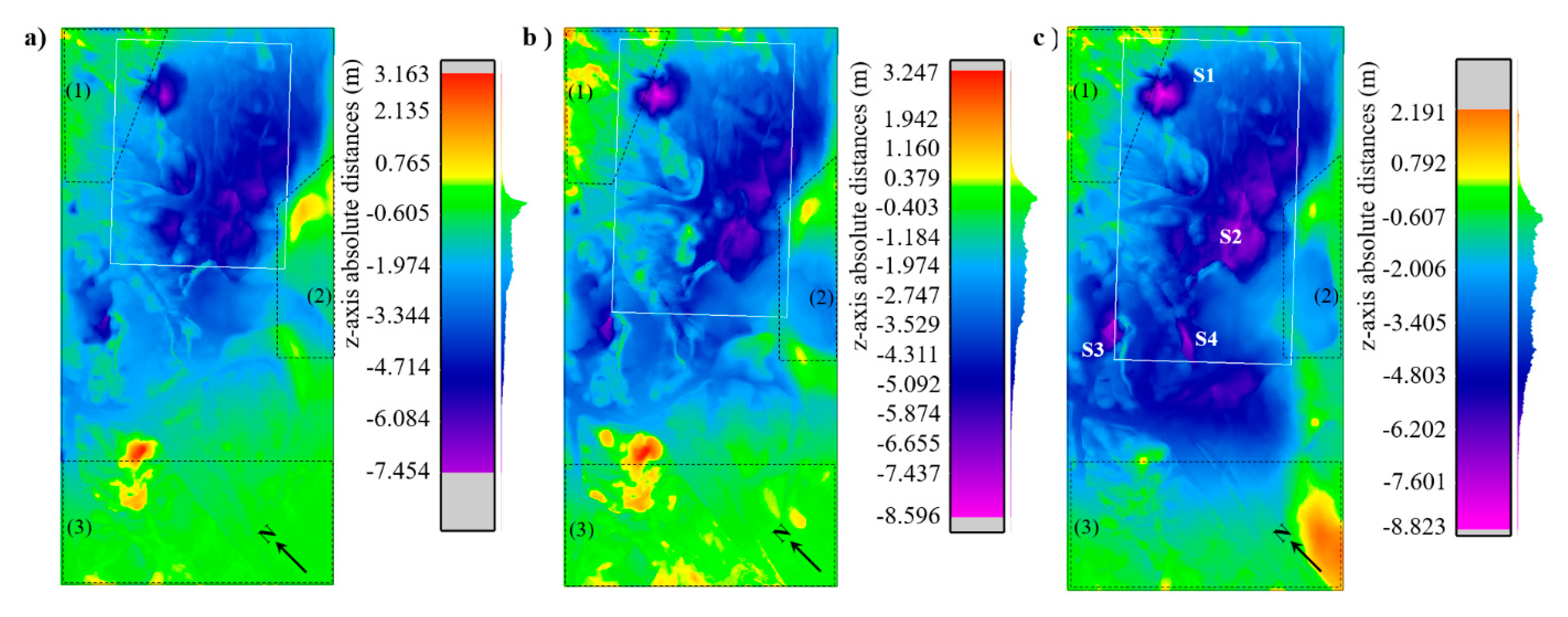
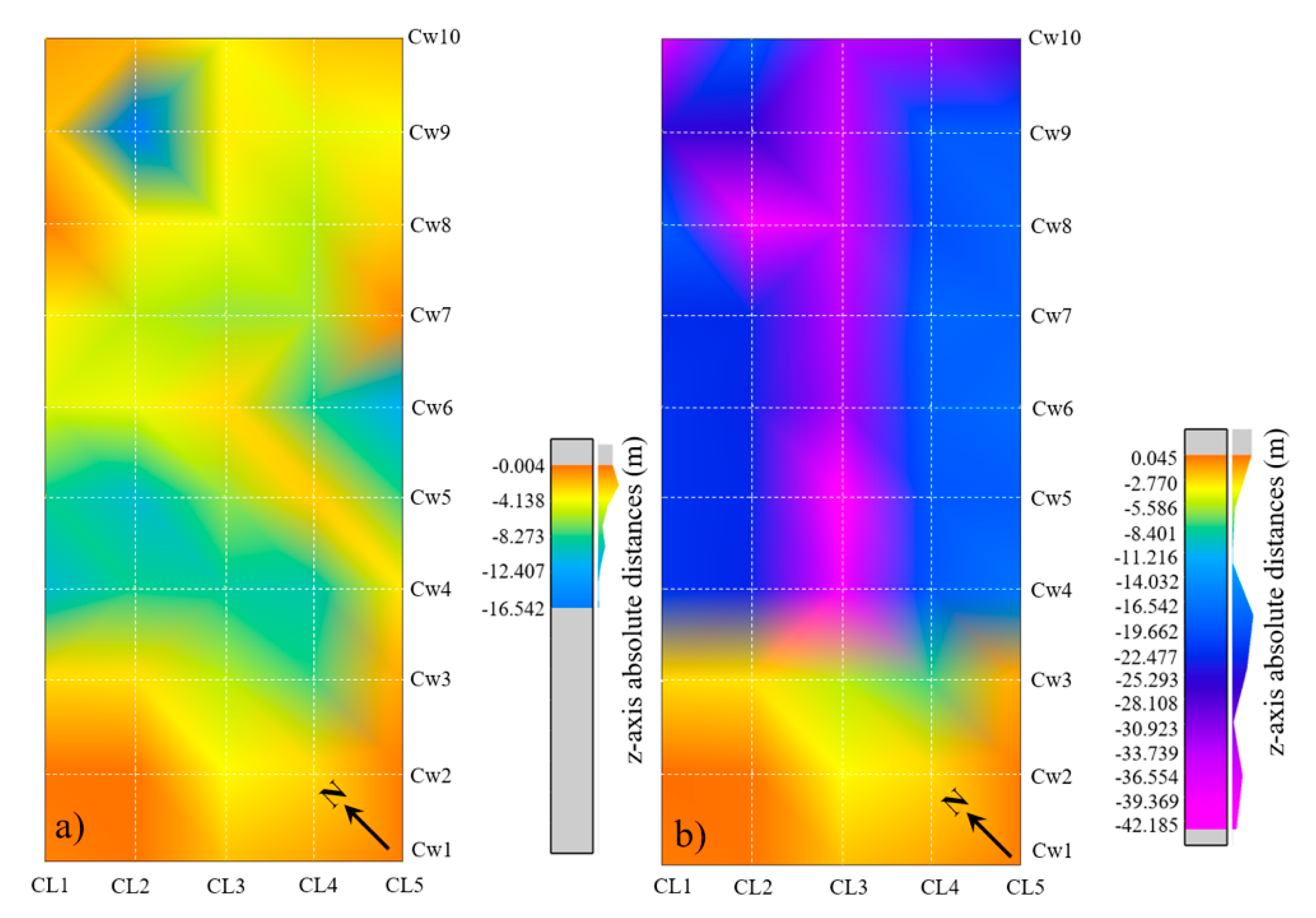
3.4. C2C Analysis of Monitoring Data
4. Discussion
5. Conclusions
- (1)
- Reliable and technically acceptable accurate prognosis of surface subsidence is only possible through concrete monitoring. Due to their special and general importance, prognosis approaches are covered by mining laws and technical regulations, due to broader social or ecological needs, as well as the profession itself.
- (2)
- Inclusion of 3D point clouds in the prediction model means a different and more complete approach to solving the problem of surface subsidence. Dividing bigger 3D point clouds into smaller ones and establishing a sectors layout within the observation area enables plane-fitting to point clouds of each sector. Using centroids, calculated for every plane in all epochs, subsidence prognosis can be applied on any point in the centroid layout. The approach with sectors and centroids enabled control and predictions of the subsidence trough along profiles in the length and width of the excavation.
- (3)
- Use of the FNSE model to predict the time of consolidation and estimate active subsidence value made it possible to produce terrain reclamation categorization based on the layout of sectors in the observational area. This, from the point of view of the practical application, provides the necessary information for the qualitative determination of the intensity and location of the required reclamation of the terrain, which must be maintained to ensure the stability of the observation area (embankment).
- (4)
- Considering that the actual excavation height of a point represents the maximum subsidence of that same point on the surface above excavation, the initial heights of the centroids can be adjusted for this value. Reducing initial heights determined total subsidence that will occur in a longer period, after excavation operations come to a stop.
- (5)
- A spatial representation of the distribution of centroids, when consolidation has been achieved or total subsidence have occurred, gives comprehensive information on the predicted subsidence trough, both in geometric and value terms. Giving an insight into the consolidated and final state of the terrain, the reclamation can be suitably adapted to the expected volume loss. A C2C analysis of the predicted consolidation values and the determined one-year centroid height values, gave an approximation of volume loss of the order of 733.825 m3.
- (6)
- Comparing actual 3D point clouds, obtained from monitoring, provides a method for quantifying occurred subsidence and terrain elevations between two epochs. Verification of terrain height changes by epochs, when initial cloud in the reference of comparison, lead to identification of subsidence, terrain reclamation areas, and sinking holes. The C2C analysis was conducted in CloudCompare 2.9.1 and overlapped with records of intense reclamation areas and excavation progress drawings.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, J.; Tian, C.; Xing, L.; Bian, Z.; Miao, X. Green and sustainable mining: Underground coal mine fully mechanized solid dense stowing-mining method. Sustainability 2017, 9, 1418. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Guo, G.; Liu, H.; Yang, X. Surface subsidence prediction method of backfill-strip mining in coal mining. Bull. Eng. Geol. Environ. 2019, 78, 6235–6248. [Google Scholar] [CrossRef]
- Can, E.; Kuşcu, T.; Mekik, C. Determination of underground mining induced displacements using GPS observations in Zonguldak-Kozlu Hard Coal Basin. Int. J. Coal Geol. 2012, 89, 62–69. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Tang, Y.; Zhang, H.; Fu, Q. Analysis of ground subsidence at a coal-mining area in Huainan using time-series InSAR. Int. J. Remote Sens. 2015, 36, 5790–5810. [Google Scholar] [CrossRef]
- Kratzsch, H.A. Mining Subsidence Engineering; Springer: Berlin, Germany, 2007. [Google Scholar]
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurence, Prediction and Control; Elsevier: Amsterdam, The Netherland, 1989. [Google Scholar]
- Ren, F.; Zhang, D.; Cao, J.; Yu, M.; Li, S. Study on the Rock Mass Caving and Surface Subsidence Mechanism Based on an in Situ Geological Investigation and Numerical Analysis. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Bell, F.G.; Stacey, T.R.; Genske, D.D. Mining subsidence and its effect in the environment: Some differing examples. Environ. Geol. 2000, 40, 135–152. [Google Scholar] [CrossRef]
- Li, L.; Wu, K.; Zhou, D.W. AutoCAD-based prediction of 3D dynamic ground movement for underground coal mining. Int. J. Rock Mech. Min. Sci. 2014, 71, 194–203. [Google Scholar] [CrossRef]
- Luo, Y. Systematic approach to assess and mitigate longwall subsidence influences on surface structures. J. Coal Sci. Eng. 2008, 14, 407–414. [Google Scholar] [CrossRef]
- Yan, W.; Chen, J.; Yan, Y. A new model for predicting surface mining subsidence: The improved lognormal function model. Geosci. J. 2019, 23, 165–174. [Google Scholar] [CrossRef]
- Lian, X.G.; Jarosz, A.; Saavedra-Rosas, J.; Dai, H.-Y. Extending dynamic models of mining subsidence. Trans. Nonferr. Met. Soc. China 2011, 21 (Suppl. 3), s536–s542. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B. Mine subsidence investigations over a longwall working and the prediction of subsidence parameters for Indian mines. Int. J. Rock Mech. Min. Sci. 1973, 10, 151–172. [Google Scholar] [CrossRef]
- Bahuguna, P.P.; Srivastava, A.M.C.; Saxena, N.C. A critical review of mine subsidence prediction methods. Min. Sci. Technol. 1991, 13, 369–382. [Google Scholar] [CrossRef]
- Asadi, A.; Shahriar, K.; Goshtasbi, K.; Najm, K. Development of a new mathematical model for prediction of surface subsidence due to inclined coal-seam mining. J. S. Afr. Inst. Min. Metall. 2005, 105, 15–20. [Google Scholar]
- Medved, M. Prispevek k Poznavanju Degradacije Okolja Pri Jamskem Pridobivanju Debelih Slojev Premoga. Ph.D. Thesis, Faculty of Natural Sciences and Engineering, Ljubljana, Slovenia, 1994. [Google Scholar]
- Sheorey, P.R.; Loui, J.P.; Singh, K.B.; Singh, S.K. Ground subsidence observations and a modified influence function method for complete subsidence prediction. Int. J. Rock Mech. Min. Sci. 2000, 37, 801–818. [Google Scholar] [CrossRef]
- Luo, Y.; Cheng, J.W. An influence function method based subsidence prediction program for longwall mining operations in inclined coal seams. Min. Sci. Technol. 2009, 19, 592–598. [Google Scholar] [CrossRef]
- Ren, G.; Whittaker, B.N.; Reddish, D.J. Mining subsidence and displacement prediction using influence function methods for steep seams. Min. Sci. Technol. 1989, 8, 235–251. [Google Scholar] [CrossRef]
- Polanin, P. Application of two parameter groups of the Knothe–Budryk theory in subsidence prediction. J. Sustain. Min. 2015, 14, 67–75. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Xu, J.; Wang, F.; Wang, F. Movement boundary shape of overburden strata and its influencing factors. Energies 2018, 11, 742. [Google Scholar] [CrossRef] [Green Version]
- Ghabraie, B.; Ren, G.; Barbato, J.; Smith, J.V. A predictive methodology for multi-seam mining induced subsidence. International J. Rock Mech. Min. Sci. 2017, 93, 280–294. [Google Scholar] [CrossRef]
- Jeromel, G.; Medved, M.; Likar, J. An analysis of the geomechanical processes in coal mining using the velenje mining method. Acta Geotech. Slov. 2010, 7, 31–45. [Google Scholar]
- Likar, J.; Medved, M.; Lenart, M.; Mayer, J.; Malenković, V.; Jeromel, G.; Dervarič, E. Analysis of geomechanical changes in hanging wall caused by longwall multi top caving in coal mining. J. Min. Sci. 2012, 48, 135–145. [Google Scholar] [CrossRef]
- Wesołowski, M. Numerical modeling of exploitation relics and faults influence on rock mass deformations. Arch. Min. Sci. 2016, 61, 893–906. [Google Scholar] [CrossRef] [Green Version]
- Sikora, P. Simulation of rock mass horizontal displacements with usage of cellular automata theory. Arch. Min. Sci. 2016, 61, 749–763. [Google Scholar] [CrossRef] [Green Version]
- Orwat, J.; Mielimąka, R. Average course approximation of measured subsidence and inclinations of mining area by smooth splines. J. Sustain. Min. 2017, 16, 8–13. [Google Scholar] [CrossRef]
- Thongprapha, T.; Fuenkajorn, K.; Daemen, J.J.K. Study of surface subsidence above an underground opening using a trap door apparatus. Tunn. Undergr. Space Technol. 2015, 46, 94–103. [Google Scholar] [CrossRef]
- Ghabraie, B.; Ren, G.; Smith, J.V. Characterising the multi-seam subsidence due to varying mining configuration, insights from physical modelling. Int. J. Rock Mech. Min. Sci. 2017, 93, 269–279. [Google Scholar] [CrossRef]
- Brezigar, A. Premogova plast Rudnika lignita Velenje/Coal seam of the Velenje coal mine. Geologija 1985, 28, 319. [Google Scholar]
- Dsurvey. Available online: https://www.3dsurvey.si/ (accessed on 15 January 2020).
- Vulić, M. Optimalna Ravnina Oblaka Točk; Internal Mine Surveying Lecture Series; University of Ljubljana, Faculty of Natural Sciences and Engineering: Ljubljana, Slovenia, 2017. [Google Scholar]
- Rošer, J.; Potočnik, D.; Vulić, M. Analysis of dynamic surface subsidence at the underground coal mining site in Velenje, Slovenia through modified sigmoidal function. Minerals 2018, 8, 74. [Google Scholar] [CrossRef] [Green Version]
- Vulić, M. Sigmoidna Funckija; Internal Mine Surveying Lecture Series; University of Ljubljana, Faculty of Natural Sciences and Engineering: Ljubljana, Slovenia, 2013. [Google Scholar]
- Hayter, J.A. Probability and Statistics for Engineers and Scientists, 4th ed.; Brooks/Cole: Boston, MA, USA, 2013. [Google Scholar]





| Epoch | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| x (m) | −0.0035 | 0.0025 | −0.0007 | 0.0023 | −0.0008 | −0.0007 | 0.0011 | −0.0001 | 0.0017 | −0.0013 |
| y (m) | −0.0045 | 0.0011 | −0.0004 | −0.0011 | 0.0002 | −0.0017 | 0.0009 | −0.0019 | −0.0023 | −0.0043 |
| z (m) | −0.0002 | 0.0010 | 0.0044 | −0.0078 | −0.0033 | 0.0000 | −0.0040 | −0.0063 | −0.0280 | −0.0111 |
| Epoch | Point ID | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| Total Excavation Height (m) | |||||||||||||||||
| 0 | 33.8 | 35.5 | 36.0 | 36.7 | 37.3 | 37.8 | 38.9 | 40.1 | 24.3 | 26.0 | 26.6 | 26.8 | 26.6 | 27.7 | 27.2 | 42.6 | 21.3 |
| 1 | 28.8 | 30.5 | 31.8 | 33.6 | 34.0 | 34.3 | 34.7 | 39.0 | 20.1 | 6.9 | 6.7 | 7.8 | 8.9 | 9.9 | 9.1 | 8.9 | 9.3 |
| 2 | 17.9 | 19.0 | 20.2 | 20.3 | 21.8 | 22.3 | 22.6 | 35.1 | 23.9 | 8.3 | 8.0 | 8.0 | 7.6 | 8.1 | 8.4 | 8.1 | 7.9 |
| 3 | 14.7 | 16.1 | 18.1 | 18.4 | 19.3 | 20.1 | 20.4 | 35.5 | 22.5 | 9.8 | 9.6 | 9.8 | 9.6 | 9.7 | 9.4 | 9.1 | 9.0 |
| 4 | 12.8 | 13.3 | 14.2 | 14.8 | 15.6 | 16.5 | 16.7 | 30.2 | 30.0 | 11.7 | 11.4 | 11.0 | 10.7 | 10.2 | 10.2 | 9.7 | 9.6 |
| 5 | 15.5 | 15.5 | 15.5 | 16.1 | 16.1 | 16.1 | 18.2 | 30.5 | 31.0 | 13.0 | 11.9 | 11.6 | 11.3 | 11.0 | 10.2 | 10.4 | 10.5 |
| 6 | 14.5 | 15.0 | 15.8 | 16.3 | 17.2 | 17.6 | 18.1 | 32.2 | 32.2 | 13.4 | 13.3 | 12.2 | 11.4 | 9.8 | 9.7 | 10.5 | 10.8 |
| 7 | 15.4 | 15.8 | 16.5 | 16.9 | 17.5 | 18.2 | 18.7 | 33.7 | 33.8 | 14.4 | 13.3 | 12.4 | 11.5 | 10.7 | 10.0 | 9.7 | 9.6 |
| 8 | 16.7 | 17.1 | 17.3 | 17.7 | 18.1 | 18.4 | 18.2 | 33.5 | 34.1 | 15.0 | 14.2 | 13.7 | 12.8 | 12.4 | 11.8 | 11.8 | 11.8 |
| 9 | 16.6 | 16.7 | 16.4 | 16.7 | 17 | 17.9 | 31.3 | 32.3 | 33.6 | 15.0 | 13.5 | 12.9 | 12.3 | 11.5 | 10.5 | 10.4 | 10.4 |
| Epoch | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Date (2017) | 2 Feb | 15 Feb | 1 Mar | 15 Mar | 1 Apr | 21 Apr | 16 May | 2 Jun | 28 Jun | 1 Aug |
| t (days) | 0 | 13 | 27 | 41 | 58 | 78 | 103 | 120 | 146 | 180 |
| L (m) | 0.0 | 29 | 51.1 | 79.8 | 112.9 | 163 | 199.9 | 216.8 | 262.6 | 306.4 |
| Epoch | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Centroid ID | Height (m) | |||||||||
| 3 | 272.942 | 272.975 | 273.032 | 272.825 | 272.767 | 272.765 | 272.735 | 272.779 | 273.093 | 272.324 |
| 8 | 276.326 | 276.273 | 276.230 | 276.033 | 276.057 | 276.015 | 275.863 | 275.793 | 275.886 | 274.635 |
| 13 | 279.961 | 279.807 | 279.594 | 279.610 | 279.557 | 279.413 | 279.227 | 279.012 | 278.845 | 276.483 |
| 18 | 279.330 | 279.255 | 279.078 | 278.901 | 278.821 | 278.614 | 278.327 | 277.773 | 277.015 | 274.269 |
| 23 | 278.483 | 278.506 | 278.287 | 277.904 | 277.701 | 277.264 | 276.904 | 275.731 | 275.101 | 273.866 |
| 28 | 280.632 | 280.549 | 280.088 | 279.633 | 279.110 | 278.433 | 277.924 | 276.824 | 276.628 | 276.038 |
| 31 | 285.594 | 285.638 | 285.416 | 285.089 | 284.796 | 284.538 | 284.306 | 283.884 | 283.928 | 283.662 |
| 32 | 288.598 | 288.547 | 287.672 | 287.572 | 286.945 | 286.544 | 286.071 | 285.531 | 286.180 | 285.405 |
| 33 | 287.849 | 287.551 | 286.527 | 286.281 | 285.292 | 284.777 | 283.877 | 283.036 | 283.932 | 282.570 |
| 34 | 281.491 | 281.294 | 280.451 | 279.850 | 279.088 | 278.600 | 277.920 | 276.846 | 276.397 | 275.839 |
| 35 | 276.440 | 276.301 | 277.036 | 277.212 | 276.958 | 276.879 | 276.374 | 276.242 | 275.699 | 275.451 |
| 38 | 290.253 | 289.890 | 288.601 | 288.327 | 287.431 | 287.049 | 286.587 | 285.943 | 286.752 | 286.172 |
| 43 | 290.219 | 289.845 | 288.634 | 288.287 | 287.440 | 287.110 | 286.990 | 286.691 | 286.802 | 286.570 |
| 48 | 290.378 | 290.004 | 289.243 | 289.066 | 288.590 | 288.305 | 288.341 | 288.111 | 288.385 | 288.132 |
| Category | ΔH (m) | Necessary Measures |
|---|---|---|
| I | ≤1 | none |
| II | ≤3 | terrain reclamation needed |
| III | ≤6 | intense terrain reclamation needed |
| IV | >6 | intense terrain reclamation needed and a chance for sinkhole occurrence |
| Centroid ID | Initial Epoch | Consolidation | Final Subsidence (75%) | Final Subsidence (90%) |
|---|---|---|---|---|
| (/) | H (m) | H (m) | H (m) | H (m) |
| 3 | 272.942 | 272.584 | 272.584 | 272.584 |
| 8 | 276.326 | 270.787 | 270.787 | 270.787 |
| 13 | 279.961 | 273.898 | 273.898 | 273.898 |
| 18 | 279.330 | 270.455 | 239.430 | 231.450 |
| 23 | 278.483 | 271.858 | 234.833 | 226.103 |
| 28 | 280.632 | 275.504 | 245.232 | 238.152 |
| 31 | 285.594 | 282.304 | 261.894 | 257.154 |
| 32 | 288.598 | 284.631 | 265.348 | 260.698 |
| 33 | 287.849 | 281.670 | 252.234 | 245.111 |
| 34 | 281.491 | 274.223 | 260.941 | 256.831 |
| 35 | 276.440 | 275.504 | 256.490 | 252.500 |
| 38 | 290.253 | 286.136 | 253.953 | 246.693 |
| 43 | 290.219 | 286.582 | 254.894 | 247.829 |
| 48 | 290.378 | 286.582 | 255.803 | 248.888 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, A.; Rošer, J.; Vulić, M. Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis. Minerals 2020, 10, 82. https://doi.org/10.3390/min10010082
Pal A, Rošer J, Vulić M. Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis. Minerals. 2020; 10(1):82. https://doi.org/10.3390/min10010082
Chicago/Turabian StylePal, Andrej, Janez Rošer, and Milivoj Vulić. 2020. "Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis" Minerals 10, no. 1: 82. https://doi.org/10.3390/min10010082
APA StylePal, A., Rošer, J., & Vulić, M. (2020). Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis. Minerals, 10(1), 82. https://doi.org/10.3390/min10010082





