A New Ore Grade Estimation Using Combine Machine Learning Algorithms
Abstract
1. Introduction
2. Data Attributes and Preparation
- Step 1. Creating a composite data: Raw data comes from 123 drill holes were composited in 1 m length, which is equal to the average sample length in one run. Table 1 presents the descriptive statistics of the composite dataset.
- Step 2. Data pre-processing: Each sample is described by five attributes including coordinates (easting, northing, and altitude), rock type, and alteration level. The original raw data contains 25 different rock types and 5 different alteration types. To generalise the geological distribution, we combined similar lithologies to reduce the original rock type to 10 and used only level of argillic alteration (a0, a1, ..., a4) that shows the high correlation with gold grade.
- Step 3. Transformation of the categorical data into numerical values: Neural Network (NN) algorithm performs numerical calculations; therefore, it can only operate with numerical numbers; however, lithology code and alteration level that is present in the dataset has categorical values denoted by characters (GG, AC, a1, a4, etc.). To feed the ANN with numerical information, original categorical values were transformed into Boolean variables through hot-encoding, as can be seen in Table 2. This resulted in representing each of the rock types and alteration level in a series of 0 or 1 values which indicate the absence or presence of a specified condition.
- Step 4. Data normalisation: In order to handle various data types and ranges existing in the dataset (i.e., geographical coordinates and grades), the values in each feature were normalised based on the mean and standard deviation. This was performed to scale different values of features into a common scale [54]. The value of a data point in each feature was recalculated by subtracting the population mean of a given feature from an individual point and then dividing the difference by the standard deviation of the population [55]. Each instance, of the data is transformed into as follows:where and denote the mean and standard deviation of ith feature respectively [56].
- Step 5. Splitting dataset into training/test sets: To evaluate the model performance, the dataset was randomly divided into training (80% of the data) and testing sets (20% of the data). The model was only trained using the training data. Its performance was validated using testing dataset. It is important to point out that these two data sets have similar statistical attributes.
3. Model Development and Implementations
3.1. Lithology and Alteration Prediction
3.2. Neural Network Model for Grade Estimation
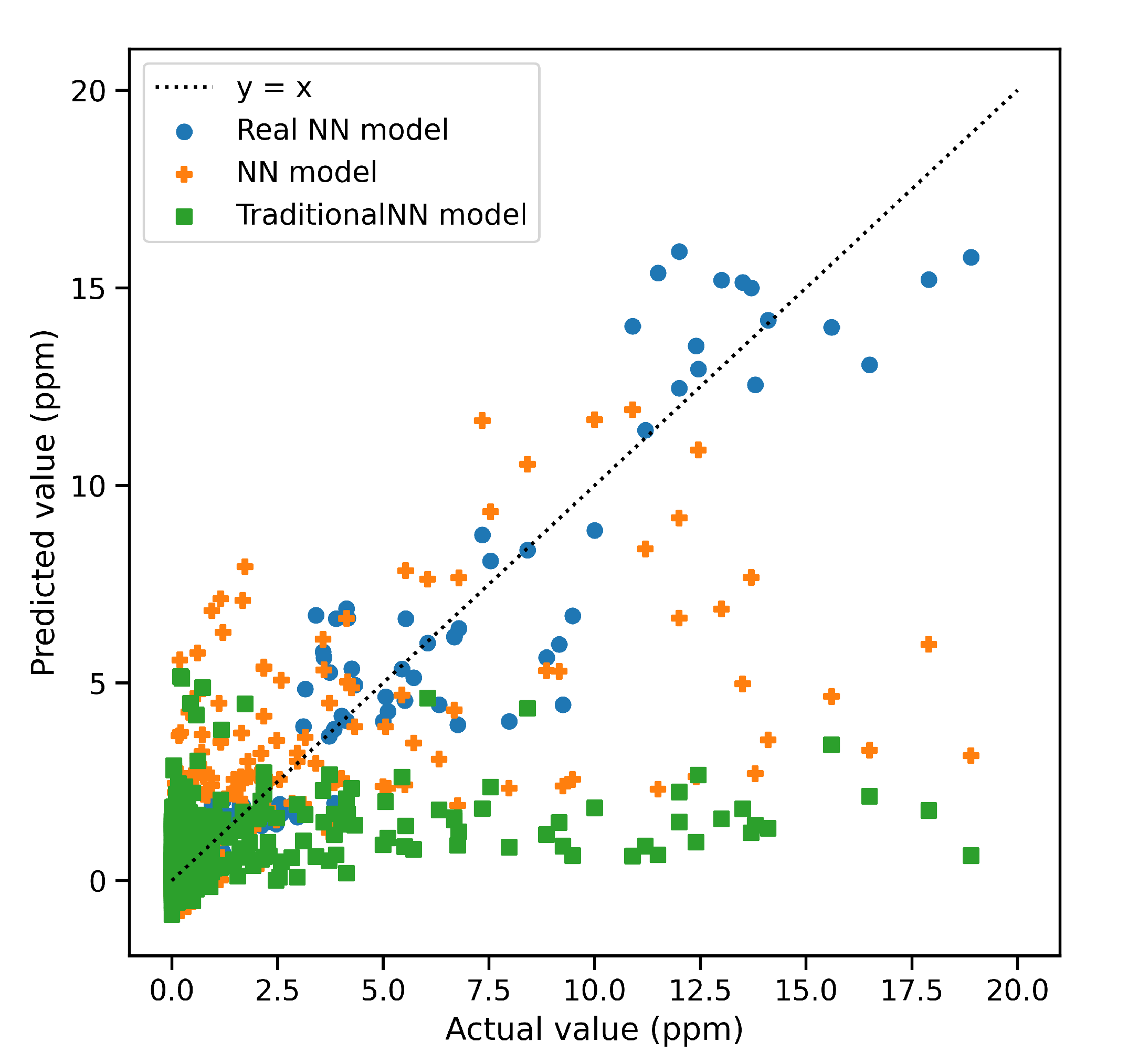
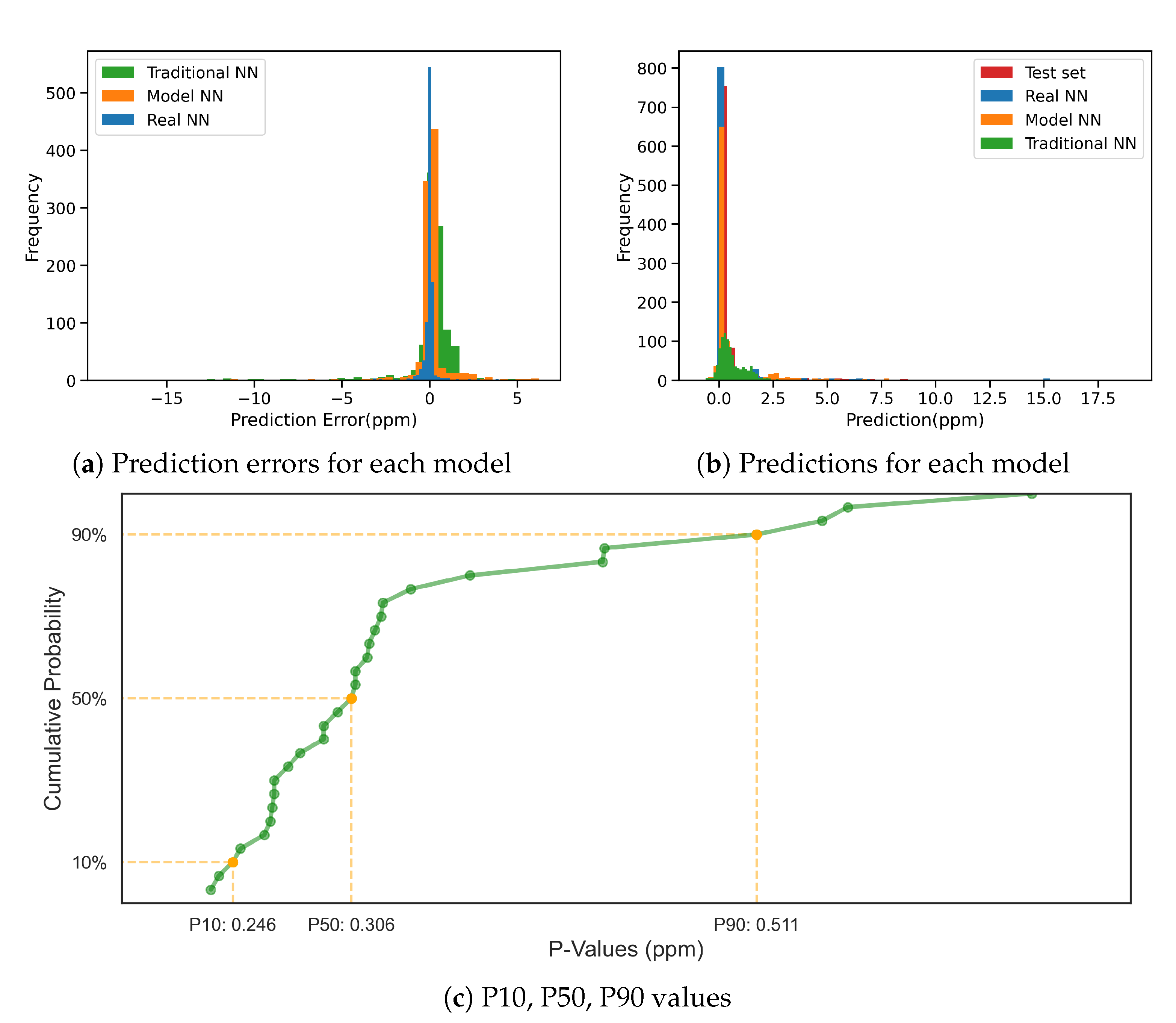
4. Results and Discussion
5. Conclusions
- The grade estimation can be more accurately modelled by having an intermediate modelling step that predicts rock types and alteration features as an input for the subsequent NN model.
- The suggested model does not require any assumptions on the input variables as in geostatistics.
- The method can be easily modified and applied into other mining resources as compared to classical resource estimation techniques.
- Inadequate data and depth of network can easily cause over-fitting issues in complex NN structures. The network is highly sensitive to following hyper-parameters: number of hidden layers, activation function type, number of epoch, and learning rate.
- The suggested model is based on lithological control of mineralization and is highly sensitive to the existence of geological discontinuities.
Author Contributions
Funding
Conflicts of Interest
References
- Weeks, R.M. Ore reserve estimation and grade control at the Quemont mine. In Proceedings of the Ore Reserve Estimation and Grade Control: A Canadian Centennial Conference Sponsored by the Geology and Metal Mining Divisions of the CIM, Ville d’Esterel, QC, Canada, 25–27 September 1967; Canadian Institute of Mining and Metallurgy: Westmount, QC, Canada, 1968; Volume 9, p. 123. [Google Scholar]
- Sinclair, A.J.; Blackwell, G.H. Applied Mineral Inventory Estimation; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Akbari, A.D.; Osanloo, M.; Shirazi, M.A. Reserve estimation of an open pit mine under price uncertainty by real option approach. Min. Sci. Technol. 2009, 19, 709–717. [Google Scholar] [CrossRef]
- Rendu, J.M. An Introduction to Cut-Off Grade Estimation; Society for Mining, Metallurgy, and Exploration: Englewood, CO, USA, 2014. [Google Scholar]
- Joseph, V.R. Limit kriging. Technometrics 2006, 48, 458–466. [Google Scholar] [CrossRef]
- Armstrong, M. Problems with universal kriging. J. Int. Assoc. Math. Geol. 1984, 16, 101–108. [Google Scholar] [CrossRef]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, M.R. Applied Geostatistics; Number 551.72 ISA; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978; Volume 600. [Google Scholar]
- Rendu, J. Kriging, logarithmic Kriging, and conditional expectation: Comparison of theory with actual results. In Proceedings of the 16th APCOM Symposium, Tucson, Arizona, 17–19 October 1979; pp. 199–212. [Google Scholar]
- Cressie, N. Spatial prediction and ordinary kriging. Math. Geol. 1988, 20, 405–421. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Chiles, J.P.; Delfiner, P. Modeling spatial uncertainty. In Geostatistics, Wiley Series in Probability and Statistics; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- David, M. Geostatistical Ore Reserve Estimation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Paithankar, A.; Chatterjee, S. Grade and tonnage uncertainty analysis of an african copper deposit using multiple-point geostatistics and sequential Gaussian simulation. Nat. Resour. Res. 2018, 27, 419–436. [Google Scholar] [CrossRef]
- Badel, M.; Angorani, S.; Panahi, M.S. The application of median indicator kriging and neural network in modeling mixed population in an iron ore deposit. Comput. Geosci. 2011, 37, 530–540. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A. Application of a modular feedforward neural network for grade estimation. Nat. Resour. Res. 2011, 20, 25–32. [Google Scholar] [CrossRef]
- Pan, G.; Harris, D.P.; Heiner, T. Fundamental issues in quantitative estimation of mineral resources. Nonrenew. Resour. 1992, 1, 281–292. [Google Scholar] [CrossRef]
- Jang, H.; Topal, E. A review of soft computing technology applications in several mining problems. Appl. Soft Comput. 2014, 22, 638–651. [Google Scholar] [CrossRef]
- Singer, D.A.; Kouda, R. Application of a feedforward neural network in the search for Kuroko deposits in the Hokuroku district, Japan. Math. Geol. 1996, 28, 1017–1023. [Google Scholar] [CrossRef]
- Denby, B.; Burnett, C. A neural network based tool for grade estimation. In Proceedings of the 24th International Symposium on the Application of Computer and Operation Research in the Mineral Industries (APCOM), Montreal, QC, Canada, 31 October–3 November 1993. [Google Scholar]
- Clarici, E.; Owen, D.; Durucan, S.; Ravencroft, P. Recoverable reserve estimation using a neural network. In Proceedings of the 24th International Symposium on the Application of Computer and Operation Research in the Mineral Industries (APCOM), Montreal, QC, Canada, 31 October–3 November 1993; pp. 145–152. [Google Scholar]
- Ke, J. Neural Network Modeling of Placer Ore Grade Spatial Variability. Ph.D. Thesis, University of Alaska Fairbanks, Fairbanks, AK, USA, 2002. [Google Scholar]
- Koike, K.; Matsuda, S. Characterizing content distributions of impurities in a limestone mine using a feedforward neural network. Nat. Resour. Res. 2003, 12, 209–222. [Google Scholar] [CrossRef]
- Koike, K.; Matsuda, S.; Gu, B. Evaluation of interpolation accuracy of neural kriging with application to temperature-distribution analysis. Math. Geol. 2001, 33, 421–448. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.; Hale, M. A hybrid neuro-fuzzy model for mineral potential mapping. Math. Geol. 2004, 36, 803–826. [Google Scholar] [CrossRef]
- Samanta, B.; Bandopadhyay, S.; Ganguli, R. Data segmentation and genetic algorithms for sparse data division in Nome placer gold grade estimation using neural network and geostatistics. Explor. Min. Geol. 2002, 11, 69–76. [Google Scholar] [CrossRef]
- Samanta, B.; Ganguli, R.; Bandopadhyay, S. Comparing the predictive performance of neural networks with ordinary kriging in a bauxite deposit. Min. Technol. 2005, 114, 129–139. [Google Scholar] [CrossRef]
- Singer, D.A. Typing mineral deposits using their associated rocks, grades and tonnages using a probabilistic neural network. Math. Geol. 2006, 38, 465–474. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bhattacherjee, A.; Samanta, B.; Pal, S.K. Ore grade estimation of a limestone deposit in India using an artificial neural network. Appl. GIS 2006, 2, 1–20. [Google Scholar] [CrossRef]
- Misra, D.; Samanta, B.; Dutta, S.; Bandopadhyay, S. Evaluation of artificial neural networks and kriging for the prediction of arsenic in Alaskan bedrock-derived stream sediments using gold concentration data. Int. J. Min. Reclam. Environ. 2007, 21, 282–294. [Google Scholar] [CrossRef]
- Dutta, S.; Bandopadhyay, S.; Ganguli, R.; Misra, D. Machine learning algorithms and their application to ore reserve estimation of sparse and imprecise data. J. Intell. Learn. Syst. Appl. 2010, 2, 86. [Google Scholar] [CrossRef][Green Version]
- Pham, T.D. Grade estimation using fuzzy-set algorithms. Math. Geol. 1997, 29, 291–305. [Google Scholar] [CrossRef]
- Tutmez, B. An uncertainty oriented fuzzy methodology for grade estimation. Comput. Geosci. 2007, 33, 280–288. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A. Application of adaptive neuro-fuzzy inference system for grade estimation; case study, Sarcheshmeh porphyry copper deposit, Kerman, Iran. Aust. J. Basic Appl. Sci. 2010, 4, 408–420. [Google Scholar]
- Tahmasebi, P.; Hezarkhani, A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Comput. Geosci. 2012, 42, 18–27. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N.; Suárez, A. Advanced machine learning methods for copper ore grade estimation. In Proceedings of the Near Surface Geoscience 2016-22nd European Meeting of Environmental and Engineering Geophysics, Helsinki, Finland, 4–6 September 2006; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2016. Number 1. p. cp-495-00087. [Google Scholar] [CrossRef]
- Das Goswami, A.; Mishra, M.; Patra, D. Investigation of general regression neural network architecture for grade estimation of an Indian iron ore deposit. Arab. J. Geosci. 2017, 10, 80. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation. Neurocomputing 2017, 235, 217–227. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, J. Method of Predicting Ore Dilution Based on a Neural Network and Its Application. Sustainability 2020, 12, 1550. [Google Scholar] [CrossRef]
- Maleki, M.; Jélvez, E.; Emery, X.; Morales, N. Stochastic Open-Pit Mine Production Scheduling: A Case Study of an Iron Deposit. Minerals 2020, 10, 585. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, Y. Reserve estimation using neural network techniques. Comput. Geosci. 1993, 19, 567–575. [Google Scholar] [CrossRef]
- Yama, B.; Lineberry, G. Artificial neural network application for a predictive task in mining. Min. Eng. 1999, 51, 59–64. [Google Scholar]
- Kapageridis, I.; Denby, B. Ore grade estimation with modular neural network systems—A case study. In Information Technology in the Mineral Industry; Panagiotou, G.N., Michalakopoulos, T.N., Eds.; AA Balkema Publishers: Rotterdam, The Netherlands, 1998; p. 52. [Google Scholar]
- Koike, K.; Matsuda, S.; Suzuki, T.; Ohmi, M. Neural network-based estimation of principal metal contents in the Hokuroku district, northern Japan, for exploring Kuroko-type deposits. Nat. Resour. Res. 2002, 11, 135–156. [Google Scholar] [CrossRef]
- Matias, J.; Vaamonde, A.; Taboada, J.; González-Manteiga, W. Comparison of kriging and neural networks with application to the exploitation of a slate mine. Math. Geol. 2004, 36, 463–486. [Google Scholar] [CrossRef]
- Samanta, B. Radial basis function network for ore grade estimation. Nat. Resour. Res. 2010, 19, 91–102. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N.; Suárez, A. Comparison of machine learning methods for copper ore grade estimation. Comput. Geosci. 2018, 22, 1371–1388. [Google Scholar] [CrossRef]
- Chaturvedi, D. Factors affecting the performance of artificial neural network models. In Soft Computing: Techniques and Its Applications in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2008; pp. 51–85. [Google Scholar]
- Mahmoudabadi, H.; Izadi, M.; Menhaj, M.B. A hybrid method for grade estimation using genetic algorithm and neural networks. Comput. Geosci. 2009, 13, 91–101. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bandopadhyay, S.; Machuca, D. Ore grade prediction using a genetic algorithm and clustering based ensemble neural network model. Math. Geosci. 2010, 42, 309–326. [Google Scholar] [CrossRef]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Larsen, R.J.; Marx, M.L. An Introduction to Mathematical Statistics and Its Applications; Prentice Hall: London, UK, 2005. [Google Scholar]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2019, 105524. [Google Scholar] [CrossRef]
- Kaplan, U.E. Method for Determining Ore Grade Using Artificial Neural Network in a Reserve Estimation. Australia Patent Au2019101145, 30 September 2019. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Davis, J.C. Introduction to Statistical Pattern Recognition. Comput. Geosci. 1996, 7, 833–834. [Google Scholar] [CrossRef]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 25 February 2019).
- Parker, D.B. Learning Logic. Invention Report S81-64, File 1; Oce of Technology Licensing; Stanford University: Paolo Alto, CA, USA, 1982. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited 2012, 14, 1–31. [Google Scholar]
- Harrell, F.E., Jr. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Pagel, J.F.; Kirshtein, P. Machine Dreaming and Consciousness; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]








| Easting 1 | Northing 1 | Altitude | Au (ppm) | |
|---|---|---|---|---|
| count | 4721 | 4721 | 4721 | 4721 |
| mean | 17,879 | 48,663 | 306 | 0.623 |
| std | 142 | 189 | 42 | 2.079 |
| min | 17,575 | 48,275 | 139 | 0.000 |
| 25% | 17,729 | 48,494 | 285 | 0.010 |
| 50% | 17,924 | 48,654 | 314 | 0.060 |
| 75% | 18,005 | 48,832 | 334 | 0.240 |
| max | 18,106 | 49,025 | 386 | 19.900 |
| ID | Easting | Northing | Altitude | GG | AC | ACBX | ACC | LT | BX | GLM | QST | QV | QVS | a0 | a1 | a2 | a3 | a4 | Grade (ppm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0161 | 17,700 | 49,000 | 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0.003 |
| S1231 | 17,750 | 48,800 | 103 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0.034 |
| S2578 | 17,500 | 48,500 | 145 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1.045 |
| S3121 | 17,800 | 48,300 | 146 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 6.483 |
| Hyper-Parameters | Search Range | Model Parameters | |
|---|---|---|---|
| Lithology/Alteration | n-neighbors | 1–15 | 3 |
| leaf-size | 1–40 | 5 | |
| ‘minkowski’ | |||
| metric | ‘euclidean’ | ‘minkowski’ | |
| ‘manhattan’ |
| Proposed Model | Eror Min (abs) | Error Max (abs) | MAE | std | var |
|---|---|---|---|---|---|
| Simulation 1 | 0.0001 | 16.481 | 0.433 | 0.918 | 0.844 |
| Simulation2 | 0.0001 | 15.552 | 0.280 | 0.707 | 0.500 |
| Simulation 3 | 0.0006 | 15.658 | 0.321 | 0.814 | 0.663 |
| Simulation 4 | 0.0004 | 15.768 | 0.267 | 0.718 | 0.516 |
| Simulation 5 | 0.0000 | 16.980 | 0.557 | 1.111 | 1.235 |
| Simulation 6 | 0.0003 | 16.055 | 0.299 | 0.831 | 0.691 |
| Simulation 7 | 0.0000 | 16.055 | 0.266 | 0.676 | 0.457 |
| Simulation 8 | 0.0001 | 16.138 | 0.315 | 0.822 | 0.675 |
| Simulation 9 | 0.0002 | 16.197 | 0.267 | 0.674 | 0.454 |
| Simulation 10 | 0.0002 | 16.370 | 0.306 | 0.844 | 0.712 |
| Simulation 11 | 0.0002 | 14.433 | 0.235 | 0.567 | 0.322 |
| Simulation 12 | 0.0008 | 15.656 | 0.292 | 0.738 | 0.545 |
| Simulation 13 | 0.0001 | 15.968 | 0.308 | 0.798 | 0.637 |
| Simulation 14 | 0.0004 | 14.702 | 0.336 | 0.640 | 0.409 |
| Simulation 15 | 0.0000 | 15.034 | 0.246 | 0.622 | 0.386 |
| Simulation 16 | 0.0004 | 15.236 | 0.650 | 1.161 | 1.349 |
| Simulation 17 | 0.0000 | 14.639 | 0.239 | 0.568 | 0.322 |
| Simulation 18 | 0.0000 | 15.113 | 0.274 | 0.691 | 0.478 |
| Simulation 19 | 0.0005 | 15.787 | 0.322 | 0.829 | 0.687 |
| Simulation 20 | 0.0001 | 16.247 | 0.434 | 0.915 | 0.837 |
| Simulation 21 | 0.0001 | 15.636 | 0.318 | 0.844 | 0.712 |
| Simulation 22 | 0.0009 | 15.079 | 0.366 | 0.678 | 0.460 |
| Simulation 23 | 0.0005 | 15.740 | 0.507 | 1.402 | 1.967 |
| Simulation 24 | 0.0001 | 15.844 | 0.544 | 1.001 | 1.003 |
| Simulation 25 | 0.0000 | 15.623 | 0.250 | 0.662 | 0.438 |
| Simulation 26 | 0.0000 | 15.220 | 0.265 | 0.644 | 0.414 |
| Simulation 27 | 0.0003 | 15.850 | 0.308 | 0.804 | 0.646 |
| Simulation 28 | 0.0001 | 16.272 | 0.511 | 0.921 | 0.849 |
| Simulation 29 | 0.0000 | 15.984 | 0.314 | 0.769 | 0.592 |
| Simulation 30 | 0.0009 | 15.473 | 0.292 | 0.703 | 0.494 |
| Predicted True | GG | AC | ACBX | ACC | LT | BX | GML | QST | QV | All |
|---|---|---|---|---|---|---|---|---|---|---|
| GG | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 |
| AC | 1 | 450 | 0 | 1 | 3 | 0 | 0 | 20 | 24 | 499 |
| ACBX | 0 | 0 | 12 | 2 | 2 | 0 | 0 | 0 | 0 | 16 |
| ACC | 0 | 2 | 0 | 159 | 4 | 0 | 0 | 6 | 3 | 174 |
| LT | 0 | 0 | 0 | 1 | 21 | 0 | 0 | 0 | 0 | 22 |
| BX | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 4 |
| GML | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 |
| QST | 0 | 41 | 0 | 1 | 1 | 0 | 0 | 39 | 5 | 87 |
| QV | 0 | 27 | 1 | 12 | 0 | 1 | 0 | 7 | 77 | 125 |
| QVS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | 9 |
| All | 8 | 521 | 13 | 176 | 31 | 4 | 2 | 73 | 117 | 945 |
| Lithology | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| GG | 0.88 | 1.00 | 0.93 | 7 |
| AC | 0.86 | 0.90 | 0.88 | 499 |
| ACBX | 0.92 | 0.75 | 0.83 | 16 |
| ACC | 0.90 | 0.91 | 0.91 | 174 |
| LT | 0.68 | 0.95 | 0.79 | 22 |
| BX | 0.75 | 0.75 | 0.75 | 4 |
| GML | 1.00 | 1.00 | 1.00 | 2 |
| QST | 0.53 | 0.45 | 0.49 | 87 |
| QV + QVS | 0.73 | 0.62 | 0.64 | 134 |
| Accuracy | 0.81 | 945 | ||
| Macro avg | 0.72 | 0.73 | 0.72 | 945 |
| Weighted avg | 0.80 | 0.81 | 0.81 | 945 |
| Predicted | Alt0 | Alt1 | Alt2 | Alt3 | Alt4 | All |
|---|---|---|---|---|---|---|
| True | ||||||
| Alt0 | 138 | 28 | 4 | 2 | 0 | 172 |
| Alt1 | 18 | 319 | 44 | 5 | 3 | 389 |
| Alt2 | 5 | 49 | 203 | 14 | 2 | 273 |
| Alt3 | 3 | 11 | 21 | 30 | 1 | 66 |
| Alt4 | 6 | 9 | 13 | 4 | 13 | 45 |
| All | 170 | 416 | 285 | 55 | 19 | 945 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| a0 | 0.81 | 0.80 | 0.81 | 172 |
| a1 | 0.77 | 0.82 | 0.79 | 389 |
| a2 | 0.71 | 0.74 | 0.73 | 273 |
| a3 | 0.55 | 0.45 | 0.50 | 66 |
| a4 | 0.68 | 0.29 | 0.41 | 45 |
| Accuracy | 0.74 | 945 | ||
| Macro avg | 0.70 | 0.62 | 0.65 | 945 |
| Weighted avg | 0.74 | 0.74 | 0.74 | 945 |
| R2 | MAE | MSE | |
|---|---|---|---|
| Real NN Model | 0.948 | 0.1849 | 0.281 |
| NN Model | 0.529 | 0.5072 | 2.236 |
| Traditional NN Model | 0.112 | 0.8624 | 4.163 |
| Sample ID | Actual Grade (ppm) | Real NN Model | NN Model | Traditional NN | |||
|---|---|---|---|---|---|---|---|
| Prediction | Error | Prediction | Error | Prediction | Error | ||
| 800 | 0.430 | 0.048 | −0.382 | 0.084 | −0.346 | 1.723 | 1.293 |
| 801 | 0.000 | 0.076 | 0.076 | −0.029 | −0.029 | 0.091 | 0.091 |
| 802 | 0.020 | 0.118 | 0.098 | 0.122 | 0.102 | 0.489 | 0.469 |
| 803 | 0.040 | 0.049 | 0.009 | 0.022 | −0.018 | 0.585 | 0.545 |
| 804 | 0.010 | 0.104 | 0.094 | 0.076 | 0.066 | 0.161 | 0.151 |
| 805 | 0.070 | 0.062 | −0.008 | 0.239 | 0.169 | 1.024 | 0.954 |
| 806 | 0.100 | 0.086 | −0.014 | 0.046 | −0.054 | 0.709 | 0.609 |
| 807 | 0.010 | 0.231 | 0.221 | 0.239 | 0.229 | −0.013 | −0.023 |
| 808 | 0.240 | 0.197 | −0.043 | 0.410 | 0.170 | 1.492 | 1.252 |
| 809 | 0.500 | 0.121 | −0.379 | 0.067 | −0.433 | −0.507 | −1.007 |
| 810 | 0.190 | 0.197 | 0.007 | 0.203 | 0.013 | 0.852 | 0.662 |
| 811 | 1.150 | 1.398 | 0.248 | 0.026 | −1.124 | 0.324 | −0.826 |
| 812 | 2.310 | 1.757 | −0.553 | 2.503 | 0.193 | 0.625 | −1.685 |
| 813 | 0.040 | 0.102 | 0.062 | 0.196 | 0.156 | 0.077 | 0.037 |
| 814 | 0.000 | 0.157 | 0.157 | 0.273 | 0.273 | 0.135 | 0.135 |
| 815 | 0.010 | 0.036 | 0.026 | 0.159 | 0.149 | 0.146 | 0.136 |
| 816 | 0.400 | 0.171 | −0.229 | 0.405 | 0.005 | 1.247 | 0.847 |
| 817 | 0.090 | 0.036 | −0.054 | 0.136 | 0.046 | 0.141 | 0.051 |
| 818 | 0.160 | 0.102 | −0.058 | 0.260 | 0.100 | 0.379 | 0.219 |
| 819 | 0.040 | 0.140 | 0.100 | 0.244 | 0.204 | 1.788 | 1.748 |
| 820 | 0.020 | 0.098 | 0.078 | 0.233 | 0.213 | 1.463 | 1.443 |
| 821 | 0.140 | 0.148 | 0.008 | 0.010 | −0.130 | 0.289 | 0.149 |
| 822 | 0.150 | 0.080 | −0.070 | 0.213 | 0.063 | 1.597 | 1.447 |
| 823 | 0.220 | 0.108 | −0.112 | 0.138 | −0.082 | 1.155 | 0.935 |
| 824 | 0.760 | 0.537 | −0.223 | 2.629 | 1.869 | 1.370 | 0.610 |
| 825 | 0.080 | 0.125 | 0.045 | 0.125 | 0.045 | 1.213 | 1.133 |
| 826 | 0.000 | −0.064 | −0.064 | 0.343 | 0.343 | 0.324 | 0.324 |
| 827 | 0.010 | 0.066 | 0.056 | 0.086 | 0.076 | 0.001 | −0.009 |
| 828 | 0.000 | 0.071 | 0.071 | 0.131 | 0.131 | 0.501 | 0.501 |
| 829 | 0.490 | 0.362 | −0.128 | 0.115 | −0.375 | 1.120 | 0.630 |
| 830 | 1.560 | 1.616 | 0.056 | 2.339 | 0.779 | 0.117 | −1.443 |
| 831 | 1.200 | 0.736 | −0.464 | 1.078 | −0.122 | 0.384 | −0.816 |
| 832 | 0.160 | 0.043 | −0.117 | 0.287 | 0.127 | −0.294 | −0.454 |
| 833 | 0.340 | 0.181 | −0.159 | 0.314 | −0.026 | 1.528 | 1.188 |
| 834 | 0.020 | 0.031 | 0.011 | 0.003 | −0.017 | 0.412 | 0.392 |
| 835 | 0.030 | 0.086 | 0.056 | −0.007 | −0.037 | 0.129 | 0.099 |
| 836 | 0.050 | 0.173 | 0.123 | 0.545 | 0.495 | 0.220 | 0.170 |
| 837 | 0.060 | 0.069 | 0.009 | 0.179 | 0.119 | 0.759 | 0.699 |
| 838 | 0.150 | 0.113 | −0.037 | −0.231 | −0.381 | 0.177 | 0.027 |
| 839 | 0.000 | 0.108 | 0.108 | 0.169 | 0.169 | 0.329 | 0.329 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaplan, U.E.; Topal, E. A New Ore Grade Estimation Using Combine Machine Learning Algorithms. Minerals 2020, 10, 847. https://doi.org/10.3390/min10100847
Kaplan UE, Topal E. A New Ore Grade Estimation Using Combine Machine Learning Algorithms. Minerals. 2020; 10(10):847. https://doi.org/10.3390/min10100847
Chicago/Turabian StyleKaplan, Umit Emrah, and Erkan Topal. 2020. "A New Ore Grade Estimation Using Combine Machine Learning Algorithms" Minerals 10, no. 10: 847. https://doi.org/10.3390/min10100847
APA StyleKaplan, U. E., & Topal, E. (2020). A New Ore Grade Estimation Using Combine Machine Learning Algorithms. Minerals, 10(10), 847. https://doi.org/10.3390/min10100847






