A New Ore Grade Estimation Using Combine Machine Learning Algorithms

Abstract

Accurate prediction of mineral grades is a fundamental step in mineral exploration and resource estimation, which plays a significant role in the economic evaluation of mining projects. Currently available methods are based either on geometrical approaches or geostatistical techniques that often considers the grade as a regionalised variable. In this paper, we propose a grade estimation technique that combines multilayer feed-forward neural network (NN) and k-nearest neighbour (kNN) models to estimate the grade distribution within a mineral deposit. The models were created by using the available geological information (lithology and alteration) as well as sample locations (easting, northing, and altitude) obtained from the drill hole data. The proposed approach explicitly maintains pattern recognition over the geological features and the chemical composition (mineral grade) of the data. Prior to the estimation of grades, rock types and alterations were predicted at unsampled locations using the kNN algorithm. The presented case study demonstrates that the proposed approach can predict the grades on a test dataset with a mean absolute error (MAE) of $0.507$ and $R^2=0.528$, whereas the traditional model, which only uses the coordinates of sample points as an input, yielded an MAE value of $0.862$ and $R^2=0.112$. The proposed approach is promising and could be an alternative way to estimates grades in a similar modelling tasks.

1. Introduction

One of the critical tasks in mining value chain is to accurately estimate the grades of interest within a mineral deposit. The grades can be in the form of observation or estimation and are used in several stages of mining that ranges from exploration to exploitation. Resource estimation, being one of the initial stages of a mining activity, is an essential step in feasibility studies as well as mine planning [1,2,3,4]. Although the state-of-the-art methodologies used in resource estimation are reasonably advanced in the mining industry, generic application of such methodologies might not be applicable for every complex geological environment [5,6,7,8,9]. Various researchers, therefore, have proposed substantial grade prediction models using diverse techniques such as inverse distance weighing (IDW), kriging and its various versions (simple kriging, ordinary kriging, lognormal kriging, indicator kriging, co-kriging, etc.), and stochastic simulations (sequential Gaussian simulation and sequential indicator simulation) [10,11,12,13,14,15,16]; however, the above-mentioned methods require an assumption in relation to the spatial correlation between samples to be estimated at non-sampled locations [17,18]. In some cases, due to the complex relationships between the grade distribution and spatial pattern variability, geostatistical methods may not give the best estimation results [19]. Consequently, these limitations and complexities inspired researchers to investigate alternative approaches that can be utilised to overcome such obstacles. Over the past few decades, several researchers focused on various computational learning techniques that can predict grades more accurately without having to rely on an underlying assumption [20]. In recent years, machine learning methods, including support vector machine (SVM), random forest (RF), artificial neural network (ANN), and their variations such as support vector regression (SVR) and adaptive neuro-fuzzy inference system (ANFIS), have been used rather extensively to make reliable grade estimations [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Wu and Zhou, and Yama and Lineberry [44,45] are one of the earliest researchers that used ANN techniques for the grade estimation with an initial success. Kapageridis [46] has utilised a modular neural network system on a randomly sampled iron ore deposit. The comparison made with their proposed approach and kriging demonstrated that the ANN techniques can deliver similar estimate results and requires far less knowledge to be effectively utilised in the estimation. Koike et al. [47] trained an artificial neural network to recognise the relation between the major metal content, location, and lithology of a sample point in the Hokuroku district in Japan. The network model was able to produce a model including many high-content zones based on sample data. Matias et al. [48] compared kriging with regularisation networks (RN), multilayer perceptron (MLP), and radial basis function (RBF) networks for the estimation of the quality of a slate mine. The MLP network showed sufficient results in terms of test error and training speed. Samanta [49] highlights the performance of a radial basis function (RBF) network for ore grade estimation in an offshore placer gold deposit. It was demonstrated that the RBF model produced estimates with the $R^2=0.39$ whereas $R^2=0.19$ for the traditional kriging prediction method. Jafrasteh et al. [50] investigated the grade prediction performance of machine learning techniques, such as ANN, random forest (RF) and Gaussian process (GP) in the porphyry copper deposit in South-eastern Iran. Their results revealed that GP performed with the best overall accuracy, followed by widely used traditional estimation technique, indicator kriging; however, developing a multilayered ANN model for grade estimation requires the selection of network complexity, which has a direct impact on prediction performance. Network complexity broadly depends on (a) neuron complexity, (b) number of neurons in each layer, (c) number of layers, and (d) number and type of interconnecting weights [51]. Consequently, a number of studies have attempted to solve these problems by combining ANN with other computational techniques. Mahmoudabadi et al. [52] proposed a hybrid method that utilizes the combination of the Levenberg–Marquardt (LM) method and genetic algorithm (GA) to identify the ANNs optimal initial weights. Chatterjee et al. [53] suggest an ensemble of neural networks utilising a genetic algorithm (GA) and k-means clustering modelling of a lead–zinc deposit. Several network models were trained, and the best models were selected for improving the accuracy of the ensemble model. Results revealed that the GA-based model outperformed the other models considered. Although the literature review highlights the potential benefits of machine learning methods in accurate grade estimation on variety of case studies, they also mention various drawbacks as well. For instance, there is no certain rule to determine the network hyper-parameters. Proper structure can only be achieved by trial and error, which is a computationally intensive procedure. Another critical issue is that once an ANN provides a solution, it does not give any explanation regarding the possible relationship with input; therefore, there is still room for further investigation of data-driven learning models in order to obtain accurate grade estimation.

The aim of this paper is to present a new grade modelling approach that combines k-nearest neighbour (kNN) and ANN models to perform grade estimations of a mineral deposit. The proposed approach utilises geological information (lithology and alteration) and spatial information (easting, northing, and altitude) for the model creation. The model creation is comprised of two steps. First, the kNN model is trained to predict rock types and alteration levels. This model allows us to estimate the geological information at non-sampled locations as a first step. Second, the ANN model is trained to predict grades using the geological and spatial information. The ANN model utilises the geological information predictions made by the kNN model as well as the geographic information as input variables. When the model is trained with sufficient data, the network is able to learn the relationship between input variables (rock type, alteration level, and geographic position) and the output variable, which is grade.

This article is organised as follows: Section 2 presents brief information on the dataset used to demonstrate the methodology and data pre-processing. Section 3 presents the model development and implementations on a real case study. Section 4 presents the analyses of the results and discusses the findings. Finally, the conclusions of the paper are presented in Section 5.

2. Data Attributes and Preparation

In this study, data were collected from a gold deposit during the second phase of a resource drilling program. Most of the study area is underlain by mafic, intermediate, more rarely felsic volcanic rocks and associated volcano-sedimentary formations that are cross-cut by post tectonic granitoids. Due to confidentiality agreement, Authors do not have a permission to refer the name of deposit, location, or any other mineralization characteristics that might expose the deposit and/or the mining company. The study area extends over 2 × 3 km² and the data contains gold grade values (ppm) from 123 drill holes. The average distance between drill holes is approximately 25 m (Figure 1). The average length of the boreholes is about 100 m. Samples from the boreholes were collected at intervals of 1 m. The ore is extracted from ten different lithologies. For the present study, raw borehole data were composited based on the lithology, which produced 4721 composited intervals altogether.

Raw borehole data that comes from a drill hole is unusable for neural network training due to (a) intense spatial grade variability, (b) unequal sample length, (c) noise due to outlier data points that differs significantly from other observations, and (d) varying range of numerical values existing in the dataset for different variables. Several preparation steps had to be performed to be able to use the raw data in the ANN model. These steps are as follows:

• Step 1. Creating a composite data: Raw data comes from 123 drill holes were composited in 1 m length, which is equal to the average sample length in one run.

  Table 1. Basic statistics of the composited dataset.

  	Easting 1	Northing 1	Altitude	Au (ppm)
  count	4721	4721	4721	4721
  mean	17,879	48,663	306	0.623
  std	142	189	42	2.079
  min	17,575	48,275	139	0.000
  25%	17,729	48,494	285	0.010
  50%	17,924	48,654	314	0.060
  75%	18,005	48,832	334	0.240
  max	18,106	49,025	386	19.900

  ¹ local coordinates.

  presents the descriptive statistics of the composite dataset.
• Step 2. Data pre-processing: Each sample is described by five attributes including coordinates (easting, northing, and altitude), rock type, and alteration level. The original raw data contains 25 different rock types and 5 different alteration types. To generalise the geological distribution, we combined similar lithologies to reduce the original rock type to 10 and used only level of argillic alteration (a0, a1, ..., a4) that shows the high correlation with gold grade.
• Step 3. Transformation of the categorical data into numerical values: Neural Network (NN) algorithm performs numerical calculations; therefore, it can only operate with numerical numbers; however, lithology code and alteration level that is present in the dataset has categorical values denoted by characters (GG, AC, a1, a4, etc.). To feed the ANN with numerical information, original categorical values were transformed into Boolean variables through hot-encoding, as can be seen in

  Table 2. Some of sample points from the training dataset.

  ID	Easting	Northing	Altitude	GG	AC	ACBX	ACC	LT	BX	GLM	QST	QV	QVS	a0	a1	a2	a3	a4	Grade (ppm)
  S0161	17,700	49,000	101	0	0	1	0	0	0	0	0	0	0	1	0	0	0	0	0.003
  S1231	17,750	48,800	103	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0.034
  S2578	17,500	48,500	145	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1.045
  S3121	17,800	48,300	146	0	0	0	0	0	0	1	0	0	0	0	0	0	0	1	6.483

  . This resulted in representing each of the rock types and alteration level in a series of 0 or 1 values which indicate the absence or presence of a specified condition.
• Step 4. Data normalisation: In order to handle various data types and ranges existing in the dataset (i.e., geographical coordinates and grades), the values in each feature were normalised based on the mean and standard deviation. This was performed to scale different values of features into a common scale [54]. The value of a data point in each feature was recalculated by subtracting the population mean of a given feature from an individual point and then dividing the difference by the standard deviation of the population [55]. Each instance, $x_{i,n}$ of the data is transformed into $x{{}^{\prime }}_{i,n}$ as follows:

  $$x{{}^{\prime }}_{i,n}=\frac{x_{i,n}-{\mu }_i}{{\sigma }_i}$$

  (1)

  where $\mu$ and $\sigma$ denote the mean and standard deviation of ith feature respectively [56].
• Step 5. Splitting dataset into training/test sets: To evaluate the model performance, the dataset was randomly divided into training (80% of the data) and testing sets (20% of the data). The model was only trained using the training data. Its performance was validated using testing dataset. It is important to point out that these two data sets have similar statistical attributes.

3. Model Development and Implementations

To construct the NN model in this study, spatial positions (easting, northing, and altitude), rock types, and alteration levels were used as inputs to predict the Au grade [57]. To make a prediction at each sample point, it is essential to provide the rock type and alteration information. In fact, this information is only available at the borehole locations. Hence, to use the NN model, rock type and alteration information need be provided for each non-sampled location at which the grade values are to be estimated. This was achieved by using the trained kNN model to make predictions at non-sampled locations.

3.1. Lithology and Alteration Prediction

Since its introduction by Thomas Cover [58], kNN has been widely used to solve nearly every regression and classification problem. For a given test query, kNN algorithm finds k-closest points in feature space and performs a prediction based on the values at k-closest neighbours. It repeats this for all the test data; therefore, it is often classified as “instance-based learning”, or “lazy learning”. Detailed descriptions of the kNN algorithm can be found in a number of textbooks [59,60,61,62]. In this study, a kNN model was developed to predict rock types and alterations at unknown locations. Python 3.6.9 [63] programming language and Scikit-learn [64] machine learning library were used to create the kNN model. The model requires the specification of k-number of neighbours to be used as a hyper-parameter, which is highly specific for a given dataset; therefore, choosing of the optimal k-value is needed prior to the model creation. A small k-value could add noise that would have significant influence on the final model. In contrast, a large k-value would create over-fitting. In this research, grid search with k-fold (K-5) cross-validation was used for determining optimal hyper-parameters for kNN algorithm. Given an acceptable search range, a grid search was applied on all possible values and “best” parameter setting minimising the losses was picked. Once the k parameter was specified, the kNN model was created and the performance of it was evaluated using the test dataset. It should be noted that the training dataset used to create the kNN model was also used for the development of the ANN model. Chosen hyper-parameters of the kNN model can be seen in

Table 3. Hyper-parameters for the k-nearest neighbours (kNN) model.

	Hyper-Parameters	Search Range	Model Parameters
Lithology/Alteration	n-neighbors	1–15	3
	leaf-size	1–40	5
		‘minkowski’
	metric	‘euclidean’	‘minkowski’
		‘manhattan’

.

3.2. Neural Network Model for Grade Estimation

Since the chemical composition of mineral deposit is highly correlated with alteration and lithology, building a three-dimensional geologic model is a crucial step for predicting an accurate grade distribution. After trying a variety of NN configuration, best results with minimum error rate were obtained by an NN architecture comprising one input layer which consists of 18 neurons, 2 hidden layers each of which has 64 neurons, and 1 neuron output layer (Figure 2). The model was built using the Python 3.6.9 programming language and Keras 2.2.5 [65] deep learning library.

In order to compare the model performance against the traditional NN modelling approach in literature, we first created a separate NN model for comparison purposes. This model only uses the sample locations (coordinates) as input variables for the network to predict the Au grade. We then created the proposed model, which not only utilises the sample locations to model the grade distribution, but also the rock type and alteration levels that were predicted by the kNN algorithm. This model corresponds to the NN model. To compare the network prediction performance, NN was fed by location, rock type, and alteration, which already known. This model corresponds to real NN model. Once the three models were created, they were run on the independent test set (unseen and unused by model) to evaluate the model accuracies.

The back-propagation algorithm was used for training the neural network. It is a widely used iterative gradient algorithm designed to minimise the error between the true and predicted model outputs [66,67]. As an optimisation algorithm, RMSProp has been applied to update the weight tensors ($w_i$) during training. RMSProp utilises an adaptive learning rate rather than a predefined one. It uses a moving average squared gradient to normalise the gradients [68]. A user defined loss function is used to evaluate the predictions against the targets and produces an error value, which is used during training to update the weights (Figure 3).

To determine the hyper-parameters of the NN model, k-fold cross validation [69] was used. We set the k-value to 5; therefore, our training set comprised 5 different equally sized partitions, each of which is comprised of 80% training dataset as for training the model and 20% of the training dataset as for model validation. For each partition, we train a network model on the remaining ‘K-1’ partitions and evaluate its accuracy on partition ‘K’ (Figure 4). Average of the losses obtained from the folds is used for the training loss. Training hyper-parameters such as number of epochs, optimiser, and learning rate were determined based on trial and error method.

In this paper, three performance metrics, mean absolute error (MAE), mean square error (MSE), and coefficient of determination ($R^2$), were used to evaluate the prediction performance. Figure 5 shows MAE improvement for each epoch on training data set. To avoid network over-fitting, which is a typical issue for NN applications, 400 epoch were used for model prediction.

4. Results and Discussion

To assess the model prediction performance, the dataset was randomly divided 30 subsets as described earlier in Section 2.

Table 4. NN model simulation summary.

Proposed Model	Eror Min (abs)	Error Max (abs)	MAE	std	var
Simulation 1	0.0001	16.481	0.433	0.918	0.844
Simulation2	0.0001	15.552	0.280	0.707	0.500
Simulation 3	0.0006	15.658	0.321	0.814	0.663
Simulation 4	0.0004	15.768	0.267	0.718	0.516
Simulation 5	0.0000	16.980	0.557	1.111	1.235
Simulation 6	0.0003	16.055	0.299	0.831	0.691
Simulation 7	0.0000	16.055	0.266	0.676	0.457
Simulation 8	0.0001	16.138	0.315	0.822	0.675
Simulation 9	0.0002	16.197	0.267	0.674	0.454
Simulation 10	0.0002	16.370	0.306	0.844	0.712
Simulation 11	0.0002	14.433	0.235	0.567	0.322
Simulation 12	0.0008	15.656	0.292	0.738	0.545
Simulation 13	0.0001	15.968	0.308	0.798	0.637
Simulation 14	0.0004	14.702	0.336	0.640	0.409
Simulation 15	0.0000	15.034	0.246	0.622	0.386
Simulation 16	0.0004	15.236	0.650	1.161	1.349
Simulation 17	0.0000	14.639	0.239	0.568	0.322
Simulation 18	0.0000	15.113	0.274	0.691	0.478
Simulation 19	0.0005	15.787	0.322	0.829	0.687
Simulation 20	0.0001	16.247	0.434	0.915	0.837
Simulation 21	0.0001	15.636	0.318	0.844	0.712
Simulation 22	0.0009	15.079	0.366	0.678	0.460
Simulation 23	0.0005	15.740	0.507	1.402	1.967
Simulation 24	0.0001	15.844	0.544	1.001	1.003
Simulation 25	0.0000	15.623	0.250	0.662	0.438
Simulation 26	0.0000	15.220	0.265	0.644	0.414
Simulation 27	0.0003	15.850	0.308	0.804	0.646
Simulation 28	0.0001	16.272	0.511	0.921	0.849
Simulation 29	0.0000	15.984	0.314	0.769	0.592
Simulation 30	0.0009	15.473	0.292	0.703	0.494

and Figure 6 summarizes the Au grade prediction results for every simulation using each subset of data. For each simulation, the test subsets were used for evaluating the performance of the kNN and NN models. Results of Simulation 23 shown in

Table 5. kNN model lithology predictions.

Predicted True	GG	AC	ACBX	ACC	LT	BX	GML	QST	QV	All
GG	7	0	0	0	0	0	0	0	0	7
AC	1	450	0	1	3	0	0	20	24	499
ACBX	0	0	12	2	2	0	0	0	0	16
ACC	0	2	0	159	4	0	0	6	3	174
LT	0	0	0	1	21	0	0	0	0	22
BX	0	1	0	0	0	3	0	0	0	4
GML	0	0	0	0	0	0	2	0	0	2
QST	0	41	0	1	1	0	0	39	5	87
QV	0	27	1	12	0	1	0	7	77	125
QVS	0	0	0	0	0	0	0	1	8	9
All	8	521	13	176	31	4	2	73	117	945

,

Table 6. kNN model lithology prediction score.

Lithology	Precision	Recall	F1-Score	Support
GG	0.88	1.00	0.93	7
AC	0.86	0.90	0.88	499
ACBX	0.92	0.75	0.83	16
ACC	0.90	0.91	0.91	174
LT	0.68	0.95	0.79	22
BX	0.75	0.75	0.75	4
GML	1.00	1.00	1.00	2
QST	0.53	0.45	0.49	87
QV + QVS	0.73	0.62	0.64	134
Accuracy			0.81	945
Macro avg	0.72	0.73	0.72	945
Weighted avg	0.80	0.81	0.81	945

,

Table 7. kNN model alteration predictions.

Predicted	Alt0	Alt1	Alt2	Alt3	Alt4	All
True
Alt0	138	28	4	2	0	172
Alt1	18	319	44	5	3	389
Alt2	5	49	203	14	2	273
Alt3	3	11	21	30	1	66
Alt4	6	9	13	4	13	45
All	170	416	285	55	19	945

,

Table 8. kNN model alteration prediction score.

	Precision	Recall	F1-Score	Support
a0	0.81	0.80	0.81	172
a1	0.77	0.82	0.79	389
a2	0.71	0.74	0.73	273
a3	0.55	0.45	0.50	66
a4	0.68	0.29	0.41	45
Accuracy			0.74	945
Macro avg	0.70	0.62	0.65	945
Weighted avg	0.74	0.74	0.74	945

,

Table 9. Performance comparison.

	R2	MAE	MSE
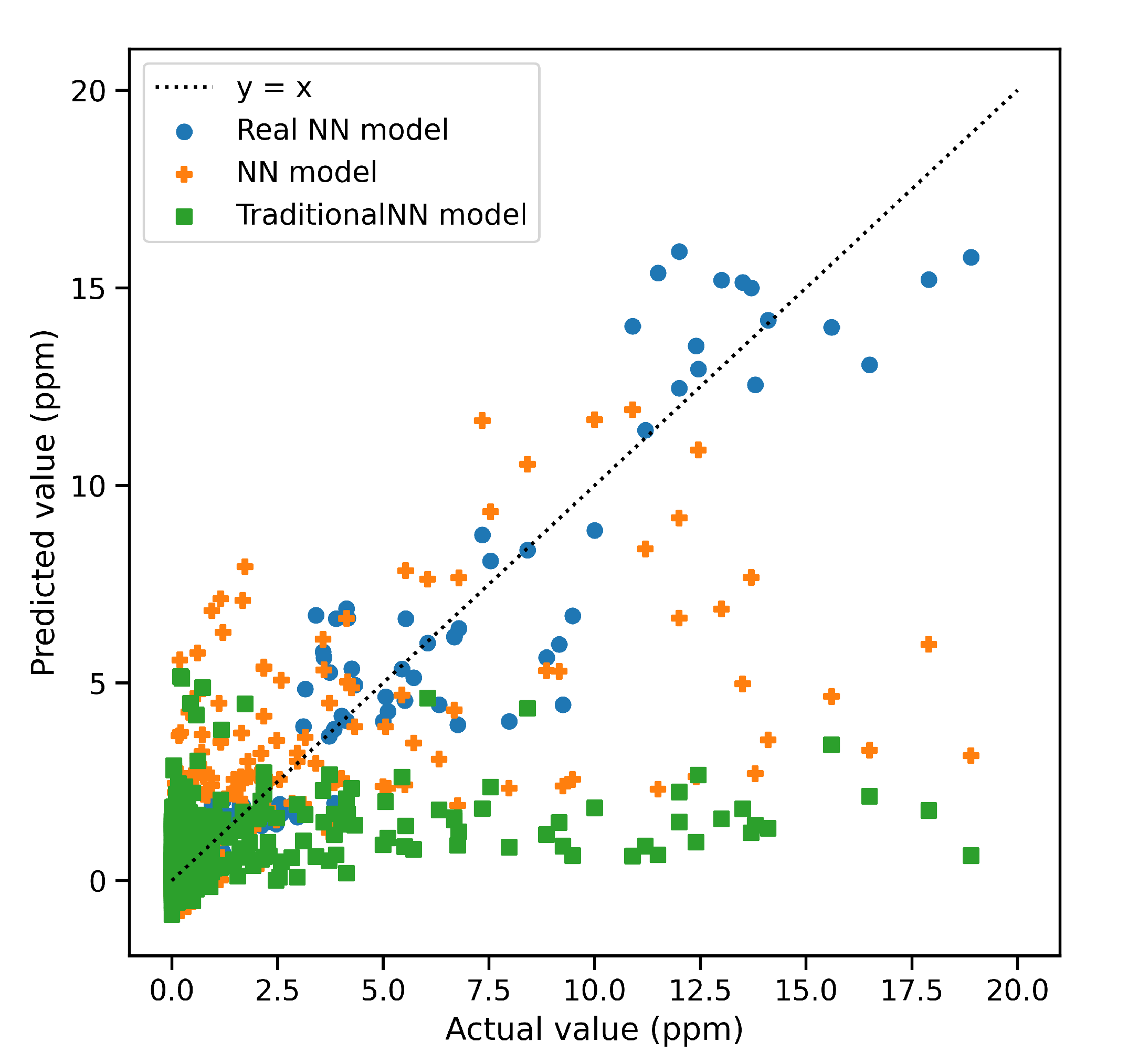
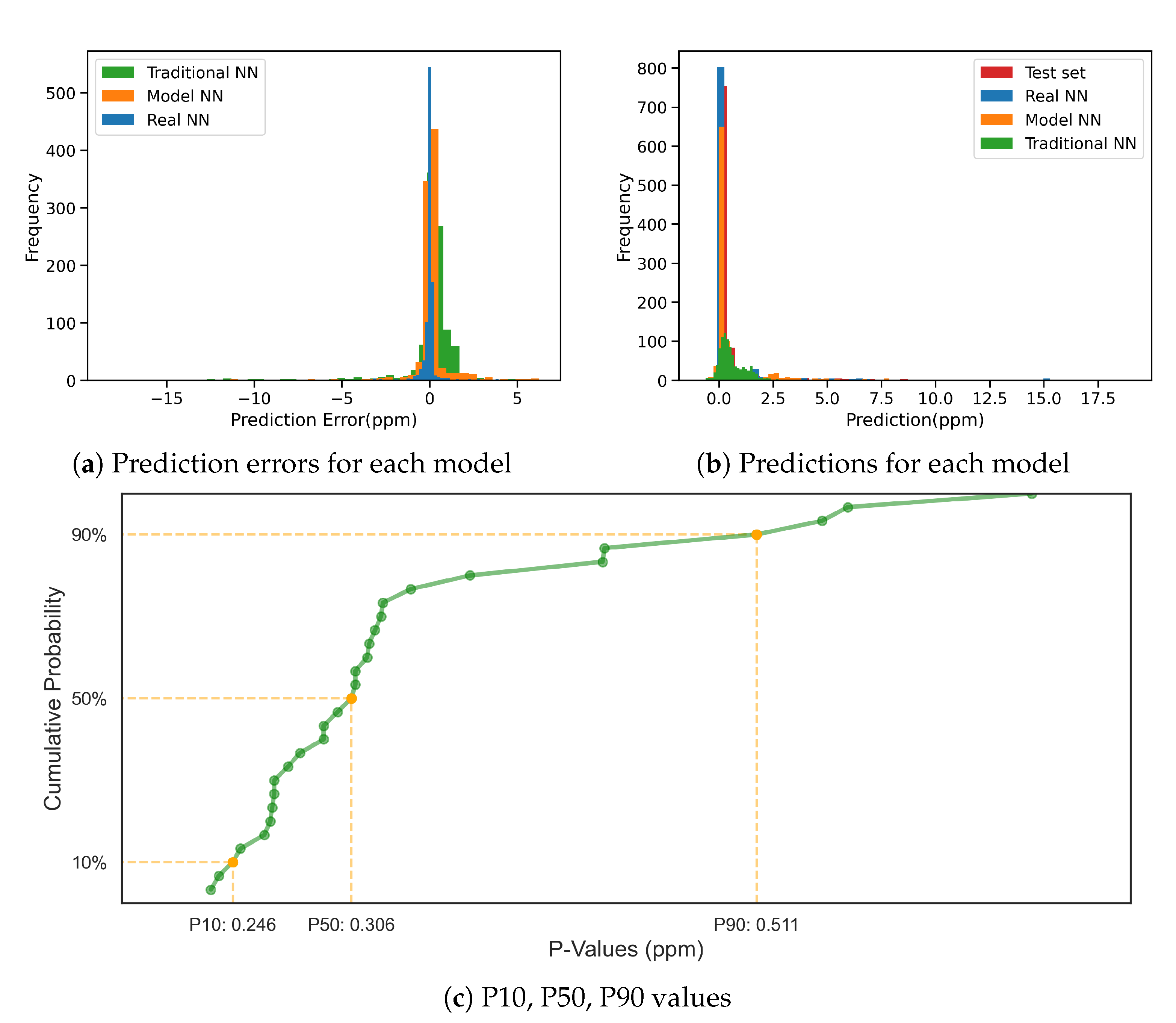
Real NN Model	0.948	0.1849	0.281
NN Model	0.529	0.5072	2.236
Traditional NN Model	0.112	0.8624	4.163

and

Table 10. Simulation 23, Comparison of NN models predictions.

Sample ID	Actual Grade (ppm)	Real NN Model		NN Model		Traditional NN
		Prediction	Error	Prediction	Error	Prediction	Error
800	0.430	0.048	−0.382	0.084	−0.346	1.723	1.293
801	0.000	0.076	0.076	−0.029	−0.029	0.091	0.091
802	0.020	0.118	0.098	0.122	0.102	0.489	0.469
803	0.040	0.049	0.009	0.022	−0.018	0.585	0.545
804	0.010	0.104	0.094	0.076	0.066	0.161	0.151
805	0.070	0.062	−0.008	0.239	0.169	1.024	0.954
806	0.100	0.086	−0.014	0.046	−0.054	0.709	0.609
807	0.010	0.231	0.221	0.239	0.229	−0.013	−0.023
808	0.240	0.197	−0.043	0.410	0.170	1.492	1.252
809	0.500	0.121	−0.379	0.067	−0.433	−0.507	−1.007
810	0.190	0.197	0.007	0.203	0.013	0.852	0.662
811	1.150	1.398	0.248	0.026	−1.124	0.324	−0.826
812	2.310	1.757	−0.553	2.503	0.193	0.625	−1.685
813	0.040	0.102	0.062	0.196	0.156	0.077	0.037
814	0.000	0.157	0.157	0.273	0.273	0.135	0.135
815	0.010	0.036	0.026	0.159	0.149	0.146	0.136
816	0.400	0.171	−0.229	0.405	0.005	1.247	0.847
817	0.090	0.036	−0.054	0.136	0.046	0.141	0.051
818	0.160	0.102	−0.058	0.260	0.100	0.379	0.219
819	0.040	0.140	0.100	0.244	0.204	1.788	1.748
820	0.020	0.098	0.078	0.233	0.213	1.463	1.443
821	0.140	0.148	0.008	0.010	−0.130	0.289	0.149
822	0.150	0.080	−0.070	0.213	0.063	1.597	1.447
823	0.220	0.108	−0.112	0.138	−0.082	1.155	0.935
824	0.760	0.537	−0.223	2.629	1.869	1.370	0.610
825	0.080	0.125	0.045	0.125	0.045	1.213	1.133
826	0.000	−0.064	−0.064	0.343	0.343	0.324	0.324
827	0.010	0.066	0.056	0.086	0.076	0.001	−0.009
828	0.000	0.071	0.071	0.131	0.131	0.501	0.501
829	0.490	0.362	−0.128	0.115	−0.375	1.120	0.630
830	1.560	1.616	0.056	2.339	0.779	0.117	−1.443
831	1.200	0.736	−0.464	1.078	−0.122	0.384	−0.816
832	0.160	0.043	−0.117	0.287	0.127	−0.294	−0.454
833	0.340	0.181	−0.159	0.314	−0.026	1.528	1.188
834	0.020	0.031	0.011	0.003	−0.017	0.412	0.392
835	0.030	0.086	0.056	−0.007	−0.037	0.129	0.099
836	0.050	0.173	0.123	0.545	0.495	0.220	0.170
837	0.060	0.069	0.009	0.179	0.119	0.759	0.699
838	0.150	0.113	−0.037	−0.231	−0.381	0.177	0.027
839	0.000	0.108	0.108	0.169	0.169	0.329	0.329

, the prediction performances of the created kNN model on rock type estimations is similar to that of alteration (80% and 74%, respectively). Although the kNN model appears to have a reasonable estimation accuracy for high rock type estimations, the model did not make any QVS lithology predictions. This is considered to be stemming from the insufficient QVS samples in the training set. Actual QVS lithologies were confused with QV lithologies.

For each test point, sample locations (easting, northing, and altitude) and lithological features were used as input values to get the mineral grade estimates. The suggested NN model in literature yielded a $0.507$ for MAE and $0.529$ for $R^2$ in Simulation 23. When the model only used the sample locations as input variables (traditional ANN model), MAE of $0.862$ and $R^2$ of $0.112$ were obtained (Table 9). This demonstrates the fact that the grades can be better estimated if lithological features such as rock type and alteration levels were also used (Figure 7, Figure 8 and Figure 9).

As it can be seen in Figure 10, Model NN and Real NN models provide the closest real distribution grades as compared to traditional NN.

The results have shown that the suggested model has underestimated any grades between 15 ppm and 20 ppm range. Close examination of sample points shows that in the condition where mineralization is controlled by the structure and a test point located near a fault, the network could not ignore the effect of discontinuity of lithology. The proposed model stands on lithological control of mineralization, and it is relatively immune to systems that is structurally controlled. Another notable outcome is that the NN model failed to predict some of the sample points that have a high number of samples in the training set. It could be partly due to a neural network can be successfully utilised to execute probabilistic functions [70]; however, no matter how much network is trained in order to improve the prediction, independent stochastic events cannot be predicted by any neural network models.

5. Conclusions

Accurate grade estimation is a significant part of a mining project, as it highly influences the decisions made in both exploration and exploitation stages of mining process. In this paper, we proposed a grade estimation methodology that utilises kNN and multilayer feed forward neural network that incorporates sample locations, lithological features, and alteration levels. It has been shown in the paper that the a kNN–NN hybrid model can be successfully utilised in a grade estimation task. The proposed model does not require complicated mathematical knowledge or deep assumptions. It is a data-driven method to that utilises the relationship between input and output values. Since the model incorporated geological features, alteration levels, and sample coordinates in the learning process, it can be tailored to fit any other grade modelling tasks. Although the model successfully figured out the relationship between the input and output variables, it ignored the structural influence of mineralization, which is expected as it is generally difficult to recognise. The proposed approach primarily provides the following advantages:

• The grade estimation can be more accurately modelled by having an intermediate modelling step that predicts rock types and alteration features as an input for the subsequent NN model.
• The suggested model does not require any assumptions on the input variables as in geostatistics.
• The method can be easily modified and applied into other mining resources as compared to classical resource estimation techniques.

While the proposed method has the significant advantages, the following drawbacks requires further attention in the application of the proposed method in different cases.

• Inadequate data and depth of network can easily cause over-fitting issues in complex NN structures. The network is highly sensitive to following hyper-parameters: number of hidden layers, activation function type, number of epoch, and learning rate.
• The suggested model is based on lithological control of mineralization and is highly sensitive to the existence of geological discontinuities.

It would be worth it to compare the proposed method with the traditional geostatistical methods on a case study. Furthermore, log of the grade values can be use instead of direct grades itself in the ANN model generations. Comparison of the predicted grades generated by direct value of grades itself vs. log value of the grades can be investigated as future research.