Data Evaluation for Cassiterite and Coltan Fingerprinting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples, Database, Sample Preparation and Analysis
2.1.1. Samples and Database
2.1.2. Sample Preparation
2.1.3. Analysis
2.2. Data Evaluation
2.2.1. KS-D Approach
2.2.2. Areas Ratio Approach
3. Results and Discussion
3.1. Reference Samples Database
3.2. Performance of the Data Evaluation Approaches
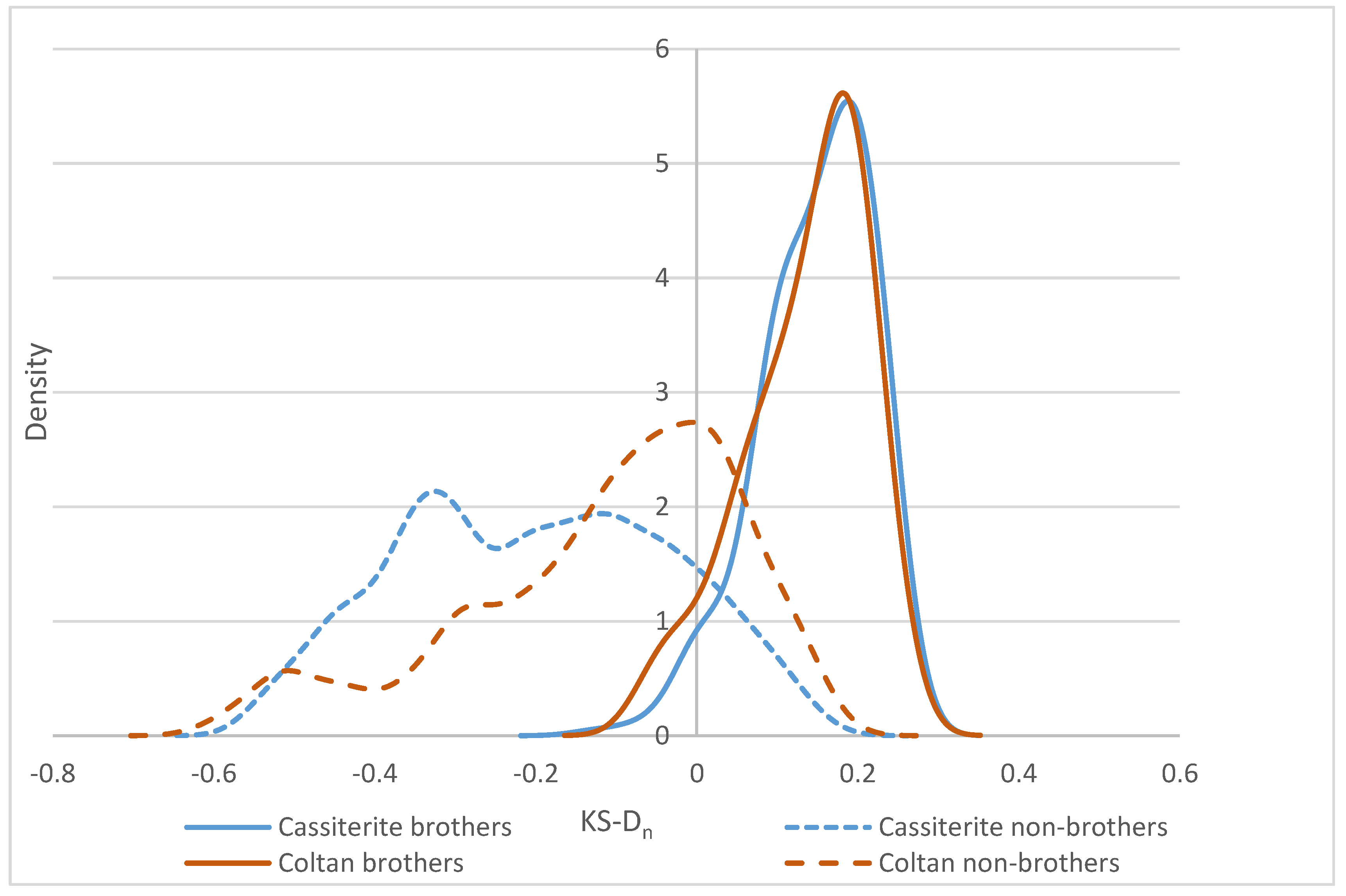
3.2.1. KS-D Approach
3.2.2. Areas Ratio Approach
3.2.3. Comparison of the Performance of Both Data Evaluation Approaches
3.3. Case Studies
3.3.1. Case Study Coltan
KS-D Approach
Areas Ratio Approach
3.3.2. Case Study Cassiterite
KS-D Approach with Deposit-Specific DC
KS-D Approach with Standard DC
Areas Ratio Approach
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- US Congress. Dodd-Frank Wall Street Reform and Consumer Protection Act; Section 1501, Public Law No. 111-203, 21 July 2010, Section 1502; US Congress: Washington, DC, USA, 2010.
- European Parliament and Council. Regulation (EU) 2017/821 of the European Parliament and of the Council of 17 May 2017 laying down supply chain due diligence obligations for Union importers of tin, tantalum and tungsten, their ores, and gold originating from conflict-affected and high-risk areas. Off. J. Eur. Union 2017, 130, 1–20. [Google Scholar]
- OECD. OECD Due Diligence Guidance for Responsible Supply Chains of Minerals from Conflict-Affected and High-Risk Areas, 3rd ed.; OECD Publishing: Paris, France, 2016. [Google Scholar]
- Vogel, C.; Raeymaekers, T. Terr(it)or(ies) of Peace? The Congolese Mining Frontier and the Fight Against “Conflict Minerals”. Antipode 2016, 48, 1102–1121. [Google Scholar] [CrossRef]
- Schütte, P. International mineral trade on the background of due diligence regulation: A case study of tantalum and tin supply chains from East and Central Africa. Resour. Policy 2019, 62, 674–689. [Google Scholar] [CrossRef]
- Franken, G.; Vasters, J.; Dorner, U.; Melcher, F.; Sitnikova, M.; Goldmann, S. Certified Trading Chains in Mineral Production: A Way to Improve Responsibility in Mining. In Non-Renewable Resource Issues: Geoscientific and Societal Challenges; Sinding-Larsen, R., Wellmer, F.-W., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 213–227. [Google Scholar] [CrossRef]
- Young, S.B. Field vignette: Sourcing “conflict-free” minerals from central Africa. In Africa’s Mineral Fortune: The Science and Politics of Mining and Sustainable Development; Taylor and Francis: London, UK, 2018; pp. 300–301. [Google Scholar] [CrossRef]
- Wakenge, C.I.; Dijkzeul, D.; Vlassenroot, K. Regulating the old game of smuggling? Coltan mining, trade and reforms in the Democratic Republic of the Congo. J. Mod. Afr. Stud. 2018, 56, 497–522. [Google Scholar] [CrossRef] [Green Version]
- Zwaan, J.C.; Mertz-Kraus, R.; Renfro, N.D.; McClure, S.F.; Laurs, B.M. Rhodochrosite Gems: Properties and Provenance. J. Gemmol. 2018, 36, 14. [Google Scholar]
- Dalpé, C.; Hudon, P.; Ballantyne, D.J.; Williams, D.; Marcotte, D. Trace Element Analysis of Rough Diamond by LA-ICP-MS: A Case of Source Discrimination? J. Forensic Sci. 2010, 55, 1443–1456. [Google Scholar] [CrossRef]
- Ahmadjan Abduriyim, H.K. Applications of laser ablation–inductively coupled plasma–mass spectrometry (LA-ICP-MS) to gemology. Gems Gemol. 2006, 42, 98–118. [Google Scholar]
- Pornwilard, M.-M.; Hansawek, R.; Shiowatana, J.; Siripinyanond, A. Geographical origin classification of gem corundum using elemental fingerprint analysis by laser ablation inductively coupled plasma mass spectrometry. Int. J. Mass Spectrom. 2011, 306, 57–62. [Google Scholar] [CrossRef]
- Roberts, R.J.; Dixon, R.D.; Merkle, R.K.W. Distinguishing Between Legally and Illegally Produced Gold in South Africa. J. Forensic Sci. 2016, 61, S230–S236. [Google Scholar] [CrossRef] [Green Version]
- Watling, R.J.; Herbert, H.K.; Delev, D.; Abell, I.D. Gold fingerprinting by laser ablation inductively coupled plasma mass spectrometry. Spectrochim. ACTA Part B At. Spectrosc. 1994, 49, 205–219. [Google Scholar] [CrossRef]
- Sirven, J.; Pailloux, A.; M’Baye, Y.; Coulon, N.; Alpettaza, T.; Stephane, G. Towards the determination of the geographical origin of yellow cake samples by laser-induced breakdown spectroscopy and chemometrics. J. Anal. At. Spectrom. 2009, 24, 451–459. [Google Scholar]
- Machault, J.; Barbanson, L.; Augé, T.; Bailly, L.; Orgeval, J.-J. Mineralogical and microtextural parameters in metals ores traceability studies. Ore Geol. Rev. 2014, 63, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Melcher, F.; Sitnikova, M.; Graupner, T.; Martin, N.; Oberthür, T.; Henjes-Kunst, F.; Gäbler, E.; Gerdes, A.; Brätz, H.; Davis, D.; et al. Fingerprinting of conflict minerals: Columbite-tantalite (“coltan”) ores. SGA News 2008, 23, 1–14. [Google Scholar]
- Gäbler, H.-E.; Melcher, F.; Graupner, T.; Bahr, A.; Sitnikova, M.A.; Henjes-Kunst, F.; Oberthür, T.; Brätz, H.; Gerdes, A. Speeding Up the Analytical Workflow for Coltan Fingerprinting by an Integrated Mineral Liberation Analysis/LA-ICP-MS Approach. Geostand. Geoanalytical Res. 2011, 35, 431–448. [Google Scholar] [CrossRef]
- Savu-Krohn, C.; Rantitsch, G.; Auer, P.; Melcher, F.; Graupner, T. Geochemical Fingerprinting of Coltan Ores by Machine Learning on Uneven Datasets. Nat. Resour. Res. 2011, 20, 177–191. [Google Scholar] [CrossRef]
- Gäbler, H.-E.; Rehder, S.; Bahr, A.; Melcher, F.; Goldmann, S. Cassiterite fingerprinting by LA-ICP-MS. J. Anal. At. Spectrom. 2013, 28, 1247–1255. [Google Scholar] [CrossRef]
- Gäbler, H.-E.; Schink, W.; Goldmann, S.; Bahr, A.; Gawronski, T. Analytical Fingerprint of Wolframite Ore Concentrates. J. Forensic Sci. 2017, 62, 881–888. [Google Scholar] [CrossRef]
- Martyna, A.; Gäbler, H.-E.; Bahr, A.; Zadora, G. Geochemical wolframite fingerprinting—the likelihood ratio approach for laser ablation ICP-MS data. Anal. Bioanal. Chem. 2018, 410, 3073–3091. [Google Scholar] [CrossRef] [Green Version]
- Varmuza, K.; Filzmoser, P. Introduction to Multivariate Statistical Analysis in Chemometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef] [Green Version]


| Element | 5th Percentile (mg·kg−1) | 50th Percentile (mg·kg−1) | 95th Percentile (mg·kg−1) |
|---|---|---|---|
| Al | 5.7 | 89.1 | 2440.8 |
| As | <0.22 | 0.22 | 8.83 |
| Ba | <0.18 | <0.18 | 3.26 |
| Bi | <0.03 | <0.03 | 0.96 |
| Ca | <10 | <10 | 44 |
| Cr | <1.2 | <1.2 | 8.2 |
| Fe | 98 | 1115 | 8126 |
| Ga | 0.08 | 1.39 | 22.35 |
| Ge | <0.15 | 0.15 | 1.42 |
| Hf | 0.07 | 36.40 | 430.51 |
| In | <1.9 | <1.9 | 25.9 |
| Mg | <0.1 | <0.1 | 25.7 |
| Mn | <1 | 14 | 1441 |
| Nb | 2 | 1168 | 16,386 |
| Pb | 0.02 | 0.47 | 9.25 |
| Sb | 0.20 | 0.62 | 18.94 |
| Sc | <0.12 | 4.00 | 85.98 |
| Si | <121 | 436 | 2419 |
| Sr | <0.03 | 0.03 | 1.73 |
| Ta | 0.04 | 1738 | 41,480 |
| Th | <0.01 | 0.01 | 1.23 |
| Ti | 26 | 1071 | 5699 |
| U | 0.13 | 1.50 | 19.07 |
| V | <0.24 | 3.67 | 85.77 |
| W | 0.8 | 11.2 | 1357.6 |
| Y | <0.03 | 0.03 | 2.15 |
| Zn | <0.9 | 0.9 | 57.3 |
| Zr | 2 | 389 | 1779 |
| Element | 5th Percentile (mg·kg−1) | 50th Percentile (mg·kg−1) | 95th Percentile (mg·kg−1) |
|---|---|---|---|
| Ta2O5 (%) | 8.9 | 36.2 | 70.1 |
| Nb2O5 (%) | 12.6 | 44.2 | 68.3 |
| MnO (%] | 1.9 | 8.8 | 17.6 |
| FeO (%) | 0.56 | 9.35 | 17.18 |
| SnO2 (%) | 0.01 | 0.13 | 0.76 |
| TiO2 (%) | 0.02 | 0.28 | 1.57 |
| WO3 (%) | 0.01 | 0.12 | 0.93 |
| Al | 9 | 57 | 1360 |
| As | <0.4 | 0.4 | 14.2 |
| Ba | <0.3 | 0.3 | 52.2 |
| Be | <0.9 | <0.9 | 1.8 |
| Bi | <0.11 | 0.11 | 30.86 |
| Ca | <63 | <63 | 460 |
| Ce | <0.03 | 0.13 | 39.86 |
| Dy | <0.08 | 0.78 | 94.21 |
| Er | <0.06 | 0.39 | 39.56 |
| Eu | <0.05 | <0.05 | 1.01 |
| Gd | <0.15 | 0.23 | 35.78 |
| Hf | 18 | 95 | 624 |
| Ho | <0.04 | 0.12 | 14.13 |
| La | <0.04 | 0.03 | 8.99 |
| Li | <7 | 7 | 102 |
| Lu | <0.03 | 0.13 | 12.31 |
| Mg | <4 | 35 | 1273 |
| Mo | <1.3 | 1.9 | 7.6 |
| Nd | <0.08 | 0.08 | 17.60 |
| Pb | 2.7 | 34.2 | 656.5 |
| Pr | <0.01 | 0.01 | 3.13 |
| Rb | <0.4 | <0.4 | 8.3 |
| Sb | <0.04 | <0.04 | 3.98 |
| Sc | 0.5 | 5.9 | 306.0 |
| Si | <281 | 281 | 1842 |
| Sm | <0.10 | 0.10 | 16.23 |
| Sr | <0.2 | 0.2 | 29.8 |
| Tb | <0.05 | 0.11 | 15.29 |
| Th | 0.18 | 3.00 | 73.22 |
| Tl | <0.03 | 0.03 | 7.99 |
| Tm | <0.04 | 0.08 | 8.95 |
| U | 19 | 204 | 1743 |
| Y | 0.05 | 3.94 | 491.92 |
| Yb | <0.10 | 0.83 | 80.75 |
| Zr | 126 | 737 | 4028 |
| Sample | CS1_1 | CS1_2 | CS1_3 | CS1_4 |
|---|---|---|---|---|
| CS1_1 | 0.20 | 0.20 | 0.27 | |
| CS1_2 | 0.20 | 0.18 | 0.25 | |
| CS1_3 | 0.20 | 0.21 | 0.23 | |
| CS1_4 | 0.23 | 0.24 | 0.23 |
| Sample | CS1_1 | CS1_2 | CS1_3 | CS1_4 | CS1_5 | CS1_6 | CS1_7 |
|---|---|---|---|---|---|---|---|
| CS1_1 | 0.27 | 0.33 | 0.26 | −0.26 | −0.06 | −0.24 | |
| CS1_2 | 0.30 | 0.33 | 0.28 | −0.08 | 0.13 | −0.19 | |
| CS1_3 | 0.32 | 0.32 | 0.33 | −0.03 | 0.09 | −0.13 | |
| CS1_4 | 0.26 | 0.29 | 0.30 | 0.05 | 0.07 | −0.13 |
| Sample Left Out | CS2_1 | CS2_2 | CS2_3 | CS2_4 | CS2_5 | CS2_6 | CS2_7 |
|---|---|---|---|---|---|---|---|
| mean | 0.232 | 0.243 | 0.238 | 0.232 | 0.232 | 0.217 | 0.220 |
| sd | 0.041 | 0.035 | 0.037 | 0.040 | 0.045 | 0.035 | 0.039 |
| DC_3sigma | 0.355 | 0.349 | 0.347 | 0.353 | 0.368 | 0.322 | 0.337 |
| DC_2sigma | 0.314 | 0.313 | 0.311 | 0.313 | 0.322 | 0.287 | 0.298 |
| FN_3sigma | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| FN_2sigma | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 50.0% | 16.7% |
| Sample | CS2_1 | CS2_2 | CS2_3 | CS2_4 | CS2_5 | CS2_6 | CS_7 |
|---|---|---|---|---|---|---|---|
| CS2_1 | 0.18 | 0.19 | 0.24 | 0.23 | 0.29 | 0.29 | |
| CS2_2 | 0.18 | 0.15 | 0.17 | 0.22 | 0.25 | 0.24 | |
| CS2_3 | 0.19 | 0.15 | 0.19 | 0.22 | 0.28 | 0.27 | |
| CS2_4 | 0.24 | 0.17 | 0.19 | 0.26 | 0.30 | 0.23 | |
| CS2_5 | 0.19 | 0.21 | 0.20 | 0.24 | 0.23 | 0.25 | |
| CS2_6 | 0.24 | 0.23 | 0.26 | 0.28 | 0.23 | 0.30 | |
| CS2_7 | 0.25 | 0.22 | 0.25 | 0.22 | 0.26 | 0.30 |
| Sample | CS2_1 | CS2_2 | CS2_3 | CS2_4 | CS2_5 | CS2_6 | CS2_7 | CS2_8 | CS2_9 | CS2_10 |
|---|---|---|---|---|---|---|---|---|---|---|
| CS2_1 | 0.63 | 0.58 | 0.56 | 0.49 | 0.38 | 0.52 | −0.80 | −0.08 | −0.37 | |
| CS2_2 | 0.65 | 0.60 | 0.49 | 0.48 | 0.41 | 0.48 | −0.93 | −0.07 | −0.49 | |
| CS2_3 | 0.56 | 0.52 | 0.51 | 0.42 | 0.31 | 0.38 | −0.89 | −0.08 | −0.48 | |
| CS2_4 | 0.62 | 0.62 | 0.62 | 0.43 | 0.43 | 0.50 | −0.90 | −0.11 | −0.45 | |
| CS2_5 | 0.54 | 0.45 | 0.41 | 0.41 | 0.44 | 0.49 | −0.88 | −0.04 | −0.39 | |
| CS2_6 | 0.42 | 0.44 | 0.47 | 0.34 | 0.56 | 0.50 | −0.87 | −0.07 | −0.52 | |
| CS2_7 | 0.57 | 0.54 | 0.45 | 0.50 | 0.59 | 0.46 | −0.81 | −0.17 | −0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gäbler, H.-E.; Schink, W.; Gawronski, T. Data Evaluation for Cassiterite and Coltan Fingerprinting. Minerals 2020, 10, 926. https://doi.org/10.3390/min10100926
Gäbler H-E, Schink W, Gawronski T. Data Evaluation for Cassiterite and Coltan Fingerprinting. Minerals. 2020; 10(10):926. https://doi.org/10.3390/min10100926
Chicago/Turabian StyleGäbler, Hans-Eike, Wilhelm Schink, and Timo Gawronski. 2020. "Data Evaluation for Cassiterite and Coltan Fingerprinting" Minerals 10, no. 10: 926. https://doi.org/10.3390/min10100926
APA StyleGäbler, H.-E., Schink, W., & Gawronski, T. (2020). Data Evaluation for Cassiterite and Coltan Fingerprinting. Minerals, 10(10), 926. https://doi.org/10.3390/min10100926




