The Differences in Evaluation of Flotation Kinetics of Talc Ore Using Statistical Analysis and Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Flotation Test
2.3. Separation Efficiency
2.4. Statistical Analysis and RSM
+ b14X1X4 + b23X2X3 + b24X2X4 + b34X3X4
3. Results and Discussion
3.1. Analysis of Variance and Covariance
- MIBC increases froth yield by increasing the recovery of talc. This has a positive effect on separation efficiency.
- SHMP lowers the yield of the froth product by lowering the recovery of both talc and gangue minerals. However, the drop in gangue minerals recovery is relatively higher, which positively affects froth grade. Effect of SHMP on separation efficiency cannot be statistically proven by the ANOVA test.
- SS negatively affects froth yield by lowering the recovery of both talc and gangue minerals, like SHMP. However, the use of SS results in unambiguously lower separation efficiency.
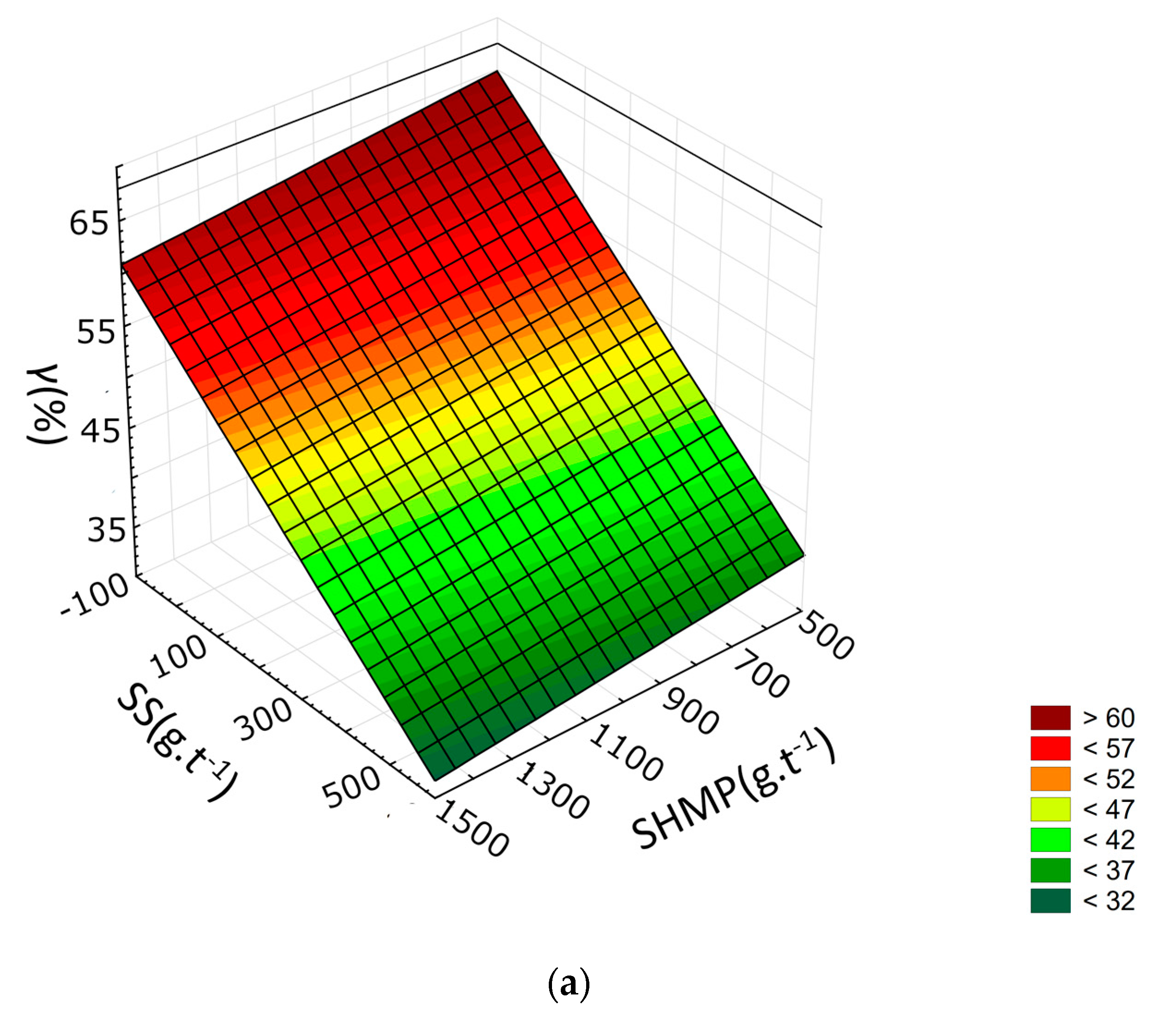
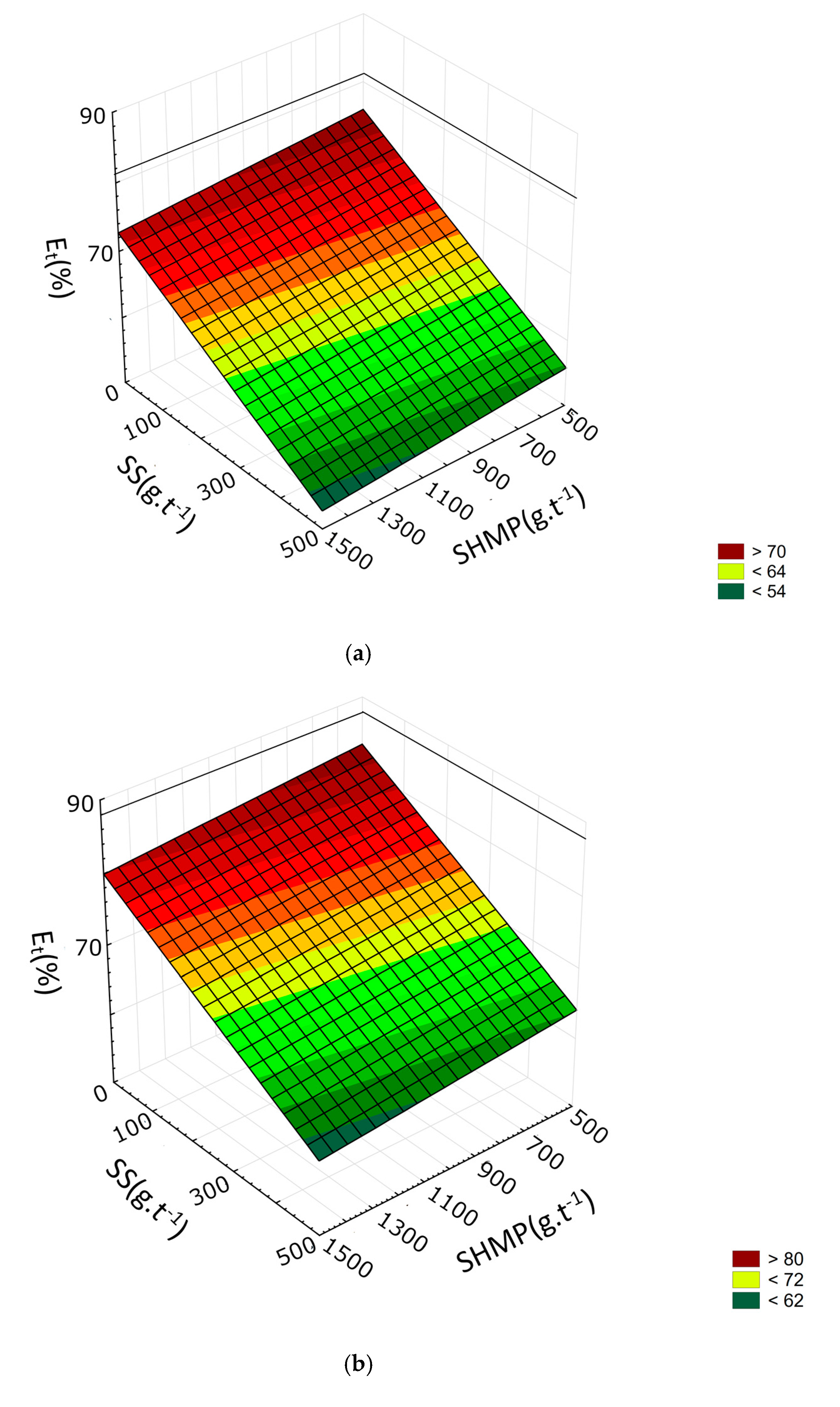
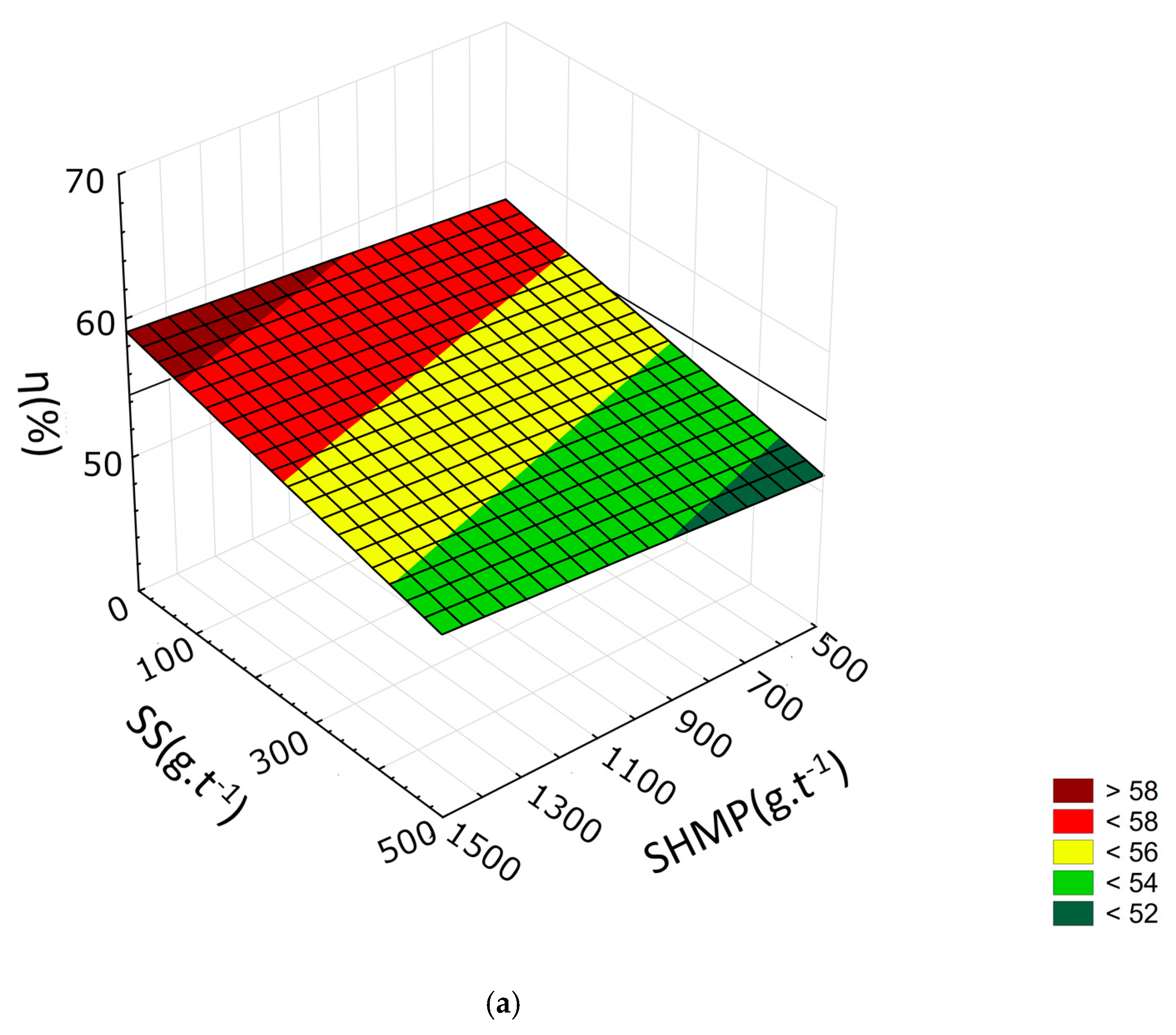
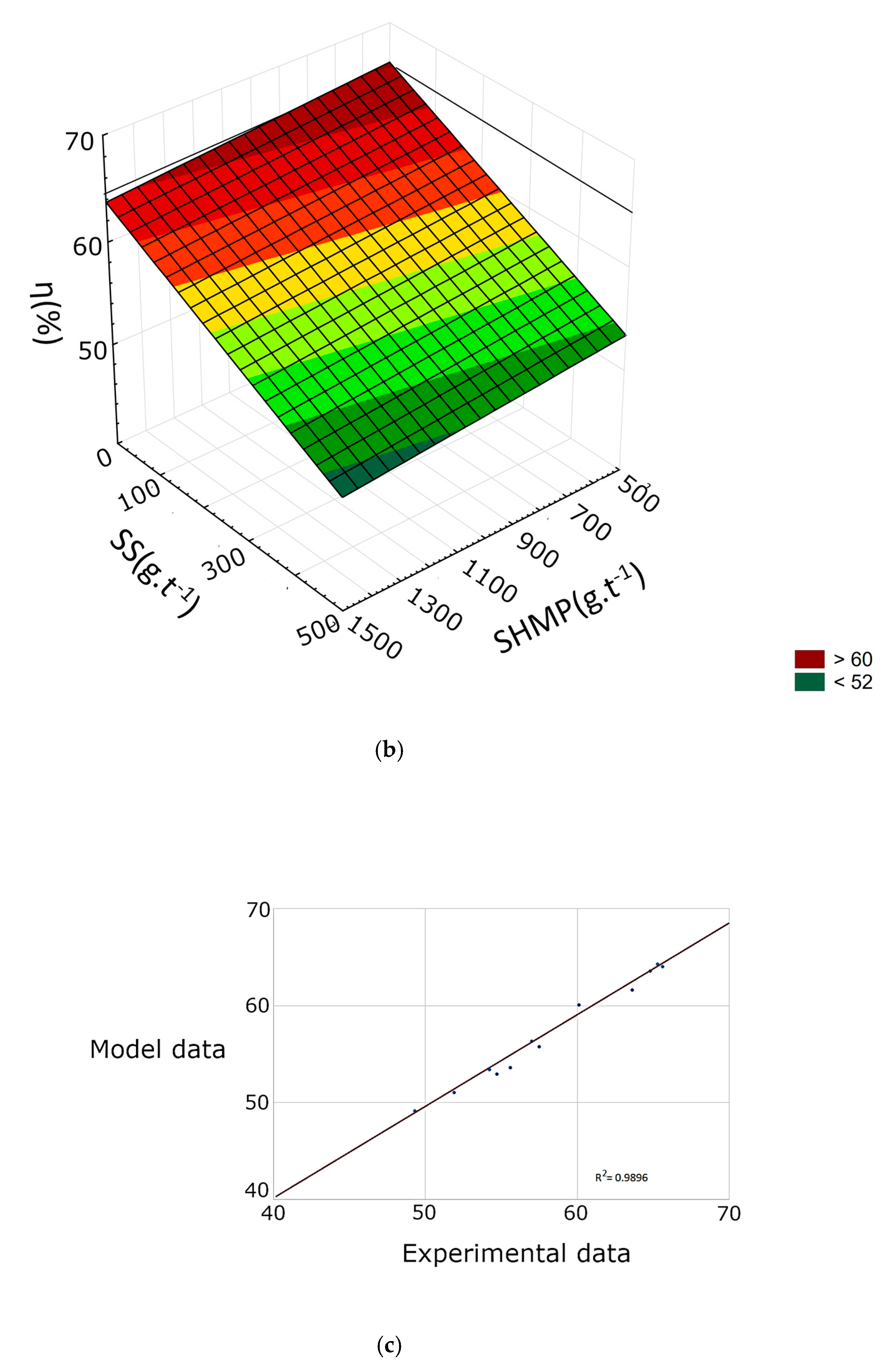
3.2. Response Surface Methodology
4. Conclusions
- SHMP lowers the yield of the froth product by lowering the recovery of both talc and gangue minerals. However, the drop in gangue minerals recovery is relatively higher. SHMP can thus be used to improve froth grade.
- SHMP positively affects separation efficiency, but the effect is more noticeable at lower dosages of the frother. When higher frother dosage is used, there is only a minor increase in separation efficiency caused by SHMP.
- It is not recommended to use SHMP along with SS as it further decreases separation efficiency and only has a minor positive effect on the froth grade.
Author Contributions
Funding
Conflicts of Interest
References
- Shean, B.; Cilliers, J. A review of froth flotation control. Int. J. Miner. Process. 2011, 100, 57–71. [Google Scholar] [CrossRef]
- Wang, G.; Nguyen, A.V.; Mitra, S.; Joshi, J.B.; Jameson, G.J.; Evans, G.M. A review of the mechanisms and models of bubble-particle detachment in froth flotation. Sep. Purif. Technol. 2016, 170, 155–172. [Google Scholar] [CrossRef] [Green Version]
- Bulatovic, S.M. Handbook of Flotation Reagents. In Handbook of Flotation Reagents; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Brezani, I.; Zelenak, F.; Zelenak, M. Collectorless flotation of talc-magnesite ore with respect to particle size. Acta Montan. Slovaca 2013, 18, 176–183. [Google Scholar]
- Yuan, D.; Xie, L.; Shi, X.; Yi, L.; Zhang, G.; Zhang, H.; Liu, Q.; Zeng, H. Selective flotation separation of molybdenite and talc by humic substances. Miner. Eng. 2018, 117, 34–41. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Ibrahim, G.A.; Hassan, M.M. Improvement of Egyptian talc quality for industrial uses by flotation process and leaching. Int. J. Miner. Process. 2007, 83, 132–145. [Google Scholar] [CrossRef]
- Yehia, A.; Al-Wakeel, M. Talc separation from talc-carbonate ore to be suitable for different industrial applications. Miner. Eng. 2000, 13, 111–116. [Google Scholar] [CrossRef]
- Zheng, X.; Manton, P. A potential application of collectorless flotation in a copper/gold operation. Miner. Eng. 2010, 23, 895–902. [Google Scholar] [CrossRef]
- Aghazadeh, S.; Mousavinezhad, S.K.; Gharabaghi, M. Chemical and colloidal aspects of collectorless flotation behavior of sulfide and non-sulfide minerals. Adv. Colloid Interface Sci. 2015, 225, 203–217. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharyya, K. Split and collectorless flotation to medium coking coal fines for multi-product zero waste concept. Fuel Process. Technol. 2007, 88, 585–590. [Google Scholar] [CrossRef]
- Ozdemir, O. Specific ion effect of chloride salts on collectorless flotation of coal. Physicochem. Probl. Miner. Process. 2013, 49, 511–524. [Google Scholar]
- Nguyen, A. Froth Flotation. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Zhang, J.; Subasinghe, N. Development of a flotation model incorporating liberation characteristics. Miner. Eng. 2016, 98, 1–8. [Google Scholar] [CrossRef]
- Gupta, A.; Yan, D. Chapter 16—flotation. In Mineral Processing Design and Operation; Gupta, A., Yan, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lotter, N.; Whiteman, E.; Bradshaw, D. Modern practice of laboratory flotation testing for flowsheet development–A review. Miner. Eng. 2014, 66, 2–12. [Google Scholar] [CrossRef]
- Ruuska, J.; Lamberg, P.; Leiviskä, K. Flotation model based on floatability component approach–PGE minerals case. IFAC Proc. Vol. 2012, 45, 19–24. [Google Scholar] [CrossRef]
- Yianatos, J.; Carrasco, C.; Bergh, L.; Vinnett, L.; Torres, C. Modelling and simulation of rougher flotation circuits. Int. J. Miner. Process. 2012, 112, 63–70. [Google Scholar] [CrossRef]
- Yalcin, E.; Kelebek, S. Flotation kinetics of a pyritic gold ore. Int. J. Miner. Process. 2011, 98, 48–54. [Google Scholar] [CrossRef]
- Szczerkowska, S.; Wiertel-Pochopien, A.; Zawala, J.; Larsen, E.; Kowalczuk, P.B. Kinetics of froth flotation of naturally hydrophobic solids with different shapes. Miner. Eng. 2018, 121, 90–99. [Google Scholar] [CrossRef]
- Censori, M.; La Marca, F.; Carvalho, M.T. Separation of plastics: The importance of kinetics knowledge in the evaluation of froth flotation. Waste Manag. 2016, 54, 39–43. [Google Scholar] [CrossRef]
- Brezani, I.; Marcin, M.; Sisol, M. The effect of sodium hexametaphosphate on natural flotation kinetics of talc ore. In International Conference on Environment and Mineral Processing; Technical University of Ostrava: Ostrava, Czech Republic, 2017; Volume 21, pp. 49–54. ISBN 978-80-248-4049-9. [Google Scholar]
- Andreola, F.; Castellini, E.; Ferreira, J.; Olhero, S.; Romagnoli, M. Effect of sodium hexametaphosphate and ageing on the rheological behaviour of kaolin dispersions. Appl. Clay Sci. 2006, 31, 56–64. [Google Scholar] [CrossRef]
- Feng, B.; Lu, Y.; Feng, Q.; Zhang, M.; Gu, Y. Talc–serpentine interactions and implications for talc depression. Miner. Eng. 2012, 32, 68–73. [Google Scholar] [CrossRef]
- Schulz, N. Separation Efficiency. In Transactions of the Society for Mining Engineers, American Institute of Mining, Metallurgy and Exploration; Society for Mining Metallurgy: Englewood, CO, USA, 1970; Volume 247, pp. 81–87. [Google Scholar]
- Maldonado, M.; Araya, R.; Finch, J. Optimizing flotation bank performance by recovery profiling. Miner. Eng. 2011, 24, 939–943. [Google Scholar] [CrossRef]
- Zanin, M.; Lambert, H.; Du Plessis, C. Lime use and functionality in sulphide mineral flotation: A review. Miner. Eng. 2019, 143, 105922. [Google Scholar] [CrossRef]
- Zhang, N.-N.; Zhou, C.-C.; Pan, J.-H.; Xia, W.; Liu, C.; Tang, M.-C.; Cao, S.-S. The response of diasporic-bauxite flotation to particle size based on flotation to particle size based on flotation kinetic study and neural network simulation. Powder Technol. 2017, 318, 272–281. [Google Scholar] [CrossRef]
- Hadler, K. The link between froth surface grade and flotation feed grade. Miner. Eng. 2015, 78, 32–37. [Google Scholar] [CrossRef]
- Brezani, I.; Zelenak, F. Matlab real-time data acquisition for laboratory froth flotation automation. Acta Montan. Slovaca 2011, 18, 198–205. [Google Scholar]
- Wiese, J.; Becker, M.; Yorath, G.; O’Connor, C. An investigation into the relationship between particle shape and entrainment. Miner. Eng. 2015, 83, 211–216. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K. Entrainment in froth flotation: The degree of entrainment and its contributing factors. Powder Technol. 2016, 288, 202–211. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Zhang, W.; Song, S.; Li, H. A novel method to improve carboxymethyl cellulose performance in the flotation of talc. Miner. Eng. 2019, 131, 23–27. [Google Scholar] [CrossRef]
- Yadav, A.M.; Nikkam, S.; Gajbhiye, P.; Tyeb, M.H. Modeling and optimization of coal oil agglomeration using response surface methodology and artificial neural network approaches. Int. J. Miner. Process. 2017, 163, 55–63. [Google Scholar] [CrossRef]
- Vieceli, N.; Durão, F.; Guimarães, C.; Nogueira, C.A.; Pereira, M.; Margarido, F. Grade-recovery modelling and optimization of the froth flotation process of a lepidolite ore. Int. J. Miner. Process. 2016, 157, 184–194. [Google Scholar] [CrossRef]



| Talc | Silicate I | Silicate II | Quartz | Dolomite | Pyrite | ||
|---|---|---|---|---|---|---|---|
| LOI | (%) | 4.54 | 1.97 | 3.55 | 2.09 | 47.54 | 32.75 |
| SiO2 | (%) | 61.32 | 58.1 | 64.82 | 85.32 | 3.44 | - |
| MgO | (%) | 30.84 | 10.45 | 11.61 | 7.74 | 19.75 | - |
| CaO | (%) | 0.52 | 2.15 | 3.23 | 2.15 | 27.46 | - |
| Fe2O3 | (%) | 0.87 | 2.96 | 3.45 | 0.69 | 0.99 | 63.74 |
| Al2O3 | (%) | 0.42 | 17.58 | 12.64 | 1.27 | 0.19 | 0.59 |
| Mn | (%) | 0.202 | 0.234 | 0.245 | 0.169 | 0.215 | 0.312 |
| Cu | (%) | 0.074 | 0.08 | 0.095 | 0.064 | 0.054 | 0.115 |
| Zn | (%) | 0.006 | 0.01 | 0.012 | 0.008 | 0.009 | 0.006 |
| Pb | (%) | 0.007 | 0.012 | 0.022 | 0.015 | 0.028 | 0.021 |
| ∑ | (%) | 98.799 | 93.546 | 99.674 | 99.516 | 99.676 | 97.534 |
| # | 100 | 110 | 111 | 112 | 120 | 121 | 200 | 210 | 211 | 220 | 221 | 222 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MIBC | 50 | 50 | 50 | 50 | 50 | 50 | 80 | 80 | 80 | 80 | 80 | 80 |
| SHMP | 0 | 500 | 500 | 500 | 1500 | 1500 | 0 | 500 | 500 | 1500 | 1500 | 1500 |
| SS | 0 | 0 | 250 | 500 | 0 | 250 | 0 | 0 | 250 | 0 | 250 | 500 |
| # | Froth Yield (%) | Froth Grade (%) | Talc Recovery (%) | Gangue Recovery (%) | Efficiency (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2γ | 5γ | 10γ | 2c | 5c | 10c | cc | 2Εt | 5Εt | 10Εt | 2Εg | 5Εg | 10Εg | 2η | 5η | 10η | |
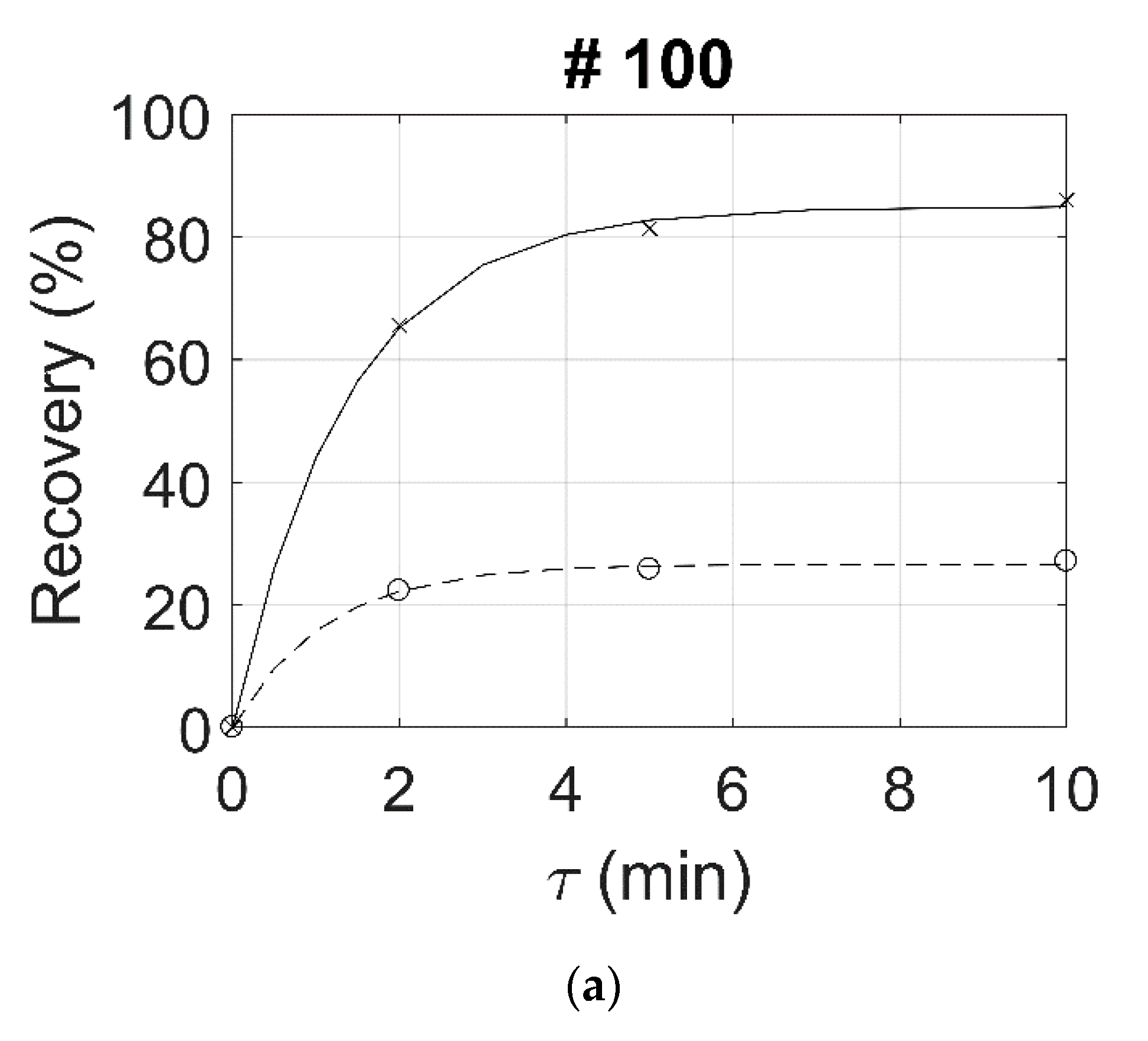
| 100 | 54.2 | 66.7 | 70.5 | 89.2 | 89.8 | 89.9 | 34.9 | 65.6 | 81.4 | 86.0 | 22.3 | 25.8 | 27.1 | 43.3 | 55.6 | 58.9 |
| 110 | 49.0 | 57.7 | 62.2 | 93.3 | 93.4 | 93.4 | 43.2 | 61.4 | 72.3 | 78.1 | 12.8 | 14.9 | 16.0 | 48.7 | 57.5 | 62.1 |
| 111 | 34.0 | 45.7 | 52.4 | 95.5 | 95.2 | 95.1 | 43.4 | 46.1 | 61.7 | 70.7 | 5.2 | 7.5 | 8.7 | 40.9 | 54.2 | 62.0 |
| 112 | 28.8 | 41.4 | 48.7 | 96.1 | 95.9 | 95.5 | 44.0 | 40.1 | 57.4 | 67.3 | 3.6 | 5.5 | 7.2 | 36.5 | 51.9 | 60.1 |
| 120 | 48.0 | 57.2 | 61.3 | 93.2 | 93.4 | 93.5 | 39.1 | 61.8 | 73.8 | 79.1 | 11.8 | 13.7 | 14.5 | 50.0 | 60.1 | 64.6 |
| 121 | 37.8 | 47.8 | 53.8 | 95.2 | 94.7 | 94.4 | 44.3 | 50.5 | 63.6 | 71.3 | 6.3 | 8.8 | 10.5 | 44.2 | 54.7 | 60.8 |
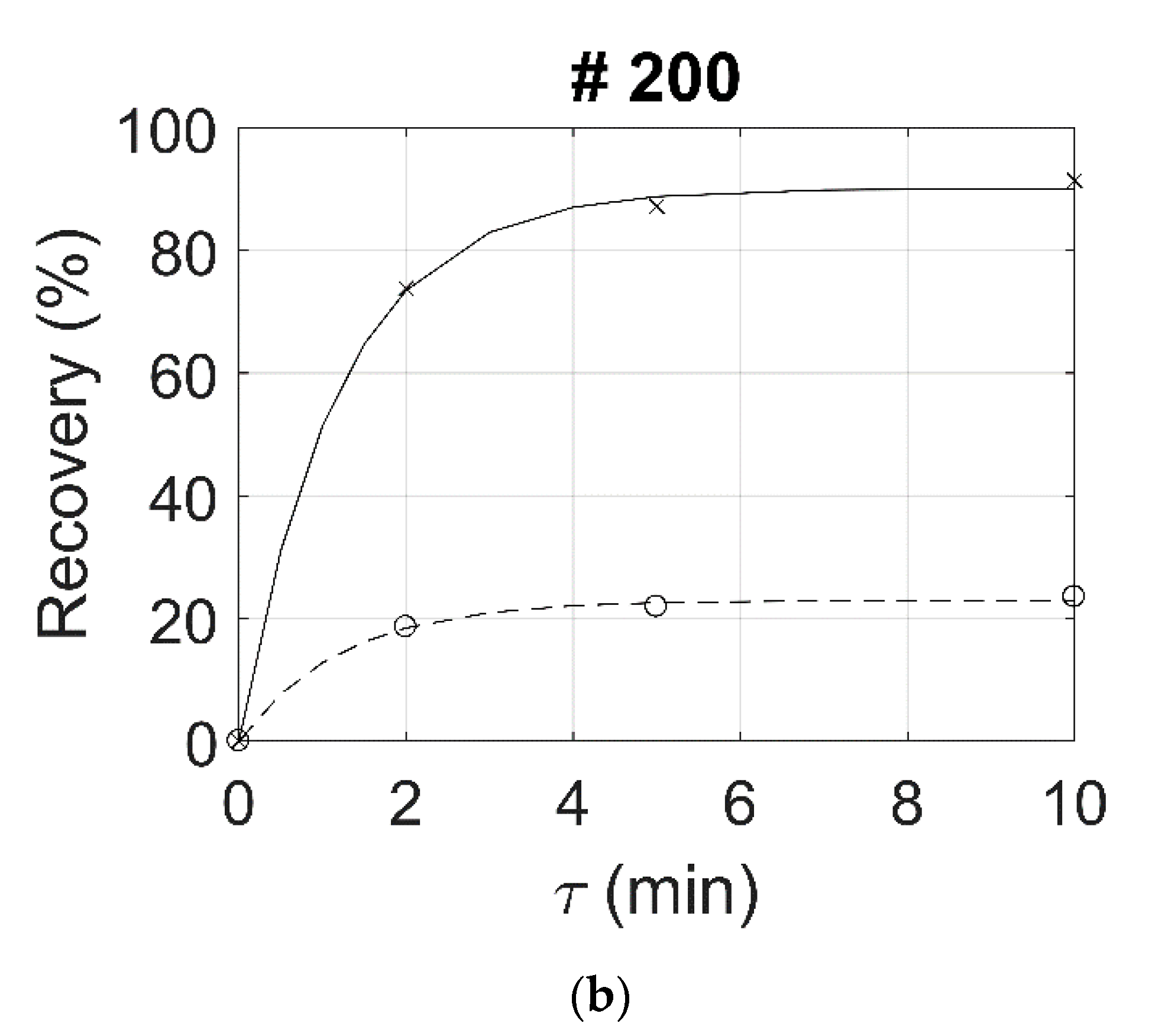
| 200 | 57.4 | 67.8 | 71.2 | 90.3 | 90.4 | 90.2 | 20.9 | 73.8 | 87.2 | 91.4 | 18.6 | 21.9 | 23.5 | 55.1 | 65.3 | 67.9 |
| 210 | 50.8 | 60.1 | 64.1 | 93.0 | 93.1 | 93.1 | 29.3 | 67.3 | 79.6 | 85.0 | 12.0 | 14.0 | 14.8 | 55.3 | 65.6 | 70.2 |
| 211 | 45.4 | 55.2 | 60.6 | 94.5 | 94.r | 93.7 | 32.8 | 61.6 | 74.4 | 81.5 | 8.3 | 10.8 | 12.6 | 53.3 | 63.6 | 68.9 |
| 220 | 53.0 | 61.6 | 65.7 | 92.9 | 92.8 | 92.7 | 30.1 | 69.1 | 80.2 | 85.5 | 13.1 | 15.4 | 16.6 | 55.9 | 64.8 | 68.9 |
| 221 | 46.3 | 56.2 | 60.6 | 93.2 | 92.3 | 92.4 | 40.4 | 60.2 | 72.4 | 77.8 | 11.1 | 15.3 | 17.1 | 49.1 | 57.0 | 60.7 |
| 222 | 32.6 | 44.1 | 51.1 | 93.8 | 93.1 | 92.7 | 44.6 | 44.2 | 59.2 | 68.5 | 6.6 | 9.9 | 12.1 | 37.6 | 49.3 | 56.4 |
| Froth Yield | Froth Grade | Talc Recovery | Gangue Recovery | Efficiency | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2γ | 5γ | 10γ | 2c | 5c | 10c | 2Εt | 5Εt | 10Εt | 2Εg | 5Εg | 10Εg | 2η | 5η | 10η | |
| MIBC | 0.009 | 0.013 | 0.012 | 0.174 | 0.082 | 0.045 | 0.002 | 0.002 | 0.001 | 0.394 | 0.323 | 0.272 | 0.004 | 0.017 | 0.046 |
| SHMP | 0.097 | 0.019 | 0.012 | 0.005 | 0.008 | 0.006 | 0.195 | 0.022 | 0.016 | 0.010 | 0.012 | 0.010 | 0.383 | 0.405 | 0.220 |
| SS | 0.000 | 0.000 | 0.001 | 0.042 | 0.175 | 0.341 | 0.000 | 0.000 | 0.000 | 0.011 | 0.042 | 0.083 | 0.002 | 0.012 | 0.062 |
| 5γ | 5c | 5Εt | 5Εg | 5η | |
|---|---|---|---|---|---|
| MIBC | + | NA | + | NA | + |
| SHMP | − | + | − | − | NA |
| SS | − | NA | − | − | − |
| Froth Yield (%) | Talc Recovery (%) | Separation Efficiency (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2γ | 5γ | 10γ | 2Ε | 5Ε | 10Ε | 2η | 5η | 10η | |
| R2 | 0.9332 | 0.9046 | 0.9005 | 0.9511 | 0.9248 | 0.9289 | 0.9631 | 0.9896 | 0.9546 |
| b0 | 44.9773 | 58.8772 | 63.9344 | 47.5381 | 64.4784 | 70.7007 | 24.2172 | 37.6106 | 42.8651 |
| b1 | 1.312 × 10−1 | 8.302 × 10−2 | 6.552 × 10−2 | 3.077 × 10−1 | 2.589 × 10−1 | 2.393 × 10−1 | 3.941 × 10−1 | 3.546 × 10−1 | 3.298 × 10−1 |
| b2 | −4.137 × 10−3 | −7.963 × 10−3 | −7.758 × 10−3 | 1.528 × 10−3 | −2.632 × 10−3 | −2.161 × 10−3 | 1.366 × 10−2 | 1.142 × 10−2 | 1.245 × 10−2 |
| b3 | −5.818 × 10−2 | −5.237 × 10−2 | −4.433 × 10−2 | −5.487 × 10−2 | −4.201 × 10−2 | −2.977 × 10−2 | −1.532 × 10−2 | 1.220 × 10−3 | 1.354 × 10−2 |
| b12 | 3.023 × 10−5 | 6.560 × 10−5 | 6.407 × 10−5 | −4.588 × 10−5 | −1.150 × 10−5 | −1.576 × 10−5 | −1.672 × 10−4 | −1.542 × 10−4 | −1.576 × 10−4 |
| b13 | 1.974 × 10−4 | 1.311 × 10−4 | 1.162 × 10−4 | 1.608 × 10−4 | 2.884 × 10−5 | 6.233 × 10−6 | 9.357 × 10−5 | −4.262 × 10−5 | −7.875 × 10−5 |
| b23 | 3.585 × 10−6 | 6.964 × 10−6 | 6.208 × 10−6 | −2.345 × 10−6 | 8.731 × 10−7 | −1.039 × 10−6 | −1.753 × 10−5 | −1.842 × 10−5 | −2.134 × 10−5 |
| γ | Εt | η | |
|---|---|---|---|
| R2 | 0.9419 | 0.9235 | 0.9769 |
| b0 | 39.1267 | 39.8691 | 14.7392 |
| b1 | 1.3586 | 3.3401 × 10−1 | 4.4712 × 10−1 |
| b2 | −5.4260 × 10−3 | 9.5193 × 10−4 | 1.4026 × 10−2 |
| b3 | −6.2395 × 10−2 | −5.8103 × 10−2 | −1.3931 × 10−2 |
| b4 | 2.5204 × 101 | 3.1809 × 101 | 3.0238 × 101 |
| b12 | 5.3303 × 10−5 | −2.5306 × 10−5 | −1.5965 × 10−4 |
| b13 | 1.4821 × 10−4 | 6.6291 × 10−5 | −9.2658 × 10−6 |
| b14 | −6.3902 × 10−2 | −9.8966 × 10−2 | −1.3145 × 10−1 |
| b23 | 5.5854 × 10−6 | −8.6916 × 10−7 | −1.9094 × 10−5 |
| b24 | −1.7899 × 10−3 | −2.9662 × 10−3 | −2.4739 × 10−3 |
| b34 | 1.6149 × 10−2 | 2.4385 × 10−2 | 2.0616 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcin, M.; Sisol, M.; Kudelas, D.; Ďuriška, I.; Holub, T. The Differences in Evaluation of Flotation Kinetics of Talc Ore Using Statistical Analysis and Response Surface Methodology. Minerals 2020, 10, 1003. https://doi.org/10.3390/min10111003
Marcin M, Sisol M, Kudelas D, Ďuriška I, Holub T. The Differences in Evaluation of Flotation Kinetics of Talc Ore Using Statistical Analysis and Response Surface Methodology. Minerals. 2020; 10(11):1003. https://doi.org/10.3390/min10111003
Chicago/Turabian StyleMarcin, Michal, Martin Sisol, Dušan Kudelas, Igor Ďuriška, and Tomáš Holub. 2020. "The Differences in Evaluation of Flotation Kinetics of Talc Ore Using Statistical Analysis and Response Surface Methodology" Minerals 10, no. 11: 1003. https://doi.org/10.3390/min10111003
APA StyleMarcin, M., Sisol, M., Kudelas, D., Ďuriška, I., & Holub, T. (2020). The Differences in Evaluation of Flotation Kinetics of Talc Ore Using Statistical Analysis and Response Surface Methodology. Minerals, 10(11), 1003. https://doi.org/10.3390/min10111003








