1. Introduction
With the progress of deep-sea exploration technology and depletion of terrestrial mineral resources, the exploration for seafloor mineral resources has been paid considerable attention by various countries [
1]. Since the first discovery of seafloor hydrothermal vent at mid-ocean ridges in the late 1970s [
2]
, the seafloor polymetallic sulfides have gradually become a new type of mineral resources rich in metallic elements of Cu, Fe, Zn, Mn, and Pb [
3,
4]. Due to its great potential value, it will become an important part of exploitable marine mineral resource, and it is also one of the strategic alternative resources for sustainable development in the 21st century. In July 2011, the International Seabed Authority (ISA) approved China’s application for a 10,000 km
2 region of the seafloor along the Southwest Indian Ridge (SWIR), and China have granted to exclusive exploration rights and preferential commercial mining rights in the area [
5]. As regulated by the contract, by 2021 China can only retain exploration and mining rights of 25% of its area. In this regard, application of mineral prospectivity mapping (MPM) techniques to delineate potential areas that likely contain sulfide occurrences in this region of interest is urgent.
In the past decades, researches on MPM techniques have mainly focused on the following four aspects [
6,
7,
8]: (1) MPM based on probability statistics (e.g., the weights-of-evidence); (2) MPM based on non-linear theory (e.g., fractal and multifractal); (3) MPM based on 3D modeling technology; and (4) MPM based on big data and machine learning (e.g., logistic regression, artificial neural network etc.). Generally, those MPM techniques can be divided into two categories of data-driven and knowledge-driven according to the types for assigning weights to each evidence layer [
9,
10]. The data-driven method analyzes and quantifies the spatial correlation between each evidential layer and the deposit location of common genesis, which is very applicable for well-explored areas [
11]. Data-driven methods consist of logistic regression [
12], weight of evidence [
13], artificial neural network [
14,
15,
16], support vector machine [
6], random forest [
17], and evidence belief function [
18]. Incontrast, based on expert knowledge and judgment, the knowledge-driven approach qualitatively evaluates the relationship between each evidence layer and the deposits sought [
13]. Analysts use expert opinions to evaluate the relative importance of spatial evidence and provide effective support for decision-making [
19]. Common methods include fuzzy logic [
20], index overlay [
20], boolean logic [
13] and fuzzy analytic hierarchy process (AHP) [
19,
21]. Comparing this approach to the data-driven method required a certain number of discovered mineral deposits; the knowledge-driven techniques are suitable for undeveloped areas where no or very few mineral deposits are known to occur. Due to a small number of hydrothermal points occurring in the study area, the knowledge-driven methods were selected for prediction in our research.
In this paper, fuzzy logic and fuzzy AHP were applied to quantitatively predict seafloor sulfide resources in the Southwest Indian Ridge between 46° and 52°E. The objectives include the demonstration of two knowledge-driven methods for MPM in seafloor sulfides, generation of seafloor sulfide prospectivity map for further exploration, and comparison of the performance of the two methods.
2. Geological Background
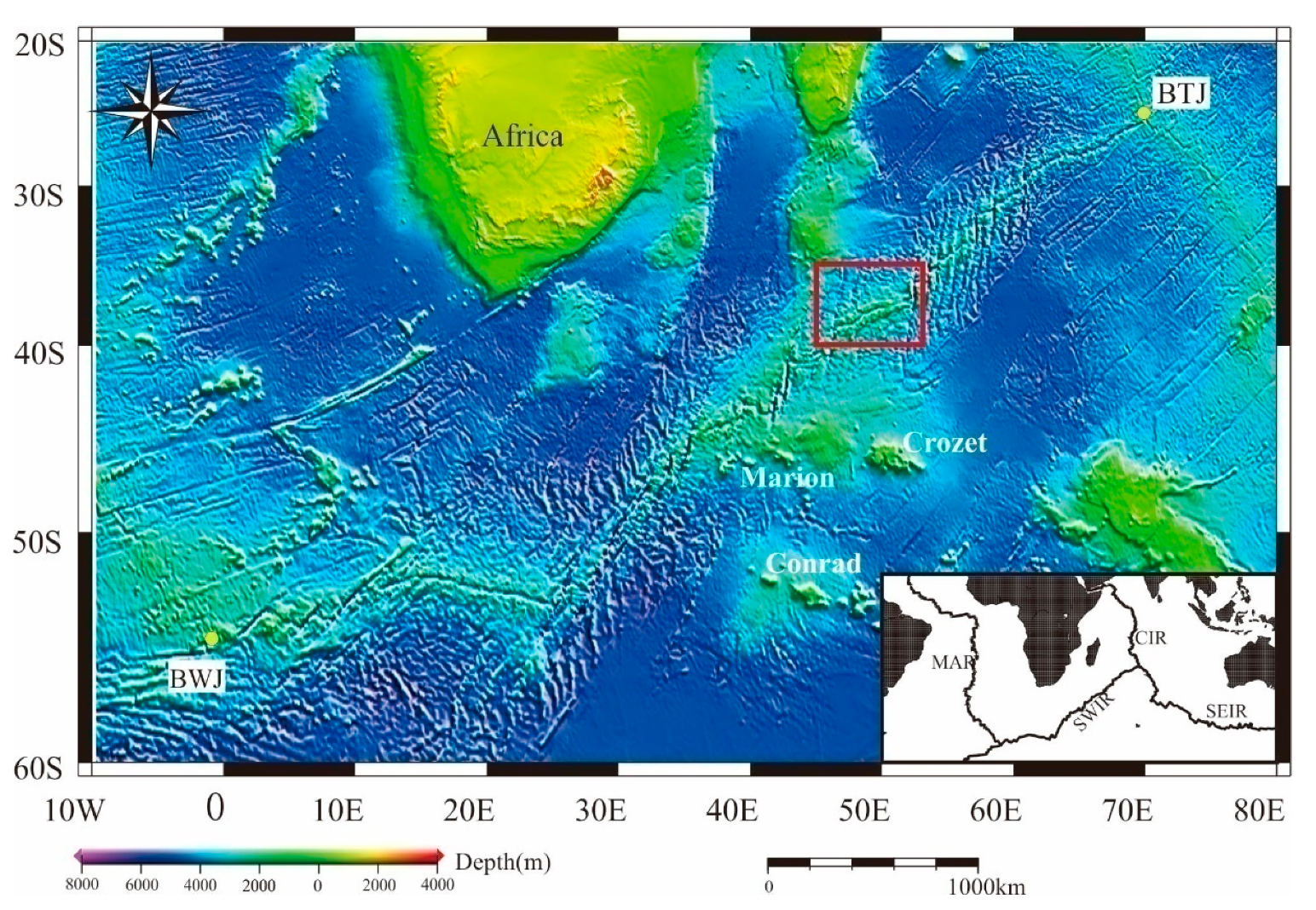
The Southwest Indian Ridge (SWIR), separating the Antarctic and African Plates, is the ultraslow spreading ridges with a full spreading rate of 14 km/Ma [
22]. The west side of SWIR intersects with the Mid-Atlantic Ridge (MAR) and America-Antarctic Ridge (AAR) at the Bouvet Triple Junction (BTJ, 55° S, 00°40′ W), while the east side intersects with the Central Indian Ridge (CIR) and the Southeast Indian Ridge (SEIR) at the Rodrigues Triple Junction (RTJ, 25°30′ S, 70° E) (
Figure 1), with a total length of about 8000 km [
23]. Along-axis topographic and geophysical surveys revealed that the SWIR may be separated into some subsections, differing in the crustal thickness, obliquity of the ridge axis, topographic and geomorphological characteristics, mantle composition, and magmatic activity [
1,
24,
25,
26].
The study area belongs to the subsection between the Indomed and Gallieni transform faults and displays constant and slight overall obliquities, with a water depth varying from ~1500 m to ~4000 m [
27]. The ridge axis in this region is E-NE striking with rugged terrain and well-developed central rift. The dominant rock in exposed seafloor is basalt, also including diabase, gabbro, and peridotite [
25]. Previous studies have proved that this region has favorable conditions to generate seafloor hydrothermal activity and form sulfide deposits [
26].It presents strong negative Bouguer gravity anomalies in this region, indicating active crust-mantle exchange to provide a heat source [
26,
27,
28]. Melt inclusion and host glass compositions indicate higher degrees of melting fractions in the mantle melting column [
29]. The detachment fault has exposed lower crust and mantle materials on the seafloor inferred by gravity, magnetic, borehole and seismic geophysical surveys, favoring the formation of an oceanic core complex and hydrothermal circulation system [
30]. In addition, hydrothermal activity in this region is significantly associated with hot spots such as Crozet, Conrad, and Marion, indicating the strong ridge–hotspot interactions [
23]. More and more countries and studies have paid increasing attention to this segment. The polymetallic sulfide exploration contract zone of China is also mainly located in this area. Since the Longqi hydrothermal field discovered in this region in 2007, some other hydrothermal fields have been discovered consecutively by Chinese Dayang cruises, such as Yuhuang, Duanqiao hydrothermal fields, etc. [
1,
28].
3. Data Acquisition and Method
3.1. Data
The study area is located in the southern hemisphere, with an area of about 350,000 km
2. Data sets of topographic, geophysical, geological, and other information are used as evidence sources for mineralization prediction. Topographic information mainly includes water depth and slope conditions. Geophysical information includes gravity and magnetic conditions. Geological information includes structure, ocean crust age, and sediment thickness. Other information mainly includes the distribution characteristics of seismic points and the size of the spreading rates. The datum is derived from the public data of GeoMapApp. Water depth data and seismic point data are from the US Geological Survey. The former is a 30″resolutions, which are a fusion of multi-beam sounding and satellite altimetry. The latter selects data with magnitudes greater than 5 from 1950 to 2013. Gravity, magnetic data and spreading rate data are from the US National Geophysical Data Center, with a resolution of 2′. The structure is mainly derived from the inference of geophysical information. Ocean crust age data (resolution 2′) and sediment thickness data (resolution 5′) are from the National Oceanic and Atmospheric Administration. Hydrothermal point data in the study area mainly come from the hydrothermal vent database and published research results [
1]. A spatial database was constructed using ArcGIS in accordance with Chinese database standards and specifications using geographic coordinate system GCS_WGS_1984.
3.2. Fuzzy Logic
In 1965, American mathematician L. Zadeh first proposed the fuzzy set theory, marking the birth of fuzzy mathematics [
31].In order to establish a mathematical model of fuzzy objects, L. Zadeh generalized the concept of ordinary sets that only take two values of 0 and 1 as the concept of fuzzy sets that take infinitely many values in the interval [0, 1], and used the concept of “membership” to accurately characterize the relationship between elements and fuzzy sets. The value of fuzzy membership can also be assigned through the fuzzification process [
32]. After assigning fuzzy membership values to each category of dataset, the data set must be combined with one or more fuzzy factors to generate a map of mineral potential.
If
X is a collection of all evidence layers
Xi (i = 1, 2, 3,...
n), each evidence layer has
r levels and is defined as (
j = 1, 2, 3,...,
r), then the
n fuzzy sets
Ai (i = 1,2,3,...,
n) of the evidence layer
X can be defined as
where
μA is a membership function. When 0.5 <
μA <1,
xij is favorable for mineralization. When
μA = 0.5, whether
xij is favorable for mineralization cannot be judged. When 0 <
μA < 0.5,
xij is not favorable for mineralization. There are various forms of membership functions [
33], and we uses the s-shaped membership function, which can be expressed as
In this formula, xij calculated by xij = wi × wj represents the j-th level of the i-th evidence layer, a and b are determined by the shape of the function. Here, the value of a and b are assigned 0.1 and 50, respectively.
A fuzzy set operator is used to synthesize
Ai to generate a comprehensive fuzzy set
F. Fuzzy AND, fuzzy OR, fuzzy algebraic sum, fuzzy algebraic product, and fuzzy gamma are the common fuzzy operators [
34].
F is the final score for each category of the evidence, which can be expressed as
3.3. Fuzzy AHP
The concept of analytic hierarchy process was originally proposed by Satty in the mid-1970s, and is a well-known technique in the multiple criteria decision-making techniques [
35,
36]. The technology can address complex problems by converting them into simple forms [
37,
38]. In this paper, a fuzzy AHP method using triangular fuzzy number processing is used to establish a mineral potential prediction model. Seven steps involved in applying fuzzy AHP for MPM are summarized as follows [
39,
40]:
(1) Construction of a hierarchy. In the first step, the complex decision-making problem is reduced to a hierarchical structure of interrelated decision-making elements. Based on expert opinions, the evaluation system for mineral prediction is divided into three levels: the target level, the criterion level, and the plan level.
(2) Preparation of evidential layers. Map layers are converted into rasters in the GIS environment.
(3) Construction of pairwise comparison matrix. Pairwise comparisons can be obtained by asking experts about the association between the criterion and the target.
(4) Checking for consistency ratio (CR).
If the pairwise comparison matrix A = (
aij)
m ×
m satisfies
aij =
aikakj, I, j, k = 1,.., m, then A is considered to be completely consistent, otherwise it is considered to be inconsistent. A can be tested by the consistency ratio (CR) defined below. If CR ≤ 0.1, A is considered to be consistent; otherwise, the pairwise comparison matrix must be modified to satisfy the condition.
where
λmax is the maximum eigenvalue of the matrix, and RI is the average random consistency index. The consistency of the pairwise comparison judgments can not only measure the consistency of decision makers but also evaluates the quality of the model.
(5) Construction of fuzzy evaluation matrix.
The fuzzy comprehensiveness value of the
i-th target is defined as
Among them,
(j = 1,2,..., m) is a triangular fuzzy number. If M
1 = (l
1, m
1, μ
1) and M
2 = (l
2, m
2, μ
2), then the probability of M
1 > M
2 is
(6) Calculation of normalized weights.
(7) Using fuzzy operators.
The final vision map is generated after the data of all scheme layers and weights are synthesized using fuzzy operators.
4. Conceptual Model of Seafloor Polymetallic Sulfide Deposit
Seafloor polymetallic sulfide deposit is formed by water–rock hydrothermal processes in the oceanic crust, which are closely related to tectonic and magmatic activities and wall rock properties [
41]. Many geological factors, such as water depth, stability of hydrothermal system, permeability, mixing process, fluid boiling, venting, and geological cap rock conditions, influence the metallogenic processes and control the occurrence of polymetallic sulfides [
42,
43]. As shown in the metallogenic model (
Figure 2), the formation of Duanqiao hydrothermal field for polymetallic sulfides was largely due to the role of the normal faults with high angle as well as long-term and stable supply of magma and heat sources from axial magma chamber (AMC) [
43].Hydrothermal circulation strongly influenced by magmatic and tectonic processes, controlled the transfer of energy and material [
5].
The mineral systems approach is usually proposed to the identify crucial criteria and establish a conceptual model, and its major components are as follows: (i) sources of mineralizing fluids and metallic element compositions; (ii) energy gradients that drive the movement of fluids; (iii) migration pathways for large amount of fluids; (iv) physical and chemical traps for ore precipitation; and finally (v) preservation of the deposits. In the seafloor sulfide mineral system of this research, three groups of factors are considered to be essential, which are source, pathway of ore-forming fluids, and favorable physico–chemical conditions for sulfide deposition and preservation. On the basis of the latest data of global hydrothermal vent sites and the results of seafloor polymetallic sulfide deposits in SWIR [
1,
5,
23,
44,
45], the conceptual model that constrains the formation and distribution of seafloor sulfide deposits was established. The exploration criteria can be inferred from various datasets to extract direct or indirect criteria in the form of evidential layers.
(1) Hydrothermal sites. Hydrothermal vents and related sulfide samples are discovered by the near-bottom surveys, such as deep-sea tows, remotely operated underwater vehicles, human occupied vehicles, and autonomous underwater vehicles [
1]. Previous works have also focused on characterizing hydrothermal plume patterns to explore new hydrothermal sites [
46]. There will be a higher possibility to find sulfides near or in the vicinity of the hydrothermal locality compared to other areas. In this regard, hydrothermal sites directly provide material source information.
(2) Topography factor. Topography is closely related to the physico–chemical conditions. Hydrothermal activity in different tectonic environments has significantly different water depth distribution characteristics. Water depth plays a crucial role in the formation and distribution of polymetallic sulfides on the ocean floor. Studies have shown that most seafloor polymetallic sulfide occurrences occur at the water depth range between 2000 and 3000 m [
47].Modern submarine hydrothermal activity is mainly distributed on negative terrain in high-bottom terrain, so slope can be used as a predictive factor.
(3) Geological factors. Geological factors are directly associated with the pathway of ore-forming fluids (e.g., Subsea fault) and physico–chemical conditions (e.g., the sedimentary cap). Subsea fault structure is the most important ore-conducting and ore-holding channel in the hydrothermal active area. Submarine hydrothermal activity and its mineralization are closely related to the tectonic evolution of the oceanic plate. The distance between the position of the hydrothermal point and the ocean ridge can be limited by the age of the ocean crust. In the hydrothermal active zone, the presence of the sedimentary cap layer facilitates the precipitation and aggregation of metal elements, which can obviously promote the formation of hydrothermal products such as hydrothermal sulfides on a larger scale.
(4) Geophysical factor. Geophysical factors can also indirectly support the physico–chemical information. If the seafloor hydrothermal sulfide area has thick sedimentary layers and the thickness of the sedimentary layer changes greatly, the density difference will become larger. There is a certain magnetic difference between the sulfide deposit and the surrounding rocks, which can indicate the existence of the sulfide deposit. Therefore, gravity and magnetic anomalies are important prospecting indicators in the exploration of seabed polymetallic sulfide resources.
(5) Others. Seismic and volcanic activities on the sea floor mean that regional crustal activity is more active. Different spreading rates of the mid-ocean ridge tectonic environment have significantly different characteristics of deep magmatic activity, fault structure, and crustal thickness. They can indirectly reflect the material source and pathway of ore-forming fluids information.
These ore-controlling layers in the SWIR were used as evidence, which is summarized as follows: water depth, slope, gravity, magnetic force, structure, ocean crust age, sediment thickness, seismic point density, and spreading rate. The results of each layer are shown in
Figure 3. Buffer analysis was conducted on the structural data using ArcGIS. The central buffer radius was 5000m, the buffer interval was set to 5000 m, and the maximum radius was 30,000 m. The dilation rate was analyzed by inverse distance weighting. Constructed data were reclassified based on buffer level; other data were reclassified with quantiles at intervals.
7. Conclusions
This paper mainly discusses the application of knowledge-driven approaches to predict the seafloor polymetallic sulfides deposits in the mid-ridge of the Southwest Indian Ocean by integrating nine spatial evidential layers representing the controlling factors. The following conclusions were obtained. First, both fuzzy logic and fuzzy AHP can prioritize the prospect area effectively, which can transform the qualitative knowledge of experts into quantitative evaluation. Integrating fuzzy theory to obtain weight, those methods can overcome the shortage of binary response, and make expert opinions closer to reality. Second, a gamma operator can used to synthesize the evidence layer, the optimal γ values were determined to be 0.95 and 0.9 for fuzzy logic and fuzzy AHP using P-A plots, respectively. Third, The ROC curve and AUC were utilized to measure the performance of the prospectivity models, which show that the models are highly capable of mapping prospectivity because the AUC is greater than 0.5 and close to 1. The prospectivity mapping confirmed that there is significant potential for sulfide mineralization, which opens up new avenues for further exploration.