On the Calculation of Van der Waals Force between Clay Particles
Abstract
:1. Introduction
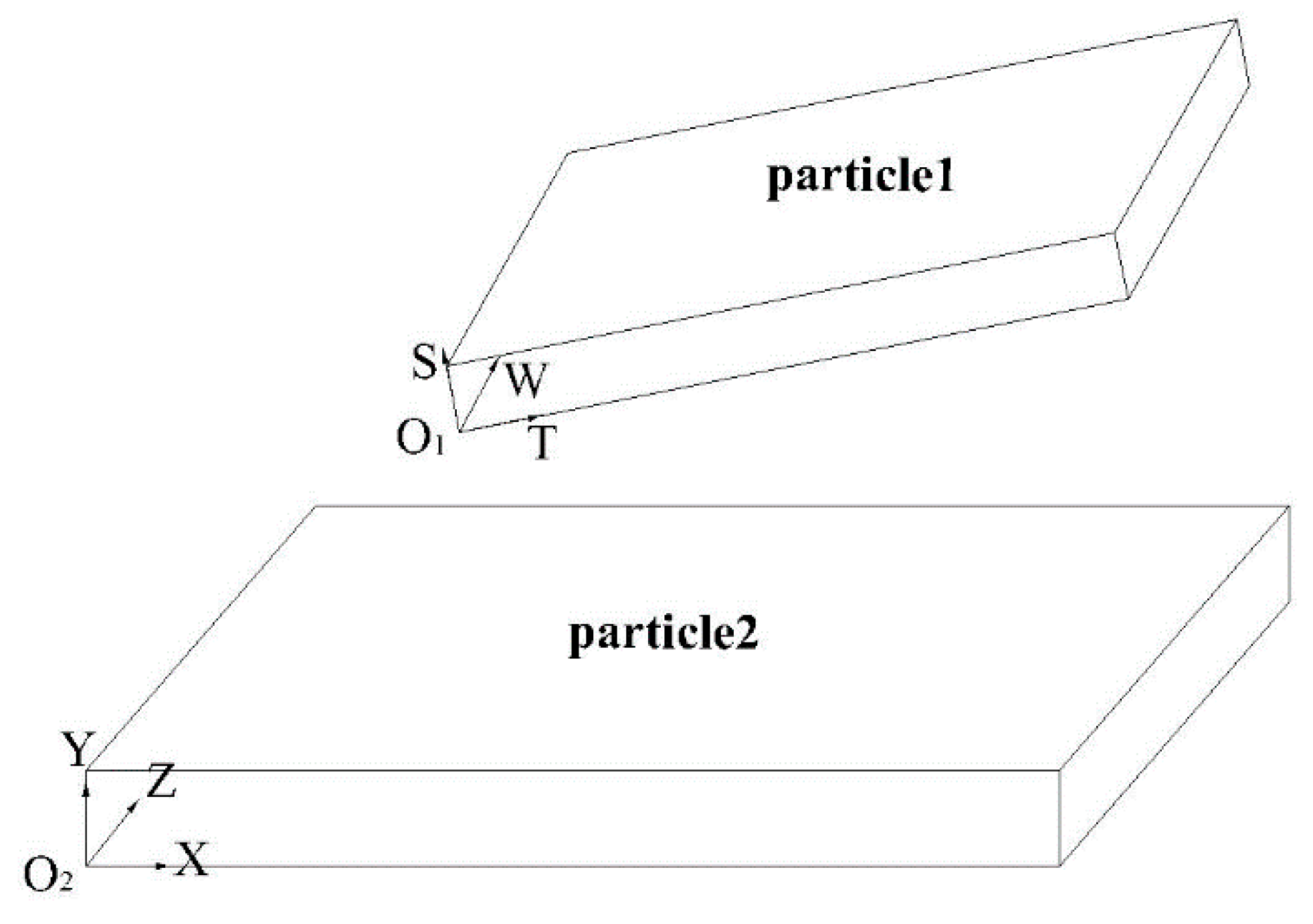
2. New Rigorous Plate-Plate Model and Its Numerical Solution
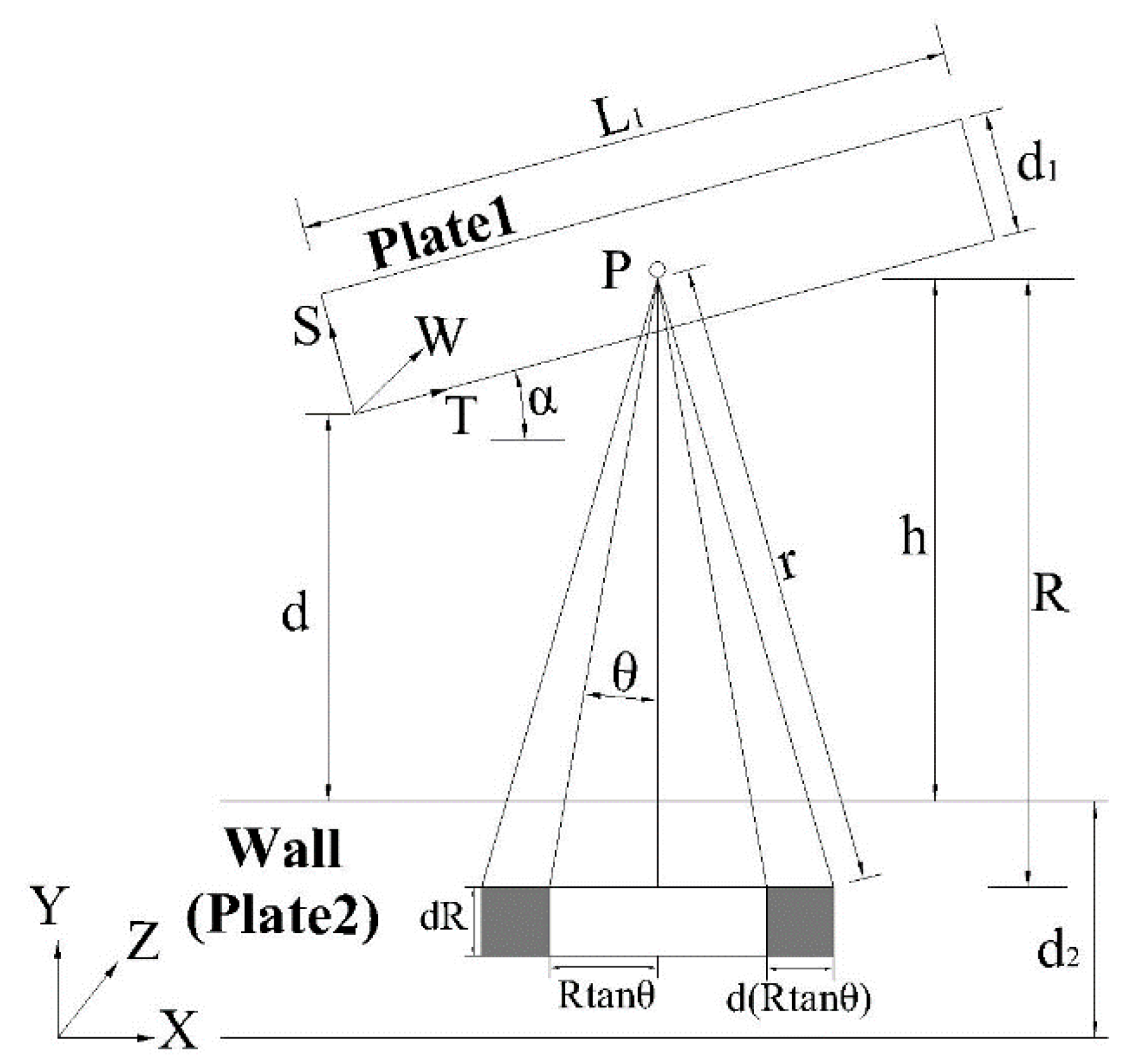
2.1. Van der Waals Force for the New Rigorous Plate-Plate Model
2.2. Numerical Solution of van der Waals Force of the New Model
2.3. Verification of the Obtained Numerical Solution
3. Effect of the Choice of Ideal Wall
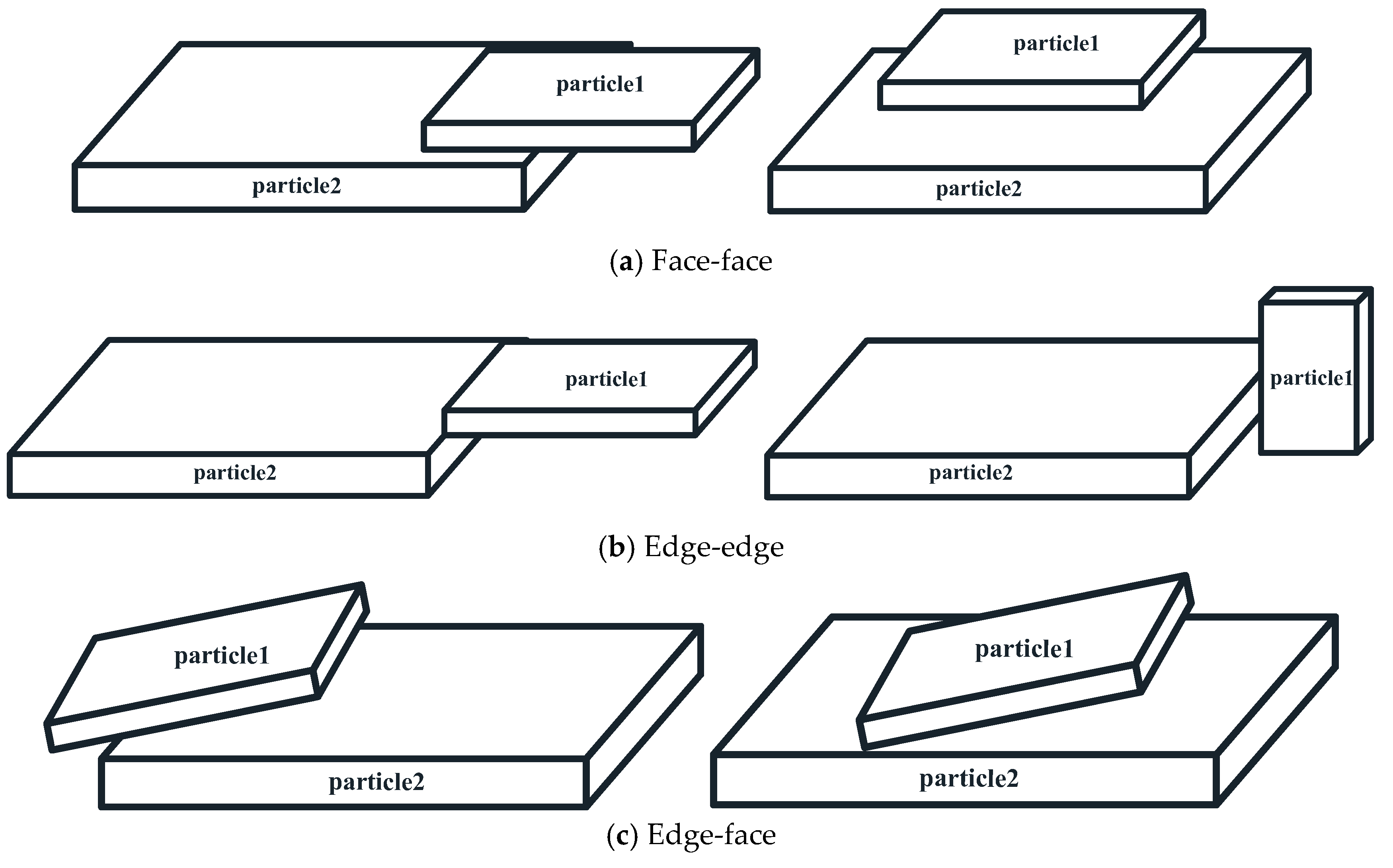
3.1. Face-Face Type
3.2. Edge-Edge Type
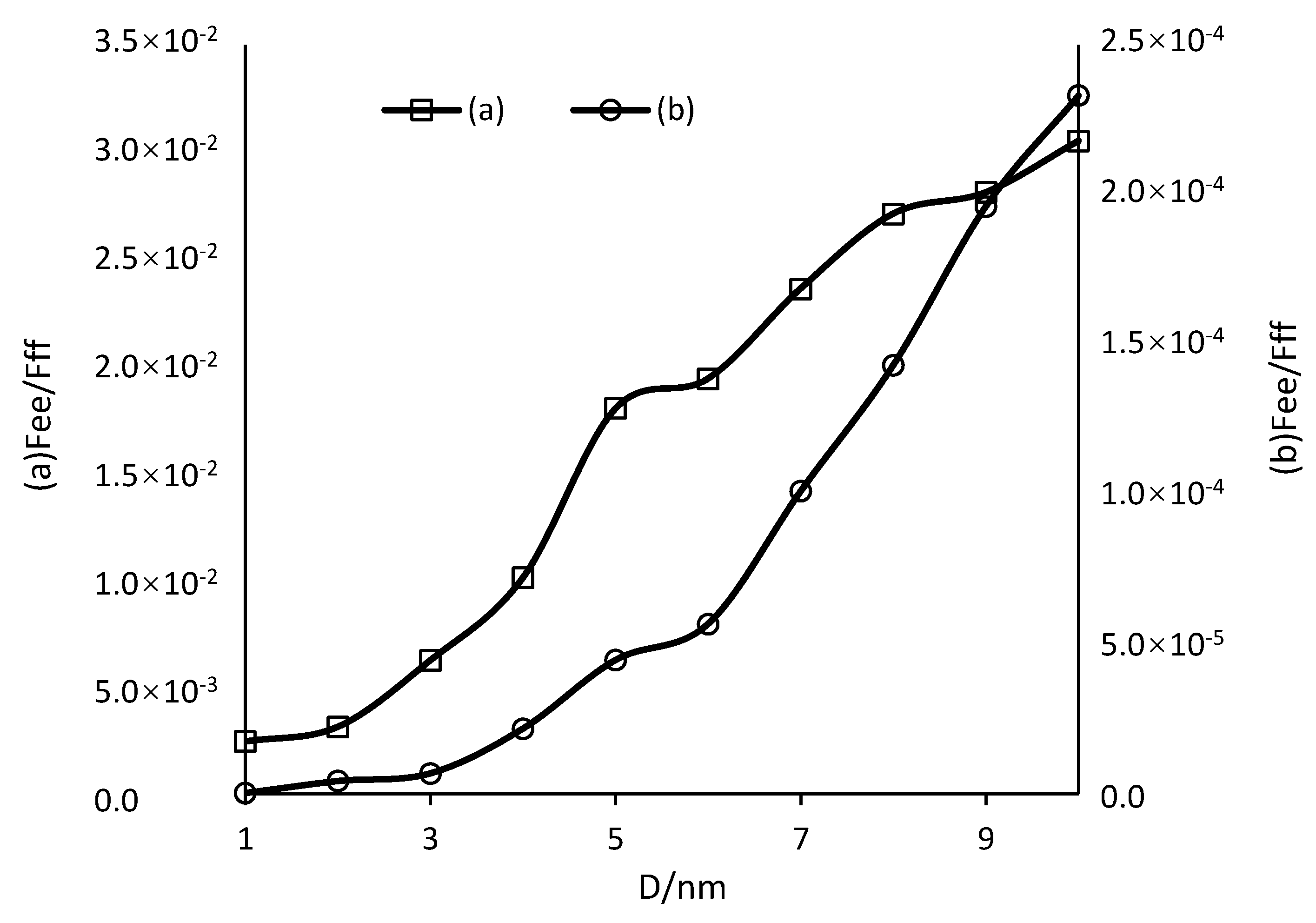
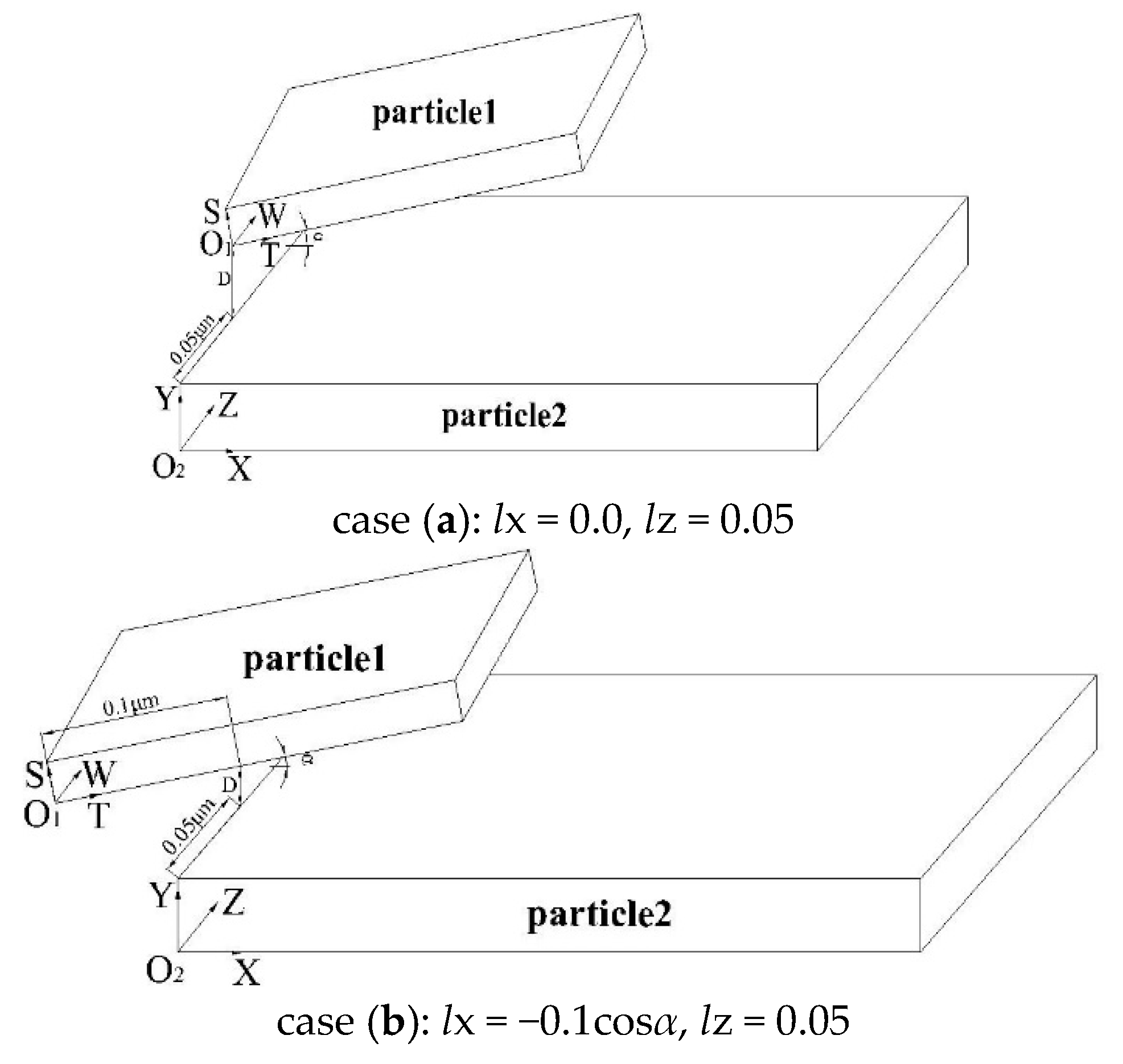
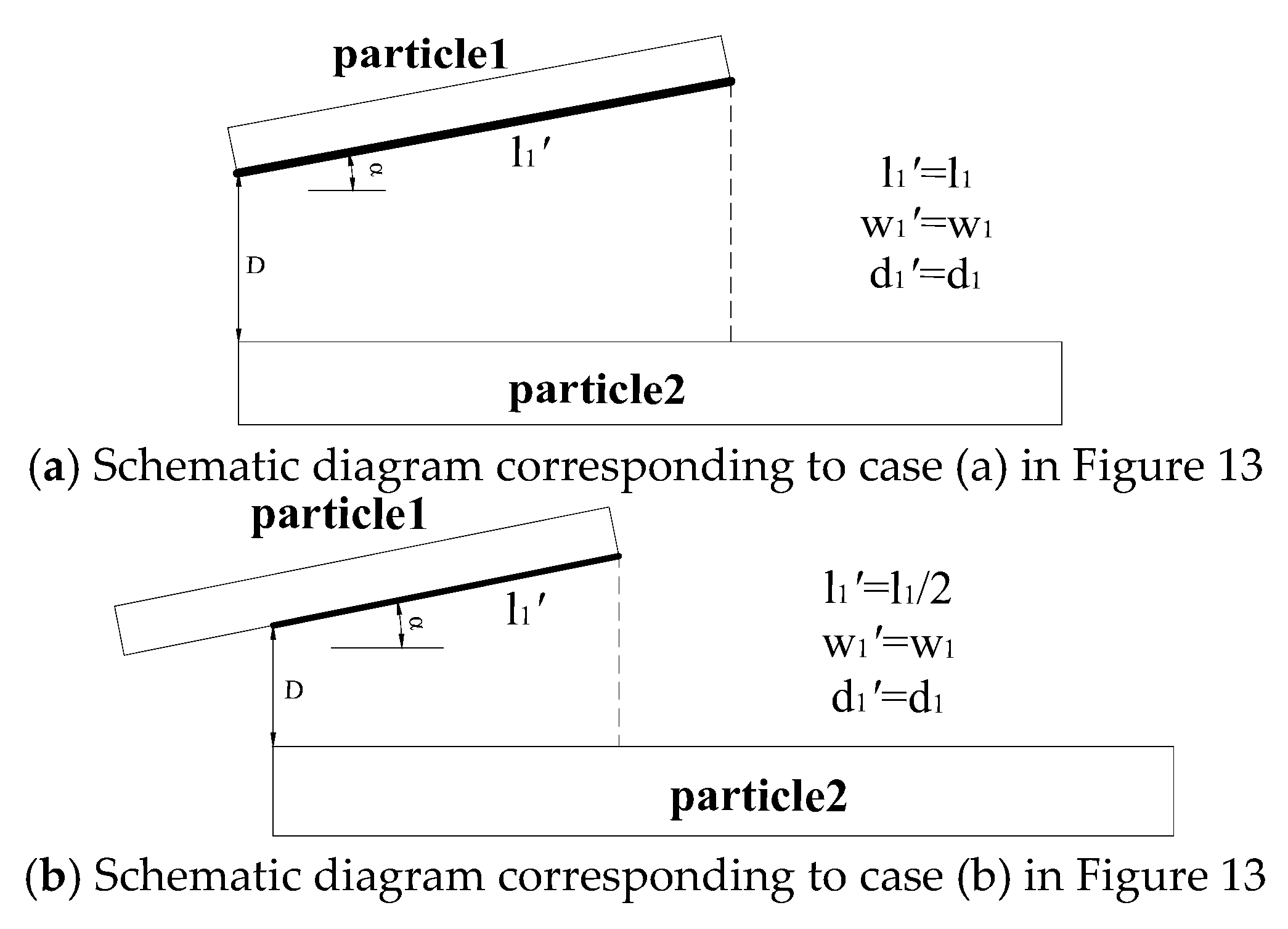
3.3. Edge-Face Type
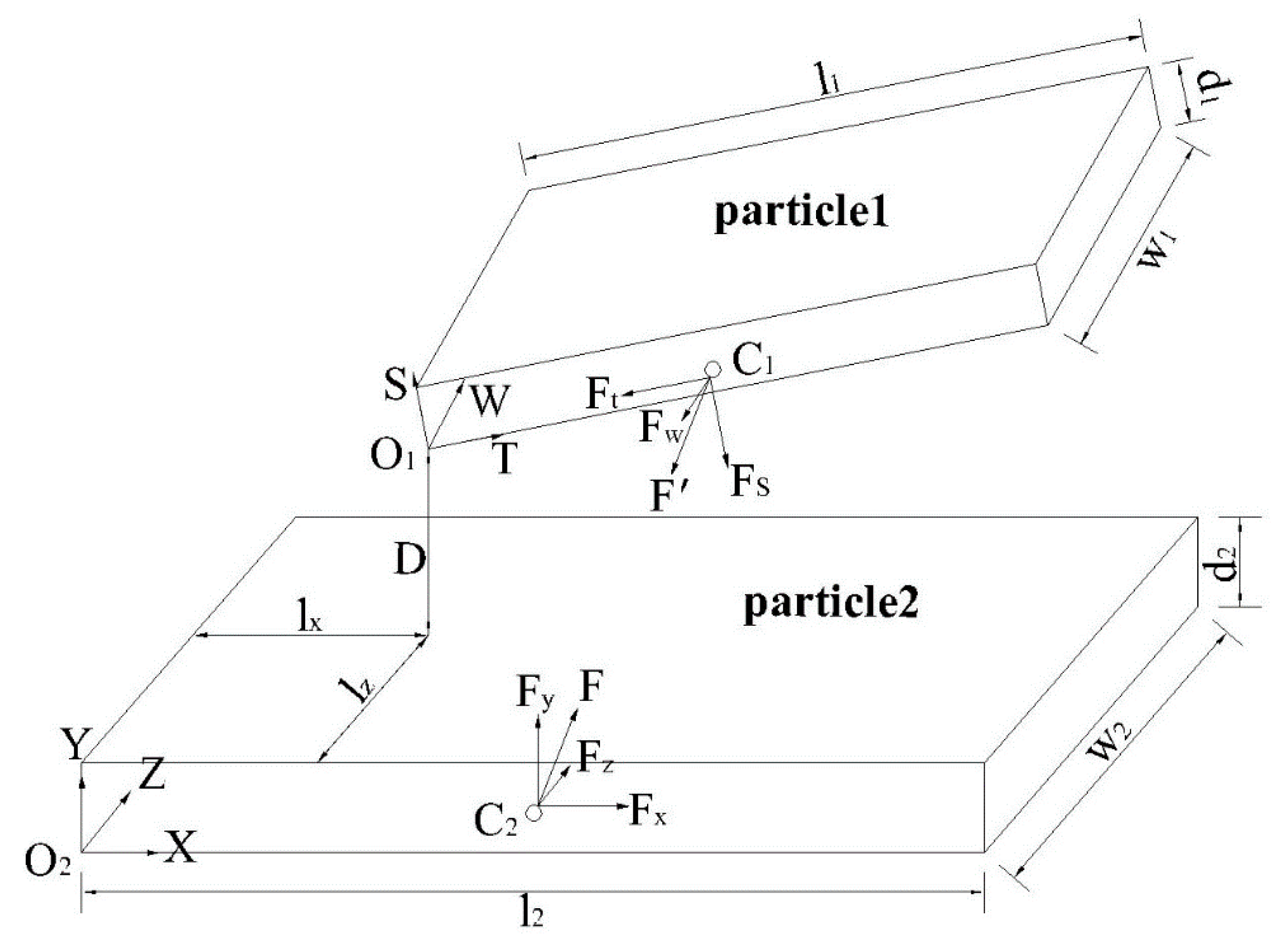
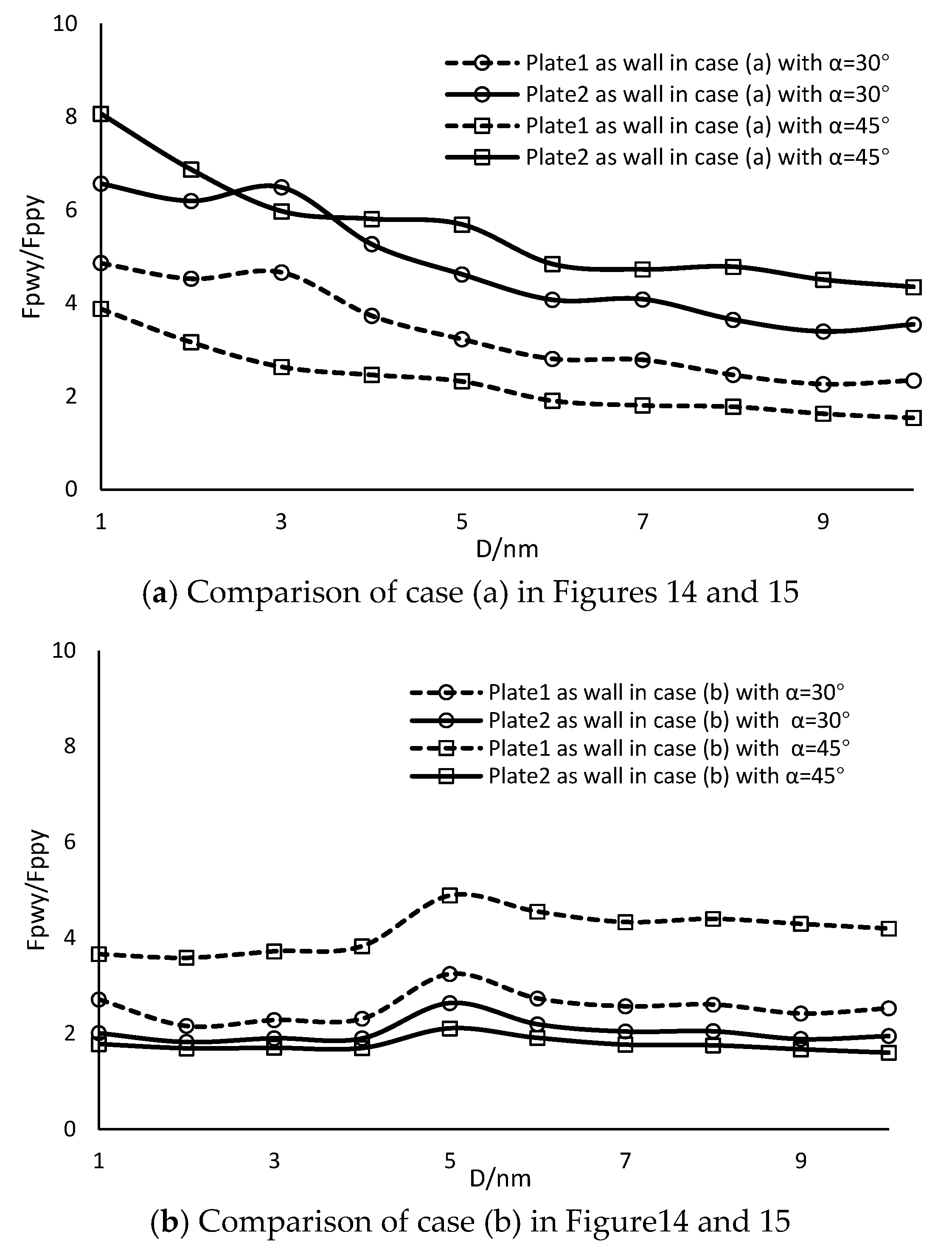
3.3.1. Magnitude of the Calculated Forces
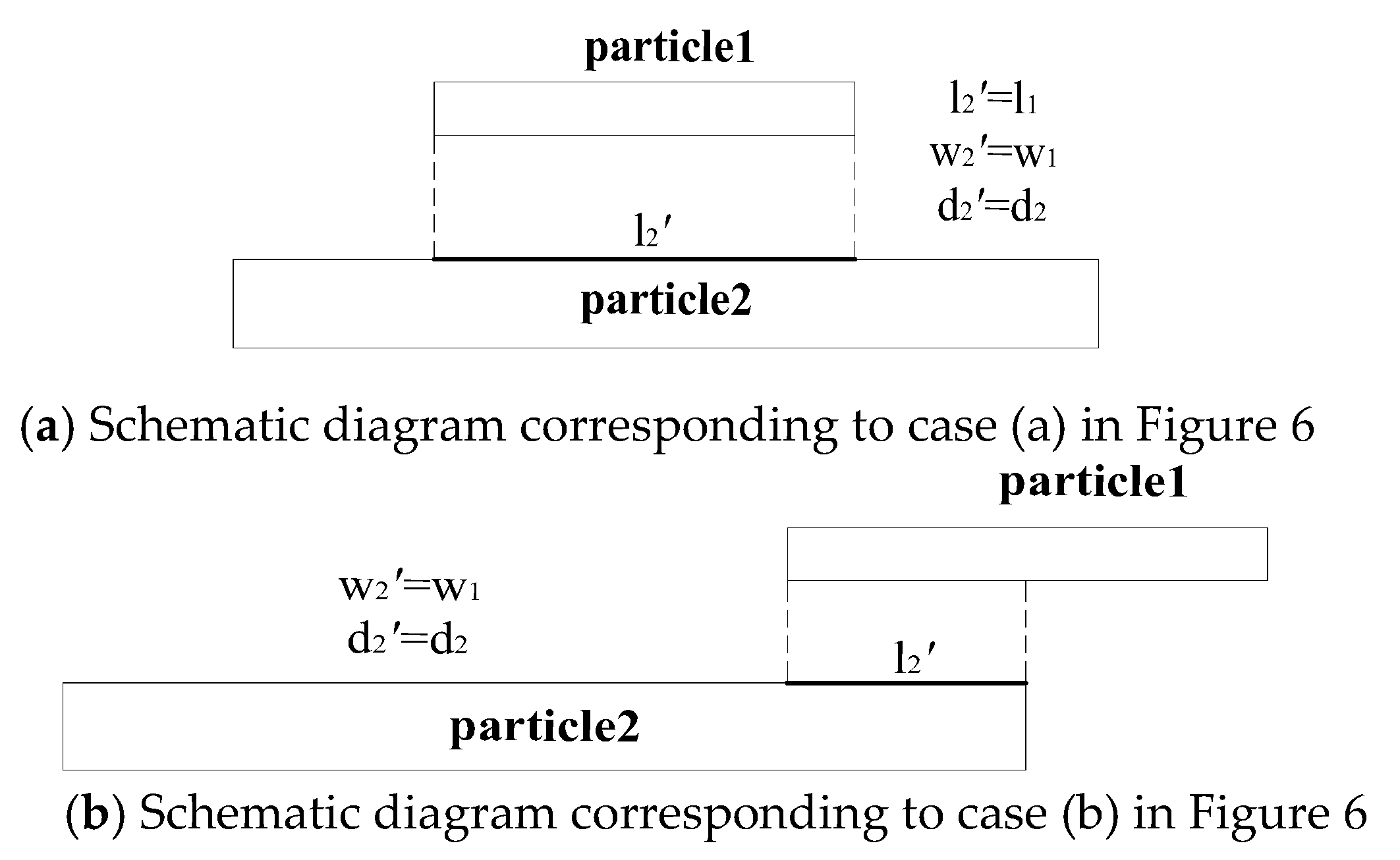
3.3.2. Direction and Location of the Calculated Forces
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Yu, Z.H.; Zheng, Y.Y.; Zhang, J.B.; Zhang, C.Z.; Ma, D.H.; Chen, L.; Cai, T.Y. Importance of soil interparticle forces and organic matter for aggregate stability in a temperate soil and a subtropical soil. Geoderma 2020, 362, 114088. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, X.J.; Liang, L.X.; Wei, X.C.; Xu, P. Investigation of the factors influencing methane adsorption on illite. Energy Sci. Eng. 2019, 7, 3317–3331. [Google Scholar] [CrossRef]
- Ndabambi, M.; Kwon, J.H. Benzalkonium ion sorption to peat and clays: Relative contributions of ion exchange and van der Waals interactions. Chemosphere 2020, 247, 125924. [Google Scholar] [CrossRef] [PubMed]
- Hattab, M.; Chang, C.S. Interaggregate forces and energy potential effect on clay deformation. J. Eng. Mech. 2015, 141, 04015014. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.K.; Soga, K.I. Fundamentals of Soil Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Amarasinghe, P.M.; Anandarajah, A.; Ghosh, P. Molecular dynamic study of capillary forces on clay particles. Appl. Clay Sci. 2014, 89, 170–177. [Google Scholar] [CrossRef]
- Tournassat, C.; Bourg, I.C.; Holmboe, M.; Sposito, G.; Steefel, C.I. Molecular dynamics simulations of anion exclusion in clay interlayer nanopores. Clays Clay Miner. 2016, 64, 374–388. [Google Scholar] [CrossRef] [Green Version]
- Underwood, T.R.; Bourg, I.C. Large-scale molecular dynamics simulation of the dehydration of a suspension of smectite clay nanoparticles. J. Phys. Chem. C 2020, 124, 3702–3714. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, D.; Pellenq, R.J.M.; Whittle, A.J. Mesoscale simulation of clay aggregate formation and mechanical properties. Granul. Matter 2016, 18, 49. [Google Scholar] [CrossRef] [Green Version]
- Sjoblom, K.J. Coarse-grained molecular dynamics approach to simulate clay behavior. J. Geotech. Geoenvironmental Eng. 2016, 142, 06015013. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Jaradat, K.A.; Abdelaziz, S.L. On the use of discrete element method for multi-scale assessment of clay behavior. Comput. Geotech. 2019, 112, 329–341. [Google Scholar] [CrossRef]
- Anandaraiah, A. Numerical simulation of one-dimensional behaviours of a kaolinite. Geotechnique 2000, 50, 509–519. [Google Scholar] [CrossRef]
- Yao, M.; Anandarajah, A. Three-dimensional discrete element method of analysis of clays. J. Eng. Mech. 2003, 129, 585–596. [Google Scholar] [CrossRef]
- Chen, J. Physico-Chemical Analysis of Contaminated Clay; The Johns Hopkins University: Baltimore, MD, USA, 1996. [Google Scholar]
- Anandarajah, A.; Chen, J. Van Der Walls attractive force between clay particles in water and contaminants. Soils Found. 1997, 37, 27–37. [Google Scholar] [CrossRef] [Green Version]
- Katti, D.R.; Matar, M.I.; Katti, K.S.; Amarasinghe, P.M.A. Multiscale modeling of swelling clays: A computational and experimental approach. KSCE J. Civ. Eng. 2009, 13, 243–255. [Google Scholar] [CrossRef]
- Anandarajah, A.; Amarasinghe, P.M. Discrete-element study of the swelling behaviour of Na-montmorillonite. Geotechnique 2012, 63, 674–681. [Google Scholar] [CrossRef]
- Ueberhuber, C.W. Numerical Computation 2: Methods, Software, and Analysis; Springer: Berlin, Germany, 1997. [Google Scholar]
- Dick, J.; Kuo, F.Y.; Sloan, I.H. High-dimensional integration: The quasi-Monte Carlo way. Acta Numer. 2013, 22, 133–288. [Google Scholar] [CrossRef]
- Zhu, L. High-dimensional Cotes optimization integral numerical method and estimation of other terms. Coll. Math. 2008, 24, 75–79. [Google Scholar]

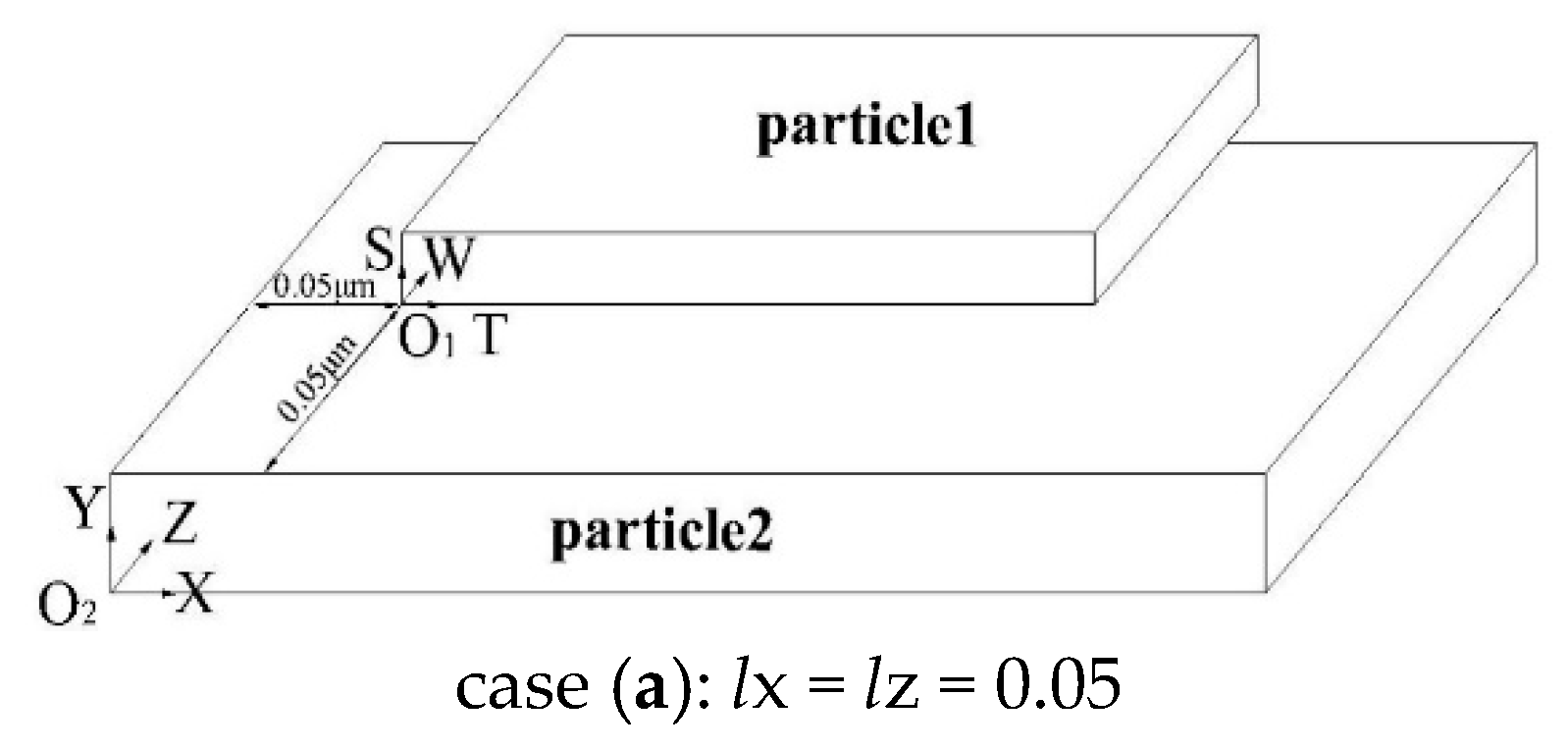
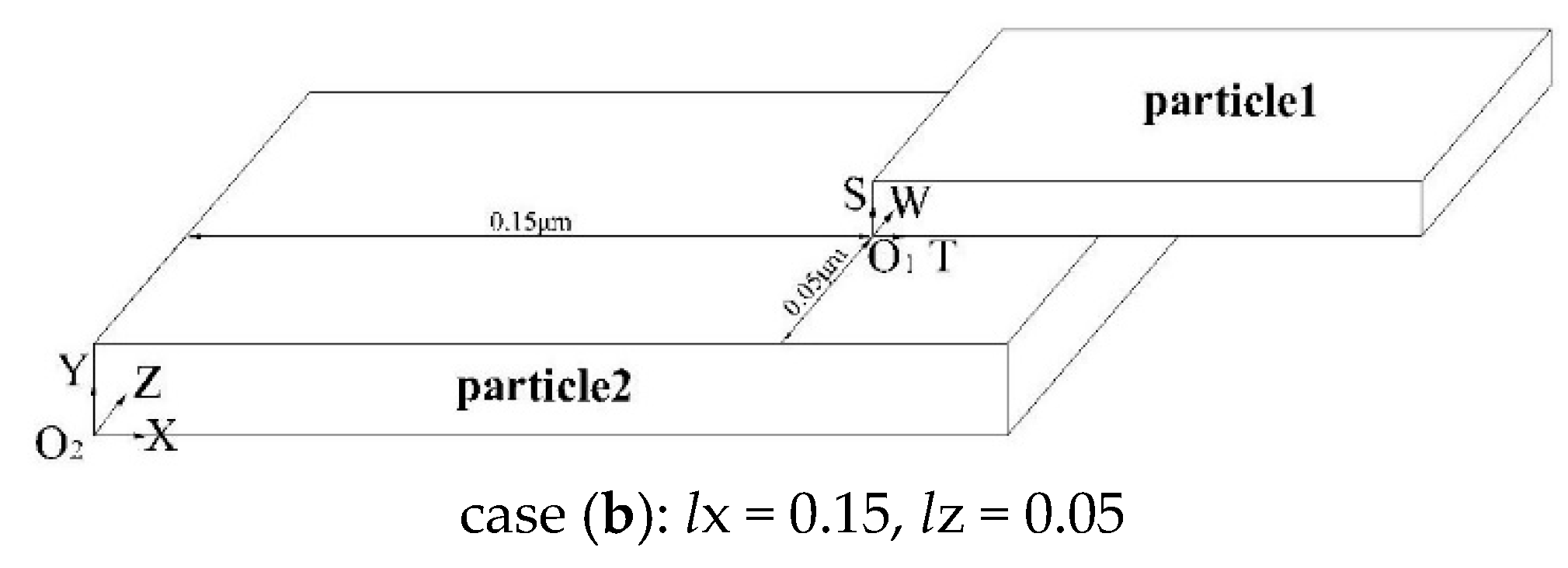
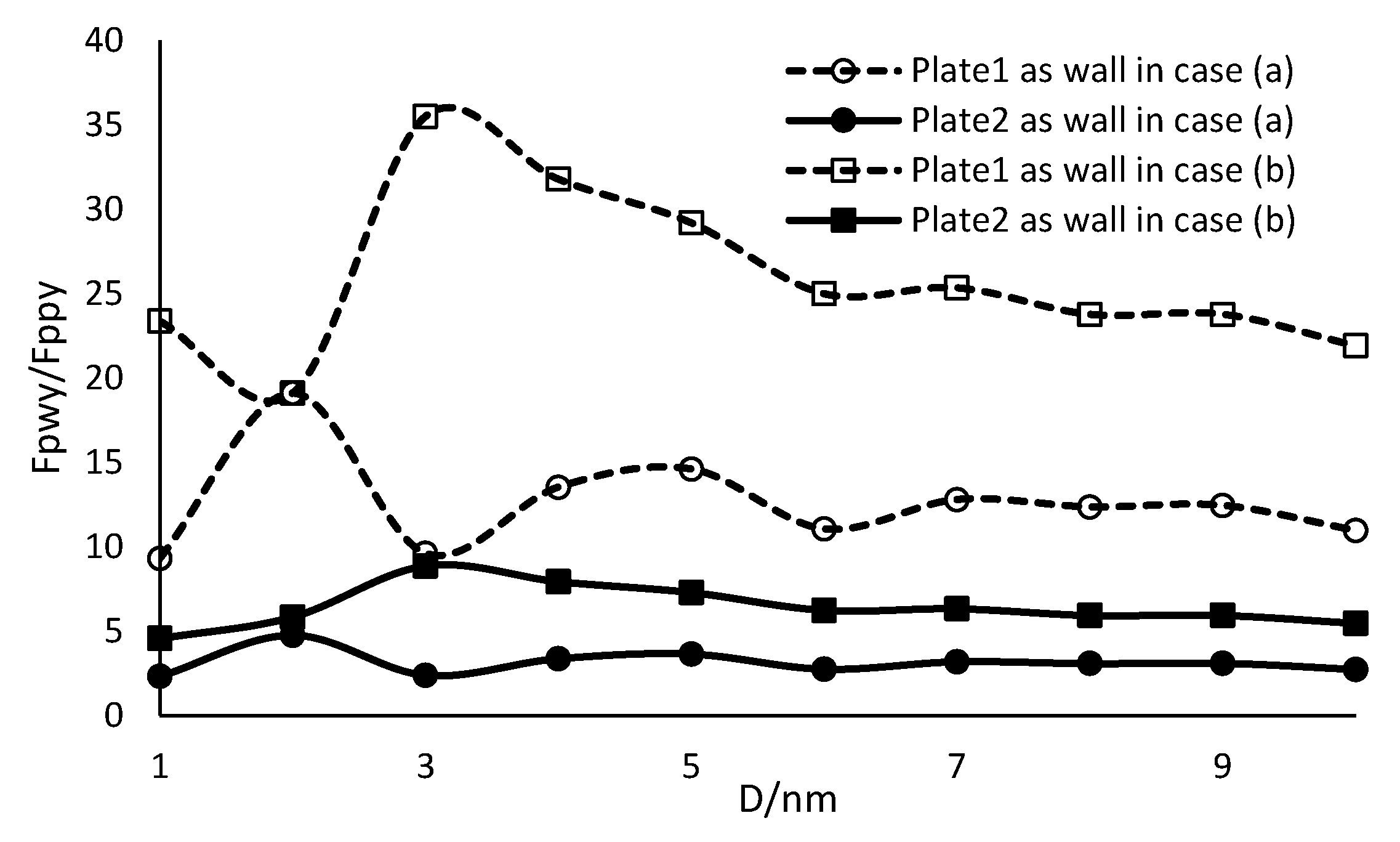

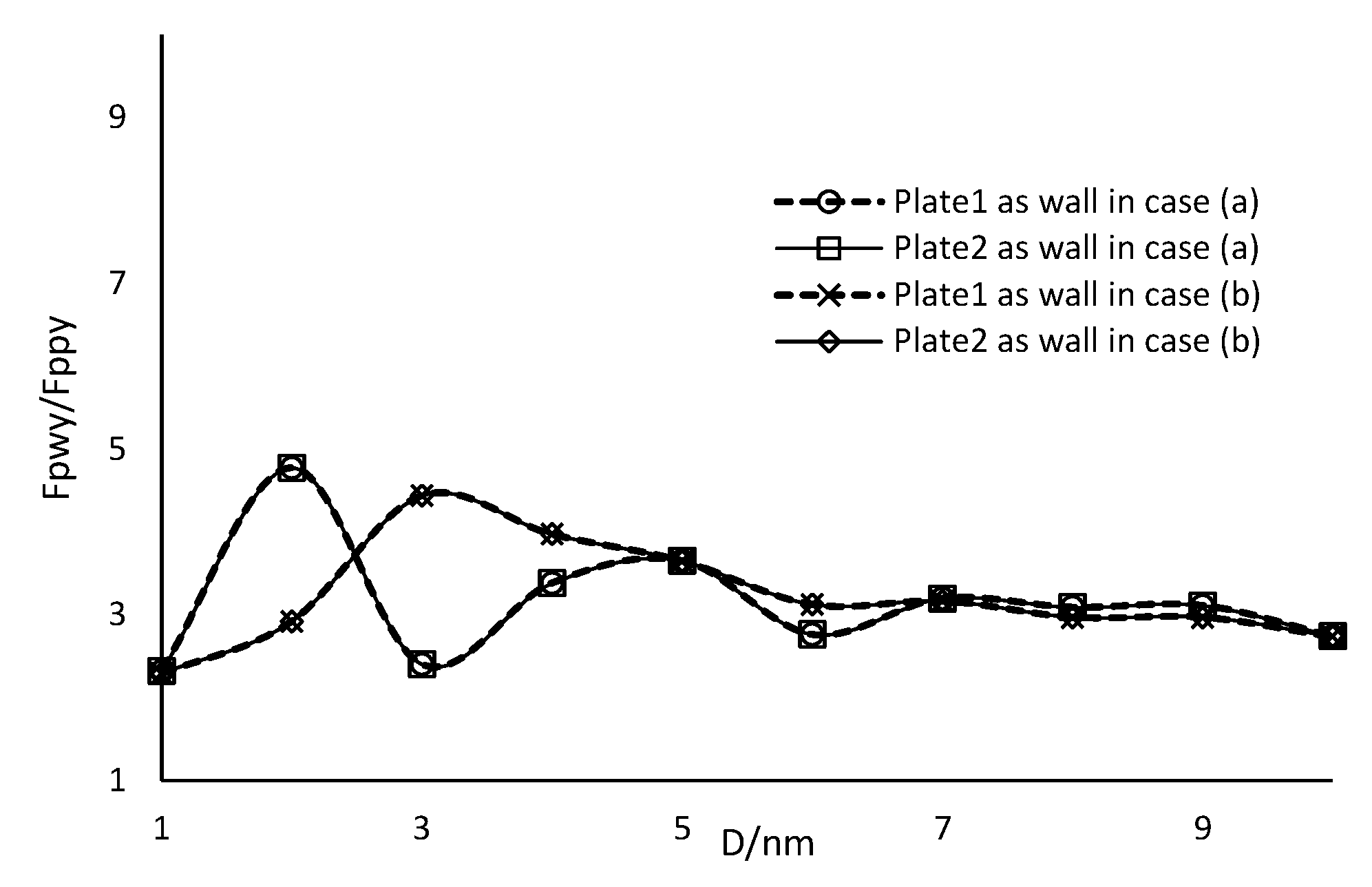
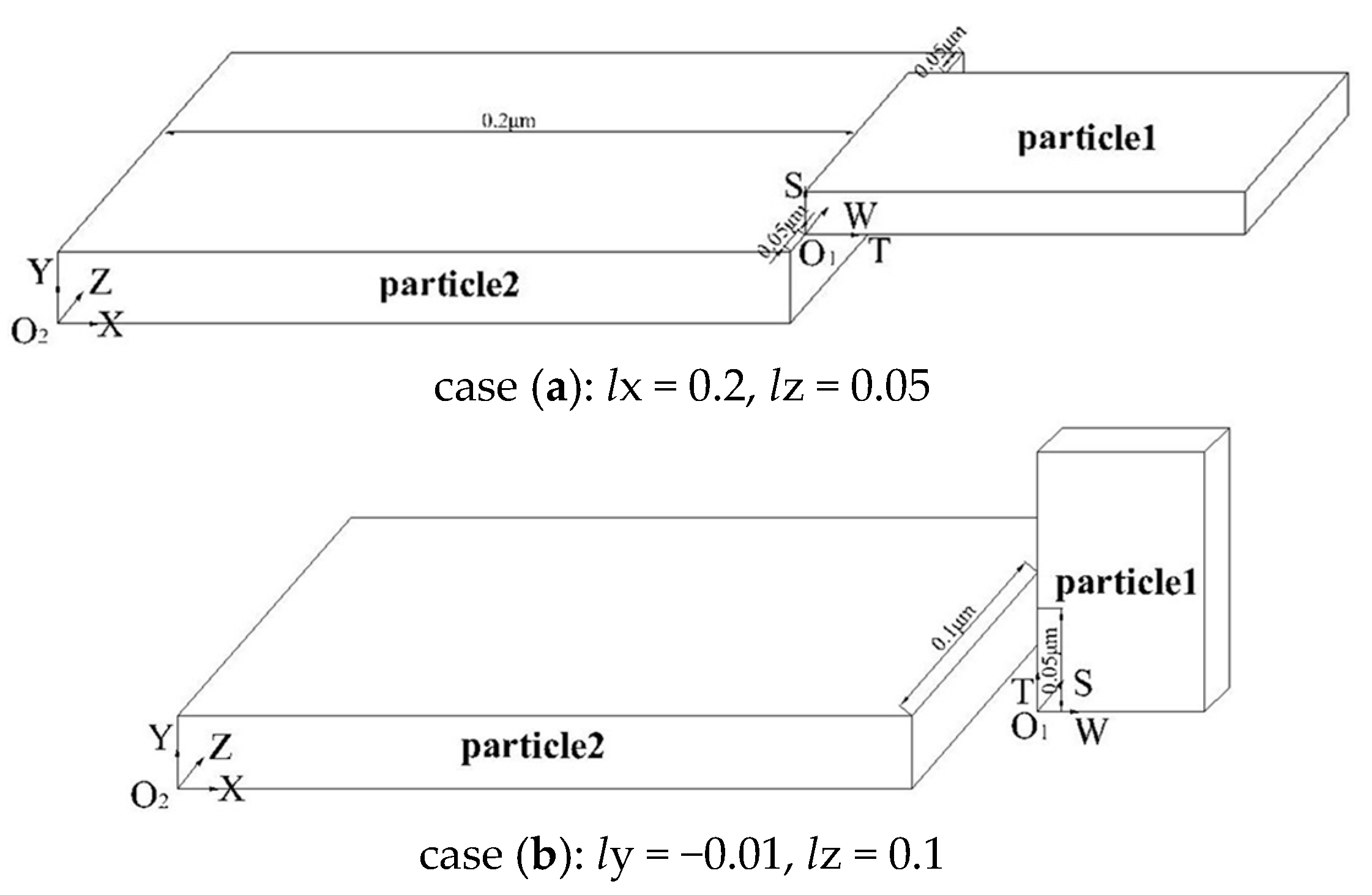

| α = 0, d1 = d2 = 0.01, D = 0.001, l1 = w1 = 0.1, l2 = w2 | |||
|---|---|---|---|
| l2/l1 | Fpwy/10−9N | Fppy/10−9N | Fppy/Fpwy |
| 1(lx = lz = 0, m = 27.5) | 8.10 | 2.84 | 0.35 |
| 2(lx = lz = 0.05, m = 27.5) | 3.49 | 0.43 | |
| 3(lx = lz = 0.1, m = 27.5) | 3.87 | 0.48 | |
| 10(lx = lz = 0.45, m = 27.5) | 4.58 | 0.57 | |
| 100(lx = lz = 4.95, m = 27.5) | 5.91 | 0.73 | |
| 1000(lx = lz= 0, m = 49.95, m = 37.5) | 7.56 | 0.93 | |
| α | Fppx/10−9N | Fppy/10−9N | Fppz/10−9N | Fppx/Fppy | Fpwx/Fpwy |
|---|---|---|---|---|---|
| 15° | −4.02 × 10−3 | 2.86 × 10−2 | 5.85 × 10−5 | −0.141 | −0.268 |
| 30° | −2.78 × 10−3 | 1.37 × 10−2 | 2.58 × 10−5 | −0.203 | −0.577 |
| 45° | −2.32 × 10−3 | 9.60 × 10−3 | 1.75 × 10−5 | −0.241 | −1.0 |
| 60° | −2.33 × 10−3 | 8.15 × 10−3 | 1.54 × 10−5 | −0.286 | −1.732 |
| 75° | −2.80 × 10−3 | 7.86 × 10−3 | 1.62 × 10−5 | −0.357 | −3.732 |
| α | Xpw/Xpp | Ypw/Ypp | Zpw/Zpp |
|---|---|---|---|
| 15° | 0.845424352 | 0.987905290 | 1.000105178 |
| 30° | 1.067378334 | 0.989210020 | 1.000041638 |
| 45° | 1.715227995 | 0.966569502 | 1.000008018 |
| 60° | 3.244969855 | 0.879831892 | 1.00000768 |
| 75° | 7.722029849 | 0.696792073 | 1.000036639 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, X.-Y.; Zhao, K.; Qian, W.-X.; Zhu, Q.-Y.; Zhou, G.-Q. On the Calculation of Van der Waals Force between Clay Particles. Minerals 2020, 10, 993. https://doi.org/10.3390/min10110993
Shang X-Y, Zhao K, Qian W-X, Zhu Q-Y, Zhou G-Q. On the Calculation of Van der Waals Force between Clay Particles. Minerals. 2020; 10(11):993. https://doi.org/10.3390/min10110993
Chicago/Turabian StyleShang, Xiang-Yu, Kang Zhao, Wan-Xiong Qian, Qi-Yin Zhu, and Guo-Qing Zhou. 2020. "On the Calculation of Van der Waals Force between Clay Particles" Minerals 10, no. 11: 993. https://doi.org/10.3390/min10110993
APA StyleShang, X.-Y., Zhao, K., Qian, W.-X., Zhu, Q.-Y., & Zhou, G.-Q. (2020). On the Calculation of Van der Waals Force between Clay Particles. Minerals, 10(11), 993. https://doi.org/10.3390/min10110993





