A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China
Abstract
1. Introduction
2. Study Area and Data Preparation
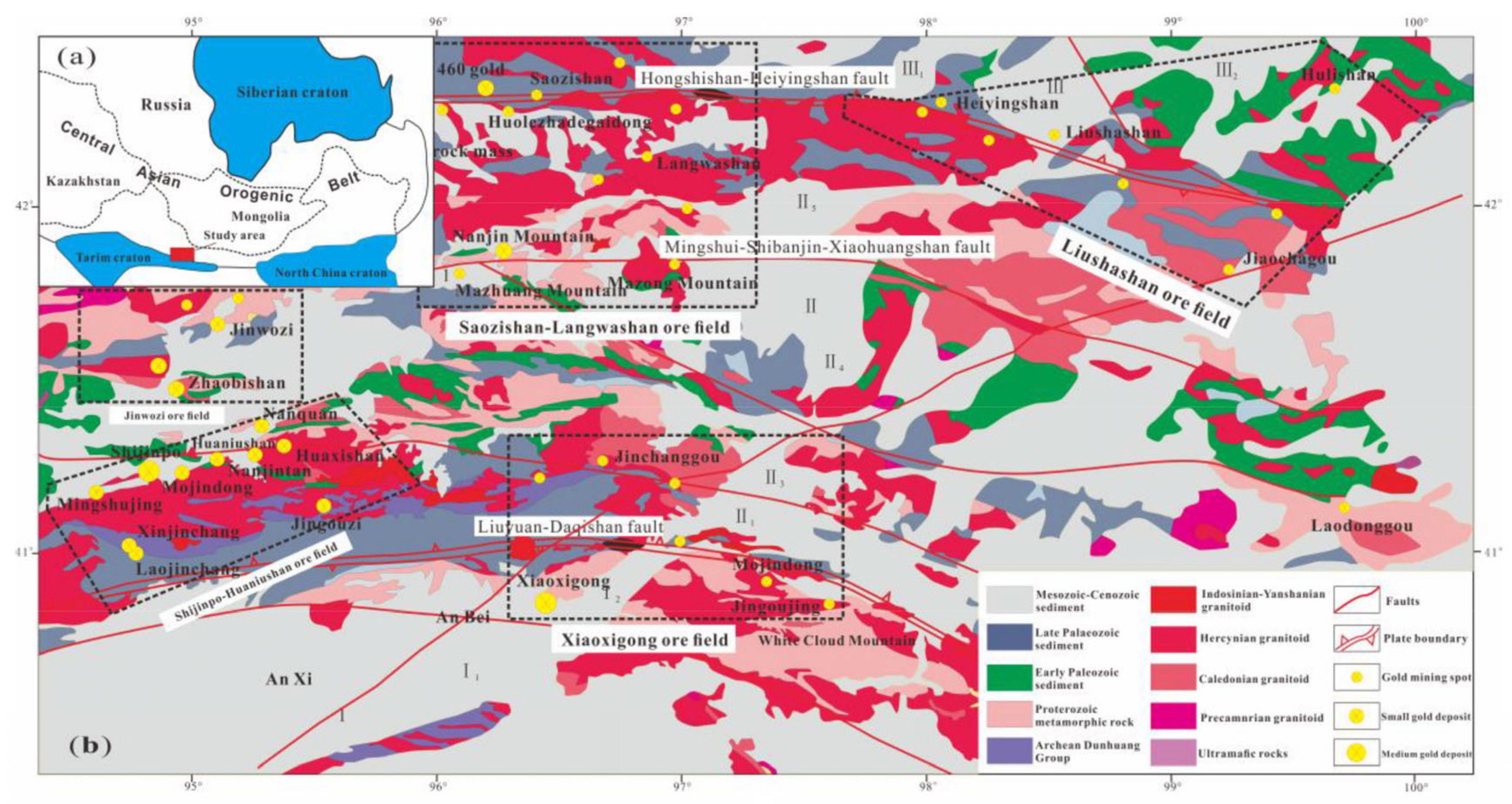
2.1. Study Area
2.2. Data Preparation
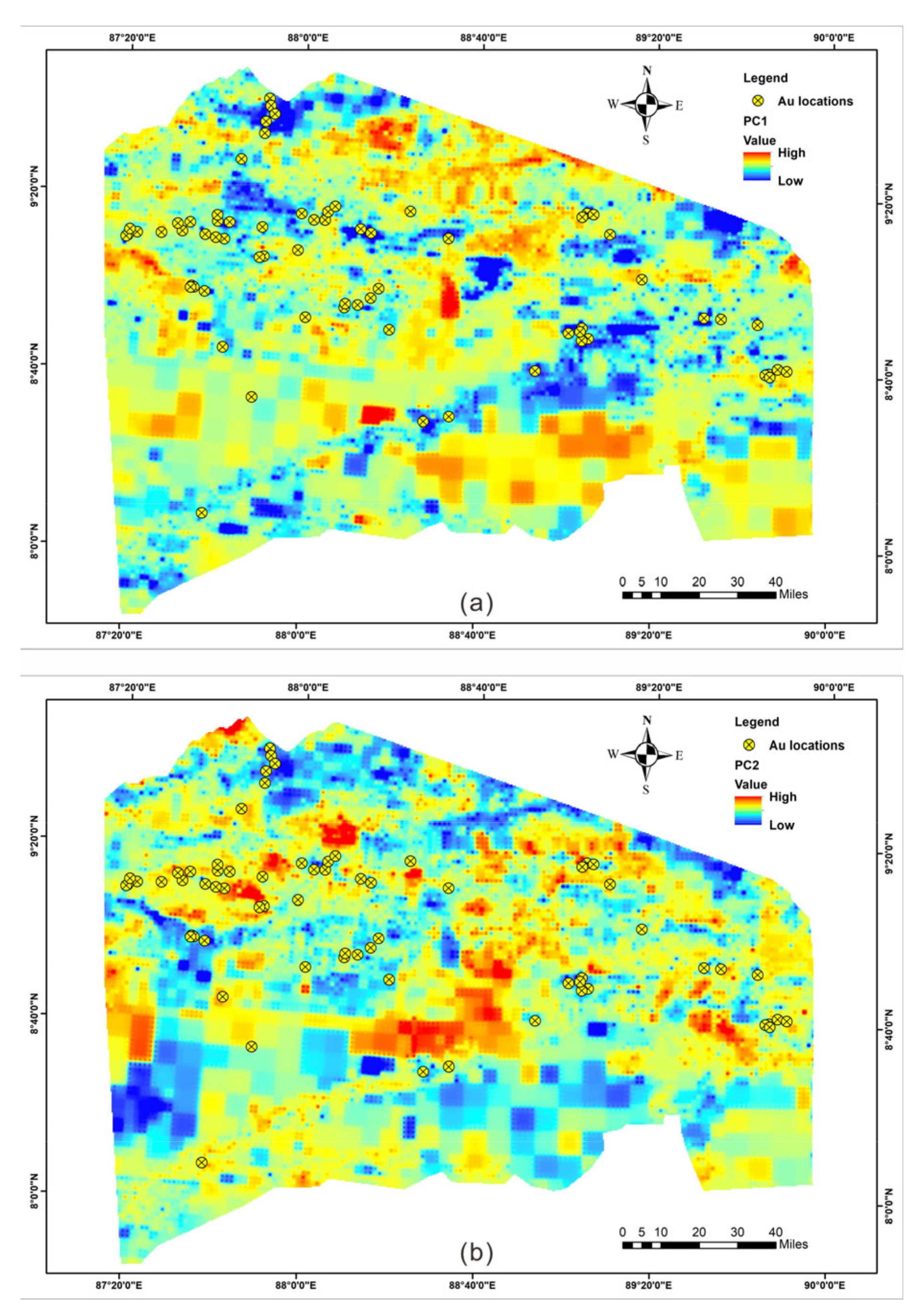
2.2.1. Spatial Datasets
2.2.2. Targets
- (1)
- Selection of non-deposit locations was randomly spatially distributed.
- (2)
- Non-deposits were distal from any known Au deposits to avoid similar multivariate spatial data characteristics to known mineralisation areas.
- (3)
- An equal number of non-deposits and deposits were used to balance the number of positive and negative examples, and achieve the optimal model [35].
2.2.3. Predictor Maps
- (1)
- Intrusive Rock Contact Zone
- (2)
- Fault System
- (3)
- Geochemical Data
3. Methodology
3.1. Random Forest
3.2. Support Vector Machine
3.3. Maximum Entropy Model
- (1)
- It is possible to integrate both discrete and continuous variables, and the output result provides a minimum deviation estimate of the target distribution [43];
- (2)
- It requires only presence data, along with evidential maps for the study area [44];
- (3)
- It can apply regularisation parameters to reduce the risk of data overfitting (which determines the error bounds around the mean of the observed data) and optimise the function to fit the data distribution trends [46].
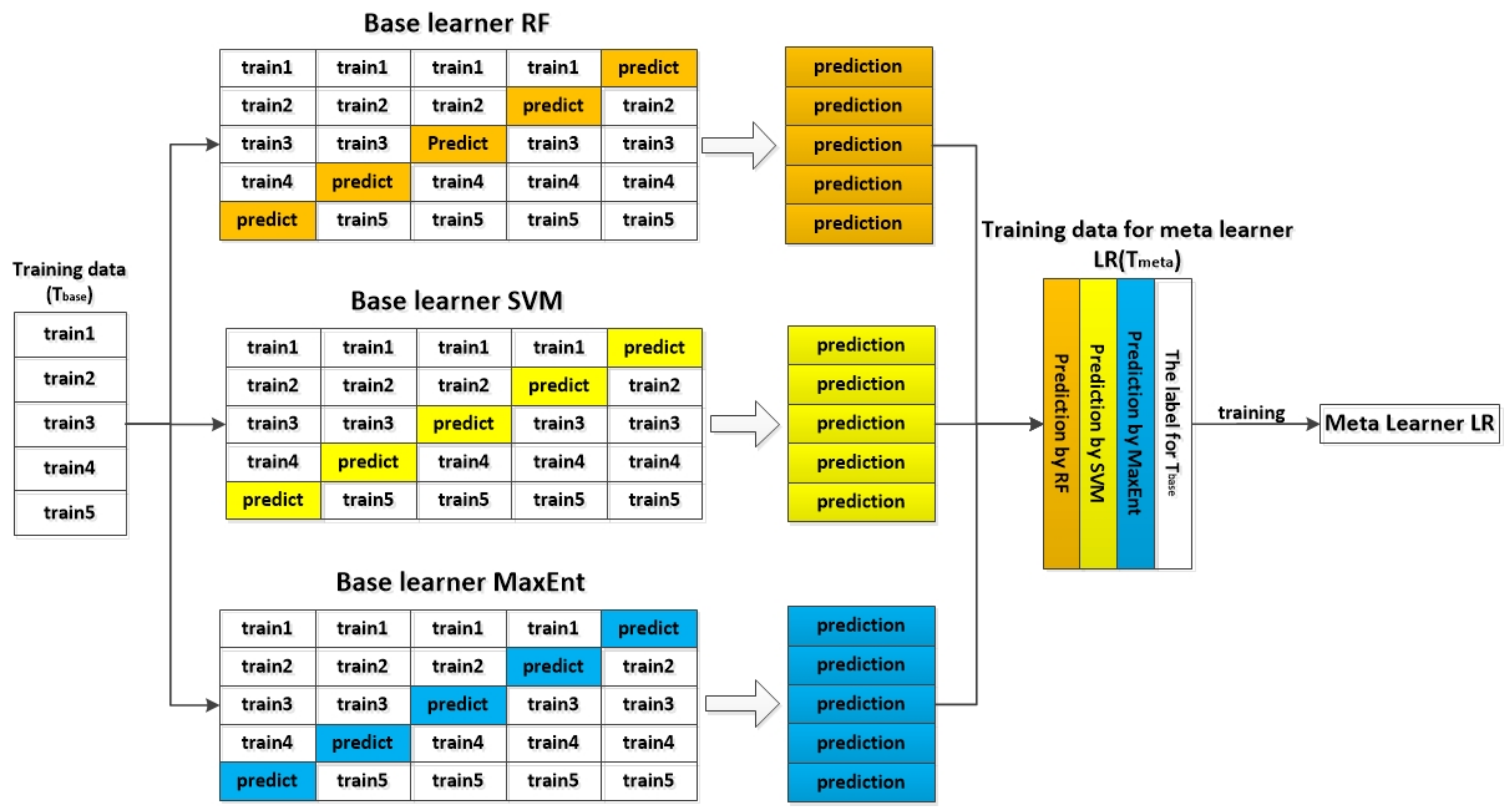
3.4. Ensemble Learning Method Framework
- (1)
- The base algorithms are trained by using k-fold cross-validation (usually k = 5 or 10) on the same datasets.
- (2)
- The three base models with remarkable performances are selected to provide predictions, and the k-fold cross-validation is also used.
- (3)
- The mean value of the three base learners’ k-fold cross-validation results are regarded as the new representations.
- (4)
- A senior model can be trained given the new representations.
3.5. Model Evaluation Metrics
4. Experiments and Results
4.1. Experiments
4.1.1. Data Processing
4.1.2. Training Base Models
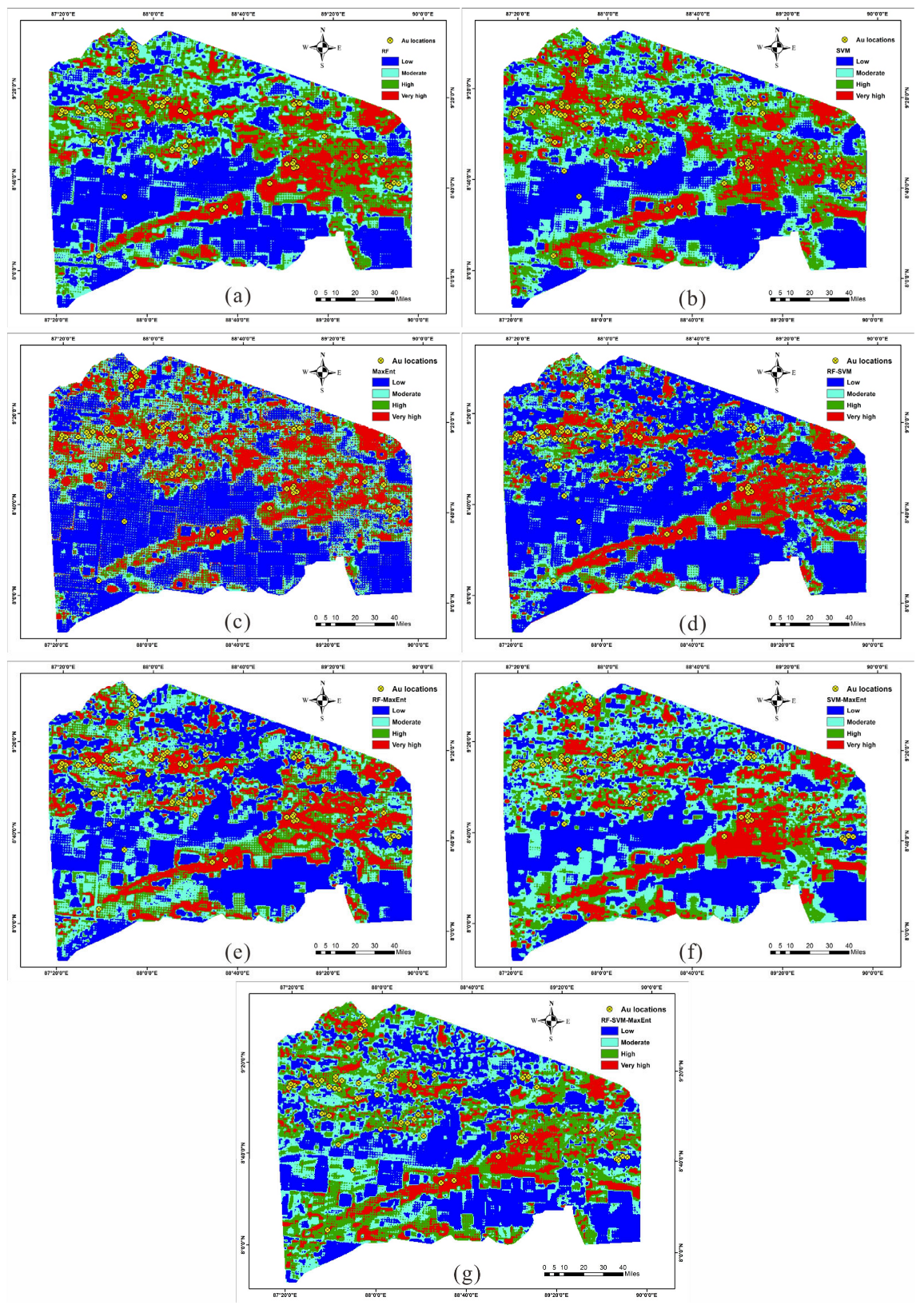
4.1.3. Constructing Mineral Prospectivity Maps
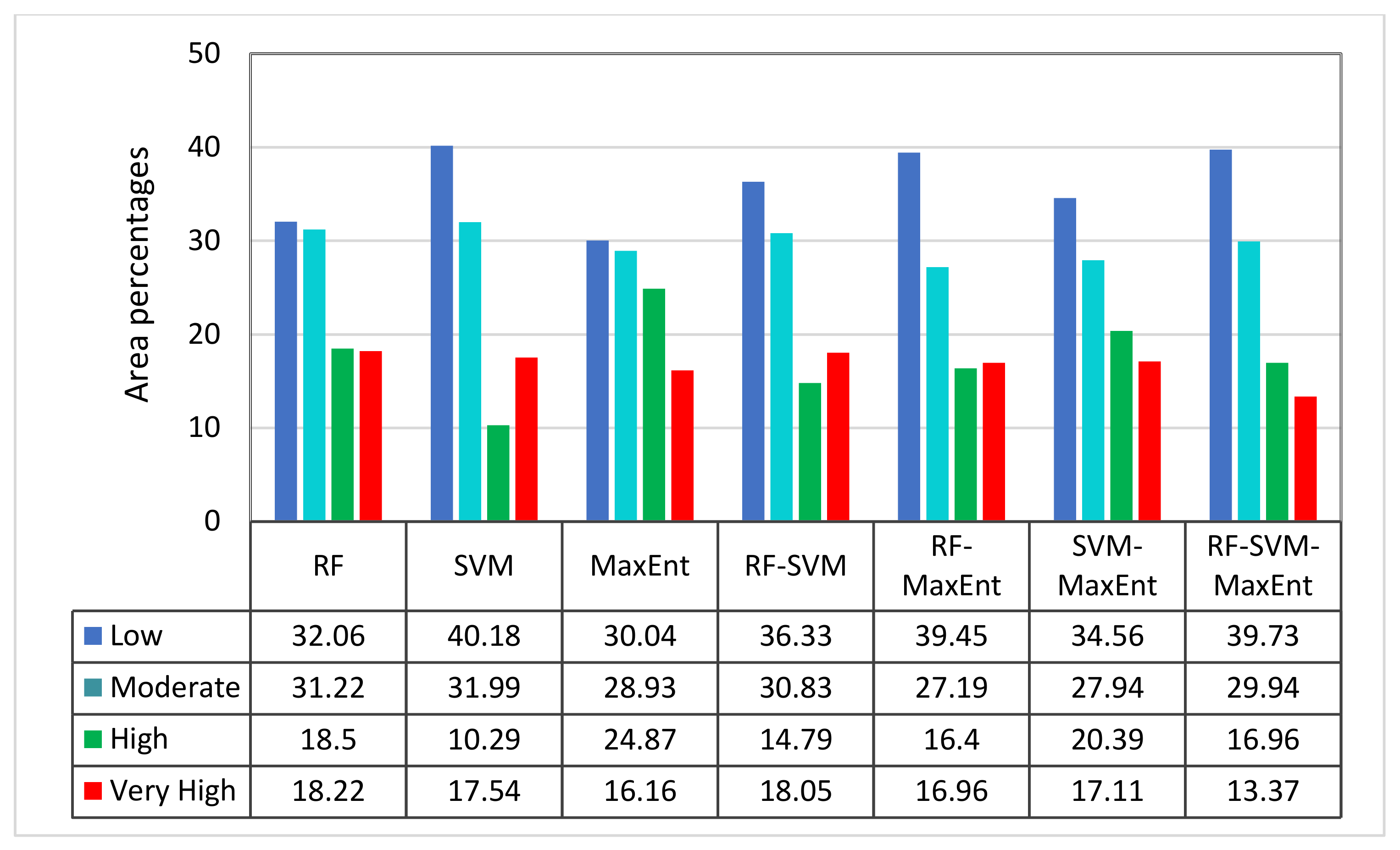
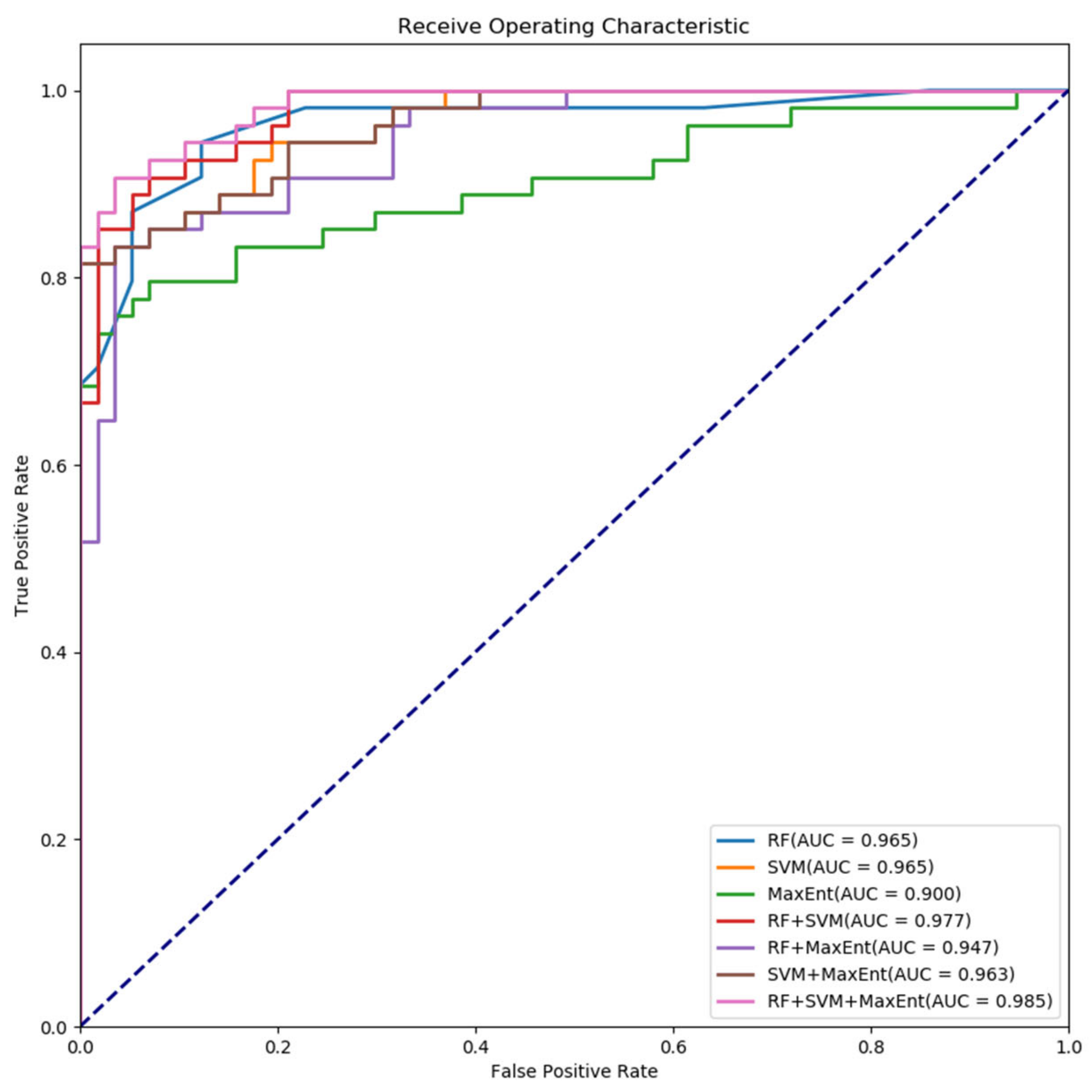
4.2. Comparison of Prediction Results
5. Discussion
5.1. Prediction Performance of Different Methods
5.2. Importance of Variables
5.3. Reliability from a Geological Perspective
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chicaolmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Arndt, N.T.; Fontboté, L.; Hedenquist, J.W.; Kesler, S.E.; Thompson, J.F.H.; Wood, D.G. Future Global Mineral Resources. Geochem. Pers. 2017, 6, 1–171. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.; Liu, W.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Li, B.; Liu, B.; Guo, K.; Li, C.; Wang, B. Application of a Maximum Entropy Model for Mineral Prospectivity Maps. Minerals 2019, 9, 556. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Leite, E.P.; Filho, C.R.D.S. Probabilistic neural networks applied to mineral potential mapping for platinum group elements in the Serra Leste region, Carajás Mineral Province, Brazil. Comput. Geosci. 2009, 35, 675–687. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Weights of Evidence Modeling of Mineral Potential: A Case Study Using Small Number of Prospects, Abra, Philippines. Nat. Resour. Res. 2004, 13, 173–187. [Google Scholar] [CrossRef]
- Qiuming, C.; Agterberg, F.P. Fuzzy Weights of Evidence Method and Its Application in Mineral Potential Mapping. Nat. Resour. Res. 1999, 8, 27–35. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.; Hale, M. Bayesian network classifiers for mineral potential mapping. Comput. Geosci. 2006, 32, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Yuan, F.; Zhang, M.; Jowitt, S.M.; Ord, A.; Zhou, T.; Dai, W. 3D computational simulation-based mineral prospectivity modeling for exploration for concealed Fe-Cu skarn-type mineralisation within the Yueshan orefield, Anqing district, Anhui Province, China. Ore. Geol. Rev. 2019, 105, 1–17. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M. Introduction to the Special Issue: GIS-based mineral potential modelling and geological data analyses for mineral exploration. Ore Geol. Rev. 2015, 71, 477–483. [Google Scholar] [CrossRef]
- Loh, Y.W. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. GIS-based rare events logistic regression for mineral prospectivity mapping. Comput. Geosci. 2018, 111, 18–25. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, K.; Xia, Q. A MaxEnt Model for Mineral Prospectivity Mapping. Nat. Resour. Res. 2017, 27, 299–313. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of Random Forests algorithm. Ore Geol. Rev. 2015, 71, 777–787. [Google Scholar] [CrossRef]
- Zhang, D.; Agterberg, F.; Cheng, Q.; Zuo, R. A Comparison of Modified Fuzzy Weights of Evidence, Fuzzy Weights of Evidence, and Logistic Regression for Mapping Mineral Prospectivity. Math. Geosci. 2013, 46, 869–885. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y. Big Data Analytics of Identifying Geochemical Anomalies Supported by Machine Learning Methods. Nat. Resour. Res. 2017, 27, 5–13. [Google Scholar] [CrossRef]
- Shabankareh, M.; Hezarkhani, A. Application of support vector machines for copper potential mapping in Kerman region, Iran. J. Afr. Earth Sci. 2017, 128, 116–126. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-Driven Predictive Modelling of Mineral Prospectivity Using Machine Learning and Deep Learning Methods: A Case Study from Southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Fang, Z.; Peng, L.; Hong, H. Potential of Ensemble Learning to Improve Tree-Based Classifiers for Landslide Susceptibility Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 4642–4662. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Han, S.; Ren, Q.; Shi, J. Intelligent Identification for Rock-Mineral Microscopic Images Using Ensemble Machine Learning Algorithms. Sensors 2019, 19, 3914. [Google Scholar] [CrossRef] [PubMed]
- Graczyk, M.; Lasota, T.; Trawiński, B.; Trawiński, K. Comparison of Bagging, Boosting and Stacking Ensembles Applied to Real Estate Appraisal. Compu. Sci. 2010, 340–350. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2020, 1–27. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Carranza, E.J.M.; Yang, F. Maximum Entropy and Random Forest Modeling of Mineral Potential: Analysis of Gold Prospectivity in the Hezuo–Meiwu District, West Qinling Orogen, China. Nat. Resour. Res. 2019, 28, 645–664. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, J.; Shu, S.; Lai, C.; Xu, B.; Sun, H. Genesis of the Xiuwenghala Gold Deposit in the Beishan Orogen, Northwest China: Evidence from Geology, Fluid Inclusion, and H-O-S-Pb Isotopes. Resour. Geol. 2019, 69, 211–226. [Google Scholar] [CrossRef]
- Jiang, S.-H.; Nie, F.-J.; Lie, Y. Gold Deposits in Beishan Mountain, Northwestern China. Resour. Geol. 2004, 54, 325–340. [Google Scholar] [CrossRef]
- Chen, S.; Guo, Z.; Qi, J.; Zhang, Y.; Pe-Piper, G.; Piper, D.J. Early Permian volcano-sedimentary successions, Beishan, NW China: Peperites demonstrate an evolving rift basin. J. Volcanol. Geotherm. Res. 2016, 309, 31–44. [Google Scholar] [CrossRef]
- Su, B.-X.; Qin, K.-Z.; Sakyi, P.A.; Liu, P.-P.; Tang, D.-M.; Malaviarachchi, S.P.; Xiao, Q.-H.; Sun, H.; Dai, Y.-C.; Yan, H. Geochemistry and geochronology of acidic rocks in the Beishan region, NW China: Petrogenesis and tectonic implications. J. Asian Earth Sci. 2011, 41, 31–43. [Google Scholar] [CrossRef]
- Su, B.; Qin, K.; Sakyi, P.A.; Tang, D.; Liu, P.; Malaviarachchi, S.P.K.; Xiao, Q.; Sun, H. Geochronologic-petrochemical studies of the Hongshishan mafic-ultramaflc intrusion, Beishan area, Xinjiang (NW China) petrogenesis and tectonic implications. Inter. Geol. Rev. 2012, 54, 270–289. [Google Scholar] [CrossRef]
- Xiao, W.; Huang, B.; Han, C.; Sun, S.; Li, J. A review of the western part of the Altaids: A key to understanding the architecture of accretionary orogens. Gondwana Res. 2010, 18, 253–273. [Google Scholar] [CrossRef]
- Yue, Y.; Liou, J.G.; Graham, S.A. Tectonic correlation of Beishan and Inner Mongolia orogens and its implications for the palinspastic reconstruction of north China. Mem. Geol. Soc. Am. 2001, 194, 101–116. [Google Scholar] [CrossRef]
- Schill, W.; JöCKEL, K.H. Logistic analysis in case-control studies under validation sampling. Great Br. 1993, 80, 339–352. [Google Scholar] [CrossRef]
- Cheng, Q.-M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, K.; Qiuming, C. A new method for geochemical anomaly separation based on the distribution patterns of singularity indices. Comput. Geosci. 2017, 105, 139–147. [Google Scholar] [CrossRef]
- Faith, M.K. Centered Log-Ratio (clr) Transformation and Robust Principal Component Analysis of Long-Term NDVI Data Reveal Vegetation Activity Linked to Climate Processes. Climate 2015, 3, 135–149. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z. Consensus RNA Secondary Structure Prediction Based on Support Vector Machine Classification. Chin. J. Biotechnol. 2008, 24, 1140–1148. [Google Scholar] [CrossRef]
- Smirnoff, A.; Boisvert, É.; Paradis, S.J. Support vector machine for 3D modelling from sparse geological information of various origins. Comput. Geosci. 2008, 34, 127–143. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. A Maximum Entropy Approach to Species Distribution Modeling. In Proceedings of the Twenty-First International Conference on Machine Learning—ICML 04, New York, NY, USA, 4 July 2004; p. 83. [Google Scholar]
- Hernández, S.; Baldomir, A.; Díaz, J.; Pereira, F. An Enhanced Formulation of the Maximum Entropy Method for Structural Optimization. Compu. Mater. Cont. 2012, 32, 219–239. [Google Scholar]
- Liu, Y.; Zhou, K.; Zhang, N.; Wangid, J. Maximum entropy modeling for orogenic gold prospectivity mapping in the Tangbale-Hatu belt, western Junggar, China. Ore Geol. Rev. 2018, 100, 133–147. [Google Scholar] [CrossRef]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2010, 17, 43–57. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2009, 33, 1–39. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Nykänen, V.; Lahti, I.; Niiranen, T.; Korhonen, K. Receiver operating characteristics (ROC) as validation tool for prospectivity models—A magmatic Ni-Cu case study from the Central Lapland Greenstone Belt, Northern Finland. Ore Geol. Rev. 2015, 71, 853–860. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Objective selection of suitable unit cell size in data-driven modeling of mineral prospectivity. Comput. Geosci. 2009, 35, 2032–2046. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Beguería, S. Validation and Evaluation of Predictive Models in Hazard Assessment and Risk Management. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef]
- Baeza, C.; Lantada, N.; Moya, J. Influence of sample and terrain unit on landslide susceptibility assessment at La Pobla de Lillet, Eastern Pyrenees, Spain. Environ. Earth Sci. 2009, 60, 155–167. [Google Scholar] [CrossRef]
- Li, T.; Wang, Z.; Xiong, Y.; Peng, Y. Random-Drop Data Augmentation of Deep Convolutional Neural Network for Mineral Prospectivity Mapping. Nat. Resour. Res. 2020, 1–12. [Google Scholar] [CrossRef]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G. Validation of Spatial Prediction Models for Landslide Hazard Mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Rokach, L. Taxonomy for characterising ensemble methods in classification tasks: A review and annotated bibliography. Compu. Statis. Data Anal. 2009, 53, 4046–4072. [Google Scholar] [CrossRef]
- Zhang, M. Analysis on the causes and prospecting direction of gold deposits in North Mt. area of Gansu Province. World Nonferrous Metals 2019, 7, 297–298. (In Chinese) [Google Scholar]
- Jiang, S.-H.; Nie, F.-J. Geology and ore genesis of the Nanjinshan gold deposit in Beishan Mountain area, northwestern China. Miner. Depos. Res. Meet. Glob. Chall. 2005, 537–540. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q. Tectonics of orogenic belts in Beishan Mts., western China and their evolution. Geosci. Res. 1995, 28, 37–48. (In Chinese) [Google Scholar]



| Methods | Performance | ||||
|---|---|---|---|---|---|
| Accuracy | Recall | Precision | F-measure | Kappa | |
| RF | 0.910 | 0.870 | 0.940 | 0.904 | 0.819 |
| SVM | 0.856 | 0.944 | 0.800 | 0.864 | 0.713 |
| MaxEnt | 0.823 | 0.926 | 0.702 | 0.730 | 0.798 |
| RF–SVM | 0.901 | 0.926 | 0.877 | 0.901 | 0.802 |
| RF–MaxEnt | 0.829 | 0.870 | 0.797 | 0.832 | 0.708 |
| SVM–MaxEnt | 0.859 | 0.907 | 0.817 | 0.860 | 0.723 |
| RF–SVM–MaxEnt | 0.928 | 0.907 | 0.942 | 0.925 | 0.856 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Zheng, X.; Wang, G.; Liu, D.; Cui, N. A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China. Minerals 2020, 10, 1126. https://doi.org/10.3390/min10121126
Wang K, Zheng X, Wang G, Liu D, Cui N. A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China. Minerals. 2020; 10(12):1126. https://doi.org/10.3390/min10121126
Chicago/Turabian StyleWang, Kaijian, Xinqi Zheng, Gongwen Wang, Dongya Liu, and Ning Cui. 2020. "A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China" Minerals 10, no. 12: 1126. https://doi.org/10.3390/min10121126
APA StyleWang, K., Zheng, X., Wang, G., Liu, D., & Cui, N. (2020). A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China. Minerals, 10(12), 1126. https://doi.org/10.3390/min10121126








