The exploitation of mining resources has been fundamental for the development of humanity since before industrialization. After hundreds of years of exploitation of mining resources, the demand for these resources has continued to increase, and without a doubt, will be maintained and increased in the future to face the great challenges of engineering [1] and society [2]. Not only will traditional materials be needed but new mining resources, such as those classified as critical materials, will be required as well [2,3]. A series of challenges will need to be addressed in order to meet those demands, including low grade ore, more complex minerals, more stringent environmental regulations, to name just a few. To face these challenges, tools are needed to help understand, improve, and facilitate the development of more effective solutions. The use of modeling of various types and levels will undoubtedly be required. The advantages include not only the possibility of cutting the times and costs of experimentation but also the study of phenomena where experimentation is difficult or impossible to employ. On the other hand, a common feature in the processing of mining resources is the presence of multiphase systems. A multiphase system is defined as one in which two or more different phases (i.e., gas, liquid, or solid) are present, including systems with the same type of phases (e.g., liquid–liquid). As such, a series of phenomena associated with processes such as flotation, grinding, magnetic separation, and thickening are related to multiphase systems. With these antecedents, in considering the importance of modeling activities and multiphase systems, we have developed this Special Issue dedicated to the modeling, design, and optimization of multiphase systems in mineral processing to promote discussion, analysis, and cooperation between research groups. The Special Issue contains a review article and eleven articles that cover different methodologies of modeling, design, optimization, and analysis in problems of adsorption, leaching, flotation, and magnetic separation, among others.
Multiphase systems are analyzed at different time and size scales in the review article [4] because the modeling and post-modeling activities depend on those scales (see Figure 1a). For example, molecular modeling is necessary to understand the phenomena that occur at the atomic or molecular level, such as the adsorption of chemical agents on the surface of minerals, while computational fluid dynamics is a suitable tool at the fluid level. The application of molecular modeling is recent in the area of study and has been used to complement experimental studies. Given that the type of information that it delivers cannot be determined experimentally, and the software currently available, numerous new applications are expected. Simulations using computational fluid dynamics codes can give comprehensive information about fluid flow and mass transfer in mineral processing processes and devices, and this can increase the understanding of a given process. The capacity and scope of computational fluid dynamics methodologies have been considerably expanded, and this type of simulation has been utilized to help in understanding a given process and in conducting new process developments. The modeling of experimental results using response surface methodology is also analyzed, given its wide use in mineral processing. Response surface methodology is based on the result of the design of experiment which intends to explain and represent the variation of output variables under conditions that are assumed to reflect the variation. The most commonly used experimental designs in mineral processing are central composite and Box–Behnken designs. One of the limitations of the response surface methodology is the use of second-order polynomials, a behavior rarely observed in multiphasic phenomena. Several applications give reasonable results because the range of the input variables is small. However, a significant amount of work using this modeling strategy has unacceptable or questionable adjustment levels. To solve this problem, new modeling strategies must be proposed, possibly based on artificial intelligence. Precisely, several applications of artificial intelligence in the design, optimization, and modeling of multiphase systems were analyzed in the review [4], including artificial neural networks and support vector machines. In fact, there has been an exponential growth in research associated with artificial intelligence; in 1990, there were 29 publications that included artificial neural networks in their title, while last year this figure was 1430 in Web of Science. Similar behavior was observed in other subjects. Publications that include support vector machine in the title grew over 2600% from 2000 to 2019. In the coming years, with the advancement of these techniques and hardware improvements, many more applications are expected. One of the strategies currently used to understand and model systems is multiscale modeling [5,6,7]. We have to promote this type of simulation to be able to combine different phenomena that occur at different scales in multiphase systems. The integration of computational fluid dynamic modeling and discrete element simulation, which integrates phenomena at the particle and fluid level, has been an example of an approach that has produced very satisfactory results in terms of its ability to improve the current understanding of the complexity of mineral processing phenomena. Nevertheless, greater efforts are needed in the integration of meso-, micro-, and macro-scales modeling in order to understand and improve multiphase systems, as has been observed in other areas [8]. Uncertainty, both epistemic and stochastic, is an important issue in mineral processing because several phenomena are not well known or difficult to measure, and because several variables (e.g., metal price, particle size, mineral grade) have random variations [9]. Therefore, modeling tools such as uncertainty analysis and global sensitivity analysis were included in the review. Both tools have been shown to be good approaches for considering uncertainties [10,11,12]. These and other topics are included in the review paper, and readers are recommended to read this review if they are interested in the topic or as an introduction to reading the other articles that cover specific themes.
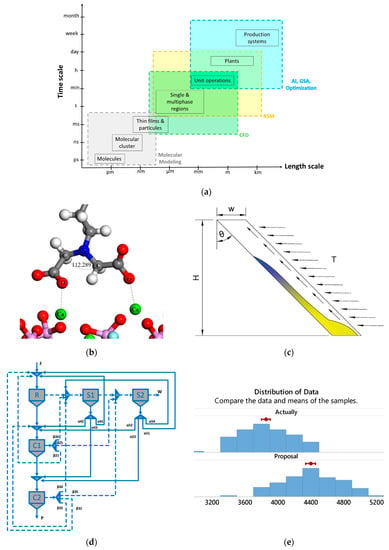
Figure 1.
Figures from the special issue. (a) Levels of length and time alongside the modeling and optimization tools [4]; (b) Adsorption configuration of collector N-(carboxymethyl)-N-tetradecylglycine on fluorapatite. (Ca—green; phosphorus—purple; O—red; H—white; fluorine—light blue; N—dark blue) [14]; (c) Scheme of the inclined settler [16]; (d) Superstructure for flotation circuit design [17]; (e) Production comparison between strategies that do and do not consider changes in the manner of operation [18].
Published articles can be analyzed following the same scale logic. Molecular modeling has allowed for an improved understanding of the mechanisms of interaction between minerals, the aqueous medium, and flotation reagents [13,14,15]. For example, studies on the behavior and molecular mechanism of adsorption of the collector sodium oleate were carried out by density functional theory and experimental techniques [13]. A similar study, but of the adsorption of flotation collector N-(carboxymethyl)-N-tetradecylglycine on a fluorapatite surface, was investigated (Figure 1b) [14]. Density functional theory is one of the most used methods in quantum calculations of the electronic structure of matter. Usually, functional density theory is combined with experimental studies; for example, molecular modeling helps identify the most stable structure of ionic species and identify active sites, while experimental techniques such as electrospray ionization-mass spectrometry and ultraviolet-visible spectroscopy allow the existence of molecules or complexes to be validated qualitatively and quantitatively [15]. These three manuscripts are good examples of the useful tool that molecular modeling can be for understanding the performance and development of new reagents.
Two manuscripts were published on the numerical simulation of equipment [16,19]. In the first, different turbulent models were compared using computational fluid dynamics in the simulation of cyclonic fields, which are important in cyclonic static microbubble flotation columns. The comparison with experimental values provides important information about which model is most suitable for modeling the different variables in these systems [19]. The second article shows how simulation can be used in the development or improvement of new equipment. Two-dimensional numerical simulations were used to analyze the possibility of improving the separation of particles in inclined settlers [16]. The inclined settler, whose scheme is shown in Figure 1c, has one of its walls exposed to heating. Results show that heating one wall has a significant effect on the particle settling velocity and can help the sedimentation of small particles of the order of 10 µm. These effects can be explained by the change of properties within the settler produced by the temperature profiles. Simulation of kinetic phenomena in multi-phase reactions are also present in this special issue [20,21], although the simulation of the phenomena in these papers have followed traditional methodologies using unreacted shrinking core and progressive conversion models, which have been shown to be unsuitable in several cases [22]. In this sense, it is necessary to move towards multiscale simulation using mesoscale simulation techniques to describe, for example, diffusion and reactive molecular dynamics [23] tools to describe the processes occurring within the interface in order to generate a procedure that can be used to increase our understanding of the heterogeneous gas–solid, liquid–solid, or other multiphase reactions in mineral processing. At the plant level, several articles are included. The use of the tabu search algorithm was applied to determine the optimal flotation circuit within a set of possibilities represented by a superstructure, as shown in Figure 1d [17]. The tabu search algorithm is a method of mathematical optimization classified as a metaheuristic algorithm, which in this work showed a tendency to give better results than the exact methods. The design and optimization at the separation circuit level is an active area in multiphase separation in mineral processing, and several reviews are available in the literature [24,25]. As such, it is not surprising that another study analyzes this same problem [26] but uses analytical methods that significantly simplify the problem, although that can lead to important errors or omissions [27]. A larger time scale problem was considered in the manuscript presented by a multidisciplinary research team [18]. The discrete-event simulation combination with analytical models of leaching processes was used to optimize mineral extraction processes. The methodology helps the planning process by incorporating different possibilities of operation according to the mineralogical changes of the feed. Thus, by simulating a discrete sequence of events over time it is possible to consider the stochastic uncertainties that naturally occur in the mineral. This simulation at the plant level, together with models at the unit operation level, allows for the integration of phenomena that occur at the level of weeks with problems at the level of months or years of operation, giving flexibility to the value chain by adjusting the mineral recovery to the mineralogical variation. This strategy allows for production to be improved compared to strategies that do not consider changes in the manner of operation (Figure 1e).
This Special Issue considered different problems in several areas of multiphase systems in mineral processing. Thus, various strategies and tools were presented to solve or face those problems. On the whole, I hope that this Special Issue will contribute to a superior understanding of multiphase phenomena and will promote future research in the modeling, design, and optimization of multiphase systems in minerals processing.
Authors’ contributions from China, Chile, Canada, Germany, Iran, Mexico, and Spain were received. I thank all of them for their contributions that helped in the development of this Special Issue. Finally, I would like to thank the referees and editorial staff of Minerals for their valuable efforts that contributed to the success of this initiative.
Acknowledgments
The author is thankful for financial support from the Chilean National Commission for Science and Technology (Fondecyt 1180826) and MINEDUCUA project (code ANT1856).
Conflicts of Interest
The author declares no conflict of interest.
References
- Mote, C.D.; Dowling, D.A.; Zhou, J. The power of an idea: The international impacts of the grand challenges for engineering. Engineering 2016, 2, 4–7. [Google Scholar] [CrossRef]
- Schlör, H.; Venghaus, S.; Zapp, P.; Marx, J.; Schreiber, A.; Hake, J.F. The energy-mineral-society nexus—A social LCA model. Appl. Energy 2018, 228, 999–1008. [Google Scholar] [CrossRef]
- Cai, M.; Brown, E.T. Challenges in the mining and utilization of deep mineral resources. Engineering 2017, 3, 432–433. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.A.; Botero, Y.L. Trends in modeling, design, and optimization of multiphase systems in minerals processing. Minerals 2019, 10, 22. [Google Scholar] [CrossRef]
- Shu, S.; Vidal, D.; Bertrand, F.; Chaouki, J. Multiscale multiphase phenomena in bubble column reactors: A review. Renew. Energy 2019, 141, 613–631. [Google Scholar] [CrossRef]
- Engquist, B.; Li, X.; Ren, W.; Vanden-Eijnden, E. Heterogeneous multiscale methods: A review. Commun. Comput. Phys. 2007, 2, 367–450. [Google Scholar]
- Liu, T.Y.; Schwarz, M.P. CFD-based multiscale modelling of bubble–particle collision efficiency in a turbulent flotation cell. Chem. Eng. Sci. 2009, 64, 5287–5301. [Google Scholar] [CrossRef]
- Ludwig, A.; Kharicha, A.; Wu, M. Modeling of multiscale and multiphase phenomena in materials processing. Metall. Mater. Trans. B 2014, 45, 36–43. [Google Scholar] [CrossRef]
- Jamett, N.; Cisternas, L.A.; Vielma, J.P. Solution strategies to the stochastic design of mineral flotation plants. Chem. Eng. Sci. 2015, 134, 850–860. [Google Scholar] [CrossRef]
- Sepúlveda, F.D.; Cisternas, L.A.; Gálvez, E.D. The use of global sensitivity analysis for improving processes: Applications to mineral processing. Comput. Chem. Eng. 2014, 66, 221–232. [Google Scholar] [CrossRef]
- Lucay, F.A.; Gálvez, E.D.; Salez-Cruz, M.; Cisternas, L.A. Improving milling operation using uncertainty and global sensitivity analyses. Miner. Eng. 2019, 131, 249–261. [Google Scholar] [CrossRef]
- Lucay, F.; Cisternas, L.A.; Gálvez, E.D. Global sensitivity analysis for identifying critical process design decisions. Chem. Eng. Res. Des. 2015, 103, 74–83. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Z.; Hu, Y.; He, J.; Tian, M.; Zhou, J.; Zhou, Q.; Chen, S.; Chen, D.; Chen, P.; et al. Novel insights into the hydroxylation behaviors of α-quartz (101) surface and its effects on the adsorption of sodium oleate. Minerals 2019, 9, 450. [Google Scholar] [CrossRef]
- Nan, N.; Zhu, Y.; Han, Y.; Liu, J. Molecular modeling of interactions between N-(Carboxymethyl)-N-tetradecylglycine and fluorapatite. Minerals 2019, 9, 278. [Google Scholar] [CrossRef]
- He, J.; Han, H.; Zhang, C.; Hu, Y.; Yuan, D.; Tian, M.; Chen, D.; Sun, W. New insights into the configurations of lead(II)-benzohydroxamic acid coordination compounds in aqueous solution: A combined experimental and computational study. Minerals 2018, 8, 368. [Google Scholar] [CrossRef]
- Reyes, C.; Ihle, C.F.; Apaz, F.; Cisternas, L.A. Heat-assisted batch settling of mineral suspensions in inclined containers. Minerals 2019, 9, 228. [Google Scholar] [CrossRef]
- Lucay, F.; Gálvez, E.; Cisternas, L. Design of flotation circuits using tabu-search algorithms: Multispecies, equipment design, and profitability parameters. Minerals 2019, 9, 181. [Google Scholar] [CrossRef]
- Saldaña, M.; Toro, N.; Castillo, J.; Hernández, P.; Navarra, A. Optimization of the heap leaching process through changes in modes of operation and discrete event simulation. Minerals 2019, 9, 421. [Google Scholar] [CrossRef]
- Meng, S.; Li, X.; Yan, X.; Wang, L.; Zhang, H.; Cao, Y. Turbulence models for single phase flow simulation of cyclonic flotation columns. Minerals 2019, 9, 464. [Google Scholar] [CrossRef]
- Juárez Tapia, J.; Patiño Cardona, F.; Roca Vallmajor, A.; Teja Ruiz, A.; Reyes Domínguez, I.; Reyes Pérez, M.; Pérez Labra, M.; Flores Guerrero, M. Determination of dissolution rates of Ag contained in metallurgical and mining residues in the S2O32−-O2-Cu2+ system: Kinetic analysis. Minerals 2018, 8, 309. [Google Scholar] [CrossRef]
- Liu, S.; Han, C.; Liu, J. Study of K-feldspar and lime hydrothermal REACTION: Phase and mechanism with reaction temperature and increasing Ca/Si ratio. Minerals 2019, 9, 46. [Google Scholar] [CrossRef]
- Liddell, K.C. Shrinking core models in hydrometallurgy: What students are not being told about the pseudo-steady approximation. Hydrometallurgy 2005, 79, 62–68. [Google Scholar] [CrossRef]
- Meuwly, M. Reactive molecular dynamics: From small molecules to proteins. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1386. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.A.; Acosta-Flores, R.; Gálvez, E.D. A quasi-review of conceptual flotation design methods based on computational optimization. Miner. Eng. 2018, 117, 24–33. [Google Scholar] [CrossRef]
- Noble, A.; Luttrell, G.H.; Amini, S.H. Linear circuit analysis: A tool for addressing challenges and identifying opportunities in process circuit design. Mining, Metall. Explor. 2019, 36, 159–171. [Google Scholar] [CrossRef]
- Radmehr, V.; Shafaei, S.; Noaparast, M.; Abdollahi, H. Optimizing flotation circuit recovery by effective stage arrangements: A case study. Minerals 2018, 8, 417. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Acosta-Flores, R.; Gálvez, E.D. Some limitations and disadvantages of linear circuit analysis. In Proceedings of the 7th International Computational Modelling Symposium (Computational Modelling ’19), Falmouth, UK, 11–12 June 2019. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).