Interphase REE Partitioning at the Boundary between the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments and Atomistic Modeling
by
Anastasia P. Tamarova
1,*, 
Ekaterina I. Marchenko
1,
Andrey V. Bobrov
1,2,3,
Nikolay N. Eremin
1,
Nina G. Zinov’eva
1,
Tetsuo Irifune
4,
Takafumi Hirata
5 and
Yoshiki Makino
5 1
Geological Faculty, Moscow State University, Leninskie Gory, 119991 Moscow, Russia
2
Vernadsky Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, ul. Kosygina 19, 119991 Moscow, Russia
3
Korzhinskii Institute of Experimental Mineralogy, Russian Academy of Sciences, ul. Akademika Osipyana 4, Chernogolovka, 142432 Moscow oblast, Russia
4
Geodynamics Research Center, Ehime University, 2-5 Bunkyo-cho, Matsuyama Ehime 790-8577, Japan
5
Geochemical Research Center, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
*
Author to whom correspondence should be addressed.
Minerals 2020, 10(3), 262; https://doi.org/10.3390/min10030262
Submission received: 1 February 2020
/
Revised: 10 March 2020
/
Accepted: 12 March 2020
/
Published: 14 March 2020
(This article belongs to the Special Issue Minerals of Kimberlites: An Insight into Petrogenesis and the Diamond Potential of Deep Mantle Magmas)
Abstract
:Trace elements play a significant role in interpretation of different processes in the deep Earth. However, the systematics of interphase rare-earth element (REE) partitioning under the conditions of the uppermost lower mantle are poorly understood. We performed high-pressure experiments to study the phase relations in key solid-phase reactions CaMgSi2O6 = CaSiO3-perovskite + MgSiO3-bridgmanite and (Mg,Fe)2SiO4-ringwoodite = (Mg,Fe)SiO3-bridgmanite + (Mg,Fe)O with addition of 1 wt % of REE oxides. Atomistic modeling was used to obtain more accurate quantitative estimates of the interphase REE partitioning and displayed the ideal model for the high-pressure minerals. HREE (Er, Tm, Yb, and Lu) are mostly accumulated in bridgmanite, while LREE are predominantly redistributed into CaSiO3. On the basis of the results of experiments and atomistic modeling, REE in bridgmanite are clearly divided into two groups (from La to Gd and from Gd to Lu). Interphase REE partition coefficients in solid-state reactions were calculated at 21.5 and 24 GPa for the first time. The new data are applicable for interpretation of the trace-element composition of the lower mantle inclusions in natural diamonds from kimberlite; the experimentally determined effect of pressure on the interphase (bridgmanite/CaSiO3-perovskite) REE partition coefficients can be a potential qualitative geobarometer for mineral inclusions in super-deep diamonds.
1. Introduction
The data on the systematics of interphase partitioning and mechanisms of incorporation of rare-earth elements (REE) in minerals are of key importance for understanding of the geochemical processes in the Earth’s deep mantle. Among the major rock-forming phases of the transition zone are the ringwoodite–arensite solid solution Mg2SiO4–Fe2SiO4 [1] and majoritic garnet (Ca,Mg,Fe)3Al2Si3O12–(Mg,Fe)4Si4O12 [2]. At a depth of 660 km, ringwoodite decomposes to form bridgmanite (Mg,Fe)SiO3 [3] and ferropericlase (Mg,Fe)O. Majoritic garnet also breaks down with the formation of CaSiO3-perovskite and bridgmanite.
The data on REE partitioning between the abovementioned phases and melts are quite limited. The concentration of REE in bridgmanite (Brd) is low with a slight enrichment in HREE. The Brd/melt REE partitioning coefficient increases with the atomic number and decreases with ionic radii from essentially incompatible La (DLa = 0.01) to rather compatible Lu (DLu up to ~1.5) [4]. It is expected that incorporation of Al in Brd (quite common admixture in natural samples) should increase the content of trivalent and tetravalent ions of trace elements in bridgmanite [5].
The concentration of REE in ferropericlase (fPer) ranges broadly [6]. This phase is often enriched in Li, Ta, Th, and U, and sometimes HREE. As is evident from the fPer/melt partitioning coefficients, most of minor elements, except for Cr, Fe, Mg, and Ni, are incompatible for fPer. In particular, the D values for REE are <0.1 [7]. Nevertheless, these experimental data are somewhat different from the results of the study of trace elements in natural ferropericlase grains. In particular, the REE patterns for inclusions of these phases in Brazilian diamonds show an increase in the content by almost an order of magnitude from the chondrite level towards HREE [6].
The data on ringwoodite (Rgw) are more limited. By analogy with wadsleyite and olivine, it is assumed that REE, U, and Th are very incompatible in this this phase, and Rgw does not accumulate the minor elements [5].
Natural CaSiO3-perovskite (CaPrv) demonstrates enrichment in LREE [6]. The mixing energies for elements with charges 3+ and 4+ in the system CaPrv/minerals are >1, which suggests accumulation of minor elements in this phase of the Earth’s lower mantle [8]. However, the abundance of CaSiO3-perovskite in the bulk mantle is very limited, as is evident from the experimental data (8% to 10%), as well as from the data on natural inclusions in ultradeep diamonds (10% to 14%) [6]. This fact forces us to shift our attention to the study of accumulation of trace elements in other, more common phases.
Our study was aimed at experimental and theoretical modeling of REE interphase partitioning between the major high-pressure phases. The REE distribution was studied experimentally for two solid-phase model reactions typical of the transition zone and lower mantle boundary: (Mg,Fe)2SiO4 → (Mg,Fe)SiO3 + (Mg,Fe)O; CaMgSi2O6 → CaSiO3 + MgSiO3. The results obtained were compared with the data of atomistic modeling of MgSiO3, CaSiO3, and (Mg,Fe)O solid solutions with REE components and with the data on REE concentrations in mineral inclusions in UHP diamonds from kimberlites.
2. Materials and Methods
Oxides mixed in the desired proportions were used in our runs as starting materials. We performed two series of experiments with the different concentration of trace elements. The first series included only three REE elements (La, Sm, and Lu); the second, a mixture of trace elements.
Each experimental cell assembly included two samples with the following compositions: (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + REE (1 wt %) (the samples of the ringwoodite composition) and CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + REE (1 wt %) (the samples of the diopside composition). The composition of ringwoodite (10 wt % FeO) was close to that of natural inclusions in ultradeep diamonds. Mixtures of only three REE oxides (3REE, La2O3 + Sm2O3 + Lu2O3) were applied in the first run series. In the second series of experiments, we used the multicomponent mixture (mixREE) of La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, Y, Hf, Zr, Nb, Sc, Ta, Pb, and Zn oxides, RbCl, and Sr, Ba, and Li carbonates (30 mg each). The starting materials were mixed for 1 h and, then, were stored in a desiccator.
The experiments at pressures of 21.5 and 24 GPa and a temperature of 1600 °C were performed on an Orange-2000 multianvil high-pressure apparatus [9]. This apparatus operated in a 2000 t hydraulic ram, in which pressures up to 30 GPa and temperatures of 2500 °C are produced. An octahedral cell assembly with an edge of 8 mm composed of MgO with Co (17 wt %) was applied in our runs. The samples were loaded into the Re capsules. The cell assembly used in our experiments was described in [10]. A cylindrical LaCrO3 heater with 3.2 and 2.0 outer and inner diameters and a length of 4 mm was applied. The sample volume after pressurization was ~1.0 mm3.
The pressure was calibrated at a room temperature using the phase transitions in Bi (2.55 and 7.7 GPa), ZnS (15.5 GPa), and GaAs (18.3 GPa) [11]. An effect of temperature on pressure was further corrected using the phase transitions between the α-β and β-γ Mg2SiO4 polymorphs [12]. The temperature was controlled using a W97Re3−W75Re25 thermocouple. Temperature variations in our runs were within ±10 °C. The run durations were 2 to 5 h. After runs, the samples were quenched by switching off the power supply, which provided a rapid temperature decrease by a few hundred °C during 3 to 5 s.
The obtained specimens were mounted in an epoxy and polished using 800-, 1000-, and 2000-mesh sandpaper. The final polishing was carried out on a Struers machine, on a cloth substrate using a diamond suspension of different grain sizes (9, 6, 3, 1 μm). Alcohol was used as a lubricant. Before switching to a finer grain size, the sample was cleaned in an ultrasonic bath.
A precise study of the samples was performed at the Laboratory of Local Methods of Matter Study, Geological Faculty, Moscow State University (Moscow, Russia), using a JSM-6480LV scanning electron microscope (Jeol, Tokyo, Japan) with a tungsten thermionic emission cathode and an INCA-Energy 350 energy dispersive spectrometer with a 10 mm2 Li–Si semiconductor detector and an ATW-2 ultrathin window (resolution 129 eV on K Mn). The results were processed using professional licensed software, SEM Control User Interface, version 7.11 (Jeol Technics LTD) and INCA, version 17a (Oxford Instruments). At this stage, the concentration of REE in high-pressure phases was estimated semiquantitatively in order to select the grains for further analysis.
A detailed analysis of trace elements was performed by the ICP-mass spectrometer (iCAP TQ, Thermo Fisher Scientific, Bremen, Germany) equipped with the 193 nm ArF excimer laser (Analyte excite, Teledyne Cetac, NE, USA).
The diameter of an ablation crater was 15 μm with a laser repetition rate of 50 Hz. Calibration of the element content was performed using NIST SRM 610 and NIST SRM 612 as an external calibration sample and Si and Mg as internal standards. The measurement error was estimated by the repeatability of intensities obtained from the standard sample (NIST610) used in the measurement.
An effective alternative approach is the computer simulation of the properties of such multicomponent systems. An appropriate particular modeling method for these systems should predict a desired set of properties with a high accuracy and optimal computational cost.
A theoretical assessment of the nature of the distribution of REE in the lower mantle MgSiO3 and CaSiO3 perovskites was performed using a semi-empirical approach. In order to compare the properties in a wide range of compositions, it is important to use the same approximations for all particular compositions, regardless of their specific structural and chemical features, which requires models with high transferability. The structural parameters of the end-members of solid solutions involving REE with occupancies of one-third of Ca/Mg sites were calculated using a self-consistent transferable model of interatomic interaction potentials for pairs of REE–O atoms from [13] and for Ca–O, Mg–O, Si–O, O–O from [14]. To describe interatomic interactions, the potential of the Morse species was used as
where three variable potential parameters DM (eV), α (Å-1), and r0 (Å) have the starting physical meaning of the energy of bond dissociation between atoms, the softness parameter of the chemical bond, and the optimal length of the pair interatomic contact, respectively.
V(r) = DM × [exp(− 2α(r − r0)) − 2exp(− α(r − r0))],
The values of the potential parameters are given in Table S1. Parametrization was performed using the GULP 5.0 software (Curtin Institute for Computation, Curtin University, Perth, WA, Australia) [15]. The deviation from the starting values of the cell parameters, angles, and atomic coordinates does not exceed 1%. A mixing enthalpy ΔHmix was determined as
where Hlatt (x) is the lattice enthalpy of solid solution; Hlatt1 and Hlatt2 are the lattice enthalpies of pure components of solid solutions.
ΔHmix = Hlatt (x) − x1Hlatt1 − x2Hlatt2
3. Results
3.1. Textural Relationships, Phase Assemblages, and Major-Element Compositions of Minerals in Run Products
The results of the experiments in the systems Rgw-3REE, Di-3REE, Rgw-mixREE, and Di-mixREE including the run conditions, starting materials, and chemical compositions of synthetic phases are presented in Table 1. Back-scattered electron (BSE) images of the samples after runs are shown in Figure 1.
Our study included four experiments at a temperature of 1600 °C and pressures of 21.5 and 24 GPa. As a result, three main phase assemblages were obtained. Samples with the “diopside starting composition” are composed of CaSiO3-perovskite (CaPrv) and bridgmanite (Brd) in almost equal proportions (Figure 1a–d).
Of special interest is the presence of bridgmanite at 21.5 GPa (Figure 1a,c). In experimental works, where the phase transformations of CaMgSi2O6 were studied, the stability of the occurrence of two minerals of the perovskite-type structure (Brd and CaPrv) was determined to be at least 22.5 GPa [16,17]. We can also assume that the presence of trace elements in the “diopside” starting composition (in our case, in total 2 wt % REE, Ti, and Cr) leads to an even greater decrease in pressure at which the assemblage of Brd and CaPrv is formed.
CaSiO3-perovskite is represented by a crystalline aggregate with a size of individual grains up to 10 μm. Therefore, it is rather difficult to analyze the composition of this phase; however, in our experimental samples, it is fairly homogeneous with 44.74 to 47.56 wt % CaO and 48.36 to 49.66 wt % SiO2. An admixture of MgO oxide reaches 0.51 wt % in some grains. The contents of TiO2 and Cr2O3 are also constant and vary from 0.52 to 0.85 wt % and from 0.46 to 0.75 wt %, respectively. The correlations of the concentrations of these elements with pressure were not detected. ”Bridgmanite” occurs in the samples as aggregates of small fractured crystals with a size up to 30 μm. The CaO, TiO2, and Cr2O3 contents in Brd reach 0.36, 0.11, and 0.46 wt %, respectively. This phase is characterized by a high content of SiO2 (58.63 to 61.73 wt %). Moreover, at a higher pressure (24 GPa), the silica content is higher than that at 21.5 GPa by an average of 3 wt %. The total content of REE in both phases does not exceed 0.1 wt %.
The following two main phase assemblages were detected in the samples with the starting composition of “ringwoodite”: ringwoodite (Rgw) + minor ferropericlase (fPer), sometimes accompanied by SiO2 (stishovite) at 21.5 GPa (Figure 1e,g) and Rgw + Brd + fPer at 24 GPa (Figure 1f,h). This is due to the reaction of Rgw decomposition via the reaction (Mg,Fe)2SiO4 → 2(Mg,Fe)O + SiO2, close to the upper boundary of Rgw stability. Ringwoodite is represented by euhedral crystals with a size up to 250 μm. The iron content in Rgw ranges from 9.71 to 11.07 wt % FeO (7 to 8 mol % FeSiO3) (Table 1). Rgw contains up to 0.37 wt % TiO2 and 0.58 wt % Cr2O3. The correlations of these elements with pressure were not detected in Rgw as well. “Ferropericlase” is represented by anhedral crystals up to 70 μm in size. The content of FeO varies from 23.61 to 38.56 wt %. The TiO2 content reaches 0.09 wt %, while the Cr2O3 content is quite high (1.53 wt %). Bridgmanite in these samples forms fractured crystals up to 100 μm in size. It contains up to 4.88 wt% FeO. It is important to note that the concentrations of Cr2O3 (up to 0.86 wt %) and TiO2 (up to 1.52 wt %) are much higher in Brd produced from the ringwoodite starting composition in comparison with this phase in the diopside system (Table 1).
3.2. REE Composition
The REE compositional patterns are different for two types of starting materials. REE in the samples with the diopside starting composition are predominantly accumulated in CaPrv (Table 2). The spectra show enrichment in La, although not significant (about 2000 ppm), over other two elements. At 24 GPa, the total content of REE is lower (~2000 to 3000 ppm for all three REE). The average content of REE varies from 6000 to 9000 ppm with predomination of La. At 21.5 GPa, the total REE content is higher than that at 24 GPa (up to 11,000 ppm) (Table 2), and all values are fairly close to each other (ranging from 8500 to 11,000 ppm). Brd, the second phase obtained in the samples with the diopside starting composition, is characterized by a quite high REE content at 21.5 GPa and could exceed 2000 ppm (for Lu). At 24 GPa, the REE content in bridgmanite significantly decreases and ranges from 80 (La and Sm) to 400 ppm (Lu). The partition coefficients DCaPrv/Brd for REE are shown in Figure 2a; all coefficients are significantly higher than 1. The partition coefficients are lower for Lu than those for La. All these facts are consistent with incorporation of REE in calcium perovskite.
In the samples of the ringwoodite starting composition (in the absence of CaPrv), REE are accumulated in Brd at 24 GPa. The Lu content in this mineral reaches 2500 ppm. The Lu partition coefficients DBrd/min are significantly higher than 1 for all phases in the sample of the ringwoodite composition. The content of La and Sm in Brd is low and ranges from the detection limits to 50 ppm. As is evident from Figure 2b, the partition coefficients for Sm and Lu exceed 1, and the pattern shows the positive slope from La to Lu. The content of REE in Rgw and fPer at 21.5 GPa is at the level of a few tens of ppm (Table 3).
It is important to note that at 24 GPa, the content of REE in Brd and fPer is lower than that at 21.5 GPa. The greatest difference is observed for fPer. The La content at 21.5 GPa reaches 1143 ppm; Sm, 453 ppm; and Lu, 537 ppm. However, this could be a result of capture of a fine phase with a high content of REE, because it was shown in [5], that fPer does not tend to accumulate REE.
The results of experiments with a REE mixture demonstrate some additional correlations for Brd and Rgw (Table 3). As is evident from Figure 3, the REE pattern is similar to those obtained in the system with 3REE. The partition coefficients increase from LREE to HREE, but with a gentler slope. The average content of trace elements is low, hardly reaching ten ppm for both Brd and Rgw. The Lu content in some Brd grains reaches 100 ppm. The REE content increases unevenly from La to Lu (Table 3). Such low concentrations do not demonstrate an effect of pressure on REE contents in these run series.
3.3. Computational Results
The thermodynamic mixing properties of MgSiO3 and CaSiO3 solid solutions containing REE were calculated using a semi-empirical method in supercells. We revealed a fundamentally different nature of the distribution of LREE and HREE between MgSiO3 and CaSiO3. Figure 4 shows the calculated REE partition coefficients for the La–Lu series in relation to the lower-mantle perovskites and the dependence of mixing enthalpy on the composition of solid solutions of the studied mineral phases with hypothetical REE end members. It can be concluded that HREE (Er, Tm, Yb, and Lu) are mostly accumulated in MgSiO3, and LREE in CaSiO3. Such REE partitioning between CaSiO3 perovskite and MgSiO3 bridgmanite can be explained by the proximity of the ionic radii of Er, Tm, Yb, and Lu to Mg, rather than to Ca. In addition, our calculations show that the isomorphic capacity of the studied phases for REE decreases with pressure, in accordance with the rule of depression of isomorphism (Figure 5, Table S2).
4. Discussion
The data on the REE composition of the phases in lower mantle diamonds are scarce. As is evident from the composition of inclusions in superdeep diamonds [6], the content of trace elements in natural bridgmanite is low, with an average REE content not exceeding 0.1 ppm (Table 2); for some elements, it is below the detection limits (e.g., La, Tb, etc. [18,20]) (Figure 6). The REE content in CaPrv from inclusions in natural diamonds is much higher, with LREE concentrations reaching 1000 ppm and regular decrease towards HREE [18]. There are also some data on the concentration of trace elements in natural ferropericlase illustrating general incompatibility of REE [6]. The data on the content of REE in ringwoodite inclusions in natural diamonds are absent.
Due to the extremely limited information on the trace-element composition of inclusions in superdeep diamonds, many issues related to understanding of the patterns of REE behavior in the uppermost lower mantle are discussed using data of experiments [4,21,22] and computer modeling [8]. Such data make it possible to evaluate the compositions of lower mantle melts that are in equilibrium with the minerals of the perovskite-type structure. In most experimental studies, the distribution of REE between mantle perovskites and melt is considered. In particular, very low bridgmanite/melt REE partitioning coefficients calculated for the high-pressure conditions (~10−3 for La to ~1 for Lu) [23] suggest the primary origin of Brd grains with their further trapping by host superdeep diamonds, but not crystallization of bridgmanite from melt, as is suggested in some studies [24]. In contrast, CaSiO3-perovskite/melt partition coefficients for REE are much higher [25], which causes the higher concentrations of REE (by up to two to three orders of magnitude) with significant enrichment in LREE in natural CaPrv in relation to Brd. As some CaPrv grains demonstrate positive Eu anomalies, their occurrence as inclusions in diamonds indicates the processes of the crust–mantle interaction at lower-mantle depths.
The present results are consistent with the previous data on the partial melt compositions estimated in the systems with addition of trace elements to the lower mantle phases (Brd and CaPrv). The concentrations of REE in Brd in our samples are similar to those in previous studies [4] (Table 3). In some bridgmanites, LREE and MREE concentrations do not exceed a few tens of ppm, but the Lu content reaches hundreds ppm (sometimes >500 ppm).
At the same time, the results of modeling of the distribution of REE between solid phases, in particular, those of the perovskite-type structure, were practically absent until recently. Our experiments show the distribution of elements in solid-phase reactions, which corresponds to the most common conditions in the transition zone and lower mantle. In the current study, we examined the interaction of these phases with each other and the distribution of minor elements and REE between them. Although the basic patterns of REE incorporation in high-pressure phases were confirmed in our experiments (Figure 2 and Figure 3), some new important features can be distinguished. In particular, we demonstrate that in the absence of melt and calcium perovskite (runs with the ringwoodite starting material), bridgmanite may accumulate significant concentrations (>2000 ppm) of REE.
Our studies significantly expand the set of data on the interphase REE partitioning in the bridgmanite/CaSiO3-perovskite pair. Until recently, such data was obtained only in one study [18] for diamond containing inclusions of these phases. A comparison of these data with the coefficients calculated in our study (Table 4 and Table 5, Figure 6) demonstrates similar patterns in the behavior of REE with a decrease in the DCaPrv/Brd partition coefficient towards HREE and significantly higher values for La in natural minerals. A similar comparison can be made with experimental work [19], in which bridgmanite and calcium perovskite were obtained at 25 GPa. The partition coefficients for La, Sm, and Lu/Yb plot in the range of our data (Figure 6).
Comparison of the results of experiments at 21.5 and 24 GPa allows us to understand the effect of pressure on the trace-element composition of mantle phases and on the interphase REE partition coefficients. In fact, in our study, we obtained the first quantitative data on the change in the coefficients of interphase REE partitioning with pressure, which can be used as a potential geobarometer. Previously, based on experiments with an amphibolite starting composition, [19] demonstrated a regular change in the trace-element composition only for CaSiO3-perovskite, since the different phase associations were obtained at different pressures (garnet + CaSiO3-perovskite at 20 GPa and bridgmanite and CaSiO3-perovskite at 25 GPa). The authors of the cited work showed that the compositions of CaSiO3-perovskites for different pressures regularly differ by 5 to 125 ppm, but the concentrations of each trace element at 20 GPa are lower than those at 25 GPa.
In this study, we used computer calculations to obtain the more accurate quantitative estimates of the interphase REE partitioning. Atomistic modeling was based on the results of our experiments and displayed the ideal REE partitioning model for the high-pressure minerals. Since the compositions of inclusions in natural diamonds and the phases obtained in our runs (the presence of Ti, Cr, and other trace elements in the mixture) are more complicated, there are some discrepancies with the model. Nevertheless, the basic systematics of the interphase REE partitioning demonstrate good agreement between the experimental and computational models.
At 24 GPa, the total content of trace elements is lower than that at 21.5 GPa (Table 2 and Table 3), as predicted by the theoretical calculations. This fact is true for all phases that were obtained in experiments (except for ringwoodite, but REE content in this phase rarely exceeds a few tens of ppm). In addition, REE patterns for Brd, CaPrv, and Rgw match with the results of atomistic modeling. Based on the theoretical considerations, Brd should be enriched in HREE. Moreover, Figure 4a shows that the mixing enthalpies of Brd plot into two groups (La–Gd and Tb–Lu). The experimental results are in a good agreement with the following such scenario: the Sm and La contents are equal, while the Lu content is significantly higher in the system with 3REE (ringwoodite starting material). There are also two groups of REE in the system with REE mixture (except for La and Ce) (Table 3). The concentrations of Nd–Gd reach a few tens of ppm, while those of Gd–Lu are hundreds of ppm (Gd in some cases changes the group). For the diopside starting composition, we observe a similar behavior of the partition coefficient DCaPrv/Brd, which is equal for Sm and La, but is lower for Lu. CaPrv is enriched in LREE, as is predicted by the atomistic modeling; the REE concentrations decrease smoothly from La to Lu.
5. Conclusions
- We performed high-pressure experiments to study the phase relations in key solid-phase reactions CaMgSi2O6 = CaSiO3-perovskite + MgSiO3-bridgmanite and (Mg,Fe)2SiO4-ringwoodite = (Mg,Fe)SiO3-bridgmanite + (Mg,Fe)O with addition of 1 wt % of REE oxides. It was shown that HREE (Er, Tm, Yb, and Lu) are mostly accumulated in bridgmanite, while LREE are predominantly redistributed into CaSiO3. Interphase REE partition coefficients in solid-state reactions were calculated at 21.5 and 24 GPa for the first time.
- The thermodynamic mixing properties of MgSiO3 and CaSiO3 solid solutions containing REE were calculated using a semi-empirical method in supercells. Atomistic modeling displayed the ideal model for the high-pressure minerals. Predominant distribution of HREE (Er, Tm, Yb, and Lu) into bridgmanite and LREE into CaSiO3-perovskite is explained by the proximity of the ionic radii of Er, Tm, Yb, and Lu to Mg, rather than to Ca. Our calculations show that the isomorphic capacity of the studied phases for REE decreases with pressure, in accordance with the rule of depression of isomorphism.
- Comparison of the results of experiments at 21.5 and 24 GPa allows us to estimate an effect of pressure on the trace-element composition of mantle phases and on the interphase REE partition coefficients; both total REE concentrations and CaPrv/Brd interphase REE partition coefficients decrease with pressure. The new data are applicable to interpretation of the trace-element composition of the lower mantle inclusions in natural diamonds from kimberlite; the experimentally determined effect of pressure on the interphase (bridgmanite/CaSiO3-perovskite) REE partition coefficients can be a potential qualitative geobarometer for mineral inclusions in superdeep diamonds.
Supplementary Materials
The following are available online at https://www.mdpi.com/2075-163X/10/3/262/s1, Table S1: Interatomic potential parameters of Morse function used in the calculations [13], Table S2: Enthalpy of solid solutions of CaSiO3 and MgSiO3 with hypothetical REE perovskites with a Сa/Mg site occupation of 0.5.
Author Contributions
Conceptualization, A.P.T., A.V.B., and N.N.E.; Funding acquisition, A.V.B.; Investigation, A.P.T., A.V.B., E.I.M., and N.N.E.; Methodology, E.I.M, N.N.E., N.G.Z., T.I., T.H., and Y.M.; Writing—original draft, A.P.T., A.V.B., and E.I.M.; Writing—review & editing, A.P.T., A.V.B., N.N.E., and T.I. All authors have read and agreed to the published version of the manuscript.
Funding
This study was performed as a part of the scientific plan of the Laboratory of Deep Geospheres, Geological Faculty, Moscow State University, and was supported by the Russian Science Foundation, project no. 17-17-01169.
Acknowledgments
We thank two anonymous referees for constructive comments and I.S. Sharygin for editorial handling. Experiments were carried out at the Geodynamics Research Center, Ehime University, Matsuyama, Japan. The SEM and EDS studies of experimental samples were performed at the laboratory of Local Methods of Matter Study, Department of Geology, Moscow State University. The La-ICP-MS studies of experimental samples were performed at the Geochemical Research Center, University of Tokyo, Tokyo, Japan. We are grateful to V.O. Yapaskurt and E.V. Guseva for their help in the analytical work. The atomistic modeling was carried out using the equipment of the shared research facilities of HPC computing resources at the Lomonosov Moscow State University and the computational cluster of the Division of Crystallography and Crystallochemistry, Department of Geology, Moscow State University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ringwood, A.E. Phase transformations and their bearing on the constitution and dynamics of the mantle. Geochim. Cosmochim. Acta 1991, 55, 2083–2110. [Google Scholar] [CrossRef]
- Akaogi, M.; Akimoto, S.I. Pyroxene-garnet solid-solution equilibria in the systems Mg4Si4O12–Mg3Al2Si3O12 and Fe4Si4O12–Fe3Al2Si3O12 at high pressures and temperatures. Phys. Earth Planet. Inter. 1977, 15, 90–106. [Google Scholar] [CrossRef]
- Tschauner, O.; Ma, C.; Beckett, J.R.; Prescher, C.; Prakapenka, V.B.; Rossman, G.R. Discovery of bridgmanite, the most abundant mineral in Earth, in a shocked meteorite. Science 2014, 346, 1100–1102. [Google Scholar] [CrossRef] [Green Version]
- Liebske, C.; Corgne, A.; Frost, D.J.; Rubie, D.C.; Wood, B.J. Compositional effects on element partitioning between Mg-silicate perovskite and silicate melts. Contrib. Mineral. Petrol. 2005, 149, 113–128. [Google Scholar] [CrossRef]
- Wood, B.J.; Corgne, A. Mineralogy of the Earth: Trace elements and hydrogen in the Earth’s transition zone and lower mantle. Treatise Geophys. 2009, 2, 63–89. [Google Scholar]
- Kaminsky, F.V. The Earth’s Lower Mantle; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Walter, M.J.; Nakamura, E.; Tronnes, R.G.; Frost, D.J. Experimental constraints on crystallization differentiation in a deep magma ocean. Geochim. Cosmochim. Acta 2004, 68, 4267–4284. [Google Scholar] [CrossRef]
- Corgne, A.; Allan, N.L.; Wood, B.J. Atomistic simulations of trace element incorporation into the large site of MgSiO3 and CaSiO3 perovskites. Phys. Earth Planet. Inter. 2003, 139, 113–127. [Google Scholar] [CrossRef]
- Kawai, N.; Endo, S. The generation of ultrahigh hydrostatic pressures by a split sphere apparatus. Rev. Sci. Instrum. 1970, 41, 1178–1181. [Google Scholar] [CrossRef]
- Sirotkina, E.A.; Bobrov, A.V.; Bindi, L.; Irifune, T. Phase relations and formation of chromium-rich phases in the system Mg4Si4O12–Mg3Cr2Si3O12 at 10–24 GPa and 1600 °C. Contrib. Mineral. Petrol. 2015, 169, 2. [Google Scholar] [CrossRef]
- Irifune, T.; Kurio, A.; Sakamoto, S.; Inoue, T.; Sumiya, H.; Funakoshi, K.I. Formation of pure polycrystalline diamond by direct conversion of graphite at high pressure and high temperature. Phys. Earth Planet. Inter. 2004, 143, 593–600. [Google Scholar] [CrossRef]
- Katsura, T.; Ito, E. The system Mg2SiO4–Fe2SiO4 at high pressures and temperatures: Precise determination of stabilities of olivine, modified spinel, and spinel. J. Geophys. Res. Solid Earth 1989, 94, 15663–15670. [Google Scholar] [CrossRef]
- Eremin, N.N.; Marchenko, E.I.; Petrov, V.G.; Mitrofanov, A.A.; Ulanova, A.S. Solid solutions of monazites and xenotimes of lanthanides and plutonium: Atomistic model of crystal structures, point defects and mixing properties. Comput. Mater. Sci. 2019, 157, 43–50. [Google Scholar] [CrossRef]
- Pedone, A.; Malavasi, G.; Menziani, M.C.; Cormack, A.N.; Segre, U. A New Self-Consistent Empirical Interatomic Potential Model for Oxides, Silicates, and Silica-Based Glasses. J. Phys. Chem. B 2006, 110, 11780–11795. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Akaogi, M.; Yano, M.; Tejima, Y.; Iijima, M.; Kojitani, H. High-pressure transitions of diopside and wollastonite: Phase equilibria and thermochemistry of CaMgSi2O6, CaSiO3, and CaSi2O5–CaTiSiO5 system. Phys. Earth Planet. Inter. 2004, 143, 145–156. [Google Scholar] [CrossRef]
- Bobrov, A.V.; Kojitani, H.; Akaogi, M.; Litvin, Y.A. Phase relations on the diopside-hedenbergite-jadeite join up to 24 GPa and stability of Na-bearing majoritic garnet. Geochim. Cosmochim. Acta 2008, 72, 2392–2408. [Google Scholar] [CrossRef]
- Stachel, T.; Harris, J.W.; Brey, G.P.; Joswig, W. Kankan diamonds (Guinea) II: Lower mantle inclusion parageneses. Contrib. Mineral. Petrol. 2000, 140, 16–27. [Google Scholar] [CrossRef]
- Wang, W.; Gasparik, T.; Rapp, R. Partitioning of rare earth elements between CaSiO3 perovskite and coexisting phases: Constraints on the formation of CaSiO3 inclusions in diamond. Earth Planet. Sci. Lett. 2000, 181, 291–300. [Google Scholar] [CrossRef]
- Burnham, A.D.; Bulanova, G.P.; Smith, C.B.; Whitehead, S.C.; Kohn, S.C.; Gobbo, L.; Walter, M.J. Diamonds from the Machado River alluvial deposit, Rondônia, Brazil, derived from both lithospheric and sublithospheric mantle. Lithos 2016, 265, 199–213. [Google Scholar] [CrossRef] [Green Version]
- Corgne, A.; Wood, B.J. Trace element partitioning and substitution mechanisms in calcium perovskites, Contrib. Mineral. Petrol. 2005, 149, 85–97. [Google Scholar] [CrossRef]
- Corgne, A.; Liebske, C.; Wood, B.J.; Rubie, D.C.; Frost, D.J. Silicate perovskite-melt partitioning of trace elements and geochemical signature of a deep perovskitic reservoir. Geochim. Cosmochim. Acta 2005, 146, 249–260. [Google Scholar] [CrossRef]
- Thomson, A.R.; Kohn, S.C.; Bulanova, G.P.; Smith, C.B.; Araujo, D.; Walter, M.J. Trace element composition of silicate inclusions in sub-lithospheric diamonds from the Juina-5 kimberlite: Evidence for diamond growth from slab melts. Lithos 2016, 265, 108–124. [Google Scholar] [CrossRef] [Green Version]
- Litvin, Y.A.; Spivak, A.V.; Kuzyura, A.V. Fundamentals of the mantle carbonatite concept of diamond genesis. Geochem. Int. 2016, 54, 839–857. [Google Scholar] [CrossRef]
- Righter, K.; Danielson, L.; Drake, M.J.; Domanik, K. Partition coefficients at high pressure and temperature. In Treatise on Geochemistry, 2nd ed.; Carlson, R.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 3, pp. 449–477. [Google Scholar]
Figure 1.
Back-scattered electron (BSE) images illustrating the phase assemblages and textural relationships in the samples obtained at 21.5 and 24 GPa from different starting compositions: (a,b): CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (c,d): CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE (Rare Earth Elements) oxides) (1 wt %). (e,f): (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (g,h): (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %).
Figure 1.
Back-scattered electron (BSE) images illustrating the phase assemblages and textural relationships in the samples obtained at 21.5 and 24 GPa from different starting compositions: (a,b): CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (c,d): CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE (Rare Earth Elements) oxides) (1 wt %). (e,f): (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (g,h): (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %).
Figure 2.
(a) Change in the CaSiO3 perovskite/bridgmanite REE partition coefficients with pressure in the system diopside-3REE. Samples 3224-1 and 3214-2; (b) REE partition coefficients for bridgmanite and ringwoodite in the system ringwoodite-3REE showing the positive slope from La to Lu. Sample 3224-1, the pressure is 24 GPa; the temperature for all samples is 1600 °C.
Figure 2.
(a) Change in the CaSiO3 perovskite/bridgmanite REE partition coefficients with pressure in the system diopside-3REE. Samples 3224-1 and 3214-2; (b) REE partition coefficients for bridgmanite and ringwoodite in the system ringwoodite-3REE showing the positive slope from La to Lu. Sample 3224-1, the pressure is 24 GPa; the temperature for all samples is 1600 °C.
Figure 3.
REE partition coefficients for bridgmanite and ringwoodite in the system ringwoodite-mixREE. Sample 3526-1, the pressure is 24 GPa and the temperature is 1600 °C.
Figure 3.
REE partition coefficients for bridgmanite and ringwoodite in the system ringwoodite-mixREE. Sample 3526-1, the pressure is 24 GPa and the temperature is 1600 °C.
Figure 4.
Mixing enthalpy of solid solutions of CaSiO3 (a) and MgSiO3 (b) with hypothetical REE perovskites.
Figure 4.
Mixing enthalpy of solid solutions of CaSiO3 (a) and MgSiO3 (b) with hypothetical REE perovskites.
Figure 5.
Calculated ratios of mixing enthalpies of CaSiO3-perovskite and bridgmanite at 0 and 24 GPa illustrating an increase in the CaPrv/Brd REE partitioning coefficients with pressure.
Figure 5.
Calculated ratios of mixing enthalpies of CaSiO3-perovskite and bridgmanite at 0 and 24 GPa illustrating an increase in the CaPrv/Brd REE partitioning coefficients with pressure.
Figure 6.
Comparison of REE partition coefficients for bridgmanite and CaSiO3-perovskite (Samples 3224-1 and 3214-2, the temperature for all samples is 1600 °C) with the coefficients obtained for the association of Brd + CaPrv from natural diamond [18,19].
Table 1.
Mean composition of phases produced in experiments at 21.5 and 24 GPa and 1600 °C. Starting compositions: (A) (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (B) CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (С) (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %); (D) CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %).
Table 1.
Mean composition of phases produced in experiments at 21.5 and 24 GPa and 1600 °C. Starting compositions: (A) (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (B) CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (La2O3 + Sm2O3 + Lu2O3) (1 wt %); (С) (Mg,Fe)SiO4 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %); (D) CaMgSi2O6 (98 wt %) + TiO2 (0.5 wt %) + Cr2O3 (0.5 wt %) + (REE oxides) (1 wt %).
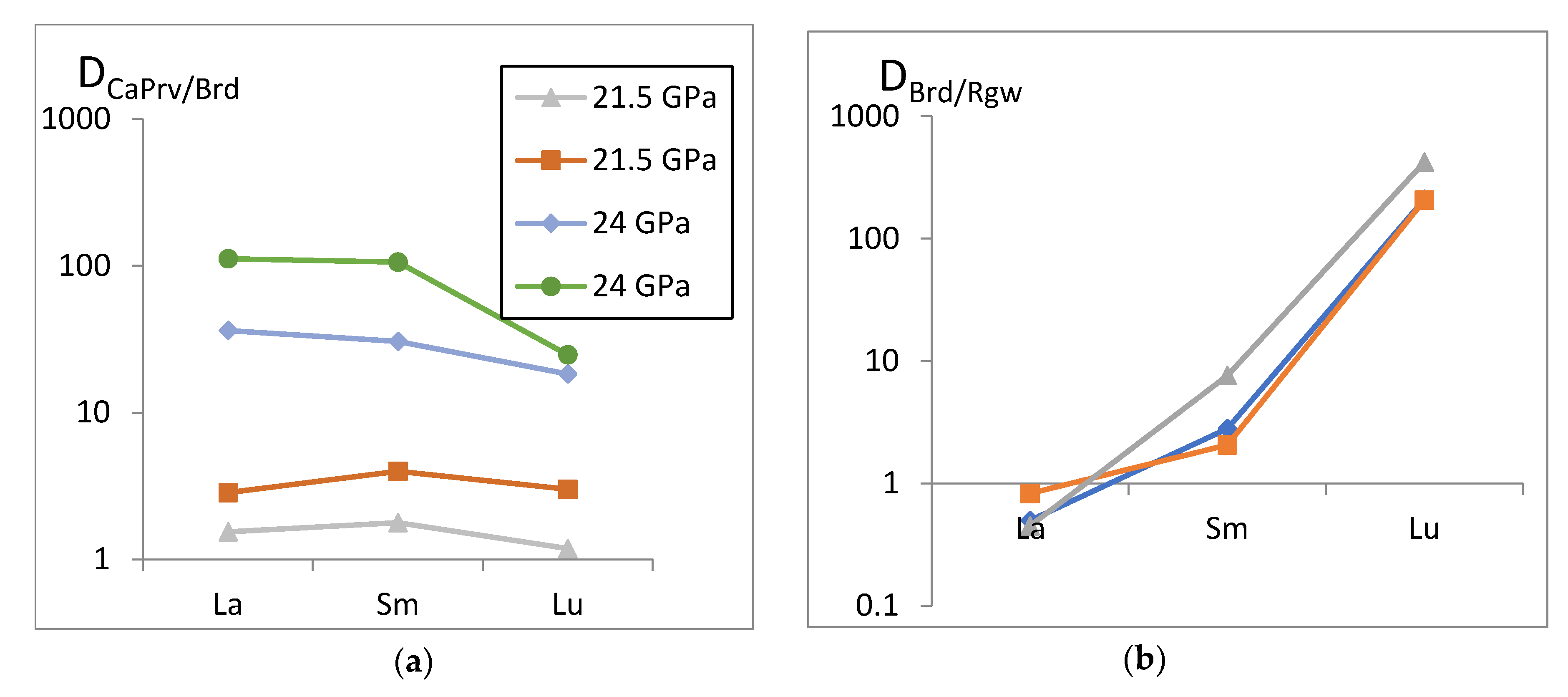
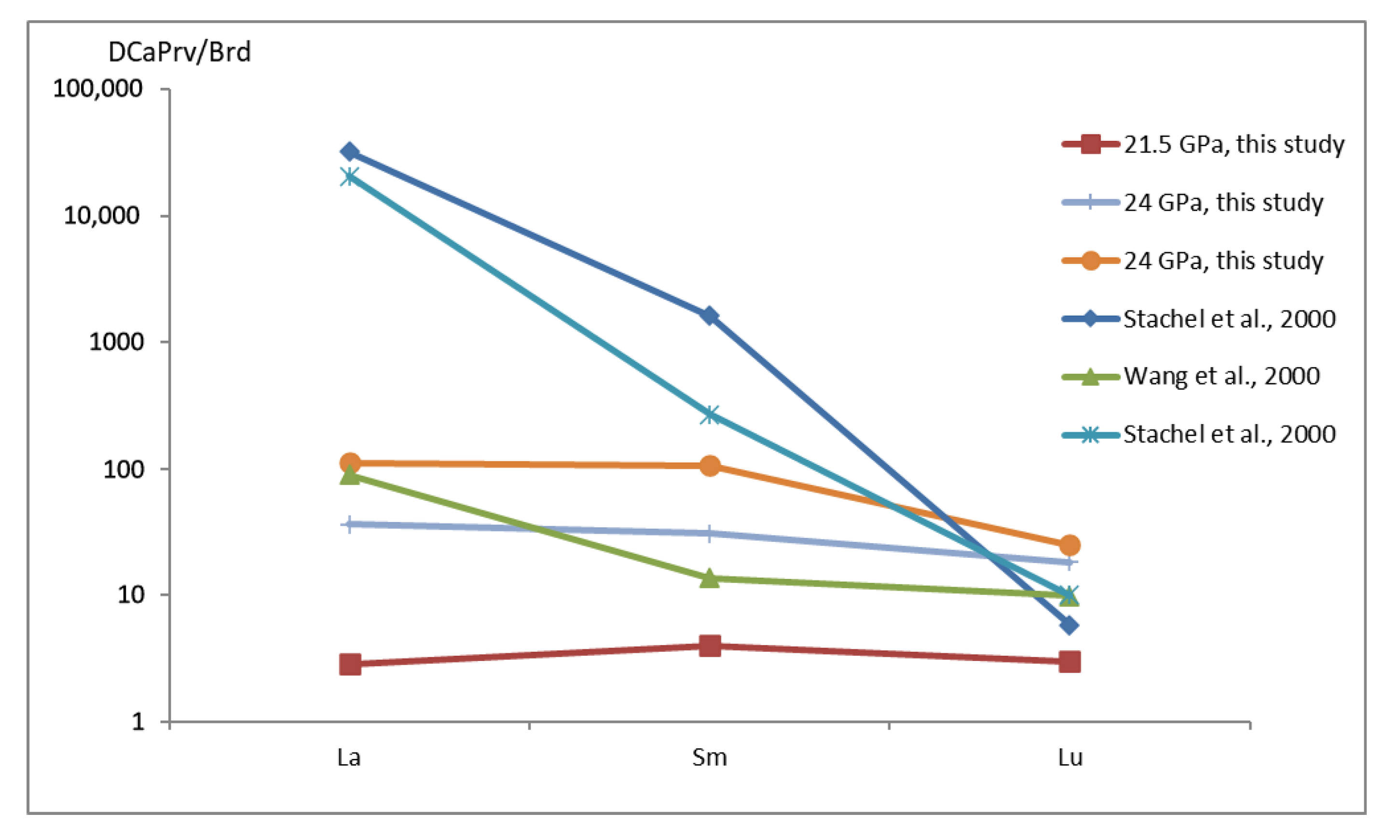
| Sample | OS3224-2 (B) | OS3214-2 (B) | OS3638-1 (D) | OS3526-2 (D) | OS3216-1 (A) | ||||
| GPa | 21.5 | 24 | 21.5 | 24 | 21.5 | ||||
| Phase | Brd | CaPrv | Brd | CaPrv | Brd | CaPrv | Brd | CaPrv | Rgw |
| SiO2 | 58.98 (0.35) | 49.28 (0.59) | 61.73 (0.38) | 48.36 (0.43) | 60.56 (0.42) | 49.66 (0.66) | 59.57 (0.43) | 49.02 (0.65) | 40.39 (0.32) |
| MgO | 40.82 (0.27) | 0.35 (0.04) | 38.13 (0.51) | 0.42 (0.02) | 39.04 (0.33) | 0.51 (0.09) | 39.2 (0.72) | 0.27 (0.04) | 47.83 (0.73) |
| FeO | - | - | - | - | - | - | - | - | 11.07 (0.62) |
| CaO | 0.13 (0.01) | 44.74 (0.49) | 0.23 (0.01) | 44.6 (0.17) | 0.28 (0.03) | 47.33 (0.60) | 0.36 (0.06) | 47.56 (0.18) | - |
| TiO2 | b.d.l. | 0.85 (0.09) | 0.09 (0.01) | 0.66 (0.09) | 0.11 (0.02) | 0.52 (0.05) | 0.06 (0.09) | 0.66 (0.08) | 0.27 (0.01) |
| Cr2O3 | 0.18 (0.04) | 0.75 (0.04) | 0.16 (0.02) | 0.58 (0.09) | 0.24 (0.01) | 0.46 (0.03) | 0.46 (0.02) | 0.47 (0.05) | 0.41 (0.03) |
| Total | 100.45 | 99.97 | 100.51 | 98.28 | 100.5 | 98.97 | 100.1 | 98.65 | 100.08 |
| Formula units per given O | |||||||||
| O | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
| Si4+ | 1.002 | 0.994 | 1.027 | 0.987 | 1.011 | 0.978 | 0.984 | 1.022 | 0.996 |
| Mg2+ | 0.995 | 0.011 | 0.946 | 0.013 | 0.975 | 0.015 | 1.003 | 0.008 | 1.759 |
| Fe2+ | - | - | - | - | - | - | - | - | 0.228 |
| Ca2+ | 0.002 | 0.967 | 0.004 | 0.975 | 0.005 | 0.998 | 0.006 | 1.007 | - |
| Ti4+ | - | 0.013 | 0.001 | 0.01 | 0.001 | 0.005 | 0.001 | 0.01 | 0.005 |
| Cr3+ | 0.002 | 0.012 | 0.002 | 0.009 | 0.003 | 0.004 | 0.006 | 0.007 | 0.008 |
| Sample | OS3216-1 (A) | OS3214-1 (A) | OS3538-2 (C) | OS3526-1 (C) | |||||
| GPa | 21.5 | 24 | 21.5 | 24 | |||||
| Phase | fPer | Brd | Rgw | fPer | Rgw | fPer | Rgw | Brd | fPer |
| SiO2 | 0.13 (0.05) | 55.8 (0.66) | 40.24 (0.21) | b.d.l. 1 | 40.94 (0.50) | 0.2 (0.01) | 41.31 (0.42) | 56.74 (0.77) | b.d.l. |
| MgO | 58.86 (0.88) | 36.31 (0.45) | 48.77 (0.27) | 72.89 (0.44) | 48.48 (0.68) | 66.47 (0.76) | 48.92 (0.33) | 36.44 (0.52) | 73.84 (0.76) |
| FeO | 38.56 (0.73) | 4.68 (0.09) | 9.71 (0.34) | 23.61 (0.19) | 9.97 (0.52) | 29.9 (0.67) | 10.55 (0.58) | 4.88 (0.11) | 24.91 (0.89) |
| CaO | - | - | - | - | - | - | - | - | - |
| TiO2 | b.d.l. | 1.52 (0.07) | 0.19 (0.04) | 0.09 (0.02) | 0.37 (0.09) | 0.08 (0.03) | 0.14 (0.06) | 0.56 (0.05) | 0.08 (0.01) |
| Cr2O3 | 1.09 (0.04) | 0.86 (0.02) | 0.34 (0.02) | 1.53 (0.03) | 0.58 (0.08) | 1.46 (0.09) | 0.14 (0.07) | 0.54 (0.04) | 0.69 (0.09) |
| Total | 98.63 | 99.96 | 99.38 | 98.58 | 100.09 | 98.22 | 100.61 | 99.46 | 99.82 |
| Formula units per given O | |||||||||
| O | 1 | 3 | 4 | 1 | 4 | 1 | 4 | 3 | 1 |
| Si4+ | 0.001 | 0.964 | 0.993 | - | 1.004 | 0.001 | 1.005 | 0.978 | - |
| Mg2+ | 0.725 | 0.935 | 1.793 | 0.837 | 1.773 | 0.788 | 1.775 | 0.937 | 0.836 |
| Fe2+ | 0.266 | 0.068 | 0.2 | 0.152 | 0.225 | 0.199 | 0.215 | 0.07 | 0.16 |
| Ca2+ | - | - | - | - | - | - | - | - | - |
| Ti4+ | - | 0.02 | 0.004 | 0.001 | 0.007 | 0.001 | 0.003 | 0.007 | 0.001 |
| Cr3+ | 0.007 | 0.012 | 0.007 | 0.009 | 0.011 | 0.009 | 0.003 | 0.007 | 0.004 |
1 b.d.l.—below the detection limit.
Table 2.
Concentrations of trace elements and measurement errors in synthetic phases (ppm, La-ICP-MS analyses) as compared with some natural [18] and experimental [19] data.
| Sample | os3224-2 (B) | |||||
| P, GPa | 21.5 | |||||
| Phase | CaPrv | +/- 1 | CaPrv | +/- | Brd | +/- |
| La | 10,476.04 | 862.44 | 11,928.96 | 982.05 | 2523.71 | 272.47 |
| Sm | 10,274.47 | 1705.93 | 10,563.46 | 1753.92 | 2333.13 | 387.38 |
| Lu | 8668.9 | 712.45 | 11,605.78 | 953.82 | 3233.54 | 207.4 |
| Sample | os3214-2 (B) | |||||
| P, GPa | 24 | |||||
| Phase | CaPrv | +/- | Brd | +/- | Brd | +/- |
| La | 9049.01 | 744.96 | 81.24 | 6.69 | 252.41 | 20.78 |
| Sm | 8643.95 | 1435.21 | 81.6 | 13.55 | 258.73 | 42.96 |
| Lu | 6314.99 | 519 | 254.43 | 20.91 | 407.29 | 33.47 |
| Sample | os3216-1 (A) | |||||
| P, GPa | 21.5 | |||||
| Phase | Rgw | +/- | Rgw | +/- | fPer | +/- |
| La | 15.35 | 1.26 | 0.51 | 0.04 | 1143.44 | 94.13 |
| Sm | 6.13 | 1.02 | 0.02 | 0.02 | 453.09 | 75.23 |
| Lu | 7.74 | 0.64 | 4.47 | 0.37 | 537.81 | 44.2 |
| Sample | os3214-1 (A) | |||||
| P, GPa | 24 | |||||
| Phase | Brd | +/- | Rgw | +/- | fPer | +/- |
| La | 11.52 | 0.95 | 13.85 | 1.14 | 334.34 | 27.53 |
| Sm | 17.58 | 2.92 | 8.55 | 1.42 | 8.56 | 1.42 |
| Lu | 2574.34 | 211.57 | 12.44 | 1.02 | 12.96 | 1.07 |
| Sample | os3214-1 (A) | [18] | [19] | |||
| P, GPa | 24 | |||||
| Phase | fPer | +/- | CaSiO3 | MgSiO3 | MgSiO3 | CaSiO3 |
| La | 20.97 | 1.73 | 161.45 | 0 | 1.28 | 115.2 |
| Sm | 4.52 | 0.75 | 96.99 | 0.06 | 2.92 | 40 |
| Lu(Yb) | 6.35 | 0.52 | 0.52 | 0.09 | 3.44 | 34.04 |
1 +/- analytical error that was estimated by the repeatability of intensities obtained from the standard sample (NIST610) used in the analysis.
Table 3.
Concentrations and measurement errors of trace elements in synthetic phases (La-ICP-MS analyses) as compared with experimental data [4] and the temperature for all samples is 1600 °C.
Table 3.
Concentrations and measurement errors of trace elements in synthetic phases (La-ICP-MS analyses) as compared with experimental data [4] and the temperature for all samples is 1600 °C.
| Samp. | os3526-1 (C) | os3538-2 (D) | [4] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P, GPa | 24 | 21.5 | |||||||||||
| Phase | Rgw | +/- | Brd | +/- | Brd | +/- | fPer | +/- | Rgw | +/- | fPer | +/- | MgSiO3 |
| La | 5.06 | 0.75 | 21.29 | 3.17 | 15.85 | 2.36 | 10.67 | 1.59 | 5.61 | 0.83 | 34.18 | 5.08 | 1 |
| Ce | 3.10 | 0.46 | 7.55 | 1.11 | 10.10 | 1.49 | 8.77 | 1.29 | 2.85 | 0.42 | 9.61 | 1.41 | 8 |
| Pr | 5.31 | 0.66 | 8.65 | 1.07 | 10.44 | 1.30 | 10.24 | 1.27 | 5.29 | 0.66 | 11.57 | 1.44 | n.a.1 |
| Nd | 3.28 | 1.34 | 7.85 | 3.19 | 5.77 | 2.35 | 11.87 | 4.83 | 3.61 | 1.47 | 7.38 | 3.00 | 36 |
| Sm | 3.52 | 1.82 | 6.55 | 3.38 | 5.89 | 3.05 | 0.83 | 0.43 | 3.52 | 1.82 | 3.85 | 1.99 | 72 |
| Eu | 3.14 | 0.39 | 7.24 | 0.91 | 6.69 | 0.84 | 5.11 | 0.64 | 2.07 | 0.26 | 5.61 | 0.70 | 39 |
| Gd | 4.19 | 0.52 | 10.42 | 1.30 | 9.74 | 1.22 | 4.11 | 0.51 | 4.10 | 0.51 | 7.40 | 0.93 | n.a. |
| Tb | 4.08 | 0.48 | 13.87 | 1.62 | 11.16 | 1.30 | 10.74 | 1.26 | 4.04 | 0.47 | 12.20 | 1.43 | n.a. |
| Dy | 5.62 | 1.45 | 18.27 | 4.72 | 12.80 | 3.31 | 8.71 | 2.25 | 5.83 | 1.51 | 12.46 | 3.22 | n.a. |
| Ho | 5.31 | 0.68 | 12.83 | 1.64 | 12.77 | 1.64 | 4.04 | 0.52 | 5.36 | 0.69 | 10.49 | 1.34 | n.a. |
| Er | 6.60 | 0.87 | 34.45 | 4.54 | 28.04 | 3.69 | 12.20 | 1.61 | 6.49 | 0.85 | 9.20 | 1.21 | n.a. |
| Tm | 6.18 | 0.43 | 45.07 | 3.10 | 37.33 | 2.57 | 17.26 | 1.19 | 5.61 | 0.39 | 13.34 | 0.92 | n.a. |
| Yb | 3.59 | 0.52 | 68.26 | 9.97 | 45.42 | 6.63 | 25.17 | 3.68 | 2.70 | 0.39 | 24.50 | 3.58 | n.a. |
| Lu | 6.28 | 1.09 | 85.63 | 14.80 | 65.29 | 11.28 | 28.57 | 4.94 | 5.49 | 0.95 | 21.40 | 3.70 | 576 |
1 n.a.—not analyzed.
Table 4.
Partition coefficients for synthetic phases from runs at 1600 °C with 3REE starting composition.
Table 4.
Partition coefficients for synthetic phases from runs at 1600 °C with 3REE starting composition.
| D Coeff | La | Sm | Lu | Sample | P, GPa |
|---|---|---|---|---|---|
| DRgw/fPer | 0.66 | 1.89 | 1.96 | os3214-1 | 24 |
| DBrd/Rgw | 0.50 | 2.80 | 209.07 | ||
| DBrd/Rgw | 0.83 | 2.06 | 206.94 | ||
| DRgw/fPer | 0.01 | 0.01 | 0.01 | os3216-1 | 21.5 |
| DCaPrv/Brd | 41.50 | 39.71 | 21.28 | os3214-2 | 24 |
| DCaPrv/Brd | 111.39 | 105.93 | 24.82 | ||
| DCaPrv/Brd | 36.30 | 30.58 | 18.27 | ||
| DCaPrv/Brd | 1.95 | 2.03 | 1.82 | os3224-2 | 21.5 |
| DCaPrv/Brd | 2.86 | 3.99 | 3.00 | ||
| DCaPrv/Brd | 1.54 | 1.79 | 1.18 |
Table 5.
Partition coefficients for synthetic phases from runs at 1600 °C with mixREE starting composition.
Table 5.
Partition coefficients for synthetic phases from runs at 1600 °C with mixREE starting composition.
| Sample | os3526-1 | os3538-2 | |||||
|---|---|---|---|---|---|---|---|
| P, GPa | 24 | 21.5 | |||||
| D Coeff | DBrd/Rgw | DBrd/Rgw | DBrd/Rgw | DRgw/fPer | DRgw/fPer | DRgw/fPer | DRgw/fPer |
| La | 2.03 | 9.38 | 3.92 | 0.27 | 0.09 | 0.16 | 0.15 |
| Ce | 1.81 | 7.73 | 3.26 | 0.40 | 0.30 | 0.28 | 0.27 |
| Pr | 1.29 | 4.16 | 1.97 | 0.52 | 0.41 | 0.45 | 0.45 |
| Nd | 1.73 | 4.60 | 1.76 | 1.57 | 1.13 | 0.44 | 0.44 |
| Sm | 0.93 | 4.00 | 1.67 | 1.02 | 0.51 | 0.91 | 0.91 |
| Eu | 1.53 | 5.79 | 2.13 | 0.77 | 0.51 | 0.37 | 0.37 |
| Gd | 1.86 | 4.63 | 2.33 | 0.52 | 0.39 | 0.55 | 0.46 |
| Tb | 2.16 | 5.79 | 2.74 | 0.47 | 0.30 | 0.32 | 0.32 |
| Dy | 2.42 | 4.80 | 2.28 | 0.47 | 0.35 | 0.45 | 0.45 |
| Ho | 1.71 | 3.35 | 2.40 | 0.44 | 0.31 | 0.52 | 0.51 |
| Er | 3.08 | 6.19 | 4.25 | 1.81 | 1.06 | 0.66 | 0.66 |
| Tm | 3.06 | 9.84 | 6.04 | 1.56 | 0.66 | 0.42 | 0.40 |
| Yb | 3.84 | 23.72 | 12.65 | 0.75 | 0.15 | 0.12 | 0.11 |
| Lu | 3.32 | 17.22 | 10.39 | 1.81 | 0.44 | 0.26 | 0.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Tamarova, A.P.; Marchenko, E.I.; Bobrov, A.V.; Eremin, N.N.; Zinov’eva, N.G.; Irifune, T.; Hirata, T.; Makino, Y. Interphase REE Partitioning at the Boundary between the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments and Atomistic Modeling. Minerals 2020, 10, 262. https://doi.org/10.3390/min10030262
AMA Style
Tamarova AP, Marchenko EI, Bobrov AV, Eremin NN, Zinov’eva NG, Irifune T, Hirata T, Makino Y. Interphase REE Partitioning at the Boundary between the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments and Atomistic Modeling. Minerals. 2020; 10(3):262. https://doi.org/10.3390/min10030262
Chicago/Turabian StyleTamarova, Anastasia P., Ekaterina I. Marchenko, Andrey V. Bobrov, Nikolay N. Eremin, Nina G. Zinov’eva, Tetsuo Irifune, Takafumi Hirata, and Yoshiki Makino. 2020. "Interphase REE Partitioning at the Boundary between the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments and Atomistic Modeling" Minerals 10, no. 3: 262. https://doi.org/10.3390/min10030262
APA StyleTamarova, A. P., Marchenko, E. I., Bobrov, A. V., Eremin, N. N., Zinov’eva, N. G., Irifune, T., Hirata, T., & Makino, Y. (2020). Interphase REE Partitioning at the Boundary between the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments and Atomistic Modeling. Minerals, 10(3), 262. https://doi.org/10.3390/min10030262
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
