The Simultaneous Removal of Zinc and Cadmium from Multicomponent Aqueous Solutions by Their Sorption onto Selected Natural and Synthetic Zeolites
Abstract
1. Introduction
2. Materials and Methods
- For the determination of the % of sorption:where CINI is the initial concentration of the given metal ion in the test solution in [cmol/L] Ce—concentration of the given metal ion in the solution at equilibrium in [cmol/L].% sorption = [(CINI − Ce)/CINI] × 100
- For the determination of the distribution constant Kd:where Ce is the concentration of the given metal ion in the solution at equilibrium in [cmol/L] and Csorb is the concentration of the given metal ion adsorbed onto the mineral sorbent at equilibrium in [cmol/kg].Kd = Csorb/Ce [L/kg]
3. Results and Their Discussion
- (1)
- Chemistry of the solution, such as pH and ionic strength;
- (2)
- Properties of sorbate concentration, ionic size, ionic charge, ionic weight, and standard redox potential;
- (3)
- Character of binding sites, functional groups, surface properties, etc.
- (1)
- Atomic weight, for Zn2+ M = 65.38 [g/mol] and for Cd2+ M = 112.41 [g/mol];
- (2)
- Hydrolysis constant, for Zn2+ Ka = 9.0 and for Cd2+ pKa = 10.1;
- (3)
- Ionic radius, for Zn2+ it is 0.074 nm and for Cd2+ 0.097 nm;
- (4)
- Hydrated ion radius, for Zn2+ it is 0.430 nm and for Cd2+ 0.426 nm;
- (5)
- Hydration energy, also called hydration enthalpy, being −1955 kJ/mol for Zn2+ and −1807 kJ/mol for Cd2+.
4. Conclusions
- (1)
- The tested synthetic zeolites, 3A, 10Am and 13X, were more efficient in the simultaneous removal of Cd2+ and Zn2+ ions from aqueous solutions than the tested natural zeolite, which may be related to their higher mineralogical homogeneity;
- (2)
- The analysis of the performance of the tested zeolites, based on the analysis of the parameters of sorption isotherm models, showed that the most efficient in simultaneous removal of Cd2+ and Zn2+ ions from aqueous solutions were zeolite 3A and zeolite 10A. Therefore, those two sorbents should be recommended to be used for rapid reduction of the level of pollution with those two elements and their spreading in the environment;
- (3)
- Zeolite 10A displayed a relatively high and constant sorption capacity over a broader range of concentrations, which indicates that it will be efficient in coping with prolonged low- and medium-level pollution of aquatic environment with cadmium and zinc;
- (4)
- The identified, on the basis of the adsorption energies, mechanism of sorption was, for all tested zeolites, physisorption, which may be explained by the fact that the sorption was examined in a multisolute system;
- (5)
- The synthetic zeolites 10A and 13X displayed higher selectivity to Cd2+ than to Zn2+, while in the case of the natural zeolite and synthetic zeolite 3A that relationship was reversed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karlaviciene, V.; Svendine, S.; Marciulioniene, D.E.; Randerson, P.; Rimeika, M.; Hogland, W. The impact of storm water runoff on a small urban stream. J. Soils Sediment. 2009, 9, 6–12. [Google Scholar] [CrossRef]
- Lynch, S.F.L.; Batty, L.C.; Byrne, P. Environmental Risk of Metal Mining Contaminated River Bank Sediment at Redox-Transitional Zones. Minerals 2014, 4, 52–73. [Google Scholar] [CrossRef]
- Newman, M.C. Fundamentals of Ecotoxicology. The Science of Pollution, 4th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2015; passim. [Google Scholar]
- Hudson-Edwards, K.A.; Dold, E. Mine Waste Characterization, Management and Remediation. Minerals 2015, 5, 82–85. [Google Scholar] [CrossRef]
- Ramesh, K.; Elango, L. Impact of Groundwater Quality from Industrial East Coastal Town, Southern India. Int. J. Eng. Res. Appl. 2014, 4, 346–354. [Google Scholar]
- Pierzynski, G.M.; Sims, T.J.; Vance, G.F. Soils and Environmental Quality, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2000; passim. [Google Scholar]
- Kabata-Pendias, A. Trace Elements in Soils and Plants, 3nd ed.; CRC Press: Boca Raton, FL, USA, 2001; passim. [Google Scholar] [CrossRef]
- Kabata-Pendias, A.; Mukherjee, A.B. Trace Elements from Soil to Human; Springer: Berlin, Germany, 2007; passim. [Google Scholar] [CrossRef]
- Alloway, B.J. (Ed.) Heavy Metals in Soils, 3nd ed.; Springer: Berlin, Germany, 2013; passim. [Google Scholar] [CrossRef]
- Frausto da Silva, J.J.R.; Williams, R.J.P. The Biological Chemistry of the Elements. The Inorganic Chemistry of Life, 2nd ed.; Oxford University Press: Oxford, UK, 2001; passim. [Google Scholar]
- Blanchard, G.; Maunaye, M.; Martin, G. Removal of heavy metals from waters by means of natural zeolites. Water Res. 1984, 18, 1501–1507. [Google Scholar] [CrossRef]
- Gworek, B. Inactivation of cadmium in contaminated Soils using synthetic zeolites. Environ. Pollut. 1992, 75, 269–271. [Google Scholar] [CrossRef]
- Gworek, B. Inactivation of lead anthropogenic soils by synthetic zeolites and plants growth. Plant Soil 1992, 143, 71–74. [Google Scholar] [CrossRef]
- Gworek, B. The Effect of Zeolites on Cooper Uptake by plants Growing in Contaminated Soils. J. Incl. Phenom. Mol. Recognit. Chem. 1993, 15, 1–7. [Google Scholar] [CrossRef]
- Oste, L.A.; Lexmond, T.M.; Van Riemsdijk, W.H. Metal Immobilization in Soils Using Synthetic Zeolites. J. Environ. Qual. 2002, 31, 813–821. [Google Scholar] [CrossRef]
- Wingenfelder, U.; Hansen, C.; Furrer Schulin, R. Removal of Heavy Metals from Mine Waters by Natural Zeolites. Environ. Sci. Technol. 2005, 39, 4606–4613. [Google Scholar] [CrossRef]
- Sprynskyy, M.; Buszewski, B.; Terzyk, A.P.; Namieśnik, J. Study of the selection mechanism of heavy metal (Pb2+, Cu2+, Ni2+, and Cd2+) adsorption on clinoptilolite. J. Colloid Interface Sci. 2006, 304, 21–28. [Google Scholar] [CrossRef]
- Usman, A.; Yakov, R.A.; Kuzyakov, Y.; Lorenz, K.; Stahr, K. Remediation of a soil contaminated with heavy metals by immobilizing compounds. J. Plant Nutr. Soil Sci. 2006, 169, 205–212. [Google Scholar] [CrossRef]
- Bhattacharyya, K.G.; Gupta, S.S. Adsorptive accumulation of Cd(II), Co(II), Cu(II), Pb(II), and Ni(II) from water on montmorillonite: Influence of acid activation. J. Colloid Interface Sci. 2007, 310, 411–424. [Google Scholar] [CrossRef]
- Ibrahim, H.S.; Jamil, T.; Hegazy, E.Z. Application of Zeolite Prepared from Egyptian Kaolin for the Removal of Heavy Metals: II. Isotherm Models. J. Hazard. Mater. 2010, 182, 842–847. [Google Scholar] [CrossRef]
- Karatas, M. Removal of Pb(II) from water by natural zeolitic tuff: Kinetics and thermodynamics. J. Hazard. Mater. 2012, 199–200, 383–389. [Google Scholar] [CrossRef]
- Zhao, Y. Review of the Natural, Modified, and Synthetic Zeolites for Heavy Metals Removal from Wastewater. Environ. Eng. Sci. 2016, 33, 443–454. [Google Scholar] [CrossRef]
- El-Azim, H.A.; Mourad, F.A. Removal of Heavy Metals Cd (II), Fe (III) and Ni (II), from Aqueous Solutions by Natural (Clinoptilolite) Zeolites and Application to Industrial Wastewater. Asian J. Environ. Ecol. 2018, 7, 1–13. [Google Scholar] [CrossRef]
- Fanta, F.T.; Dubale, A.A.; Bebizuh, D.F.; Atlabachew, M. Copper doped zeolite composite for antimicrobial activity and heavy metal removal from waste water. BMC Chem. 2019, 13, 12. [Google Scholar] [CrossRef]
- Ahmaruzzaman, M. Industrial Wastes as Low-Cost Potential Adsorbents fo4r the Treatment of Wastewater Laden with Heavy Metals. Adv. Colloid Interface Sci. 2011, 166, 36–59. [Google Scholar] [CrossRef]
- Uddin, M.K. A review on the adsorption of heavy metals by clay minerals, with special focus on the past decade. Chem. Eng. J. 2017, 308, 438–462. [Google Scholar] [CrossRef]
- Qin, F.; Wen, B.; Shan, X.-Q.; Xie, Y.N.; Liu, T.; Zhang, S.Z.; Khan, S.U. Mechanisms of competitive adsorption of Pb, Cu and Cd on peat. Environ. Pollut. 2006, 144, 669–680. [Google Scholar] [CrossRef]
- Mahamadi, C.; Nharingo, T. Competitive adsorption of Pb2+, Cd2+ and Zn2+ ions onto Eichhornia crassipes in binary and ternary systems. Bioresour. Technol. 2010, 101, 859–864. [Google Scholar] [CrossRef]
- Eloussaief, M.; Hamza, W.; Kallel, N.; Bnezina, M. Wastewaters Decontamination: Mechanisms of Pb(II), Zn (II) and Cd (II) Competitive Adsorption on Tunisian Smectite in Single and Multi-Solute Systems. Environ. Prog. Sustain. Energy 2013, 32, 229–238. [Google Scholar] [CrossRef]
- OECD. OECD Guideline for the Testing of Chemicals No. 106 Adsorption-Desorption Using a Batch Equilibrium Method; OECD: Paris, France, 2000. [Google Scholar] [CrossRef]
- Balaz, B.; Alacova, A.; Briancin, J. Sensivity of Freundlich equation constant 1/n for zinc sorption on changes introduced by calcite by mechanical activation. Chem. Eng. J. 2005, 114, 115–121. [Google Scholar] [CrossRef]
- Toth, J. Uniform interpretation of gas/solid adsorption. Adv. Colloid Interface Sci. 1995, 55, 1–239. [Google Scholar] [CrossRef]
- Otake, Y.; Kalili, N.; Chang, T.H.; Furuya, E. Relationship between Freundlich-type equation constants and molecular orbital properties. Sep. Purif. Technol. 2004, 39, 67–72. [Google Scholar] [CrossRef]
- Kupiec, K.; Georgiou, A. Analysis of thermal effects in a spherical adsorbent pellet. Int. J. Heat Mass Transf. 2005, 48, 5047–5057. [Google Scholar] [CrossRef]
- Milonjic, S.K. A consideration of the corrected calculation of thermodynamic parameters of adsorption. J. Serb. Chem. Soc. 2007, 72, 1363–1367. [Google Scholar] [CrossRef]
- Rudzinski, W.; Plazinski, W. Theoretical description of the kinetics of solute adsorption at heterogeneous solid/solution interfaces. On the possibility of distinguishing between the diffusional and surface reaction kinetics models. Appl. Surf. Sci. 2007, 253, 5827–5840. [Google Scholar] [CrossRef]
- Mobacherpour, I.; Salahi, E.; Pazouki, M. Comparative of the removal of Pb2+, Cd2+ and Ni2+ by nano crystallite hydroxyapatite from aqueous solutions: Adsorption isotherms study. Arab. J. Chem. 2012, 5, 439–446. [Google Scholar] [CrossRef]
- Allen, S.J.; Mckay, G.; Porter, J.F. Adsorption isotherm models for basic dye adsorption by peat in single and binary component system. Colloid Interface Sci. 2004, 280, 322–333. [Google Scholar] [CrossRef]
- Yang, K.; Wang, X.; Zhu, L.; Xing, B. Competitive Sorption of Pyrene, Phenantrene and Naphtalene on Multiwalled Carbon Nanotubes. Environ. Sci. Technol. 2006, 40, 5804–5810. [Google Scholar] [CrossRef]
- Swayampakula, K.; Boddu, V.M.; Nadavala, S.K.; Abburi, K.M. Competitive adsorption of Cu(II), Co (II) and Ni (II) from their binary and tertiary aqueous solutions using chitosan-coated perlite beads as biosorbent. J. Hazard. Mater. 2009, 170, 680–689. [Google Scholar] [CrossRef]
- Tofighy, M.A.; Mohammadi, T. Adsorption of divalent heavy metal ions from water using carbon nanotube sheets. J. Hazard. Mater. 2011, 185, 140–147. [Google Scholar] [CrossRef]
- Bouhamed, P.; Elouear, Z.; Bouzid, J.; Ouddane, B. Multi-component adsorption of copper, nickel and zinc from aqueous solutions onto activated carbon prepared from date stones. Environ. Sci. Pollut. Res. 2016, 23, 15801–15806. [Google Scholar] [CrossRef]
- Yurekli, Y. Determination of adsorption characteristics of synthetic NaX nanoparticles. J. Hazard. Mater. 2019, 378, 120743. [Google Scholar] [CrossRef]
- Ho, Y.-S. Selection of optimum sorption isotherm. Carbon 2004, 42, 2115–2116. [Google Scholar] [CrossRef]
- Kumar, K.V.; Sivanesan, S. Prediction of optimum sorption isotherm: Comparison of linear and non-linear method. J. Hazard. Mater. 2005, 126, 198–201. [Google Scholar] [CrossRef]
- Ncibik, M.C. Applicability of some statistical tools to predict optimum adsorption isotherm after linear and non-linear regression analysis. J. Hazard. Mater. 2008, 153, 207–212. [Google Scholar] [CrossRef]
- Parimal, S.; Prasad, M.; Bhaskar, U. Prediction of Equilibrium Sorption Isotherms: Comparison of Linear and Nonlinear Methods. Ind. Eng. Chem. Res. 2010, 49, 2882–2888. [Google Scholar] [CrossRef]
- Osmani, T.A.; Gallon, R.; Schwaab, M.; Barbosa-Coutinho, E.; Severo, J.B., Jr.; Pinto, J.C. Statistical Analysis of Linear and Non-Linear Regression for the Estimation of Adsorption Isotherm Parameters. Adsorpt. Sci. Technol. 2013, 31, 433–458. [Google Scholar] [CrossRef]
- Hutson, N.D.; Yang, R.T. Theoretical Basis for the Dubinin-Radushkievitch (D-R) Adsorption Isotherm Equation. Adsorption 1997, 3, 189–197. [Google Scholar] [CrossRef]
- Dabrowski, A. Adsorption—From theory to practice. Adv. Colloid Interface Sci. 2001, 93, 135–224. [Google Scholar] [CrossRef]
- Meghea, A.; Rehner, H.H.; Peleanu, I.; Mihalache, R. Test-fitting on adsorption isotherms of organic pollutants from waste waters on activated carbon. J. Radioanal. Nuclear Chem. 1998, 229, 105–110. [Google Scholar] [CrossRef]
- Krishna, B.S.; Murty, D.S.R.; Prakash, B.S.J. Thermodynamics of chromium (VI) anionic species sorption onto surfactant-modified montmorillonite clay. J. Colloid Interface Sci. 2000, 229, 230–236. [Google Scholar] [CrossRef]
- Lin, S.H.; Juang, R.S. Heavy metal removal from water by sorption using surfactant-modified montmorillonite. J. Hazard. Mater. B 2002, 92, 315–326. [Google Scholar] [CrossRef]
- Wang, C.C.; Juang, L.C.; Lee, C.K.; Hsua, T.C.; Leeb, J.F.; Chaob, H.P. Effects of exchanged surfactant cations on the pore structure and adsorption characteristics of montmorillonite. J. Colloid Interface Sci. 2004, 280, 27–35. [Google Scholar] [CrossRef]
- Alipour, D.; Keshtkar, A.R.; Moosavian, M.A. Adsorption of thorium (IV) from simulated radioactive solutions using a novel electrospun PVA/TiO2/ZnO nanofiber adsorbent functionalized with mercapto groups: Study in single and multi-component systems. Appl. Surf. Sci. 2016, 306, 19–29. [Google Scholar] [CrossRef]
- Essomba, J.S.; Ndi Nsami, J.; Belibi Belibi, P.D.; Tagne, G.M.; Ketcha Mbadcam, J. Adsorption of Cadmium (II) Ions from Aqueous Solution onto Kaolinite and Metakaolinite. Pure Appl. Chem. Sci. 2014, 2, 11–30. [Google Scholar] [CrossRef][Green Version]
- Chen, C.; Liu, H.; Chen, T.; Chen, D.; Frost, R.L. An insight into the removal of Pb(II), Cu(II), Cd(II), Zn(II), Ag(I), Hg(I), Cr(VI) by Na(I)-montmorillonite and Ca(II)-montmorillonite. Appl. Clay Sci. 2015, 118, 239–247. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Z. Application of Dubinin-Radushkevich isotherm model at the solid/solution interface: A theoretical analysis. J. Mol. Liq. 2019, 277, 646–648. [Google Scholar] [CrossRef]
- Erdem, E.; Karapinar, N.; Donat, R. The removal of heavy metals by natural zeolites. J. Colloid Interface Sci. 2004, 280, 309–314. [Google Scholar] [CrossRef]
- Apiratikul, R.; Pavasant, P. Sorption of Cu2+, Cd2+ and Pb2+ using modified zeolite from coal fly ash. Chem. Eng. J. 2008, 144, 245–258. [Google Scholar] [CrossRef]
- Kralik, M. Adsorption, chemisorption, and catalysis. Chem. Pap. 2014, 68, 1625–1638. [Google Scholar] [CrossRef]
- Abollino, O.; Giacomino, A.; Malandrino, M.; Mentasti, E. Interaction of metal ions with montmorillonite and vermiculite. Appl. Clay Sci. 2008, 38, 227–238. [Google Scholar] [CrossRef]
- Zhu, C.; Dong, X.; Chen, Z.; Naidu, R. Adsorption of aqueous Pb(VI), Cu(II), Zn(II) ions by amorphous tin (VI) phosphate: An excellent inorganic sorbent. Int. J. Environ. Sci. Technol. 2016, 13, 1257–1268. [Google Scholar] [CrossRef]
- Baker, H.M. A study of thye binding strength and thermodynamics aspects of cadmiu and lead ions with natural silicate minerals in aqueous solutions. Desalination 2009, 242, 115–127. [Google Scholar] [CrossRef]
- Baker, H.M.; Massadeh, A.M.; Younes, H.A. Natural Jordanian zeolite: Removal of heavy metal ions from water samples using column and batch methods. Environ. Monit. Assess. 2009, 157, 319–330. [Google Scholar] [CrossRef]
- Alvarez-ayuso, E.; Garcia-Sanchez, A.; Queval, X. Purification of metal electroplating waste waters using zeolites. Water Res. 2003, 37, 4858–4862. [Google Scholar] [CrossRef]
- Rao, G.P.C.; Satyaveni, S.; Ramesh, A.; Seshaiah, K.; Murthy, K.S.N.; Choudary, N.V. Sorption of cadmium and zinc from aqueous solutions by zeolite 4A, zeolite 13X and bentonite. J. Environ. Manag. 2006, 81, 265–272. [Google Scholar] [CrossRef]
- Tseng, R.-L.; Wu, F.-C. Inferring the favorable adsorption level and the concurrent multi-stage process with the Freundlich constant. J. Hazard. Mater. 2008, 155, 277–287. [Google Scholar] [CrossRef]
- De Gisi, S.; Giusy, L.; Grassi, M.; Notarnicola, M. Characteristics and adsorption capacities of low-cost sorbents for wastewater treatment: A review. Sustain. Mater. Technol. 2016, 9, 10–40. [Google Scholar] [CrossRef]
- Du, T.; Zhou, L.-F.; Zhang, Q.; Liu, L.-Y.; Li, G.; Luo, W.-B.; Liu, H.-K. Mesoporous structured aluminosilicate with excellent adsorption performances for water purification. Sustain. Mater. Technol. 2018, 17, e00080. [Google Scholar] [CrossRef]
- Kumari, P.; Alam, M.; Siddiqi, W.A. Usage of nanoparticles as adsorbents for waste water treatment: An emerging trend. Sustain. Mater. Technol. 2019, 22, e00128. [Google Scholar] [CrossRef]
| Property | Minerals | ||||
|---|---|---|---|---|---|
| Natural Zeolite | Synthetic Zeolites | ||||
| 3A | 10A | 13X | |||
| Grain size [mm] | <0.2 | 1.0 | 1.0 | 1.0 | |
| pH | in H2O | 6.1 | 0.2 | 9.4 | 10.1 |
| in 1M KCl | 4.7 | 8.8 | 7.9 | 8.9 | |
| Content of exchangeable cations [cmol/kg] | Total–CEC | 93.9 | 354.1 | 377.9 | 235.2 |
| Na+ | 1.7 | 146.5 | 364.2 | 223.7 | |
| K+ | 46.1 | 200.3 | 8.4 | 3.8 | |
| Mg2+ | 1.5 | 0.5 | 2.4 | 1.5 | |
| Ca2+ | 44.6 | 6.8 | 2.9 | 6.2 | |
| Dominant cations | K+ and Ca2+ | K+ and Na+ | Na+ | Na+ | |
| Sorbent: Natural Zeolite | |||||||
| Sorbed Element: Zn2+ | Sorbed Element: Cd2+ | ||||||
| Initial Concentration of Zn2+ in Solution Expressed: | % Sorption | Kd [L/kg] | Initial Concentration of Cd2+ in Solution Expressed: | % Sorption | Kd [L/kg] | ||
| in [cmol/L] | as % CEC | in [cmol/L] | as % CEC | ||||
| 0.02 | 2 | 50.00 | 25.00 | 0.02 | 2 | 100.00 | n. c.* |
| 0.10 | 10 | 60.00 | 37.50 | 0.10 | 10 | 50.00 | 25.00 |
| 0.20 | 20 | 54.50 | 20.45 | 0.20 | 20 | 35.00 | 13.46 |
| 0.30 | 30 | 43.33 | 19.12 | 0.30 | 30 | 30.00 | 10.71 |
| 0.50 | 50 | 34.00 | 12.88 | 0.50 | 50 | 20.00 | 6.25 |
| 0.70 | 75 | 31.43 | 11.46 | 0.70 | 75 | 18.57 | 5.70 |
| 0.99 | 100 | 29.29 | 10.36 | 1.00 | 100 | 16.00 | 4.76 |
| Sorbent: Zeolite 3A | |||||||
| Sorbed Element: Zn2+ | Sorbed Element: Cd2+ | ||||||
| Initial Concentration of Zn2+ in Solution Expressed: | % Sorption | Kd [L/kg] | Initial Concentration of Cd2+ in Solution Expressed: | % Sorption | Kd [L/kg] | ||
| in [cmol/L] | as % CEC | in [cmol/L] | as % CEC | ||||
| 0.07 | 2 | 57.14 | 33.33 | 0.07 | 2 | 57.14 | 33.33 |
| 0.37 | 10 | 40.54 | 17.04 | 0.36 | 10 | 41.67 | 17.86 |
| 0.74 | 20 | 64.86 | 46.51 | 0.73 | 20 | 52.05 | 27.14 |
| 1.10 | 30 | 60.00 | 37.50 | 1.09 | 30 | 49.54 | 24.54 |
| 1.84 | 50 | 53.26 | 28.49 | 1.81 | 50 | 50.28 | 25.28 |
| 2.58 | 75 | 38.76 | 15.82 | 2.54 | 75 | 33.46 | 12.57 |
| 3.68 | 100 | 38.31 | 14.21 | 3.63 | 100 | 32.78 | 12.19 |
| Sorbent: Zeolite 10A | |||||||
| Sorbed Element: Zn2+ | Sorbed Element: Cd2+ | ||||||
| Initial Concentration of Zn2+ in Solution Expressed: | % Sorption | Kd [L/kg] | Initial Concentration of Cd2+ in Solution Expressed: | % Sorption | Kd [L/kg] | ||
| in [cmol/L] | as % CEC | in [cmol/L] | as % CEC | ||||
| 0.07 | 2 | 0.00 | n. c.* | 0.07 | 2 | 16.66 | 4.17 |
| 0.37 | 10 | 45.95 | 21.25 | 0.36 | 10 | 33.33 | 12.50 |
| 0.74 | 20 | 43.24 | 19.05 | 0.73 | 20 | 45.20 | 20.63 |
| 1.10 | 30 | 41.82 | 17.97 | 1.09 | 30 | 44.04 | 19.67 |
| 1.84 | 50 | 47.28 | 22.42 | 1.81 | 50 | 52.49 | 27.62 |
| 2.58 | 75 | 37.60 | 15.06 | 2.54 | 75 | 42.52 | 18.49 |
| 3.68 | 100 | 31.52 | 11.51 | 3.63 | 100 | 37.74 | 15.15 |
| Sorbent: Zeolite 13X | |||||||
| Sorbed Element: Zn2+ | Sorbed Element: Cd2+ | ||||||
| Initial Concentration of Zn2+ in Solution Expressed: | % Sorption | Kd [L/kg] | Initial Concentration of Cd2+ in Solution Expressed: | % Sorption | Kd [L/kg] | ||
| in [cmol/L] | as % CEC | in [cmol/L] | as % CEC | ||||
| 0.05 | 2 | 100.00 | n. c.* | 0.05 | 2 | 100.00 | n. c.* |
| 0.24 | 10 | 75.00 | 75.00 | 0.27 | 10 | 77.78 | 87.50 |
| 0.48 | 20 | 68.75 | 55.00 | 0.53 | 20 | 67.92 | 52.94 |
| 0.72 | 30 | 51.39 | 26.43 | 0.80 | 30 | 55.00 | 30.56 |
| 1.20 | 50 | 40.83 | 17.25 | 1.33 | 50 | 45.11 | 20.55 |
| 1.69 | 75 | 35.50 | 13.76 | 1.87 | 75 | 34.76 | 13.73 |
| 2.41 | 100 | 26.14 | 8.85 | 2.67 | 100 | 23.60 | 7.72 |
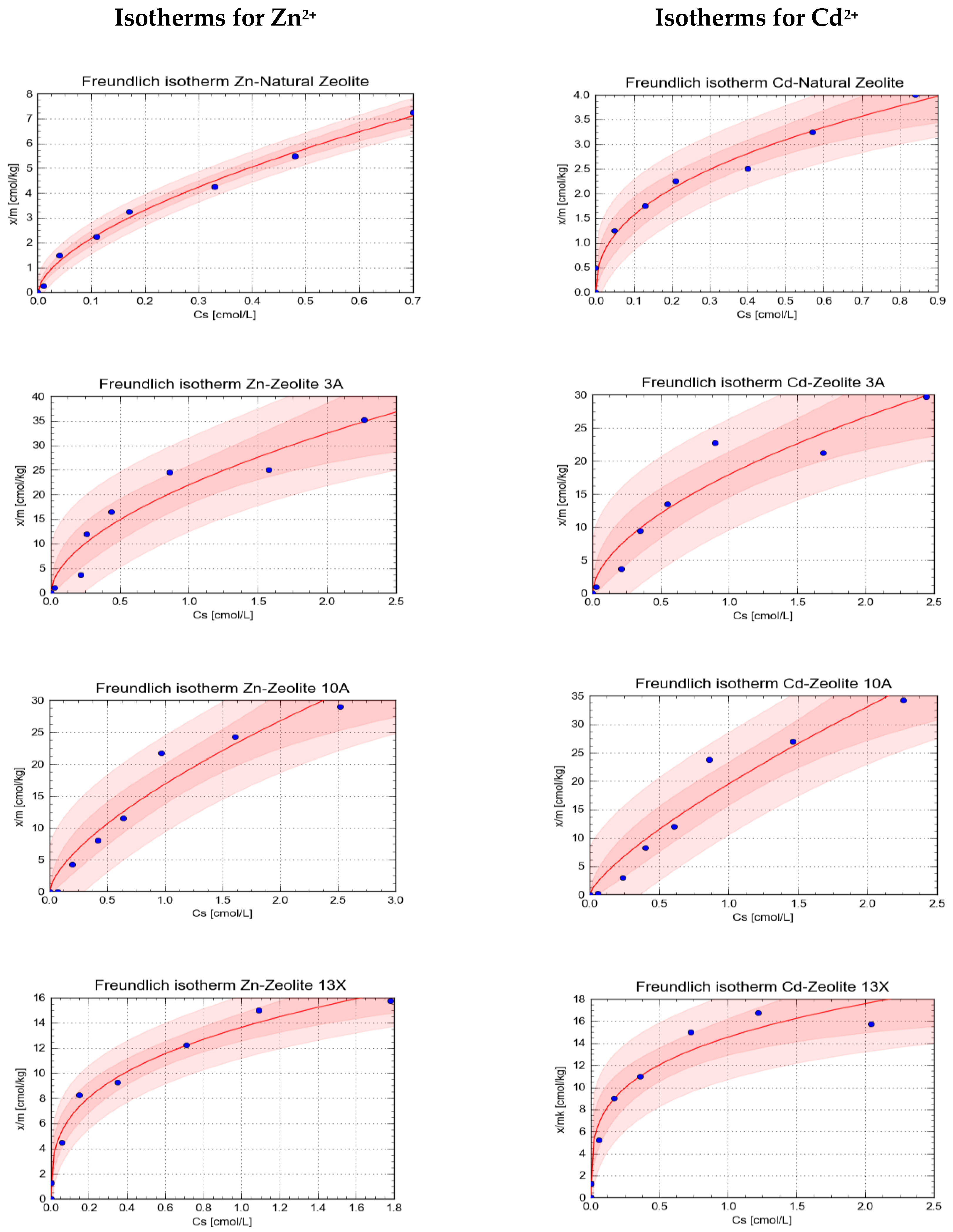
| Sorbent | Sorbed Element | Parameters of Freundlich Isotherm | Statistical Parameters of the Isotherm | |||||
|---|---|---|---|---|---|---|---|---|
| Adsorption Constant Kf [L/kg] | 1/n | SD | r | R2 | ||||
| Value | SD | Value | SD | |||||
| Natural Zeolite | Zn2+ | 8.82 | 0.311 | 0.609 | 0.034 | 0.229 | 0.9965 | 0.9931 |
| Cd2+ | 4.15 | 0.245 | 0.426 | 0.057 | 0.256 | 0.9846 | 0.9694 | |
| Zeolite 3A | Zn2+ | 21.96 | 1.602 | 0.564 | 0.096 | 3.566 | 0.9665 | 0.9342 |
| Cd2+ | 17.94 | 1.401 | 0.572 | 0.101 | 3.130 | 0.9650 | 0.9311 | |
| Zeolite 10A | Zn2+ | 16.85 | 1.282 | 0.666 | 0.100 | 2.803 | 0.9734 | 0.9475 |
| Cd2+ | 19.50 | 1.553 | 0.763 | 0.116 | 3.332 | 0.9722 | 0.9452 | |
| Zeolite 13X | Zn2+ | 13.64 | 0.450 | 0.327 | 0.037 | 0.906 | 0.9901 | 0.9803 |
| Cd2+ | 14.54 | 0.676 | 0.274 | 0.048 | 1.424 | 0.9795 | 0.9595 | |
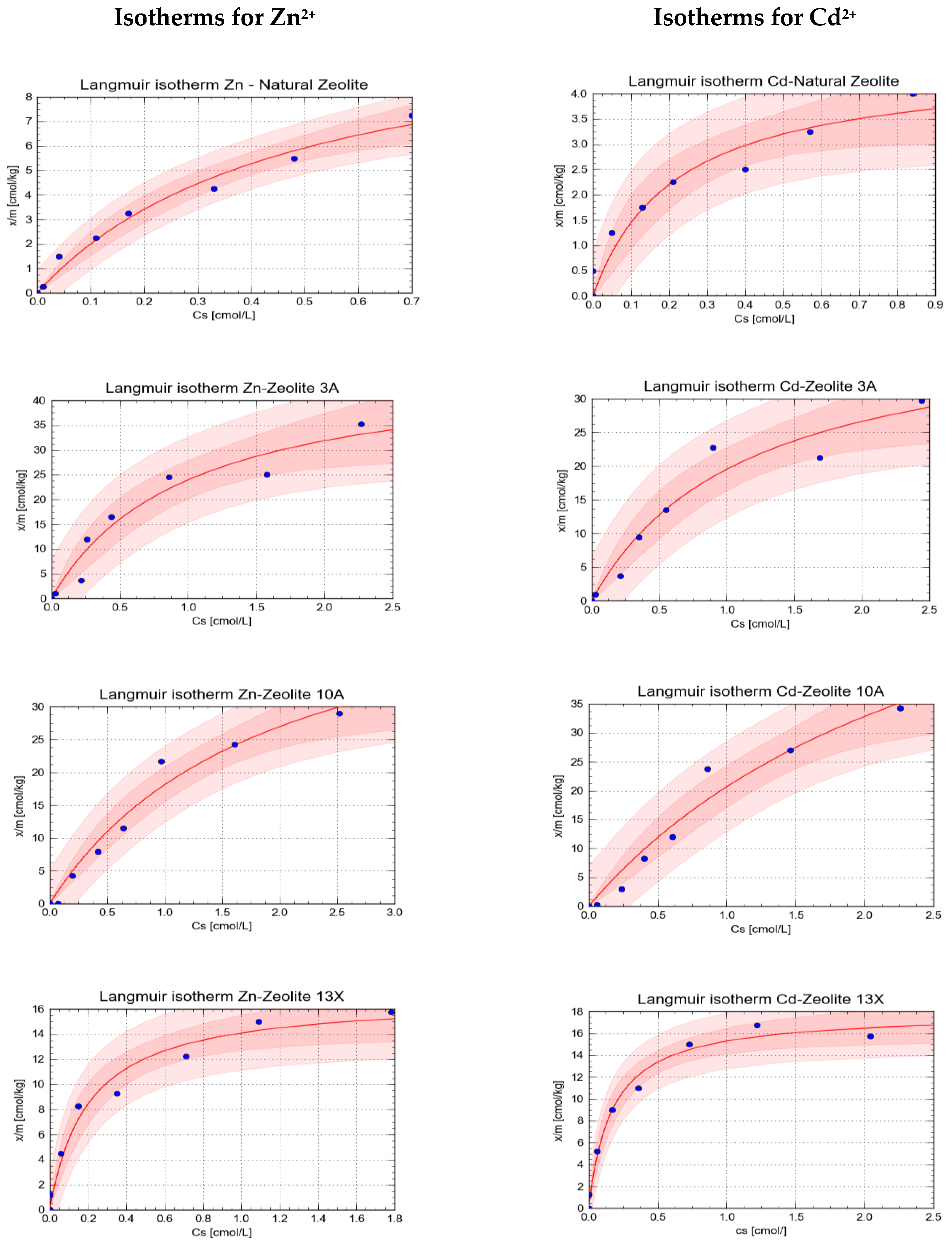
| Sorbent | Sorbed Element | Parameters of Langmuir Isotherm | Statistical Parameters of the Isotherm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| KL [L/kg] | KL∗N | N [cmol/kg] | SD | r | R2 | ||||
| Value | SD | Value | SD | ||||||
| Natural Zeolite | Zn2+ | 2.09 | 0.609 | 24.18 | 3.531 | 11.58 | 0.382 | 0.9903 | 0.9807 |
| Cd2+ | 4.59 | 1.785 | 21.08 | 5.599 | 4.60 | 0.356 | 0.9697 | 0.9403 | |
| Zeolite 3A | Zn2+ | 1.01 | 0.400 | 48.19 | 11.264 | 47.59 | 3.170 | 0.9736 | 0.9480 |
| Cd2+ | 0.87 | 0.343 | 36.62 | 8.230 | 41.8 | 2.634 | 0.9753 | 0.9513 | |
| Zeolite 10A | Zn2+ | 0.53 | 0.189 | 27.72 | 4.680 | 52.46 | 2.091 | 0.9853 | 0.9708 |
| Cd2+ | 0.35 | 0.183 | 27.97 | 5.305 | 79.34 | 2.816 | 0.9802 | 0.9609 | |
| Zeolite 13X | Zn2+ | 4.95 | 1.266 | 83.83 | 16.936 | 16.93 | 1.026 | 0.9861 | 0.9724 |
| Cd2+ | 5.92 | 1.188 | 105.75 | 17.313 | 17.87 | 0.927 | 0.9914 | 0.9828 | |
| Sorbent | Sorbed Element | Parameters of the DKR Isotherm | Statistical Parameters of the Isotherm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| lnXm | β [mol2/kJ2] | Xm [cmol/kg] | E [kJ/mol] | SD | r | R2 | ||||
| Value | SD | Value | SD | |||||||
| Natural Zeolite | Zn2+ | 1.852 | 0.095 | −0.02554 | 0.00017 | 6.37 | 4.425 | 0.1832 | 0.9890 | 09781 |
| Cd2+ | 1.256 | 0.096 | −0.02046 | 0.0036 | 3.51 | 4.94 | 0.156 | 0.9433 | 0.8898 | |
| Zeolite 3A | Zn2+ | 3.315 | 0.238 | −0.04508 | 0.0018 | 27.51 | 3.30 | 0.513 | 0.9285 | 0.8621 |
| Cd2+ | 2.954 | 0.222 | −0.04285 | 0.0076 | 19.18 | 3.42 | 0.486 | 0.9301 | 0.8651 | |
| Zeolite 10A | Zn2+ | 3.262 | 0.138 | −0.1039 | 0.0154 | 26.10 | 2.19 | 0.237 | 0.9588 | 0.9194 |
| Cd2+ | 3.265 | 0.179 | −0.09952 | 0.00909 | 26.17 | 2.29 | 0.375 | 0.9802 | 0.9608 | |
| Zeolite 13X | Zn2+ | 2.680 | 0.068 | −0.02449 | 0.00308 | 14.59 | 4.52 | 0.124 | 0.9717 | 0.9442 |
| Cd2+ | 2.774 | 0.048 | −0.02368 | 0.00216 | 16.03 | 4.59 | 0.089 | 0.9838 | 0.9679 | |
| Sorbent | Sorbed Element | Maximum Sorption Capacity N–Langmuir’s Isotherm, Expressed in: | Maximum Sorption Capacity Xm–DKR Isotherm, Expressed in: | Ratio N:Xm | ||||
|---|---|---|---|---|---|---|---|---|
| [cmol/kg] | [mmol/g] | [mg/g] | [cmol/kg] | [mmol/g] | [mg/g] | |||
| Natural Zeolite | Zn2+ | 11.58 | 0.1158 | 7.57 | 6.37 | 0.0637 | 4.16 | 1.82:1 |
| Cd2+ | 4.60 | 0.0460 | 5.17 | 3.51 | 0.0351 | 3.95 | 1.31:1 | |
| Zeolite 3A | Zn2+ | 47.59 | 0.4759 | 31.11 | 27.51 | 0.2751 | 17.99 | 1.73:1 |
| Cd2+ | 41.8 | 0.4180 | 46.99 | 19.18 | 0.1981 | 22.27 | 2.18:1 | |
| Zeolite 10A | Zn2+ | 52.46 | 0.5246 | 34.30 | 26.10 | 0.2610 | 17.06 | 2.01:1 |
| Cd2+ | 79.34 | 0.7934 | 89.19 | 26.17 | 0.2617 | 29.42 | 3.03:1 | |
| Zeolite 13X | Zn2+ | 16.93 | 0.1693 | 11.07 | 14.59 | 0.1459 | 9.54 | 1.16:1 |
| Cd2+ | 17.87 | 0.1787 | 20.09 | 16.03 | 0.1603 | 18.02 | 1.11:1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozera-Sucharda, B.; Gworek, B.; Kondzielski, I. The Simultaneous Removal of Zinc and Cadmium from Multicomponent Aqueous Solutions by Their Sorption onto Selected Natural and Synthetic Zeolites. Minerals 2020, 10, 343. https://doi.org/10.3390/min10040343
Kozera-Sucharda B, Gworek B, Kondzielski I. The Simultaneous Removal of Zinc and Cadmium from Multicomponent Aqueous Solutions by Their Sorption onto Selected Natural and Synthetic Zeolites. Minerals. 2020; 10(4):343. https://doi.org/10.3390/min10040343
Chicago/Turabian StyleKozera-Sucharda, Bożena, Barbara Gworek, and Igor Kondzielski. 2020. "The Simultaneous Removal of Zinc and Cadmium from Multicomponent Aqueous Solutions by Their Sorption onto Selected Natural and Synthetic Zeolites" Minerals 10, no. 4: 343. https://doi.org/10.3390/min10040343
APA StyleKozera-Sucharda, B., Gworek, B., & Kondzielski, I. (2020). The Simultaneous Removal of Zinc and Cadmium from Multicomponent Aqueous Solutions by Their Sorption onto Selected Natural and Synthetic Zeolites. Minerals, 10(4), 343. https://doi.org/10.3390/min10040343