Mineralogical Prediction of Flotation Performance for a Sediment-Hosted Copper–Cobalt Sulphide Ore
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Preparation
2.2. Flotation Tests
2.2.1. Reagents
2.2.2. Flotation Procedure
2.2.3. Chemical Analysis
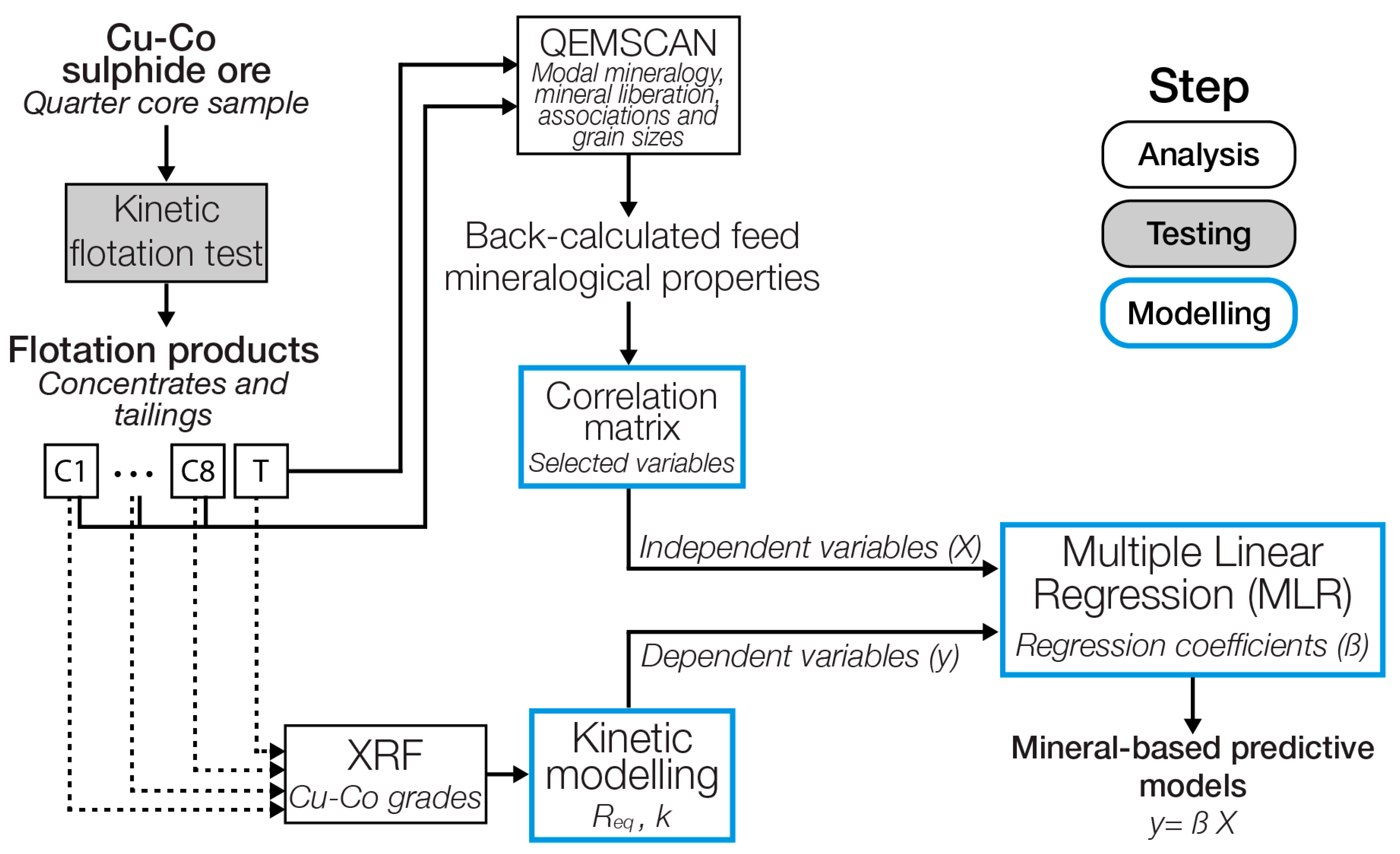
2.2.4. Mineralogical Analysis
2.3. Flotation Kinetics Modelling
2.4. Regression Analysis
2.4.1. Variable Selection
2.4.2. Multiple Linear Regression
2.4.3. Cross Validation
2.5. Methodology
3. Results and Discussion
3.1. Feed Characteristics
3.1.1. Feed Grade and Modal Mineralogy
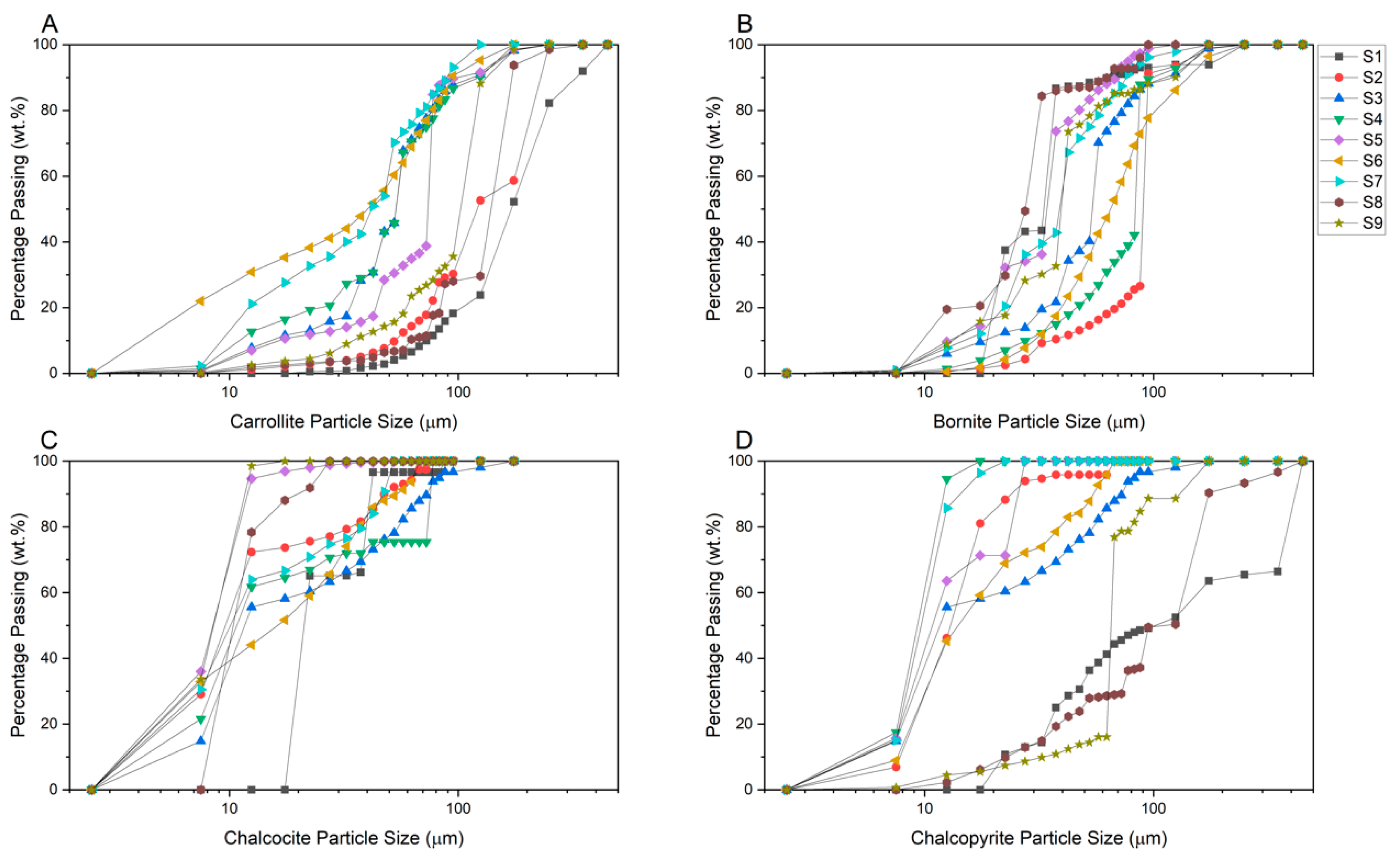
3.1.2. Feed Mineral Particle Size
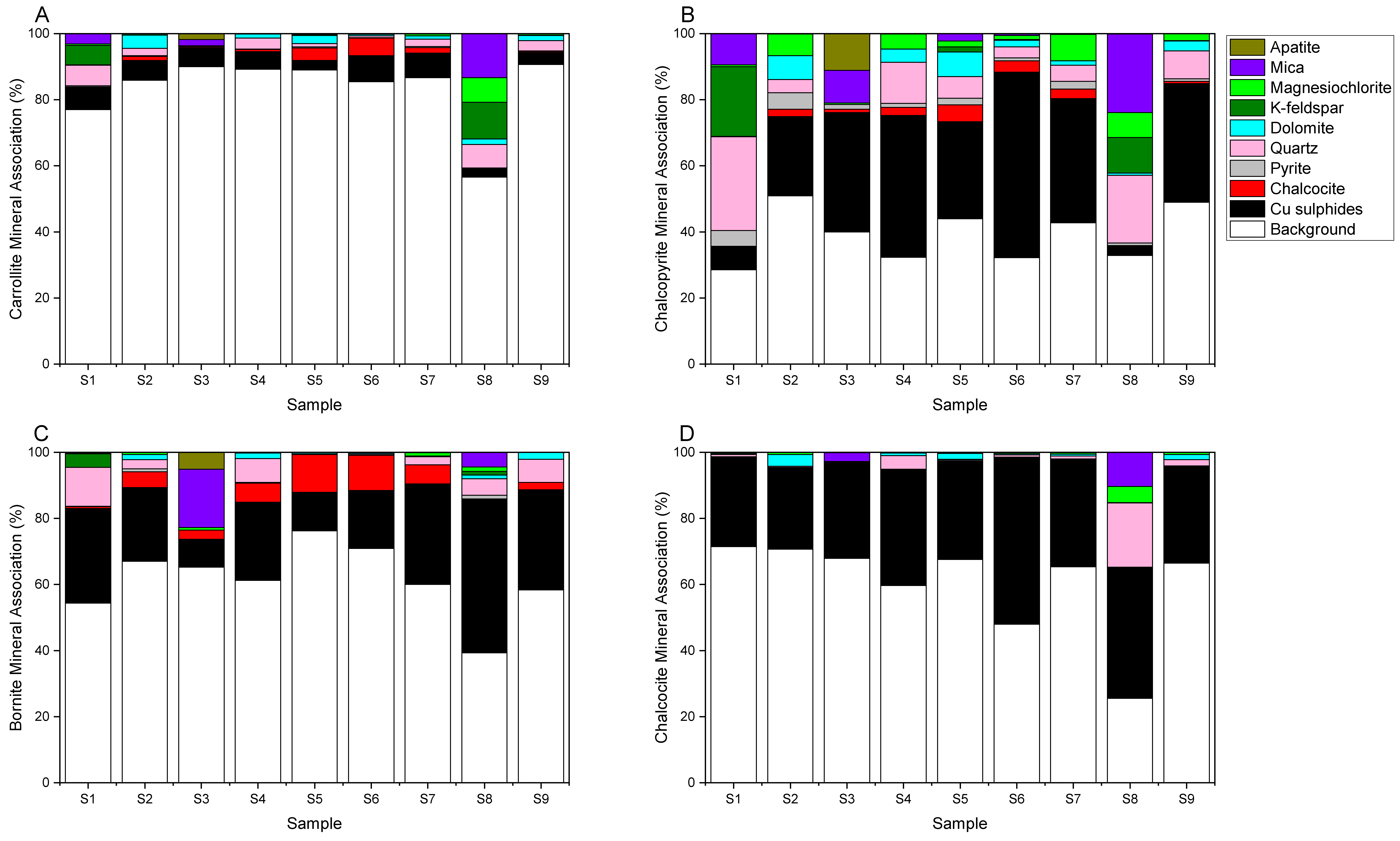
3.1.3. Feed Liberation and Mineral Association
3.2. Flotation Performance
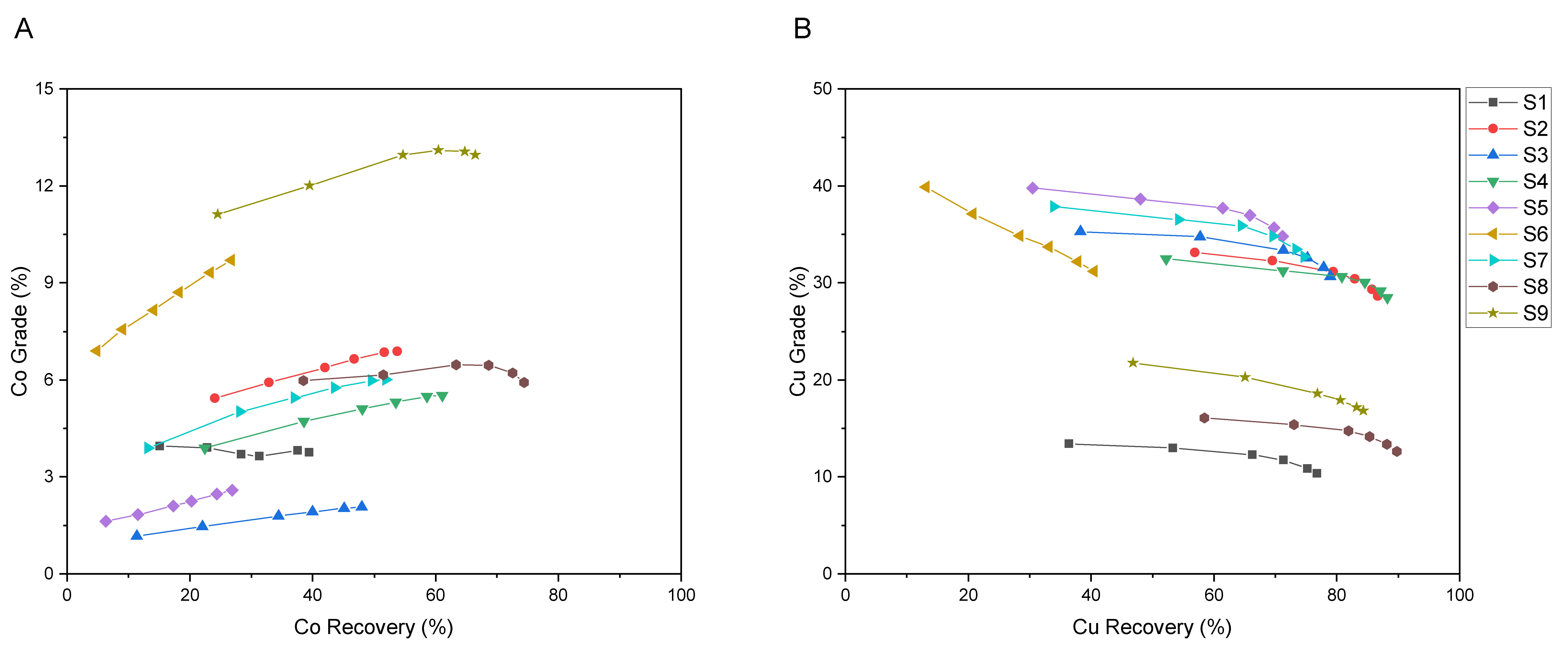
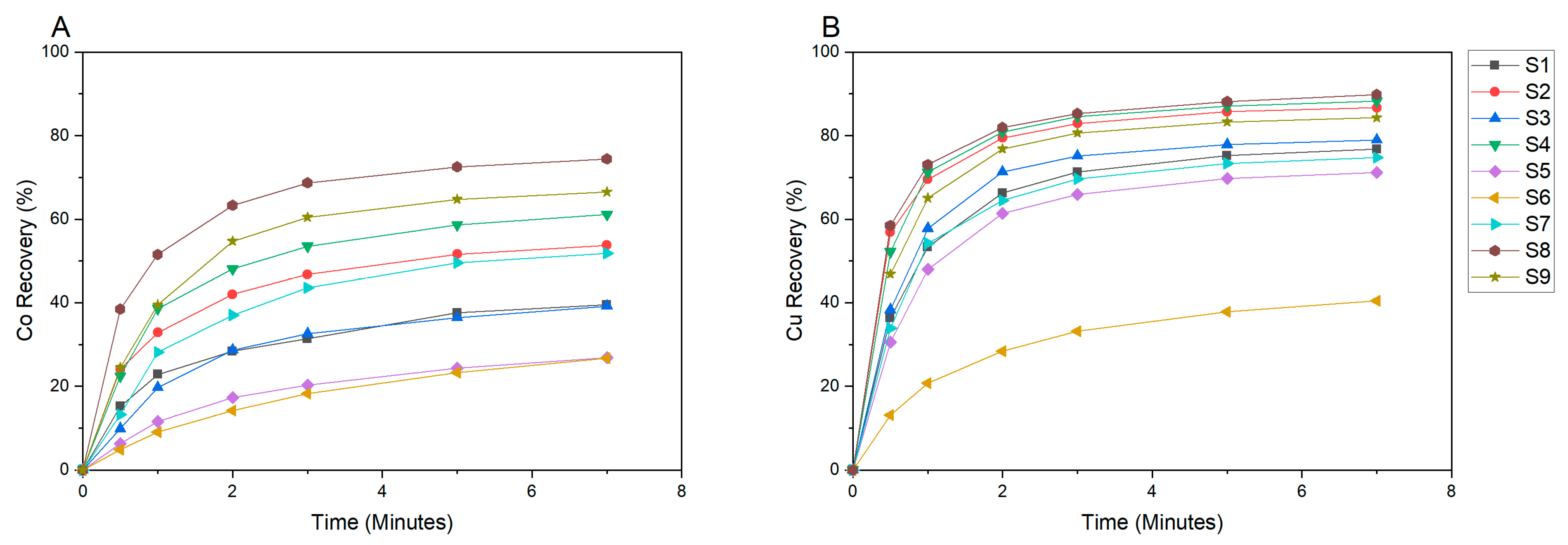
3.2.1. Copper and Cobalt Grade-Recovery Curves
3.2.2. Copper and Cobalt Flotation Kinetics
3.2.3. Fitting of Flotation Models to Metal Recovery Data
3.3. Regression Analysis
3.3.1. Selection of Regression Variables
3.3.2. Multiple Linear Regression Results for Selected Variables
3.3.3. Regression Models Cross Validation
3.4. Model Limitations and Further Development
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Sample | Index | Model 1 | Model 2 | Model 3 | Model 4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Cobalt | Copper | Cobalt | Copper | Cobalt | Copper | Cobalt | Copper | ||
| S1 | R2 | 0.98 | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 |
| RMSE | 2.30 | 1.77 | 1.60 | 0.17 | 1.11 | 1.24 | 0.88 | 1.91 | |
| S2 | R2 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| RMSE | 2.48 | 2.93 | 1.37 | 0.84 | 0.61 | 0.35 | 0.28 | 0.86 | |
| S3 | R2 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 |
| RMSE | 0.73 | 1.77 | 0.93 | 0.17 | 1.46 | 1.24 | 1.76 | 1.91 | |
| S4 | R2 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 2.77 | 0.99 | 1.00 |
| RMSE | 1.96 | 0.45 | 1.17 | 0.72 | 1.42 | 1.66 | 1.76 | 2.33 | |
| S5 | R2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 |
| RMSE | 0.65 | 1.12 | 0.41 | 0.82 | 0.29 | 1.85 | 0.34 | 2.46 | |
| S6 | R2 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| RMSE | 0.44 | 1.31 | 0.33 | 0.72 | 0.18 | 0.21 | 0.14 | 0.22 | |
| S7 | R2 | 0.99 | 1.00 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 |
| RMSE | 1.66 | 1.83 | 1.51 | 1.35 | 1.77 | 2.17 | 2.01 | 2.74 | |
| S8 | R2 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| RMSE | 2.72 | 2.78 | 1.00 | 0.52 | 0.37 | 0.42 | 0.85 | 1.02 | |
| S9 | R2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 |
| RMSE | 0.66 | 1.63 | 0.76 | 1.22 | 1.76 | 1.63 | 2.31 | 1.02 | |
Appendix B
| Parameter | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Measured pulp pH | 8.1 | 9.5 | 9.1 | 9.3 | 9.4 | 9.2 | 9.2 | 8.8 | 9.3 |
| Cu minerals P80 | 295.2 | 114.7 | 73.5 | 84.5 | 43.9 | 91.6 | 58.5 | 160.8 | 91.6 |
| Cu minerals F100 | 65.2 | 14.6 | 8.6 | 7.3 | 2.1 | 10.8 | 1.6 | 55.2 | 10.9 |
| Cu minerals liberation | 68.0 | 80.8 | 72.1 | 75.2 | 77.8 | 84.0 | 61.8 | 53.8 | 80.8 |
| MA CuD Apatite | 0.0 | 0.0 | 4.3 | 0.0 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 |
| MA CuD Background | 56.2 | 69.0 | 65.7 | 63.8 | 75.2 | 69.8 | 61.0 | 32.6 | 73.6 |
| MA CuD Barite | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.1 |
| MA CuD Biotite | 2.2 | 0.0 | 8.9 | 0.0 | 0.1 | 0.0 | 0.0 | 7.4 | 0.0 |
| MA CuD Bornite | 0.1 | 1.3 | 1.9 | 1.8 | 4.5 | 4.8 | 2.1 | 0.6 | 2.6 |
| MA CuD Carrollite | 2.3 | 5.4 | 1.8 | 3.8 | 5.6 | 5.3 | 3.2 | 0.9 | 4.5 |
| MA CuD Chalcocite | 0.1 | 3.7 | 2.2 | 4.7 | 6.1 | 8.7 | 4.7 | 0.1 | 1.0 |
| MA CuD Chalcopyrite | 4.3 | 12.0 | 4.8 | 15.4 | 4.5 | 9.3 | 21.6 | 1.3 | 8.4 |
| MA CuD Chrysocolla | 4.4 | 2.2 | 0.2 | 1.9 | 1.6 | 1.0 | 3.0 | 19.8 | 2.1 |
| MA CuD Dolomite | 0.1 | 2.2 | 0.0 | 1.6 | 1.3 | 0.3 | 0.3 | 0.8 | 1.8 |
| MA CuD Fe Dolomite/Ankerite | 0.0 | 0.0 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| MA CuD Fe-Ox/CO3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.1 |
| MA CuD Gypsum | 0.0 | 0.2 | 0.5 | 0.0 | 0.2 | 0.0 | 0.1 | 0.0 | 0.1 |
| MA CuD Heterogenite | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MA CuD Ilmenite | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MA CuD Kaolinite | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 |
| MA CuD K-feldspar | 10.5 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 8.5 | 0.0 |
| MA CuD Magnesiochlorite | 0.4 | 0.6 | 0.6 | 0.2 | 0.0 | 0.1 | 1.1 | 5.8 | 0.4 |
| MA CuD Magnesite | 0.0 | 0.0 | 2.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 |
| MA CuD Mg silicates | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.1 | 0.3 |
| MA CuD Monazite | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MA CuD Muscovite/Illite | 2.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 |
| MA CuD Others | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 |
| MA CuD Phlogopite | 0.1 | 0.0 | 5.1 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 0.0 |
| MA CuD Plagioclase | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 0.0 |
| MA CuD Pyrite | 1.8 | 0.8 | 0.0 | 0.1 | 0.2 | 0.0 | 0.1 | 0.4 | 0.1 |
| MA CuD Quartz | 13.2 | 2.5 | 0.0 | 6.5 | 0.4 | 0.5 | 2.4 | 11.9 | 4.7 |
| MA CuD Rutile | 0.4 | 0.0 | 1.1 | 0.0 | 0.0 | 0.0 | 0.1 | 1.1 | 0.1 |
| MA CuD Zircon | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Appendix C
| Feed Parameter | %Car | %Cc | %Mgc | Car F100 | Car lib | Car MA Mgc | Car MA Dol |
| %Car | 1.00 | 0.46 | −0.49 | −0.57 | 0.58 | −0.48 | 0.03 |
| %Cc | 0.46 | 1.00 | −0.45 | −0.50 | 0.35 | −0.31 | 0.14 |
| %Mgc | −0.49 | −0.45 | 1.00 | 0.16 | −0.40 | 0.35 | 0.32 |
| Car F100 | −0.57 | −0.50 | 0.16 | 1.00 | −0.55 | 0.57 | 0.11 |
| Car lib | 0.58 | 0.35 | −0.40 | −0.55 | 1.00 | −0.95 | −0.06 |
| Car MA Mgc | −0.48 | −0.31 | 0.35 | 0.57 | −0.95 | 1.00 | 0.06 |
| Car Ma Dol | 0.03 | 0.14 | 0.32 | 0.11 | −0.06 | 0.06 | 1.00 |
| Feed Parameter | %Car | %Cc | %Bn | %Sul | CuF100 | Cu MA Mgc | Cu Ma Dol |
| %Car | 1.00 | 0.46 | 0.29 | 0.66 | −0.49 | −0.55 | 0.27 |
| %Cc | 0.46 | 1.00 | 0.35 | 0.54 | −0.48 | −0.36 | −0.03 |
| %Bn | 0.29 | 0.35 | 1.00 | 0.90 | −0.67 | −0.42 | −0.30 |
| %Sul | 0.66 | 0.54 | 0.90 | 1.00 | −0.70 | −0.52 | −0.16 |
| Cu F100 | −0.49 | −0.48 | −0.67 | −0.70 | 1.00 | 0.56 | −0.29 |
| Cu MA Mgc | −0.55 | −0.36 | −0.42 | −0.52 | 0.56 | 1.00 | −0.11 |
| Cu Ma Dol | 0.27 | −0.03 | −0.30 | −0.16 | −0.29 | −0.11 | 1.00 |
References
- Lund, C.; Lamberg, P. Geometallurgy-A tool for better resource efficiency. Eur. Geol. 2014, 37, 39–43. [Google Scholar]
- Dehaine, Q.; Filippov, L.O.; Glass, H.J.; Rollinson, G. Rare-metal granites as a potential source of critical metals: A geometallurgical case study. Ore Geol. Rev. 2019, 104, 384–402. [Google Scholar] [CrossRef]
- Alruiz, O.M.; Morrell, S.; Suazo, C.J.; Naranjo, A. A novel approach to the geometallurgical modelling of the Collahuasi grinding circuit. Miner. Eng. 2009, 22, 1060–1067. [Google Scholar] [CrossRef]
- Navarra, A.; Grammatikopoulos, T.; Waters, K. Incorporation of geometallurgical modelling into long-term production planning. Miner. Eng. 2018, 120, 118–126. [Google Scholar] [CrossRef]
- Lamberg, P. Particles–the bridge between geology and metallurgy. In Proceedings of the Conference in Mineral Engineering, Luleå, Sweden, 8–9 February 2011; pp. 1–16. [Google Scholar]
- Schmidt, T.; Buchert, M.; Schebek, L. Investigation of the primary production routes of nickel and cobalt products used for Li-ion batteries. Resour. Conserv. Recycl. 2016, 112, 107–122. [Google Scholar] [CrossRef]
- Fisher, K.G.; Treadgold, L.G. Design Considerations for the Cobalt Recovery Circuit of the Kol (Kov) Copper/Cobalt Refinery, DRC. In Proceedings of the ALTA Nickel-Cobalt Conference, Perth, Australia, 25–27 May 2009. [Google Scholar]
- Crundwell, F.K.; Moats, M.S.; Ramachandran, V.; Robinson, T.G.; Davenport, W.G.; Crundwell, F.K.; Moats, M.S.; Ramachandran, V.; Robinson, T.G.; Davenport, W.G. Production of Cobalt from the Copper–Cobalt Ores of the Central African Copperbelt. In Extractive Metallurgy of Nickel, Cobalt and Platinum Group Metals; Elsevier: Amsterdam, The Netherlands, 2011; pp. 377–391. ISBN 9780080968094. [Google Scholar]
- Mainza, A.N.; Simukanga, S.; Witika, L.K. Technical note evaluating the performance of new collectors on feed to Nkana concentrator’s flotation circuit. Miner. Eng. 1999, 12, 571–577. [Google Scholar] [CrossRef]
- Musuku, B. Enhancing the Recoveries and Grades of Cobalt from Nchanga and Konkola Ores of KCM. Master’s Thesis, University of Zambia, Lusaka, Zambia, 2011. [Google Scholar]
- Tijsseling, L.T.; Dehaine, Q.; Rollinson, G.K.; Glass, H.J. Flotation of mixed oxide sulphide copper-cobalt minerals using xanthate, dithiophosphate, thiocarbamate and blended collector. Miner. Eng. 2019, 138, 246–256. [Google Scholar] [CrossRef]
- Lamberg, P.; Rosenkranz, J. Systematic diagnosis of flotation circuit performance based on process mineralogical methods. In Proceedings of the 14th International Mineral Processing Symposium, Kuşadası, Turkey, 15–17 October 2014; pp. 417–423. [Google Scholar]
- Keeney, L. The Development of a Novel Method for Integrating Geometallurgical Mapping and Orebody Modelling. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2010. [Google Scholar]
- Gharai, M.; Venugopal, R. Modeling of flotation process-An overview of different approaches. Miner. Process. Extr. Metall. Rev. 2016, 37, 120–133. [Google Scholar] [CrossRef]
- Whiteman, E.; Lotter, N.O.; Amos, S.R. Process mineralogy as a predictive tool for flowsheet design to advance the Kamoa project. Miner. Eng. 2016, 96–97, 185–193. [Google Scholar] [CrossRef]
- Rincon, J.; Gaydardzhiev, S.; Stamenov, L. Investigation on the flotation recovery of copper sulphosalts through an integrated mineralogical approach. Miner. Eng. 2019, 130, 36–47. [Google Scholar] [CrossRef]
- Little, L.; Mclennan, Q.; Prinsloo, A.; Muchima, K.; Kaputula, B.; Siame, C. Relationship between ore mineralogy and copper recovery across different processing circuits at Kansanshi mine. J. S. Afr. Inst. Min. Metall. 2018, 118, 1155–1162. [Google Scholar] [CrossRef]
- Anderson, K.F.E.; Wall, F.; Rollinson, G.K.; Moon, C.J. Quantitative mineralogical and chemical assessment of the Nkout iron ore deposit, Southern Cameroon. Ore Geol. Rev. 2014, 62, 25–39. [Google Scholar] [CrossRef]
- Gottlieb, P.; Wilkie, G.; Sutherland, D.; Ho-Tun, E.; Suthers, S.; Perera, K.; Jenkins, B.; Spencer, S.; Butcher, A.; Rayner, J. Using Quantitaive Electron Microscopy for Process Mineralogy Applications. J. Miner. Met. Mater. Soc. 2000, 52, 24–25. [Google Scholar] [CrossRef]
- Pirrie, D.; Butcher, A.R.; Power, M.R.; Gottlieb, P.; Miller, G.L. Rapid quantitative mineral and phase analysis using automated scanning electron microscopy (QemSCAN); potential applications in forensic geoscience. Geol. Soc. London Spec. Publ. 2004, 232, 123–136. [Google Scholar] [CrossRef]
- Rollinson, G.K.; Andersen, J.C.Ø.; Stickland, R.J.; Boni, M.; Fairhurst, R. Characterisation of non-sulphide zinc deposits using QEMSCAN®. Miner. Eng. 2011, 24, 778–787. [Google Scholar] [CrossRef]
- Bu, X.; Xie, G.; Peng, Y.; Ge, L.; Ni, C. Kinetics of flotation. Order of process, rate constant distribution and ultimate recovery. Physicochem. Probl. Miner. Process. 2017, 53, 342–365. [Google Scholar]
- Garcia-Zungina, H. The efficiency obtained by flotation is an exponential function of time. Bol. Min. 1935, 47, 83–86. [Google Scholar]
- Klimpel, R.R. Selection of Chemical Reagents for Flotation. Organ. Soc. Min. Metall. Explor. 1980, 2, 907–934. [Google Scholar]
- Arbiter, N. Flotation rates and flotation efficiency. Trans. AIME. Sept. 1951, 791, 796. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7137-0. [Google Scholar]
- Wills, B.A.; Finch, J.A. Wills’ Mineral Processing Technology an Introduction to the Practical Aspects; Butterworth-Heinemann: Oxford, UK, 2016; ISBN 9780080970530. [Google Scholar]
- Lotter, N.O.; Bradshaw, D.J.; Barnes, A.R. Classification of the Major Copper Sulphides into semiconductor types, and associated flotation characteristics. Miner. Eng. 2016, 96–97, 177–184. [Google Scholar] [CrossRef]
- Guy, P.J.; Trahar, W.J. The effects of oxidation and mineral interaction on sulphide flotation. In Flotation of Sulphide Minerals; Stiftelsen Mineral Teknisk Forshning: Stockholm, Sweden, 1985; pp. 91–103. [Google Scholar]
- Trahar, W.J.; Senior, G.D.; Shannon, L.K. Interactions between sulphide minerals-the collectorless flotation of pyrite. Int. J. Miner. Process. 1994, 40, 287–321. [Google Scholar] [CrossRef]
- Owusu, C.; Addai-Mensah, J.; Fornasiero, D.; Zanin, M. Estimating the electrochemical reactivity of pyrite ores-their impact on pulp chemistry and chalcopyrite flotation behaviour. Adv. Powder Technol. 2013, 24, 801–809. [Google Scholar] [CrossRef]
- Owusu, C.; Brito, E.; Abreu, S.; Skinner, W.; Addai-Mensah, J.; Zanin, M. The influence of pyrite content on the flotation of chalcopyrite/pyrite mixtures. Miner. Eng. 2014, 55, 87–95. [Google Scholar] [CrossRef]
- Woods, R. Electrochemical potential controlling flotation. Int. J. Miner. Process. 2003, 72, 151–162. [Google Scholar] [CrossRef]
- Mesa, D.; Brito-Parada, P.R. Scale-up in froth flotation: A state-of-the-art review. Sep. Purif. Technol. 2019, 210, 950–962. [Google Scholar] [CrossRef]




| Phase | Stage | Cumulative Timing | Conditioning | Flotation | MIBC | DF245 |
|---|---|---|---|---|---|---|
| min | min | min | g/t | g/t | ||
| Rougher | 1. Conditioning collector | 0 | 3 | - | - | 30 |
| 2. Conditioning frother | 3 | 1 | - | 50 | - | |
| 3. Concentrate 1 | 4 | - | 0.5 | - | - | |
| 4. Concentrate 2 | 4.5 | - | 0.5 | - | - | |
| 5. Concentrate 3 | 5 | - | 1 | - | - | |
| 6. Concentrate 4 | 6 | - | 1 | - | - | |
| 7. Concentrate 5 | 7 | - | 2 | - | - | |
| 8. Concentrate 6 | 9 | - | 2 | - | - | |
| Scavenger | 9. Conditioning collector | 11 | 3 | - | - | 30 |
| 10. Concentrate 7 | 14 | - | 1 | - | - | |
| 11. Concentrate 8 | 15 | - | 2 | - | - |
| Mineral/Element | Formula | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Carrollite | CuCo2S4 | 11.1 | 13.1 | 8.5 | 15.6 | 18.9 | 28.8 | 15.1 | 5.5 | 29.1 |
| Chalcopyrite | CuFeS2 | 3.7 | 0.6 | 0.7 | 0.7 | 0.2 | 1.3 | 1.6 | 7.2 | 1.7 |
| Bornite | Cu5FeS4 | <0.1 | 14.7 | 32.6 | 27.3 | 11.1 | 41.6 | 31.1 | 0.1 | 6.4 |
| Chalcocite | Cu2S | <0.1 | 0.8 | 0.5 | 0.8 | 5.7 | 4.4 | 1.5 | <0.1 | 0.1 |
| Pyrite | FeS2 | 1.0 | 0.1 | 0.1 | 0.3 | 0.1 | 0.2 | 0.3 | <0.1 | 0.1 |
| Chrysocolla | (Cu,Al)2H2Si2O5(OH)4·nH2O | 0.3 | 0.2 | 0.1 | 0.2 | 0.1 | 0.3 | 0.6 | 0.3 | 0.2 |
| Goethite | FeO(OH) | 0.1 | 0.3 | 0.8 | 0.6 | 1.0 | 0.3 | 1.1 | 0.2 | 0.6 |
| Rutile | TiO2 | 1.0 | 0.1 | 0.2 | 0.1 | 0.2 | 0.1 | 0.3 | 1.1 | 0.1 |
| Dolomite/Ankerite | CaMg(CO3)2 | 2.5 | 44.6 | 16.7 | 18.1 | 44.9 | 10.7 | 12.9 | 12.1 | 27.3 |
| Apatite | Ca5(PO4)3(F,Cl,OH) | 0.4 | 0.3 | 0.6 | 0.2 | 0.3 | 0.2 | 0.7 | 0.6 | 0.4 |
| Magnesite | MgCO3 | <0.1 | <0.1 | 2.0 | 0.1 | 0.2 | 0.1 | 0.6 | <0.1 | 2.0 |
| Quartz | SiO2 | 31.4 | 12.5 | 28.0 | 34.1 | 12.2 | 10.2 | 19.6 | 23.4 | 25.9 |
| Plagioclase | (Ca,Na)(Al,Si)4O8 | 0.8 | <0.1 | <0.1 | <0.1 | 0.1 | <0.1 | 0.1 | 0.9 | <0.1 |
| K-feldspar | KAlSi3O8 | 31.1 | <0.1 | <0.1 | <0.1 | 2.5 | 0.3 | 0.2 | 21.0 | 0.1 |
| Muscovite/Illite | (Al,Mg,Fe)2(Si,Al)4O10[(OH)2,(H2O)] | 10.0 | <0.1 | <0.1 | <0.1 | 1.0 | 0.1 | 0.1 | 4.1 | <0.1 |
| Biotite | KFe3(AlSi3O10)(F,OH)2 | 2.4 | <0.1 | <0.1 | <0.1 | 0.2 | <0.1 | <0.1 | 0.8 | <0.1 |
| Phlogopite | KMg3(AlSi3O10)(F,OH)2 | 2.0 | <0.1 | <0.1 | <0.1 | 0.1 | 0.1 | 0.4 | 13.2 | <0.1 |
| Magnesiochlorite | (Fe,Mg,Al)6(Si,Al)4O10(OH)8 | 1.9 | 11.4 | 7.7 | 1.5 | 1.0 | 1.2 | 11.5 | 9.2 | 4.2 |
| Mg silicates | Mg3Si4O10(OH)2 | <0.1 | 1.1 | 1.3 | 0.3 | 0.2 | 0.1 | 2.0 | 0.1 | 1.6 |
| Others | 0.3 | 0.1 | 0.1 | 0.1 | 0.1 | <0.1 | 0.1 | 0.1 | 0.1 | |
| Mineral Total | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| Cobalt | Co | 1.5 | 3.1 | 1.6 | 3.7 | 6.5 | 8.6 | 4.2 | 1.4 | 6.3 |
| Copper | Cu | 2.1 | 7.8 | 14.3 | 13.1 | 11.5 | 18.2 | 15.7 | 2.5 | 6.4 |
| Flotation Performance Parameters | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Co rate constant () | 1.76 | 2.20 | 1.13 | 1.95 | 0.95 | 0.59 | 1.31 | 2.96 | 1.85 |
| Co equilibrium recovery () | 41.32 | 56.19 | 55.33 | 65.30 | 31.08 | 34.63 | 58.34 | 77.44 | 72.84 |
| Co final grade () | 3.76 | 6.88 | 2.07 | 5.53 | 2.59 | 9.69 | 6.00 | 5.92 | 12.95 |
| Cu rate constant () | 2.69 | 4.93 | 2.91 | 4.15 | 2.39 | 1.38 | 2.71 | 4.99 | 3.61 |
| Cu equilibrium recovery | 81.21 | 88.84 | 84.22 | 91.79 | 76.35 | 44.26 | 79.31 | 91.72 | 88.44 |
| Cu final grade | 10.37 | 28.61 | 30.64 | 28.50 | 34.78 | 31.22 | 32.68 | 12.63 | 16.83 |
| R2 | 0.98 | 0.95 | 0.99 | 0.93 | 0.97 | >0.99 |
| RMSE | 3.74 | 4.29 | 0.17 | 2.48 | 3.99 | 0.04 |
| F-value | 47.77 | 29.69 | 105.69 | 23.95 | 32.17 | 633.98 |
| Prob > F | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Model Parameter | Variable | Value | Standard Error | t-Value | Prob > |t| |
|---|---|---|---|---|---|
| Intercept | 28.64 | 2.23 | 12.82 | <0.01 | |
| Chalcocite content (%Cc) | 10.30 | 2.17 | 4.71 | 0.01 | |
| Carrollite content (%Car) | −9.67 | 2.28 | −4.24 | 0.01 | |
| Bornite content (%Bn) | 6.68 | 2.45 | 2.72 | 0.05 | |
| Cu sulphide F100 (Cu F100) | −17.06 | 2.72 | 6.26 | <0.01 | |
| Intercept | 114.13 | 4.44 | 25.69 | <0.01 | |
| Chalcocite content (%Cc) | −20.24 | 5.04 | −4.01 | 0.01 | |
| Total sulphide content (%Sul) | −49.22 | 7.55 | −6.52 | <0.01 | |
| Cu sulphide F100 (Cu F100) | −29.36 | 5.83 | −5.04 | <0.01 | |
| Intercept | 2.98 | 0.14 | 21.39 | <0.01 | |
| Chalcocite content (%Cc) | −1.13 | 0.19 | −6.03 | <0.01 | |
| Carrollite content (%Car) | −1.23 | 0.22 | −5.54 | 0.01 | |
| Cu MA dolomite (Cu MA Dol) | 2.34 | 0.17 | 13.97 | <0.01 | |
| Cu MA magnesiochlorite (Cu MA Mgc) | 1.20 | 0.22 | 5.35 | 0.01 | |
| Intercept | 5.82 | 1.06 | 5.48 | <0.01 | |
| Chalcocite content (%Cc) | −5.08 | 1.23 | −5.12 | 0.01 | |
| Carrollite content (%Car) | 12.20 | 1.46 | 8.33 | <0.01 | |
| Carrollite liberation (Car lib) | −4.82 | 1.54 | −3.13 | 0.03 | |
| Intercept | 66.77 | 2.82 | 23.68 | <0.01 | |
| Chalcocite content (%Cc) | −42.17 | 4.61 | −9.16 | <0.01 | |
| Carrollite F100 (Car F100) | −28.18 | 4.88 | −5.78 | <0.01 | |
| Carrollite MA magnesiochlorite (Car MA Mgc) | 31.39 | 5.30 | 5.92 | <0.01 | |
| Carrollite MA dolomite (Car MA Dol) | 13.81 | 4.59 | 3.01 | 0.04 | |
| Intercept | 2.91 | 0.05 | 56.83 | <0.01 | |
| Chalcocite content (%Cc) | −1.42 | 0.05 | −29.61 | <0.01 | |
| Magnesiochlorite content (%Mgc) | −0.51 | 0.04 | −11.72 | <0.01 | |
| Carrollite liberation (Car lib) | −1.35 | 0.05 | −26.52 | <0.01 | |
| Carrollite MA dolomite (Car MA Dol) | 1.16 | 0.05 | 23.07 | <0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tijsseling, L.T.; Dehaine, Q.; Rollinson, G.K.; Glass, H.J. Mineralogical Prediction of Flotation Performance for a Sediment-Hosted Copper–Cobalt Sulphide Ore. Minerals 2020, 10, 474. https://doi.org/10.3390/min10050474
Tijsseling LT, Dehaine Q, Rollinson GK, Glass HJ. Mineralogical Prediction of Flotation Performance for a Sediment-Hosted Copper–Cobalt Sulphide Ore. Minerals. 2020; 10(5):474. https://doi.org/10.3390/min10050474
Chicago/Turabian StyleTijsseling, Laurens T., Quentin Dehaine, Gavyn K. Rollinson, and Hylke J. Glass. 2020. "Mineralogical Prediction of Flotation Performance for a Sediment-Hosted Copper–Cobalt Sulphide Ore" Minerals 10, no. 5: 474. https://doi.org/10.3390/min10050474
APA StyleTijsseling, L. T., Dehaine, Q., Rollinson, G. K., & Glass, H. J. (2020). Mineralogical Prediction of Flotation Performance for a Sediment-Hosted Copper–Cobalt Sulphide Ore. Minerals, 10(5), 474. https://doi.org/10.3390/min10050474






