The Effect of Carbon Defects in the Coal–Pyrite Vacancy on the Electronic Structure and Optical Properties: A DFT + U Study
Abstract
:1. Introduction
2. Model and Calculation Method
3. Results and Discussion
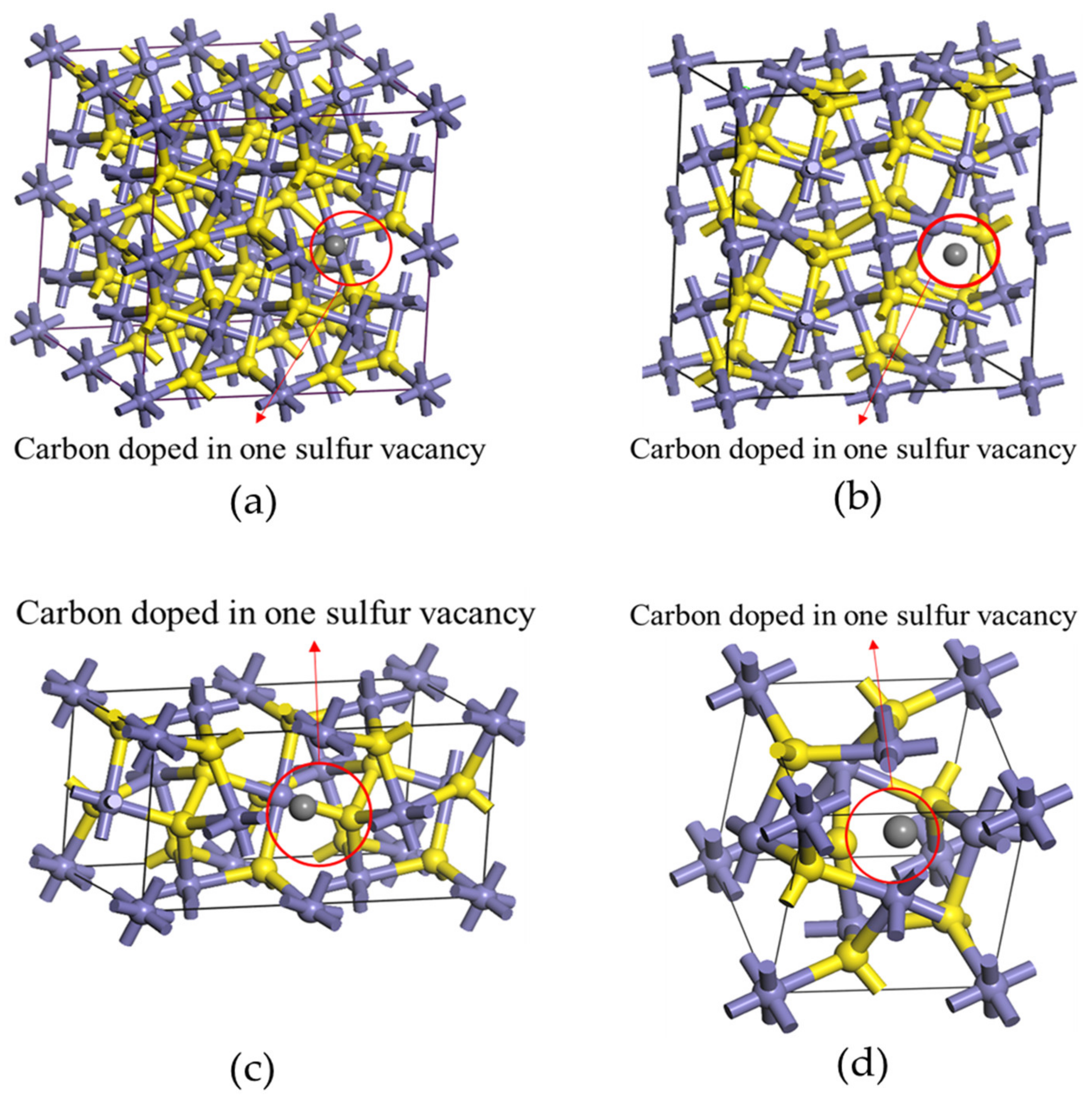
3.1. The Effect of Different Carbon Impurity Defects on the Crystal Structure of Pyrite
3.2. Effect of Carbon Occurrence on Electronic Structure and Optical Properties in Vacancy Defects of Pyrite
3.2.1. Electronic Structure
3.2.2. Effect of Optical Properties
3.3. Effects of Carbon Doping Concentrations on the Electronic Structure and Optical Properties of Coal–Pyrite
3.3.1. Electronic Structure
3.3.2. Effect of Optical Properties
3.4. Effect of the Distribution of Carbon Impurities on the Electronic Structure and Optical Properties of Pyrite at the Same Doping Concentration
3.4.1. Electronic Structure
3.4.2. Effects of Optical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schlegel, A.; Wachter, P. Optical properties, phonons and electronic structure of iron pyrite (FeS2). J. Phys. C Solid State Phys. 1976, 9, 3363–3369. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.M.; Law, M.; Wu, R.Q. First-principles studies of the electronic properties of native and substitutional anionic defects in bulk iron pyrite. Phys. Rev. B 2012, 85, 085203. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.K.; Cai, S.; Jin, Z.G.; Yan, Z.P. Evolutions of composition, microstructure and optical properties of Mn-doped pyrite (FeS2) films prepared by chemical bath deposition. Mater. Res. Bull. 2013, 48, 3601–3606. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, J. Feasibility of band gap engineering of iron pyrite (FeS2) by codoping Os, Ru or Zn together with O. Mater. Chem. Phys. 2020, 244, 122742. [Google Scholar] [CrossRef]
- Voigt, B.; Moore, W.; Manno, M.; Walter, J.; Jeremiason, J.D.; Aydil, E.S.; Leighton, C. Transport evidence for sulfur vacancies as the origin of unintentional n-Type doping in pyrite FeS2. ACS Appl. Mater. Interfaces 2019, 11, 15552–15563. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, J. The electronic, magnetic and optical properties of Co doped marcasite FeS2. J. Phys. Chem. Solids 2018, 121, 285–291. [Google Scholar] [CrossRef]
- Li, Y.Q.; Chen J., H.; Zhao, C. Influence of external electric field on the electronic structure and optical properties of pyrite. RSC Adv. 2017, 7, 56676–56681. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Chan, M.K.Y.; Kang, S.Y.; Ceder, G. Intrinsic stoichiometry and oxygen-induced p-type conductivity of pyrite FeS2. Phys. Rev. B. 2011, 84, 035212. [Google Scholar] [CrossRef]
- Lehner, S.W.; Newman, N.; van Schilfgaarde, M.; Bandyopadhyay, S.; Savage, K.; Buseck, P.R. Defect energy levels and electronic behavior of Ni-, Co-, and As-doped synthetic pyrite (FeS2). J. Appl. Phys. 2012, 111, 2072–2077. [Google Scholar] [CrossRef]
- Ferrer, I.J.; Delasheras, C.; Sanchez, C. Physical properties of Cu-doped FeS2 pyrite thin films. Appl. Surf. Sci. 1993, 70, 588–592. [Google Scholar] [CrossRef]
- Li, Y.Q. First Principle Study of the Influences of Lattice Defects on the Electronic Structures and Flotation Behaviours of Pyrite Crytal. Ph.D. Thesis, Guangxi University, Nanning, China, 2011. [Google Scholar]
- Yu, J.X. Study on the Physical and Chemical Characteristics of Coal-Pyrite and Its Inhibitors. Ph.D. Thesis, University of Mining and Technology, Beijing, China, 2013. [Google Scholar]
- Yu, J.X. Influence of carbon on electronic properties and flotation behavior of pyrite. Min. Metall. Eng. 2013, 33, 63–67. [Google Scholar]
- Qi, X.; Zhang, H.J.; Li, Y.Q.; Chen, J.H. Density functional theory study of the structure and properties of C-doped pyrite. Phys. B Condens. Matter. 2019, 572, 168–174. [Google Scholar] [CrossRef]
- Xi, P.; Ma, R.; Liu, W. Research on the Effect of carbon defects on the hydrophilicity of coal pyrite surface from the insight of quantum chemistry. Molecules 2019, 24, 228–512. [Google Scholar] [CrossRef] [Green Version]
- Xi, P.; Wang, D.H.; Liu, W.L.; Shi, C.S. DFT study into the Influence of carbon material on the hydrophobicity of a coal pyrite surface. Molecules 2019, 24, 3534. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.H. Principles of the Flotation of Sulphide Minerals Bearing Lattice Defects; Central South University Press: Changsha, China, 2012. [Google Scholar]
- Guo, J.; Li, Y.Q.; Chen, J.H. Density functional theory study of influence of impurity on electronic properties and reactivity of pyrite. Trans. Nonferrous Metals Soc. China 2011, 21, 1887–1895. [Google Scholar]
- Li, Y.Q.; Chen, J.H.; Chen, Y. Electronic structures and flotation behavior of pyrite containing vacancy defects. Acta Physico-Chimica Sinica 2010, 26, 1435–1441. [Google Scholar]
- Li, Y.Q. Density functional theory calculation of surface properties of pyrite (100) with implications for flotation. Chinese J. Nonferrous Metals 2011, 21, 919–926. [Google Scholar]
- Liu, Y.; Dang, H.; Li, Y.; Charoensuppanimit, P.; Mohammad, S.A.; Gasem, K.A.M.; Wang, S. Sequestration of carbon dioxide in coal: Energetics and bonding from first-principles calculations. Comput. Mater. Sci. 2017, 133, 145–151. [Google Scholar] [CrossRef]
- Ren, K.; Sun, M.L.; Luo, Y.; Wan, S.; Yu, J.; Tang, W.C. First-principle study of electronic and optical properties of two-dimensional materials-based heterostructures based on transition metal dichalcogenides and boron phosphide. Appl. Surf. Sci. 2019, 476, 70–75. [Google Scholar] [CrossRef]
- Deng, X.Z.; Zhao, Q.Q.; Zhao, Y.Q.; Cai, M.Q. Theoretical study on photoelectric properties of lead-free mixed inorganic perovskite RbGe1−xSnxI3. Curr. Appl. Phys. 2019, 19, 279–284. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467–R5470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulik, H.J.; Cococcioni, M.; Scherlis, D.A.; Marzari, N. Density functional theory in transition-metal chemistry: A self-consistent Hubbard U approach. Phys. Rev. Lett. 2006, 97, 103001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Thomas, M.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.N.; Hu, J.; Law, M.; Wu, R.Q. Effect of surface stoichiometry on the band gap of the pyrite FeS2(100) surface. Phys. Rev. B 2012, 85, 085314. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Sun, R.S.; Chan, M.K.Y.; Kang, S.Y.; Ceder, G. First-principles electronic structure and relative stability of pyrite and marcasite: Implications for photovoltaic performance. Phys. Rev. B 2011, 83, 235311. [Google Scholar] [CrossRef] [Green Version]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 4, 7892–7895. [Google Scholar] [CrossRef]
- Fiechter, S.; Birkholz, M.; Hartmann, A.; Dulski, P.; Giersig, M.; Tributsch, H.; Tilley, R.J.D. The microstructure and stoichiometry of pyrite FeS2−x. J. Mater. Res. 1992, 7, 1829–1838. [Google Scholar] [CrossRef]
- Andersson, K.J.; Ogasawara, H.; Nordlund, D.; Brown, G.E.J.; Nilsson, A. Preparation, structure, and orientation of pyrite FeS2{100} surfaces: Anisotropy, sulfur monomers, dimer vacancies, and a possible FeS surface phase. J. Phys. Chem. C 2014, 118, 21896–21903. [Google Scholar] [CrossRef]
- Andersson, K.; Nyberg, M.; Ogasawara, H.; Nordlund, D.; Kendelewicz, T.; Doyle, C.S.; Brown, G.E., Jr.; Pettersson, L.G.M.; Nilsson, A. Experimental and theoretical characterization of the structure of defects at the pyrite FeS2(100) surface. Phys. Rev. B 2004, 70, 195404. [Google Scholar] [CrossRef]
- Luck, J.; Hartmann, A.; Fiechter, S. Stoichiometry and impurity concentration in synthetically grown iron pyrite crystals and their constituents. Fresenius’ Z. Anal. Chem. 1989, 334, 441–446. [Google Scholar] [CrossRef]
- Choi, S.G.; Hu, J.; Abdallah, L.S.; Limpinsel, M.; Zhang, Y.N.; Zollner, S.; Wu, R.Q.; Law, M. Pseudodielectric function and critical-point energies of iron pyrite. Phys. Rev. B 2012, 86, 115207. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zhang, Y.N.; Law, M.; Wu, R.Q. Increasing the band gap of iron pyrite by alloying with oxygen. J. Am. Chem. Soc. 2012, 134, 13216–13219. [Google Scholar] [CrossRef] [PubMed]












| Defect | |
|---|---|
| Fe3S8C-1 | 3.83 |
| Fe4S7C-1 | 0.24 |
| Fe3S8C-2 | 3.32 |
| Fe4S7C-2 | 0.25 |
| Fe3S8 | 869.36 |
| Fe4S7 | 282.19 |
| Defect | Cell Parameters | ||||||
|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | V (Å3) | |
| Fe4S8 | 5.363115 | 5.363115 | 5.363115 | 90 | 90 | 90 | 154.26 |
| Fe3S8C-1 | 5.423741 | 5.423622 | 5.42234 | 90.21932 | 89.7674 | 89.78359 | 159.50 |
| Fe4S7C-1 | 5.311265 | 5.310937 | 5.318768 | 89.73857 | 89.21195 | 90.01553 | 150.02 |
| Fe3S8 | 5.45302 | 5.453499 | 5.453304 | 89.53321 | 89.55751 | 90.5055 | 162.15 |
| Fe4S7 | 5.451625 | 5.45459 | 5.451475 | 91.85461 | 91.85182 | 91.87544 | 161.85 |
| Fe3S8C-2 | 5.347074 | 5.560031 | 5.462908 | 84.79421 | 90.23497 | 90.06698 | 161.74 |
| Fe4S7C-2 | 5.319118 | 5.311358 | 5.312286 | 90.02449 | 89.75348 | 89.19101 | 150.06 |
| Species | Bond | Length (Å) |
|---|---|---|
| Fe3S8C-1 | C–S | 2.361 |
| 2.361 | ||
| 2.359 | ||
| C–Fe | 3.827 | |
| Fe3S8C-2 | C–S | 1.777 |
| 1.778 | ||
| 1.779 | ||
| C–Fe | 3.532 | |
| Fe4S7C-1 | C–S | 1.831 |
| C–Fe | 2.166 | |
| 2.059 | ||
| Fe4S7C-2 | C–S | 2.971 |
| C–Fe | 1.943 | |
| 1.958 |
| Defect | Band Gap (eV) |
|---|---|
| Fe4S8 | 1.156 |
| Fe3S8C-1 | 0.119 |
| Fe4S7C-1 | 0.068 |
| Fe3S8C-2 | 0.018 |
| Fe4S7C-2 | 0.175 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Cheng, C.; Ke, B. The Effect of Carbon Defects in the Coal–Pyrite Vacancy on the Electronic Structure and Optical Properties: A DFT + U Study. Minerals 2020, 10, 815. https://doi.org/10.3390/min10090815
Cheng W, Cheng C, Ke B. The Effect of Carbon Defects in the Coal–Pyrite Vacancy on the Electronic Structure and Optical Properties: A DFT + U Study. Minerals. 2020; 10(9):815. https://doi.org/10.3390/min10090815
Chicago/Turabian StyleCheng, Wei, Chen Cheng, and Baolin Ke. 2020. "The Effect of Carbon Defects in the Coal–Pyrite Vacancy on the Electronic Structure and Optical Properties: A DFT + U Study" Minerals 10, no. 9: 815. https://doi.org/10.3390/min10090815
APA StyleCheng, W., Cheng, C., & Ke, B. (2020). The Effect of Carbon Defects in the Coal–Pyrite Vacancy on the Electronic Structure and Optical Properties: A DFT + U Study. Minerals, 10(9), 815. https://doi.org/10.3390/min10090815






