Advances on the Fragmentation-Energy Fan Concept and the Swebrec Function in Modeling Drop Weight Testing
Abstract
:1. Introduction
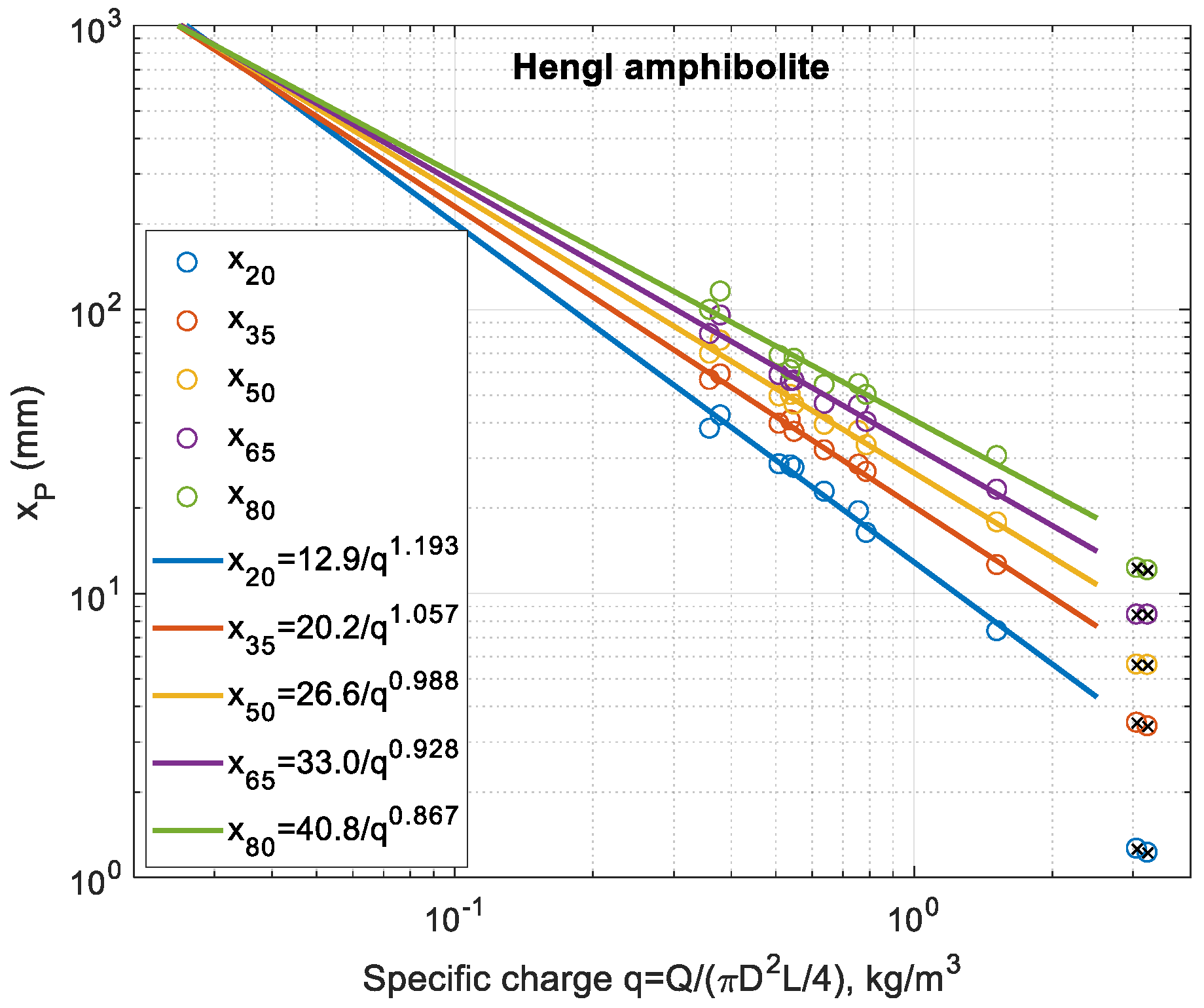
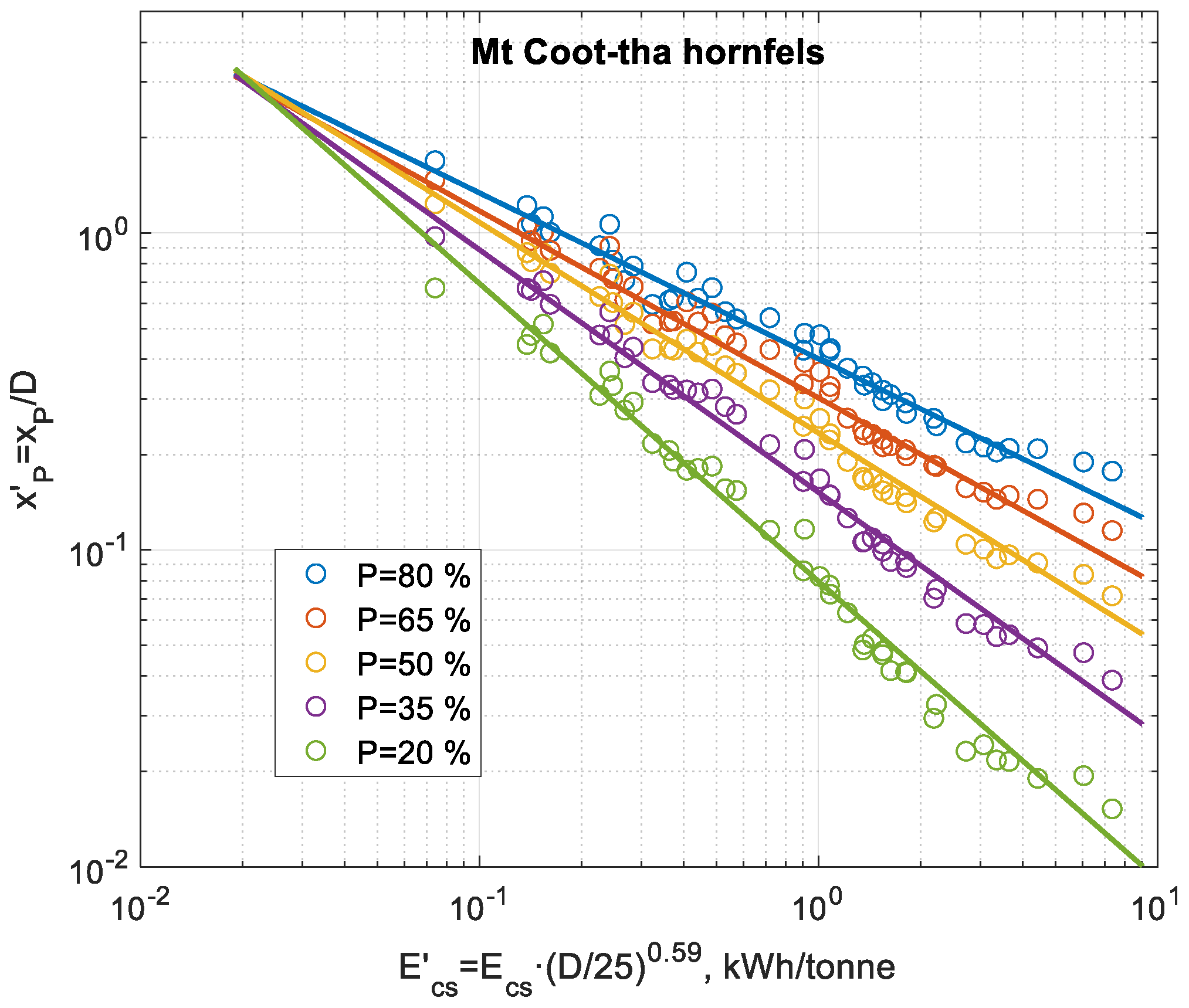
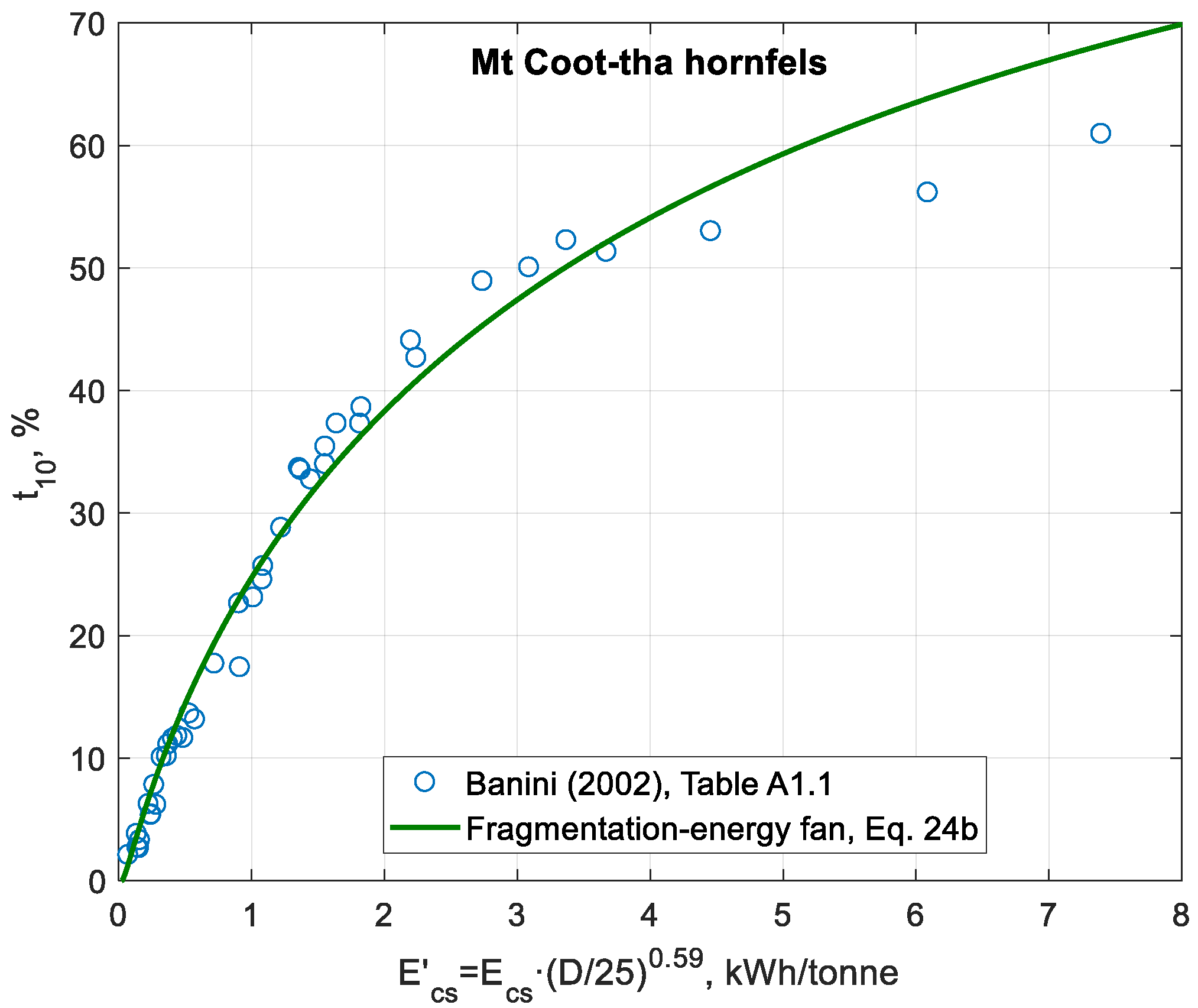
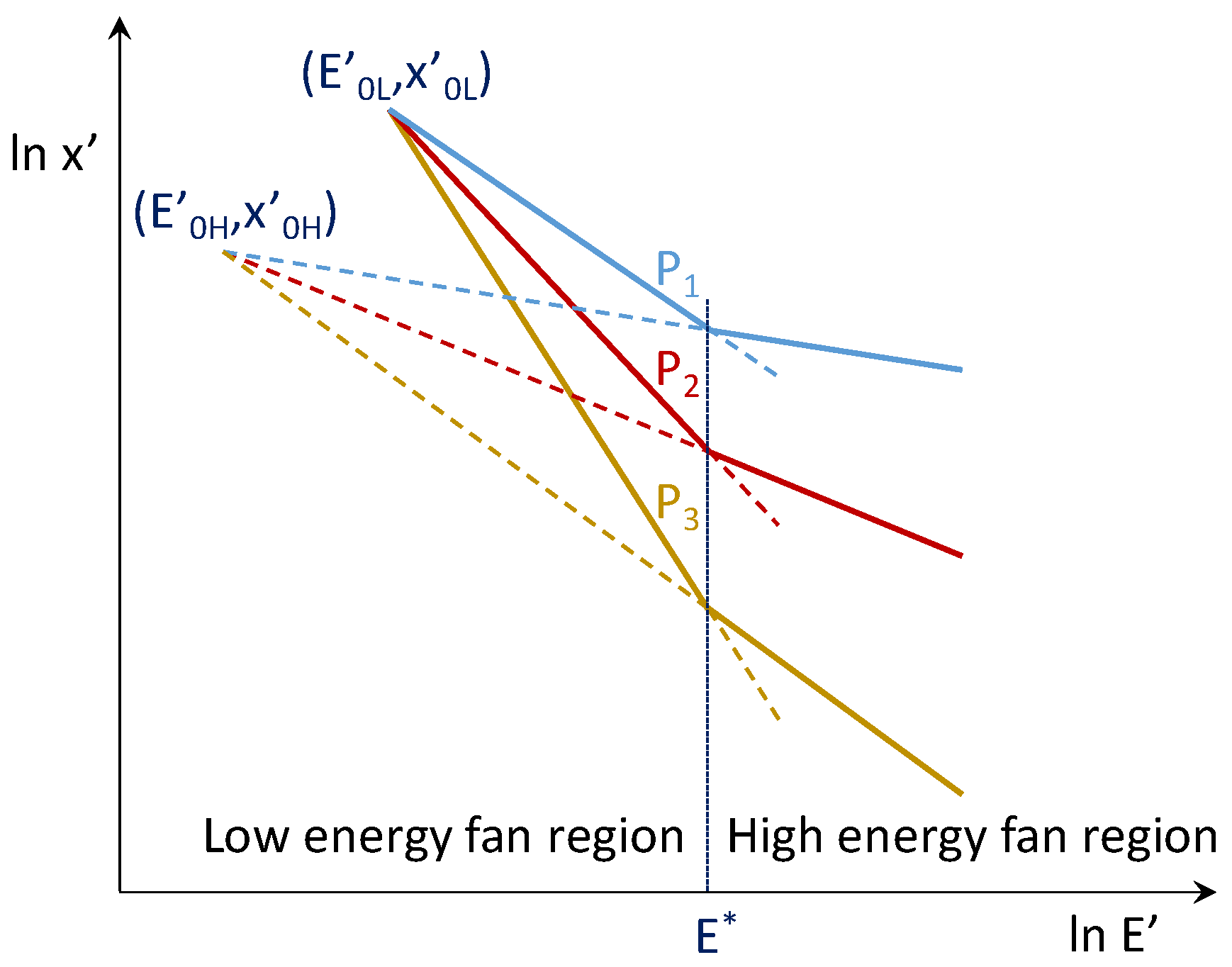

- Banini [19] needs the interpolation splines data to obtain plus 14–18 parameters to determine in his first analysis. When he introduces the size scaling he needs, instead, 3 parameters plus the splines data. Shi and Kojovic [22] need the splines data plus 4 parameters; , , and . With this they obtain a higher fidelity.
- The basic, linear fan method needs 6 parameters to describe ; namely the size scaling exponent , the position of the focal point , the two slope values and plus the Swebrec exponent . Calculating the last two parameters via the slope values and is better. These parameters follow from the fan fitting though, but the fidelity is not as good as that of the JK new BIE [22].
- The double fan method needs the 6 parameters for the primary fan plus the focal point of the secondary fan and the energy value of the kink point, in all 9 parameters but no splines data because and derive from the same function. The fidelity is now almost good as that of the JK new BIE.
- The size scaling of the impact energy in the fan method is more transparent than that used by the others since it lets the scaled energy retain the same units as the impact energy , [kWh/tonne].
- The fan method uses the -values directly or values interpolated from the sieving curves. This loses less information than converting them to -values based on a Rosin-Rammler interpolation.
- The fan method contains information not only on but also on for arbitrary values of . This makes the use of the interpolated representation unnecessary.
| Author | Material Type |
|---|---|
| Banini [19] | hornfels, Cu-ores (2), Pb-Zn ores (3), Au-ores (2) |
| Avsar [23] | cement clinker and trass |
| Genç et al. [24] | cement clinker (2), clay, colemanite, copper ore, gypsum, limestone, quartz (2) and trass |
| Genç [25] | salt ore |
| Yu [26] | Au-Cu porphyry ore |
| Faramarzi [27] | ores 1–4: 1—hard, fresh basalt, 2, 3—hard and 4—soft |
2. Data and Analysis
2.1. Available Sieving Data
2.2. Analysis of Sieving Data: Formulation of Breakage Index Equations
2.2.1. The Earlier Standard JK DWT Analysis
2.2.2. The JK Size-Dependent Breakage Index Equation or the JK New BIE
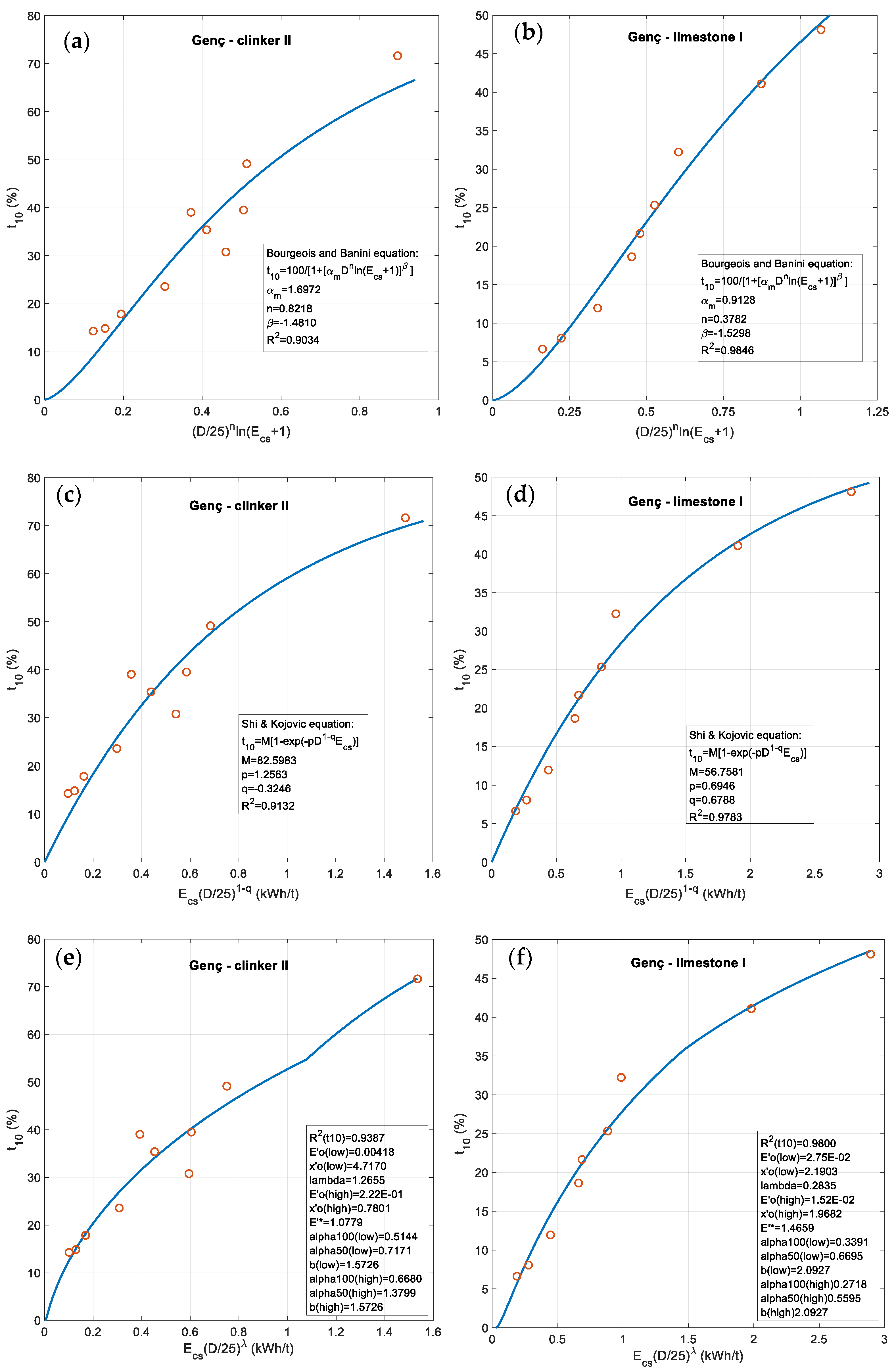
2.2.3. The Banini-Bourgeois Size-Dependent Breakage Index Equation
2.2.4. The 4D-m and 4D-mq Model Equations
- The Greek - and -parameters are not pure material parameters, they were calibrated for specific ranges of particle sizes and impact energies for the Cadia ore. Even for that material, what happens when the top particle size and top impact energy change is not known, nor what happens when the material changes.
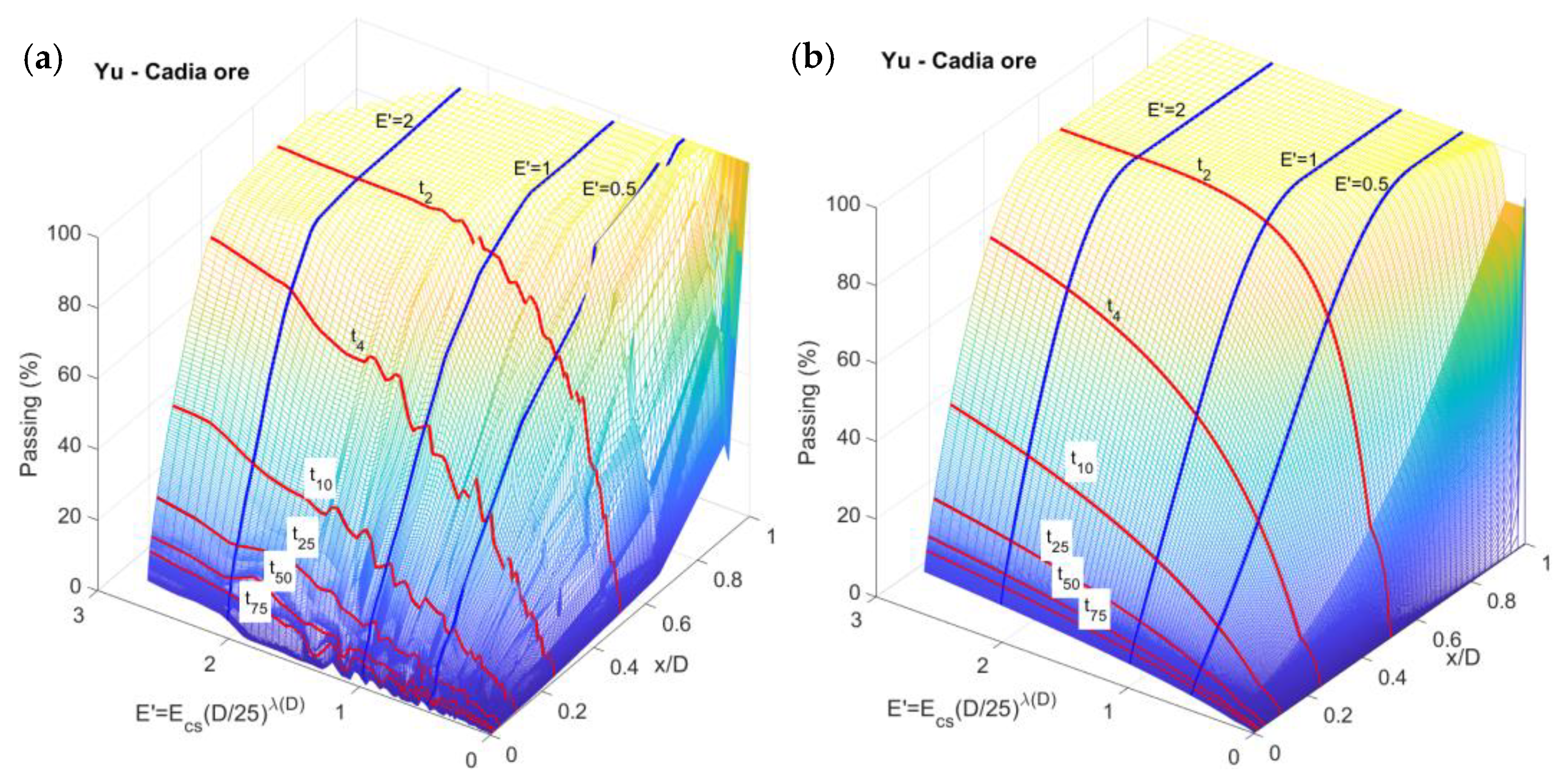
- The procedure used by Yu to determine the - and -parameters is not described in sufficient detail; a “cut-and-trial” fitting method is mentioned, but only vaguely described.
- Yu ([26], p 133) appears to use the geometric mean to characterize particle and progeny size associated with the progeny mass passing. The upper bin limits seem more appropriate.
- Before Equation (14), Yu et al. ([28]) seem to mean that they, apart from 45 cases of bottom sieves have mass passing data for all 20 sieving bin sizes for all 59 progeny CDF, i.e., 1180 − 45 = 1135 data points. The data tables in his thesis, pp 202–205 [26] have only 745 entries including the points . To add dummy points to the curve fitting could have deleterious effects.
2.2.5. The Fragmentation Energy Fan Equations
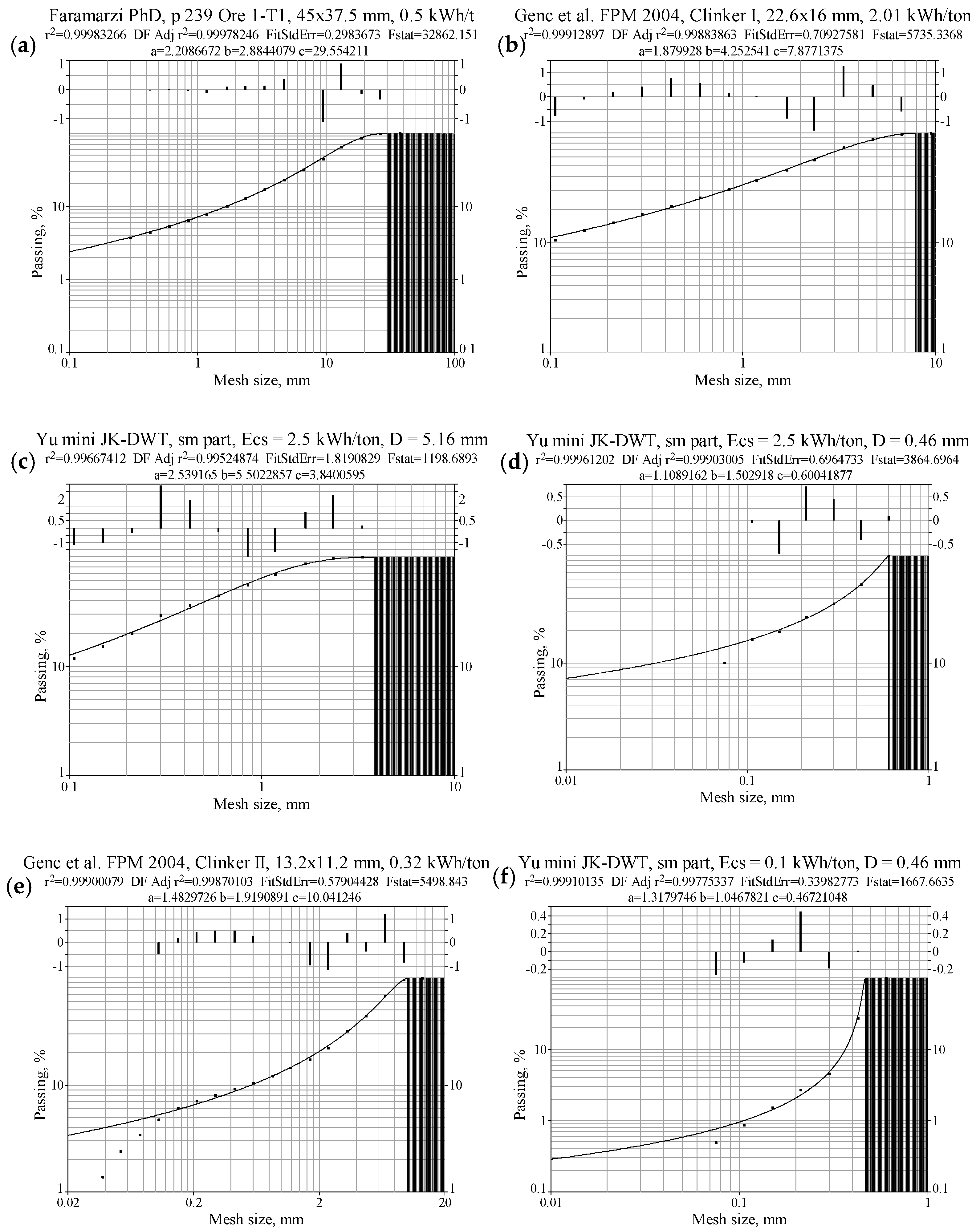
2.3. Size Distributions of Sieving Data: Swebrec Function Fitting
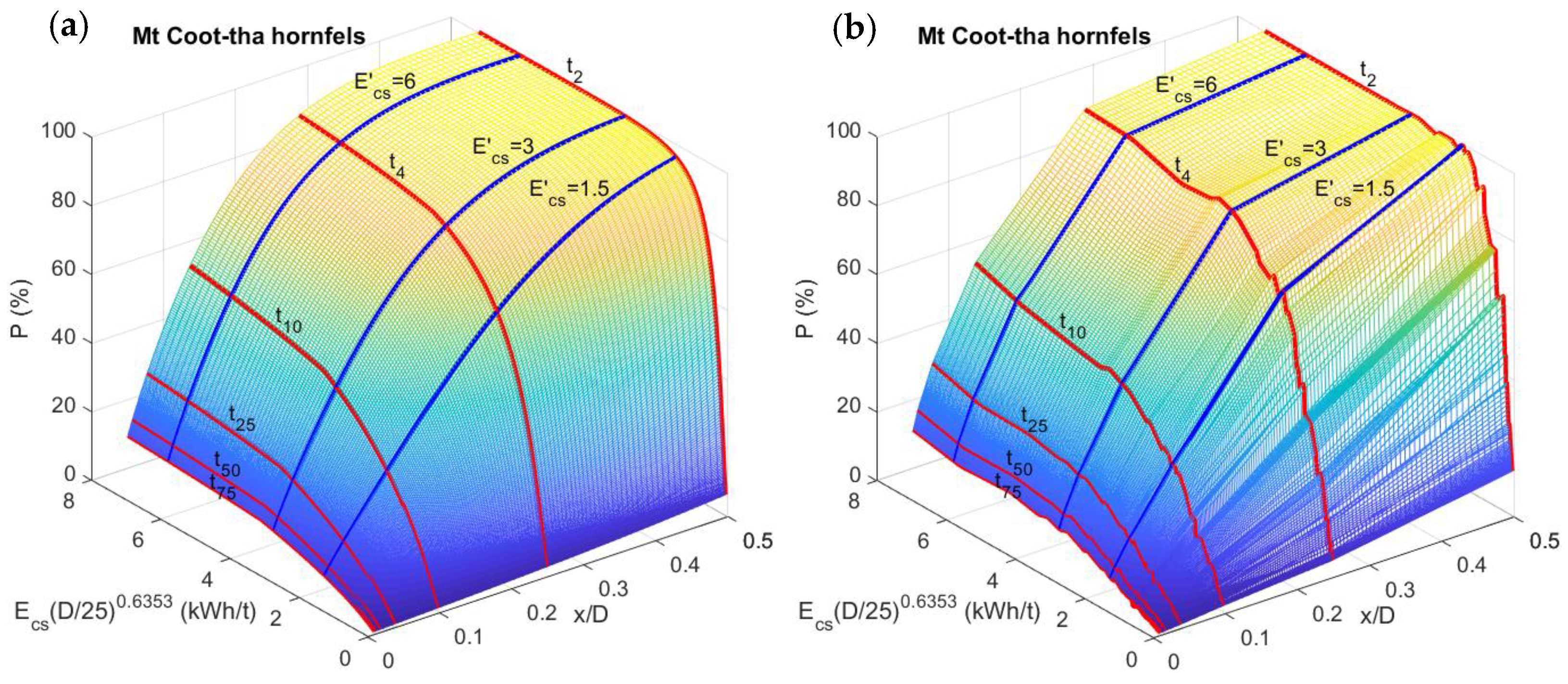
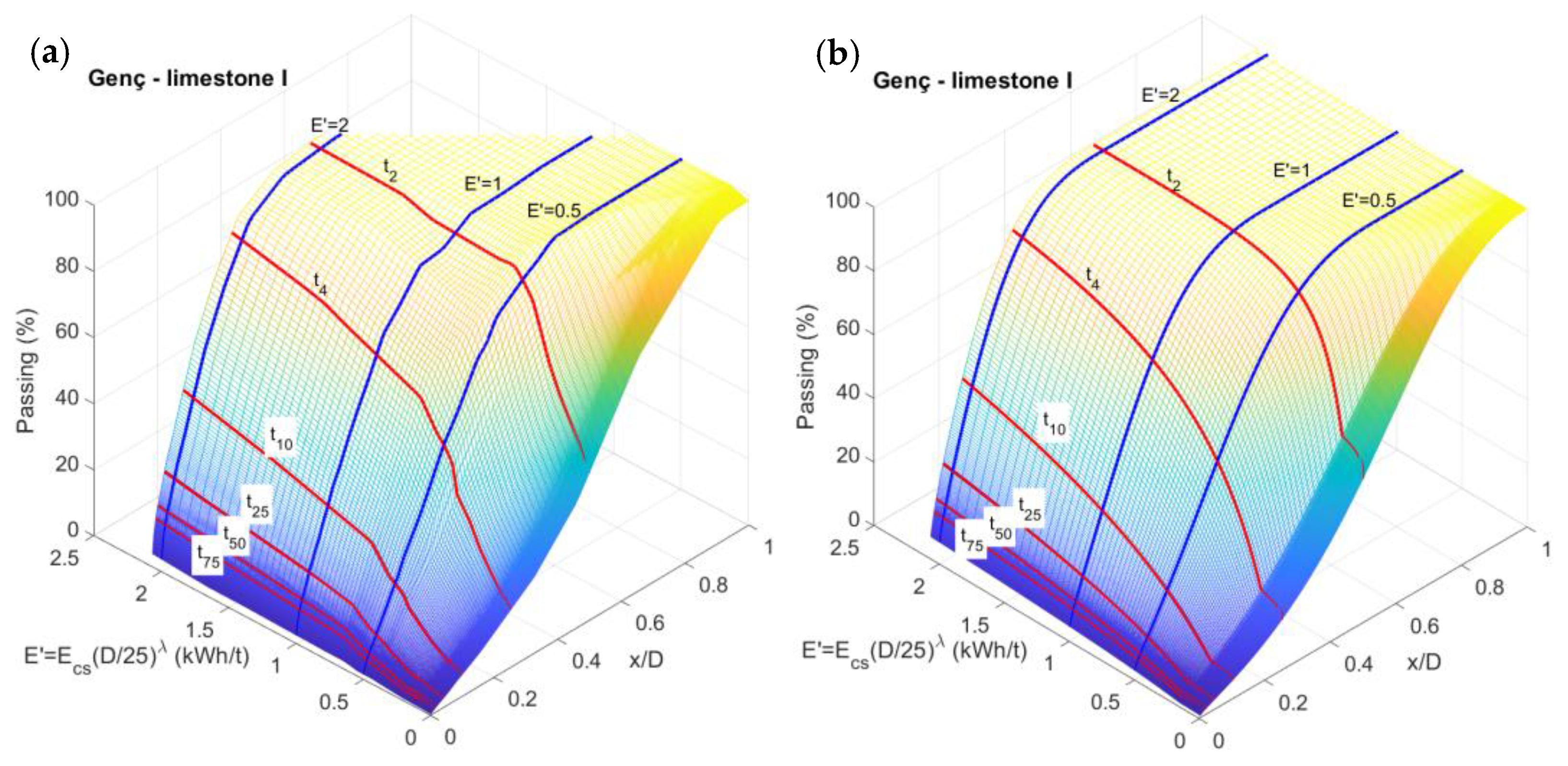
3. Fragmentation-Energy Fans and Breakage Index Equations for New Materials
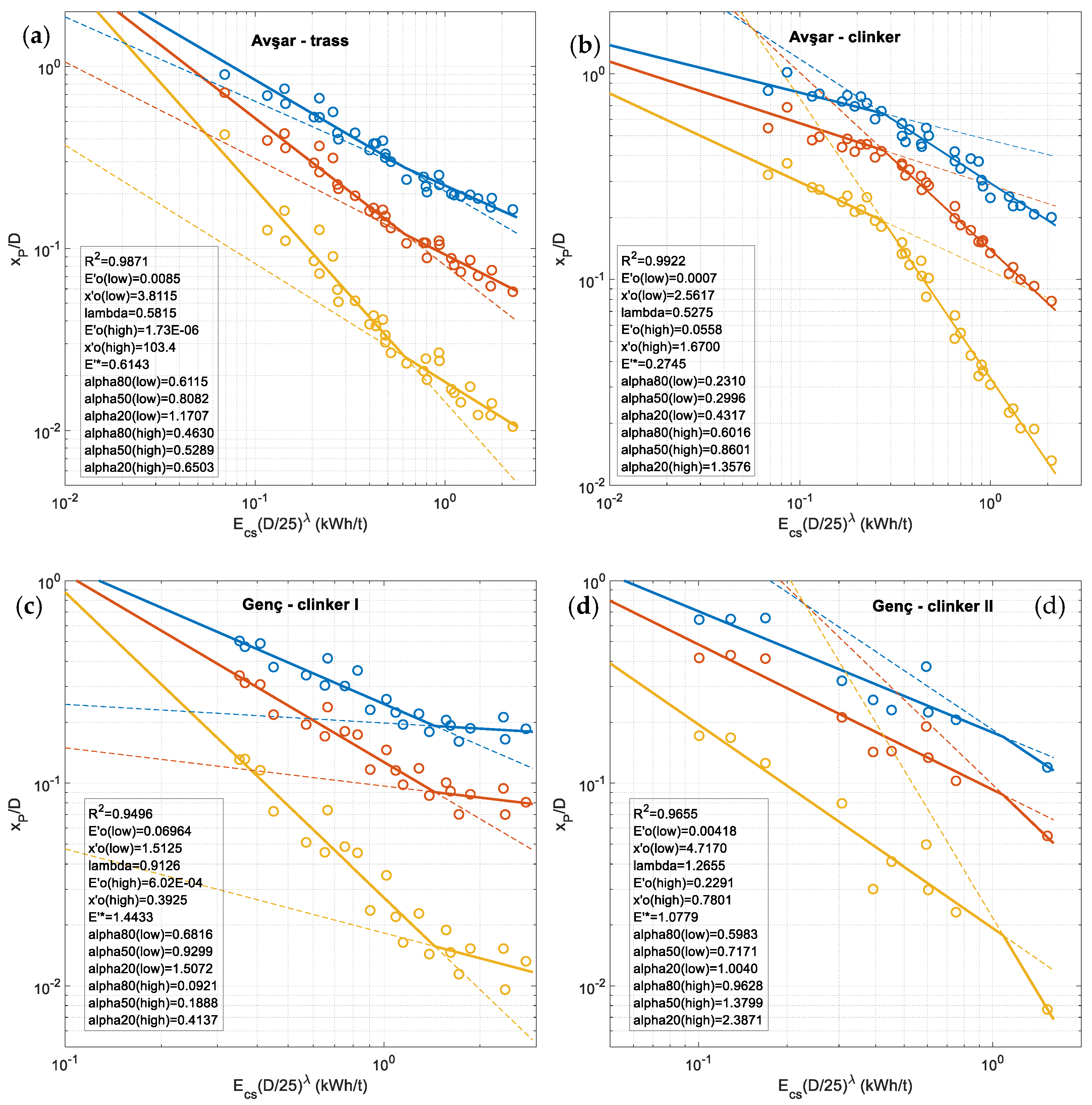
3.1. Basic Double Fragmentation-Energy Fans for New Rocks
3.2. Basic Breakage Index Equations
- The JK new BIE is the simplest in the sense that the curve is always convex (up) in the plotting space but it levels out below 100% and is questionable.
- The Banini BIE levels out at 100%. It is convex for the most part but turns concave near the origin, a fact that is probably due to the logarithmic abscissa.
- The double fan BIE also levels out at 100% and the curve has a kink, which e.g., could be caused by a change in breakage mode but that remains to be proven.
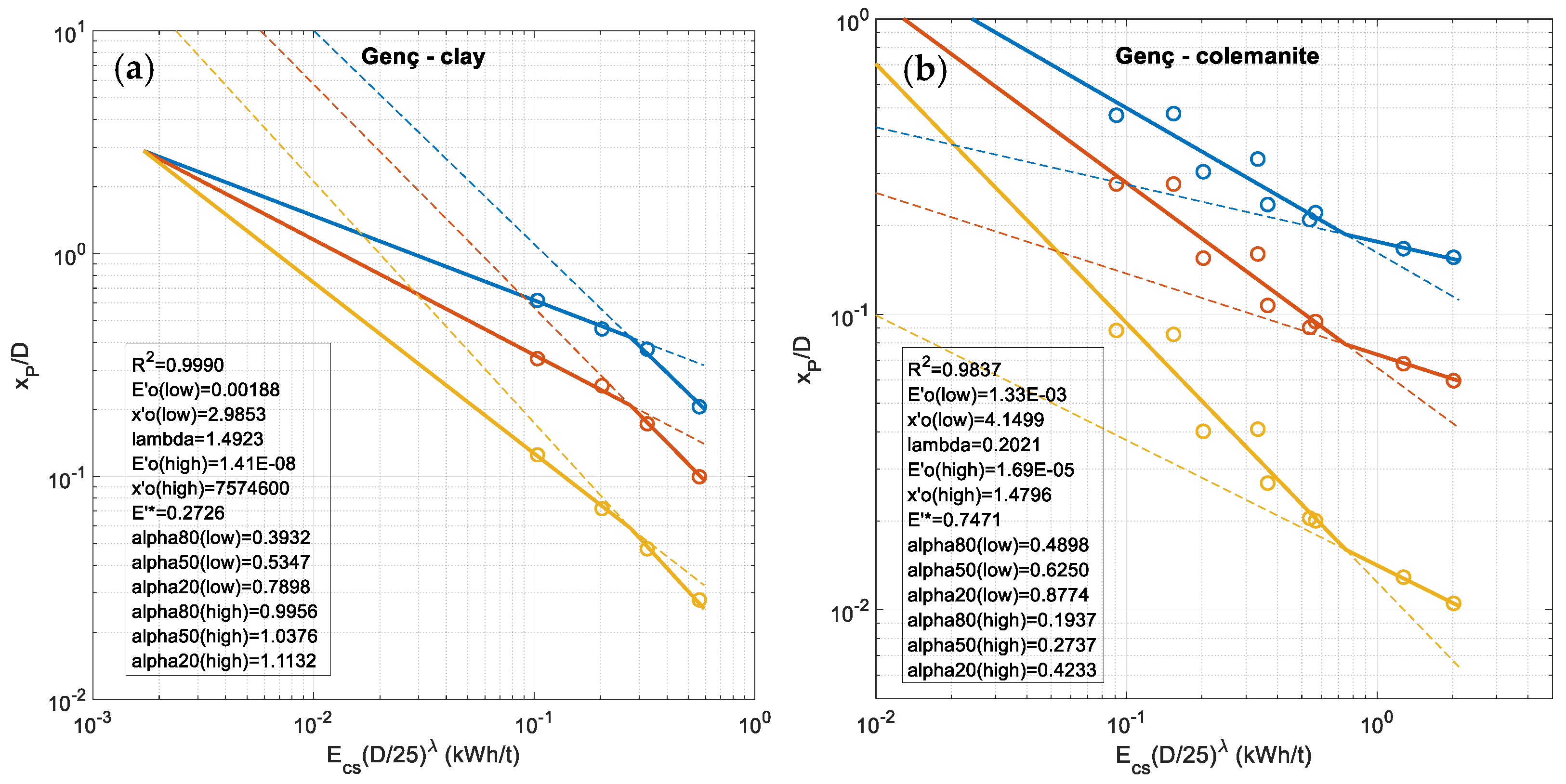
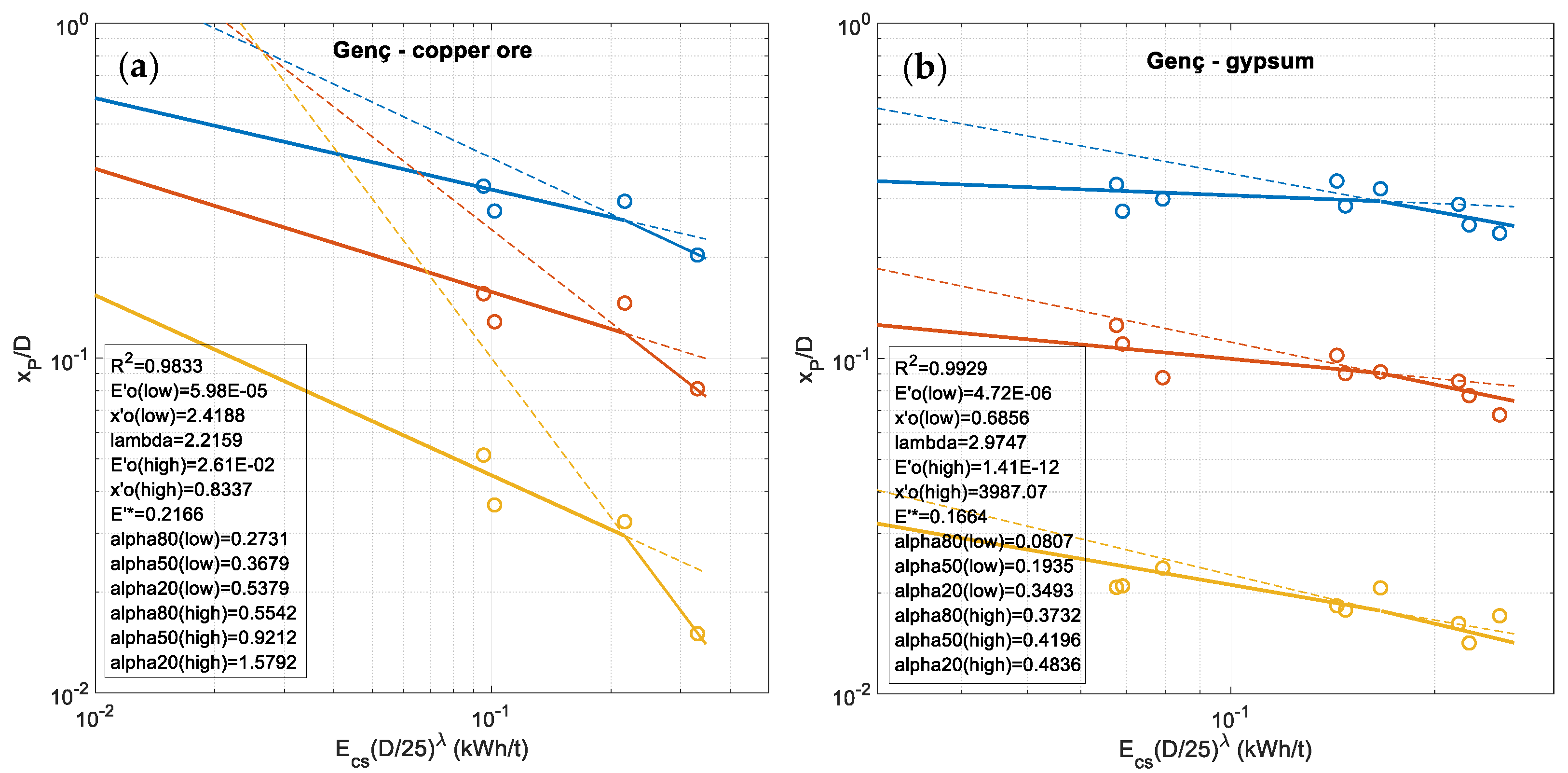
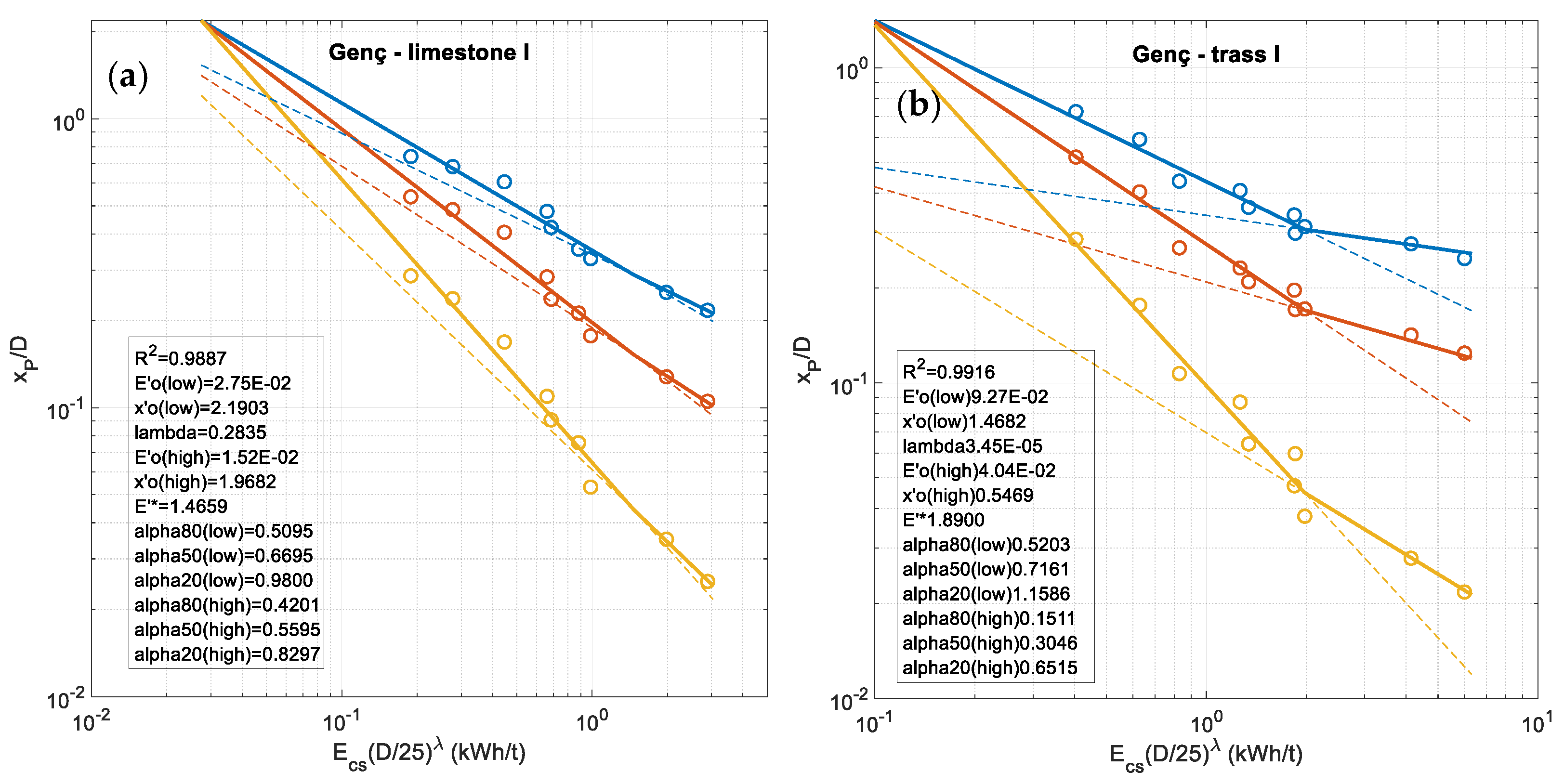
3.3. Improved Double Fragmentation-Energy Fan BIE
- I-1.
- 3 fan lines ( = 20%, 50%, 80%), constant plus an -value, 10 parameters.
- I-2.
- 3 fan lines ( = 20%, 50%, 80%) plus varying but no , 12 parameters.
- I-3.
- 5 fan lines ( = 20%, 35%, 50%, 65%, 80%) plus varying but no , 12 parameters.
- I-4.
- 5 fan lines with -values inside the range of measured -values plus varying but no , 12 parameters.
- I-5.
- Direct fit of whole mesh size-passing-sample size-energy space with the equivalents to Equations (13a,b):
4. Discussion
5. Conclusions
- For each curve calculate the decile fragment sizes , and and divide by particle size .
- Plot, e.g., the normalized fragment size vs. impact energy in log-log scale for some particle sizes, the data should fall on roughly parallel lines.
- Trial the size scaling multiplier for that makes these lines collapse best on one line, e.g., in Excel.
- Choose a suitable reference size and plot log() vs. log() where .
- Add decile fragment sizes and to the plot; each set should fall on a separate line with different slopes.
- Draw three “representative” lines for these data that have a common focal point, i.e., the fan.
- Read off the line slope values , and plus the focal point coordinates and .
- Calculate and the undulation exponent with Equation (12), and insert the parameter values in Equations (13a) or (16a).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


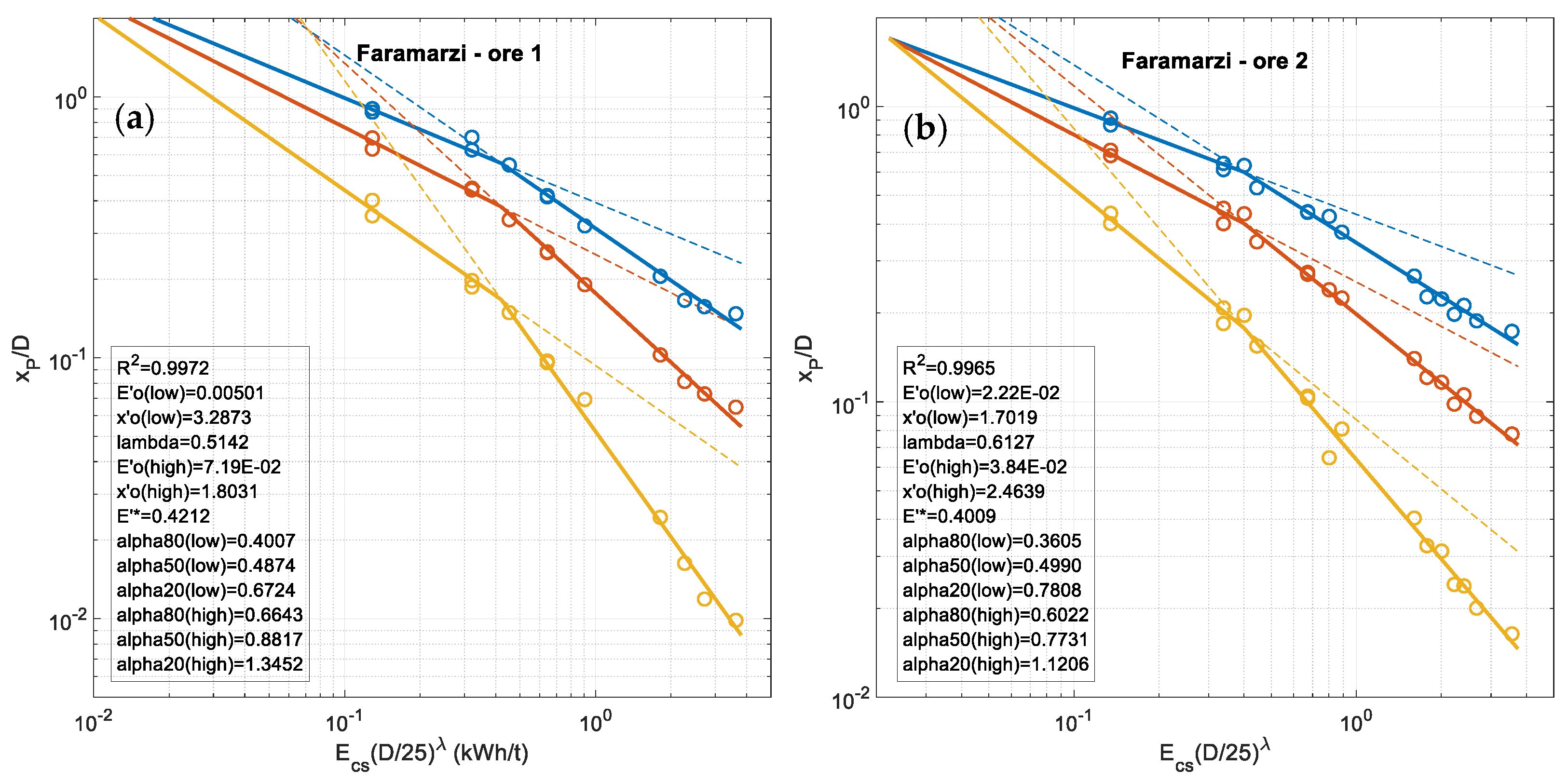

Appendix B

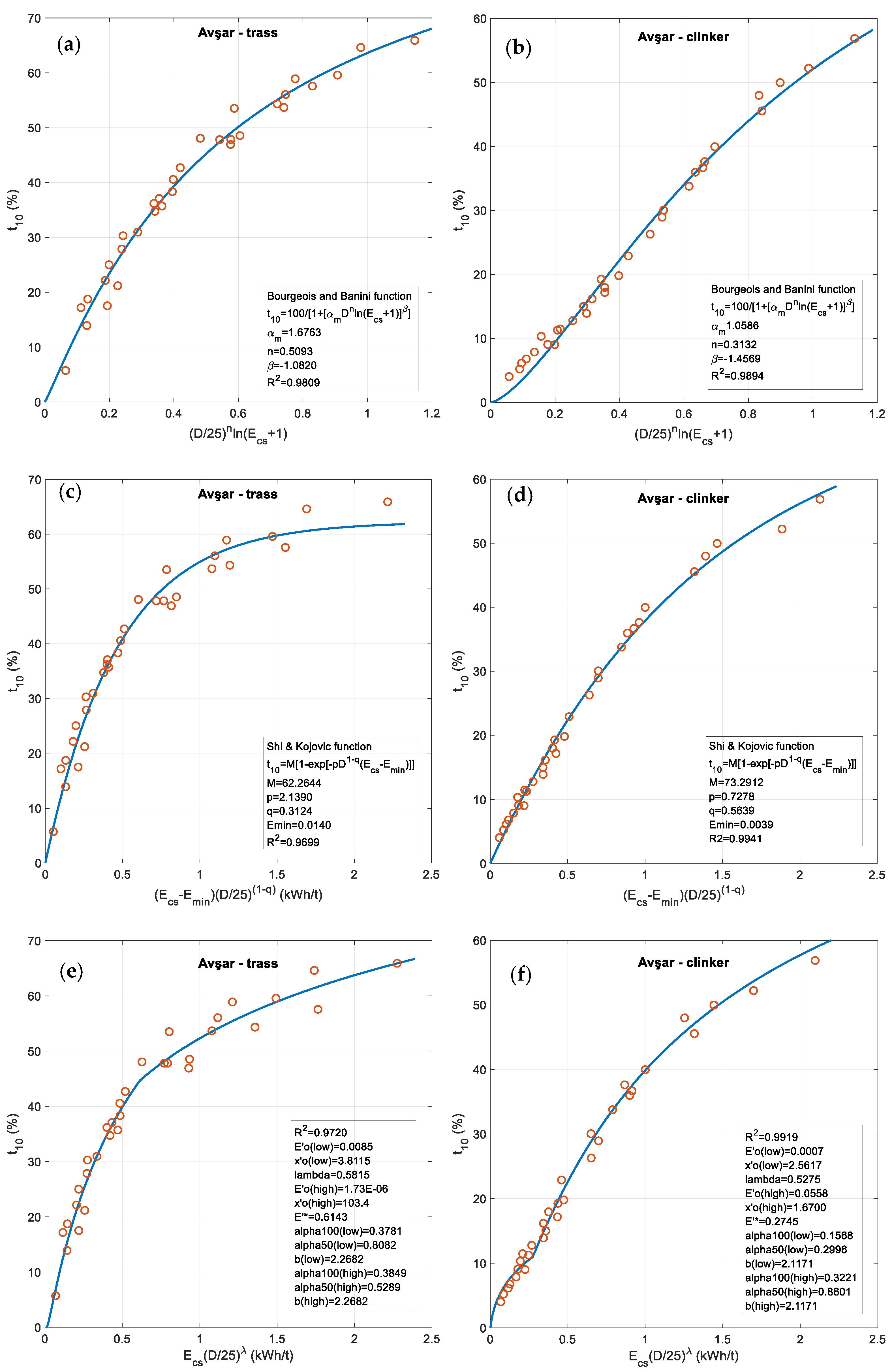
Appendix C
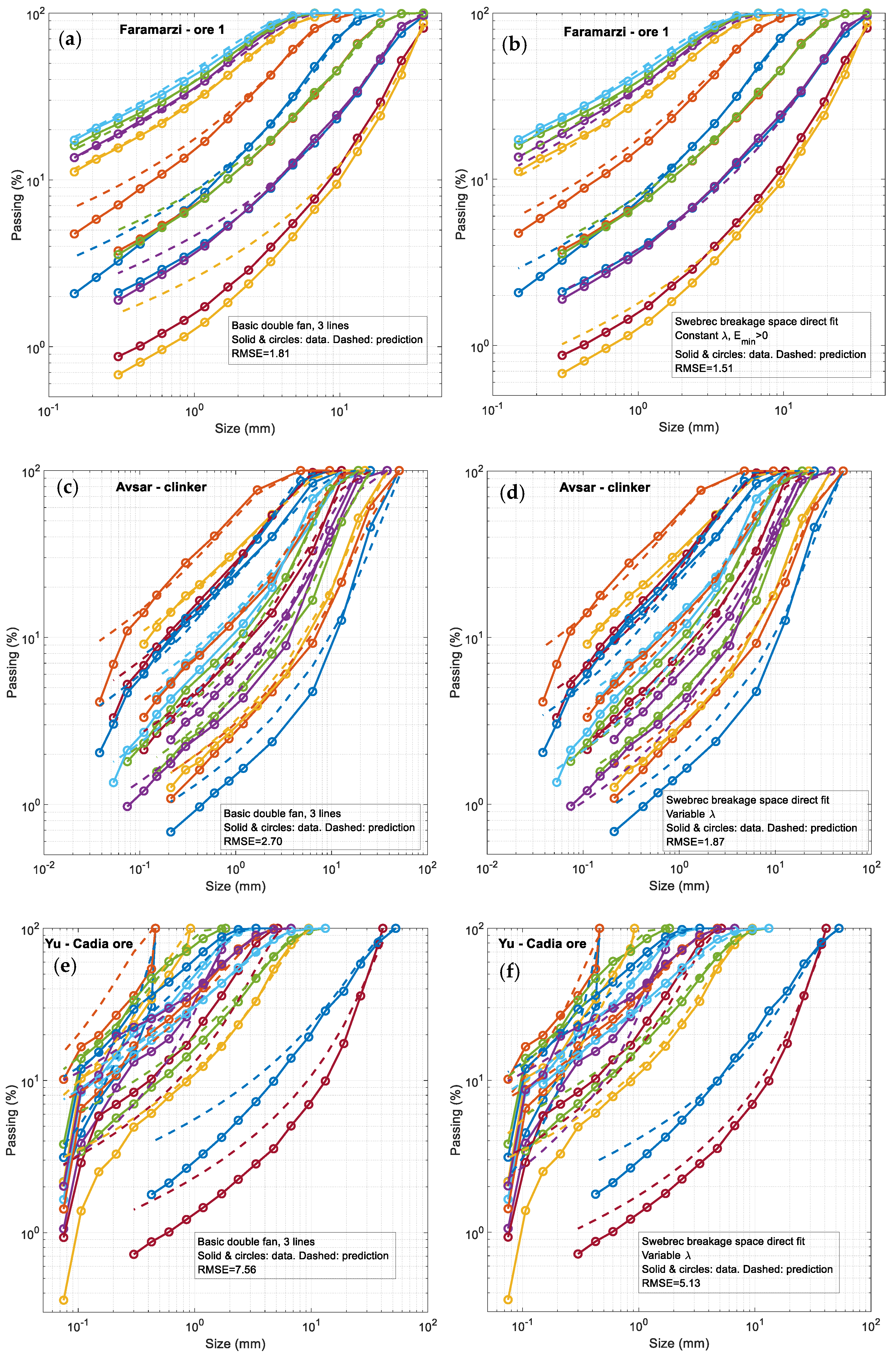
Appendix D
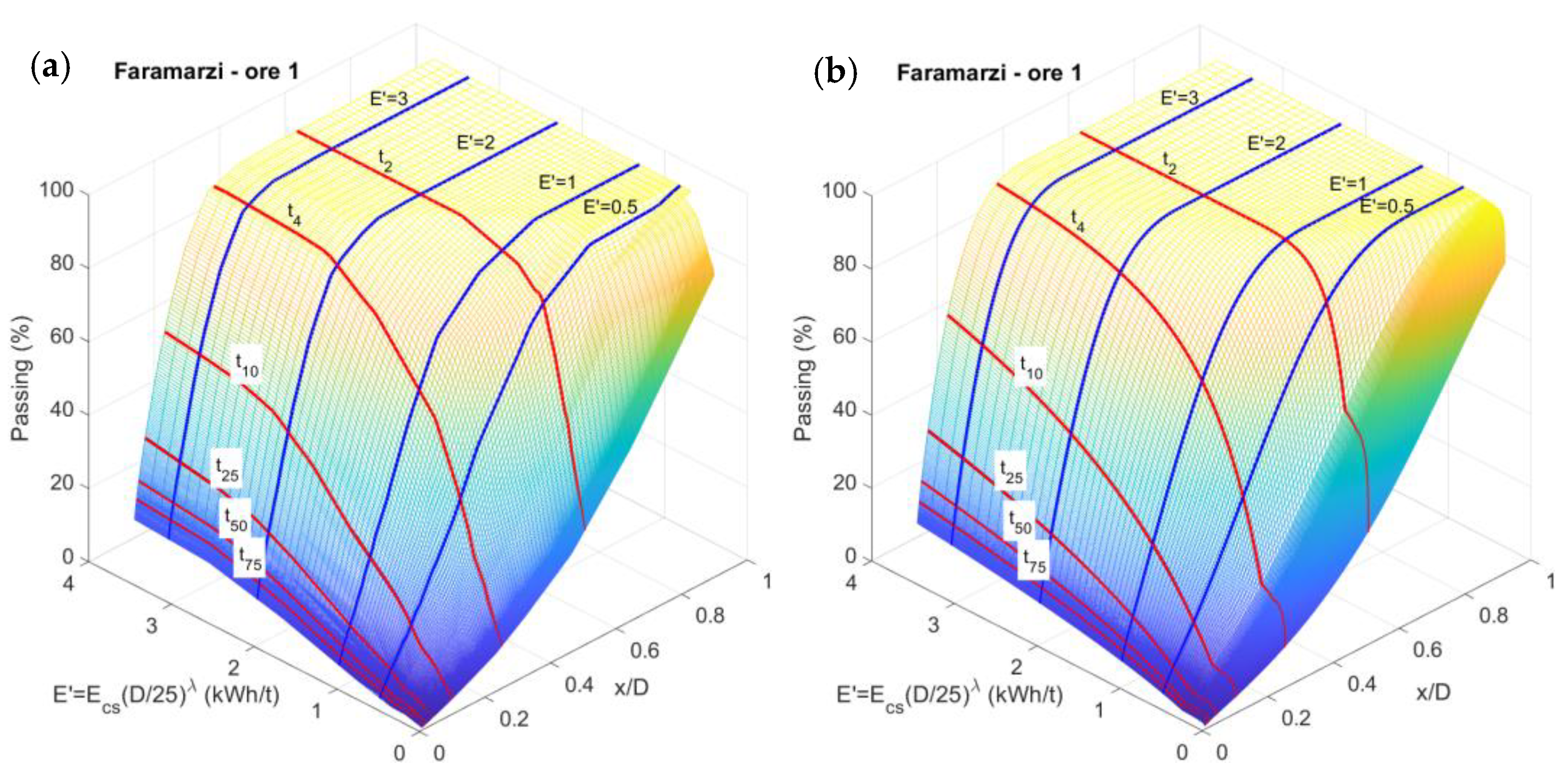

References
- Rosin, P.; Rammler, E. The laws governing fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Cunningham, C.V.B. The Kuz-Ram model for prediction of fragmentation from blasting. In Proceedings of the 1st International Symposium on Rock Fragmentation by Blasting, Luleå University of Technology, Luleå, Sweden, 22–26 August 1983; pp. 439–453. [Google Scholar]
- Cunningham, C.V.B. Fragmentation estimations and the Kuz-Ram model—Four years on. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23–26 August 1987; pp. 475–487. [Google Scholar]
- Cunningham, C.V.B. The Kuz-Ram fragmentation model—20 years on. In Proceedings of the 3rd European Federation of Explosives Engineers (EFEE), World Conference on Explosives and Blasting, Brighton, UK, 13–16 September 2005; pp. 201–210. [Google Scholar]
- Ouchterlony, F.; Sanchidrián, J.A. A review of development of better prediction equations for blast fragmentation. J. Rock Mech. Geotech. Eng. 2019, 11, 1094–1109. [Google Scholar] [CrossRef]
- Ouchterlony, F. ‘Bend it Like Beckham’ or a Wide-Range Yet Simple Fragment Size Distribution for Blasted and Crushed Rock; Technical Report 78; EU project GRD-2000-25224 ‘Less Fines’; European Commission: Brussels, Belgium, 2003. [Google Scholar]
- Ouchterlony, F. The Swebrec© function, linking fragmentation by blasting and crushing. Min. Technol. 2005, 114, A29–A44. [Google Scholar] [CrossRef] [Green Version]
- Sanchidrián, J.A.; Ouchterlony, F.; Moser, P.; Segarra, P.; López, L.M. Performance of some distributions to describe rock fragmentation data. Int. J. Rock Mech. Min. Sci. 2012, 53, 18–31. [Google Scholar] [CrossRef]
- Sanchidrián, J.A.; Segarra, P.; López, L.M.; Ouchterlony, F.; Moser, P. On the performance of truncated distributions to describe rock fragmentation. In Measurement and Analysis of Blast Fragmentation; Taylor and Francis: London, UK, 2013; pp. 87–96. [Google Scholar]
- Sanchidrián, J.A.; Ouchterlony, F.; Segarra, P.; Moser, P. Size distribution functions for rock fragments. Int. J. Rock Mech. Min. Sci. 2014, 71, 381–394. [Google Scholar] [CrossRef]
- Sanchidrián, J.A. Ranges of validity of some distribution functions for blast-fragmented rock. In Fragblast 11, Proceedings of the 11th International Symposium Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015; AusIMM: Carlton, VIC, Australia, 2015; pp. 741–748. [Google Scholar]
- Sanchidrián, J.A.; Ouchterlony, F. A distribution-free description of fragmentation by blasting based on dimensional analysis. Rock Mech. Rock Eng. 2017, 50, 781–806. [Google Scholar] [CrossRef] [Green Version]
- Ouchterlony, F.; Sanchidrián, J.A.; Moser, P. Percentile fragment size predictions for blasted rock and the fragmentation–energy fan. Rock Mech. Rock Eng. 2017, 50, 751–779. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, S.S. Development of a Laboratory Single Particle Breakage Technique and Its Application to Ball Mill Scale-Up. Ph.D. Thesis, Julius Kruttschnitt Mineral Research Centre, University of Queensland, Indooroopilly, QLD, Australia, 1985. [Google Scholar]
- Narayanan, S.S.; Whiten, W.J. Breakage characteristics of ores for ball mill modelling. Proc. Australas. Inst. Min. Metall. 1983, 286, 31–39. [Google Scholar]
- Leung, K.; Morrison, R.D.; Whiten, W.J. An energy based ore specific model of autogenous and semi-autogenous grinding. In Copper 87; Chilean Institute of Mining Engineers: Viña del Mar, Chile, 1987. [Google Scholar]
- Andersen, J.S. Development of a Cone Crusher Model. Master’s Thesis, University of Queensland (JKMRC), Indooroopilly, QLD, Australia, 1988. [Google Scholar]
- Napier-Munn, T.J.; Morrell, S.; Morrison, R.D.; Kojovic, T. Mineral Comminution Circuits: Their Operation and Optimization; Julius Kruttschnitt Mineral Research Centre: Indoroopilly, QLD, Australia, 1996. [Google Scholar]
- Banini, G.A. An Integrated Description of Rock Breakage in Comminution Machines. Ph.D. Thesis, Julius Kruttschnitt Mineral Research Centre, University of Queensland, Indoroopilly, QLD, Australia, 2002. [Google Scholar]
- Shi, F. A review of the applications of the JK size-dependent breakage model Part 1: Ore and coal breakage characterization. Int. J. Miner. Process. 2016, 155, 118–129. [Google Scholar] [CrossRef] [Green Version]
- Ouchterlony, F.; Sanchidrián, J.A. The fragmentation-energy fan concept and the Swebrec function in modeling drop weight testing. Rock Mech. Rock Eng. 2018, 51, 3129–3156. [Google Scholar] [CrossRef]
- Shi, F.; Kojovic, T. Validation of a model for impact breakage incorporating particle size effect. Int. J. Miner. Process. 2007, 82, 156–163. [Google Scholar] [CrossRef]
- Avsar, C. Breakage Characteristics of Cement Components. Ph.D. Thesis, Department of Mining Engineering, Middle East Tech University, Ankara, Turkey, 2003. [Google Scholar]
- Genç, Ö.; Ergün, L.; Benzer, H. Single particle impact breakage characterization of materials by drop weight testing. Physicochem Prob. Min. Proc. 2004, 38, 241–255. [Google Scholar]
- Genç, Ö.; Muğla Sıtkı Koçman University, Muğla, Turkey. Sieving Data for Salt Ore. Personal Communication. 2019. [Google Scholar]
- Yu, P. A Generic Dynamic Model Structure for Tumbling Mills. Ph.D. Thesis, Sustainable Minerals Institute, University of Queensland, Indoroopilly, QLD, Australia, 2016. [Google Scholar]
- Faramarzi, F. The Measurement of Variability in Ore Competence and Its Impact on Process Performance. Ph.D. Thesis, Sustainable Minerals Institute, University of Queensland, Indoroopilly, QLD, Australia, 2019. [Google Scholar]
- Yu, P.; Xie, W.; Liu, L.X.; Powell, M.S. The development of the wide-range 4D appearance function for breakage characterisation in grinding mills. Miner. Eng. 2017, 110, 1–11. [Google Scholar] [CrossRef]
- Faramarzi, F.; Jokovic, V.; Morrison, R.; Kanchibotla, S.S. Quantifying variability of ore breakage by impact—Implications for SAG mill performance. Miner. Eng. 2018, 127, 81–89. [Google Scholar] [CrossRef]
- Genç, Ö. An Investigation of the Breakage Distribution Functions of Clinker and Additive Materials. Master’s Thesis, Hacettepe University, Mining Engineering Department, Ankara, Turkey, 2002. [Google Scholar]
- Bourgeois, F. Single-Particle Fracture as a Basis for Microscale Modeling of Comminution Processes. Ph.D. Thesis, Department of Metallurgical Engineering, University of Utah, Salt Lake City, UT, USA, 1993. [Google Scholar]
- Lynch, A.J. (Ed.) Comminution Handbook; AusIMM: Carlton VIC, Australia, 2015. [Google Scholar]
- Ouchterlony, F. Fragmentation characterization; the Swebrec function and its use in blast engineering. In Fragblast 9, Proceedings of the 9th International Rock Fragmentation by Blasting, Granada, Spain, 13–17 September 2009; Sanchidrián, J.A., Ed.; Taylor & Francis: London, UK, 2009; pp. 3–22. [Google Scholar]
- Ouchterlony, F.; Moser, P. Lessons from single-hole blasting in mortar, concrete and rocks. In Fragblast 10, Proceedings of the 10th International Symposium Rock Fragmentation by Blasting, New Delhi, India, 26–29 November 2012; Singh, S., Ed.; Taylor & Francis: London, UK, 2013; pp. 3–14. [Google Scholar]

| Fitted BIE | Coot-Tha Hornfels | Newcrest Gold Ore | Mt Isa HG Cu Ore | Mt Isa LG Cu Ore | Mt Isa Pb-Zn Ore 1 | Mt Isa Pb-Zn Ore 2 | Broken Hill Pb-Zn | Big Bell Gold Ore |
|---|---|---|---|---|---|---|---|---|
| Linear fan | 0.982 | 0.980 | 0.980 | 0.960 | 0.960 | 0.967 | 0.965 | 0.954 |
| JK new BIE | 0.993 | 0.987 | 0.989 | 0.981 | 0.982 | 0.982 | 0.981 | 0.980 |
| Double fan | 0.992 | 0.984 | 0.983 | 0.983 | 0.988 | 0.993 | 0.960 | 0.946 |
| Rock Type | Sieving | ||||||
|---|---|---|---|---|---|---|---|
| Curves | Range | Median | >0.995 | Range | Mean | Std Dev | |
| Banini [19] | |||||||
| hornfels | 42 | 0.9977–0.9999 | 0.9995 | 42 | 1.99–3.91 | 2.48 | 0.35 |
| gold ore | 72 | 0.9985–1.0000 | 0.9998 | 72 | 0.75–3.20 | 2.20 | 0.41 |
| HG Cu ore | 61 | 0.9979–1.0000 | 0.9996 | 61 | 1.69–4.56 | 2.31 | 0.42 |
| LG Cu ore | 70 | 0.9978–1.0000 | 0.9997 | 70 | 1.77–3.61 | 2.31 | 0.41 |
| Pb/Zn ore 1 | 70 | 0.9983–1.0000 | 0.9999 | 70 | 1.77–5.48 | 2.46 | 0.64 |
| Pb/Zn ore 2 | 65 | 0.9946–1.0000 | 0.9999 | 64 | 2.00–5.54b | 2.57 | 0.53 |
| Pb/Zn ore | 47 | 0.9905–1.0000 | 0.9976 | 42 | 0.92–5.38 | 2.23 | 1.03 |
| gold ore | 53 | 0.9812–1.0000 | 0.9991 | 39 | 0.91–5.29 | 1.49 | 0.69 |
| Genç et al. [24] | |||||||
| clay | 4 | 0.9916–0.9997 | 0.9973 | 3 | 2.68–3.34 | 2.95 | 0.31 |
| clinker I | 21 | 0.9974–0.9994 | 0.9989 | 21 | 1.62–2.12 | 1.82 | 0.14 |
| clinker II | 9 | 0.9970–0.9995 | 0.9986 | 9 | 1.44–2.16 | 1.69 | 0.26 |
| colemanite | 9 | 0.9933–0.9988 | 0.9980 | 7 | 2.42–3.30 | 2.81 | 0.27 |
| copper ore | 4 | 0.9979–0.9997 | 0.9987 | 4 | 2.56–4.01 | 3.10 | 0.64 |
| gypsuma | 9 | 0.9886–0.9996 | 0.9983 | 7 | 2.66–17.25 | 10.7 | 5.5 |
| limestone I | 9 | 0.9957–0.9997 | 0.9991 | 9 | 2.03–2.81 | 2.39 | 0.26 |
| quartzite I | 14 | 0.9955–0.9994 | 0.9979 | 14 | 2.20–3.83a | 3.05 | 0.41 |
| quartzite II | 11 | 0.9975–0.9997 | 0.9992 | 11 | 1.77–2.87 | 2.34 | 0.38 |
| trass I | 10 | 0.9978–0.9996 | 0.9986 | 10 | 1.66–2.20 | 1.83 | 0.18 |
| salt orec | 5 | 0.9968–0.9989 | 0.9975 | 5 | 3.58–4.34 | 4.11 | 0.36 |
| Faramarzi [27] | |||||||
| ore 1 | 12 | 0.9984–0.9999 | 0.9996 | 12 | 1.82–2.58 | 2.19 | 0.27 |
| ore 2 | 17 | 0.9966–0.9999 | 0.9996 | 17 | 1.80–2.52 | 2.21 | 0.19 |
| ore 2 | 12 | 0.9978–0.9998 | 0.9990 | 12 | 1.49–2.30 | 1.87 | 0.25 |
| ore 4 | 12 | 0.9993–1.0000 | 0.9996 | 12 | 2.19–2.64 | 2.40 | 0.16 |
| Yu [26] | |||||||
| Cadia porphyry ore | 59 | 0.9893–0.9999 | 0.9976 | 49 | 0.89–3.73 | 2.09 | 0.55 |
| Avsar [23] | |||||||
| clinker | 32 | 0.9956–0.9999 | 0.9985 | 32 | 0.96–2.78 | 2.00 | 0.34 |
| trass | 32 | 0.9953–0.9992 | 0.9971 | 32 | 1.74–3.48 | 2.58 | 0.38 |
| Statistics: | <0.995 | ||||||
| Banini | 480 | min: | 0.9971 | 4.2% | mean: | 2.27 | 0.56 |
| New data | 281 | max: | 0.9999 | 7.8% | mean: | 2.27 | 0.31 |
| Total | 761 | median: | 0.9990 | 5.5% | mean: | 2.27 | 0.47 |
| Material | Material | Material | ||||||
|---|---|---|---|---|---|---|---|---|
| clinker | 2.12 | 2.00 | copper ore | 2.37 | 3.10 | salt | 4.03 | 4.11 |
| trass | 2.27 | 2.58 | gypsum | 4.30 | 10.7 | ore 1 | 1.83 | 2.19 |
| clay | 2.35 | 2.95 | limestone I | 2.09 | 2.39 | ore 2 | 1.95 | 2.21 |
| clinker I | 1.64 | 1.82 | quartz I | 2.30 | 3.05 | ore 2 | 1.62 | 1.87 |
| cinker II | 1.57 | 1.69 | quartz II | 2.43 | 2.34 | ore 4 | 2.28 | 2.40 |
| colemanite | 2.22 | 2.81 | trass I | 1.70 | 1.83 | Cadia ore | 1.87 | 2.09 |
| Material | %–% | JK new BIE | JK New BIE | JK New BIE | Banini BIE Equation (7) | Double Fan Const |
|---|---|---|---|---|---|---|
| 3 param. | 4 param. | 4 param. | 3 param. | 9 param. | ||
| Genç et al. [24] | ||||||
| clay | 16.6–50.1 | 0.9963 | 0.9963 | 1.0000 | 0.9939 | 0.9920 |
| clinker I | 16.2–61.3 | 0.9131 | 0.9199 | 0.9199 | 0.8992 | 0.9289 |
| clinker II | 15.7–71.7 | 0.9132 | 0.9132 | 0.9295 | 0.9034 | 0.9387 |
| colemanite | 22.4–64.8 | 0.9310 | 0.9310 | 0.9451 | 0.9341 | 0.9424 |
| copper ore | 35.6–55.4 | 0.5649 | 0.5649 | 0.7258 | 0.7100 | 0.7908 |
| gypsum | 46.0–60.0 | 0.5797 | 0.5797 | 0.7991 | 0.8353 | 0.6459 |
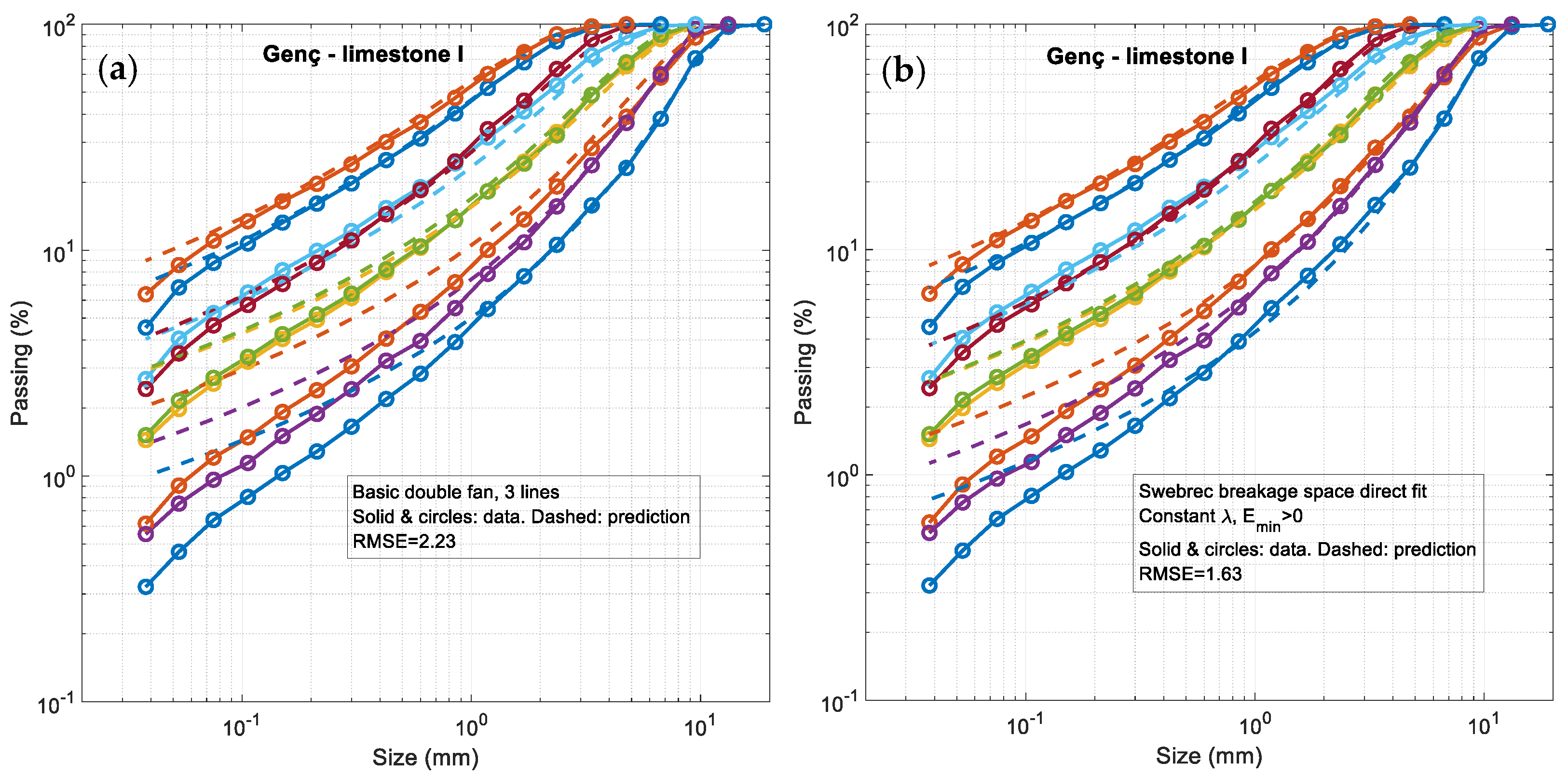
| limestone I | 6.6–48.1 | 0.9783 | 0.9833 | 0.9833 | 0.9846 | 0.9800 |
| quartz I | 11.4–66.0 | 0.9708 | 0.9708 | 0.9742 | 0.9730 | 0.9750 |
| quartz II | 4.8–15.8 | 0.9456 | 0.9456 | 0.9588 | 0.9553 | 0.8903 |
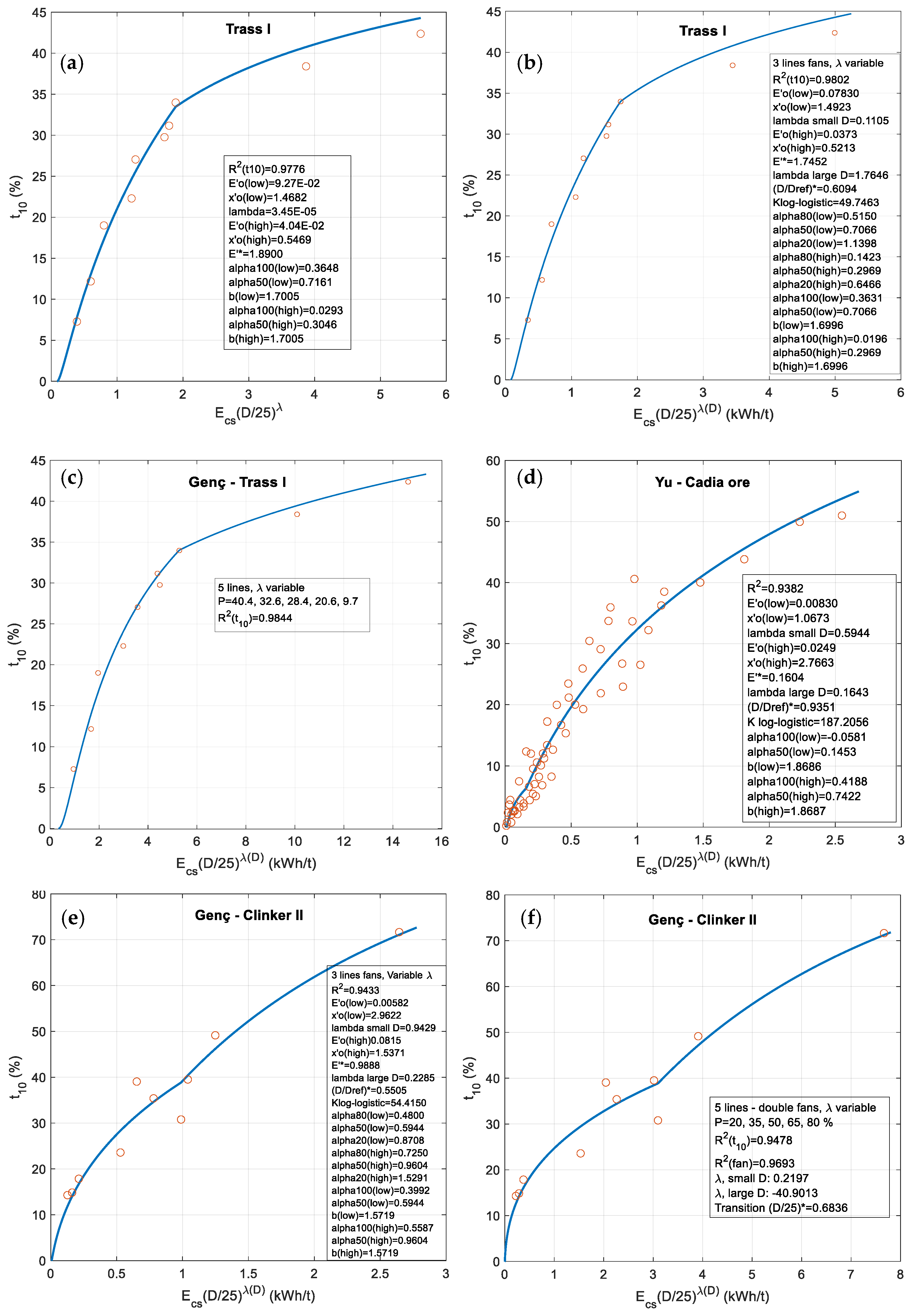
| trass I | 7.3–42.4 | 0.9712 | 0.9836 | 0.9836 | 0.9571 | 0.9776 |
| salt ore b | 25.2–60.8 | 0.9134 | 0.9134 | 0.9998 | 0.9864 | 0.9944 |
| Faramarzi [27] | ||||||
| ore 1 | 4.0–64.7 | 0.9946 | 0.9952 | 0.9952 | 0.9931 | 0.9943 |
| ore 2 | 3.9–58.0 | 0.9919 | 0.9925 | 0.9925 | 0.9923 | 0.9916 |
| ore 3 | 4.4–54.9 | 0.9965 | 0.9965 | 0.9969 | 0.9939 | 0.9943 |
| ore 4 | 14.0–60.5 | 0.9867 | 0.9867 | 0.9960 | 0.9918 | 0.9943 |
| Yu [26] | ||||||
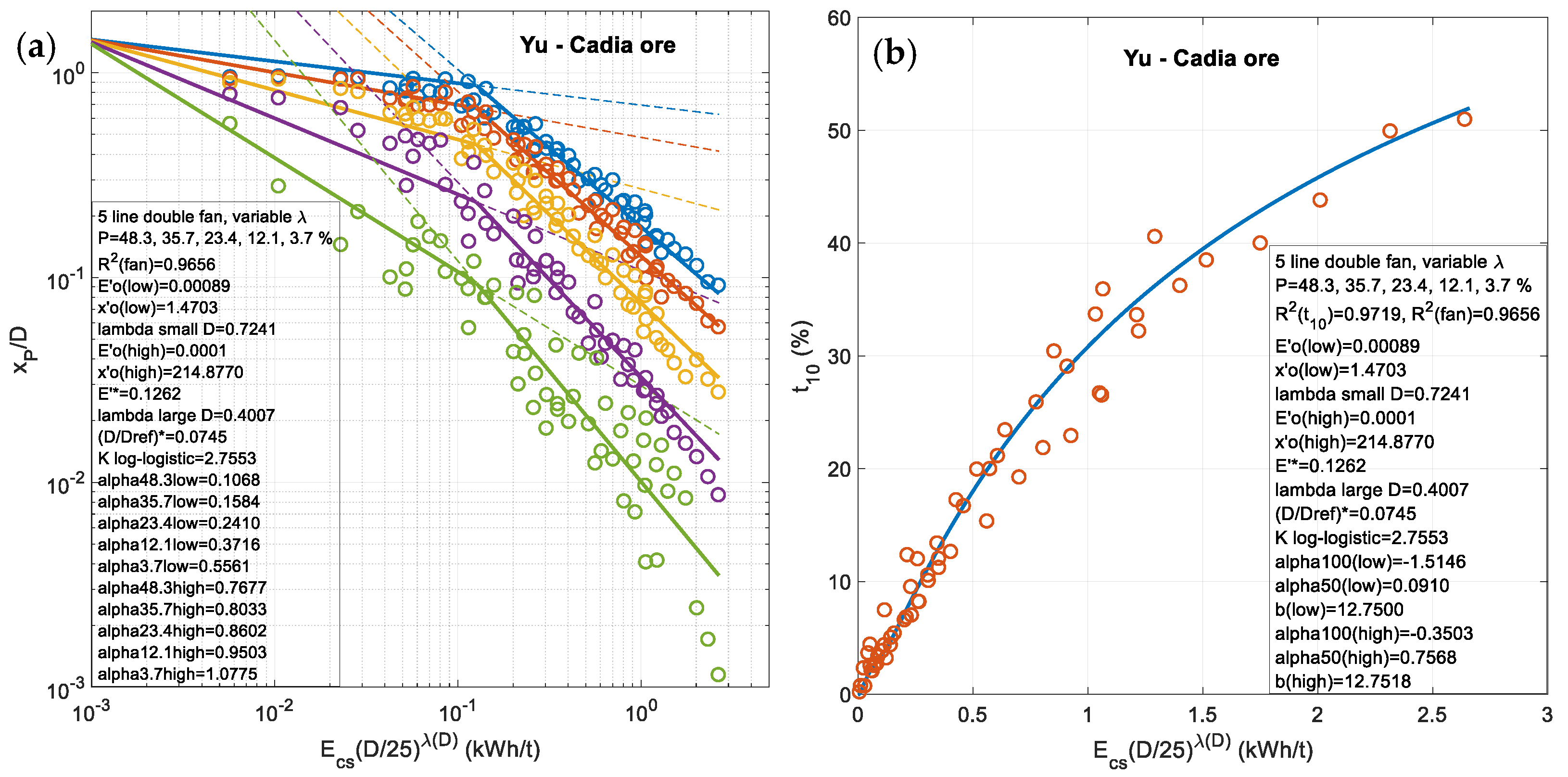
| Cadia ore | 0.2–51.0 | 0.9353 | 0.9365 | 0.9365 | 0.9333 | 0.9313 |
| Avsar [23] | ||||||
| clinker | 4.0–56.9 | 0.9940 | 0.9941 | 0.9941 | 0.9894 | 0.9919 |
| trass | 5.7–65.9 | 0.9689 | 0.9699 | 0.9699 | 0.9809 | 0.9720 |
| Median: | 0.9699 | 0.9704 | 0.9788 | 0.9770 | 0.9763 | |
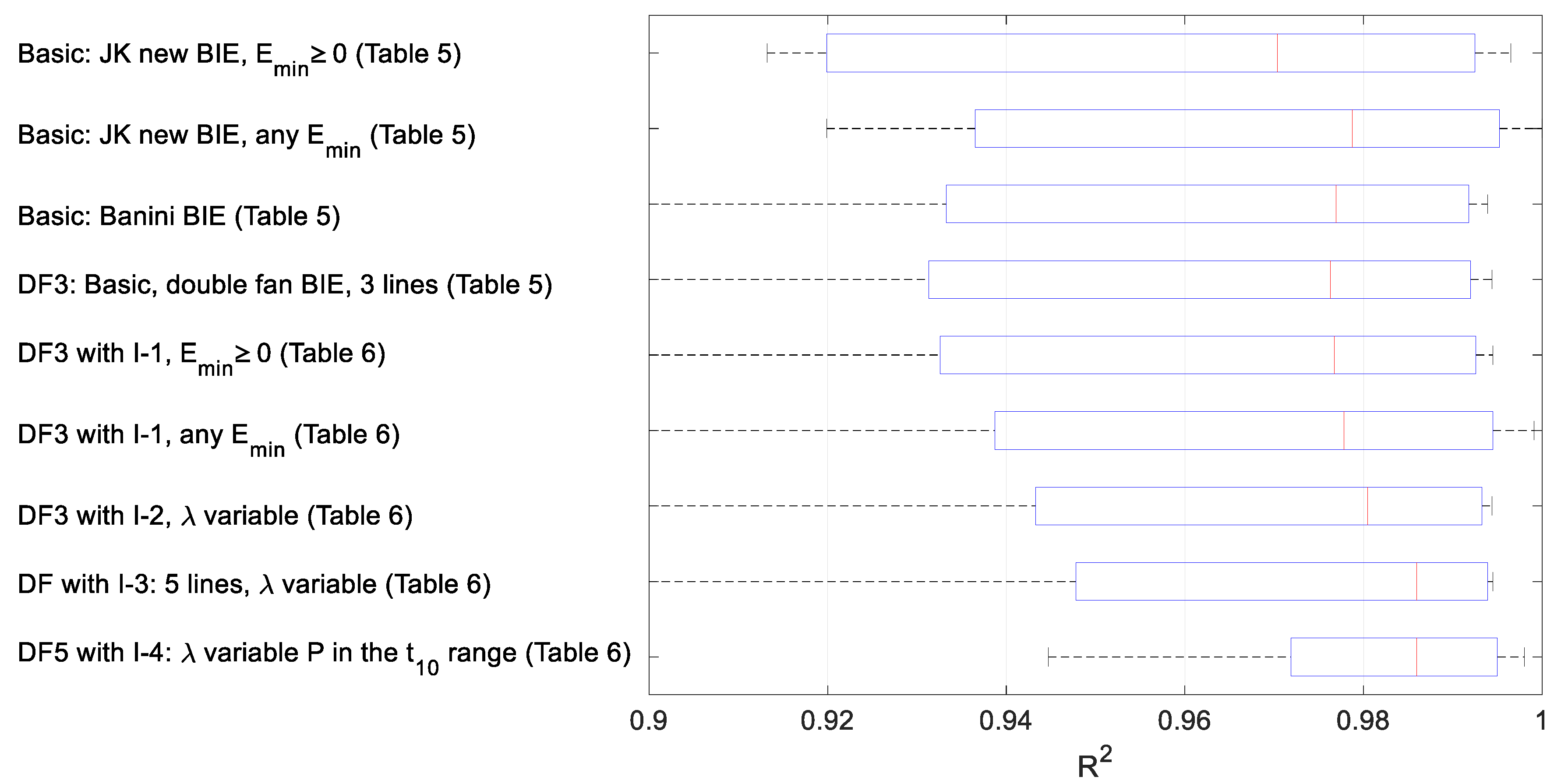
| Material | Max Fidelity Basic BIE | Type of BIE | Double Fan I-1: 3 Lines ≥ 0a | Double Fan I-1: 3 Lines Any | Double Fan I-2: 3 Lines Variable | Double Fan I-3: 5 Lines Variable | Double Fan I-4: 5 Lines Adapted Variable | Double Fan I-5: Direct Fit Const RMSE | Double Fan I-5: Direct Fit Variable RMSE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 param | 10 param | 12 param | 12 param | 12 param | 10 param | 12 param | ||||
| clay | 1.0000 | JK E < 0 | 0.9920 | 0.9945 | few data | 0.9942 | 0.9980 | 1.81 | <0 | 1.85 |
| clink. I | 0.9289 | fan | 0.9300 | 0.9308 | 0.9666 | 0.9662 | 0.9659 | 3.34 | >0 | 2.51 |
| clink. II | 0.9387 | fan | 0.9387 | 0.9387 | 0.9433 | 0.9478 | 0.9482 | 4.36 | >0 | 4.16 |
| colema. | 0.9451 | JK E < 0 | 0.9424 | 0.9447 | 0.9433 | 0.9389 | 0.9447 | 3.03 | <0 | 3.23 |
| Cu ore | 0.7908 | fan | 0.7908 | 0.9623 | few data | 0.9901 | 0.9971 | 1.83 | <0 | 1.46 |
| gyps. | 0.8353 | Banini | 0.6459 | 0.6459 | 0.6464 | 0.7097 | 0.8442 | 2.80 | <0 | 2.79 |
| Lime. I | 0.9846 | Banini | 0.9858 | 0.9977 | 0.9807 | 0.9799 | 0.9829 | 1.63 | >0 | 2.06 |
| qrtz. I | 0.9750 | fan | 0.9750 | 0.9779 | 0.9791 | 0.9755 | 0.9748 | 3.32 | <0 | 3.32 |
| qrtz. II | 0.9588 | JK E < 0 | 0.8903 | 0.8903 | 0.8936 | 0.8941 | 0.9842 | 1.28 | <0 | 1.17 |
| trass I | 0.9836 | JK E ≥ 0 | 0.9777 | 0.9777 | 0.9802 | 0.9818 | 0.9844 | 1.93 | >0 | 1.97 |
| salt ore | 0.9998 | JK E < 0 | 0.9944 | 0.9944 | 0.9941 | 0.9939 | 0.9960 | 2.12 | >0 | 2.17 |
| ore 1 | 0.9952 | JK E ≥ 0 | 0.9944 | 0.9991 | 0.9944 | 0.9940 | 0.9972 | 1.40 | <0 | 1.54 |
| ore 2 | 0.9925 | JK E ≥ 0 | 0.9926 | 0.9926 | 0.9917 | 0.9918 | 0.9921 | 1.60 | <0 | 1.56 |
| ore 3 | 0.9969 | JK E < 0 | 0.9945 | 0.9955 | 0.9943 | 0.9941 | 0.9938 | 1.95 | >0 | 2.02 |
| ore 4 | 0.9960 | JK E < 0 | 0.9943 | 0.9945 | 0.9941 | 0.9945 | 0.9950 | 1.15 | <0 | 1.23 |
| Cadia | 0.9365 | JK E ≥ 0 | 0.9326 | 0.9326 | 0.9382 | 0.9397 | 0.9719 | 6.32(5.11 a) | >0 | 5.13(4.15 a) |
| clinker | 0.9941 | JK E ≥ 0 | 0.9919 | 0.9919 | 0.9924 | 0.9918 | 0.9875 | 1.84 | <0 | 1.87 |
| trass | 0.9809 | Banini | 0.9758 | 0.9758 | 0.9918 | 0.9928 | 0.9917 | 2.34 | >0 | 1.75 |
| Median: | 0.9823 | 0.9768 | 0.9778 | 0.9805 | 0.9860 | 0.9860 | 1.94 | 2.00 |
| Material | DF3: Basic, Double Fan, 3 Fan Lines λ Const. | DF3 w. I-1 Emin ≥ 0 | DF3 w. I-1 Any Emin | DF3 w. I-2 λ Variable | DF5 w. I-3 5 Fan Lines λ Variable | DF5 w. I-4 λ Variable P in t10 Range | Direct Fit Double Fan λ Const. Emin ≥ 0 | Direct Fit Double Fan λ Const. Any Emin | Direct Fit Double Fan λ Variable |
|---|---|---|---|---|---|---|---|---|---|
| No. param. | 9 | 10 | 10 | 12 | 12 | 12 | 10 | 10 | 12 |
| Genç’s | |||||||||
| limestone I | 2.23 | 1.78 | 1.59 | 2.20 | 2.20 | 3.05 | 1.63 | 1.37 | 2.06 |
| Faramarzi’s | |||||||||
| ore 1 | 1.81 | 1.81 | 1.62 | 1.80 | 1.83 | 3.05 | 1.51 | 1.40 | 1.54 |
| Avsar’s | |||||||||
| clinker | 2.70 | 2.70* | 2.54 | 2.55 | 2.46 | 4.70 | 2.11* | 1.84 | 1.87 |
| Yu’s | |||||||||
| Cadia ore | 7.56 | 7.76 | 7.76 | 7.27 | 7.80 | 11.63 | 6.32 | 6.32 | 5.13 |
| 1135 data ** | 6.12 | 6.28 | 6.28 | 5.88 | 6.31 | 9.40 | 5.11 | 5.11 | 4.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouchterlony, F.; Sanchidrián, J.A.; Genç, Ö. Advances on the Fragmentation-Energy Fan Concept and the Swebrec Function in Modeling Drop Weight Testing. Minerals 2021, 11, 1262. https://doi.org/10.3390/min11111262
Ouchterlony F, Sanchidrián JA, Genç Ö. Advances on the Fragmentation-Energy Fan Concept and the Swebrec Function in Modeling Drop Weight Testing. Minerals. 2021; 11(11):1262. https://doi.org/10.3390/min11111262
Chicago/Turabian StyleOuchterlony, Finn, José A. Sanchidrián, and Ömürden Genç. 2021. "Advances on the Fragmentation-Energy Fan Concept and the Swebrec Function in Modeling Drop Weight Testing" Minerals 11, no. 11: 1262. https://doi.org/10.3390/min11111262
APA StyleOuchterlony, F., Sanchidrián, J. A., & Genç, Ö. (2021). Advances on the Fragmentation-Energy Fan Concept and the Swebrec Function in Modeling Drop Weight Testing. Minerals, 11(11), 1262. https://doi.org/10.3390/min11111262






