A Numerical Study on the Optimization of the Material Pressure of the Feeding System
Abstract
:1. Introduction
2. Materials and Methods
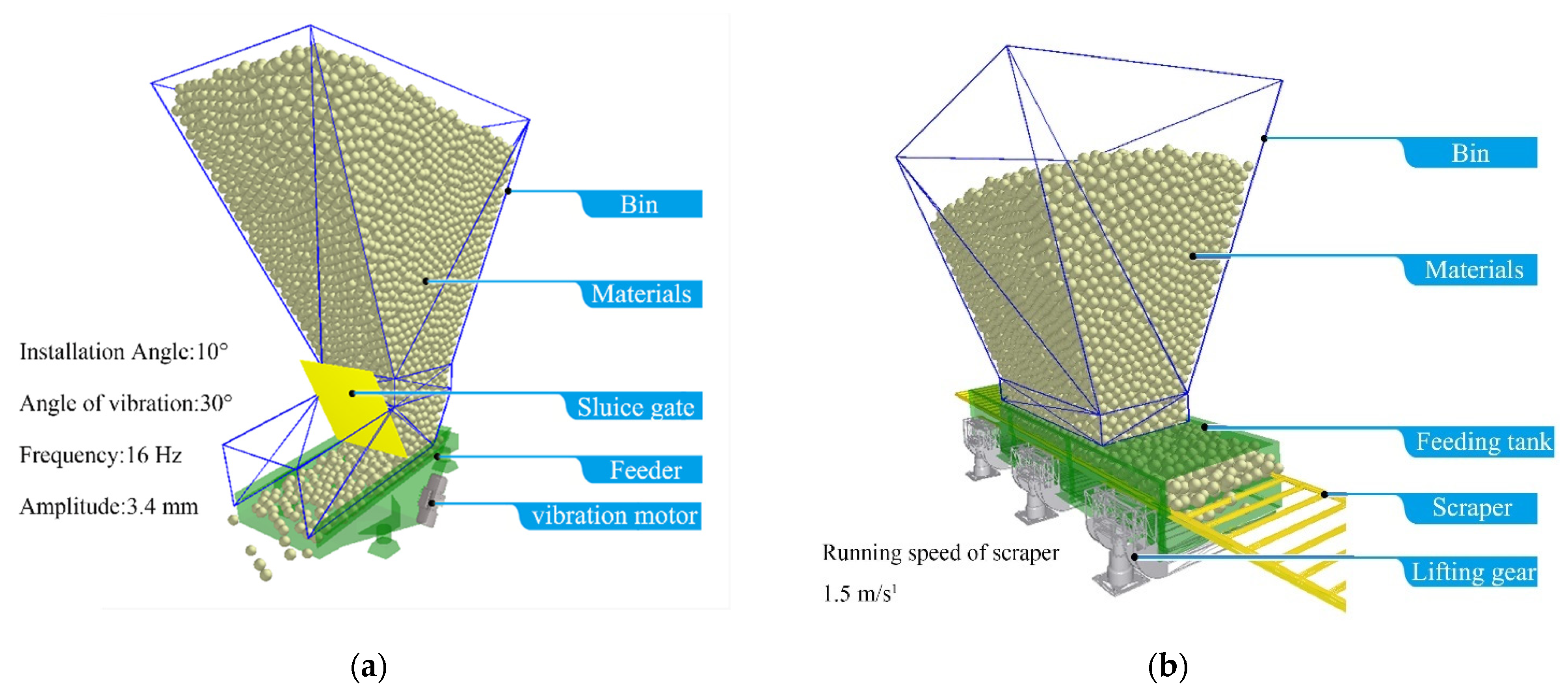
2.1. EDEM Simulation Parameter Setting
2.2. Experimental Materials and Equipment
3. Results and Discussion
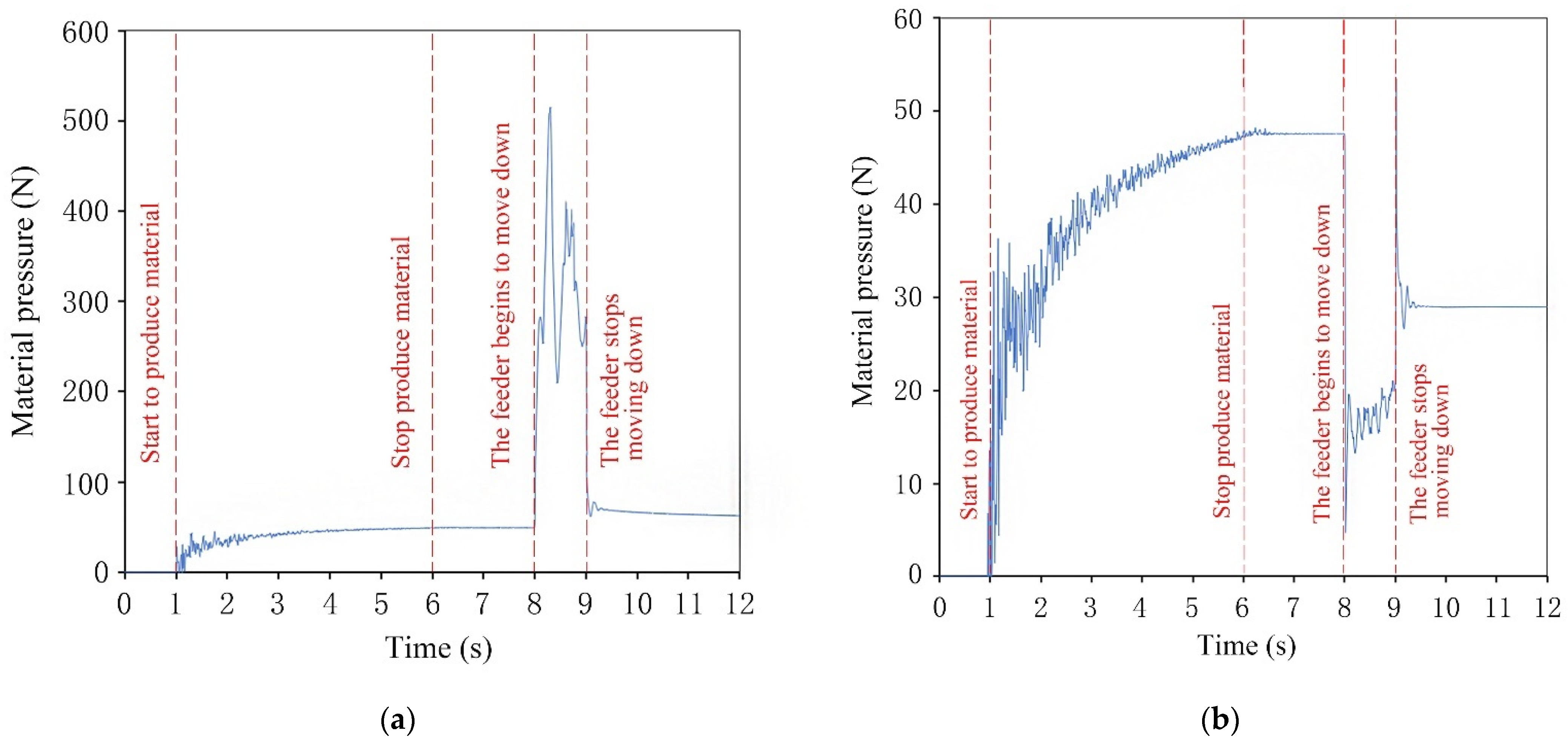
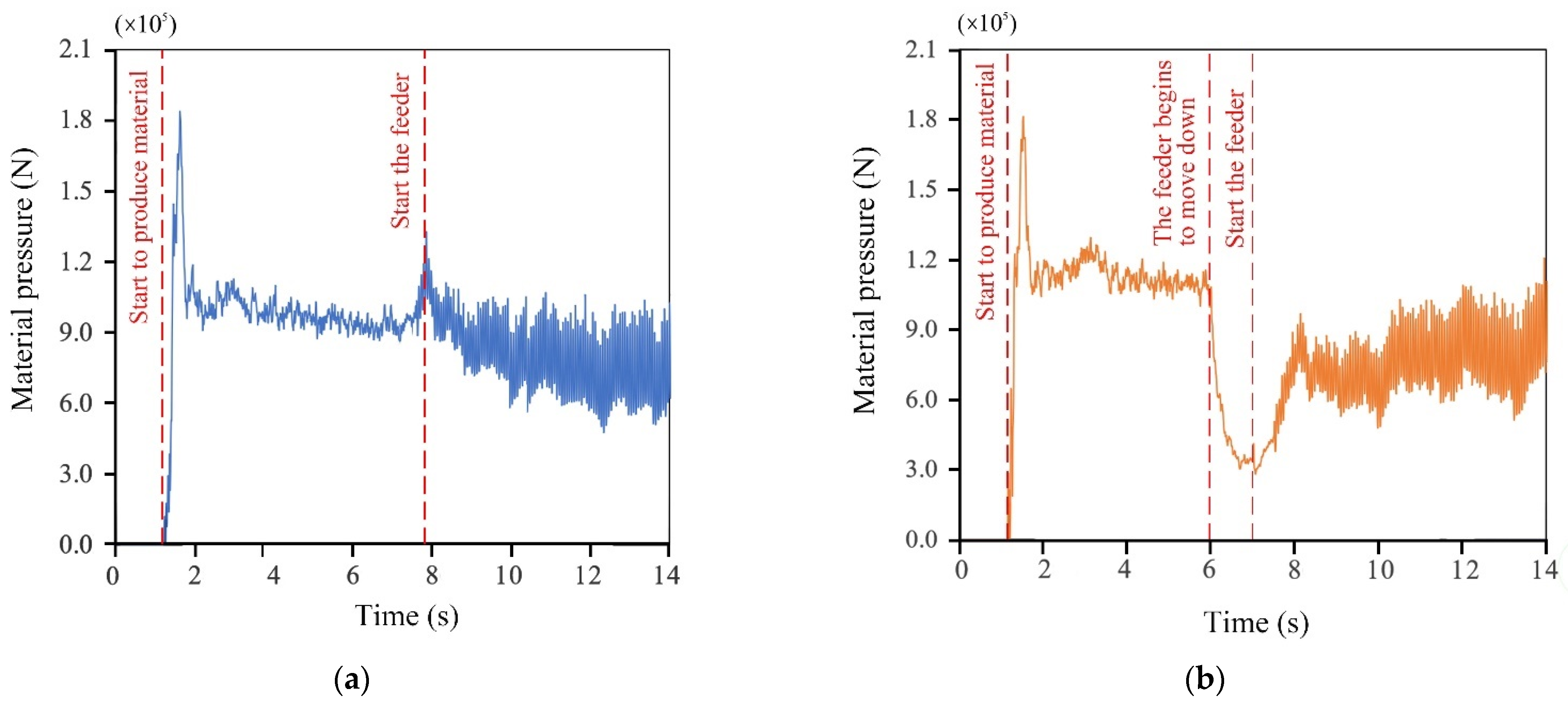
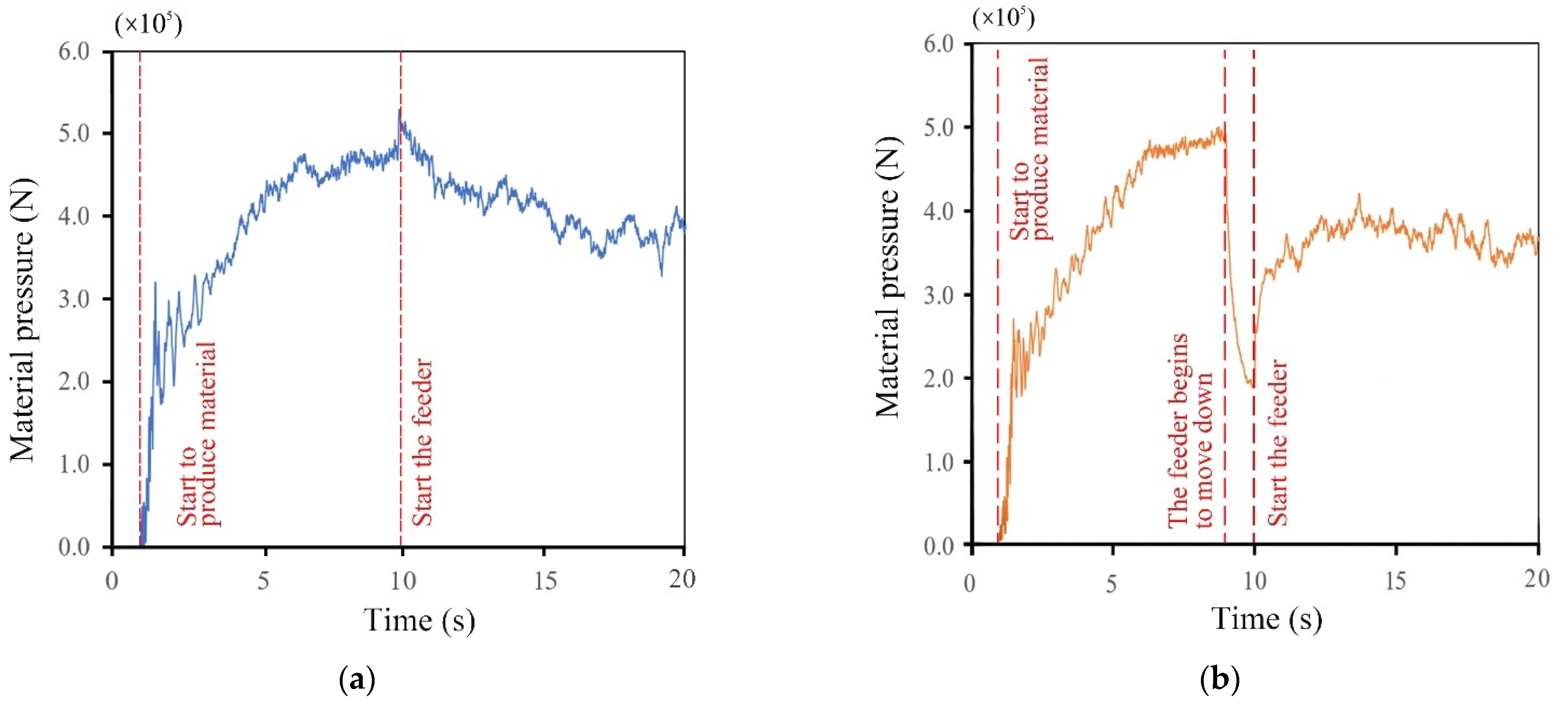
3.1. Influence of the Movement Direction of the Feeder
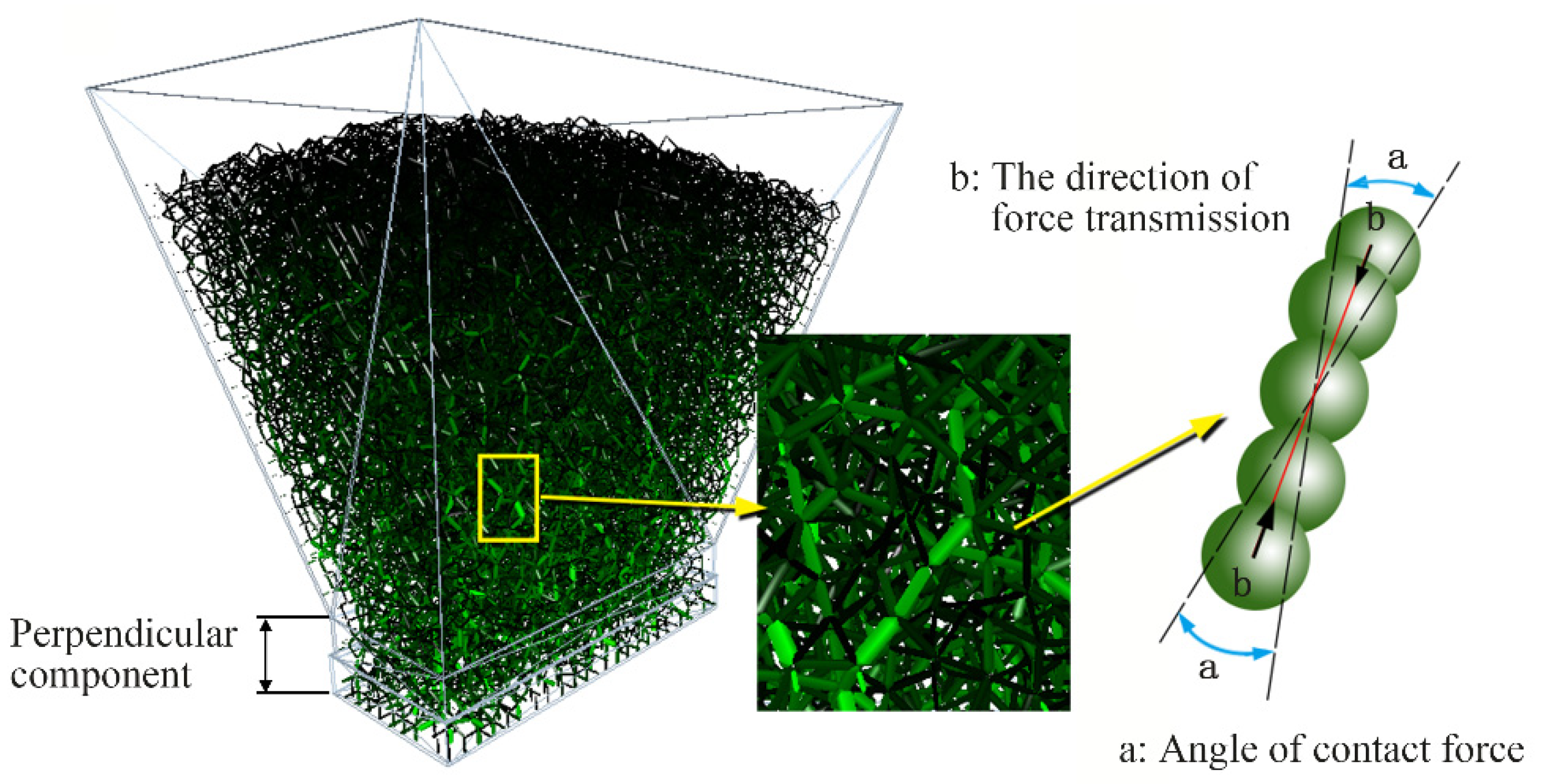
3.2. Evolution Law of Force Chain
3.3. Influencing Factors of Material Pressure Changes
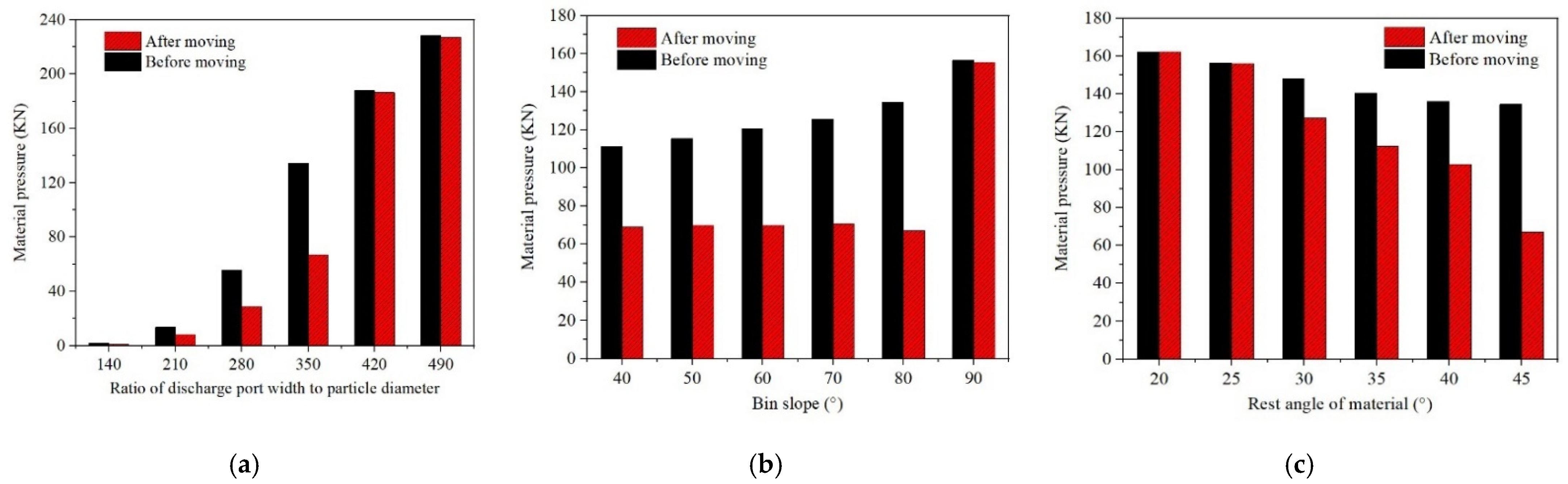
3.3.1. The Influence of Bin Size
3.3.2. The Influence of the Bin Body Slope
3.3.3. The Influence of Material Resting Angle
3.4. Influence Law of Motion State on Material Pressure
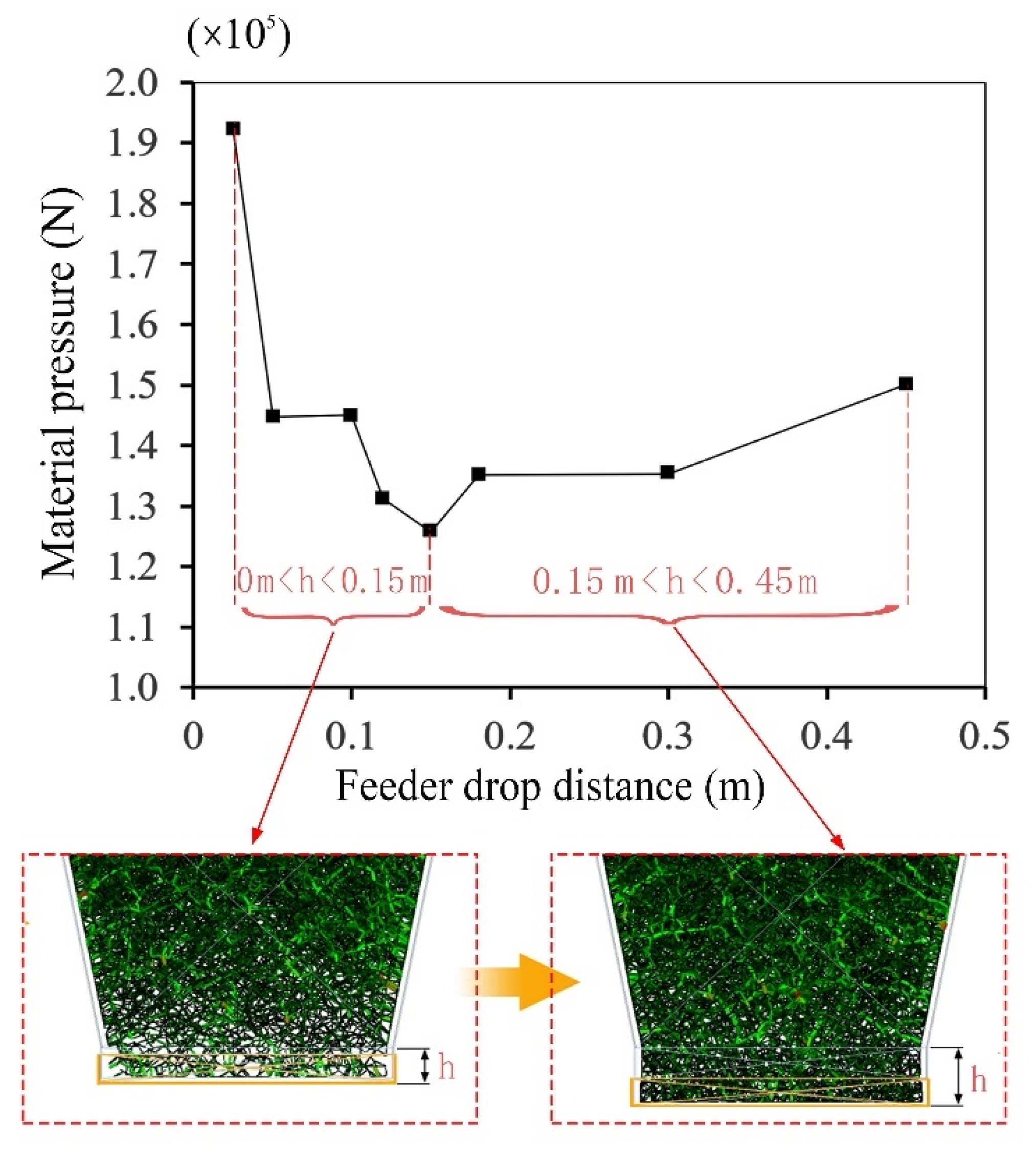
3.4.1. Influence Law of Movement Distance on Material Pressure
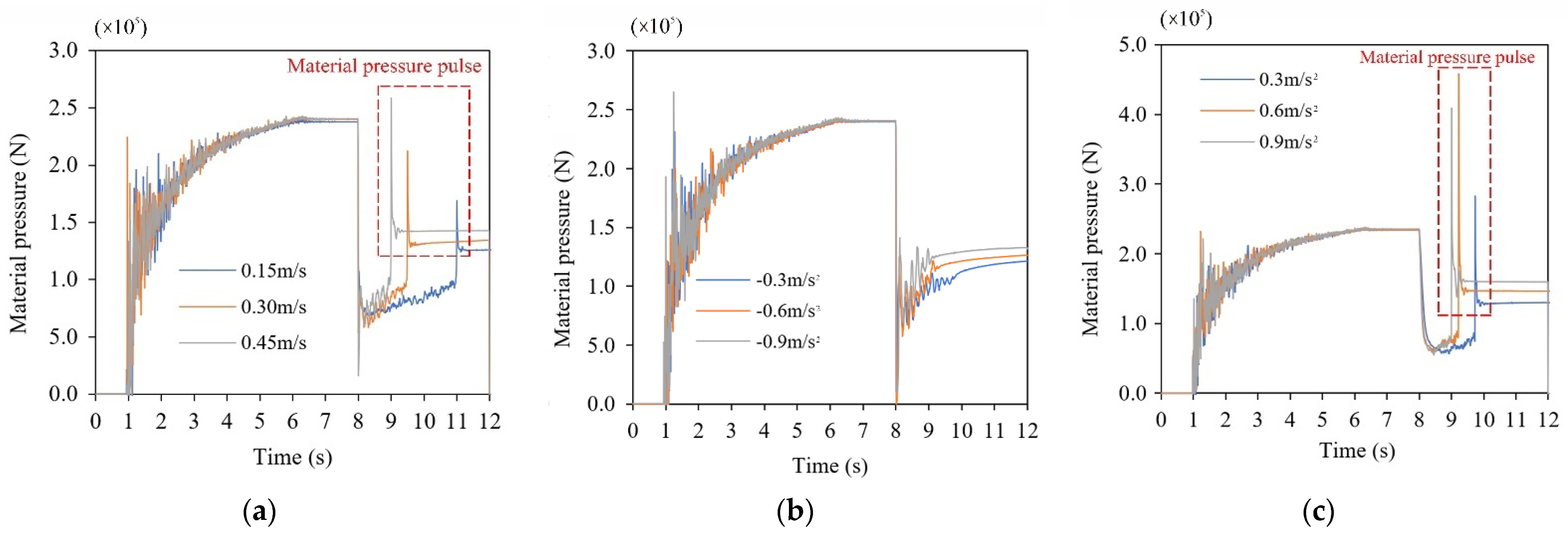
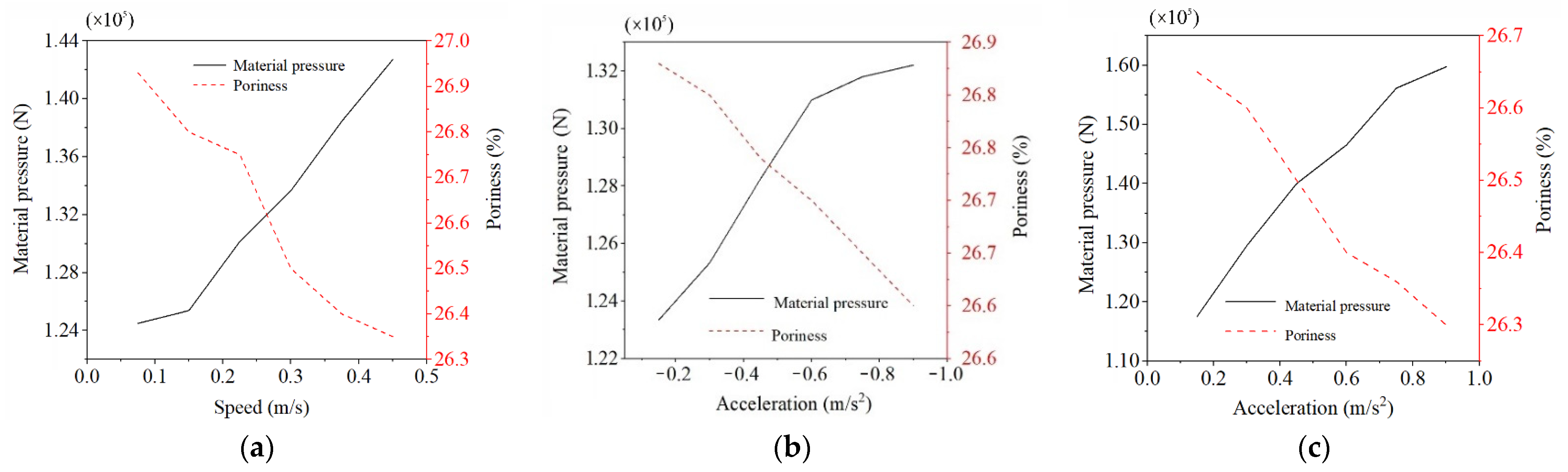
3.4.2. Influence Law of Descending Speed and Acceleration on Material Pressure
3.5. Response Surface BBD Optimization Experiment
- Investigate the material rest angle, bin body slope, and RWD to determine whether the downward movement of the feeder can cause the material pressure to decrease.
- Design a reasonable descent process of the feeder; there should be enough deceleration time before the feeder stops to eliminate the inertial impact of the material.
- Appropriate optimization methods can be applied to optimize the designed descent process.
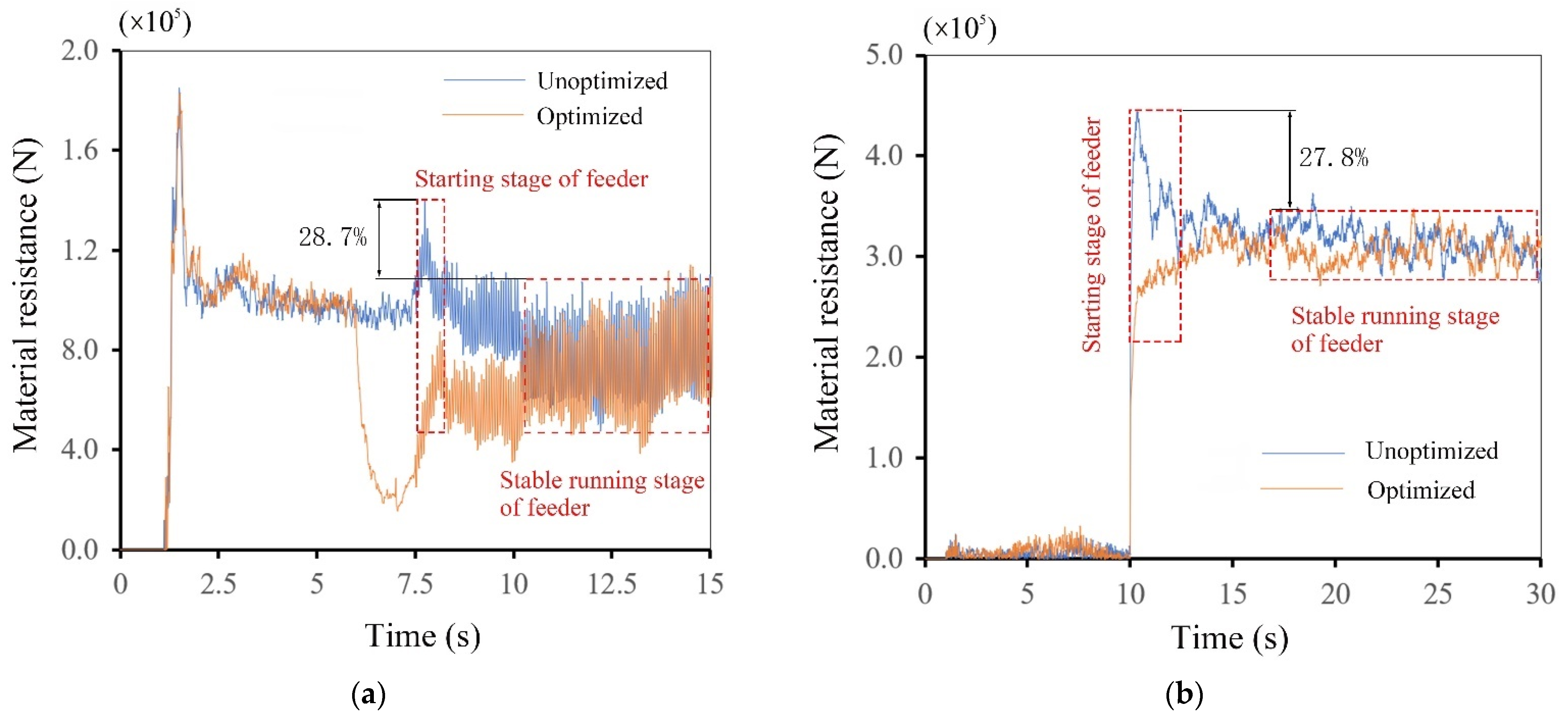
4. Example Analysis of Feeding System
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Y. Discussion on the Influence of Warehouse Pressure Calculation on the Design of Belt Conveyor. Hoisting Conveying Mach. 2012, 2, 55–58. [Google Scholar]
- Li, P.; Wang, N.N.; Si, H.; Chang, J.M. Feeding characteristics of a novel double-bin pneumatic feeder of biomass particles. Powder Technol. 2020, 363, 735–744. [Google Scholar] [CrossRef]
- Shie, C.Y.; Shu, S.H. The simulation and experimental study of granular materials discharged from a silo with the placement of inserts. Powder Technol. 2001, 120, 244–255. [Google Scholar]
- Zhang, Q. An Intermittent Arch Model for Predicting Dynamic Pressures during Discharge in Grain Storage Bins. Trans. ASABE 2014, 57, 1839–1844. [Google Scholar]
- Zhang, Q.; Ge, T. Development of a predictive model for arch destruction by vibration in storage bins for cohesive bulk solids. Trans. ASAE 2005, 48, 1905–1910. [Google Scholar]
- Sun, Q.; Wang, G.; Hu, K. Considerations on several key problems in the mechanics of particulate matter. Prog. Nat. Sci. 2008, 10, 1104–1110. [Google Scholar]
- Wang, J.A.; Liu, Y.; Fei, L.; Wang, C. Force chains in top coal caving mining. Int. J. Rock Mech. Min. Sci. 2020, 127, 104218. [Google Scholar] [CrossRef]
- Dai, B.B.; Yang, J.; Liu, F.; Lin, K. Characteristics and mechanism of natural accumulation of granular soil. J. Geotech. Eng. 2019, 41, 57–60. [Google Scholar]
- Meng, F.J.; Pang, M.H.; Hua, S.Z.; Liu, H.B.; Cheng, P.F.; Zhang, T.; Wu, Z.Q. Research on Mechanical Mechanism of Powder Metallurgy Uniaxial Pressing Process. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 1128–1132. [Google Scholar]
- Løvoll, G.; Máløy, K.J.; Flekkøy, E.G. Force measurements on static granular materials. Phys. Rev. E 1999, 60, 5872–5878. [Google Scholar] [CrossRef]
- Blair, D.L.; Mueggenburg, N.W.; Marshall, A.H.; Jaeger, H.M.; Nagel, S.R. Force distributions in three-dimensional granular assemblies: Effects of packing order and interparticle friction. Phys. Rev. E 2001, 63, 41304. [Google Scholar] [CrossRef] [Green Version]
- Peters, J.F.; Muthuswamy, M.; Wibowo, J.; Tordesillas, A. Characterization of force chains in granular material. Phys. Rev. E 2005, 72, 041307. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.; Zhang, X.X.; Kong, F.C.; Liu, H.S. Discrete element method simulation of collision depolymerization of wet particles. J. Appl. Phys. 2015, 64, 328–337. [Google Scholar]
- Yang, Y.; Chen, Y.M.; Wang, J.A. Exploring the contact types within mixtures of different shapes at the steady state by DEM. Powder Technol. 2016, 301, 440–448. [Google Scholar] [CrossRef]
- Meng, F.J.; Meng, X.; Hua, S.Z.; Ma, S. Fluctuation and self-diffusion research about dry granular materials under shearing. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 153. [Google Scholar] [CrossRef]
- Wang, W.; Gu, W.; Liu, K. Force chain evolution and force characteristics of shearing granular media in taylor-couette geometry by DEM. Tribol. Trans. 2015, 58, 197–206. [Google Scholar] [CrossRef]
- Xu, Y.; Kafui, K.D.; Thornton, C.S. Discharge Simulation with Different Particulate Properties Using the Distinct Element Method. Trans. Chin. Soc. Agric. Eng. 1999, 15, 65–69. [Google Scholar]
- Cleary, P.W.; Sawley, M.L. DEM modeling of industrial granular flows:3D case studies and the effect of particle shape on hopper discharge. Appl. Math. Model. 2002, 26, 89–111. [Google Scholar] [CrossRef]
- Chen, C.; Liang, X. Analysis on discrete element simulation of discharging in silos. Sci. Technol. Grain Oil Food 2008, 16, 11–13. [Google Scholar]
- Tordesillas, A.; Walker, D.M.; Lin, Q. Force cycles and force chains. Phys. Rev. E 2010, 81, 011302. [Google Scholar] [CrossRef] [PubMed]
- Staron, L.; Hinch, E.J. The spreading of a granular mass: Role of grain properties and initial conditions. Granul. Matter 2007, 9, 205–217. [Google Scholar] [CrossRef]
- Jing, L.; Yang, G.C.; Kwok, C.Y.; Sobral, Y.D. Dynamics and scaling laws of underwater granular collapse with varying aspect ratios. Phys. Rev. E 2018, 98, 042901-1–042901-15. [Google Scholar] [CrossRef]
- Girolami, L.; Hergault, V.; Vinay, G.; Wachs, A. A three-dimensional discrete-grain model for the simulation of dam-break rectangular collapses: Comparison between numerical results and experiments. Granul. Matter 2012, 14, 381–392. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, G. Distribution of Force Chains in Static Packed Particles. Acta Phys. Sin. 2008, 8, 4667–4674. [Google Scholar]
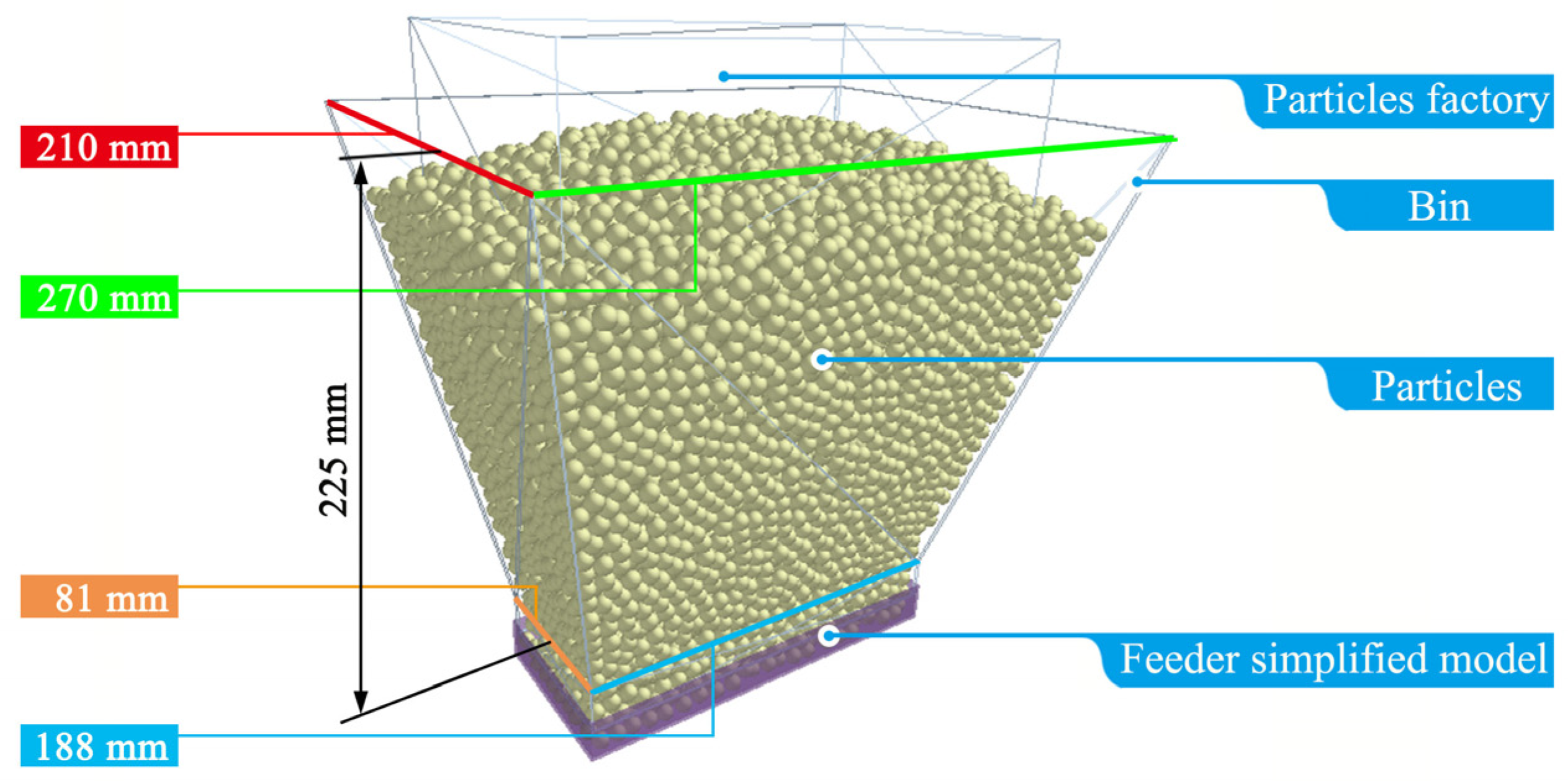
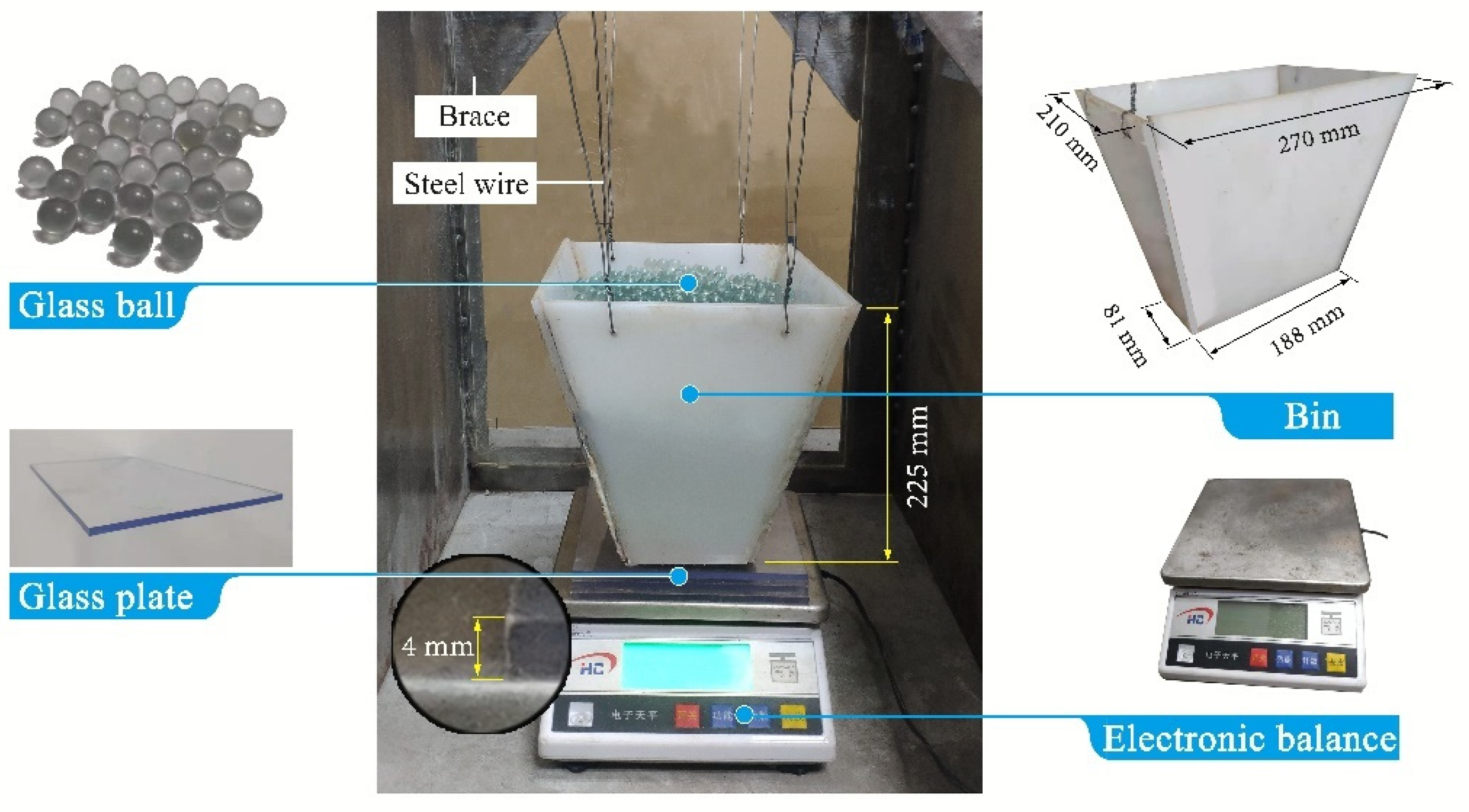




| Parameters | Polypropylene | Glass |
| Poisson’s ratio | 0.42 | 0.25 |
| Shear modulus (MPa) | 8.9 × 106 | 1.96 × 107 |
| Density (kg/m3) | 920 | 2500 |
| Contact Parameters | Polypropylene—Glass | Glass—Glass |
| Coefficient of restitution | 0.5 | 0.5 |
| Static friction coefficient | 0.6 | 0.9 |
| Coefficient of rolling friction | 0.05 | 0.05 |
| Material Pressure | Initial Material Pressure | After the Feeder Drops | After the Feeder Rises |
|---|---|---|---|
| Simulation value (N) | 47.5 | 28.9 | 62.3 |
| Experimental value (N) | 45.2 | 27.1 | 59.7 |
| Margin of error (%) | 4.84 | 6.23 | 4.17 |
| Parameters | Steel | Coal |
| Poisson’s ratio | 0.28 | 0.3 |
| Shear modulus (MPa) | 7 × 1010 | 8 × 107 |
| Density (kg/m3) | 7860 | 1400 |
| Contact Parameters | Steel—Coal | Coal—Coal |
| Coefficient of restitution | 0.5 | 0.5 |
| Static friction coefficient | 0.5 | 0.7 |
| Coefficient of rolling friction | 0.01 | 0.01 |
| No. | Drop Distance (m) | Acceleration (m/s2) | Negative Acceleration (m/s2) | Stable Material Pressure (kN) |
|---|---|---|---|---|
| 1 | 0.1625 | 0.001 | 0.001 | 93.596 |
| 2 | 0.3 | 0.0505 | 0.001 | 116.679 |
| 3 | 0.1625 | 0.1 | 0.001 | 98.571 |
| 4 | 0.3 | 0.0505 | 0.1 | 106.496 |
| 5 | 0.025 | 0.0505 | 0.001 | 93.161 |
| 6 | 0.1625 | 0.0505 | 0.0505 | 95.573 |
| 7 | 0.025 | 0.001 | 0.0505 | 93.847 |
| 8 | 0.1625 | 0.1 | 0.1 | 91.960 |
| 9 | 0.025 | 0.0505 | 0.1 | 90.960 |
| 10 | 0.1625 | 0.0505 | 0.0505 | 96.468 |
| 11 | 0.3 | 0.1 | 0.0505 | 107.395 |
| 12 | 0.3 | 0.001 | 0.0505 | 102.238 |
| 13 | 0.1625 | 0.001 | 0.1 | 94.166 |
| 14 | 0.1625 | 0.0505 | 0.0505 | 87.890 |
| 15 | 0.025 | 0.1 | 0.0505 | 96.416 |
| 16 | 0.1625 | 0.0505 | 0.0505 | 96.442 |
| 17 | 0.1625 | 0.0505 | 0.0505 | 96.020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, N.; Wang, X.; Yu, C.; Lin, D.; Zhao, G. A Numerical Study on the Optimization of the Material Pressure of the Feeding System. Minerals 2021, 11, 1333. https://doi.org/10.3390/min11121333
Xu N, Wang X, Yu C, Lin D, Zhao G. A Numerical Study on the Optimization of the Material Pressure of the Feeding System. Minerals. 2021; 11(12):1333. https://doi.org/10.3390/min11121333
Chicago/Turabian StyleXu, Ningning, Xinwen Wang, Chi Yu, Dongdong Lin, and Guofeng Zhao. 2021. "A Numerical Study on the Optimization of the Material Pressure of the Feeding System" Minerals 11, no. 12: 1333. https://doi.org/10.3390/min11121333
APA StyleXu, N., Wang, X., Yu, C., Lin, D., & Zhao, G. (2021). A Numerical Study on the Optimization of the Material Pressure of the Feeding System. Minerals, 11(12), 1333. https://doi.org/10.3390/min11121333





