Analyzing Stability Conditions and Ore Dilution in Open Stope Mining
Abstract
:1. Introduction
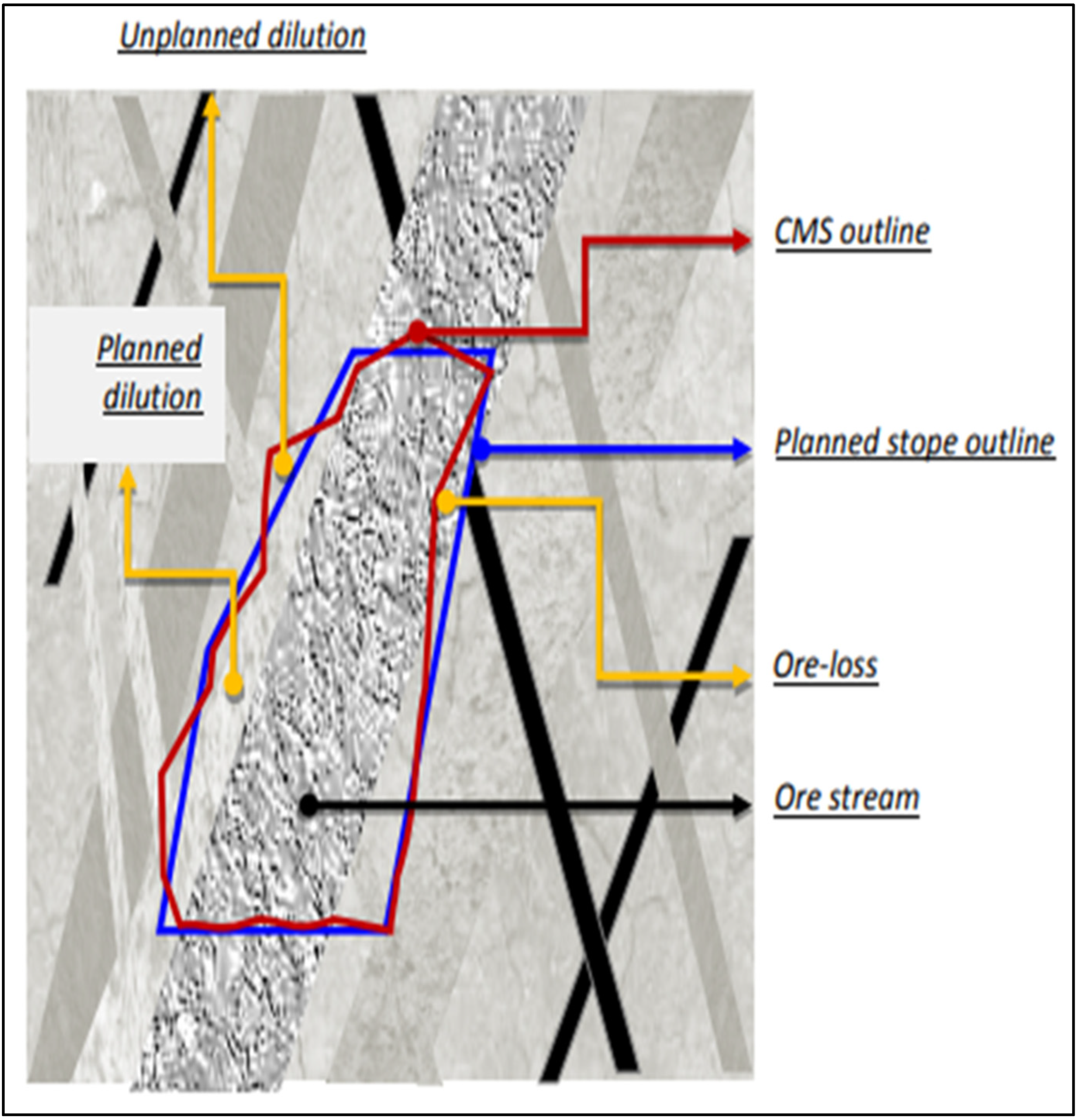
- Drilling and blasting characteristics;
- Stope design factors;
- Geological—Geotechnical factors;
- Human error and others.
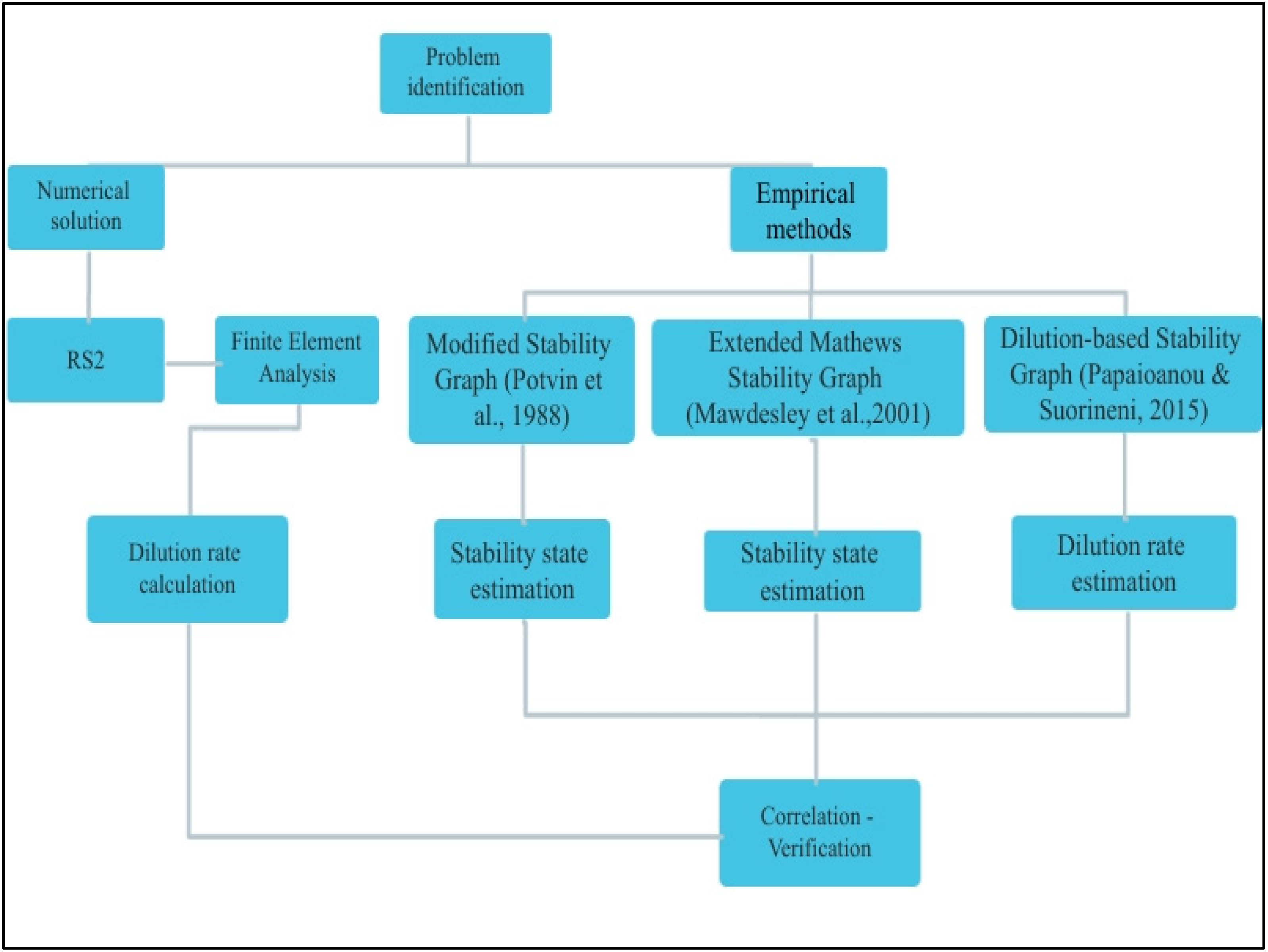
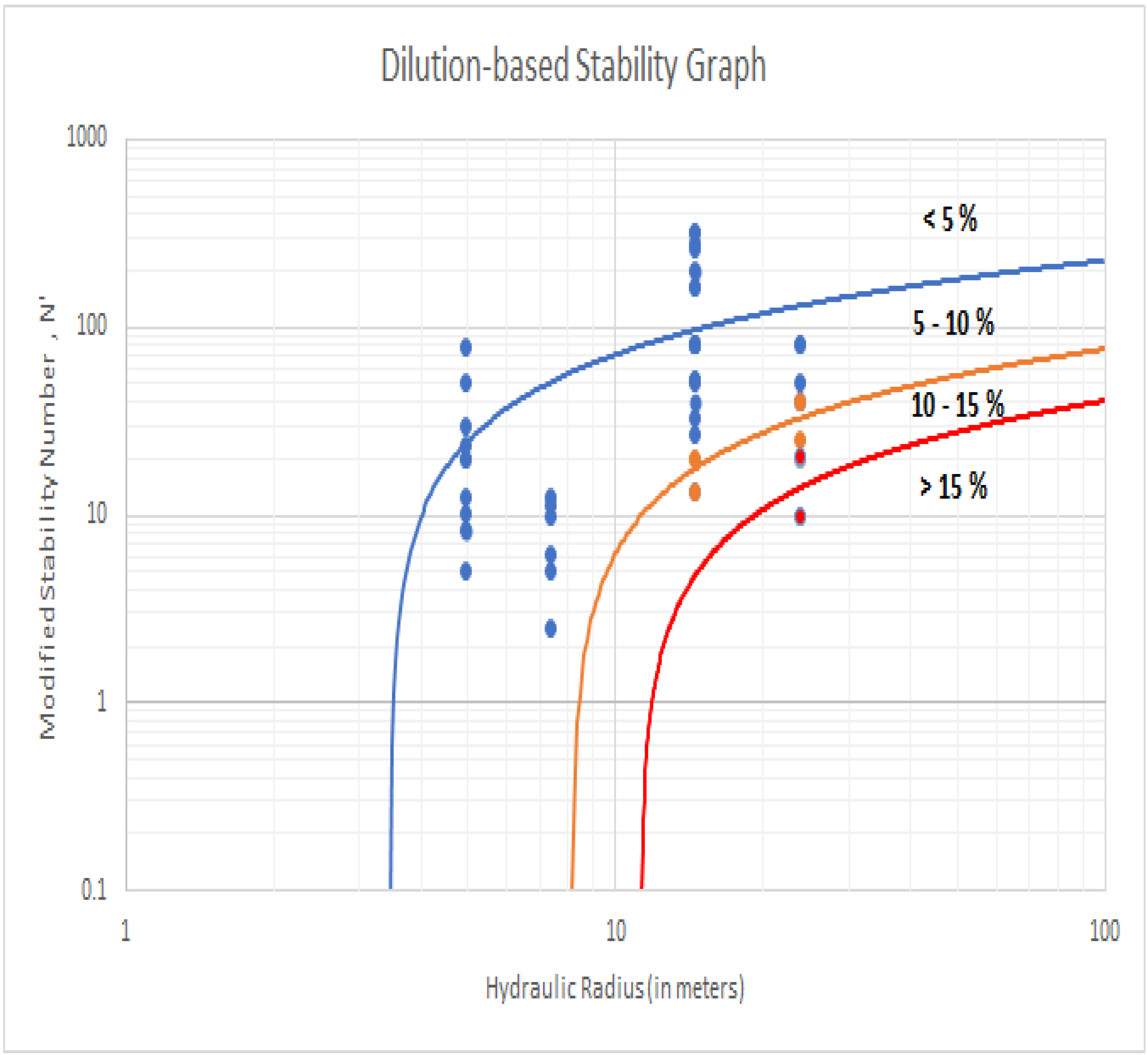
2. Materials and Methods
2.1. Introduction
2.2. Parameters: Values and Assumptions
- Material properties of the surrounding rock;
- Stopes’ geometrical characteristics;
- Infill material between joints surfaces;
- Number of joint sets;
- Inclination of joint sets.
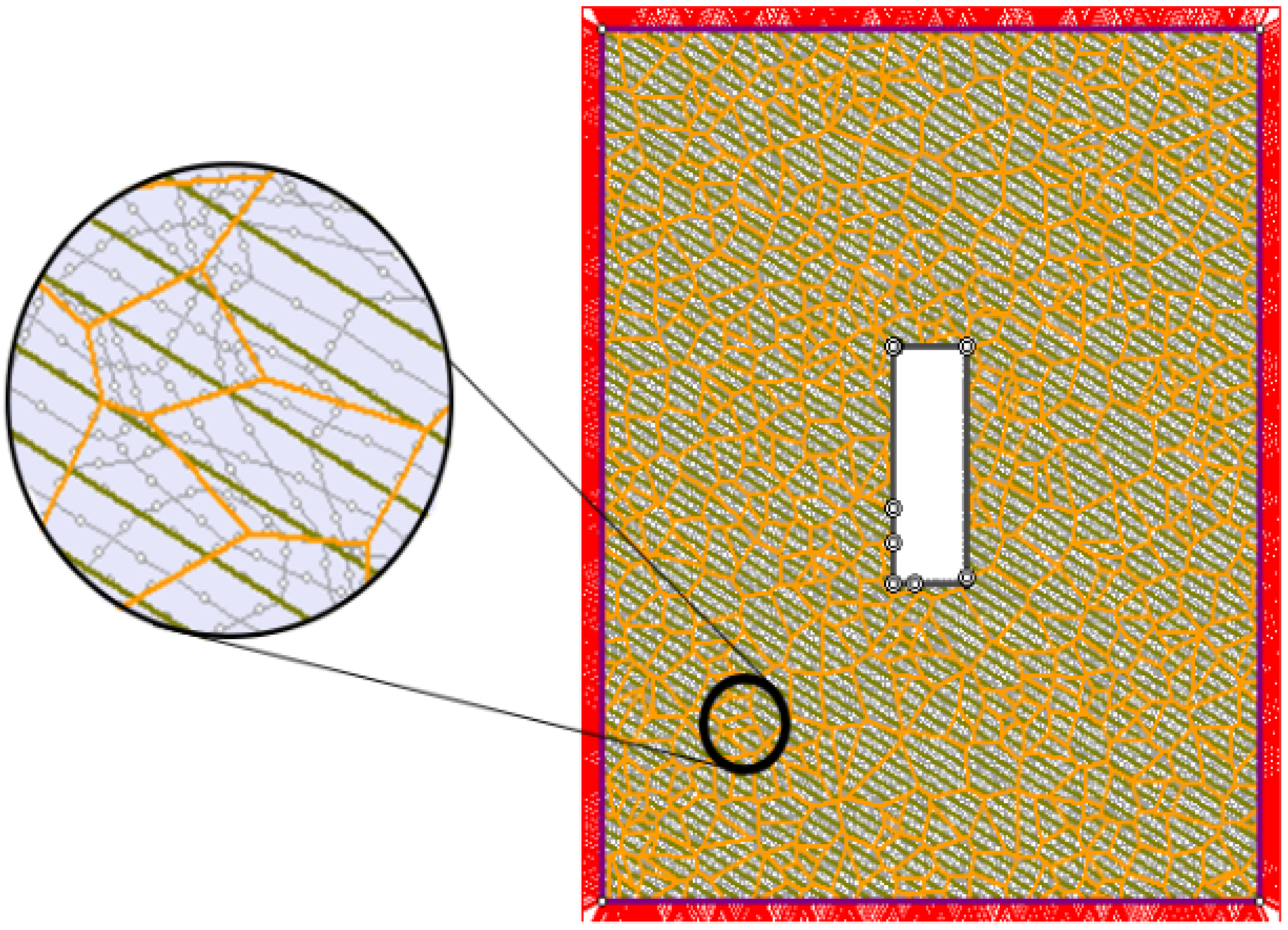
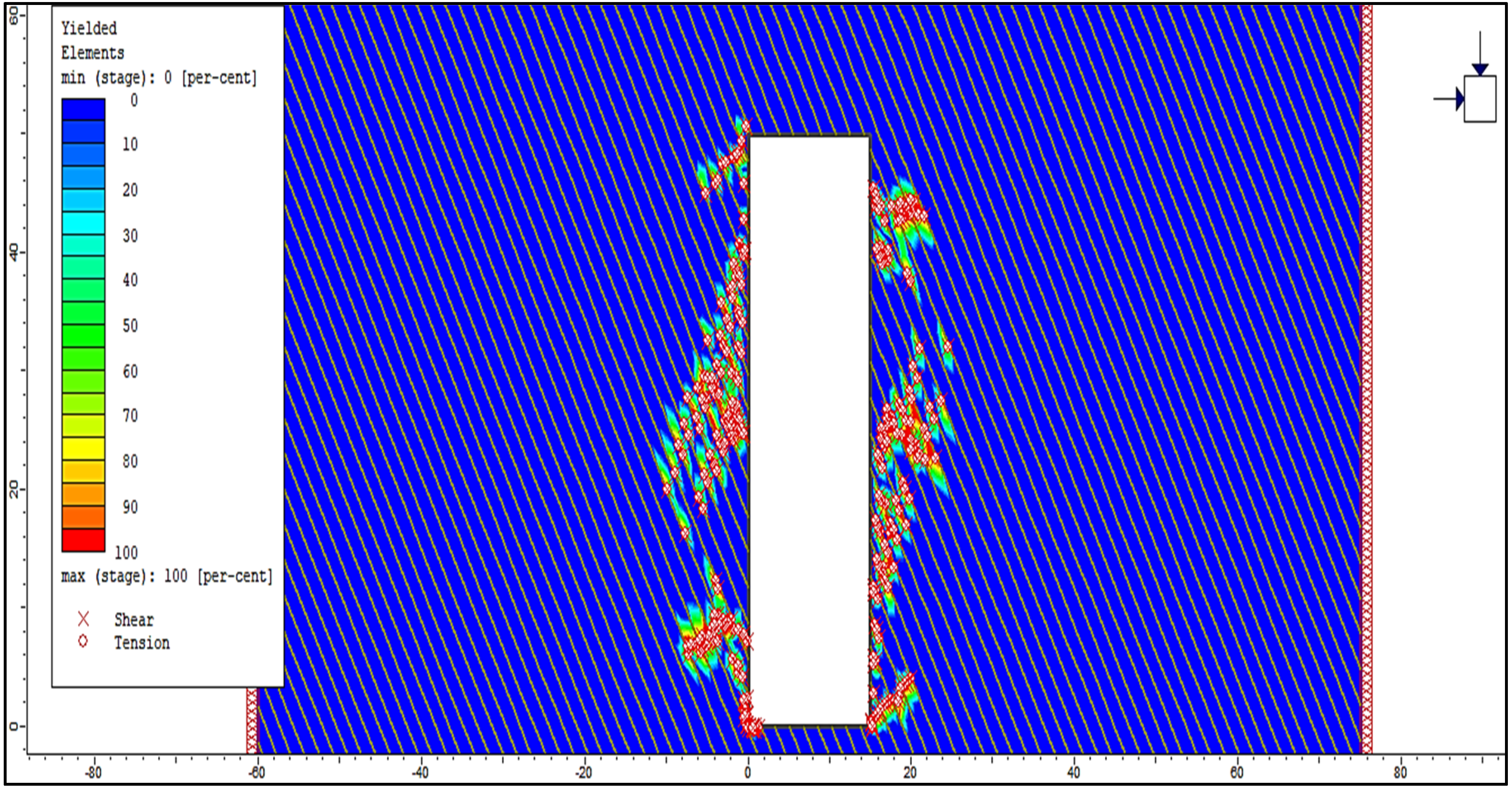
2.3. Methodology of Overbreak Estimation
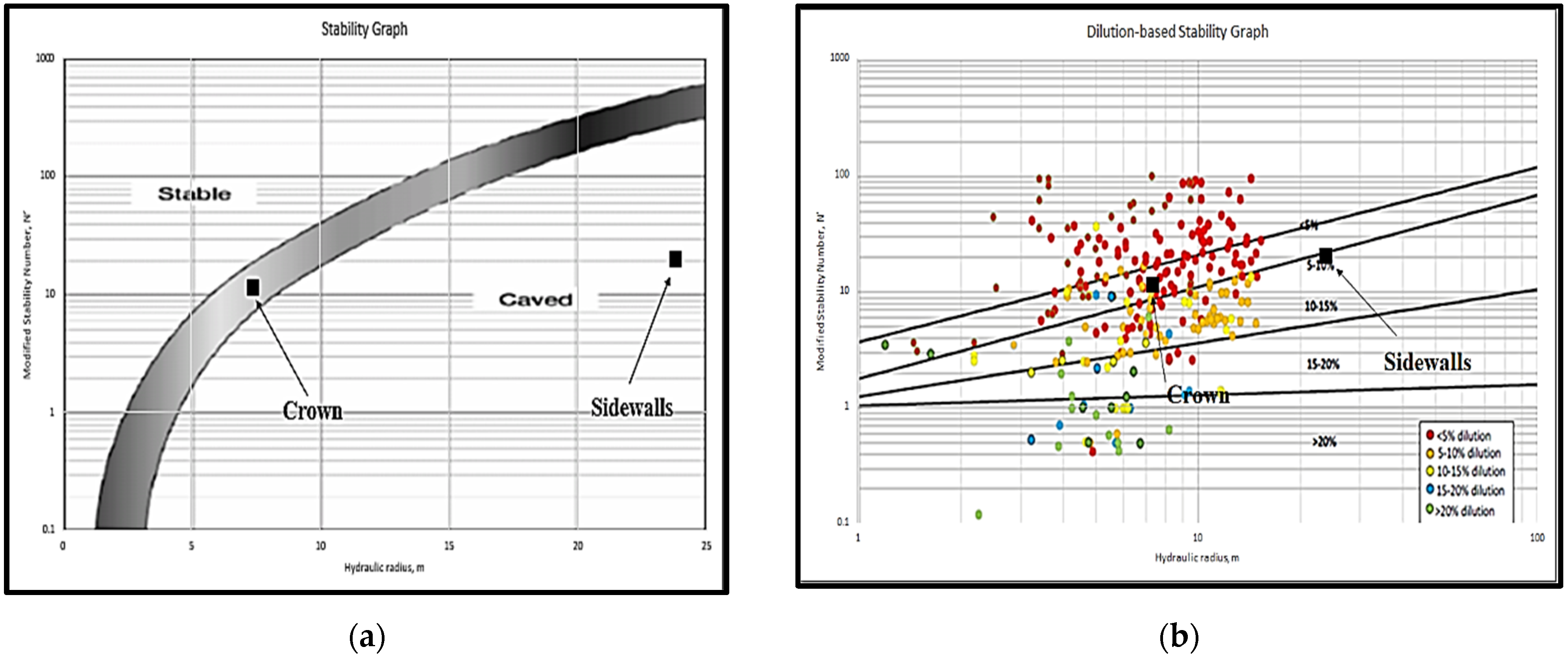
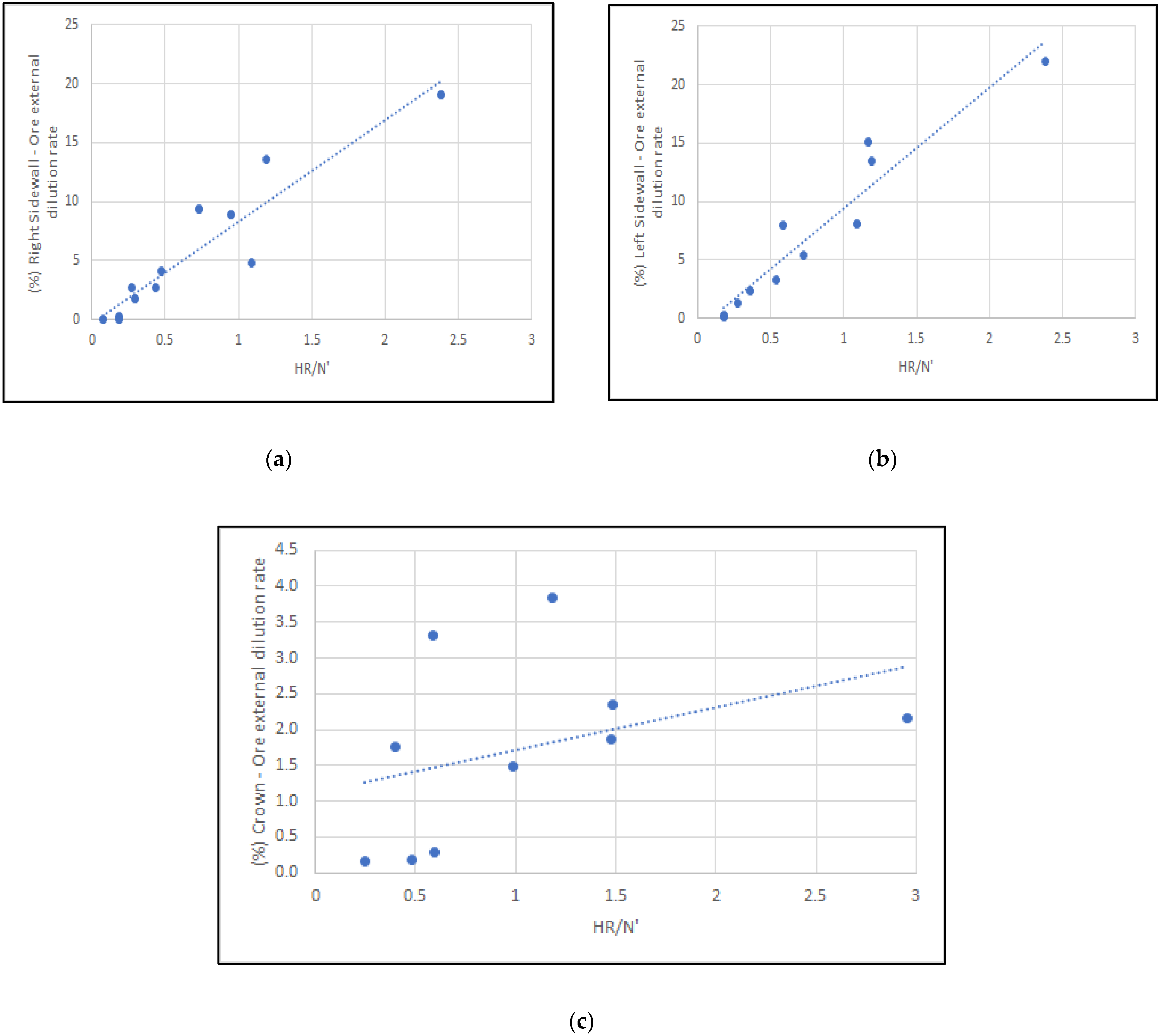
3. Results
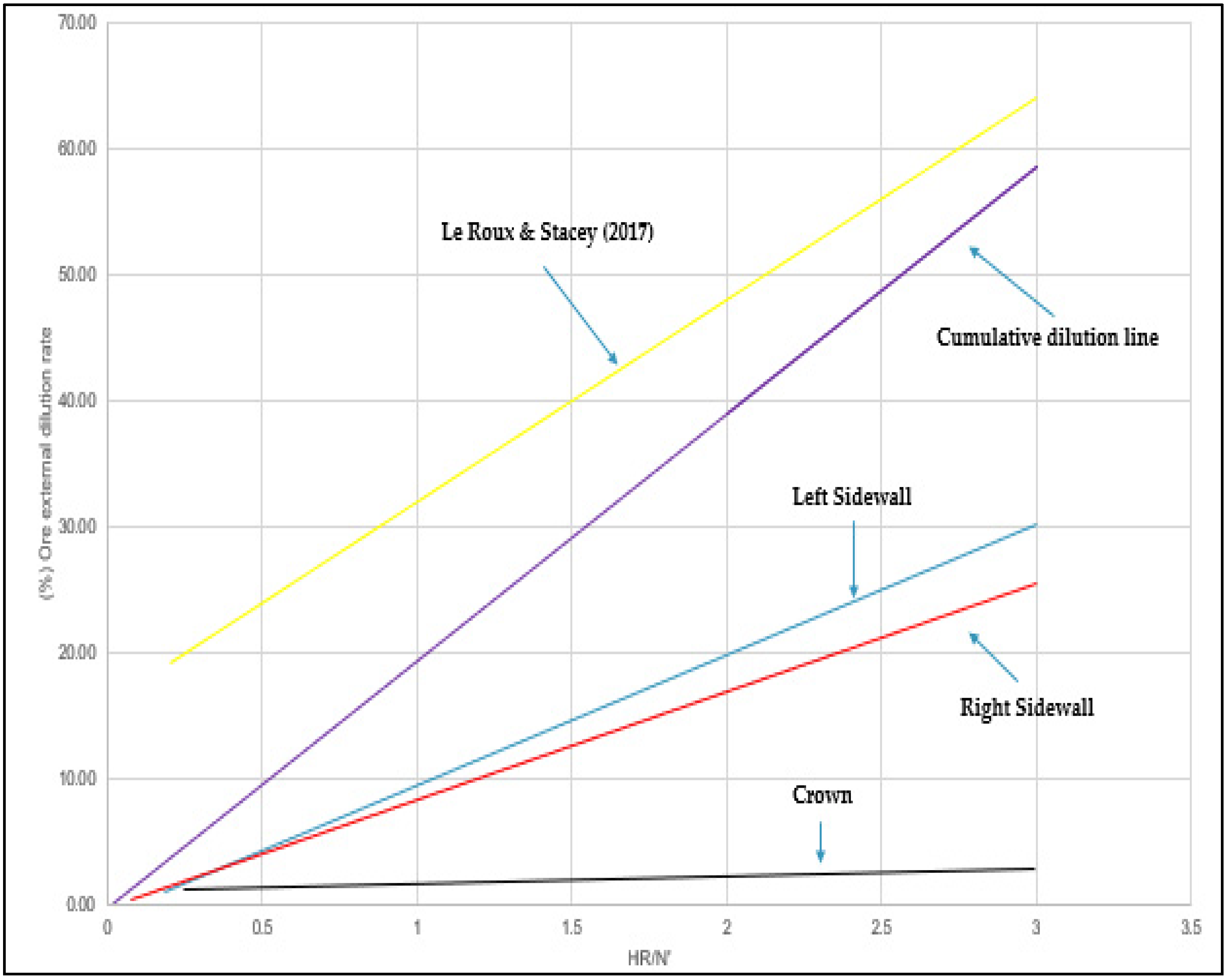
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Villaescusa, E. Geotechnical Design for Dilution Control in Underground Mining. at R. K. Singhal, Mine Planning and Equipment Selection Rotterdam: Balkema. 1998, p. 141. Available online: https://www.researchgate.net/profile/Ernesto-Villaescusa-2/publication/237618005_Geotechnical_design_for_dilution_control_in_underground_mining/links/549ca1440cf2d6581ab4869c/Geotechnical-design-for-dilution-control-in-underground-mining.pdf (accessed on 23 June 2021).
- Pakalnis, R. Empirical Stope Design at Runan Mine. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1986. [Google Scholar]
- Jang, H.D. Unplanned Dilution and Ore-Loss Optimisation in Underground Mines via Cooperative Neuro-Fuzzy Network. Ph.D. Thesis, Western Australia School of Mines, Perth, Australia, 2014. [Google Scholar]
- Planeta, S.; Bourgoin, C. The impact of rock dilution on underground mining. In Proceedings of the 92nd Canadian Institute of Mining Anual General Meeting, Ottawa, ON, Canada, 6–10 May 1990. [Google Scholar]
- Stewart, P.; Trueman, R. Strategies for Minimising and Predicting Dilution in Narrow Vein Mines—The Narrow Vein Dilution Method. In Proceedings of the Narrow Vein Mining Conference, Ballarat, VIC, Canada, 14–15 October 2008. [Google Scholar]
- Suorineni, T. A Critical Review of the Stability Graph Method for Open Stope Design, Conference Paper; MIRARCO/Geomechanics Research Centre (GRC), Laurentian University: Sudbury, ON, Canada, 2012; Available online: https://www.researchgate.net/profile/Fidelis-Suorineni/publication/271191453_A_Critical_Review_of_the_Stability_Graph_Method_for_Open_Stope_Design/links/54bf84ce0cf2f6bf4e04f678/A-Critical-Review-of-the-Stability-Graph-Method-for-Open-Stope-Design.pdf (accessed on 23 June 2021).
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Mathews, K.E.; Hoek, E.; Wylle, D.C.; Stewart, S.B.V. Prediction of Stable Excavation Spans for Mining at Depths below 1000 meters in Hard Rock; Golder Associates: Vancouver, BC, Canada, 1981; pp. 36–110. [Google Scholar]
- Nickson, S.D. Cable Support Guidelines for Underground Hard Rock Mine Operations. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1992. Unpublished work. [Google Scholar]
- Potvin, Y.; Hudyma, M.; Miller, H. The Stability Graph Method for Open Stope Design; University of British Columbia: Vancouver, BC, Canada, 1988. [Google Scholar]
- Mawdesley, C.; Trueman, R.; Whiten, W. Extending the Mathews Stability Graph for Open-Stope Design; EBSCO Publishing: Ipswich, MA, USA, 2001. [Google Scholar]
- Papaioanou, A.; Suorineni, F. Dilution-Based Stability Graph for Open Stope Design; Research Gate: Berlin, Germany, 2015. [Google Scholar]
- Suorineni, F.T. The stability graph after three decades in use:experiences and the way forward. Int. J. Min. Reclam. Environ. 2010, 24, 307–339. [Google Scholar] [CrossRef]
- Le Roux, P.; Stacey, T. Value creation in a mine operating with open stoping mining methods. J. South Afr. Inst. Min. Metall. 2017, 117, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Potvin, Y.; Milne, D. Empirical cable bolt support design. In Proceedings of the International Symposium on Rock Mechanics, Sudbury, ON, Canada, 16–19 June 1992. [Google Scholar]
- Scoble, M.J.; Moss, A. Dilution in underground bulk mining: Implications for production management, mineral resource evaluation, II. Geol. Soc. Sp. Publ. 1994, 79, 95–108. [Google Scholar] [CrossRef]
- Stewart, S.B.V.; Forsyth, W.W. The Mathews method for open stope design. CIM Bull. 1995, 88, 45–53. [Google Scholar]
- Hadjigeorgiou, J.; Leclaire, J.; Potvin, Y.Y. An update of the stability graph method of open stope design. In Proceedings of the 97th Annual General Meeting; Canadian Institute of Mining, Metallurgy and Petroleum: Halifax, NS, Canada, 1995; pp. 154–161. [Google Scholar]
- Milne, D.M.; Pakalnis, R.C.; Lunder, P.J. Approach to the quantification of hanging-wall behaviour. Trans. Inst. Min. Metall. 1996, 105, A69–A74. [Google Scholar]
- Clark, L.M.; Pakalnis, R.C. An empirical approach for estimating unplanned dilutionfrom open stope hangingwalls and footwalls. In Proceedings of the 99th Annual General Meeting; [CD-ROM]; Canadian Institute of Mining, Metallurgy and Petroleum: Vancouver, BC, Canada, 1997. [Google Scholar]
- Germain, P.; Hadjigeorgiou, J. Influence of stope geometry on mining performance. In Proceedings of the 100th Annual General Meeting; [CD-ROM]; Canadian Institute of Mining, Metallurgy and Petroleum: Vancouver, BC, Canada, 1998. [Google Scholar]
- Suorineni, F.T. Effects of Faults and Stress on Open Stope Design. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1998. [Google Scholar]
- Suorineni, F.T.; Tannant, D.D.; Kaiser, P.K. Fault factor for the stability graph method of open-stope design. Trans. Inst. Min. Metall. Sect. A. Mining Ind. 1999, 108, A92–A104. [Google Scholar]
- Diederichs, M.S.; Kaiser, P.K. Tensile strength and abutment relaxation as failure control mechanisms in underground excavations. Int. J. Rock Mech. Min. Sci. 1999, 36, 69–96. [Google Scholar] [CrossRef]
- Trueman, R.; Mikula, P.; Mawdesley, C.; Haries, N. Experience in Australiawith the application of the Mathews method of open stope design. CIM Bull. 2000, 93, 162–167. [Google Scholar]
- Trueman, R.; Mawdesley, C. Predicting cave initiation and propagation. CIM Bull. 2003, 96, 54–59. [Google Scholar]
- Suorineni, F.T.; Henning, J.G.; Kaiser, P.K. Narrow-vein mining experiences at Ashanti: Case study. In Proceedings of the International National Symposium, Mining Techniques of Narrow-Vein Deposits; Canadian Institute of Mining, Metallurgy and Petroleum: Val’Dor, QC, Canada, 2001. [Google Scholar]
- Bewick, R.; Kaiser, P.K. Numerical assessment of factor B in Mathews’ method for open stope design. In Proceedings of the 3rd CAN-US Rock Mechanics Symposium; [CD-ROM]; Canadian Rock Mechanics Association: Toronto, ON, Canada, 2009. [Google Scholar]
- Mitri, H.S.; Hughes, R.; Zhang, Y. New Rock Stress Factor for the Stability Graph Method. Int. J. Rock Mech. Min. Sci. 2011, 48, 141–145. [Google Scholar] [CrossRef]
- Rocscience RS2-2D Geotechnical Finite Element Analysis. Toronto, ON, Canada. 2020. Available online: https://www.rocscience.com/software/rs2 (accessed on 23 June 2021).


| Period | Developments |
|---|---|
| 1980–1985 |
|
| 1985–1990 |
|
| 1990–1995 |
|
| 1995–2000 |
|
| 2000–2005 | |
| 2005–2010 |
|
| 2010–to date |
|
| Material | Stope’s Geometry | Infill Material | Joint Sets | Joint Inclination |
|---|---|---|---|---|
| Gneiss | Geometry 1 | Calcite-based | One joint set | 30° |
| Marble | Geometry 2 | Clay-based | One joint set + random | 45° |
| - | - | Without infill material | - | 60° |
| Category | Rock Material | Geometry Type | Infill Material | Joint Set Numbers |
|---|---|---|---|---|
| Category 1 | Gneiss | Geometry 1 | Without infill material | One set |
| Category 2 | Marble | Geometry 1 | Without infill material | One set |
| Category 3 | Marble | Geometry 1 | Calcite-based infill material | One set |
| Category 4 | Marble | Geometry 2 | Calcite-based infill material | One set |
| Category 5 | Marble | Geometry 2 | Clay-based infill material | One set |
| Category 6 | Marble | Geometry 1 | Calcite-based infill material | One set + random |
| Material | σci (MPa) | σt (MPa) | E (MPa) | Cohesion (MPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Gneiss | 175 | 10 | 70,000 | 36.24 | 45 |
| Marble | 63.8 | 4.4 | 54,230 | 13.21 | 45 |
| Geometry Type | Height (m) | Width (m) |
|---|---|---|
| Geometry 1 | 30 | 10 |
| Geometry 2 | 50 | 15 |
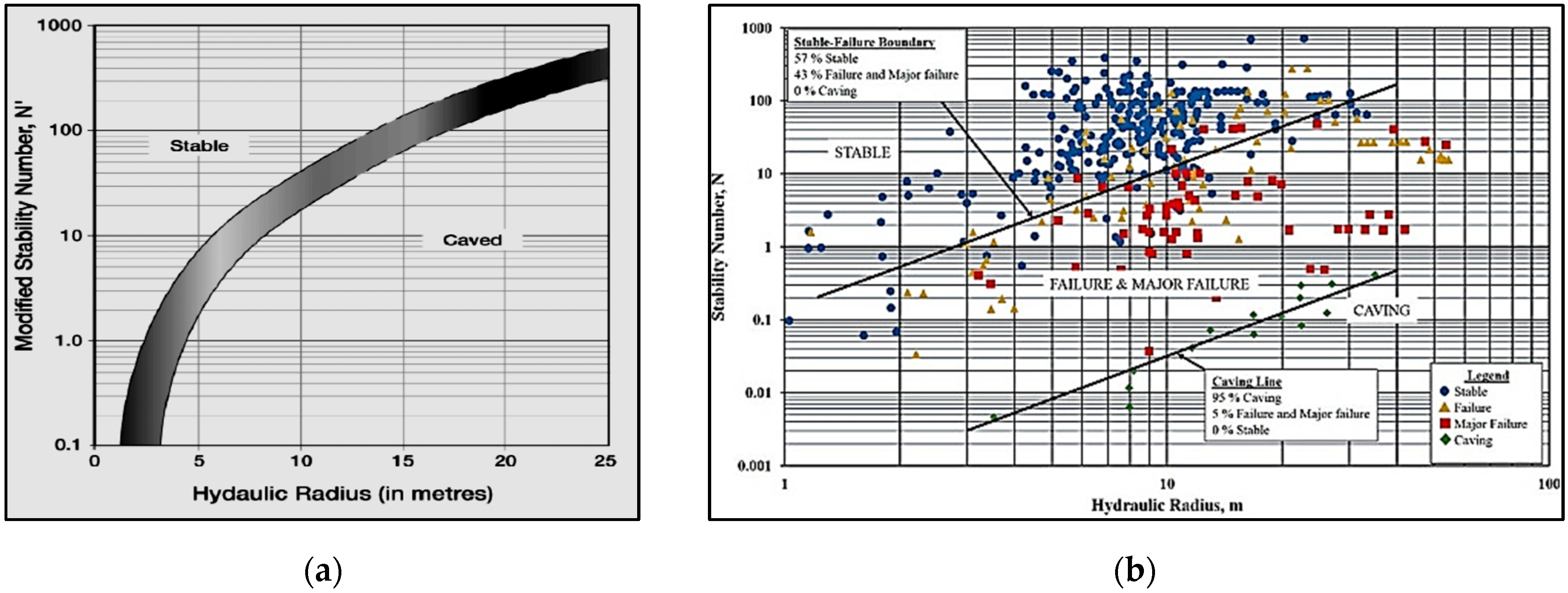
| Examined Surface | A | B | C | Q | N | N′ | HR (m) | Expected Dilution (%) [12] | Expected Stability State [10] | Calculated Dilution (%)—FEA |
|---|---|---|---|---|---|---|---|---|---|---|
| Crown | 0.58 | 0.8 | 1 | 12.5 | 5.8 | 11.2 | 7.39 | 5–10 | Caved | 0.00 |
| Left Sidewall | 1 | 0.34 | 8 | 12.5 | 34 | 20 | 23.81 | 10–15 | Caved | 13.46 |
| Right Sidewall | 1 | 0.34 | 8 | 12.5 | 34 | 20 | 23.81 | 10–15 | Transitional | 13.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delentas, A.; Benardos, A.; Nomikos, P. Analyzing Stability Conditions and Ore Dilution in Open Stope Mining. Minerals 2021, 11, 1404. https://doi.org/10.3390/min11121404
Delentas A, Benardos A, Nomikos P. Analyzing Stability Conditions and Ore Dilution in Open Stope Mining. Minerals. 2021; 11(12):1404. https://doi.org/10.3390/min11121404
Chicago/Turabian StyleDelentas, Andreas, Andreas Benardos, and Pavlos Nomikos. 2021. "Analyzing Stability Conditions and Ore Dilution in Open Stope Mining" Minerals 11, no. 12: 1404. https://doi.org/10.3390/min11121404
APA StyleDelentas, A., Benardos, A., & Nomikos, P. (2021). Analyzing Stability Conditions and Ore Dilution in Open Stope Mining. Minerals, 11(12), 1404. https://doi.org/10.3390/min11121404








