Abstract
With the goal of answering the highly debated question of whether the presence of Ni at the Earth’s inner core can make body-centered cubic (bcc) Fe stable, we performed a computational study based on first-principles calculations on bcc, hexagonal closed packed (hcp), and face-centered cubic (fcc) structures of the Fe1−xNix alloys (x = 0, 0.0312, 0.042, 0.0625, 0.084, 0.125, 0.14, 0.175) at 200–364 GPa and investigated their relative stability. Our thorough study reveals that the stability of Ni-doped bcc Fe is crucially dependent on the nature of the distribution of Ni in the Fe matrix. We confirm this observation by considering several possible configurations for a given concentration of Ni doping. Our theoretical evidence suggests that Ni-doped bcc Fe could be a stable phase at the Earth’s inner core condition as compared to its hcp and fcc counterparts.
1. Introduction
The fact that the Earth’s metallic solid inner core is dominated by iron (Fe) with 5–15% of nickel (Ni) is well established by a combination of seismology and iron-meteorite geochemical studies [1,2]. Thus, the physical properties of Fe-Ni alloy at relevant thermodynamic conditions are important to understand the chemical composition and dynamics of the Earth’s core. In the past, several studies have reported a phase diagram of pure Fe from relatively modest to high (as compared to Earth’s inner core; 330 GPa < P < 360 GPa) pressures and temperatures [3,4,5,6,7,8,9,10]. Based on these results, there is a growing consensus that pure Fe would stabilize in the hexagonal closed packed (hcp) structure at inner core conditions [11]. However, theoretical calculations and experimental results suggest that the addition of a small amount of Ni in Fe alloy may have a profound effect on the properties of Fe [10,12,13,14,15,16,17,18]. Experimental studies at modestly high pressures and temperatures (72 GPa and 3000 K, [12]; 86 GPa and 2382 K, [19]; <107 GPa and <2600 K, [13]) show that the presence of Ni prefers a face-centered cubic (fcc) structure, whereas recent experimental results on Fe with 10% Ni suggest that the hcp structure of Fe is the stable phase at Earth’s core conditions (250 GPa and 2730 K; [20]; 2011; 340 GPa and 4700 K; [10]). However, if the temperature at the inner core boundary is higher than 6400 K, a two-phase (hcp and fcc) outer region may also exist [12,21]. Mikhaylushkin et al. (2007) reported a mixture of hcp- and fcc-Fe phase at 165 GPa that was quenched from high temperature, which may be interpreted as an indication of body-centered cubic (bcc)-Fe at high pressure and temperature condition [22]. While Dubrovinsky et al. [23] showed that the presence of Ni stabilized the body-centered cubic (bcc) structure of Fe under inner-core conditions (up to 225 GPa and 3400 K) using X-ray diffraction technique in combination with the use of diamond anvil cells (DAC) to 300 GPa and 2000 K on Fe-Ni alloys, Kuwayama et al. [14] suggested that the crystallizing phase of Fe-Ni alloy depends on the amount of Ni present in the core the during early core formation period and indicated the possibility of Fe-Ni alloy taking up an fcc structure upon cooling.
Seismological observations indicate that the Earth’s inner core is elastically anisotropic with both hemispherical and depth variations [24,25,26,27]. It has been interpreted that the preferred orientation of the hcp phase of Fe may explain the seismic anisotropy at core temperatures [28,29]. However, the aligned hcp-Fe is not sufficient to explain the observed anisotropy as the c/a axial ratio of hcp-Fe becomes more ideal at higher pressures and temperatures, effectively lowering the elastic anisotropy [4,30]. In addition, aligned bcc-Fe can display a large elastic anisotropy required for explaining the inner core anisotropy [31,32]. It is worth noting here that since the bcc structure is a more open structure (with a lower atomic packing fraction, i.e., 0.68) compared to the close-packed fcc or hcp (with an atomic packing fraction = 0.74), it might partly overcome the density deficit at the inner core, exhibited by Fe in its close-packed hcp/fcc structure. The crucial issue, however, is the stability of the bcc phase of Fe at Earth’s inner core condition of pressure and temperature and the role played by the presence of Ni, which needs a careful investigation.
A recent ab initio quantum mechanical simulation [16] suggested that the fcc structure of Fe-Ni alloy is dynamically stable over bcc structure, evidenced in terms of negative phonon frequencies in Ni-doped bcc Fe structure and its absence in the fcc phase. It is to be noted that the conclusion by Côté et al. was arrived at based on calculations that considered only a specific configuration of Ni distribution in the Fe matrix. In particular, Ni atoms were placed at the body center position of each bcc motif of the supercell. In such a situation, the distance between any two Ni atoms is constant and therefore can be considered as a uniform distribution. However, there can be many other possible ways in which Ni can be distributed in the bcc matrix of Fe; e.g., Ni atoms can cluster together in the bcc-lattice, or there can be several other random distributions of Ni, where the uniform Ni-Ni distance is not maintained. Our first-principles density-functional-theory-based calculations, which take into account different possible arrangements of Ni distribution in the Fe matrix, find that apart from the atypical case where Ni is uniformly distributed in the bcc-Fe lattice, Ni doping makes bcc Fe both dynamically and thermodynamically stable at inner core conditions. This forms the central finding of our study. Although the hcp phase has been suggested to be the most stable phase at the Earth’s inner core conditions by a huge majority of experiments [3,4,7,33,34,35], nonetheless, with pure Ni crystallizing in the fcc phase, the fcc phase also forms a part of our study. We have therefore investigated the thermodynamic stability of the bcc phase with respect to both the hcp and fcc phases of Fe/Fe-Ni. Our results strongly support the idea of bcc Fe-Ni alloy as a promising candidate for the Earth’s inner core.
2. Methodology
All calculations have been performed using first-principles density functional theory (DFT) as implemented in the plane-wave based Vienna Ab initio Simulation Package (VASP) [36,37,38], within the option of Generalized Gradient Approximation (GGA) for exchange-correlation functional as implemented in the Perdew-Burke-Ernzerhof (PBE-GGA) [39] formulation. The possible correlation effect in Fe-d and Ni-d manifold on the results was cross-checked in terms of supplemented +U calculations in representative cases. It was found that the trend of the results presented here remains unchanged upon the inclusion of U. We have used projector-augmented wave (PAW) potentials, and the wave functions were expanded in a plane wave basis with a kinetic energy cut-off of 900 eV. For the valence configuration, we employed eight electrons for Fe (3d64s2) and 10 electrons for Ni (3d84s2). To ensure the convergence of electronic energies during the self-consistent run and the calculation of Hellmann-Feynman forces on atoms during structural optimization using the conjugate gradient algorithm, we used a convergence criterion of 1 × 10−8 eV and 1 × 10−3 eV/Å respectively. Our calculations suggest that under Earth’s core pressure and temperature conditions, both Fe and Ni [40,41] in Fe-Ni alloy become non-magnetic [42], though that does not rule out the possibility of some disordered magnetic moments, especially at Ni sites. In all our calculations, symmetry was switched off during structural optimization, and Fermi-smearing was implemented in order to account for the contribution of electronic excitations to the free energy.
We have considered two different cell sizes, namely 4 × 3 × 2 (48 atoms per cell) and 4 × 4 × 4 (128 atoms per cell) and varied the concentration of Ni (3.125%, 4.2%, 6.25%, 8.4%, 12.5%, 14%, and 17.5%). The effect of Ni doping was considered within the periodic set-up of DFT by replacing a fraction of Fe atoms by Ni atoms within the constructed supercell. With a given specific concentration of Ni, various different configurations can be realized. For example, the Ni atoms can be uniformly distributed such that the distance between any two nearest-neighbor Ni atoms is maintained at a constant value. This can be achieved if Ni is made to occupy the body centers of the bcc structure. A representative case of such uniform distribution of Ni is shown in the inset of Figure 1, where there are eight Ni atoms uniformly distributed in a bcc lattice containing 128 atoms. In addition to such uniform distribution, there can be many other possibilities, where the nearest-neighbor distance between the various doped Ni atoms can vary. As opposed to the uniform distribution of doped Ni atoms, we attribute such configurations as “random”, although technically they are not random and constitute one of the many different configurations of Ni-doping in the bcc-Fe lattice. A representative case of a random arrangement of eight Ni atoms in a bcc Fe lattice of total 128 atoms is shown in the inset of Figure 1. In our study, we have considered “uniform” as well as various different “random” arrangements of Ni atoms for different doping concentrations. For the Brillouin zone sampling of the bcc lattice, Monkhorst-Pack k-mesh sampling of size 4 × 6 × 8 was used for the 4 × 3 × 2 super-cell and a k-mesh sampling of 4 × 4 × 4 was used for the supercell of dimension 4 × 4 × 4. Similarly, for the hcp lattice, Monkhorst-Pack k-mesh sampling with a size of 4 × 4 × 4 was used for the 4 × 4 × 4 supercell. For the fcc lattice, Monkhorst-Pack k-mesh sampling of size 4 × 4 × 4 was used for the 4 × 4 × 2 supercell. The convergence of k-points on the calculated properties has been checked. In order to predict the volume of a given bcc-Fe-Ni alloy at Earth’s inner core pressure, we calculated the energy as a function of volume for a 128-atom unit cell containing 6.25% Ni (cf Model 2 in the inset of Figure 1). We found that third-order Birch-Murnaghan equation of state adequately describes the energy-volume results with Vo = 10.91 Å3/atom, K = 220.19 GPa, and K′ = 4.49. The P-V equation of state has been presented in the supplementary materials (Figure S1). In order to estimate the volume of hcp Fe at the Earth’s inner core pressure, we employed third-order Birch-Murnaghan’s equation of state (3 B-M EOS) [43] with Vo = 10.25 Å3/atom, bulk modulus K = 290.6 GPa and K′ = 4.29 as obtained from the DFT derived energy–volume relationship of hcp Fe-6.25%Ni. The corresponding 3 B-M EOS parameters for fcc Fe-6.25%Ni alloy were: Vo = 10.34 Å3/atom; K = 272.6 GPa; K′ = 4.4. A comparison of the EOS parameters to those we obtained with previously reported EOS parameters for pure and Ni-doped bcc, hcp, and fcc phases of Fe is presented in the SI (refer to S3). The elastic tensor has been determined from the stress–strain relationship [44]. The bulk and shear moduli were calculated subsequently from the elastic tensor using the Voight-Hill-Reuss approach [45,46]. Further, using the calculated bulk and shear moduli and the density, the P and S wave velocities, i.e., VP and Vs, were determined using the following formulas:
where K and G and ρ are, respectively, the bulk and shear moduli and density of the material. The adiabatic bulk modulus (BS) and the isothermal bulk modulus (BT) are related through
where α is the thermal volumetric expansion co-efficient and γ is the Grüneisen parameter [47].
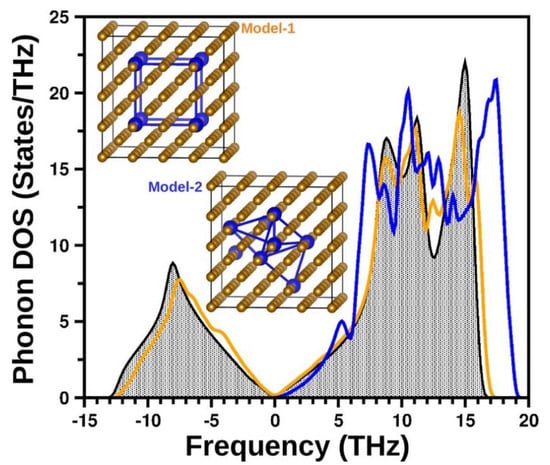
Figure 1.
Phonon density of states (DOS) for body-centered cubic (bcc)-Fe (black shaded curve), 6.25% Ni containing bcc Fe-Ni alloy in two different configurations; Model-1: uniform (orange) and Model-2: random (blue) calculated at 364 GPa. The inset shows the corresponding models of the Ni-doped cases for which the phonon DOS has been shown.
Phonon dispersion and free energies were calculated within the framework of quasi-harmonic approximation as implemented in the PHONOPY code [48]. The real space force constants were obtained using Density Functional Perturbation Theory (DFPT) as implemented in the VASP code. Starting from the Helmholtz Free energies, computed at ten different volumes within pressures range between 100–364 GPa, the effect of thermal expansion was considered within the quasi-harmonic approximation to obtain the Gibbs free energies of the different phases at Earth’s core pressure.
3. Results
We determined the dynamical stability of the Ni-doped and undoped bcc, hcp, and fcc phases of iron at inner core conditions from the calculated phonon density of states (DOS). In Figure 1, we present a comparison of the phonon density of states for bcc Fe and 6.25% Ni containing bcc Fe in two different configurations, namely uniform and one of the possible random configurations (cf inset) at 364 GPa, which corresponds to the pressure at the center of the Earth. The presence of imaginary modes (represented as negative frequencies in the figure) in the phonon DOS of undoped bcc-Fe shows that it is dynamically unstable under inner-core conditions in confirmation with previous experimental and theoretical investigations ([16] and references therein). The phonon DOS for uniformly distributed Ni atoms in the bcc lattice is also found to be unstable with large imaginary frequencies, confirming the findings of [16]. However, remarkably, the phonon DOS for the randomly distributed Ni is found to be dynamically stable. To ascertain this fact, we considered six different configurations for 3.125% (four Ni out of 128 atoms per cell) Ni containing bcc Fe-Ni alloy as shown in supplementary materials Figures S2–S7 of the SI. It was observed that when the Ni atoms are not distributed uniformly, the atoms in the resultant optimized structure are slightly displaced (~1%) from the perfect bcc lattice, maintaining the overall cubic symmetry. This slight displacement of atoms happens because Ni does not prefer a bcc structure and is known to take up an fcc structure at all temperatures. When these Ni atoms are randomly distributed, they try to distort the structure in order to increase its coordination, thereby making the lattice structure dynamically stable. However, when these Ni atoms are symmetrically placed, as is the case when they sit at the body centers of the bcc lattice, the distortion caused by one Ni atom is counter-balanced by the neighboring Ni atoms, thereby retaining the body-centered cubic structure, which is shown to be dynamically unstable. Calculation of free energy difference of uniform and random structures shows that apart from being dynamically stable, the random configuration is also energetically more favorable as compared to the symmetric arrangement of Ni. For the specific examples of the uniform and random structures shown in the inset of Figure 1, the free energy difference turned out to be 0.305 eV/atom, which is substantial.
We repeated the above exercise for different concentrations of Ni in the range of 3.125% to 17.5% in order to ascertain whether the stabilization of bcc Fe by randomly distributed Ni doping remains valid in all cases. The results are summarized in Figure 2. It is reassuring to find that the bcc Fe phase remains dynamically stable for a wide range of Ni doping if the distribution of dopants is considered to be random.
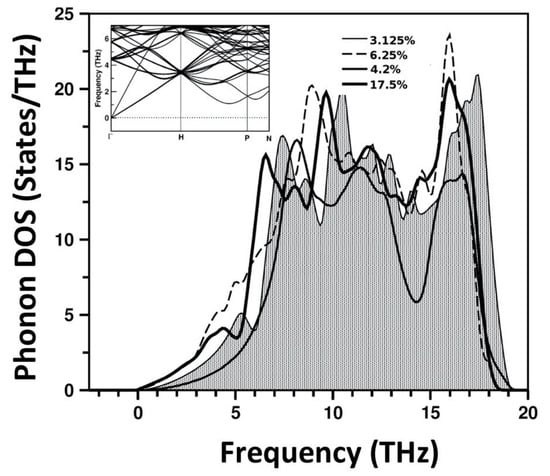
Figure 2.
DFT calculated phonon DOS at 364 GPa for Fe-Ni alloy with varied Ni concentrations. The Ni atoms were carefully distributed in a random fashion in the bcc Fe matrix. Inset shows the phonon band structure of the 3.125% Ni-containing case.
In the next stage, the thermodynamic stability of bcc Fe was further investigated in terms of enthalpy and free energy. As is already known from previous studies [49], we found that up to about 12 GPa bcc-Fe is more stable than hcp-Fe, beyond which the relationship reverts. However, a comparison of enthalpy of fcc-Fe with respect to bcc-Fe shows that the transition to fcc takes place at about 42 GPa (refer to Figure S8 of supplementary materials for details). We next consider Ni-doped systems. The calculated difference in enthalpy of the bcc phase of Fe-Ni alloy with respect to the other two competing phases, namely fcc and hcp, as a function of pressure is shown in the left panel of Figure 3, for the specific case of 6.25% Ni doping. We found that with the introduction of Ni into the system, the bcc to hcp transition pressure was barely affected, whereas the bcc-to-fcc transition takes place at a comparatively lower pressure, thereby showing that Ni-doping increases the stability field of the fcc phase of Fe. The respective transition pressures for bcc to hcp and bcc to fcc were found to be 13 GPa and 34 GPa, respectively. However, the extreme conditions of Earth’s inner core involves high-temperature conditions, in addition to high-pressure conditions. The stability analysis thus needs to be argued in terms of Gibbs energy. Considering the difference in the Gibbs energy for the Ni-doped bcc and hcp phases of Fe, we find that the difference is negative in the entire temperature range of 3000 K to 6000 K, suggesting that at 364 GPa the bcc phase is more stable over the hcp phase as the temperature is increased. Similarly, the difference in Gibbs energy between the bcc and fcc phases of 6.25% Ni-doped Fe suggests that the bcc phase is stable in the entire temperature range. We, therefore, conclude that few percentages of Ni doping in an appropriate manner can stabilize the bcc phase of Fe under Earth’s inner core conditions, both from dynamic and thermodynamic considerations. However, it is to be noted that all our calculations were performed within the purview of quasi-harmonic approximation. Previously, Alfè et al. [50] calculated the total anharmonic contribution to free energy in the case of hcp-Fe to be about 60 meV/atom at 6000 K. The fcc phase with the same packing index is expected to have a similar contribution [16]. However, for the less densely packed bcc phase, anharmonicity might have a greater contribution to free energy. However, small anharmonic perturbations to the harmonic ground states can be safely ignored because differences between small quantities are negligible relative to the total energy. Our calculations show that the Ni-doped bcc-Fe phase is stabilized by about 300 meV/atom as compared to the close-packed structure at 6000 K temperature and 364 GPa pressure.
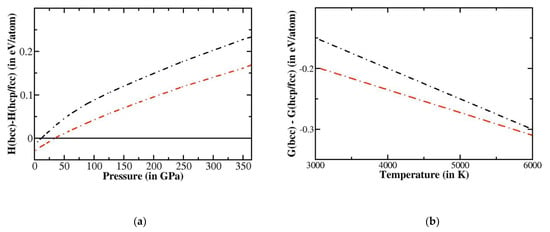
Figure 3.
(a) Enthalpy of hexagonal closed packed (hcp)-Fe [H(hcp)] and face-centered cubic (fcc)-Fe [H(fcc)] with respect to bcc-Fe [H(bcc)] plotted as a function of pressure in the presence of 6.25% Ni doping. Black dashed line: H(bcc)-H(hcp). Red dashed line: H(bcc)-H(fcc). (b) Gibbs energy of hcp-Fe [G(hcp)] and fcc-Fe [G(fcc)] with respect to bcc-Fe [G(bcc)], plotted as a function of temperature. Black dashed line: G(bcc)-G(hcp). Red dashed line: G(bcc)-G(fcc).
4. Discussion
It has been suggested that the free energy difference between hcp-, bcc-, and fcc-Fe is small (of the order of a few mRy/atom) at Earth’s inner core conditions, making all of them possible constituents of the Earth’s inner core [4,43,51,52]. While high-pressure laser heating diamond anvil cell experiments [7,10] and ab-initio calculations [43,51,53] support the possibility that the hcp-Fe or Fe-Ni alloy is the most stable phase at Earth’s inner core conditions, only a few studies suggest that the fcc phase of Fe or Fe-Ni alloy may be stable at inner core pressure and temperature conditions [14,16,54]. However, both these phases of Fe suffer from a severe drawback in terms of the over-estimation of density at Earth’s core conditions as compared to the Preliminary Reference Earth Model (PREM) [55]. This specific discrepancy in addition to a few others (most important among them being the anisotropy) can be overcome by the bcc-phase of Fe or Fe-Ni alloy, which, due to its open structure, is expected to better reproduce the measured density. Unfortunately, one of the major problems with the bcc Fe model so far has been its stability, because it is shown to be elastically and vibrationally unstable at core pressures [12,49]. In the present study, we report our detailed first-principles calculation, which establishes that the bcc-Fe structure can be stabilized at Earth’s inner core condition upon the doping of a few percentages (3% to 17.5%) of Ni, subject to the condition that the dopants are randomly distributed in the Fe matrix, thereby restoring the bcc model in discussion for possible candidates.
Sound velocities of Fe-Ni alloy at inner core conditions are essential for the interpretation of seismic observations of the Earth’s core. We have therefore calculated the adiabatic compressional-wave (VP) and shear-wave (VS) sound velocities of the two comparatively more stable phases of Fe-Ni alloy, namely, hcp and bcc as a function of density (ρ), as shown in Figure 4. It is to be noted that the computed elastic properties are static; i.e., they do not include the high-temperature effect and would therefore only approximate the actual values at Earth’s core temperatures. Our calculations find that the density of the hcp phase of Fe and Fe-Ni alloy at inner core conditions is higher than that given by PREM [55] by 5.7% and 6.4%, respectively. However, bcc Fe-Ni alloy is seen to reproduce the density of the inner core within a reasonable limit. The density of bcc-Fe-Ni alloy is found to differ by 3.3% from the actual density of the inner core as given by the PREM model. The calculated phase wave velocity was also seen to be well satisfied for the case of bcc-Fe-Ni alloy, where we find that the calculated data are lower than the PREM data by 1%, whereas in the case of hcp-Fe-Ni alloy, it is off by 16%. We compared our theoretically observed sound velocity vs. density trend with the coherent experimental results using consistent pressure scale, equation of state of hcp-Fe, etc. [33,34,56,57,58,59,60,61] and shock wave determination along the Hugoniot curve at high temperatures [62]. Mao et al. (1998) obtained the compressional wave velocity on hcp-Fe at the relatively low pressure of 16.5 GPa using pulse-echo ultrasonic techniques in multi-anvil large-volume presses. Using the impulsive stimulated light scattering (ISLS) method, Crowhurst et al. (2004) measured aggregate sound velocities of hcp-Fe up to 115 GPa, whereas, by using picosecond acoustics method in diamond anvil cell, Decremps et al. [61] reported sound velocity measurements of iron up to 152 GPa. Ohtani et al. [33] determined the compressional wave velocity of powdered hcp-Fe using high-resolution IXS and in situ X-ray powder diffraction at 300 K and pressure up to 174 GPa. Antonegeli et al. [57,58] carried out sound wave velocity measurements at 300 K and pressure up to 112 GPa using inelastic X-ray Scattering (IXS) and X-ray diffraction (XRD). The linear fit to the experimental values of sound velocities is extrapolated to inner core densities and compared to PREM, which shows slightly higher values than PREM for both VP and VS, i.e., 3% to 4% above PREM, with slightly steeper slope. This is probably due to the fact that different spectrometer techniques and absolute energy calibration were used in these experimental studies. More details can be obtained in Antonangeli and Ohtani [63] for hcp-Fe under static compression by different methods on the pressure and density dependence of the sound velocities. In addition, the most accurate nuclear resonant inelastic X-ray scattering (NRIXS) measurements [34,60] were used to compare VS at ambient temperature and pressure up to 171 GPa. In addition, the temperatures in high-pressure experiments are much lower than inner core temperatures [5]. As can be inferred from Figure 4, the computed densities of Ni-doped bcc Fe are higher than the PREM. However, the densities of Ni-doped bcc Fe decrease several percent (~3%) compared to hcp Fe and hcp Fe-Ni alloy. Our calculated Vs of bcc Fe-Ni alloy at inner core conditions deviates to a great extent from the PREM. This may be partly due to anharmonic and/or premelting activity at high-temperature [64,65,66] or frequency-dependent viscoelastic relaxations [67] as well as the presence of melt [68,69] in the inner core (as suggested by seismic observations and quantum mechanical calculations), which has the ability to lower the shear wave velocity.
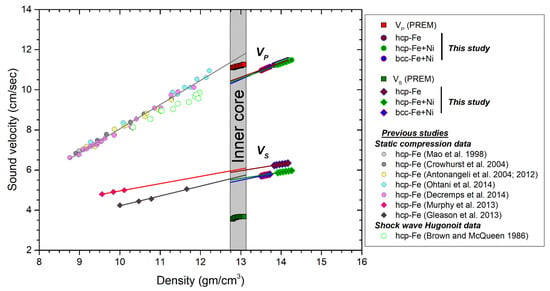
Figure 4.
Calculated compressional and shear velocities of Ni-doped bcc and hcp Fe equivalents at inner core conditions as a function of density and compared with hcp-Fe and the experimental results from 300 K to 1000 K [33,34,56,57,58,59,60,61] and PREM [55] and shock wave Hugonoit measurements at high temperatures [62]. The computed densities of hcp-Fe-Ni alloy and hcp-Fe (filled green and brown circles and diamonds, respectively) are higher than PREM. However, the density of bcc-Fe-Ni alloy (filled blue circle and diamond) is close to PREM. Light grey circle: Mao et al. [56]; grey circle: Crowhurst et al. [59]; yellow circle: Antonangeli et al. [57,58]; cyan circle: Ohtani et al. [33]; magenta circle: Decremps et al. [61]; green hexagon: Brown and McQueen, [62]; red diamond: Murphy et al. [34]; grey diamond: Gleason et al. [60]. The solid lines are a linear regression across all previous experimental results and theoretical data from the present study.
Seismological studies also suggest that there exists strong seismic anisotropy in the Earth’s inner core, with the longitudinal waves traveling faster along the Earth’s rotational axis than in the equatorial plane [24]. Several studies indicate that this seismic anisotropy can be explained in terms of the preferred lattice orientation of the hcp-Fe [70]. However, there are also conflicting reports, which suggest that since the c/a ratio of hcp-Fe comes close to the ideal 1.63 at the temperature of the inner core [71], hcp-Fe is not elastically anisotropic under inner-core conditions. A recent report by Mattesini et al. [72] on the other hand, suggests on the basis of modelling of seismic data that anisotropy of the Earth’s core can only be disclosed by a lattice-preferred orientation of a body-centered-cubic iron aggregate, having a fraction of their {111} crystal axes parallel to the Earth’s rotation axis. A few theoretical calculations and experimental studies also suggest an hcp-to-bcc transition of iron at high pressure and temperature condition [4,43,73,74]. A recent paper by Belonoshko et al. [22] shows the stability of pure bcc-Fe at temperatures of the order of 7000 K and 360 GPa pressure using ab initio molecular dynamics at constant pressure and temperature on a cell size of 1024 atoms. They suggest that the dynamical stability at high temperature is achieved by diffusion of atoms along the directions of the soft modes, which would otherwise make bcc-Fe lattice unstable at low temperatures. Such a diffusion may have profound consequences for the formation of lattice preferential orientation anisotropy, extremely low shear resistance, and high attenuation of seismic waves. Examination of their structure by extracting the snap-shots of the actual dynamics finds that the co-ordination of the atoms in the bcc lattice increases in a way such that the first co-ordination sphere contains half of the atoms from the second shell due to thermal motion, which they suggest has been misinterpreted as a closed packed structure by shock-wave experiments [75]. It is to be noted that our proposed crystal structure of Ni-doped bcc-Fe also indicates slight distortion of the bcc lattice (in an attempt to increase the co-ordination around the doped Ni-atoms). In addition, based on the melting temperature of iron at extreme conditions, a recent experimental study suggests that the predicted temperature at the inner core boundary is more than 6200 K [5]. If this is true, then Fe stabilizes the bcc structure at the Earth’s inner core condition [22]. Seismic observations suggest that the density of the solid inner core is slightly lower than pure Fe and Fe-Ni alloy under inner core pressure and temperature conditions [76], suggesting the presence of some light element such as oxygen, sulfur, silicon, and carbon in the inner core. The solid inner core also crystallizes from the liquid outer core, and therefore, a small amount (<3%) of light elements could be present in the Earth’s inner core [77]. This seems plausible, which together with our analysis of results, strongly suggests that bcc structure of Fe phase, along with few percentage points of Ni doping and few percentage points of one or more light elements with preferred orientation, may produce seismic anisotropy that could be used to explain the observed seismic anisotropy in the Earth’s inner core [78,79,80]. However, it is to be noted that a detailed investigation requires performing ab initio molecular dynamics (AIMD) simulation up to Earth’s core pressure and temperature on all possible dynamically stable configurations of Ni-doped bcc Fe. Calculations to implement this, though computationally very expensive (owing to (i) the large size of the supercell; (ii) the lack of symmetry in the calculations, and (iii) the huge number of possible “random” configurations in a large supercell), form a part of our future endeavours.
5. Concluding Remarks and Implications
Using first principles DFT, we investigate the effect of Ni doping at Earth’s inner core condition on the thermodynamic stability of the bcc phase of Fe. Our calculation finds that the manner in which the Ni atoms are distributed in the bcc-Fe lattice plays a very crucial role in making the lattice dynamically stable at inner core conditions. It was found that only those configurations where Ni is distributed randomly in the bcc-Fe lattice become dynamically stable at inner conditions as determined from our calculation of the phonon dispersion relation. However, for those configurations where the Ni atoms are distributed uniformly in the bcc-lattice, the structure turns out to be dynamically unstable at inner core conditions, as predicted previously. The calculated density of the stable 6.25% Ni-doped bcc-Fe was found to give a better agreement with PREM, differing by 3% as opposed to 6.4% for the hcp phase of Fe-Ni alloy. The remaining discrepancy in the calculated value of our predicted structure of bcc Fe-Ni alloy with respect to PREM presumably hints towards the presence of some light elements [79] in the Earth’s inner core as indicated by several geochemical and cosmochemical studies. The true nature and the incorporation mechanism of the appropriate light element, however, is a matter that needs to be studied.
Supplementary Materials
The following are available online at https://www.mdpi.com/2075-163X/11/3/258/s1, Text S1: The P-V third order Birch-Murnaghan–s equation of state for bcc-Fe-Ni alloy; Text S2: Six different models involving 3.125% Ni doped bcc Fe (i.e., there are 4 Ni atoms and 124 Fe atoms per unit cell); Text S3: The third order Birch-Murnaghan’s equation of state(3B-M) fitting parameters for the different compositions considered in this study presented in comparison with previous first principles based studies; Text S4: The calculated enthalpy of hcp-Fe and fcc-Fe with respect to bcc-Fe in eV/atom in the range 0 GPa to 100 GPa.
Author Contributions
Conceptualization: T.S.-D.; investigation: S.C.; formal analysis: S.C., S.G., T.S.-D.; software: S.C.; supervision: T.S.-D.; writing—original draft: S.C., S.G.; writing—review and editing: T.S.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge the contribution of T. Das at the initial stages of this project. We thank three anonymous reviewers for their constructive comments. Any additional data may be obtained from S.C. (swastika@iiserkol.ac.in) and S.G. (sujoy.ghosh@gg.iitkgp.ac.in).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allégre, C.J.; Poirier, J.-P.; Humler, E.; Hofmann, A.W. The chemical composition of the Earth. Earth Planet. Sci. Lett. 1995, 134, 515–526. [Google Scholar] [CrossRef]
- Anderson, D.L. Theory of the Earth; Blackwell Scientific Publications: Hoboken, NJ, USA, 1989. [Google Scholar]
- Vočadlo, L.; Brodholt, J.; Alfe, D.; Price, G.D. The structure of iron under the conditions of the Earth’s inner core. Geophys. Res. Lett. 1999, 26, 1231–1234. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Ahuja, R.; Johansson, B. Stability of the body-centred-cubic phase of iron in the Earth’s inner core. Nature 2003, 424, 1032. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 2013, 340, 464–466. [Google Scholar] [CrossRef]
- Denoeud, A.; Ozaki , N.; Benuzzi-Mounaix, A.; Uranishi , H.; Kondon, Y.; Kodama, R.; Brambrink, E.; Ravasio, A.; Bocoum, M.; Boudenne , J.-M.; et al. Dynamic X-ray diffraction observation of shocked solid iron up to 170 GPa. Proc. Natl. Acad. Sci. USA 2016, 113, 7745–7749. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Ohishi, Y.; Tatsumi, Y. The structure of iron in Earth’s inner core. Science 2010, 330, 359–361. [Google Scholar] [CrossRef]
- Luo, W.; Johansson, B.; Eriksson, O.; Arapan, S.; Souvatzis, P.; Katsnelson, M.I.; Ahuja, R. Dynamical stability of body center cubic iron at the Earth’s core conditions. Proc. Natl. Acad. Sci. USA 2010, 107, 9962. [Google Scholar] [CrossRef]
- Aquilanti, G.; Trapananti, A.; Karandikar, A.; Kantor, I.; Marini, C.; Mathon, O.; Pascarelli, S.; Boehler, R. Melting of iron determined by X-ray absorption spectroscopy to 100 GPa. Proc. Natl. Acad. Sci. USA 2015, 112, 12042–12045. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Komabayashi, T.; Ozawa, H.; Ohishi, Y. The structure of Fe-Ni alloy in Earth’s inner core. Geophys. Res. Lett. 2012, 39, L12305. [Google Scholar] [CrossRef]
- Hirose, K.; Labrosse, S.; Hernlund, J. Composition and state of the core. Ann. Rev. Earth Planet. Sci. 2013, 41, 657–691. [Google Scholar] [CrossRef]
- Mao, W.L.; Campbell, A.J.; Heinz, D.L.; Shen, G.Y. Phase relations of Fe-Ni alloys at high pressure and temperature. Phys. Earth Planet. Inter. 2006, 155, 146–151. [Google Scholar] [CrossRef]
- Komabayashi, T.; Hirose, K.; Ohishi, Y. In situ X-ray diffraction measurements of the fcc–hcp phase transition boundary of an Fe-Ni alloy in an internally heated diamond anvil cell. Phys. Chem. Miner. 2012, 39, 329–338. [Google Scholar] [CrossRef]
- Kuwayama, Y.; Hirose, K.; Sata, N.; Ohishi, Y. Phase relations of Fe and Fe-Ni alloys up to 300 GPa: Implications for composition and structure of the Earth’s inner core. Earth Planet. Sci. Lett. 2008, 273, 379–385. [Google Scholar] [CrossRef]
- Vočadlo, L.; Dobson, D.P.; Wood, I.G. Ab initio study of nickel substitution into iron. Earth Planet. Sci. Lett. 2006, 248, 132–137. [Google Scholar] [CrossRef]
- Côté, A.S.; Vočadlo, L.; Brodholt, J.P. Ab initio simulations of iron-nickel alloys at Earth’s core conditions. Earth Planet. Sci. Lett. 2012, 345, 126–130. [Google Scholar] [CrossRef][Green Version]
- Martorell, B.; Brodholt, J.; Wood, I.G.; Vočadlo, L. The effect of nickel on the properties of iron at the conditions of Earth’s inner core: Ab initio calculations of seismic wave velocities of Fe-Ni alloys. Earth Planet. Sci. Lett. 2013, 365, 143–151. [Google Scholar] [CrossRef]
- Ekholm, M.; Mikhaylushkin, A.S.; Simak, S.I.; Johansson, B.; Abrokosov, I.A. Configurational thermodynamis of Fe-Ni alloys at Earth’s core conditions. Earth Planet. Sci. Lett. 2011, 308, 90–96. [Google Scholar] [CrossRef]
- Lin, J.F.; Heinz, D.L.; Campbell, A.J.; Devine, J.M.; Mao, W.L.; Shen, G. Iron-nickel alloy in the Earth’s core. Geophys. Res. Lett. 2002, 29, 1471. [Google Scholar] [CrossRef]
- Sakai, T.; Ohtani, E.; Hirao, N.; Ohishi, Y. Stability field of the hcp-structure for Fe, Fe-Ni, and Fe-Ni-Si alloys up to 3 Mbar. Geophys. Res. Lett. 2011, 38, L09302. [Google Scholar] [CrossRef]
- Torchio, R.; Boccato, S.; Miozzi, F.; Rosa, A.D.; Ishimatsu, N.; Kantor, I.; Sévelin-Radiguet, N.; Briggs, R.; Meneghini, C.; Irifune, T.; et al. Melting curve and phase relations of Fe-Ni alloys: Implications for the Earth’s core composition. Geophys. Res. Lett. 2020, 47, e2020GL088169. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Lukinov, T.; Fu, J.; Zhao, J.; Davis, S.; Simak, S.I. Stabilization of body-centered cubic iron under inner-core condition. Nat. Geosci. 2017, 10, 312. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Narygina, O. Body-centered cubic iron-nickel alloy in Earth’s core. Science 2007, 316, 1880–1883. [Google Scholar] [CrossRef]
- Morelli, A.; Dziewonski, A.M.; Woodhouse, J.H. Anisotropy of the inner core inferred from PKIKP travel times. Geophys. Res Lett. 1986, 13, 1545–1548. [Google Scholar] [CrossRef]
- Woodhouse, J.H.; Giardini, D.; Li, X.D. Evidence for inner core anisotropy from free oscillations. Geophys. Res. Lett. 1986, 13, 1549–1552. [Google Scholar] [CrossRef]
- Song, X.D. Anisotropy of the Earth’s inner core. Rev. Geophys. 1997, 35, 297–313. [Google Scholar] [CrossRef]
- Beghein, C.; Trampert, J. Robust normal mode constraints on inner-core anisotropy from model space search. Science 2003, 229, 552–555. [Google Scholar] [CrossRef] [PubMed]
- Wenk, H.R.; Matthies, S.; Hemley, R.J.; Mao, H.K.; Shu, J. The plastic deformation of iron at pressures of the Earth’s inner core. Nature 2000, 45, 1044–1047. [Google Scholar] [CrossRef] [PubMed]
- Buffett, B.A.; Wenk, H.-R. Texturing of the Earth’s inner core by Maxwell stresses. Nature 2001, 413, 60–63. [Google Scholar] [CrossRef]
- Mattesini, M.; Belonoshko, A.B.; Tkalčić, H. Polymorphic nature of iron and degree of lattice preferred orientations beneath the Earth’s inner core boundary. Geochem. Geophys. Geosyst. 2018, 19, 292–304. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Skorodumova, N.V.; Rosengren, A.; Johansson, B. Elastic anisotropy of Earth’s inner core. Science 2008, 319, 797–800. [Google Scholar] [CrossRef]
- Mattesini, M.; Belonoshko, A.B.; Tkalčić, H.; Buforn, E.; Udias, A.; Ahuja, R. Candy wrapper for the Earth’s inner core. Sci. Rep. 2013, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ohtani, E.; Shibazaki, Y.; Sakai, T.; Mibe, K.; Fukui, H.; Kamada, S.; Sakamaki, T.; Seto, Y.; Tsutsui, S.; Baron, A.Q.R. Sound velocity of hexagonal close packed iron up to core pressures. Geophys. Res. Lett. 2013, 40, 5089–5094. [Google Scholar] [CrossRef]
- Murphy, C.A.; Jackson, J.M.; Sturhahn, W. Experimental constraints on the thermodynamics and sound velocities of hcp-Fe to core pressures. J. Geophys. Res. Solid Earth 2013, 118, 1999–2016. [Google Scholar] [CrossRef]
- Antonangeli, A.; Morard, G.; Paolasini, L.; Garbarini, G.; Murphy, C.A.; Edmund, E.; Decremps, F.; Fiquet, G.; Bosak, A.; Mezouar, M.; et al. Sound velocities and density measurements of solid hcp-Fe and hcp-Fe-Si (9 wt.%) alloy at high pressure: Constraints on the Si abundance in the Earth’s inner core. Earth Planet. Sci. Lett. 2018, 482, 446–453. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab-initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augment d-wave method. Phys. Rev. B 1999, 59, 1158–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Iota, V.; Klepeis, J.H.P.; Yoo, C.S.; Lang, J.; Haskel, D.; Srajer, G. Electronic structure and magnetism in compressed 3d transition metals. Appl. Phys. Lett. 2007, 90, 042505. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Fe melting transition: Electrical resistivity, thermal conductivity, and heat flow at the inner core boundaries of mercury and ganymede. Crystals 2019, 9, 359. [Google Scholar] [CrossRef]
- Vočadlo, L.; Alfe, D.; Gillan, M.J.; Wood, I.G.; Brodholt, J.; Price, G.D. Possible thermal and chemical stabilization of body-centred-cubic iron in the Earth’s core. Nature 2003, 424, 536–539. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Page, Y.L.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; B.G. Teubner: Leipzig, Germany, 1928. [Google Scholar]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties, A Handbook; MIT Press: Cambridge, UK, 1971; Volume 379. [Google Scholar]
- Sha, X.; Cohen, R.E. Lattice dynamics and thermodynamics of bcc iron under pressure: First principles linear response theory. Phys. Rev. B 2006, 73, 104303. [Google Scholar] [CrossRef]
- Togo and Tanaka 2015 Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Stixrude, L.; Cohen, R.E. Constraints on the crystalline structure of the inner core: Mechanical instability of bcc iron at high pressure. Geophys. Res. Lett. 1995, 22, 125–128. [Google Scholar] [CrossRef]
- Alfe, D.; Price, G.D.; Gillan, M.J. Thermodynamics of hexagonal close packed iron under Earth’s core conditions. Phys. Rev. B 2001, 64, 04512316. [Google Scholar] [CrossRef]
- Vočadlo, L.; Wood, I.G.; Alfè, D.; Price, G.D. Ab initio calculations on the free energy and high P–T elasticity of face-centred-cubic iron. Earth Planet. Sci. Lett. 2008, 268, 444–449. [Google Scholar] [CrossRef][Green Version]
- Côté, A.S.; Vočadlo, L.; Brodholt, J.P. Light elements in the core: Effects of impurities on the phase diagram of iron. Geophys. Res. Lett. 2008, 35, L05306. [Google Scholar] [CrossRef]
- Stixrude, L. Structure of Iron to 1 Gbar and 40 000 K. Phys. Rev. Lett. 2012, 108, 055505. [Google Scholar] [CrossRef]
- Mikhaylushkin, A.S.; Simak, S.I.; Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Johansson, B.; Abrikosov, I.A. Pure iron compressed and heated to extreme conditions. Phys. Rev. Lett. 2007, 99, 165505. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Mao, H.K.; Shu, J.; Shen, G.; Hemley, R.J.; Li, B.; Singh, A.K. Elasticity and rheology of iron above 220 GPa and the nature of the Earth’s inner core. Nature 1998, 396, 741–743, (correction Nature 1999, 399, 80). [Google Scholar] [CrossRef]
- Antonangeli, D.; Occelli, F.; Requardt, H.; Badro, J.; Fiquet, G.; Krisch, M. Elastic anisotropy in textured hcp-iron to 112 GPa from sound velocity wave propagation measurements. Earth Planet. Sci. Lett. 2004, 225, 243–251. [Google Scholar] [CrossRef]
- Antonangeli, D.; Komabayashi, T.; Occelli, F.; Borissenko, E.; Walters, A.C.; Fiquest, G.; Fei, Y. Simultaneous sound velocity and density measurements of hcp iron upto 93GPa and 1100K: An experimental test of the Birch’s law at high tempearture. Earth Planet. Sci. Lett. 2012, 331, 210–214. [Google Scholar] [CrossRef]
- Crowhurst, J.C.; Goncharov, A.F.; Zaug, J.M. Impulsive stimulated light scattering from opaque materials at high pressure. J. Phys. Condens. Matter 2004, 16, S1137–S1142. [Google Scholar] [CrossRef]
- Gleason, A.E.; Mao, W.L.; Zhao, J.Y. Sound velocities for hexagonally close packed iron compressed hydrostatically to 136 GPa from phonon density of states. Geophys. Res. Lett. 2013, 40, 2983–2987. [Google Scholar] [CrossRef]
- Decremps, F.; Antonangeli, D.; Gauthier, M.; Ayrinhac, S.; Morand, M.; Le Marchand, G.; Bergame, F.; Philippe, J. Sound velocity measurements of iron up to 152 GPa by picosecond acoustics in diamond anvil cell. Geophys. Res. Lett. 2014, 41, 1459. [Google Scholar] [CrossRef]
- Brown, J.M.; McQueen, R.G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. Solid Earth 1986, 91, 7485–7494. [Google Scholar] [CrossRef]
- Antonangeli, D.; Ohtani, E. Sound velocity of hcp-Fe at high pressure: Experimental constraints, extrapolations and comparison with seismic models. Prog. Earth Planet. Sci. 2015, 2, 3. [Google Scholar] [CrossRef]
- Laio, A.; Bernard, S.; Chiarotti, G.L.; Scandolo, S.; Tosatti, E. Physics of iron at Earth’s core conditions. Science 2000, 287, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
- Vočadlo, L.; Dobson, D.P.; Wood, I.G. Ab initio calculations of the elasticity of hcp-Fe as a function of temperature at inner-core pressure. Earth Planet. Sci. Lett. 2009, 288, 534–538. [Google Scholar] [CrossRef]
- Martorell, B.; Vočadlo, L.; Brodholt, J.; Wood, I.G. Strong premelting effect in the elastic properties of hcp-Fe under inner-core conditions. Science 2013, 342, 466–468. [Google Scholar] [CrossRef]
- Jackson, I.; Gerald, J.F.; Kokkonen, H. High-temperature viscoelastic relaxation in iron and its implications for the shear modulus and attenuation of the Earth’s inner core. J. Geophys. Res. 2000, 1105, 23605–23634. [Google Scholar] [CrossRef]
- Singh, S.C.; Taylor, M.A.J.; Montagner, J.P. On the presence of liquid in Earth’s inner core. Science 2000, 287, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Vočadlo, L. Ab initio calculations of the elasticity of iron and iron alloys at inner core conditions: Evidence for a partially molten inner core? Earth Planet. Sci. Lett. 2007, 254, 227–232. [Google Scholar] [CrossRef]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R.E.; Gülseren, O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 2001, 413, 57–60. [Google Scholar] [CrossRef]
- Gannarelli, C.M.S.; Alfè, D.; Gillan, M.J. The axial ratio of hcp iron at the conditions of the Earth’s inner core. Phys. Earth Planet. Inter. 2005, 152, 67–77. [Google Scholar] [CrossRef]
- Mattesini, M.; Belonoshko, A.B.; Buforn, E.; Ramírez, M.; Simak, S.I.; Udías, A.; Mao, H.K.; Ahuja, R. Hemispherical anisotropic patterns of the Earth’s inner core. Proc. Natl. Acad. Sci. USA 2010, 107, 9507–9512. [Google Scholar] [CrossRef]
- Matsui, M.; Anderson, O.L. The case for a body-centered cubic phase (α′) for iron at inner core conditions. Phys. Earth Planet. Inter. 1997, 103, 55–62. [Google Scholar] [CrossRef]
- Hrubiak, R.; Meng, Y.; Shen, G. Experimental evidence of a body centered cubic iron at the Earth’s core condition. arXiv 2018, arXiv:1804.05109. [Google Scholar]
- Ping, Y.; Coppari, F.; Hicks, D.G.; Yaakobi, B.; Fratanduono, D.E.; Hamel, S.; Eggert, J.H.; Rygg, J.R.; Smith, R.F.; Swift, D.C.; et al. Solid Iron compressed up to 560 GPa. Phys. Rev. Lett. 2013, 111, 065501. [Google Scholar] [CrossRef]
- Stevenson, D.J. Models of the Earth’s core. Science 1981, 214, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Poirier, J.P. Light elements in the Earth’s outer core: A critical review. Phys. Earth Planet. Inter. 1994, 85, 319–337. [Google Scholar] [CrossRef]
- Badro, J.; Côté, A.S.; Brodholt, J.P. A seismologically consistent compositional model of Earth’s core. Proc. Natl. Acad. Sci. USA 2014, 111, 7542–7545. [Google Scholar] [CrossRef]
- Li, J.; Fei, Y. Experimental constraints on core composition, The Mantle and Core. In Treatise on Geochemistry; Carlson, R.W., Ed.; Elsevier: Amsterdam, The Netherland, 2014; Volume 2, pp. 521–546. [Google Scholar]
- Das, T.; Chatterjee, S.; Ghosh, S.; Saha-Dasgupta, T. First-principles prediction of Si-doped Fe carbide as one of the possible constituents of Earth’s inner core. Geophys. Res. Lett. 2017, 44, 8776–8784. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).