Theoretical Study on Thermal Release of Helium-3 in Lunar Ilmenite
Abstract
:1. Introduction
2. Concentration Profile of Helium-3 Trapped in Lunar Ilmenite
2.1. Theoretical Model about Implantation of Helium-3 into Ilmenite
2.2. Concentration Profile of Implanted Helium-3 Ions in Lunar Ilmenite
3. Thermal Release Model of Helium-3
3.1. Molecular Dynamics Simulations
3.1.1. Geometric Models for Helium-3 Thermal Release
3.1.2. Potential Models for Molecular Dynamics
3.2. Similitude Analysis
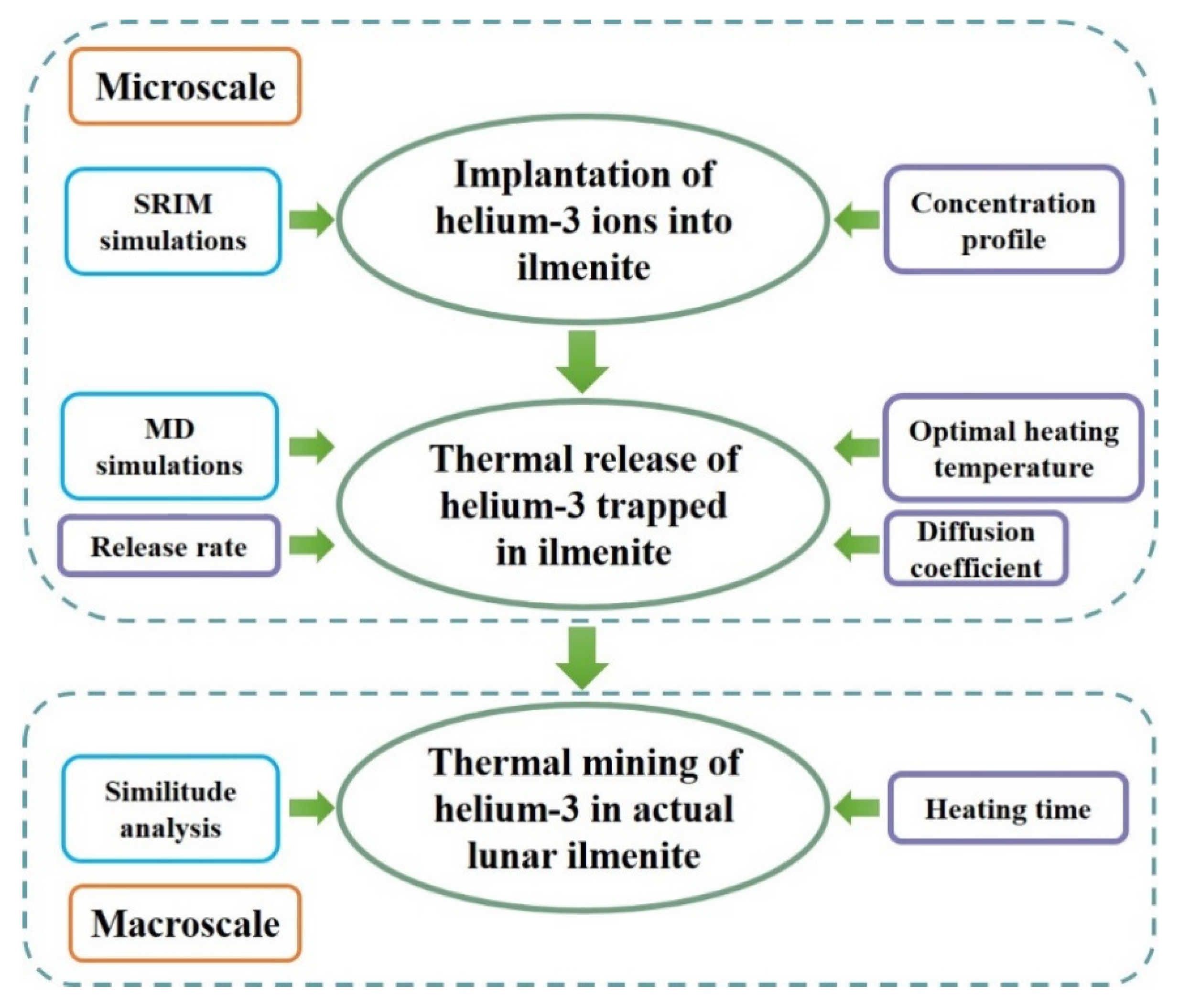
3.3. Calculation Process
4. Results and Discussion
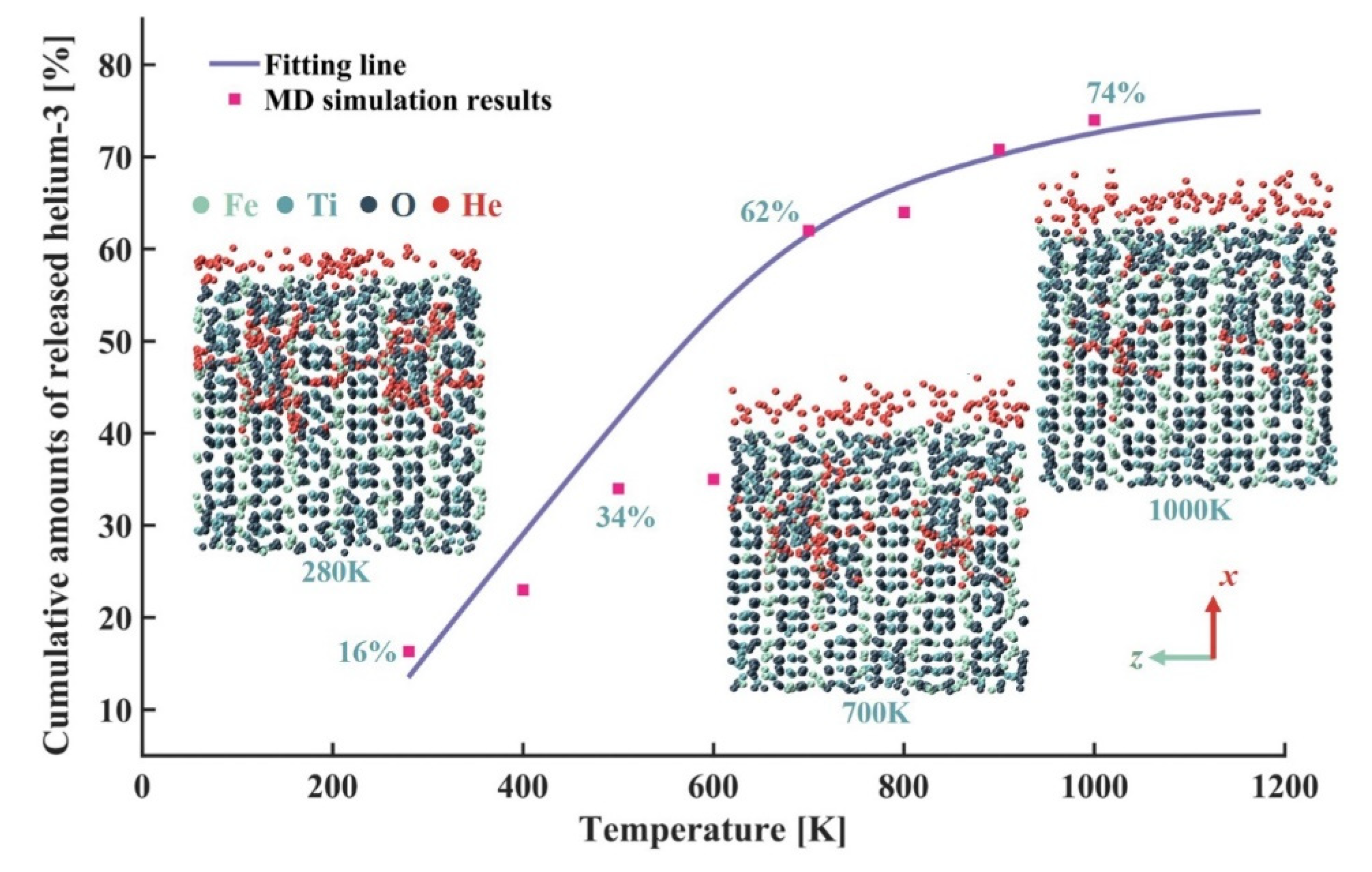
4.1. Validation of Molecular Dynamics Model
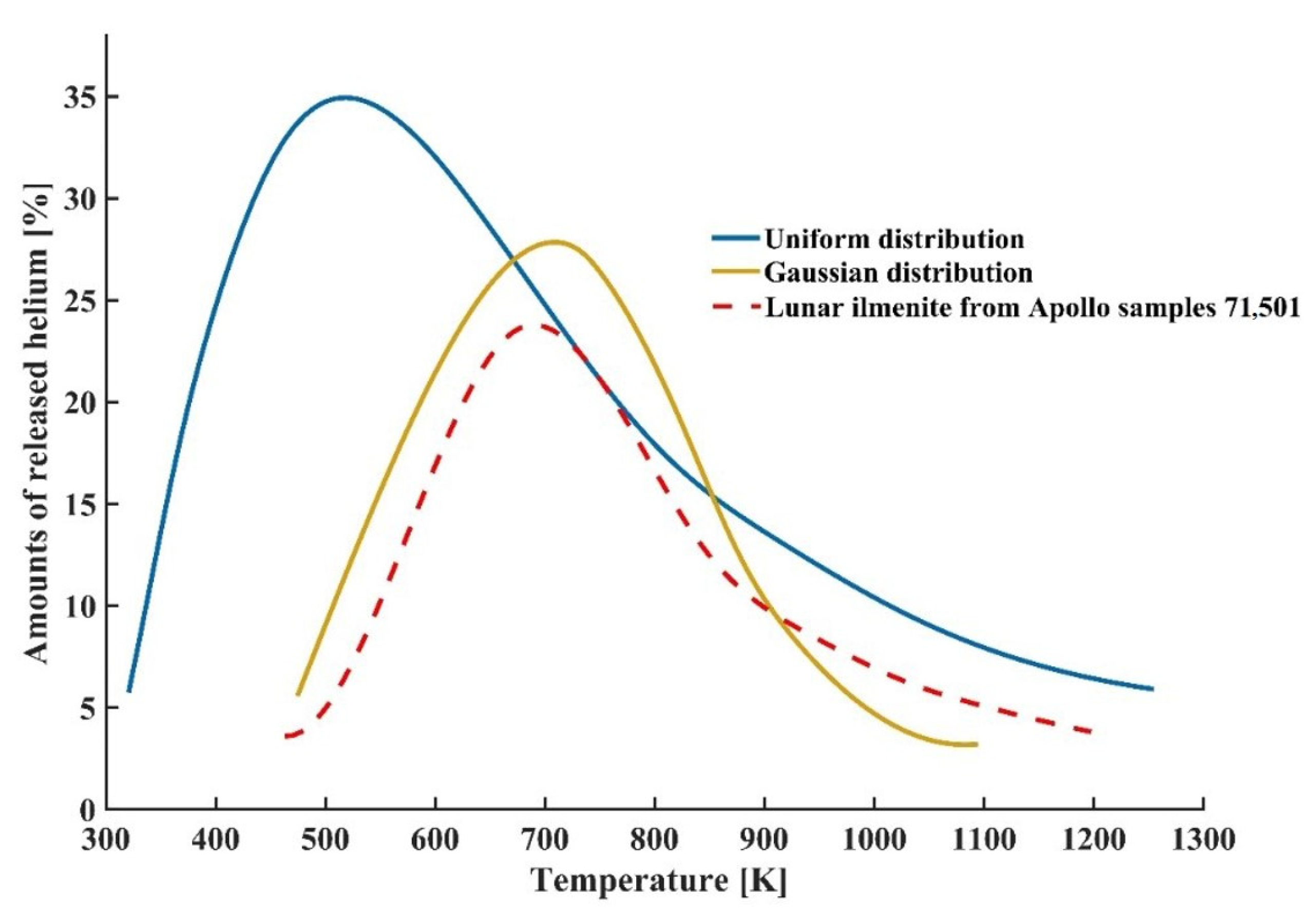
4.2. Determination of Optimal Heating Temperature
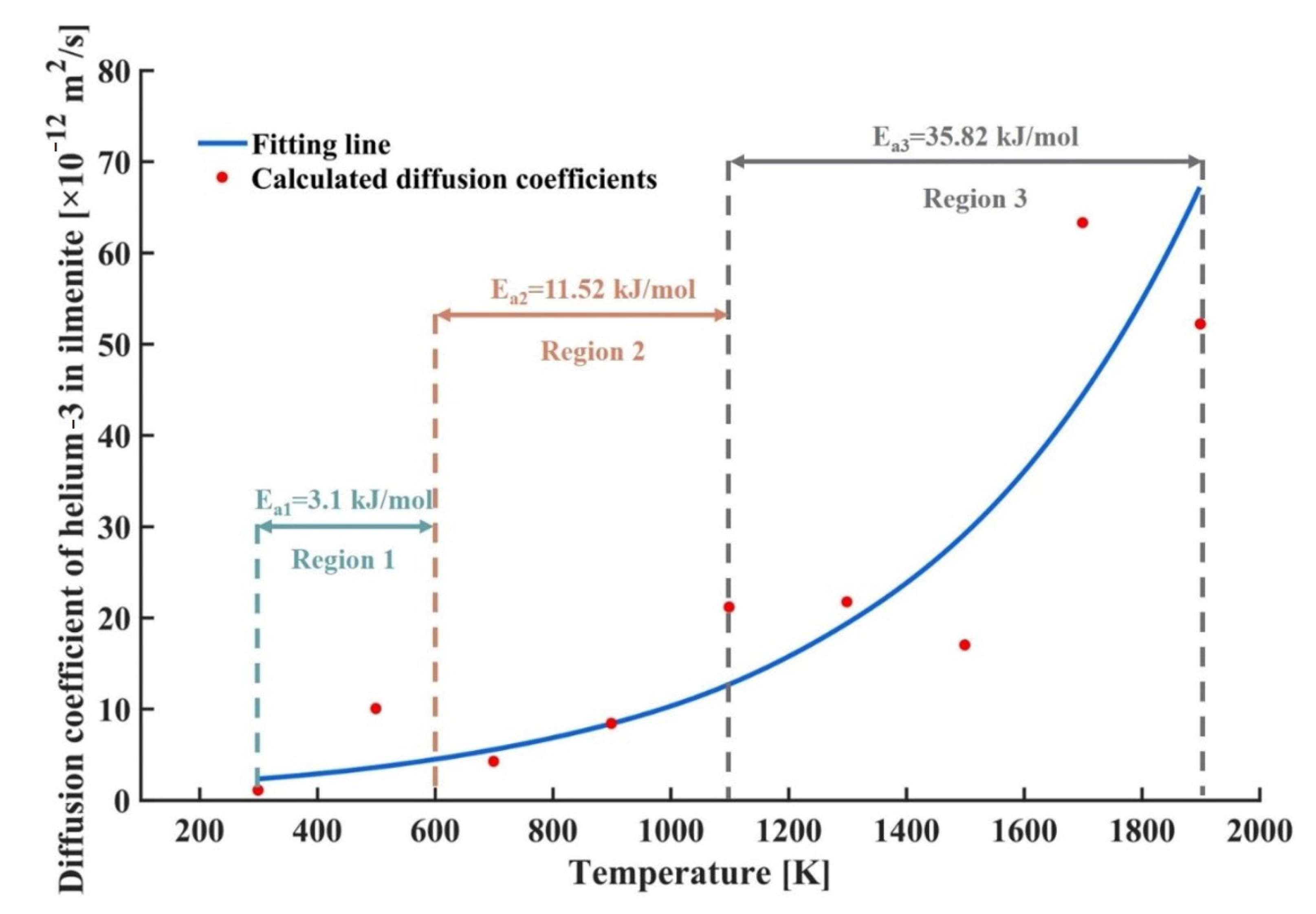
4.3. Diffusion Coefficient and Activation Energy of Helium-3 in Lunar Ilmenite
4.4. Release Rate of Helium-3 in Lunar Ilmenite
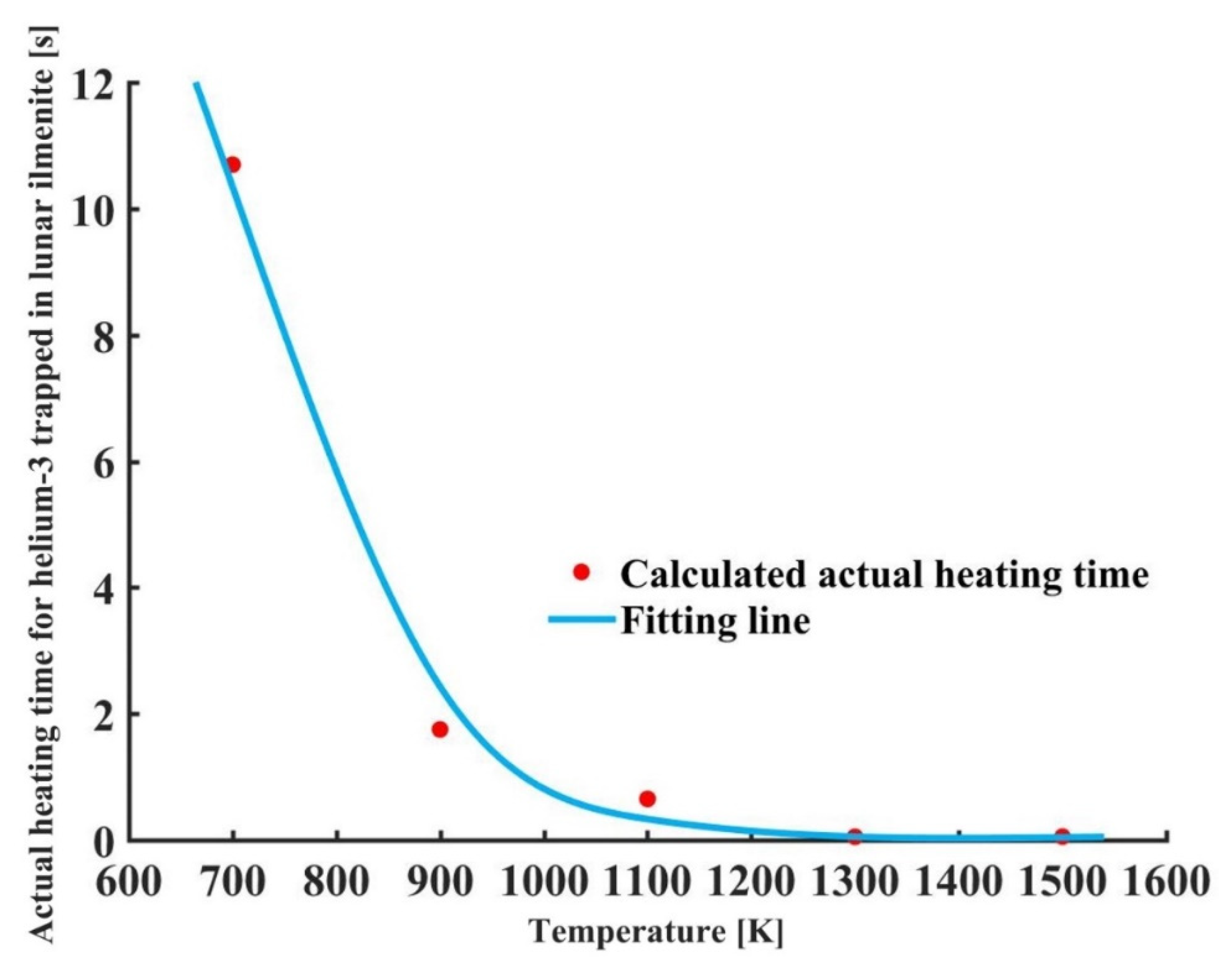
4.5. Heating Time under Actual Lunar Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anand, M.; Crawford, I.A.; Balat-Pichelin, M.; Abanades, S.; van Westrenen, W.; Péraudeau, G.; Jaumann, R.; Seboldt, W. A brief review of chemical and mineralogical resources on the Moon and likely initial in situ resource utilization (ISRU) applications. Planet. Space Sci. 2012, 74, 42–48. [Google Scholar] [CrossRef]
- Rasera, J.N.; Cilliers, J.J.; Lamamy, J.A.; Hadler, K. The beneficiation of lunar regolith for space resource utilisation: A review. Planet. Space Sci. 2020, 186, 104879. [Google Scholar] [CrossRef]
- Gou, S.; Di, K.; Yue, Z.; Liu, Z.; He, Z.; Xu, R.; Liu, B.; Peng, M.; Wan, W.; Wang, Y.; et al. Forsteritic olivine and magnesium-rich orthopyroxene materials measured by Chang’e-4 rover. Icarus 2020, 345, 113776. [Google Scholar] [CrossRef]
- Cesaretti, G.; Dini, E.; De Kestelier, X.; Colla, V.; Pambaguian, L. Building components for an outpost on the Lunar soil by means of a novel 3D printing technology. Acta Astronaut. 2014, 93, 430–450. [Google Scholar] [CrossRef]
- Gladstone, G.R.; Hurley, D.M.; Retherford, K.D.; Feldman, P.D.; Pryor, W.R.; Chaufray, J.-Y.; Versteeg, M.; Greathouse, T.K.; Steffl, A.J.; Throop, H.; et al. LRO-LAMP Observations of the LCROSS Impact Plume. Science 2010, 330, 472–476. [Google Scholar] [CrossRef]
- Li, S.; Lucey, P.G.; Milliken, R.E.; Hayne, P.O.; Fisher, E.; Williams, J.-P.; Hurley, D.M.; Elphic, R.C. Direct evidence of surface exposed water ice in the lunar polar regions. Proc. Natl. Acad. Sci. USA 2018, 115, 8907–8912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sefton-Nash, E.; Williams, J.-P.; Greenhagen, B.T.; Warren, T.J.; Bandfield, J.L.; Aye, K.-M.; Leader, F.; Siegler, M.A.; Hayne, P.O.; Bowles, N.; et al. Evidence for ultra-cold traps and surface water ice in the lunar south polar crater Amundsen. Icarus 2019, 332, 1–13. [Google Scholar] [CrossRef]
- Honniball, C.I.; Lucey, P.G.; Li, S.; Shenoy, S.; Orlando, T.M.; Hibbitts, C.A.; Hurley, D.M.; Farrell, W.M. Molecular water detected on the sunlit Moon by SOFIA. Nat. Astron. 2021, 5, 121–127. [Google Scholar] [CrossRef]
- Farrell, W.M.; Hurley, D.M.; Esposito, V.J.; McLain, J.L.; Zimmerman, M.I. The statistical mechanics of solar wind hydroxylation at the Moon, within lunar magnetic anomalies, and at Phobos. J. Geophys. Res. Planet. 2017, 122, 269–289. [Google Scholar] [CrossRef]
- Farrell, W.M.; Hurley, D.M.; Zimmerman, M.I. Solar wind implantation into lunar regolith: Hydrogen retention in a surface with defects. Icarus 2015, 255, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Grumpe, A.; Wöhler, C.; Berezhnoy, A.A.; Shevchenko, V.V. Time-of-day-dependent behavior of surficial lunar hydroxyl/water: Observations and modeling. Icarus 2019, 321, 486–507. [Google Scholar] [CrossRef]
- Sowers, G.F.; Dreyer, C.B. Ice Mining in Lunar Permanently Shadowed Regions. New Space 2019, 7, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Schwandt, C.; Hamilton, J.A.; Fray, D.J.; Crawford, I.A. The production of oxygen and metal from lunar regolith. Planet. Space Sci. 2012, 74, 49–56. [Google Scholar] [CrossRef]
- Sakurai, M.; Sone, Y.; Nishida, T.; Matsushima, H.; Fukunaka, Y. Fundamental study of water electrolysis for life support system in space. Electrochim. Acta 2013, 100, 350–357. [Google Scholar] [CrossRef]
- Fa, W.; Jin, Y.-Q. Quantitative estimation of helium-3 spatial distribution in the lunar regolith layer. Icarus 2007, 190, 15–23. [Google Scholar] [CrossRef]
- Simko, T.; Gray, M. Lunar Helium-3 Fuel for Nuclear Fusion: Technology, Economics, and Resources. World Futures Rev. 2014, 6, 158–171. [Google Scholar] [CrossRef]
- Johnson, J.R.; Swindle, T.D.; Lucey, P.G. Estimated solar wind-implanted helium-3 distribution on the Moon. Geophys. Res. Lett. 1999, 26, 385–388. [Google Scholar] [CrossRef]
- Slyuta, E.; Yakovlev, O.; Voropaev, S.; Dubrovskii, A. He implantation and concentrations in minerals and lunar regolith particles. Geochem. Int. 2013, 51, 959–967. [Google Scholar] [CrossRef]
- Curran, N.M.; Nottingham, M.; Alexander, L.; Crawford, I.A.; Füri, E.; Joy, K.H. A database of noble gases in lunar samples in preparation for mass spectrometry on the Moon. Planet. Space Sci. 2020, 182, 104823. [Google Scholar] [CrossRef]
- Kim, K.J.; Wöhler, C.; Berezhnoy, A.A.; Bhatt, M.; Grumpe, A. Prospective 3He-rich landing sites on the Moon. Planet. Space Sci. 2019, 177, 104686. [Google Scholar] [CrossRef]
- Cocks, F.H. 3He in permanently shadowed lunar polar surfaces. Icarus 2010, 206, 778–779. [Google Scholar] [CrossRef]
- Surkov, Y.; Shkuratov, Y.; Kaydash, V.; Korokhin, V.; Videen, G. Lunar ilmenite content as assessed by improved Chandrayaan-1 M3 data. Icarus 2020, 341, 113661. [Google Scholar] [CrossRef]
- Shukla, S.; Tolpekin, V.; Kumar, S.; Stein, A. Investigating the Retention of Solar Wind Implanted Helium-3 on the Moon from the Analysis of Multi-Wavelength Remote Sensing Data. Remote Sens. 2020, 12, 3350. [Google Scholar] [CrossRef]
- Shkuratov, Y.G.; Starukhina, L.; Kaidash, V.; Bondarenko, N. 3He Distribution over the Lunar Visible Hemisphere. Solar Syst. Res. 1999, 33, 409. [Google Scholar]
- Pepin, R.; Nyquist, L.; Phinney, D.; Black, D. Rare gases in Apollo 11 lunar material. Geochim. Cosmochim. Ac. Supplement 1970, 1, 1435. [Google Scholar]
- Srinivasan, B.; Hennecke, E.; Sinclair, D.; Manuel, O. A comparison of noble gases released from lunar fines (#15601.64) with noble gases in meteorites and in the earth. Lunar Planet. Sci. Conf. Proc. 1972, 2, 1927–1945. [Google Scholar]
- Baur, H.; Frick, U.; Funk, H.; Schultz, L.; Signer, P. Thermal release of helium, neon, and argon from lunar fines and minerals. Lunar Planet. Sci. Conf. Proc. 1972, 2, 1947–1966. [Google Scholar]
- Hohenberg, C.; Davis, P.; Kaiser, W.; Lewis, R.; Reynolds, J. Trapped and cosmogenic rare gases from stepwise heating of Apollo 11 samples. Geochim. Cosmochim. Acta 1970, 1, 1283. [Google Scholar]
- Pepin, R.O.; Becker, R.H.; Schlutter, D.J. Irradiation records in regolith materials. I: Isotopic compositions of solar-wind neon and argon in single lunar mineral grains. Geochim. Cosmochim. Acta 1999, 63, 2145–2162. [Google Scholar] [CrossRef]
- Burgess, K.D.; Stroud, R.M. Phase-dependent space weathering effects and spectroscopic identification of retained helium in a lunar soil grain. Geochim. Cosmochim. Acta 2018, 224, 64–79. [Google Scholar] [CrossRef]
- Anufriev, G.S. Hopping diffusion of helium isotopes from samples of lunar soil. Phys. Solid State 2010, 52, 2058–2062. [Google Scholar] [CrossRef]
- Harris-Kuhlman, K.R. Trapping and Diffusion of Helium in Lunar Minerals. Ph.D. Thesis, University of Wisconsin–Madison, Madison, WI, USA, 1998. [Google Scholar]
- Futagami, T.; Ozima, M.; Nagal, S.; Aoki, Y. Experiments on thermal release of implanted noble gases from minerals and their implications for noble gases in lunar soil grains. Geochim. Cosmochim. Acta 1993, 57, 3177–3194. [Google Scholar] [CrossRef]
- Mueller, H.; Jordan, J.; Kalbitzer, S.; Kiko, J.; Kirsten, T. Rare gas ion probe analysis of helium profiles in individual lunar soil particles. Lunar Planet. Sci. Conf. Proc. 1976, 7, 937–951. [Google Scholar]
- Wieler, R.; Baur, H.; Signer, P. Noble gases from solar energetic particles revealed by closed system stepwise etching of lunar soil minerals. Geochim. Cosmochim. Acta 1986, 50, 1997–2017. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Meth. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Saha, U.; Devan, K.; Ganesan, S. A study to compute integrated dpa for neutron and ion irradiation environments using SRIM-2013. J. Nucl. Mater. 2018, 503, 30–41. [Google Scholar] [CrossRef]
- Loeffler, M.J.; Dukes, C.A.; Baragiola, R.A. Irradiation of olivine by 4 keV He+: Simulation of space weathering by the solar wind. J. Geophys. Res. Planet. 2009, 114, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mueller, H.; Kiko, J.; Kirsten, T. High resolution depth profiles of rare gases in individual lunar soil particles. Lunar Planet. Sci. Conf. Proc. 1976, 7, 577–579. [Google Scholar]
- Fu, X.; Zou, Y.; Zheng, Y.; He, H.; Ouyang, Z. Noble gas diffusion mechanism in lunar soil simulant grains: Results from 4He+ implantation and extraction experiments. J. Earth Sci. China 2011, 22, 566. [Google Scholar] [CrossRef]
- Fan, H.; Chen, D.; Liu, P.; Duan, H.; Huang, Y.; Long, M.; Liu, T. Structural and transport properties of FeO-TiO2 system through molecular dynamics simulations. J. Non Cryst. Solids 2018, 493, 57–64. [Google Scholar] [CrossRef]
- Belashchenko, D.K.; Ostrovski, O.I.; Skvortsov, L.V. Molecular dynamics simulation of binary CaO–FeO, MgO–SiO2, FeO–SiO2, CaO–SiO2 and ternary CaO–FeO–SiO2 systems. Thermochim. Acta 2001, 372, 153–163. [Google Scholar] [CrossRef]
- Zhang, J.; Song, H.; Zhu, W.; Wang, J. Liquid Transport through Nanoscale Porous Media with Strong Wettability. Transport Porous Med. 2021, 1–15. [Google Scholar] [CrossRef]
- Govers, K.; Lemehov, S.; Hou, M.; Verwerft, M. Molecular dynamics simulation of helium and oxygen diffusion in UO2±x. J. Nucl. Mater. 2009, 395, 131–139. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Juslin, N.; Nordlund, K. Pair potential for Fe–He. J. Nucl. Mater. 2008, 382, 143–146. [Google Scholar] [CrossRef]
- Wang, J.; Hou, Q.; Sun, T.Y.; Wu, Z.C.; Long, X.G.; Wu, X.C.; Luo, S.Z. Simulation of Helium Behaviour in Titanium Crystals Using Molecular Dynamics. Chinese Phys. Lett. 2006, 23, 1666–1669. [Google Scholar] [CrossRef]
- Jin, J.; Ling, Y.; Hao, Y. Similarity analysis of parabolic-trough solar collectors. Appl. Energ. 2017, 204, 958–965. [Google Scholar] [CrossRef]
- Wang, S.; Javadpour, F.; Feng, Q. Molecular dynamics simulations of oil transport through inorganic nanopores in shale. Fuel 2016, 171, 74–86. [Google Scholar] [CrossRef]
- Watson, E.B.; Baxter, E.F. Diffusion in solid-Earth systems. Earth Planet. Sc. Lett. 2007, 253, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Kuhlman, K.R.; Kulcinski, G.L. Helium Isotopes in the Lunar Regolith–Measuring Helium Isotope Diffusivity in Lunar Analogs. Moon Springer 2012, 23–56. [Google Scholar] [CrossRef]

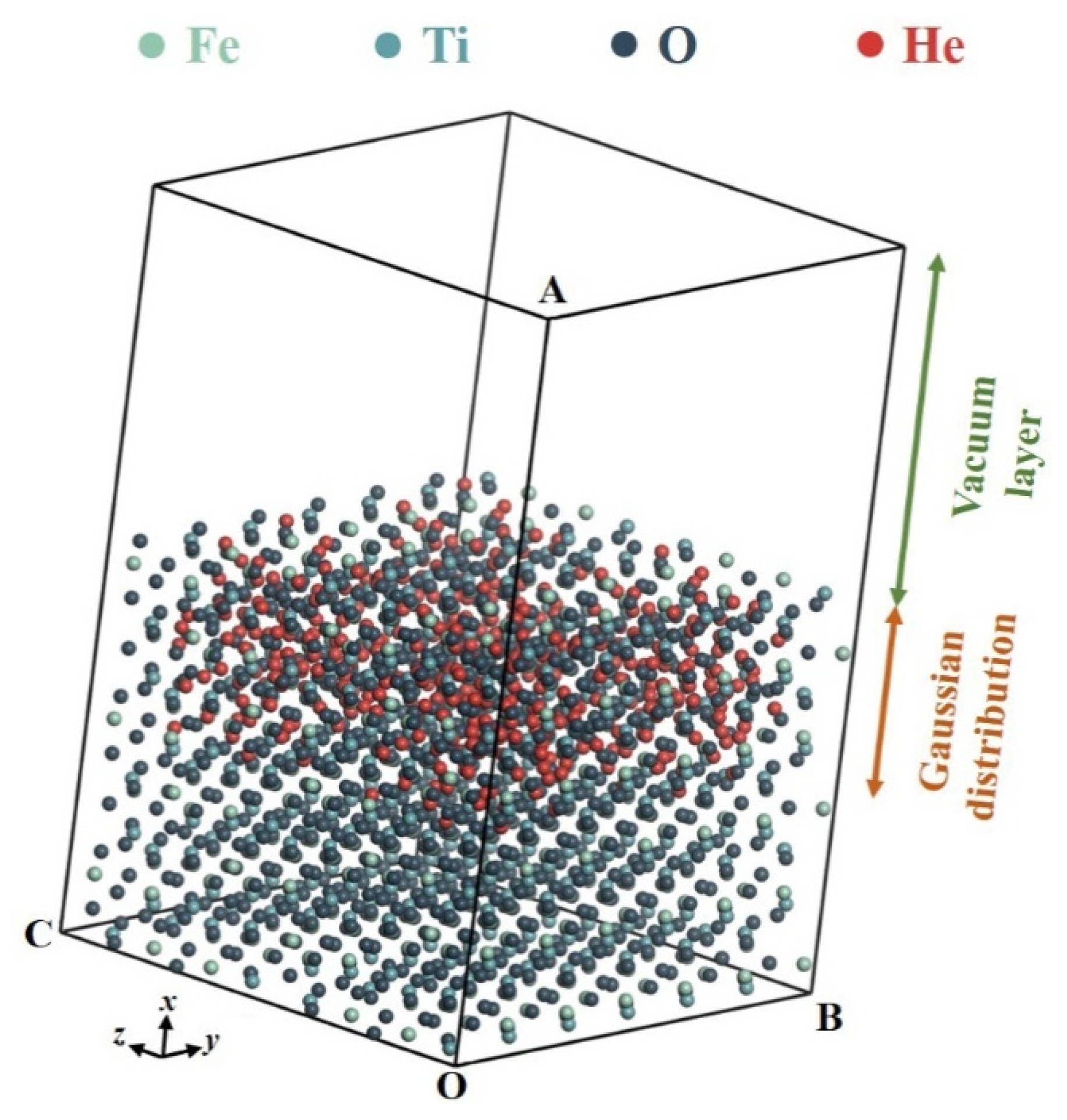

| Parameters of Incident Ions | Parameters of Target Atoms | ||||
|---|---|---|---|---|---|
| Species | Energy(keV) | Dose(ions/cm2) | Element | Stoichiometry | Density(g/cm3) |
| Helium-3 | 50 | 4 × 1013 | Fe | 1 | 4.7 |
| Ti | 1 | ||||
| O | 3 | ||||
| Atom Type | References | ||||
|---|---|---|---|---|---|
| Ti | Ti | 35,133.15 | 6.25 | 0 | [41] |
| Ti | O | 242,696.25 | 6.06 | 0 | [41] |
| O | O | 1,497,693.51 | 5.88 | 17.35 | [41] |
| Fe | O | 1900.21 | 3.45 | 0 | [42] |
| Atom Type | References | |||
|---|---|---|---|---|
| He | He | 69.3559 | 0.493712 | [44] |
| Fe | Fe | 206.4923 | 0.68 | [45] |
| Fe | Ti | 398.7154 | 1.0103 | [45] |
| Temperature(K) | Amounts of Released Helium with Uniform Distribution (%) | Amounts of Released Helium with Gaussian Distribution (%) | Differences between Two Concentration Profiles |
|---|---|---|---|
| 300 | 0 | 16 | 16 |
| 500 | 35.4 | 40 | 4.6 |
| 700 | 57.5 | 62 | 4.5 |
| 900 | 73 | 70 | −3 |
| 1100 | 82 | 75 | −7 |
| Temperature (K) | [40] | |||||
|---|---|---|---|---|---|---|
| 500 | 3.63 × 10−8 | 7.00 × 10−15 | 1.93 × 10−7 | 423 | 9.28 × 1011 | 371.13 |
| 700 | 5.61 × 10−8 | 3.75 × 10−13 | 6.69 × 10−6 | 2.67 × 1010 | 10.70 | |
| 900 | 8.39 × 10−8 | 3.43 × 10−12 | 4.09 × 10−5 | 4.38 × 109 | 1.75 | |
| 1100 | 12.75 × 10−8 | 1.40 × 10−11 | 1.10 × 10−4 | 1.63 × 109 | 0.65 | |
| 1300 | 19.48 × 10−8 | 2.69 × 10−10 | 1.38 × 10−3 | 1.30 × 108 | 0.052 | |
| 1500 | 29.24 × 10−8 | 3.88 × 10−10 | 1.33 × 10−3 | 1.35 × 108 | 0.054 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Zhang, J.; Sun, Y.; Li, Y.; Zhang, X.; Ma, D.; Kou, J. Theoretical Study on Thermal Release of Helium-3 in Lunar Ilmenite. Minerals 2021, 11, 319. https://doi.org/10.3390/min11030319
Song H, Zhang J, Sun Y, Li Y, Zhang X, Ma D, Kou J. Theoretical Study on Thermal Release of Helium-3 in Lunar Ilmenite. Minerals. 2021; 11(3):319. https://doi.org/10.3390/min11030319
Chicago/Turabian StyleSong, Hongqing, Jie Zhang, Yueqiang Sun, Yongping Li, Xianguo Zhang, Dongyu Ma, and Jue Kou. 2021. "Theoretical Study on Thermal Release of Helium-3 in Lunar Ilmenite" Minerals 11, no. 3: 319. https://doi.org/10.3390/min11030319
APA StyleSong, H., Zhang, J., Sun, Y., Li, Y., Zhang, X., Ma, D., & Kou, J. (2021). Theoretical Study on Thermal Release of Helium-3 in Lunar Ilmenite. Minerals, 11(3), 319. https://doi.org/10.3390/min11030319






