Iron Isotopes Reveal a Benthic Iron Shuttle in the Palaeoproterozoic Zaonega Formation: Basinal Restriction, Euxinia, and the Effect on Global Palaeoredox Proxies
Abstract
:1. Introduction
2. The Fe Isotope Palaeoredox Proxy
3. Geological Background
4. Materials and Methods
4.1. Sample Material
4.2. Element Concentrations
4.3. Iron Isotopes
4.4. Principal Component Analysis
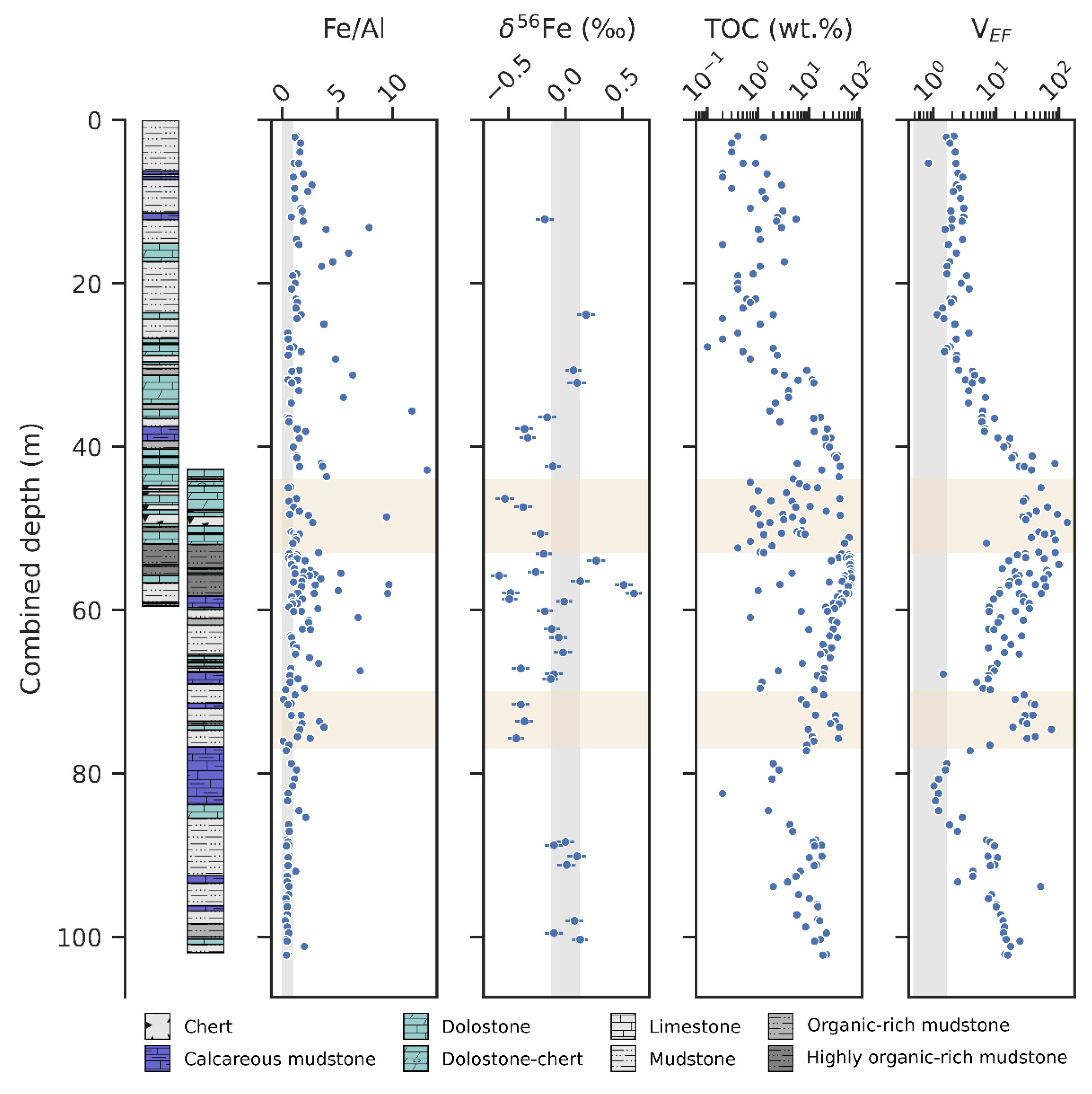
5. Results
5.1. Geochemical Data
5.2. Principal Component Analysis
6. Discussion
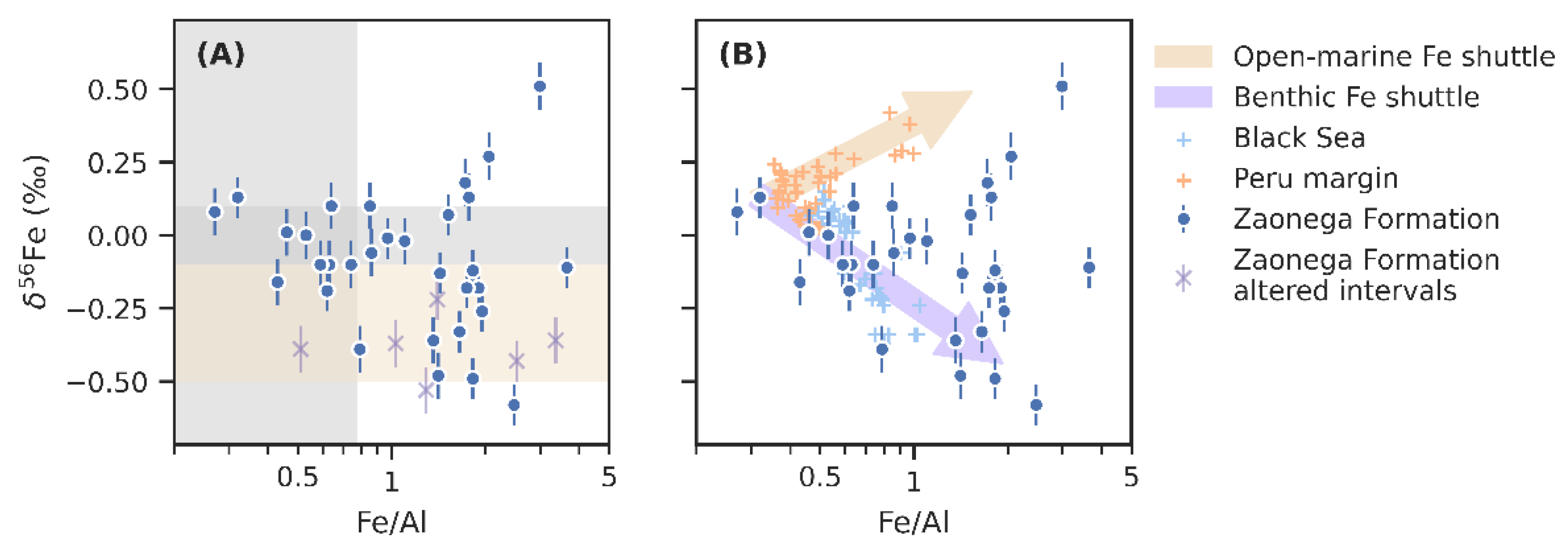
6.1. Post-Depositional Alteration
6.2. Principal Influences on Iron Geochemistry
6.3. Detrital Versus Authigenic Iron Sources
6.4. Hydrothermal Iron
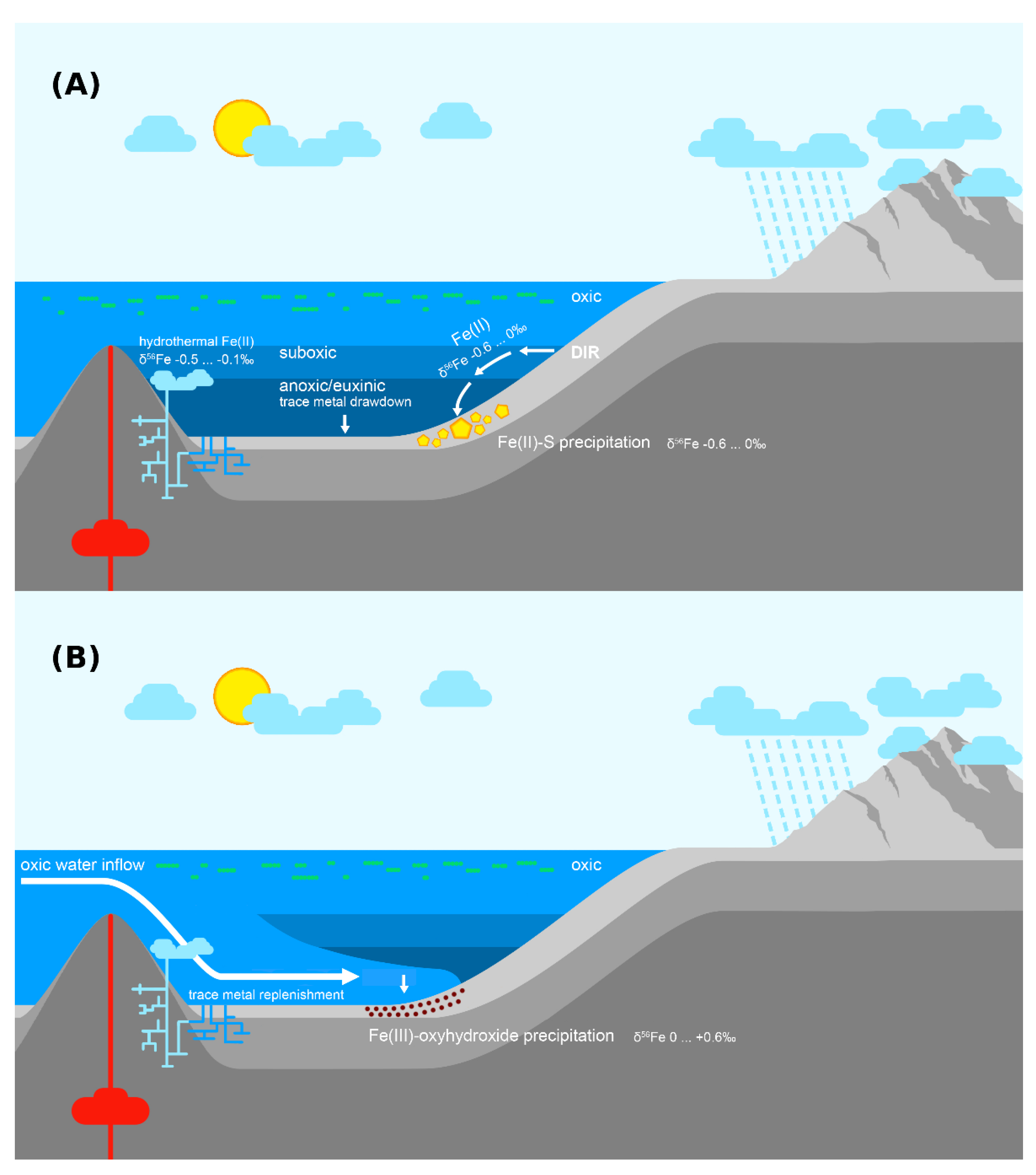
6.5. Iron Redox-Shuttling
6.6. Redox Development in the Upper Zaonega Formation
6.7. The Onega Basin Palaeoenvironment
7. Conclusions and Implications
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lyons, T.W.; Reinhard, C.T.; Planavsky, N.J. The Rise of Oxygen in Earth’s Early Ocean and Atmosphere. Nature 2014, 506, 307–315. [Google Scholar] [CrossRef]
- Bekker, A.; Holland, H.D.; Wang, P.-L.; Rumble, D.; Stein, H.J.; Hannah, J.L.; Coetzee, L.L.; Beukes, N.J. Dating the Rise of Atmospheric Oxygen. Nature 2004, 427, 117–120. [Google Scholar] [CrossRef]
- Holland, H.D. Volcanic Gases, Black Smokers, and the Great Oxidation Event. Geochim. Cosmochim. Acta 2002, 66, 3811–3826. [Google Scholar] [CrossRef]
- Warke, M.R.; Rocco, T.D.; Zerkle, A.L.; Lepland, A.; Prave, A.R.; Martin, A.P.; Ueno, Y.; Condon, D.J.; Claire, M.W. The Great Oxidation Event Preceded a Paleoproterozoic “Snowball Earth”. Proc. Natl. Acad. Sci. USA 2020, 117, 13314–13320. [Google Scholar] [CrossRef] [PubMed]
- Bekker, A.; Holland, H.D. Oxygen Overshoot and Recovery during the Early Paleoproterozoic. Earth Planet. Sci. Lett. 2012, 317–318, 295–304. [Google Scholar] [CrossRef]
- Karhu, J.A.; Holland, H.D. Carbon Isotopes and the Rise of Atmospheric Oxygen. Geology 1996, 24, 867–870. [Google Scholar] [CrossRef]
- Martin, A.P.; Condon, D.J.; Prave, A.R.; Lepland, A. A Review of Temporal Constraints for the Palaeoproterozoic Large, Positive Carbonate Carbon Isotope Excursion (the Lomagundi–Jatuli Event). Earth Sci. Rev. 2013, 127, 242–261. [Google Scholar] [CrossRef]
- Och, L.M.; Shields-Zhou, G.A. The Neoproterozoic Oxygenation Event: Environmental Perturbations and Biogeochemical Cycling. Earth Sci. Rev. 2012, 110, 26–57. [Google Scholar] [CrossRef]
- Canfield, D.E.; Ngombi-Pemba, L.; Hammarlund, E.U.; Bengtson, S.; Chaussidon, M.; Gauthier-Lafaye, F.; Meunier, A.; Riboulleau, A.; Rollion-Bard, C.; Rouxel, O.; et al. Oxygen Dynamics in the Aftermath of the Great Oxidation of Earth’s Atmosphere. Proc. Natl. Acad. Sci. USA 2013, 110, 16736–16741. [Google Scholar] [CrossRef] [Green Version]
- Kump, L.R.; Junium, C.; Arthur, M.A.; Brasier, A.; Fallick, A.; Melezhik, V.; Lepland, A.; Črne, A.E.; Luo, G. Isotopic Evidence for Massive Oxidation of Organic Matter Following the Great Oxidation Event. Science 2011, 334, 1694–1696. [Google Scholar] [CrossRef]
- Ohmoto, H.; Watanabe, Y.; Lasaga, A.C.; Naraoka, H.; Johnson, I.; Brainard, J.; Chorney, A. Oxygen, Iron, and Sulfur Geochemical Cycles on Early Earth: Paradigms and Contradictions. Geol. Soc. Am. Spec. Pap. 2014. [Google Scholar] [CrossRef]
- Kreitsmann, T.; Lepland, A.; Bau, M.; Prave, A.; Paiste, K.; Mänd, K.; Sepp, H.; Martma, T.; Romashkin, A.E.; Kirsimäe, K. Oxygenated Conditions in the Aftermath of the Lomagundi-Jatuli Event: The Carbon Isotope and Rare Earth Element Signatures of the Paleoproterozoic Zaonega Formation, Russia. Precambrian Res. 2020, 347, 105855. [Google Scholar] [CrossRef]
- Mänd, K.; Lalonde, S.V.; Robbins, L.J.; Thoby, M.; Paiste, K.; Kreitsmann, T.; Paiste, P.; Reinhard, C.T.; Romashkin, A.E.; Planavsky, N.J.; et al. Palaeoproterozoic Oxygenated Oceans Following the Lomagundi–Jatuli Event. Nat. Geosci. 2020, 13, 302–306. [Google Scholar] [CrossRef]
- Ossa Ossa, F.; Eickmann, B.; Hofmann, A.; Planavsky, N.J.; Asael, D.; Pambo, F.; Bekker, A. Two-Step Deoxygenation at the End of the Paleoproterozoic Lomagundi Event. Earth Planet. Sci. Lett. 2018, 486, 70–83. [Google Scholar] [CrossRef]
- Paiste, K.; Lepland, A.; Zerkle, A.L.; Kirsimäe, K.; Izon, G.; Patel, N.K.; McLean, F.; Kreitsmann, T.; Mänd, K.; Bui, T.H.; et al. Multiple Sulphur Isotope Records Tracking Basinal and Global Processes in the 1.98 Ga Zaonega Formation, NW Russia. Chem. Geol. 2018, 499, 151–164. [Google Scholar] [CrossRef] [Green Version]
- Paiste, K.; Pellerin, A.; Zerkle, A.L.; Kirsimäe, K.; Prave, A.R.; Romashkin, A.E.; Lepland, A. The Pyrite Multiple Sulfur Isotope Record of the 1.98 Ga Zaonega Formation: Evidence for Biogeochemical Sulfur Cycling in a Semi-Restricted Basin. Earth Planet. Sci. Lett. 2020, 534, 116092. [Google Scholar] [CrossRef]
- Scott, C.; Wing, B.A.; Bekker, A.; Planavsky, N.J.; Medvedev, P.; Bates, S.M.; Yun, M.; Lyons, T.W. Pyrite Multiple-Sulfur Isotope Evidence for Rapid Expansion and Contraction of the Early Paleoproterozoic Seawater Sulfate Reservoir. Earth Planet. Sci. Lett. 2014, 389, 95–104. [Google Scholar] [CrossRef]
- Paiste, K.; Lepland, A.; Zerkle, A.L.; Kirsimäe, K.; Kreitsmann, T.; Mänd, K.; Romashkin, A.E.; Rychanchik, D.V.; Prave, A.R. Identifying Global vs. Basinal Controls on Paleoproterozoic Organic Carbon and Sulfur Isotope Records. Earth Sci. Rev. 2020, 207, 103230. [Google Scholar] [CrossRef]
- Melezhik, V.A.; Fallick, A.E.; Filippov, M.M.; Larsen, O. Karelian Shungite—An Indication of 2.0-Ga-Old Metamorphosed Oil-Shale and Generation of Petroleum: Geology, Lithology and Geochemistry. Earth Sci. Rev. 1999, 47, 1–40. [Google Scholar] [CrossRef]
- Kreitsmann, T.; Külaviir, M.; Lepland, A.; Paiste, K.; Paiste, P.; Prave, A.R.; Sepp, H.; Romashkin, A.E.; Rychanchik, D.V.; Kirsimäe, K. Hydrothermal Dedolomitisation of Carbonate Rocks of the Paleoproterozoic Zaonega Formation, NW Russia—Implications for the Preservation of Primary C Isotope Signals. Chem. Geol. 2019, 512, 43–57. [Google Scholar] [CrossRef] [Green Version]
- Joosu, L.; Lepland, A.; Kirsimäe, K.; Romashkin, A.E.; Roberts, N.M.W.; Martin, A.P.; Črne, A.E. The REE-Composition and Petrography of Apatite in 2 Ga Zaonega Formation, Russia: The Environmental Setting for Phosphogenesis. Chem. Geol. 2015, 395, 88–107. [Google Scholar] [CrossRef]
- Kipp, M.A.; Stüeken, E.E.; Bekker, A.; Buick, R. Selenium Isotopes Record Extensive Marine Suboxia during the Great Oxidation Event. Proc. Natl. Acad. Sci. USA. 2017, 114, 875–880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kipp, M.A.; Lepland, A.; Buick, R. Redox Fluctuations, Trace Metal Enrichment and Phosphogenesis in the ∼2.0 Ga Zaonega Formation. Precambrian Res. 2020, 343, 105716. [Google Scholar] [CrossRef]
- Asael, D.; Tissot, F.L.H.; Reinhard, C.T.; Rouxel, O.; Dauphas, N.; Lyons, T.W.; Ponzevera, E.; Liorzou, C.; Chéron, S. Coupled Molybdenum, Iron and Uranium Stable Isotopes as Oceanic Paleoredox Proxies during the Paleoproterozoic Shunga Event. Chem. Geol. 2013, 362, 193–210. [Google Scholar] [CrossRef]
- Asael, D.; Rouxel, O.; Poulton, S.W.; Lyons, T.W.; Bekker, A. Molybdenum Record from Black Shales Indicates Oscillating Atmospheric Oxygen Levels in the Early Paleoproterozoic. Am. J. Sci. 2018, 318, 275–299. [Google Scholar] [CrossRef]
- Partin, C.A.; Bekker, A.; Planavsky, N.J.; Scott, C.T.; Gill, B.C.; Li, C.; Podkovyrov, V.; Maslov, A.; Konhauser, K.O.; Lalonde, S.V.; et al. Large-Scale Fluctuations in Precambrian Atmospheric and Oceanic Oxygen Levels from the Record of U in Shales. Earth Planet. Sci. Lett. 2013, 369–370, 284–293. [Google Scholar] [CrossRef]
- Scott, C.; Lyons, T.W.; Bekker, A.; Shen, Y.; Poulton, S.W.; Chu, X.; Anbar, A.D. Tracing the Stepwise Oxygenation of the Proterozoic Ocean. Nature 2008, 452, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Črne, A.E.; Melezhik, V.A.; Lepland, A.; Fallick, A.E.; Prave, A.R.; Brasier, A.T. Petrography and Geochemistry of Carbonate Rocks of the Paleoproterozoic Zaonega Formation, Russia: Documentation of 13C-Depleted Non-Primary Calcite. Precambrian Res. 2014, 240, 79–93. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Črne, A.E.; Lepland, A.; van Zuilen, M.A. Methanotrophy in a Paleoproterozoic Oil Field Ecosystem, Zaonega Formation, Karelia, Russia. Geobiology 2012, 10, 467–478. [Google Scholar] [CrossRef]
- Robbins, L.J.; Lalonde, S.V.; Planavsky, N.J.; Partin, C.A.; Reinhard, C.T.; Kendall, B.; Scott, C.; Hardisty, D.S.; Gill, B.C.; Alessi, D.S.; et al. Trace Elements at the Intersection of Marine Biological and Geochemical Evolution. Earth Sci. Rev. 2016, 163, 323–348. [Google Scholar] [CrossRef]
- Robbins, L.J.; Mänd, K.; Planavsky, N.J.; Alessi, D.S.; Konhauser, K.O. Trace Metals. In Encyclopedia of Astrobiology; Gargaud, M., Irvine, W.M., Amils, R., Cleaves, H.J., Pinti, D., Quintanilla, J.C., Viso, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–5. ISBN 978-3-642-27833-4. [Google Scholar]
- Dauphas, N.; John, S.G.; Rouxel, O. Iron Isotope Systematics. Rev. Mineral. Geochem. 2017, 82, 415–510. [Google Scholar] [CrossRef]
- Johnson, C.; Beard, B.; Weyer, S. Iron Geochemistry: An Isotopic Perspective; Advances in Isotope Geochemistry; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-33827-5. [Google Scholar]
- Poulton, S.W.; Canfield, D.E. Development of a Sequential Extraction Procedure for Iron: Implications for Iron Partitioning in Continentally Derived Particulates. Chem. Geol. 2005, 214, 209–221. [Google Scholar] [CrossRef]
- Cole, D.B.; Zhang, S.; Planavsky, N.J. A New Estimate of Detrital Redox-Sensitive Metal Concentrations and Variability in Fluxes to Marine Sediments. Geochim. Cosmochim. Acta 2017, 215, 337–353. [Google Scholar] [CrossRef]
- Lyons, T.W.; Werne, J.P.; Hollander, D.J.; Murray, R.W. Contrasting Sulfur Geochemistry and Fe/Al and Mo/Al Ratios across the Last Oxic-to-Anoxic Transition in the Cariaco Basin, Venezuela. Chem. Geol. 2003, 195, 131–157. [Google Scholar] [CrossRef]
- Raiswell, R.; Hardisty, D.S.; Lyons, T.W.; Canfield, D.E.; Owens, J.D.; Planavsky, N.J.; Poulton, S.W.; Reinhard, C.T. The Iron Paleoredox Proxies: A Guide to the Pitfalls, Problems and Proper Practice. Am. J. Sci. 2018, 318, 491–526. [Google Scholar] [CrossRef] [Green Version]
- Severmann, S.; Lyons, T.W.; Anbar, A.; McManus, J.; Gordon, G. Modern Iron Isotope Perspective on the Benthic Iron Shuttle and the Redox Evolution of Ancient Oceans. Geology 2008, 36, 487–490. [Google Scholar] [CrossRef]
- Raiswell, R.; Canfield, D.E. Sources of Iron for Pyrite Formation in Marine Sediments. Am. J. Sci. 1998, 298, 219–245. [Google Scholar] [CrossRef] [Green Version]
- Poulton, S.W.; Canfield, D.E. Ferruginous Conditions: A Dominant Feature of the Ocean through Earth’s History. Elements 2011, 7, 107–112. [Google Scholar] [CrossRef] [Green Version]
- Clarkson, M.O.; Poulton, S.W.; Guilbaud, R.; Wood, R.A. Assessing the Utility of Fe/Al and Fe-Speciation to Record Water Column Redox Conditions in Carbonate-Rich Sediments. Chem. Geol. 2014, 382, 111–122. [Google Scholar] [CrossRef]
- Raiswell, R.; Canfield, D.E.; Berner, R.A. A Comparison of Iron Extraction Methods for the Determination of Degree of Pyritisation and the Recognition of Iron-Limited Pyrite Formation. Chem. Geol. 1994, 111, 101–110. [Google Scholar] [CrossRef]
- Scholz, F. Identifying Oxygen Minimum Zone-Type Biogeochemical Cycling in Earth History Using Inorganic Geochemical Proxies. Earth Sci. Rev. 2018, 184, 29–45. [Google Scholar] [CrossRef]
- Scholz, F.; Schmidt, M.; Hensen, C.; Eroglu, S.; Geilert, S.; Gutjahr, M.; Liebetrau, V. Shelf-to-Basin Iron Shuttle in the Guaymas Basin, Gulf of California. Geochim. Cosmochim. Acta 2019, 261, 76–92. [Google Scholar] [CrossRef]
- Rico, K.I.; Sheldon, N.D. Nutrient and Iron Cycling in a Modern Analogue for the Redoxcline of a Proterozoic Ocean Shelf. Chem. Geol. 2019, 511, 42–50. [Google Scholar] [CrossRef]
- Slotznick, S.P.; Eiler, J.M.; Fischer, W.W. The Effects of Metamorphism on Iron Mineralogy and the Iron Speciation Redox Proxy. Geochim. Cosmochim. Acta 2018, 224, 96–115. [Google Scholar] [CrossRef] [Green Version]
- Beard, B.L.; Handler, R.M.; Scherer, M.M.; Wu, L.; Czaja, A.D.; Heimann, A.; Johnson, C.M. Iron Isotope Fractionation between Aqueous Ferrous Iron and Goethite. Earth Planet. Sci. Lett. 2010, 295, 241–250. [Google Scholar] [CrossRef]
- Frierdich, A.J.; Beard, B.L.; Reddy, T.R.; Scherer, M.M.; Johnson, C.M. Iron Isotope Fractionation between Aqueous Fe(II) and Goethite Revisited: New Insights Based on a Multi-Direction Approach to Equilibrium and Isotopic Exchange Rate Modification. Geochim. Cosmochim. Acta 2014, 139, 383–398. [Google Scholar] [CrossRef]
- Frierdich, A.J.; Beard, B.L.; Scherer, M.M.; Johnson, C.M. Determination of the Fe(II)Aq–Magnetite Equilibrium Iron Isotope Fractionation Factor Using the Three-Isotope Method and a Multi-Direction Approach to Equilibrium. Earth Planet. Sci. Lett. 2014, 391, 77–86. [Google Scholar] [CrossRef]
- Wu, L.; Beard, B.L.; Roden, E.E.; Johnson, C.M. Stable Iron Isotope Fractionation Between Aqueous Fe(II) and Hydrous Ferric Oxide. Environ. Sci. Technol. 2011, 45, 1847–1852. [Google Scholar] [CrossRef]
- Croal, L.R.; Johnson, C.M.; Beard, B.L.; Newman, D.K. Iron Isotope Fractionation by Fe(II)-Oxidizing Photoautotrophic Bacteria 11Associate Editor: D. E. Canfield. Geochim. Cosmochim. Acta 2004, 68, 1227–1242. [Google Scholar] [CrossRef]
- Planavsky, N.J.; Rouxel, O.J.; Bekker, A.; Hofmann, A.; Little, C.T.S.; Lyons, T.W. Iron Isotope Composition of Some Archean and Proterozoic Iron Formations. Geochim. Cosmochim. Acta 2012, 80, 158–169. [Google Scholar] [CrossRef]
- Rouxel, O.J.; Bekker, A.; Edwards, K.J. Iron Isotope Constraints on the Archean and Paleoproterozoic Ocean Redox State. Science 2005, 307, 1088–1091. [Google Scholar] [CrossRef] [Green Version]
- Beard, B.L.; Johnson, C.M.; Cox, L.; Sun, H.; Nealson, K.H.; Aguilar, C. Iron Isotope Biosignatures. Science 1999, 285, 1889–1892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crosby, H.A.; Roden, E.E.; Johnson, C.M.; Beard, B.L. The Mechanisms of Iron Isotope Fractionation Produced during Dissimilatory Fe(III) Reduction by Shewanella Putrefaciens and Geobacter Sulfurreducens. Geobiology 2007, 5, 169–189. [Google Scholar] [CrossRef]
- Icopini, G.A.; Anbar, A.D.; Ruebush, S.S.; Tien, M.; Brantley, S.L. Iron Isotope Fractionation during Microbial Reduction of Iron: The Importance of Adsorption. Geology 2004, 32, 205–208. [Google Scholar] [CrossRef]
- Conway, T.M.; John, S.G. Quantification of Dissolved Iron Sources to the North Atlantic Ocean. Nature 2014, 511, 212–215. [Google Scholar] [CrossRef]
- Fung, I.Y.; Meyn, S.K.; Tegen, I.; Doney, S.C.; John, J.G.; Bishop, J.K.B. Iron Supply and Demand in the Upper Ocean. Glob. Biogeochem. Cycles 2000, 14, 281–295. [Google Scholar] [CrossRef]
- Luther, G.W. Pyrite Synthesis via Polysulfide Compounds. Geochim. Cosmochim. Acta 1991, 55, 2839–2849. [Google Scholar] [CrossRef]
- Rickard, D. Kinetics of Pyrite Formation by the H2S Oxidation of Iron (II) Monosulfide in Aqueous Solutions between 25 and 125 °C: The Rate Equation. Geochim. Cosmochim. Acta 1997, 61, 115–134. [Google Scholar] [CrossRef]
- Guilbaud, R.; Butler, I.B.; Ellam, R.M. Abiotic Pyrite Formation Produces a Large Fe Isotope Fractionation. Science 2011, 332, 1548–1551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rolison, J.M.; Stirling, C.H.; Middag, R.; Gault-Ringold, M.; George, E.; Rijkenberg, M.J.A. Iron Isotope Fractionation during Pyrite Formation in a Sulfidic Precambrian Ocean Analogue. Earth Planet. Sci. Lett. 2018, 488, 1–13. [Google Scholar] [CrossRef]
- Mansor, M.; Fantle, M.S. A Novel Framework for Interpreting Pyrite-Based Fe Isotope Records of the Past. Geochim. Cosmochim. Acta 2019, 253, 39–62. [Google Scholar] [CrossRef]
- Anderson, T.F.; Raiswell, R. Sources and Mechanisms for the Enrichment of Highly Reactive Iron in Euxinic Black Sea Sediments. Am. J. Sci. 2004, 304, 203–233. [Google Scholar] [CrossRef] [Green Version]
- Duan, Y.; Severmann, S.; Anbar, A.D.; Lyons, T.W.; Gordon, G.W.; Sageman, B.B. Isotopic Evidence for Fe Cycling and Repartitioning in Ancient Oxygen-Deficient Settings: Examples from Black Shales of the Mid-to-Late Devonian Appalachian Basin. Earth Planet. Sci. Lett. 2010, 290, 244–253. [Google Scholar] [CrossRef]
- Scholz, F.; Severmann, S.; McManus, J.; Hensen, C. Beyond the Black Sea Paradigm: The Sedimentary Fingerprint of an Open-Marine Iron Shuttle. Geochim. Cosmochim. Acta 2014, 127, 368–380. [Google Scholar] [CrossRef]
- Melezhik, V.A.; Medvedev, P.V.; Svetov, S.A. The Onega Basin. In Reading the Archive of Earth’s Oxygenation; Melezhik, V.A., Prave, A.R., Fallick, A.E., Kump, L.R., Strauss, H., Lepland, A., Hanski, E.J., Eds.; The Palaeoproterozoic of Fennoscandia As Context for the Fennoscandian Arctic Russia-Drilling Early Earth Project; Frontiers in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 387–490. ISBN 978-3-642-29681-9. [Google Scholar]
- Melezhik, V.A.; Fallick, A.E.; Medvedev, P.V.; Makarikhin, V.V. Extreme 13Ccarb Enrichment in ca. 2.0 Ga Magnesite–Stromatolite–Dolomite–’red Beds’ Association in a Global Context: A Case for the World-Wide Signal Enhanced by a Local Environment. Earth Sci. Rev. 1999, 48, 71–120. [Google Scholar] [CrossRef]
- Puchtel, I.S.; Brügmann, G.E.; Hofmann, A.W. Precise Re–Os Mineral Isochron and Pb–Nd–Os Isotope Systematics of a Mafic–Ultramafic Sill in the 2.0 Ga Onega Plateau (Baltic Shield). Earth Planet. Sci. Lett. 1999, 170, 447–461. [Google Scholar] [CrossRef]
- Črne, A.E.; Melezhik, V.A.; Prave, A.R.; Lepland, A.; Romashkin, A.E.; Rychanchik, D.V.; Hanski, E.J.; Luo, Z.-Y. Zaonega Formation: FAR-DEEP Holes 12A and 12B, and neighbouring quarries. In Reading the Archive of Earth’s Oxygenation; Melezhik, V.A., Prave, A.R., Fallick, A.E., Hanski, E., Lepland, A., Kump, L.R., Strauss, H., Eds.; The Core Archive of the Fennoscandian Arctic Russia-Drilling Early Earth Project; Frontiers in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, pp. 946–1007. [Google Scholar]
- Črne, A.E.; Melezhik, V.A.; Prave, A.R.; Lepland, A.; Romashkin, A.E.; Rychanchik, D.V.; Hanski, E.J.; Luo, Z.-Y. Zaonega Formation: FAR-DEEP hole 13A. In Reading the Archive of Earth’s Oxygenation; Melezhik, V.A., Prave, A.R., Fallick, A.E., Hanski, E.J., Lepland, A., Kump, L.R., Strauss, H., Eds.; The Core Archive of the Fennoscandian Arctic Russia-Drilling Early Earth Project; Frontiers in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, pp. 1008–1046. [Google Scholar]
- Lepland, A.; Joosu, L.; Kirsimäe, K.; Prave, A.R.; Romashkin, A.E.; Črne, A.E.; Martin, A.P.; Fallick, A.E.; Somelar, P.; Üpraus, K.; et al. Potential Influence of Sulphur Bacteria on Palaeoproterozoic Phosphogenesis. Nat. Geosci. 2014, 7, 20–24. [Google Scholar] [CrossRef]
- Melezhik, V.A.; Filippov, M.M.; Romashkin, A.E. A Giant Palaeoproterozoic Deposit of Shungite in NW Russia: Genesis and Practical Applications. Ore Geol. Rev. 2004, 24, 135–154. [Google Scholar] [CrossRef]
- Strauss, H.; Melezhik, V.A.; Lepland, A.; Fallick, A.E.; Hanski, E.J.; Filippov, M.M.; Deines, Y.E.; Illing, C.J.; Črne, A.E.; Brasier, A.T. Enhanced accumulation of organic matter: The Shunga Event. In Reading the Archive of Earth’s Oxygenation; Melezhik, V.A., Prave, A.R., Hanski, E.J., Fallick, A.E., Lepland, A., Kump, L.R., Strauss, H., Eds.; Global Events and the Fennoscandian Arctic Russia-Drilling Earth Project; Frontiers in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 3, pp. 1195–1273. ISBN 978-3-642-29669-7. [Google Scholar]
- Ovchinnikova, G.V.; Kuznetsov, A.B.; Melezhik, V.A.; Gorokhov, I.M.; Vasil’eva, I.M.; Gorokhovskii, B.M. Pb-Pb Age of Jatulian Carbonate Rocks: The Tulomozero Formation of Southeast Karelia. Stratigr. Geol. Correl. 2007, 15, 359–372. [Google Scholar] [CrossRef]
- Melezhik, V.A.; Fallick, A.E.; Brasier, A.T.; Lepland, A. Carbonate Deposition in the Palaeoproterozoic Onega Basin from Fennoscandia: A Spotlight on the Transition from the Lomagundi-Jatuli to Shunga Events. Earth Sci. Rev. 2015, 147, 65–98. [Google Scholar] [CrossRef] [Green Version]
- Priyatkina, N.; Khudoley, A.K.; Ustinov, V.N.; Kullerud, K. 1.92 Ga Kimberlitic Rocks from Kimozero, NW Russia: Their Geochemistry, Tectonic Setting and Unusual Field Occurrence. Precambrian Res. 2014, 249, 162–179. [Google Scholar] [CrossRef]
- Stepanova, A.; Samsonov, A.; Larionov, A. The Final Episode of Middle Proterozoic Magmatism in the Onega Structure: Data on Trans-Onega Dolerites. Trans. Karelian Res. Cent. Russ. Acad. Sci. Precambrian Geol. Ser. 2014, 1, 3–16. [Google Scholar]
- Martin, A.P.; Prave, A.R.; Condon, D.J.; Lepland, A.; Fallick, A.E.; Romashkin, A.E.; Medvedev, P.V.; Rychanchik, D.V. Multiple Palaeoproterozoic Carbon Burial Episodes and Excursions. Earth Planet. Sci. Lett. 2015, 424, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Puchtel, I.S.; Arndt, N.T.; Hofmann, A.W.; Haase, K.M.; Kröner, A.; Kulikov, V.S.; Kulikova, V.V.; Garbe-Schönberg, C.-D.; Nemchin, A.A. Petrology of Mafic Lavas within the Onega Plateau, Central Karelia: Evidence for 2.0 Ga Plume-Related Continental Crustal Growth in the Baltic Shield. Contrib. Mineral. Petrol. 1998, 130, 134–153. [Google Scholar] [CrossRef]
- Bauer, A.M.; Rooney, A.D.; Lepland, A.; Cole, D.B.; Planavsky, N.J. The Dynamics of the Lomagundi-Jatuli Carbon Isotope Excursion and Implications for Early Life. In Proceedings of the Geobiology 2019 Conference Proceedings, Banff, AB, Canada, 9–13 June 2019. [Google Scholar]
- Hannah, J.L.; Stein, H.J.; Zimmerman, A.; Yang, G.; Melezhik, V.A.; Filippov, M.M.; Turgeon, S.C.; Creaser, R.A. Re-Os Geochronology of Shungite: A 2.05 Ga Fossil Oil Field in Karelia. In Proceedings of the Goldschmidt Conference Abstracts, Oslo, Norway, 16 July 2008; p. A351. [Google Scholar]
- Rouxel, O.; Sholkovitz, E.; Charette, M.; Edwards, K.J. Iron Isotope Fractionation in Subterranean Estuaries. Geochim. Cosmochim. Acta 2008, 72, 3413–3430. [Google Scholar] [CrossRef] [Green Version]
- Malinovsky, D.; Stenberg, A.; Rodushkin, I.; Andren, H.; Ingri, J.; Öhlander, B.; Baxter, C.D. Performance of High Resolution MC-ICP-MS for Fe Isotope Ratio Measurements in Sedimentary Geological Materials. J. Anal. At. Spectrom. 2003, 18, 687–695. [Google Scholar] [CrossRef]
- Poitrasson, F.; Freydier, R. Heavy Iron Isotope Composition of Granites Determined by High Resolution MC-ICP-MS. Chem. Geol. 2005, 222, 132–147. [Google Scholar] [CrossRef]
- Belshaw, N.S.; Zhu, X.K.; Guo, Y.; O’Nions, R.K. High Precision Measurement of Iron Isotopes by Plasma Source Mass Spectrometry. Int. J. Mass Spectrom. 2000, 197, 191–195. [Google Scholar] [CrossRef]
- Jochum, K.P.; Nohl, U.; Herwig, K.; Lammel, E.; Stoll, B.; Hofmann, A.W. GeoReM: A New Geochemical Database for Reference Materials and Isotopic Standards. Geostand. Geoanalytical Res. 2005, 29, 333–338. [Google Scholar] [CrossRef]
- Kassambara, A.; Mundt, F. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses. R Package Version 2020, 1, 337–354. [Google Scholar]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Williams, M.J.; Schoneveld, L.; Mao, Y.; Klump, J.; Gosses, J.; Dalton, H.; Bath, A.; Barnes, S. Pyrolite: Python for Geochemistry. J. Open Source Softw. 2020, 5, 2314. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Ikeda, Y.; Grabowski, B.; Körmann, F. Mpltern: Ternary Plots as Projections of Matplotlib; Zenodo: Genève, Switzerland, 2019. [Google Scholar]
- Waskom, M.; Botvinnik, O.; Gelbart, M.; Ostblom, J.; Hobson, P.; Lukauskas, S.; Gemperline, D.C.; Augspurger, T.; Halchenko, Y.; Warmenhoven, J.; et al. Mwaskom/Seaborn: Statistical Data Visualization; Zenodo: Genève, Switzerland, 2020. [Google Scholar]
- Algeo, T.J.; Li, C. Redox Classification and Calibration of Redox Thresholds in Sedimentary Systems. Geochim. Cosmochim. Acta 2020, 287, 8–26. [Google Scholar] [CrossRef]
- Tribovillard, N.; Algeo, T.J.; Lyons, T.; Riboulleau, A. Trace Metals as Paleoredox and Paleoproductivity Proxies: An Update. Chem. Geol. 2006, 232, 12–32. [Google Scholar] [CrossRef]
- Rudnick, R.L.; Gao, S. Composition of the Continental Crust. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–51. ISBN 978-0-08-098300-4. [Google Scholar]
- Taylor, S.R.; McLennan, S.M. The Continental Crust: Its Composition and Evolution; Blackwell Scientific Pub.: Palo Alto, CA, USA, 1985. [Google Scholar]
- Iwamori, H.; Yoshida, K.; Nakamura, H.; Kuwatani, T.; Hamada, M.; Haraguchi, S.; Ueki, K. Classification of Geochemical Data Based on Multivariate Statistical Analyses: Complementary Roles of Cluster, Principal Component, and Independent Component Analyses. Geochem. Geophys. Geosystems 2017, 18, 994–1012. [Google Scholar] [CrossRef]
- Rickard, D.; Luther, G.W. Chemistry of Iron Sulfides. Chem. Rev. 2007, 107, 514–562. [Google Scholar] [CrossRef] [PubMed]
- Beard, B.L.; Johnson, C.M.; Damm, K.L.V.; Poulson, R.L. Iron Isotope Constraints on Fe Cycling and Mass Balance in Oxygenated Earth Oceans. Geology 2003, 31, 629–632. [Google Scholar] [CrossRef]
- Rouxel, O.; Shanks, W.C.; Bach, W.; Edwards, K.J. Integrated Fe- and S-Isotope Study of Seafloor Hydrothermal Vents at East Pacific Rise 9–10° N. Chem. Geol. 2008, 252, 214–227. [Google Scholar] [CrossRef] [Green Version]
- Severmann, S.; Johnson, C.M.; Beard, B.L.; German, C.R.; Edmonds, H.N.; Chiba, H.; Green, D.R.H. The Effect of Plume Processes on the Fe Isotope Composition of Hydrothermally Derived Fe in the Deep Ocean as Inferred from the Rainbow Vent Site, Mid-Atlantic Ridge, 36°14′ N. Earth Planet. Sci. Lett. 2004, 225, 63–76. [Google Scholar] [CrossRef]
- Chan, L.-H.; Leeman, W.P.; Plank, T. Lithium Isotopic Composition of Marine Sediments. Geochem. Geophys. Geosystems 2006, 7. [Google Scholar] [CrossRef]
- Bau, M. Rare-Earth Element Mobility during Hydrothermal and Metamorphic Fluid-Rock Interaction and the Significance of the Oxidation State of Europium. Chem. Geol. 1991, 93, 219–230. [Google Scholar] [CrossRef]
- Mills, R.A.; Elderfield, H. Rare Earth Element Geochemistry of Hydrothermal Deposits from the Active TAG Mound, 26° N Mid-Atlantic Ridge. Geochim. Cosmochim. Acta 1995, 59, 3511–3524. [Google Scholar] [CrossRef]
- Weill, D.F.; Drake, M.J. Europium Anomaly in Plagioclase Feldspar: Experimental Results and Semiquantitative Model. Science 1973, 180, 1059–1060. [Google Scholar] [CrossRef]
- Wijsman, J.W.M.; Middelburg, J.J.; Heip, C.H.R. Reactive Iron in Black Sea Sediments: Implications for Iron Cycling. Mar. Geol. 2001, 172, 167–180. [Google Scholar] [CrossRef]
- Moore, J.K.; Braucher, O. Sedimentary and Mineral Dust Sources of Dissolved Iron to the World Ocean. Biogeosciences 2008, 5, 631–656. [Google Scholar] [CrossRef] [Green Version]
- Algeo, T.J.; Lyons, T.W. Mo–Total Organic Carbon Covariation in Modern Anoxic Marine Environments: Implications for Analysis of Paleoredox and Paleohydrographic Conditions. Paleoceanography 2006, 21, PA1016. [Google Scholar] [CrossRef]
- Kunzmann, M.; Gibson, T.M.; Halverson, G.P.; Hodgskiss, M.S.W.; Bui, T.H.; Carozza, D.A.; Sperling, E.A.; Poirier, A.; Cox, G.M.; Wing, B.A. Iron Isotope Biogeochemistry of Neoproterozoic Marine Shales. Geochim. Cosmochim. Acta 2017, 209, 85–105. [Google Scholar] [CrossRef]
- Coleman, M.L.; Berner, R.A.; Durand, B.; Meadows, P.S.; Eglinton, G.; Eglinton, G.; Curtis, C.D.; McKenzie, D.P.; Murchison, D.G. Geochemistry of Diagenetic Non-Silicate Minerals: Kinetic Considerations. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 315, 39–56. [Google Scholar] [CrossRef]
- Lyons, T.W.; Severmann, S. A Critical Look at Iron Paleoredox Proxies: New Insights from Modern Euxinic Marine Basins. Geochim. Cosmochim. Acta 2006, 70, 5698–5722. [Google Scholar] [CrossRef]
- Shawar, L.; Halevy, I.; Said-Ahmad, W.; Feinstein, S.; Boyko, V.; Kamyshny, A.; Amrani, A. Dynamics of Pyrite Formation and Organic Matter Sulfurization in Organic-Rich Carbonate Sediments. Geochim. Cosmochim. Acta 2018, 241, 219–239. [Google Scholar] [CrossRef]
- Blättler, C.L.; Claire, M.W.; Prave, A.R.; Kirsimäe, K.; Higgins, J.A.; Medvedev, P.V.; Romashkin, A.E.; Rychanchik, D.V.; Zerkle, A.L.; Paiste, K.; et al. Two-Billion-Year-Old Evaporites Capture Earth’s Great Oxidation. Science 2018, 360, 320–323. [Google Scholar] [CrossRef] [Green Version]
- Lenstra, W.K.; Hermans, M.; Séguret, M.J.M.; Witbaard, R.; Behrends, T.; Dijkstra, N.; van Helmond, N.A.G.M.; Kraal, P.; Laan, P.; Rijkenberg, M.J.A.; et al. The Shelf-to-Basin Iron Shuttle in the Black Sea Revisited. Chem. Geol. 2019, 511, 314–341. [Google Scholar] [CrossRef]
- Scholz, F.; McManus, J.; Sommer, S. The Manganese and Iron Shuttle in a Modern Euxinic Basin and Implications for Molybdenum Cycling at Euxinic Ocean Margins. Chem. Geol. 2013, 355, 56–68. [Google Scholar] [CrossRef]
- Heard, A.W.; Dauphas, N. Constraints on the Coevolution of Oxic and Sulfidic Ocean Iron Sinks from Archean–Paleoproterozoic Iron Isotope Records. Geology 2020, 48, 358–362. [Google Scholar] [CrossRef]
- Konhauser, K.O.; Lalonde, S.V.; Planavsky, N.J.; Pecoits, E.; Lyons, T.W.; Mojzsis, S.J.; Rouxel, O.J.; Barley, M.E.; Rosìere, C.; Fralick, P.W.; et al. Aerobic Bacterial Pyrite Oxidation and Acid Rock Drainage during the Great Oxidation Event. Nature 2011, 478, 369–373. [Google Scholar] [CrossRef] [PubMed]



| Column | PC1 | PC2 | PC3 | PC4 |
|---|---|---|---|---|
| Si | −0.38 | 0.11 | −0.11 | −0.01 |
| (Eu/Eu*)SN | −0.27 | 0.07 | −0.29 | 0.11 |
| ReEF | −0.24 | −0.14 | −0.39 | −0.11 |
| δ56Fe | −0.16 | 0.09 | 0.03 | 0.61 |
| VEF | −0.12 | −0.37 | −0.19 | −0.22 |
| UEF | −0.07 | −0.41 | −0.10 | −0.10 |
| MoEF | −0.05 | −0.42 | −0.10 | −0.05 |
| TOC | 0.02 | −0.43 | 0.06 | 0.00 |
| Fe/Al | 0.17 | −0.36 | 0.03 | 0.18 |
| Ca | 0.19 | −0.13 | −0.18 | 0.51 |
| Fe | 0.24 | −0.29 | 0.24 | 0.21 |
| Mg | 0.27 | 0.08 | −0.42 | −0.08 |
| Mn | 0.27 | 0.03 | −0.35 | 0.33 |
| Al | 0.29 | 0.00 | 0.41 | −0.12 |
| Li | 0.33 | 0.20 | −0.13 | −0.15 |
| P | 0.33 | 0.08 | −0.31 | −0.13 |
| Ti | 0.33 | −0.04 | −0.12 | −0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mänd, K.; Lalonde, S.V.; Paiste, K.; Thoby, M.; Lumiste, K.; Robbins, L.J.; Kreitsmann, T.; Romashkin, A.E.; Kirsimäe, K.; Lepland, A.; et al. Iron Isotopes Reveal a Benthic Iron Shuttle in the Palaeoproterozoic Zaonega Formation: Basinal Restriction, Euxinia, and the Effect on Global Palaeoredox Proxies. Minerals 2021, 11, 368. https://doi.org/10.3390/min11040368
Mänd K, Lalonde SV, Paiste K, Thoby M, Lumiste K, Robbins LJ, Kreitsmann T, Romashkin AE, Kirsimäe K, Lepland A, et al. Iron Isotopes Reveal a Benthic Iron Shuttle in the Palaeoproterozoic Zaonega Formation: Basinal Restriction, Euxinia, and the Effect on Global Palaeoredox Proxies. Minerals. 2021; 11(4):368. https://doi.org/10.3390/min11040368
Chicago/Turabian StyleMänd, Kaarel, Stefan V. Lalonde, Kärt Paiste, Marie Thoby, Kaarel Lumiste, Leslie J. Robbins, Timmu Kreitsmann, Alexander E. Romashkin, Kalle Kirsimäe, Aivo Lepland, and et al. 2021. "Iron Isotopes Reveal a Benthic Iron Shuttle in the Palaeoproterozoic Zaonega Formation: Basinal Restriction, Euxinia, and the Effect on Global Palaeoredox Proxies" Minerals 11, no. 4: 368. https://doi.org/10.3390/min11040368
APA StyleMänd, K., Lalonde, S. V., Paiste, K., Thoby, M., Lumiste, K., Robbins, L. J., Kreitsmann, T., Romashkin, A. E., Kirsimäe, K., Lepland, A., & Konhauser, K. O. (2021). Iron Isotopes Reveal a Benthic Iron Shuttle in the Palaeoproterozoic Zaonega Formation: Basinal Restriction, Euxinia, and the Effect on Global Palaeoredox Proxies. Minerals, 11(4), 368. https://doi.org/10.3390/min11040368






