An Accurate Model to Calculate CO₂ Solubility in Pure Water and in Seawater at Hydrate–Liquid Water Two-Phase Equilibrium

Abstract

Understanding of CO₂ hydrate–liquid water two-phase equilibrium is very important for CO₂ storage in deep sea and in submarine sediments. This study proposed an accurate thermodynamic model to calculate CO₂ solubility in pure water and in seawater at hydrate–liquid water equilibrium (HL_WE). The van der Waals–Platteeuw model coupling with angle-dependent ab initio intermolecular potentials was used to calculate the chemical potential of hydrate phase. Two methods were used to describe the aqueous phase. One is using the Pitzer model to calculate the activity of water and using the Poynting correction to calculate the fugacity of CO₂ dissolved in water. Another is using the Lennard–Jones-referenced Statistical Associating Fluid Theory (SAFT-LJ) equation of state (EOS) to calculate the activity of water and the fugacity of dissolved CO₂. There are no parameters evaluated from experimental data of HL_WE in this model. Comparison with experimental data indicates that this model can calculate CO₂ solubility in pure water and in seawater at HL_WE with high accuracy. This model predicts that CO₂ solubility at HL_WE increases with the increasing temperature, which agrees well with available experimental data. In regards to the pressure and salinity dependences of CO₂ solubility at HL_WE, there are some discrepancies among experimental data. This model predicts that CO₂ solubility at HL_WE decreases with the increasing pressure and salinity, which is consistent with most of experimental data sets. Compared to previous models, this model covers a wider range of pressure (up to 1000 bar) and is generally more accurate in CO₂ solubility in aqueous solutions and in composition of hydrate phase. A computer program for the calculation of CO₂ solubility in pure water and in seawater at hydrate–liquid water equilibrium can be obtained from the corresponding author via email.

1. Introduction

There has been a growing concern on the potential impact of rising greenhouse gas levels in the atmosphere. CO₂ is the greatest contributor to the greenhouse effect. Consequently, carbon capture and storage (CCS) becomes a promising option to reduce anthropogenic CO₂ emissions into the atmosphere. Geological storage and ocean storage are the most common storage methods for large CO₂ volumes. Proposed sites for CO₂ geological storage range from mined salt caverns, saline aquifers, depleted hydrocarbon reservoirs, unmineable coal seams, and so on [1]. Storage of CO₂ in depleted oil/gas reservoirs and unmineable coal beds is more economical than other CO₂ storage strategies due to additional oil and gas recovery, characterized geological conditions, existing installed equipment, and so on. Saline aquifers are favored due to their extended storage capacity. Storages of CO₂ in depleted oil/gas reservoirs and in saline aquifers are more technically feasible [2,3]. Tens of pilot and commercial projects for CO₂ storage in depleted oil/gas reservoirs or in saline aquifers have been launched to date [3,4]. Injecting CO₂ into the deep ocean to form CO₂ hydrate is attractive since the CO₂ storage capacity of deep oceans is huge [5]. However, this method is more controversial than other CO₂ storage methods due to the risk of leakage, local acidification of seawater, the correspondingly negative impact on the marine environment, and so on [4,6,7]. Recent studies relevant to ocean storage of CO₂ tried to develop numerical models for better evaluation of storage efficiency and risk assessment and investigate the determination and quantification of ocean site selection criteria [7,8]. In a hybrid method between ocean and geological storage, CO₂ would be injected into submarine sediments below the deep ocean floor to avoid the potential leakage of CO₂ and harm to marine ecosystems [9].

In addition to the deep ocean, CO₂ injected into shallow zones in deep-sea sediments or cold saline aquifers will dissolve in seawater or brine and then convert into CO₂ hydrate [10,11,12]. Alternatively, Ohgaki et al. [13] proposed the method to replace CH₄ in methane hydrate in the seafloor sediments with CO₂, which provides twin advantages: sequestrating CO₂ and enhancing CH₄ hydrate recovery. A recent study found that the direct use of a CO₂ + N₂ gas mixture (flue gas), instead of pure CO₂, replacing CH₄ can greatly enhance the overall CH₄ recovery rate and reduce the costs [14,15,16].

Gas hydrates, or clathrate hydrates, are non-stoichiometric crystalline solids that consist of a hydrogen-bonded network of host water molecules and enclathrated guests molecules such as CH₄, C₂H₆, N₂, and CO₂ [17]. They are thermodynamically stable at a low temperature and high pressure. Within the stable region in deep sea or subsurface aquifers, CO₂ hydrate coexists with seawater or brine while being absent of a CO₂-rich phase. Therefore, understanding CO₂ hydrate–liquid water two-phase equilibrium is very important for CO₂ storage.

The stability boundary of CO₂ hydrate, corresponding to the pressure (P)-temperature (T) conditions for CO₂ hydrate–liquid water-CO₂ vapor (HL_WV) three-phase equilibrium, has been studied extensively [18]. Based on the van der Waals–Platteeuw (vdW-P) model [19], many thermodynamic models were developed to calculate P-T conditions for HL_wV three-phase equilibrium of gas hydrates (including CO₂ hydrate). In recent years, great improvements on the vdW-P model included the calculation of interaction potentials between gas molecules and water molecules using ab initio methods or quantum mechanics [17,18,20,21,22,23,24,25,26,27,28], taking into account effects of lattice distortion and guest–guest interactions (which is essential for modeling multiple occupancy of small guests) by extension of the vdW-P model or using alternative methods [29,30,31,32,33,34,35].

Early models for three-phase equilibrium of gas hydrates adopted a Cubic equation of states (EOS), such as Redlich–Kwong EOS [36], Peng–Robinson EOS [37], Patel–Teja EOS [38], and Trebble–Bishnoi EOS [39], to calculate fugacities of gas components, and used excess Gibbs energy models (activity coefficient models), such as the NRTL model [40], the UNIQUAC model [41], and the Pitzer model [42], to calculate the activity of water in the aqueous phase containing thermodynamic inhibitors. Later, studies tried to use one model to describe both gas phase and aqueous phase involved in three-phase equilibrium of gas hydrates. Some models combining a cubic EOS with an excess Gibbs energy model have been used [27,28,43]. In recent years, molecule-based EOS, such as SAFT (Statistical Associating Fluid Theory) and CPA (Cubic plus Association) EOS, became a popular choice for the modeling of phase equilibria of fluids. The SAFT-type EOS [44,45] describes the intermolecular association (hydrogen-bonding force) based on first-order thermodynamic perturbation theory of Wertheim [46,47,48], making it suitable for fluid systems containing associating molecules (e.g., water, methanol). The CPA EOS [49], as the name suggests, is constructed by incorporating the association term derived from Wertheim’s theory into the Cubic EOS. The SAFT-type EOS and CPA EOS have been widely used to model vapor–liquid equilibrium of the CO₂-H₂O or CO₂-brine systems [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. Furthermore, many studies tried to combine the SAFT-type EOS or CPA EOS with vdW-P model to calculate three-phase equilibrium of gas hydrates [43,66,67,68,69,70,71,72,73,74,75].

In contrast to numerous studies for three-phase equilibrium of CO₂ hydrate, studies on CO₂ hydrate–liquid water two-phase equilibrium are relatively limited. Aya et al. [76], Yang et al. [77], Lee et al. [78], Servio and Englezos [79], Zhang [80], Someya et al. [81], Kim et al. [82], Zhang et al. [83], Sun et al. [84], and Geng et al. [85] measured CO₂ solubility in water at hydrate–liquid water equilibrium (HL_WE). All measurements show that CO₂ solubility at HL_WE increase with increasing temperature. In regards to the effect of pressure, available experimental data show weak pressure dependence of CO₂ solubility at HL_WE although there are some discrepancies among them.

Yang et al. [77], Hashemi et al. [86], and Zhang et al. [83] proposed models to calculate CO₂ solubility in water at HL_WE. All these models adopted the van der Waals–Platteeuw hydrate model [19] to describe the hydrate phase. Differences between them are how to calculate the Langmuir constants and how to describe the aqueous phase. The model of Yang et al. [77] used an empirical formula to calculate the Langmuir constants and used the lattice fluid equation of state to calculate thermodynamic properties of the aqueous phase. Yang’s model agrees with the experimental data reported in the same work. However, data measured by Yang et al. [77] are larger than those measured by other studies. Hashemi et al. [86] adopted the Langmuir constants reported by Parrish and Prausnitz [87] and used the Trebble–Bishnoi EOS [39] to describe the aqueous phase. Zhang et al. [83] applied the lattice distortion theory developed by Holder and co-workers [88,89,90] to calculate the Langmuir constants and used Margules equations [91] to describe the aqueous phase. Calculations of this model agree with the experimental data measured by the same study. However, the lattice distortion theory overestimates the occupancy fraction of CO₂ in small cage. Recently, Sun et al. [92] combined the Chen–Guo hydrate model [93,94] and the Patel–Teja EOS [38] to calculate CO₂ solubilities in water and aqueous NaCl solution under HL_WE. All these models predict that CO₂ solubility at HL_WE increases with the increase of temperature, which is consistent with available experimental data. About pressure dependence of CO₂ solubility at HL_WE, models of Yang et al. [77], Zhang et al. [83], and Sun et al. [92] suggested a negative trend (i.e., CO₂ solubility at HL_WE decreases with the increasing pressure at constant temperature), whereas the model of Hashemi et al. [86] gives a positive trend. Bergeron et al. [95,96] made thermodynamic analyses on temperature and pressure dependence of CO₂ solubility at HL_WE. Although SAFT EOS and CPA EOS have been widely used to model three-phase equilibrium of gas hydrates as mentioned above, they have not been used to model HL_WE of gas hydrates to date. Sun and Duan [97] applied the method to calculate Langmuir constants from ab initio intermolecular potentials to model HL_WE of CH₄ hydrate. However, this method has not been used to model HL_WE of CO₂ hydrate.

The purpose of this study is to develop a new model to predict CO₂ solubility at HL_WE in marine environments by taking into account the effect of temperature, pressure and salinity together. Van der Waals–Platteeuw basic hydrate model [19] is used to calculate the chemical potential of hydrate phase. The method to calculate Langmuir constants from angle-dependent ab initio intermolecular potentials, which can well predict cage occupancies of CO₂ molecule in small and large cages of sI hydrate [18], is followed by this study. The aqueous solution is described with two methods. One is using the Pitzer model [42] to calculate the activity of water and using the Poynting correction to calculate the fugacity of CO₂ dissolved in water. Another is using the Lennard–Jones-referenced Statistical Associating Fluid Theory (SAFT-LJ) EOS [55] to calculate the activity of water and the fugacity of dissolved CO₂. The next section will introduce the principle of the thermodynamic model proposed by this study. Section 3 compares the experimental data with predictions of this model for CO₂ solubility in aqueous solution at HL_WE. Finally, some conclusions are drawn.

2. Thermodynamic Model of Gas Hydrates

2.1. Model Framework for HL_WE

According to principles of thermodynamics, the fugacities or chemical potentials of species in the various phases must be equal at phase equilibrium. For CO₂ hydrate–liquid water two-phase equilibrium, the following equation must be satisfied:

$$\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}={\mu }_{\mathrm{W}}^{\mathsf{\beta }}-{\mu }_{\mathrm{W}}^{\mathrm{H}}={\mu }_{\mathrm{W}}^{\mathsf{\beta }}-{\mu }_{\mathrm{W}}^{\mathrm{L}}=\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}},$$

(1)

where μ is the chemical potential, Δμ is the difference of chemical potential, the subscript W represents H₂O, the superscript H represents hydrate phase, β represents the hypothetical empty hydrate lattice, and L represent liquid water (aqueous phase).

$\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ is calculated from the van der Waals–Platteeuw model [19] based on the statistical mechanics:

$$\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}\left(T,P\right)=-RT{{\displaystyle \sum }}_{i=1}^2\ln \left(1-{{\displaystyle \sum }}_{j=1}^{N_C}{\theta }_{ij}\right),$$

(2)

$${\theta }_{ij}=C_{ij}{f}_j/\left(1+{{\displaystyle \sum }}_{j=1}^{N_C}{C}_{ij}{f}_j\right),$$

(3)

where ν_i is the number of i-type cages (also called “cavities”) per water molecule, θ_ij is the fractional occupancy of i-type cavities with j-type guest molecules, and C_ij is the Langmuir constant of gas component j in i-type cavity. For sI hydrate, the number of small cavities, v₁, equals to 1/23, the number of large cages, v₂, equals to 3/23. f_j in Equation (3) is the fugacity of gas component j in the hydrate phase, which equals to the fugacity of gas component in the aqueous phase at HL_WE.

Our previous study [18] presented a method to calculate the Langmuir constant from angle-dependent ab initio intermolecular potentials, which not only can represent P-T conditions of hydrate–liquid water–vapor three-phase equilibrium of pure CH₄ hydrate and CO₂ hydrate, but can also well-predict cage occupancies of CH₄ or CO₂ in small and large cages of sI hydrate. Thus, this method was followed by this study. It is the first time to apply Langmuir constants calculated from ab initio intermolecular potentials to model HL_WE of CO₂ hydrate. In order to facilitate the application, the Langmuir constant of CO₂ in small and large cage of structure I (sI)-type hydrate, C_Is,CO2 and C_Il,CO2, calculated from angle-dependent ab initio intermolecular potentials was fit using empirical equations as follows:

$$C_{\mathrm{Is},{\mathrm{CO}}_2}=\exp \left(-25.354129+3277.0691/T\right),$$

(4)

$$C_{\mathrm{Il},{\mathrm{CO}}_2}=\exp \left(-23.632139+3697.1701/T\right).$$

(5)

Since ions (e.g., Na⁺, Cl⁻) do not enter cages of the hydrate lattice, this study neglects the influence of ions on Langmuir constants as previous studies did. $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$ in Equation (1) is calculated from the thermodynamic correction equation improved by Holder et al. [98]:

$$\frac{\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}\left(T,P\right)}{RT}=\frac{\Delta {\mu }_{\mathrm{W}}^0\left(T_0,0\right)}{RT}-{{\displaystyle \int }}_{T_0}^T\left(\frac{\Delta h_{\mathrm{W}}^{\mathrm{L}}}{R{T}^2}\right)dT+{{\displaystyle \int }}_0^P\left(\frac{\Delta V_{\mathrm{W}}^{\mathrm{L}}}{RT}\right)dP-\ln a_{\mathrm{W}},$$

(6)

where a_W is the activity of water, $\Delta {\mu }_{\mathrm{W}}^0\left(T_0,0\right)$ is the reference chemical potential difference at the reference temperature, T₀, usually taken to be 273.15 K, and zero pressure. $\Delta h_{\mathrm{W}}^{\mathrm{L}}$ is the difference of enthalpy between hydrate and liquid water. The variation of $\Delta h_{\mathrm{W}}^{\mathrm{L}}$ with temperature is described with the following equation:

$$\Delta h_{\mathrm{W}}^{\mathrm{L}}=\Delta h_{\mathrm{W}}^0\left(T_0\right)+{{\displaystyle \int }}_{T_0}^T\Delta C_p^{\mathrm{L}}dT,$$

(7)

where $\Delta h_{\mathrm{W}}^0\left(T_0\right)$ is the reference enthalpy difference at T₀, $\Delta C_p^{\mathrm{L}}$ is the difference of isobaric molar heat capacity. The variation of $\Delta C_p^{\mathrm{L}}$ with temperature is linear:

$$\Delta C_p^{\mathrm{L}}=\Delta C_p^0+b\left(T-T_0\right).$$

(8)

$\Delta {\mu }_{\mathrm{w}}^0$ and $\Delta h_{\mathrm{W}}^0$ determined by our previous study [18] and $\Delta C_p^0$ and b determined by Parrish and Prausnitz [87] is adopted by this model.

$\Delta V_W^{\mathrm{L}}$ in Equation (6) is the difference of the molar volume between hydrate and liquid water. For sI hydrate, it equals to 4.6 cm³/mol after neglecting small variations of molar volumes of hydrate lattice and liquid water with pressure.

All solutes dissolved in water, such as CO₂ and ions, will change the activity of water. The fugacity of CO₂ dissolved is affected by ions. This study adopted two methods to calculate $f_{{\mathrm{CO}}_2}$ and a_W. One is using the Pitzer model [42] to calculate the activity of water and using the Poynting correction to calculate the fugacity of CO₂ dissolved in water, as we did for HL_WE of CH₄ hydrate [97]. Another is using the SAFT-LJ EOS [55] to calculate the activity of water and the fugacity of dissolved CO₂.

2.2. Method 1: Poynting Correction + Pitzer Model

At hydrate–liquid water two-phase equilibrium, vapor CO₂ or liquid CO₂ phase is absent. The fugacity of CO₂ in hydrate phase is equal to that in aqueous phase. The latter can be calculated from the Poynting correction equation [99,100] as following:

$$f_{{\mathrm{CO}}_2}^{\mathrm{aq}}\left(\mathrm{T},P,x_{{\mathrm{CO}}_2}\right)=f_{{\mathrm{CO}}_2}^{\mathrm{sat}}\exp \left[{{\displaystyle \int }}_{P^{\mathrm{sat}}}^P\frac{{\overline{V}}_{{\mathrm{CO}}_2}^{\mathrm{aq}}dP}{RT}\right],$$

(9)

where ${\overline{V}}_{{\mathrm{CO}}_2}^{\mathrm{aq}}$ means the partial molar volume of CO₂ in aqueous solution, P^sat is defined as the pressure required to obtain a given solubility, $x_{{\mathrm{CO}}_2}$. At P^sat, CO₂-rich vapor (or liquid) coexists with H₂O-rich liquid (aqueous phase) so that P^sat can be calculated from CO₂ solubility model developed by Duan et al. [101] for vapor–liquid equilibrium (VLE). $f_{{\mathrm{CO}}_2}^{\mathrm{sat}}$ in Equation (9) represents the fugacity of CO₂ at P^sat, which is calculated from the EOS of Duan et al. [102]. ${\overline{V}}_{{\mathrm{CO}}_2}^{\mathrm{aq}}$ can be evaluated from PVTX and solubility data of the CO₂-H₂O system based on thermodynamic methods [103]. The value of ${\overline{V}}_{{\mathrm{CO}}_2}^{\mathrm{aq}}$ determined by this study is equal to 31.5 cm³/mol at temperatures below 300 K.

The Pitzer model [42] was used to calculate the activity of water in aqueous electrolytes solution containing dissolved CO₂. It is well accepted that the Pitzer model can calculate thermodynamic properties of aqueous electrolyte solutions over a wide P-T-m range (from the saturation pressure to 1000 bar, from the Eutectic temperature to 523~573 K, from dilute solution to saturated solution) with high accuracy when sufficient data are available to constrain the regression of Pitzer ion-interaction parameters. Temperature-dependent ion-ion interaction parameters determined by Spencer et al. [104] are suitable for aqueous solutions containing Na⁺, K⁺, Mg²⁺, Ca²⁺, Cl^-, and SO₄²⁻ at temperatures below 298 K. These parameters and CO₂-ion interaction parameters determined by Duan et al. [101] were adopted by Sun and Duan [18] in the model for three-phase equilibrium of CO₂ hydrate. Although some approximations had to be made to evaluate CO₂-ion interaction parameters (such as neglecting the ionization of the carbonic acid and neglecting interactions between CO₂ molecules), three-phase equilibria of CO₂ hydrate in the CO₂-H₂O-NaCl system and CO₂-seawater system have been calculated with high accuracy. Thus, this study tried to check the performance of the Pitzer model with parameters determined by Spencer et al. [104] and Duan et al. [101] in modeling HL_WE of CO₂ hydrate. The details about the Pitzer model is omitted here to keep the paper concise. The readers can find them in the paper of Duan and Sun [105].

2.3. Method 2: SAFT-LJ EOS

The Statistical Association Fluid Theory (SAFT) EOS is one type of advanced EOS based on statistical mechanics. It describes the intermolecular association (hydrogen-bonding force) based on first-order thermodynamic perturbation theory of Wertheim [46,47,48] so that it is suitable for fluid system containing associating molecules (e.g., water, methanol). Depending on the type of reference fluid selected, there are various SAFT-type EOSs, such as SAFT-VR (Variable Range) [106], SAFT1 [107], PC (Perturbed Chain)-SAFT [108], and SAFT-LJ (Lennard–Jones) [109]. The SAFT-LJ EOS improved by Sun and Dubessy [54,55], which takes into account multi-polar interaction and ion–ion interaction besides association, allows for calculation of VLE and PVTx properties of the CO₂-H₂O-NaCl system at temperatures below 573 K. It was adopted by this study to calculate thermodynamic properties of aqueous solutions. As we know, it is the first time to apply the SAFT-type EOS to modeling HL_WE. The improved SAFT-LJ EOS is defined in terms of the dimensionless residual Helmholtz energy a^res as follows:

$$a^{\mathrm{res}}=a^{\mathrm{seg}}+a^{\mathrm{chain}}+a^{\mathrm{assoc}}+a^{\mathrm{polar}}+a^{\mathrm{ion}},$$

(10)

where a represents the dimensionless molar Helmholtz energy, the superscript seg, chain, assoc, polar, and ion represent the contributions from the repulsive and the attractive forces between Lennard–Jones segments, the chain formation, the intermolecular association, the multi-polar interaction, and ion–ion interaction, respectively.

a^chain and a^assoc in Equation (10) are calculated from Wertheim’s first-order thermodynamic perturbation theory [46,47,48], a^seg, a^polar, and a^ion is calculated based on the Kolafa-Nezbeda equation [110], the Gubbins-Twu equation [111], and the primitive model of the mean-spherical approximation [112]. Detailed equations (Equations (A1)–(A30)) for a^seg, a^chain, a^assoc, a^polar, and a^ion are listed in Appendix A and can also be found in Sun and Dubessy [54,55]. Parameters for pure H₂O, CO₂ and NaCl, binary parameters for interactions between H₂O and NaCl, and binary parameters for interactions between CO₂ and NaCl determined by Sun and Dubessy [55] were followed by this study (these parameters are given in

Table A1. Parameters of SAFT-LJ EOS for pure H₂O and pure CO_2.

	H2O	CO2
ε/kB (K)	172.1 − 0.001 × (T-473.15)2	173.7
b (cm3/mol)	16.684 − 0.00476 × (T-423.15) + 1.58 × 10−5 × (T-423.15)2	19.97
εassoc/kB (K)	1430 − 1.07 × (T-273.15) − 10.5 × 10−4 × (T-273.15)2 +7.5 × 10−6 × (T-273.15)3
Κassoc	0.004
m	1	1.5
μ (10−30C·m)	7.34
Q (10−40C·m2)		−14.3

and

Table A2. SAFT-LJ parameters for NaCl-H₂O.

Parameter	Value
d (10−10 m)	4.65 + 0.00237 × (T-273.15) − 2.572 × 10−5 × (T-273.15)2
εNaCl/kB (K)	0
bNaCl (cm3/mol)	11.411 + 0.03052 × (T-273.15) − 2.389 × 10−4 × (T-273.15)2 + 3.048 × 10−7 × (T-273.15)3
εNaCl-H2O/kB (K)	283.01 − 0.0476 × (T-273.15) + 6.237 × 10−4 × (T-273.15)2
bNaCl-H2O(cm3/mol)	10.6 − 0.00521 × (T-273.15) − 6.3336 × 10−5 × (T-273.15)2

in Appendix A). Two binary parameters for interactions between H₂O and CO_2, k_1,ij and k_2,ij (their definitions can be found in Equations (A12) and (A13) in Appendix A) were re-evaluated by this study in order to improve the accuracy of the SAFT-LJ EOS at temperatures below 300 K. New parameters are listed in

Table 1. Binary parameters of the Lennard–Jones-referenced Statistical Associating Fluid Theory (SAFT-LJ) equation of state (EOS) for the CO₂-H₂O system.

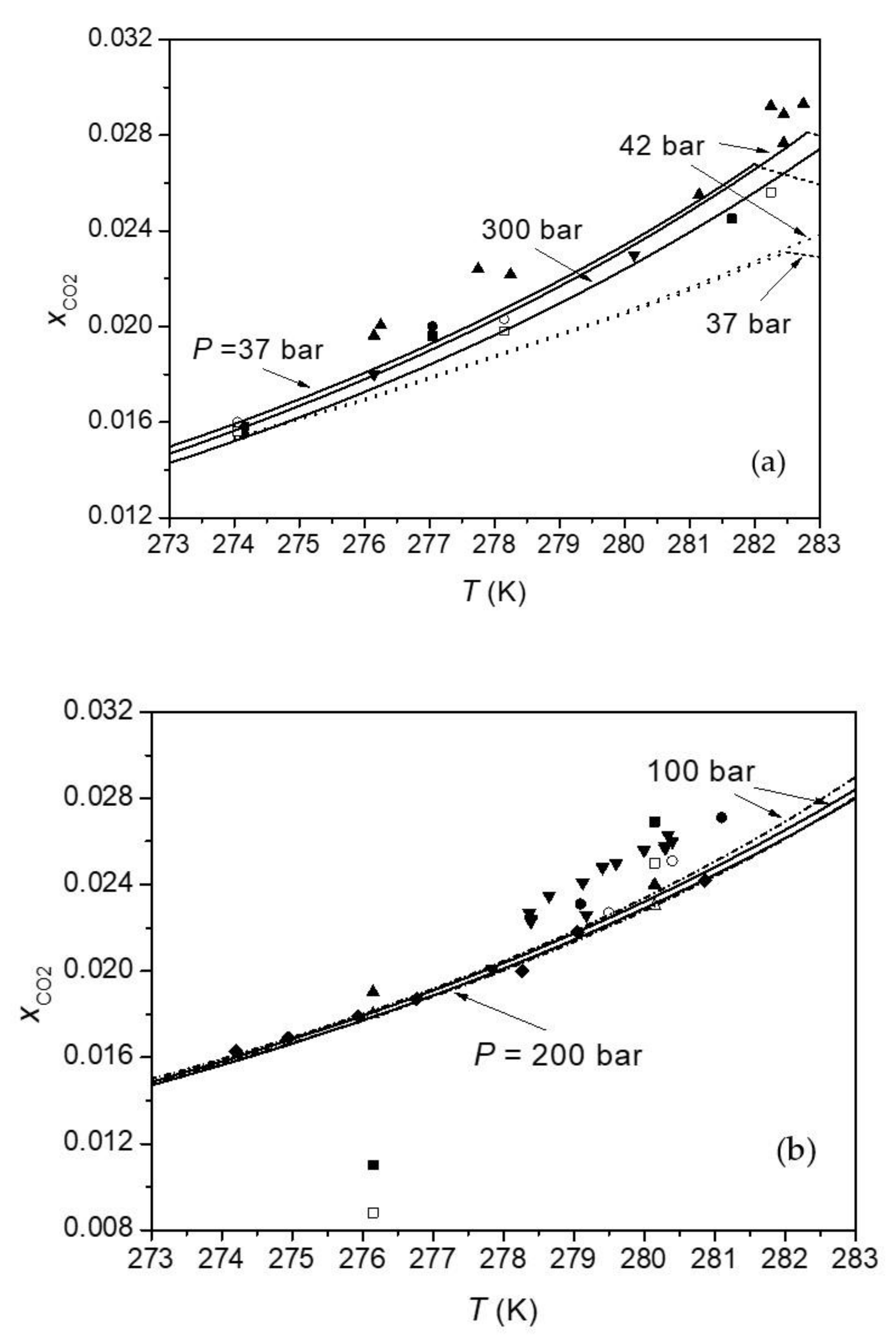
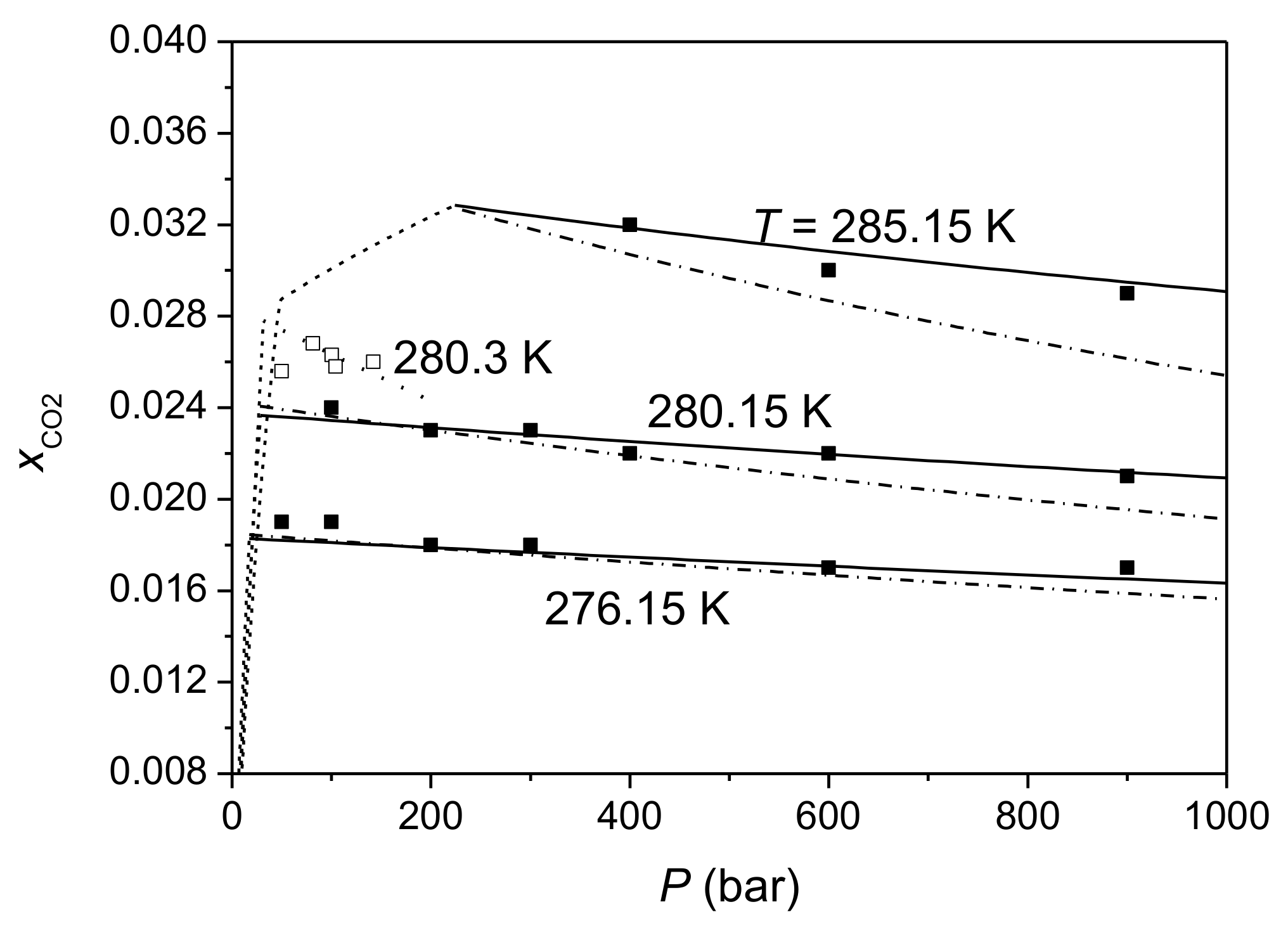
Parameter	Value
k1,ij	0.00518 + 0.001 × (T-273.15) − 5.695 × 10−7 × (T-273.15)2
k2,ij	0.9671 + 9.997 × 10−4 × (T-273.15) − 9.304 × 10−6 × (T-273.15)2

.

CO₂ solubility at H-L_W equilibrium at a given P and T can be calculated by iteration of Equation (1). For Method 1, an initial guess for the value of $x_{{\mathrm{CO}}_2}$ is made firstly. Then, P^sat is calculated from CO₂ solubility model of Duan et al. [101] for VLE, and f^sat is calculated from EOS of Duan et al. [102]. The third step is to calculate $f_{{\mathrm{CO}}_2}$ (from Equation (9)) and a_W (from the Pitzer model [42]) at P. Finally, $f_{{\mathrm{CO}}_2}$ and a_W are substituted into Equations (2), (3), and (6) to calculate $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ and $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$. If $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ equals to $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$, the current value of $x_{{\mathrm{CO}}_2}$ is the answer. If $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ does not equal to $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$, we must change the value of $x_{{\mathrm{CO}}_2}$ and repeat calculation until the answer is found. For Method 2, the first step is to guess an initial value for $x_{{\mathrm{CO}}_2}$, too. Then, both $f_{{\mathrm{CO}}_2}$ and a_W at P are calculated from the improved SAFT-LJ EOS [55]. After that, they are substituted into Equations (2), (3), and (6) to calculate $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ and $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$. If $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ does not equal to $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$, we must change the value of $x_{{\mathrm{CO}}_2}$ and repeat calculation until $\Delta {\mu }_{\mathrm{W}}^{\mathrm{H}}$ equals to $\Delta {\mu }_{\mathrm{W}}^{\mathrm{L}}$.

3. Result and Discussion

Firstly, this study compared predictions of this model for H-L_w equilibrium of the CO₂-H₂O system with available experimental data.

Table 2. The absolute average deviations (AAD) of this model for CO₂ solubility in water at hydrate–liquid water equilibrium (HL_WE) from experimental data sets.

Data Source	T (K)	P (bar)	N *	AAD a%	AAD b%
[76]	276.2–282.8	300	9	9.4	9.8
[79]	274.0–283.0	20–60	15	3.5	4.3
[78]	273.2–280.2	50–200	11	65.1	67.4
[77]	277.8–281.0	50–142	32	7.7	6.9
[80]	274.0–279.3	66–506	9	6.1	4.8
[81]	275.8–282.3	40–120	52	7.7	7.1
[82]	279.1–281.5	101–201	10	4.2	3.9
[83]	274.1–281.1	19–236	30	1.6	1.5
[85]	276.2–285.2	50–900	15	1.8	3.6
[84]	274.0–282.9	20–50	7	2.5	3.2

* Number of experimental data, ^a Method 1; ^b Method 2.

lists the absolute average deviations (AAD) of CO₂ solubilities calculated by this model from each solubility data sets. Figure 1, Figure 2, Figure 3 compare the calculated CO₂ solubility isobars, isopleths, and isotherms with experimental data, respectively. Both calculation results of Method 1 and those of Method 2 are given in Table 2 and Figure 1, Figure 2, Figure 3. It can be seen that the difference between Method 1 and Method 2 is small at pressures below 300 bar. The difference between two methods increases with pressure in that Method 2 gives larger pressure dependence of CO₂ solubility than Method 1. Figure 1, Figure 2, Figure 3 show that this model agrees well with most of experimental data sets. CO₂ solubilities calculated by this model are systematically lower than experimental data reported by Yang et al. [77] by 3–11.7%. A comparison of different experimental data sets shows that CO₂ solubilities measured by Aya et al. [76] are greater than those of Geng et al. [85] by 4–10% (Figure 1a), and CO₂ solubilities reported by Yang et al. [77] are larger than data measured by Servio and Englezos [79], Zhang et al. [83], Sun et al. [84], and Geng et al. [85] (Figure 1b). Data of Lee et al. [78] at 280 K are close to data from other studies, but data of Lee et al. [78] at 273 K and 276 K are much lower than data from other studies (Figure 1b). Calculations of this model for CO₂ solubility are consistent with measurements of Someya et al. [81] at 40 bar and 70 bar, but are lower than those measurements at 100 bar and 120 bar, since measurements of Someya et al. [81] show a positive pressure dependence of CO₂ solubility at HL_WE.

Figure 1a shows that CO₂ solubility in water at HL_WE increases with the increasing temperature whereas CO₂ solubility at VLE decreases with the increasing temperature at constant pressure. The prediction of this model for the temperature dependence of CO₂ solubility at HL_WE is consistent with experimental data. As shown in Figure 2 and Figure 3, the pressure dependence of CO₂ solubility at HL_WE predicted by this model is negative, which is consistent with experimental data of Zhang [80], Zhang et al. [83], and Geng et al. [85]. It can also be seen from Figure 3 that the decreasing gradient of CO₂ solubility with pressure at constant temperature is small. For example, CO₂ solubility decreases by 10% when the pressure increases from 100 bar to 900 bar at 276.15 K according to the measurement of Geng et al. [85] and calculations of this model with Method 1. As mentioned before, Method 2 predicts larger pressure dependence of CO₂ solubility than Method 1. Calculations of Method 1 are more consistent with data of Geng et al. [85] than Method 2, whereas calculations of Method 2 are more consistent with data of Zhang [80] than Method 1. Experimental data of Yang et al. [77], Servio and Englezos [79], and Kim et al. [82] show very weak pressure dependence of CO₂ solubility at HL_WE. Considering that the maximum pressure of these data is about 200 bar and the decrease of CO₂ solubility within 200 bar is close to the uncertainty of experimental data, it is indeed difficult to find the change tendency of CO₂ solubility with pressure from these data. On the other hand, experimental data measured by Zhang [80], Zhang et al. [83], and Geng et al. [85]), which cover a wider range of pressure than other experimental data, clearly show a negative pressure dependence of CO₂ solubility at HL_WE. Anyway, more measurements on CO₂ solubility at HL_WE are needed to verify this model.

Calculations of models of Hashemi et al. [86], Zhang et al. [83], and Yang et al. [77] were put into Figure 1, Figure 2, Figure 3, respectively. It can be seen that models of Zhang et al. [83] and Yang et al. [77] give a negative pressure dependence of CO₂ solubility at HL_WE, which is consistent with our model. In contrast, the model of Hashemi et al. [86] gives a positive pressure dependence of CO₂ solubility at HL_WE. The model of Yang et al. [77] gives a greater decrease gradient of CO₂ solubility with increasing pressure than our model using Method 2, while the decrease gradient of CO₂ solubility with increasing pressure predicted by the model of Zhang et al. [83] is comparable to that predicted by our model with Method 2. As shown in Figure 1, calculations of the model of Hashemi et al. [86] are lower than experimental data at 37 bar and 42 bar. Calculations of the model of Yang et al. [77] agree with experimental data reported in the same work, but are larger than those measured by other studies. The accuracy of the model of Zhang et al. [83] is comparable to our model since it adopted solubility models [101,113,114] which can accurately calculate CO₂ solubility at vapor–liquid equilibrium. However, the model of Zhang et al. [83] overestimates the occupancy fraction of CO₂ in small cage. Considering that composition of CO₂ hydrate phase at HL_WVE calculated by Sun and Duan [18] is accurate and the variation of composition of CO₂ hydrate phase with pressure is small, we argue that calculations of this model for composition of CO₂ hydrate phase at HL_WE are reliable. However, experimental data on composition of hydrate phase at HL_WE are needed for verifying our model. In general, this model is generally more accurate than previous models in CO₂ solubility in aqueous solutions and in composition of hydrate phase. In addition, this model covers a larger range of pressure (up to 1000 bar) compared to previous models.

There are just a few experimental measurements of CO₂ solubility in aqueous electrolyte solutions at HL_WE, including measurements of CO₂ solubility in aqueous NaCl solution made by Kim et al. [82] and Sun et al. [84], and measurement of CO₂ solubility in artificial seawater made by Zhang et al. [83]. Unfortunately, there are some discrepancies among these data. Data reported by Kim et al. [82] show a salting-in effect for CO₂ solubility at HL_WE (in another word, CO₂ solubility in NaCl solution is greater than that in pure water at the same temperature and pressure). In contrast, data measured by Zhang et al. [83] and Sun et al. [84] show a salting-out effect. The absolute average deviation of this model from experimental data of Kim et al. [82] and Sun et al. [84] are given in

Table 3. The AAD of this model for CO₂ solubility in aqueous NaCl solution at HL_WE from experimental data sets.

Data Source	T (K)	P (bar)	mNaCl (mol/kg)	N *	AAD a%	AAD b%
[82]	278.8–280.4	101–201	1.0	6	5.3	2.4
[84]	274.0–278.2	20–80	0.17–0.62	36	15.7	18.4

* number of experimental data, ^a Method 1; ^b Method 2.

. Calculations of this model for CO₂ solubility in aqueous NaCl solution at HL_WE are lower than data of Kim et al. [82] because this model predicts a salting-out effect. Predictions of this model are consistent with experimental data of Sun et al. [84] in 1 wt% NaCl solution but are greater than their data in 3 wt% and 3.6 wt% NaCl solutions by 10–30%. Figure 4 shows that predictions of this model with Method 1 for CO₂ solubility in artificial seawater agree well with data of Zhang et al. [83] (the AAD is 1.6%). Considering that the effect of 35‰ seawater on CO₂ solubility is close to that of 3.6 wt% NaCl solution, the discrepancy between this model and data of Sun et al. [84] reflects the discrepancy between data of Zhang et al. [83] and Sun et al. [84].

For the effect of pressure on CO₂ solubility in aqueous electrolyte solutions at HL_WE, experimental data measured by Zhang et al. [83] and Sun et al. [84] show a negative trends whereas data of Kim et al. [82] show very weak pressure dependence. As shown in Figure 4, this model predicts that CO₂ solubility in aqueous electrolyte solutions at HL_WE decreases with the increasing pressure, similar to CO₂ solubility in pure water. More measurements on CO₂ solubility in aqueous NaCl solutions and in seawater at HL_WE are needed to verify this model.

4. Conclusions

An accurate thermodynamic model was developed to predict CO₂ solubility in pure water and in seawater at hydrate–liquid water equilibrium. The van der Waals–Platteeuw basic hydrate model was used to describe the chemical potential of hydrate phase. Angle-dependent ab initio intermolecular potentials were used to calculate the Langmuir constants of CO₂ in hydrate cavities following our previous study. For the thermodynamic properties of the aqueous phase, two methods were adopted by this study. Method 1 is using the Pitzer model to calculate the activity of water and using the Poynting correction to calculate the fugacity of CO₂ dissolved in water, and Method 2 is using the SAFT-LJ EOS to calculate the activity of water and the fugacity of dissolved CO₂. No parameters of this model were evaluated from experimental data of HL_WE so that calculations of this model for HL_WE are predictive.

The comparison of calculations of this model with experimental data shows that this model can predict CO₂ solubility in pure water and in seawater at HL_WE with high accuracy. This model predicts that CO₂ solubility at HL_WE increases with increasing temperature, which agrees with available experimental measurements. This model predicts that CO₂ solubility at HL_WE decreases with increasing pressure and salinity. Most of the experimental data sets show negative pressure and salinity dependences of CO₂ solubility at HL_WE except one experimental data set showing a positive pressure dependence of CO₂ solubility and one data set showing a positive salinity dependence of CO₂ solubility. The predictions of this model for pressure and salinity dependences of CO₂ solubility are consistent with most of experimental data. Two different methods to describe aqueous phase give similar change rate of CO₂ solubility with temperature and salinity whereas Method 2 gives larger decrease of CO₂ solubility with increasing pressure. This model covers a wider range of pressure (up to 1000 bar) than previous models and is generally more accurate than previous models in CO₂ solubility in aqueous solutions and in composition of hydrate phase. Anyway, more measurements on CO₂ solubility at HL_WE are needed to verify this model. Extending our model to HL_WE of CH₄+CO₂+N₂ hydrate will be done in future. A computer program for the calculation of CO₂ solubility in pure water and in seawater at hydrate–liquid water equilibrium can be obtained from the corresponding author via email.