Advances in Blast-Induced Impact Prediction—A Review of Machine Learning Applications

Abstract

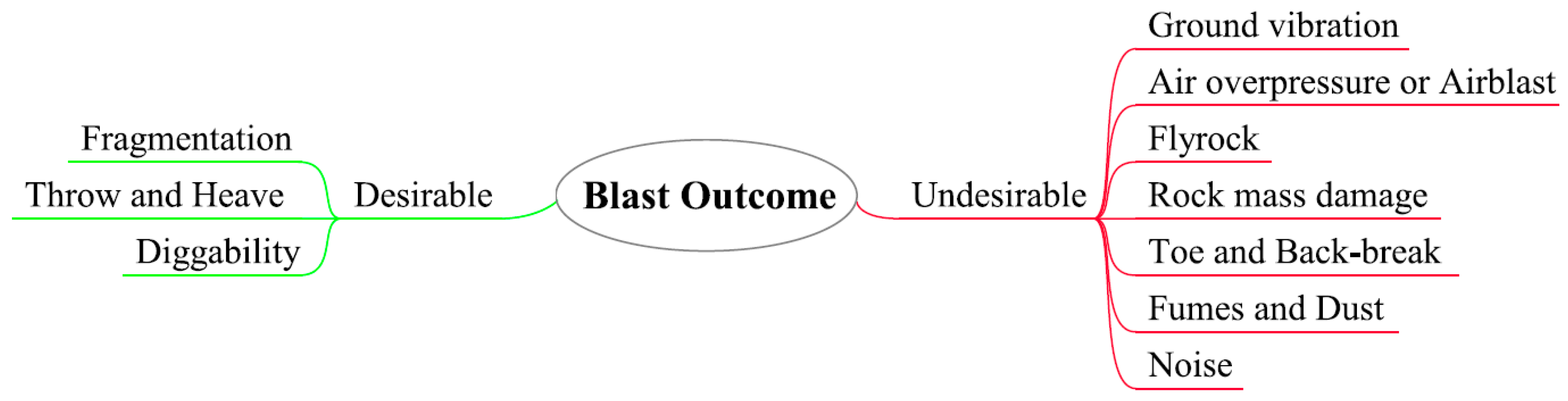
Rock fragmentation in mining and construction industries is widely achieved using drilling and blasting technique. The technique remains the most effective and efficient means of breaking down rock mass into smaller pieces. However, apart from its intended purpose of rock breakage, throw, and heave, blasting operations generate adverse impacts, such as ground vibration, airblast, flyrock, fumes, and noise, that have significant operational and environmental implications on mining activities. Consequently, blast impact studies are conducted to determine an optimum blast design that can maximize the desirable impacts and minimize the undesirable ones. To achieve this objective, several blast impact estimation empirical models have been developed. However, despite being the industry benchmark, empirical model results are based on a limited number of factors affecting the outcomes of a blast. As a result, modern-day researchers are employing machine learning (ML) techniques for blast impact prediction. The ML approach can incorporate several factors affecting the outcomes of a blast, and therefore, it is preferred over empirical and other statistical methods. This paper reviews the various blast impacts and their prediction models with a focus on empirical and machine learning methods. The details of the prediction methods for various blast impacts—including their applications, advantages, and limitations—are discussed. The literature reveals that the machine learning methods are better predictors compared to the empirical models. However, we observed that presently these ML models are mainly applied in academic research.

1. Introduction

Rock fragmentation in mining involves the breakage of hard rock into appropriate sizes to facilitate downstream handling and processing. Currently, the most economical and widely accepted ground fragmentation technique is drilling and blasting that involves the usage of commercial explosives (placed in blastholes) to break down a rock mass into pieces upon detonation [1,2,3]. The technique is also common in many civil construction projects, including the construction of tunnels, highways, subways, dams, and building demolition [4,5,6,7].

Blasting has significant environmental, operational, and cost implications, and the outcomes of a blast can impact the entire mining operation, from waste/ore transportation through beneficiation. For instance, an optimized blast fragmentation process improves excavator and dump truck production, minimizes equipment maintenance and repair costs, maximizes crusher throughput, and ultimately, minimizes operating costs [3,8,9]. There are two types of impacts for every blasting event: desirable and undesirable (see Figure 1). When an explosive detonates, it releases an enormous amount of energy in the form of gases, pressure, heat, and stress waves [10], causing the surrounding rock mass to develop cracks and get displaced. About 20–30% of the explosive energy released is utilized to fragment and throw the material [11], while the remaining 70–80% generates undesirable outcomes [12]. The undesirable outcomes include airblast/air overpressure, ground vibration, flyrock, noise, heat, fumes/dust, and backbreak. It should be noted that heat, which is a part of the undesirable outcomes, does not necessarily produce adverse effects; it is the portion of the released energy that is not fully utilized in breaking the rock mass.

The undesirable outcomes can reach elevated levels causing discomfort to humans, a threat to human safety and health, and damage to building structures and equipment close to the blast zone. It can also affect groundwater, geological structures, and slope stability. Blasting affects groundwater when soluble substances from detonators and explosives that are not fully combusted permeate groundwater [13]. It may cause short-term turbidity and long-term changes to incumbent wells due to the expansion of fractures from loss of lateral confinement [14]. There are cases reported in the literature on groundwater contamination, including elevated nitrate levels and turbidity [15]. Blasting near cave regions can cause damages to the structural integrity of caves due to vibrations and air overpressure [16]. Incidents of frequent complaints, which, in some cases, escalate into protests against mining operations due to blast impacts, have been reported in many mining jurisdictions, including Ghana, India, Brazil, Turkey, and South Africa [17,18,19,20,21]. Thus, it is important to understand these phenomena and model the potential impacts of blasting activities on catchment communities.

Studies have been performed to ascertain the distance to which the adverse effects of blasting would affect the surrounding blast areas. McKenzie [22] conducted a detailed study to predict the projection range of flyrocks and suggested calculating maximum projection distance with an appropriate safety factor to establish clearance distance. The study found that the maximum flyrock distance is a function of hole diameter, shape factor, and velocity coefficient. The velocity coefficient is calculated using the scaled length of burial, which is a function of stemming length, explosive density, hole diameter, and charge length. Blanchier [23] suggested utilizing a flyrock model developed by Chiapetta et al. [24] to estimate the flyrock speed and maximum range. The model is a function of burden, linear energy of explosives, and a coefficient that expresses the probability of attaining estimated speed [23]. Richard and Moore [25] suggested using empirical formulae developed by Lundborg et al. [26] for predicting the maximum throw and projectile size of flyrock.

Generally, mining regulations prescribe blast standards to ensure that blast impacts are maintained within a certain bound. For example, in the USA, the Title 30 Code of Federal Regulations (30 CFR) specifies that flyrock shall not be cast from the blasting site: more than one-half the distance to the nearest dwelling or other occupied structure, beyond the area of control required under, or beyond the permit boundary [27]. A similar regulatory requirement exists in other mining countries. It should be noted that blast standards are established following extensive empirical and field studies based on several factors, including geology, rock type, explosive type, ground condition, wind direction, blast direction, and building types. Some of these factors (e.g., geology, rock type, and building type) vary from one location to another; therefore, the blast standard for one geological location or country may not necessarily be the same for another geological location or country.

Table 1. Blast standards for the USA, Canada, and Australia.

Blast Impact	Country
	USA	Canada	Australia
Ground vibration	Maximum allowable PPV: 0–300 ft for PPV ≤ 1.25 in./s 301–5000 ft for PPV ≤ 1.00 in./s >5001 ft for PPV ≤ 0.75 in./s Frequency: 0.03 in for 1–3.5 Hz 0.75 in./s for 3.5–12 Hz 0.01 in. for 12–30 Hz 2.0 in./s for 30–100 Hz	PPV ≤ 12.5 mm/s measured below grade or less than 1 m above grade.	Must not exceed a PPV of 5 mm/s for nine out of any ten consecutive blasts initiated, regardless of the interval between blasts, but never over 10 mm/s for any blast.
Airblast	≤0.1 Hz: peak ≤ 134 dB ≤2 Hz: peak ≤ 133 dB ≤6 Hz: peak ≤ 129 dB C-weighted--slow response: 105 dBC	≤128 dB	Must not be more than 115 dB(lin) peak for nine out of any ten consecutive blasts initiated, regardless of the interval between blasts, but never over 120 dB(lin) peak for any blast.
Flyrock	Shall not cast: More than one-half the distance to the nearest dwelling. Beyond the area of control required under 30 CFR 816.66(c); or Beyond the permit boundary.	The blaster must take precautions for the protection of persons and property, including proper loading and stemming of holes, and where necessary, the use of cover for the blast or other effective means of controlling the blast or resultant flying material.	If debris from blasting in a surface mining operation could constitute a danger to any person or property, each responsible person at the mine must ensure that such precautions are taken as are necessary to prevent injury to persons and to minimize the risk of damage to property.
Noise	70 dBA (EPA)	≤55 dBA daytime (Leq D) ≤45 dBA at (Leq N) nighttime	No worker to be exposed to noise with a level exceeding 140 dB(lin) peak

PPV is the peak particle velocity, dBA is the A-weighted decibel, dBC is the C-weighted decibel, dB(lin) or dBZ is the unweighted decibel, and EPA is the U.S. Environmental Protection Agency.

presents a summary of blast standards for ground vibration, airblast, flyrock, and noise for the USA, Canada, and Australia.

Figure 2 indicates various zones of blast influence and the potential risk to people and structures within these zones. The risk to people and equipment is highest at the innermost circle, i.e., within the immediate vicinity of the blast zone. The blast zone is a high-risk area with the highest degree of blast-induced impacts. However, the severity of the impacts reduces as they travel outward from the blast zone towards the outer perimeter, as depicted by the blast impact profile in Figure 2. The blast impacts are not confined to a single direction; they can travel radially because the explosive energy act on all points of the blasthole simultaneously [28]. However, the intensity of the associated impacts may not be the same everywhere. Figure 2 is divided into three segments (S1, S2, and S3) to illustrate the potential impact regions. Assuming the blast design is optimal in S1, then the associated undesirable effects are limited to the buffer zone, and they would be harmless even if they exceed the buffer zone. However, with the same buffer zone, increasing the explosive charge (S2) or the number of blast shots (S3) can cause undesirable effects to exceed the buffer zone, damaging structures in the concession and beyond. Usually, for a good blast operation, it is expected that the magnitude of the blast impact beyond the buffer zone will reduce below the damage threshold. In other words, blast impacts attenuate with the increasing distance. The distances between the blast zone, buffer zone, and mine concession are usually stated in the blast standards. For instance, in Ghana, the blast standard prescribes a safe distance (buffer zone) of 500 m from the blast zone. Decreasing factors, such as the quantity of explosive charge and number of blast shots, could also reduce the magnitude of blast impacts. Blast standards mandate that all employees and equipment must be cleared from the blast area to a safe location before any scheduled blast operation to prevent injury and equipment damage.

Generally, there are two categories of factors that influence blast impacts: controllable and uncontrollable parameters. Controllable parameters are those that a blast engineer can modify and include the blast geometry (spacing, burden, blasthole depth, blasthole diameter, and stemming) and explosive parameters (type, density, powder factor, charge per delay/instantaneous charge, and delay time). The uncontrollable parameters include geological (rock type, discontinuities, and groundwater) and geotechnical properties (rock strength, density, etc.) of the rock formation that cannot be modified. Therefore, blasts must be designed to suit the prevailing ground conditions to generate optimal fragmentation with minimal environmental impact, fostering an excellent company–community relationship. Mining regulations are also major deciding factors in blast design, providing guidelines and blast impact threshold limits to ensure safe blast operations.

Over the years, studies have been conducted to examine blast impacts, which has led to the development of several blast impact prediction models. These models, many of which are based on empirical data, have primarily been applied in mining operations to predict and model the potential impacts of blasting. Several empirical models are in the literature for predicting blast-induced ground vibration, flyrock, dust/fumes, backbreak, and fragmentation. Though most of these models have a long history of use in the mining industry, they possess some inherent limitations, such as (1) a restriction to just two input parameters, (2) inability to concurrently predict more than one outputs, and (3) unsuitability to apply to all geological formations or mine conditions. Singh and Singh [29] noted that empirical models are analyzed datasets along specific geometries, which may or may not be favorable to understand the nonlinearity existing among various input/output parameters. Additionally, there are too many other interrelated controllable (blast geometry and explosive) and uncontrollable (geological and geotechnical) parameters, which are not incorporated in any of the available predictors [30]. In effect, the empirical models are not able to identify the nonlinear relationships, and this weakness influences the performance of these models.

A promising solution to this problem is the application of ML techniques in blast impact prediction. With the recent popularity of artificial intelligence (AI) in both academia and industry, many scholars are exploring machine learning as a robust tool to model blast impacts. In recent years, numerous scientific papers have been published in this area, and the number of new publications is ascending significantly. The wide application of ML can be attributed to its ease in handling complex engineering problems with several variables. ML is the study and application of computer algorithms to make intelligent systems that improve automatically through the experience without being explicitly programmed. It is classified as a subfield of AI, which is the science and engineering of making intelligent machines. ML applies computer algorithms to analyze and learn from data and makes decisions or predictions based on the data provided. Depending on the structure of available data being analyzed, ML models are categorized as supervised learning, unsupervised learning, or reinforcement learning [31].

In this paper, the authors performed a comprehensive review of scientific studies that applied ML techniques to predict blast impact. This paper covered a detailed examination of machine learning models for blast-induced ground vibration, flyrock, airblast, backbreak, and fragmentation. It is worth noting that most of the studies conducted in this field are related to blast-induced ground vibration.

The remainder of the paper is organized into five sections. Section 2 outlines the review methodology, followed by a description of the rock breakage mechanism in Section 3. Section 4 and Section 5 discuss the empirical and ML blast impact prediction models, respectively. Section 6 presents a discussion and future trends for ML applications, while Section 7 covers the concluding remarks.

2. Methodology

This review intends to summarize the existing knowledge on the application of ML in blast-induced impact predictions and identify gaps in the current research to suggest areas for further investigation. The review scope is mainly limited to only publications related to blast-induced impacts associated with surface and underground mining and quarry operations. The primary purpose of this review was to report the current status of ML usage in predicting blast-induced impacts in mining. However, a few studies on blast impacts resulting from blasting operations in dam and tunnel construction were also considered.

Based on the stated review objective and purpose, we conducted an extensive literature search to identify relevant peer-reviewed publications indexed in major scientific research databases, such as Web of Science, Google Scholar, Scopus, and ScienceDirect. To limit the search scope, we used keywords, including “blasting”, “rock fragmentation”, “machine learning”, “blast impacts”, “ground vibration”, “airblast or air overpressure”, “flyrock”, “backbreak”, “soft computing”, “neural networks”, “deep learning”, and “support vector machines”. Boolean operators and strings were adopted to improve the search results. Another search strategy employed was snowballing (e.g., forward and backward snowballing), where the original search results led to the discovery of more papers. We screened the search results for relevance by reviewing the titles and abstracts of the publications. The published articles were required to be original, peer-reviewed, and recognized in the field.

The search scope covered research articles published from 2004 to 2020. However, a few recent articles published in early 2021 were also included. This review was mostly focused on peer-reviewed journal publications, since the intention was to rely on rigorous research addressing the subject matter. Some of the notable journals where the search results were retrieved were Engineering with Computers, Safety Science, Environmental Earth Sciences, International Journal of Mining Science and Technology, Rock Mechanics and Rock Engineering, Neural Computing and Applications, and Natural Resources Research. From the research results, we noticed that the majority of the articles were published in Engineering with Computers, followed by Natural Resources Research, as evident in Figure 3. In a few cases, relevant papers in peer-reviewed conference proceedings and a thesis report were included.

Out of the 193 articles reviewed, approximately 112 focused on the prediction of blast-induced impacts using machine learning, while the remaining articles covered blast phenomenon and empirical prediction models. This is by no means an exhaustive list of all blast-induced impacts and ML-related articles published in this field within the period under consideration. Figure 4 illustrates the yearly distribution of publications on ML applications in blast-induced impact predictions. The distribution (Figure 4) shows an increasing trending in publications of ML techniques in this field. This positive trend can be attributed to the growing interest in ML applications in academia and the industry in recent years.

Table 2. Review statistics of blast-induced impacts predicted using machine learning.

Blast Impact	Count
Ground vibration	58
Flyrock	15
Fragmentation	13
Airblast	11
Backbreak	3
Overbreak	1
Noise	1
Ground vibration and airblast	3
Flyrock and fragmentation	3
Backbreak and fragmentation	2
Flyrock and backbreak	1
Ground vibration, airblast, and fragmentation	1

presents a summary of the number of ML applications in each blast-induced impact considered in this review. Most of the studies reviewed predicted only one blast-induced impact. It is interesting to note that a significant portion of ML applications were about ground vibrations, likely due to the drive to accurately measure and mitigate blast-induced vibration levels. Since blast-induced ground vibrations can cause structural damage to buildings, resulting in contention between mining companies and host communities, it is always prudent to ensure that the vibration levels are within the regulatory requirements. Therefore, relatively cheaper and more rapid techniques that allow the blast engineer to predict the vibration level before blasting are helpful in pre-blast planning as compared to field measurements. This may also indicate the importance placed on ground vibrations compared to other blast-induced impacts and the research efforts to improve the prediction results.

ML application in flyrock prediction has also received significant research attention, as flyrock is a potential hazard responsible for a large proportion of all blasting-related injuries and fatalities. The fragment size analysis and airblast have also received considerable attention, while backbreak and overbreak are blast-induced impacts with the least ML implementations. It is worth noting that, apart from a single impact prediction, a few studies have predicted two impacts, while one research predicted three impacts simultaneously.

3. Rock Fragmentation and Blast Impact Phenomena

The technique most commonly used for breaking rock with explosives involves drilling blastholes into a rock mass, placing explosive substances in the blastholes, initiating the fire sequence, and detonating the explosive, as illustrated in Figure 5. Upon initiation, the explosive charge detonates (i.e., an intense and rapid chemical reaction occurs), producing an enormous amount of energy in the form of gases at very high temperatures and pressure. The energy released by an explosive during a blast can be categorized into seismic, kinetic, backbreaks, heave, heat, or fragmentation energies [32]. The resulting detonation energy has the following effects: pressurizes the blasthole and fractures the vicinity rock mass, creates strong shock waves in the rock mass, which propagate as plastic and, ultimately, elastic waves and appear as a seismic wave or ground vibration, and displaces and heaves the fractured rock mass to form a muck pile that appears as kinetic energy imparted to the rock [33,34,35,36].

According to Changyou et al. [37], the theory that rock damage is a result of the coaction of the blast wave and explosive explosion is currently accepted by most scholars, as it matches the actual process of blast-induced rock breakage favorably. Nevertheless, the mechanism of rock breakage under explosive action is still being investigated, even after many decades of advancement in explosive technology for mining and civil applications. Recently, numerical modeling and simulation models have been applied to further the understanding of blasting [38,39,40]. Generally, the fragmentation action has been attributed to either the gases or shock waves generated or both [38,41,42].

The detonation waves from the explosive (with the velocity of detonation between 2000 and 7000 m/s, depending on the type of explosive) induce intense stresses in the blasthole due to the sudden acceleration of the rock mass by detonating gas pressure on the blasthole wall [35]. Bendezu et al. [28] stated that the energy released is converted into two main forms that are responsible for rock fracturing, creating new cracks and widening the already existing ones: blast-induced stress waves (dynamic load) and the overpressure of the explosive gases (quasi-static load). The strain waves transmitted to the surrounding rock sets up a wave motion in the ground. The strain energy carried out by these strain waves fragments the rock mass, resulting in different breakage mechanisms such as crushing, radial cracking, and reflection breakage in the presence of a free face. The crushed zone and radial fracture zone encompass a volume of permanently deformed rock. When the stress wave intensity diminishes to the level where no permanent deformation occurs in the rock mass (i.e., beyond the fragmentation zone), strain waves propagate through the medium as elastic waves, oscillating the particles through which they travel. These waves in the elastic zone are known as ground vibrations, which closely conform to viscoelastic behavior. The wave motion spreads concentrically from the blast point in all directions and attenuates as it travels farther from the origin through the rock medium.

The fragmentation action does not exhaust all the explosive energy; some portion of it is transformed into ground vibration, airblast, and flyrock. Bendezu et al. [28] pointed out that there is no clear indication about the amount of energy converted into stress wave energy; how much is available as high-pressure gases; and how much is lost to other sources, such as ground vibration, air blast, heat, and smoke/dust. The energy distribution depends on the type of explosive. However, some studies have reported that approximately 20–30% of the explosive energy is utilized to fragment and throw the rock mass, while the remaining 70–80% goes toward the generation of other blast-induced impacts [11]. Even though ground vibrations attenuate exponentially with distance, the large quantity of explosives used means that ground vibrations can still be high enough to cause damage to buildings and other structures by causing dynamic stresses that exceed the material’s strength [35]. The blast phenomena and the mechanisms of ground vibrations, airblast, flyrock, and fragmentation have been well-documented. Figure 6 depicts a blast event with its associated vibrations and undesirable effects, such as flyrock, ground vibrations, and airblast.

4. Empirical Models

Empirical blast impact prediction models are established following rigorous and extensive field studies; data collection; and site observations of several blast parameters, including blast geometry, the geology of the area, rock type, blast direction, wind direction, the location of building structures relative to a blast zone, etc. The empirical models are based on two main factors: (1) the maximum charge per delay and (2) the distance from the blast face to the monitoring point. The models are generally mine-specific due to the heterogeneity of geological formations and variations in site conditions from one location to another. To apply empirical models for site-specific predictions of blast impacts, the models are calibrated using field measurements and established site constants.

Table 3. Empirical models for predicting blast-induced ground vibrations.

Prediction Model	Equation	Reference
USBM	$PPV=k{(D/\surd Q)}^{-\beta }$	[44]
Langefors–Kihlstrom	$PPV=k{(Q^{1/2}/D^{3/4})}^{\beta }$	[45]
General predictor	$PPV=k\times D^{-\beta }\times Q^A$	[43]
Ambraseys–Hendron	$PPV={(D/\sqrt[3]{Q})}^{-\beta }$	[46]
Indian Standard	$PPV=k{(Q/D^{2/3})}^{\beta }$	[46]
Ghosh–Daemen 1	$PPV=k{(D/\sqrt{Q})}^{-\beta }\times e^{-\alpha \times D}$	[43]
Ghosh–Daemen 2	$PPV=k{(D/\sqrt[3]{Q})}^{-\beta }\times e^{-\alpha \times D}$	[43]
Gupta et al.	$PPV=k{(D/\sqrt[3]{Q})}^{-\beta }\times e^{-\alpha \times \left(D/Q\right)}$	[43]
CMRI predictor	$PPV=n+k{(D/\sqrt{Q})}^{-1}$	[43]
Rai–Singh	$PPV=k\times D^{-\beta }\times Q^A\times e^{-\alpha \times D}$	[47]

PPV is the peak particle velocity (mm/s), D is the distance between the blast face to the monitoring point (m), and Q is the cooperating charge (kg). The values k and β are the site-specific constants (coefficients) obtained through a linear regression model by plotting the graph between the PPV versus scaled distance (SD) on a log–log scale [48].

,

Table 4. Empirical models for predicting the airblast or air overpressure.

Prediction Model	Equation	Reference
USBM	$P={\beta }_1\times {(D/Q^{0.33})}^{{\beta }_2}$	[49]
NAASRA	$P=140\sqrt[3]{Q/200}/d \left(kPa\right)$	[50]
Ollofson; Persson et al.	$P=0.7\times Q^{1/3}/D\left(mbar\right)$	[51]
Holmberg-Persson	$P=k\times 0.7\times Q^{1/3}/D \left(mbar\right)$	[51]
Mckenzie	$P=165-24\log D/Q^{1/3} \left(dB\right)$	[52]

P is the airblast or overpressure, Q is the mass of the explosive charge (kg), D is the distance from the charge (m) to the monitoring point, and H and β are the site factors.

and

Table 5. Empirical models for predicting the flyrock.

Prediction Model	Equation	Reference
Lundborg et al.	$L_m=260\times d^{2/3}$ $T_b=0.1\times d^{2/3}$	[53]
Chiapetta et al.	$R_1=V_0\times (2sin 2\theta /g)$ $R_2=V_0\times cos\left(V_0 sin\theta +2V_{0 }sin\theta +2gH\right)/g$	[34]
Gupta	$L=155.2\times D^{-1.37}$	[54]

L_m is the flyrock range (m), d is the blasthole diameter (inch), T_b is the flyrock fragment size (m), L is the ratio of the length stemming the column to burden, D is the distance traveled by the flyrock (m), R₁ is the distance traveled (m) by the rock along a horizontal line at the original elevation of the rock on the face, R₂ is the total distance traveled (m) by a fragment ejected from the blast, accounting for its height above the pit floor, V₀ is the initial velocity of the flyrock, θ is the angle of departure with the horizontal, and g is the gravitational constant.

are summaries of some empirical models for predicting blast-induced ground vibrations, airblast/air overpressure, and flyrock, respectively. The models presented in these tables are not exhaustive, and references can be made to Murmu et al. [12] and Kumar et al. [43] for a more comprehensive list, particularly for blast-induced ground vibrations.

5. Machine Learning Models

AI refers to a branch of computer science concerned with building smart machines capable of performing tasks that typically require human intelligence [55]. AI techniques have been increasing steadily in many engineering fields, including image processing [56], mineral exploration [57], and mine planning [58,59]. Simeone [60] believes that the widespread use of data-driven AI methods is motivated by the successes of ML-based pattern recognition tools. ML is a branch of AI that systematically applies algorithms to synthesize the underlying relationships among data and information [61]. ML focuses on the application of computer algorithms to process large amounts of data, detect patterns or regularities in data, and improve their performance based on experience [62,63]. Such applications may offer more understanding about a system and can be used to predict or modify the future behavior of the system. Given sufficient input data and a sequence of instructions (algorithms), a computer can perform the desired task of predicting an output. Algorithms for some desired tasks can be developed easily using traditional programming (TP), and a computer will be able to execute them following all the steps required to solve the problem without learning. However, for more advanced tasks (e.g., prediction of consumer behavior or natural occurrences), it can be challenging for a human to manually create the needed algorithms. In practice, it can turn out to be more effective to help the machine develop its model rather than having human programmers specify every needed step [64,65,66]. It may be impossible to develop an explicit program of such an advanced system, but the ML models provide good and useful approximations. Unlike TP, ML automates the process of learning a model (program) that captures and subsequently predicts the relationship between the input and output variables in a dataset by searching through a set of possible prediction models that best defines the relationship between the variables [67]. A good prediction model must be able to predict events that are not in the current data, i.e., it must generalize well.

Samuel [68] described ML as the “field of study that gives computers the ability to learn without being explicitly programmed”. Alpaydin [65] also defined ML as programming computers to optimize a performance criterion using example data or experience. In other words, given a sufficient dataset (e.g., historical blast monitoring data), an ML algorithm can identify patterns; predict blast impact values (e.g., PPV, frequency, flyrock, fragment size, etc.); and improve the previous predictions as more data are made available. Once programmed, the algorithm can learn from the data and improve the learning experience with little human interference. The algorithm synthesizes the various independent variables, such as hole diameter, hole depth, blast size, spacing, burden, stemming height, explosives blasted per delay, and distance between the blast zone and measuring point, with weights that depict their influence on the dependent variable. A generalized ML implementation procedure is presented in Figure 7. The first step in the ML model development cycle (Problem definition) deals with an understanding of the problem, characterizing it, and eliciting required knowledge in acquiring the relevant data. The second step (Data collection) is the collection of all relevant and comprehensive data, followed by data preparation and feature extraction. Next, the data is divided into training, validation, and testing sets based on a predefined ratio (Data partition). Following that, an ML model is selected, trained, validated, and tested using the partitioned datasets (Train model). Here, the programmer can try different algorithms and compare their performances.

Model evaluation involves the usage of some metrics or a combination of metrics to measure the objective performance of the selected ML model (Evaluate model). The model parameters can be revised (hyperparameter-tuned) until a satisfactory performance is achieved; then, it is adopted for prediction. A few of the statistical criteria used to evaluate the performance of ML models include the mean absolute error (MAE), root mean square error (RMSE), correlation coefficient (R), and determination coefficient (R²).

The ML methods that have been employed in blast impact prediction are the artificial neural network (ANN), support vector machine (SVM), random forest (RF), gaussian processes (GP), and fuzzy theory sets. These models have been successfully applied in evaluating various blast impacts. The ANN is a computational network presenting a simplified abstraction of the human brain. Conceptually, this computational network mimics the operations of biological neural networks to recognize existing relationships in a set of data. It consists of layers of interconnected nodes that represent artificial neurons. The layers are categorized into three divisions: input layer (receives the raw data), hidden layer (process the raw data), and output layer (processed data). The number of layers and neurons (topology) in a network determines the structure of a neural network or network architecture [66]. Figure 8 depicts an ANN architecture for predicting maximum flyrock distance. The model comprises one input layer with seven neurons, two hidden layers with eight and seven neurons, respectively, and one output layer with one neuron.

SVM is an ML algorithm based on the structural risk minimization principle [69,70]. The algorithm uses the concept of decision planes that utilize decision boundaries to optimally separate data into different categories [69]. SVM can solve classification, regression, and outlier detection problems, and when it is applied to regression problems, it is called a support vector machine (SVR). The process of training an SVM decision function involves identifying a reproducible hyperplane that maximizes the distance (i.e., the “margin”) between the support vectors of both class labels, and thus, the optimal hyperplane is that which “maximizes the margin” between the classes [71].

RF is a supervised learning algorithm consisting of multiple independent decision trees (DT) that are trained independently on a random subset of data [72,73]. It is an ensemble method that uses bagging (bootstrapping and aggregation) to train several DTs in parallel (i.e., uncorrelated forest of trees) whose prediction by committee is more accurate than that of any individual trees [73,74]. RF can solve both classification and regression problems.

GP is a “collection of random variables, any finite number of which have (consistent) joint Gaussian distributions” [75]. It is characterized by mean and covariance functions. GPs are attractive because of their flexible nonparametric natures and computational simplicity, and they are designed to solve regression and probabilistic classification problems.

The fuzzy set theory uses natural language to formulate a mathematical model of vague qualitative or quantitative data by attributing a degree to which a certain object belongs to a set [76,77]. The model is based on the generalization of the classical concepts of the set and its characteristic functions. Fuzzy sets and fuzzy logic are an extension of classical set theory and built around the central concept of a fuzzy set or membership function [78]. The model provides a natural way of dealing with problems in which the source of imprecision inhabits a precise definition of class membership criteria [76]. Fuzzy set theory has been shown to cope well with the complexity of complicated and ill-defined systems flexibly and reliably [79].

The following subsections review the application of these algorithms to blast impact prediction problems. There is extensive documentation in the literature regarding the assumptions, mathematical computations, and architecture of these techniques; thus, this paper focused largely on their application.

5.1. Ground Vibration

Several ML models, including the ANN, RF, SVM, and logistic regression, have been employed in predicting and modeling blast-induced ground vibrations. Currently, ground vibrations are, by far, the most studied blast impact for many ML applications. The prediction procedure involves the selection of input parameters, a training model, and predicting the outcome. The input parameters can vary from two to as many as possible, depending on the strength of the algorithm and the computing resources available. Different studies have considered different sets of influential factors in predicting the ground vibrations and designed varying ANN architectures to ensure the accuracy of these predictions. Some of these studies only considered as few as two parameters, while others considered as many as 13 parameters to predict the blast-induced ground vibrations [80]. In fact, due to the complexity of the blast phenomenon and the many factors involved, it has been a challenge to identify the specific influential factors. Nevertheless, studies have considered explosive characteristics, blast design parameters, geological conditions, and rock mass properties as the major factors influencing blast-induced ground vibrations. Among the main factors, the distances between the blast zone and monitoring point, maximum charge per delay, velocity of detonation, blasthole depth, burden, spacing, stemming height, powder factor, rock-quality designation (RQD) and p-wave velocity were the most common factors in estimating blast-induced ground vibrations. Due to the limitations of the parameters and datasets, studies have tried to change the number of hidden layers and the hidden neurons to ensure the accuracy of their predictions [81]. For instance, Amnieh et al. [82] designed an ANN model with four hidden layers (hidden neurons in each layer: 20-17-15-10) and four influential parameters that showed better performances in predicting the PPV for a problem with 25 datasets.

Most scholarly articles applied an ANN, particularly the feed-forward back-propagation neural network (BPNN), for the prediction of blast-induced ground vibrations [29,32,48,80,81,82,83,84,85,86,87,88,89]. We present a review of some of these papers in this section. BPNN is a strong modeling technique for input/output pattern identification problems and is a commonly used ANN, often applied to solve nonlinear problems. The calculation process of BPNN is divided into two steps: forward calculation and backward propagation. The connection weights and bias values are adjusted by gradient descent algorithms. The weights of the interneuron connections are adjusted according to the difference between the predicted and the actual network outputs [81]. Normally, closer mapping is required to obtain more satisfactory model performance [90], and it is recommended that the numeric values of the pertinent parameters be normalized in a range of 0 to 1 to achieve a reasonable solution [46].

Singh et al. [91] used the ANN technique for the prediction of p-wave velocity and anisotropy, taking chemical composition and other physicomechanical properties of rocks as the input parameters. Due to data limitation, the leaving-one-out cross-validation method was used, and the network had three layers with six inputs, five hidden neurons, and two output neurons. Using the Bayesian regulation, overfitting of the data was mitigated, and the network was trained with 1500 training epochs, resulting in a high correlation coefficient and low mean absolute percentage error between the predicted and observed values, respectively. Khandelwal and Singh [80] used a BPNN consisting of three layers to predict PPV and its corresponding frequency based on the rock mass mechanical, explosive, and blast design properties. Khandelwal and Singh [92] evaluated and predicted blast-induced ground vibrations and frequencies by incorporating the rock properties, blast design, and explosive parameters into an ANN. Mohamed [93] determined the effect of varying the number of input parameters (blast variables) on the performance of a neural network for ground vibration prediction. Khandelwal et al. [94] incorporated the explosive charges per delay and blast monitoring distance to evaluate and predict ground vibrations using an ANN. With an optimum architecture of 4-10-5-1, Monjezi et al. [95] compared the performances of a BPNN model with empirical predictors and a regression analysis. The comparison revealed that the most influential parameter was the distance between the blast zone and the monitoring point, while the least effective parameter was stemming the height.

Other types of ANN applied in the prediction of blast-induced ground vibrations include GRNN, quantile regression neural network (QRNN), wavelet neural network (WNN), hybrid neural fuzzy inference system (HYFIS), adaptive neuro-fuzzy inference system (ANFIS), and group method of data handling (GMDH). Arthur et al. [96] estimated blast-induced ground vibrations by comparing five ANNs (WNN, BPNN, RBFNN, GRNN, and GMDH) and four empirical models (Indian Standard, the United State Bureau of Mines, Ambrasey-Hendron, and Langefors and Kilhstrom). The study revealed that WNN with a single hidden layer and three wavelons produced highly satisfactory results compared to the benchmark methods of BPNN and RBFNN. Xue and Yang [97] also predicted blast-induced ground vibrations and frequencies by incorporating rock properties, blast design, and explosive parameters using the general regression neural network (GRNN) technique. The GRNN model provided excellent predictions with a high degree of correlation when compared with multivariate regression analysis (MVRA). Nguyen et al. [98] argued that MLP recorded the most accurate prediction over BRNN and HYFIS. They also observed that not all ANN models (e.g., HYFIS) are useful for blast impact predictions in open-pit mines, depending on the input parameters and training algorithms.

Generally, ANN-based models are better predictors with superior performances compared to empirical models when it comes to predicting blast-induced ground vibration levels. However, this is not to say that ANN results are always accurate and are without challenges. ANN algorithms also have some weaknesses, such as overfitting [99], long training times, and falling easily into the local minimum [81]. According to Dreiseitl and Ohno-Machado [99], ANN models are more flexible and, thus, more susceptible to overfitting. This usually occurs when the ANN model begins “to memorize the training set instead of learning them and consequently loses the ability to generalize” [48]. The methods proposed for resolving it include early stopping, noise injection, cross-validation, Bayesian regularization, and the optimization approximation algorithm [48,100,101]. Paneiro et al. [102] employed bilevel optimization to avoid overfitting and reduce the complexity of an ANN-based ground vibration model. The authors concluded that the improved ANN model offered a much higher generalization ability than traditional and other ANN models applied to ground vibration predictions. Piotrowski and Napiorkowski [100] also cautioned that the ANN architecture should be kept relatively simple, as complex models are much more prone to overfitting. Dreiseitl and Ohno-Machado advised that, in constructing the model, the network size can be restricted by decreasing the number of variables and hidden neurons and by pruning the network after training. Alternatively, one can require the model output to be sufficiently smooth through regularization [99].

Studies have integrated ANN with other soft computing techniques, such as data mining and feature selection algorithms, to improve the accuracy and robustness of ANN-based ground vibration models. In some instances, preprocessing of the raw data involves data mining to find relationships and patterns in the raw data. For example, before training the ANN model, Amiri et al. [103] applied itemset mining (IM) to identify patterns and extract frequently occurring sets of items in a database. Based on the extracted knowledge, association rules were formed that helped select the best instance for training the neural network model. The proposed itemset mining and neural networks (IM–NN) model showed superior prediction results compared to the classical ANN.

To overcome the limitations associated with ANN in predicting blast-induced ground vibrations, studies have also applied other ML algorithms that are without these shortcomings. Some of the algorithms applied included SVM [104,105,106,107,108,109,110,111], relevance vector regression [112], particle swarm optimization [113,114] Bayesian network and random forest [108], Gaussian process regression [115], classification and regression trees, chi-square automatic interaction detection, random forest [1,116,117], hybrid artificial bee colony algorithm [118], fuzzy Delphi method and hybrid ANN-based systems [119], cuckoo search algorithm [120], extreme learning machine [121], extreme gradient boosting (XGBoost) [122], and the firefly algorithm [123,124,125,126].

5.2. Airblast

Airblast or air overpressure are among the undesirable effects of blasting operations. They are explosion-induced large shock waves that are refracted horizontally by density variations in the atmosphere. The atmospheric pressure waves of airblasts consist of a high audible frequency and subaudible low-frequency sound [50,127]. Airblasts can impact structures close to the blast zone by rattling windows and the roofing materials.

Several scholarly studies have attempted to predict airblasts based on some identified influential factors, such as the maximum explosive charge per delay, burden, spacing, stemming, wind direction, temperature, and distance from the blast zone to the monitoring point. There are empirical models (see Table 2) for predicting airblasts, in addition to more recent applications of machine learning techniques, such as the ANN, support vector regression, particle swarm optimization, and adaptive neuro-fuzzy inference system.

Khandelwal and Singh [128] attempted to predict airblasts using an ANN by incorporating the maximum charge per delay and distance between the blast zone and the monitoring point and demonstrated that the neural network model yields better predictions when compared to a generalized equation and conventional statistical relations. Mohamed [129] predicted airblasts using the fuzzy inference system and ANN. Comparing the results of these methods with the values obtained by a regression analysis and measured field data, Mohamed asserted that the neural network and fuzzy models had accurate predictions compared to the regression analysis. Khandelwal and Kankar [130] predicted airblasts using SVM and compared the values with the results of the generalized predictor equation. They showed that the predicted values of airblasts by SVM were much closer to the actual values as compared to the predicted values by the predictor equation. Nguyen and Bui [72] developed and combined five ANN models with an RF algorithm to form an ANN-RF model to predict blast-induced air overpressure. The input variables of the model included the maximum explosive charge capacity, monitoring distance, vertical distance, powder factor, burden, spacing, and length of stemming. The results indicate that the proposed ANN-RF model was a superior model to the empirical technique, ANN, and RF models.

Mohamad et al. [131] employed the empirical, ANN, and a hybrid model of the genetic algorithm (GA-ANN) to estimate airblasts based on a maximum charge per delay and the distance from the blast face input parameters. The results show that the GA-ANN technique can provide a higher performance in predicting airblasts compared to the ANN and empirical models. The superior performance of GA-ANN in airblast prediction was also reported by Armaghani et al. [132]. They compared it with the ANN, USBM, and MLR models and observed that, with a coefficient of determination of 0.965, GA-ANN was a better airblast predictor than the other models implemented. Hajihassani et al. [133] developed a hybrid airblast model where the particle swarm optimization (PSO) algorithm was used to train ANNs instead of the backpropagation algorithm. Using nine input parameters, the proposed model had a correlation coefficient of 0.94, suggesting a superior predictive strength compared to empirical models. AminShokravi et al. [134] evaluated the acceptability and reliability of three PSO-based airblast models (the PSO-linear, PSO-power, and PSO-quadratic models) and found that the PSO-linear model showed a higher predictive ability than the PSO-power, PSO-quadratic, ANN, and USBM models.

Armaghani et al. [135] also optimized an ANN with an imperialist competitive algorithm for airblast prediction. They also developed conventional ANN models to compare the results with the new model. The results demonstrated that the proposed model could predict airblasts more accurately than the other presented techniques. Nguyen et al. [136] investigated the feasibility of three ensemble machine learning algorithms, including the gradient boosting machine (GBM), random forest (RF), and Cubist, for predicting airblasts in open-pit mines. The ensemble model results were compared with those of an empirical model. Their findings revealed that the ensemble models yielded more precise accuracy than those of the empirical model. Of the ensemble models, the Cubist model provided a better performance than those of the RF and GBM models. Besides, they also indicated that the explosive charge capacity, spacing, stemming, monitoring distance, and air humidity were the most important inputs for the airblast predictive models using AI.

5.3. Flyrock

Flyrock is a loose rock fragment ejected from blasting processes that can travel over long distances away from the zone of influence of the blast. The Institute of Makers of Explosives (IME) defines flyrock as the rock propelled beyond the blast area by the force of an explosion [137]. According to Amini et al. [138], there are three mechanisms via which flyrock can occur (Figure 9): riffling, catering, and face bursting. Riffling occurs when the stemming material is insufficient, causing blast gases to stream up the blast hole along the path of least resistance, resulting in stemming ejection and, sometimes, ejection of the collar rock. Catering is due to the venting of gasses through the stemming region (i.e., blasthole collar), which usually contains a weakened layer due to the previous blasting from the bench above. Face bursting occurs when explosive charges are adjacent to the major geological structures or zones of weakness, allowing high-pressure gases to jet along the weakness zones [138].

Flyrock has the potential to cause serious damage to the properties or cause injuries and fatalities in communities located close to a blast zone. As a result, researchers have made efforts to develop empirical models to predict and help mitigate flyrock. Equations have also been formulated based on Newton’s law of motion with two possible solutions: an approximate numerical solution and the application of the Runge-Kutta algorithm of the fourth order to predict the maximum throw of flyrock fragments and estimate safe distances [139]. More recently, ML has proven to be a useful tool with surging applications in predicting flyrock. Amini et al. [138] tested the capability of SVM in flyrock prediction of a copper mine. Comparing the obtained results of the SVMs with those of an ANN, they concluded that the SVM model was faster and more precise than the ANN model in predicting flyrock. A new combination (FA-ANN) can be used as a powerful and practical technique in predicting the flyrock distance before blasting operations. Li et al. [140] selected the most important factor for flyrock predictions using the fuzzy Delphi method and developed a firefly algorithm (FA) and ANN model to estimate the flyrock distance. They observed that the FA-ANN model provided the best optimization of the weights and biases and recorded the lowest network error compared to the other ANN-based models.

Manoj and Monjezi [141] also analyzed flyrock predictions using the support vector machine and multivariate regression analysis. They found that the SVM results were more accurate than those of the multivariate regression analysis. Rad et al. [142] also conducted a similar study, comparing least squares support vector machines (LS-SVM) and support vector regression (SVR), and based on the performances of the two models, they concluded that the LS-SVM model was more useful than the SVR model in the estimation of blast-induced flyrock. A sensitivity analysis of the model showed that the powder factor and rock density were the most effective parameters on flyrock. Hasanipanah et al. [143] also developed a flyrock prediction equation based on particle swarm optimization (PSO) in quarry operations. For comparison purposes, multiple linear regression (MLR) was also used. Five effective parameters (burden, spacing, stemming, rock density, and powder factor) were used as the input parameters, while flyrock was considered as the output parameter. The results revealed that the proposed PSO equation was more reliable than MLR in predicting flyrock. Based on the sensitivity analysis results, it was also found that the rock density was the most effective parameter on flyrock in the studied cases.

Recently, Lu et al. [144] presented two machine learning models, including the extreme learning machine (ELM) and outlier robust ELM (ORELM), for predicting flyrock. To construct and verify the proposed ELM and ORELM models, a database including 82 datasets collected from three granite quarry sites was used. Additionally, the ANN and multiple regression models were used for comparison. The results showed that both the ELM and ORELM models performed satisfactorily, and their performances were far better compared to the performances of the ANN and multiple regression models. Armaghani et al. [145] estimated the flyrock distance using three machine learning methods: principal component regression (PCR), support vector regression (SVR), and multivariate adaptive regression splines (MARS). The SVR model showed a better performance in predicting the flyrock distance compared to the other proposed models. Further, the SVR model was optimized by gray wolf optimization (GWO), resulting in a 4% decrease in flyrock distance. The authors asserted that the SVR prediction model can be used to accurately predict the flyrock distance and properly establish the blast safety zone. An ELM was also optimized using the biogeography-based optimization (BBO) algorithm to form a hybrid flyrock prediction model [146]. Compared to the particle swarm optimization (PSO-ELM) and ELM models, the BBO-ELM proved to be a powerful model for predicting flyrock, with a superior performance. Dehghani et al. [147] used the gene expression programming (GEP) model and cuckoo optimization algorithm to predict and minimize the flyrock range. In this study, the burden, spacing, stemming, charge length, and powder factor were used as the input parameters in the GEP model; then, the equation from the GEP was used as a cost function for minimizing flyrock by the cuckoo optimization algorithm. They concluded that the GEP model showed a good performance in predicting blast-induced flyrock using the blast design parameters, and the cuckoo algorithm reduced the maximum flyrock distance relative to the values obtained from the initial blast designs. This study also revealed the powder factor as the input parameter sensitivity in the analysis and, hence, the most effective parameter on the flyrock phenomenon.

6. Discussion and Future Trends

The impacts of blasting operations have significant effects on mining in varied ways, from mineral processing to environmental sustainability. Undesirable blast impacts, such as ground vibration, airblast, and flyrock, pose severe risks, including human irritation, structural damage, injury, and even fatalities to receptor communities if a blast is not conducted properly [148]. In other words, blast results could increase a mine’s operating cost and community complaints, which can escalate to contention between the management and the community if not addressed early. Blast-induced ground vibrations, which are measured in the PPV, are, by far, the most studied blast impact; consequently, most of the blast impact models focus on this area. The popularity of ground vibrations in this field can be attributed to the fact that ground motions accompanying blast events cannot be avoided, and they often result in community complaints. It is one of the major concerns in mining with stringent environmental standards, and a slight breach or incompliance with the rules could impede production and deteriorate the cordial relationship (i.e., social license) between a mining company and a host community. For example, the La Arena gold mine in Peru owned by Tahoe Resources Inc. had to suspend operations temporarily following a protest by some community members demanding compensation for unspecified damage caused by dust and vibrations from blasting at the mine [149]. Given increasing concerns about the environmental impacts of mining, it is now more crucial than ever to ensure that blasting operations are conducted with greater precision. The goal of every blast engineer is to conduct a blast that produces optimal fragmentation, good heave, and minimal backbreak with minimal ground vibration, airblast, flyrock, and fumes. Thus, blast impact studies are vital to determine the most appropriate blast design that would optimize the desirable effects and minimize the undesirable ones. Blasting is a complex phenomenon, and many factors influence its resulting impacts. Different methods based on numerical, empirical, and, more recently, machine learning have been developed for predicting blast impacts.

Several factors affect blast impacts. As highlighted by Yan et al. [81], some common parameters identified to influence blast impacts include the burden, spacing, free face, charge structure, delays, blasthole dimension, charge parameters, stemming, and geological conditions. It is often difficult to incorporate all the influential parameters in the blast impact model, so the practice is to identify the important parameters peculiar to the problem being addressed. Additionally, due to the heterogeneity of geological formations [150], there will be variations in the site conditions (e.g., rock strength and discontinuities) from one mine to another. Therefore, the prevailing local situation, mine plan, and environmental standards must be considered when formulating a blast impact model. The parameter selections are therefore very important, and they have a significant influence on the predictive powers of a blast impact model. Indeed, a blast impact model is as powerful and accurate as the set of parameters employed in developing the model. Studies expend significant resources in deciding which parameters should be included in a model.

Even though empirical blast models are formulated following extensive field experiments and data collection on various blast impact parameters, only a few parameters are considered in the final model. Empirical models for predicting the PPV, for example, are built using mainly the maximum charge per delay, the distance between blast zone and monitoring point, and the geological conditions, which are accounted for as site-specific constants [81]. Similar parameters are used in estimating airblasts and flyrock. The limited number of parameters could result in inaccurate predictions. Cognizant of the limitations of the empirical models, Monjezi et al. [151] modified the United State Bureau of Mines (USBM) model by incorporating the effect of water in addition to the charge per delay and distance from the blast face to develop a new predictive model based on gene expression programming (GEP). They observed that the proposed model was able to predict blast-induced ground vibrations more accurately than the other developed techniques. Nevertheless, empirical models remain the most widely used blast impact predictive tools in the mining industry. This wide usage could be attributed to their computational simplicity and reasonable prediction results. Statistical blast impact models such as those used by Hudaverdi [152] also consider only the blast design parameters and consider them as ratios instead, using their actual values. Despite the wide application of the conventional blast impact models, they possess inherent inefficiencies as a result of their inability to accommodate more relevant parameters affecting the outcome of a blast.

In addressing this challenge, researchers have employed ML techniques to estimate blast impacts. These are computer models that can accommodate several input variables and deduce the relationships between them to predict an output. Considering the numerous parameters involved in estimating blast impacts, ML has proven to be a formidable tool in this area. Besides establishing complex relationships, machine learning tools are also efficient in feature selection. Again, the literature has shown that, compared to the conventional blast impact models, the ML approach is more robust and yields better prediction results. For example, Bayat et al. [125] minimized the blast-induced ground vibrations by decreasing the PPV to 17 mm/s (60%) using an ANN combined with a FA. A burden of 3.1 m, spacing of 3.9 m, and charge per delay of 247 kg were reported as the optimized blast design parameters. Similarly, the authors of [153] employed gene expression programming (GEP) and the cuckoo optimization algorithm (COA) to optimize the blast patterns in an iron mine, resulting in a considerable reduction in the PPV values (55.33%). Armaghani et al. [145] achieved a 4% decrease in the minimum flyrock distance by using SVR in a quarry operation.

Table 6. Summary of the ML-based blast-induced impact prediction models.

ML Method	Other Models	Operation	Parameter	Dataset	Impact	Performance (R2)	Reference
ANN	USBM, Langefors–Kihlstrom, Ambraseys–Hendron, Bureau of Indian Standard, CMRI predictor	Coal mine	Q, D	130	Ground vibration	0.919	[94]
ANN	MVR	Coal mine	Q, D, HD, HZ, B, ST CH, BI, E, V, PV, VOD, ED	150	Ground vibration	0.9994	[80]
SVM	USBM, Ambraseys–Hendron, Davies et al., Indian Standard	Dam construction	Q, D	80	Ground vibration	0.957	[105]
GA-ANN	ANN, USBM, and MLR	Quarry	Q, D	97	Airblast	0.965	[132]
PSO	MLR	Quarry	S, B, ST, PF, RD	76	Flyrock	0.966	[143]
PSO–ANN	ICA, GA	Quarry	HD, HZ, BS, Q, PF	262	Flyrock	0.943	[154]
ANN	MVR	Copper mine	B, S, Q, PF, ST, HD, NR, BH	135	Fragmentation	0.94	[155]

VOD is the velocity of detonation, Q is the maximum charge per delay, D is the distance from the blasting face, B is the burden, S is spacing, ST is stemming, HD is the hole diameter, HZ is the hole depth, CH is the charge length, BI is the blastability index, E is the Young’s modulus, V is Poisson’s ratio, PV is the P-wave velocity, ED is the explosive density, RD is the rock density, PF is the powder factor, BS is the burden-to-spacing ratio, NR is the number of rows, and BH is the bench height.

summarizes some of the ML techniques used to predict blast-induced impacts. The summary includes predicted impacts, techniques that are usually compared with ML, the prediction parameters, the number of datasets, and the ML model performance measure (coefficient of determination).

The most common machine learning methods used for blast impact prediction are the ANN, SVM, and PSO (Table 6). Hybrid models were also developed by combining some of these algorithms. Among these algorithms, the artificial neural network remains the most popular, with wide implementation in ground vibrations [29,80,85], airblasts [98], flyrock [95,156,157,158], fragmentation [155,159,160,161,162], backbreak analyses [159,160,163,164,165], and noise [166]. We observed that these ML techniques were generally employed to predict blast-induced impacts, just like the empirical models, and not necessarily to improve or reduce the impacts. The performances of the models were judged based on a set of statistical metrics, including the mean absolute error (MAE), root mean square error (RMSE), correlation coefficient (R), and coefficient of determination (R²), which only showed the prediction strength of the ML techniques compared to the other models. A summary of the ML-based blast impact prediction models and common parameters is presented in Figure 10.

In implementing the machine learning algorithms, feature selection is considered the first step and is usually achieved using the principal component analysis (PCA). The PCA identifies the principal independent variables and eliminates irrelevant ones [153], and it is one inherent feature of the classification and regression tree (CART) algorithm, as applied by Hasanipanah et al. [167], in predicting ground vibrations. The selected features are synthesized in the chosen machine learning algorithm to estimate the blast impact. Currently, there seems to be consensus backing ANN as a suitable blast impact predictor. However, studies have also highlighted some limitations of the ANN, including a long training period and the possibility of easily falling into the local minimum [81]. Thus, the ANN is combined with other algorithms to optimize and improve the accuracy of predicting blast impacts.

This paper discussed mostly the undesirable impacts of blasting and how machine learning models have been employed to predict these impacts. However, another aspect of blasting is the desired outcomes in terms of fragmentation and heave. Mining companies and quarries desire to produce fragment sizes that can be mucked easily and directly fed into a crusher without the need for secondary blasting. At times, there are too many fine or oversized boulders. The blast input parameters are altered to control the fragment sizes. There are empirical equations [168,169,170,171,172] for predicting the fragment size distribution as well. Examples of empirical models for predicting blast-induced fragment distribution include Kuz-Ram models, Julius Kruttschnitt Mineral Research Centre (JKMRC) models, the Bond comminution method, and the Swebrec function. Images of a blast muck pile can be analyzed using digital image processing software such as Split-Desktop^® and WipFrag 3 to determine the particle size distribution of the fragmented rock.

Additionally, attempts are being made by researchers to introduce new and improved fragment distribution models, leveraging on the advances gained in computer power in recent years. Studies such as An et al. [173], Tao et al. [174], and Yi et al. [123] have utilized numerical modeling techniques and image processing to predict fragment size distributions. One merit of the numerical approach is that it allows the researcher to simulate a series of fragment size distribution scenarios under various blast configurations and fracture patterns [174]. It is worth noting that ML applications in this area are also gaining interest in the scientific community. Generally, the process involves the provision of a set of input data (e.g., blast design parameters and muck pile image), which is processed by the ML model to generate a rock fragment size profile (Figure 11). The ML techniques being applied for evaluating the fragment size distribution are different from those used in the prediction of ground vibrations, airblasts, and flyrock. These new techniques are deep learning, a subset of ML. Deep learning naturally takes advantage of automatically discovering and extracting features and patterns from large datasets combined with modeling structures capable of capturing highly complex behaviors [175]. Examples of deep learning algorithms include convolutional neural networks (CNN), recurrent neural networks (RNNs), long short-term memory networks (LSTMs), stacked auto-encoders, deep Boltzmann machine (DBM), and deep belief networks (DBN). These algorithms have tremendously improved image classification, object detection, and natural language processing in many fields. Recent applications of deep learning in blasting include the prediction of flyrock [157], rock fragment distribution [176], and classification of mine seismic events, among others. Further, we observed that most common ML algorithms for blast-induced fragment size predictions include the ANN [159,160,161,162], SVM [104,177], PCA [177], fuzzy inference system [178,179,180], adaptive neuro-fuzzy inference system [177,181,182], bee colony algorithm [162], PSO [183,184], ant colony optimization [185], and gaussian process regression [186]. The ML-based fragment size prediction models performed significantly better than the empirical models [187].

From the literature, many of the proposed models could predict only one blast impact. Only a few models were developed to predict ground vibrations and airblasts [188,189], backbreak and rock fragmentation [160,162], and flyrock and rock fragmentation [190,191]. Meanwhile, all the blast impacts occur concurrently and are equally influenced by similar blast parameters and geological conditions. Currently, only one study (a master of a science thesis report) has been able to develop an integrated prediction model for rock fragmentation, ground vibrations, and airblasts using an ANN with 7-13-3 architecture [8]. The input parameters were the charge per delay, distance from the blast zone to the monitoring point, hole depth, stemming length, hole diameter, powder factor, and spacing-to-burden ratio, while rock fragmentation, ground vibrations, and airblasts were the corresponding output parameters. The ANN model proved to be more effective with improved fragmentation and minimal blast impacts compared to the empirical equations and multivariate regression. An integrated model of this kind saves resources and allows the blast engineer to examine the influence of the input parameters on the blast outcome in one attempt. Therefore, a more holistic and robust ML-based blast impact model should integrate all the blast impacts, both desirable and undesirable. An improved ML model development can be connecting the input (most influential blast design parameters) to the output (blast outcomes). Subsequently, with sufficient training of the ML model using an adequate dataset, the blast outcomes can be predicted before the actual blast event that would inform further modification of the input parameters to achieve the desired outcome. Compared to the other blast impacts, ML applications for blast-induced dust/fume and noise prediction have not received intensive research attention. From the existing blast features, ML models can be developed to estimate noise level and dust/fume volume and direction.

Nowadays, with automation and the internet of things (IoT), mining companies can receive real-time information on drill operations, including high-resolution rock images and ground conditions. Similarly, several measurements, such as blast images and videos, vibration results, fragment distribution, plume movement, and loading and crushing performances, can be obtained during and after a blast. With the availability of such large datasets combined with improvements in algorithms and computing power, we foresee a field-wide implementation of big data analytics coupled with deep learning applications to integrate all the aspects of mine operations, from exploration to reclamation, leading to more efficient and accurate decision-making in the industry. These applications will automatically learn from the result of each drilling and blasting operation and analyze how the parameters such as the drill pattern, hole deviation, ground condition, timing, and powder factor contribute to the resulting fragmentation and heave, material handling, and crushing performance. In fact, unlike most traditional ML algorithms applied in this field, deep learning algorithms would automatically discover, extract, and optimize the blast-induced features without human intervention. Deep learning could overcome some of the deficiencies in traditional data-driven methods as more data becomes available. Deep learning models can also make it possible for researchers to predict all blast-induced impacts simultaneously. Integrating these applications into the current systems will form part of the ongoing efforts to improve mine-to-mill processes and automate mining processes.

It is essential to mention that the foundation of a functional ML model rests upon a rich dataset. The quality, size, and partition of the dataset used in implementing ML influence the model’s performance in accuracy and generalization. Thus, the application of various AI methods, including ML and deep learning, requires a reasonably large dataset to work properly. Without an adequate dataset, the model’s usefulness and potential can be undermined or negated completely. Generally, it is widely accepted within the research community that AI demands an enormous dataset, and a too-little dataset will yield poor results. However, what constitutes an adequate dataset size is not clearly defined, as the amount of data required depends on different factors, such as the problem definition, model complexity, and algorithm type [192]. Fortunately, renowned researchers working in AI within the mining industry have put forth their experience in modeling problems relating to the mining and mineral industry and recommended good practices, especially when modeling with a sparse dataset.

Ganguli et al. [193] provided good practices regarding AI implementation in mining. They recommended a thorough understanding of the modeling process before implementation and advised caution when using business intelligence tools and software products. Their recommendation also included the random splitting of a dataset into training, testing, and validation subsets and achieving similar characteristics among the three subsets, irrespective of the data partition. Further, they suggested that the training subset should contain the highest and lowest values, and samples should be assigned to the training subset first, followed by validation and testing, during data grouping/segmentation. Moreover, the best data collection and processing practices should be observed during model development to ensure the dataset is of high quality, sufficient, and representative of the population.

7. Conclusions

A blast impact is a complex phenomenon with numerous influential factors that must be incorporated into blast impact prediction models to predict accurate results. However, the industry-accepted empirical models lack the computational capacity to accommodate all the influential factors. Thus, these models may not be accurate in their predictions. The importance of achieving accurate predictions is well-known, as it informs proper blast design and helps allay doubts about compliance with the established blast standards. Recent advances in computer power have ushered in soft computing tools that can address some of the limitations of the empirical models used in blast engineering. ML algorithms are powerful tools for solving both linear and nonlinear complex mining problems with several influential factors. ML algorithms, such as the ANN, SVM, and CART, can take several variables and predict blast impacts with high levels of accuracy. These models are promising tools for optimizing the blast parameters and blast outcomes to increase the production efficiency while reducing the costs. The models’ predictive powers could also be improved by synthesizing with other algorithms.

Future models could focus on developing a one-shop model that could estimate all the blast impacts, perhaps using deep learning, instead of predicting a single impact such as ground vibrations or airblasts. Additionally, these new models should incorporate the geological variability and consider datasets from different mine sites or operations to develop a more holistic model. The models should be user-friendly and devoid of complex mathematical language so that industry practitioners can easily implement them.