Study of Double-Deck Vibrating Flip-Flow Screen Based on Dynamic Stiffness Characteristics of Shear Springs
Abstract
:1. Introduction
2. Theoretical Model
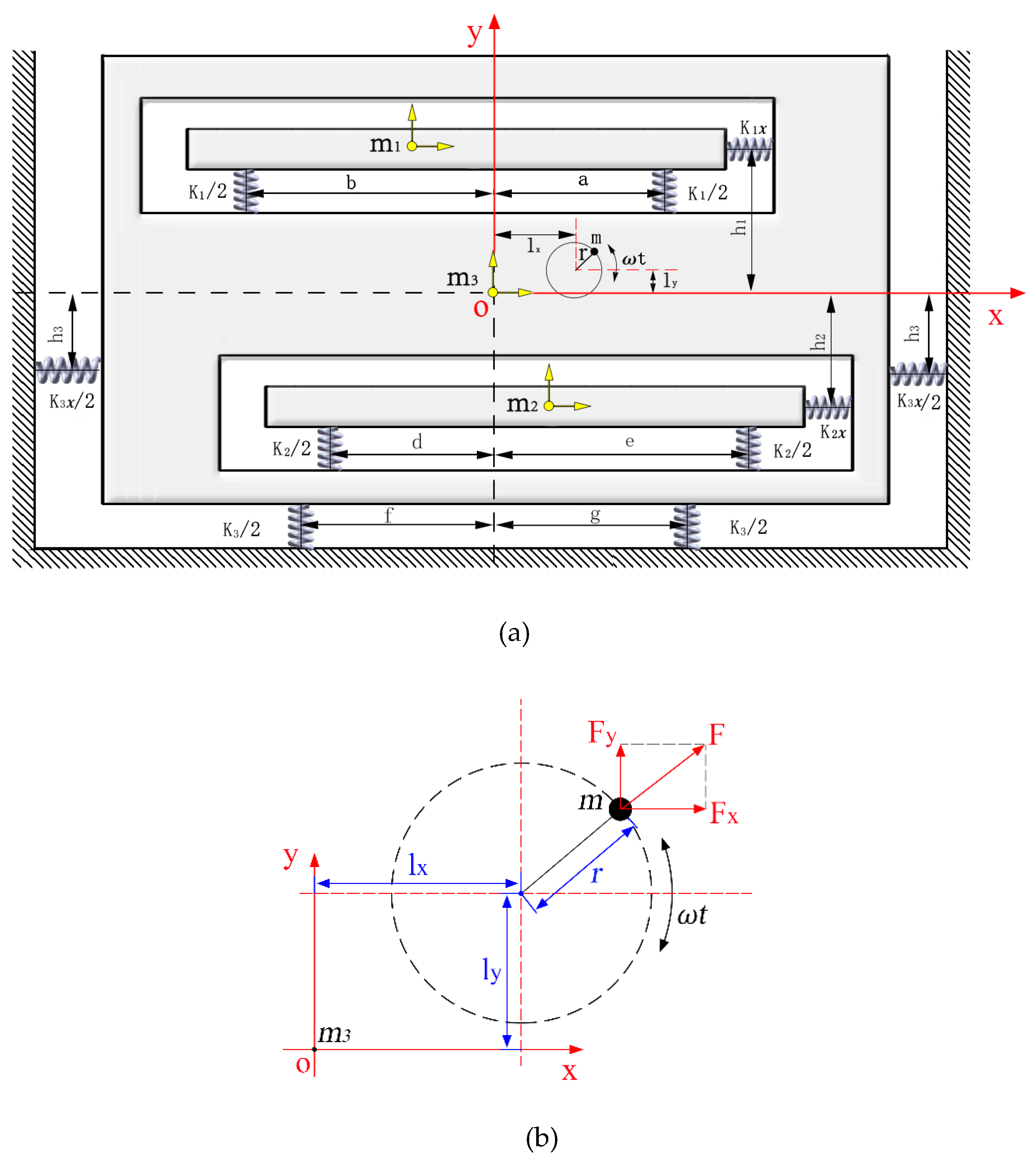
2.1. Mechanical Model
2.2. Dynamic Equation
2.3. The Parameters
3. Experimental
3.1. Experimental System
3.2. Materials
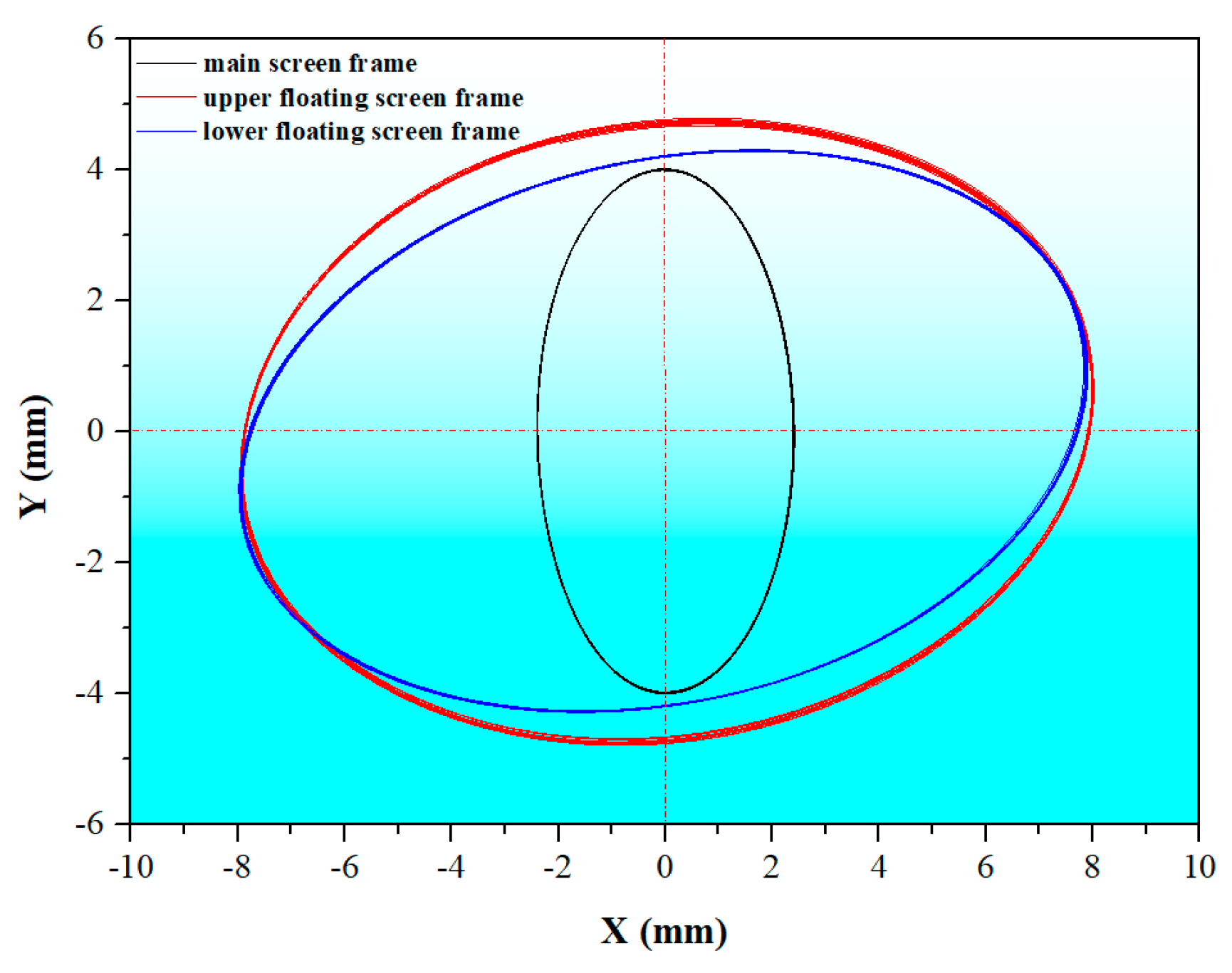
3.3. Motion Trail Test
4. Results and Discussion
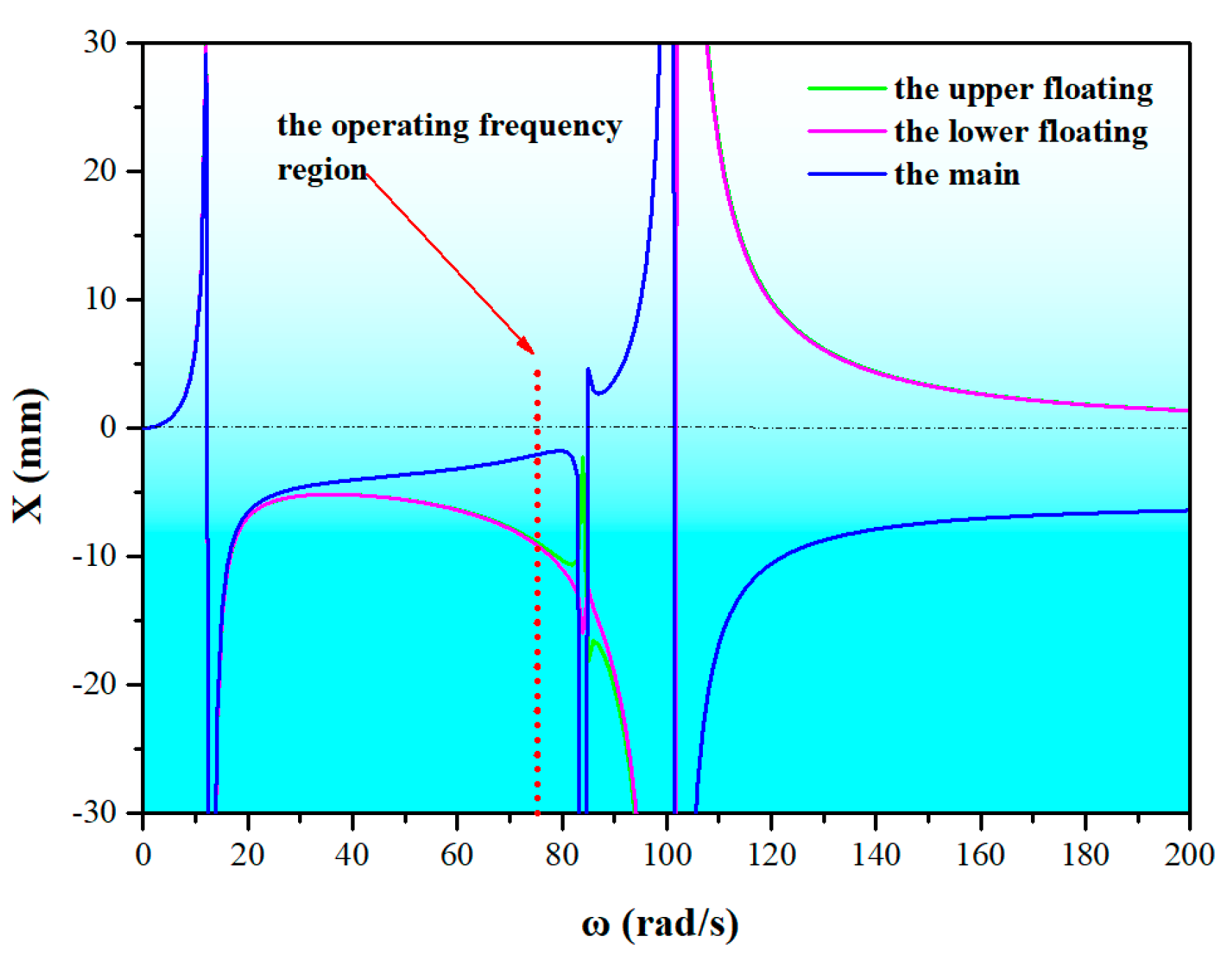
4.1. Theoretical Dynamic Amplitude–Frequency Characteristics
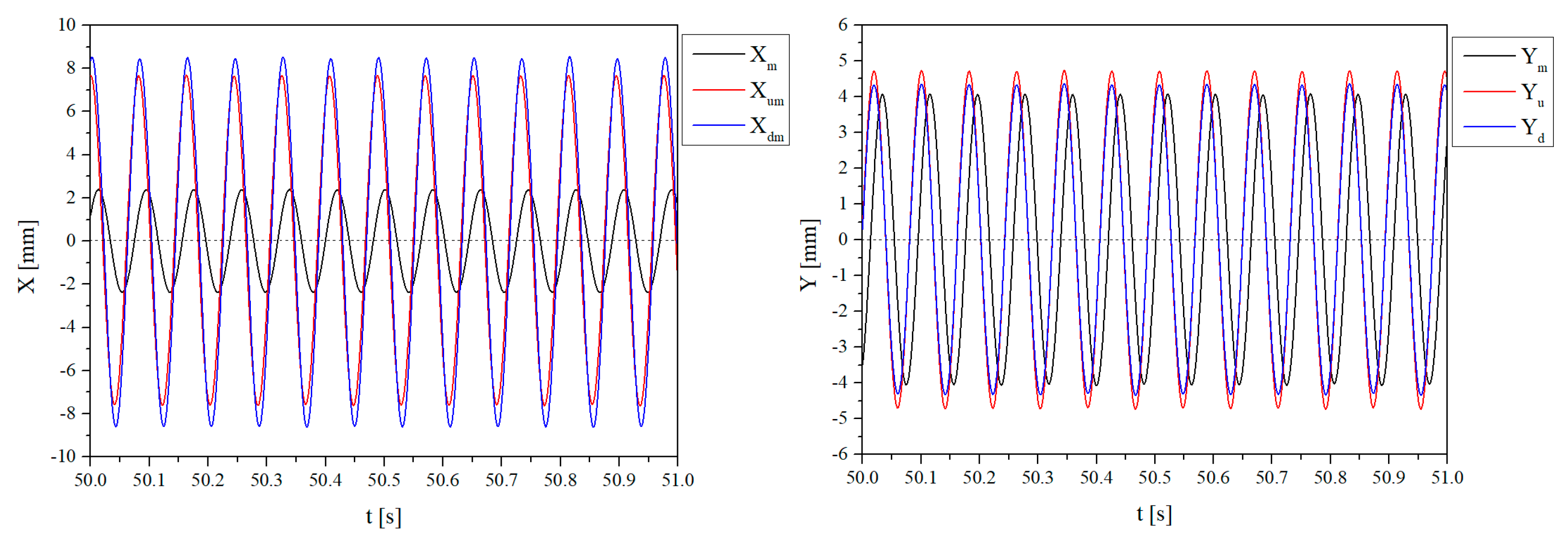
4.1.1. In the x Direction
4.1.2. In the y Direction
4.2. Experimental Dynamic Amplitude–Frequency Characteristics
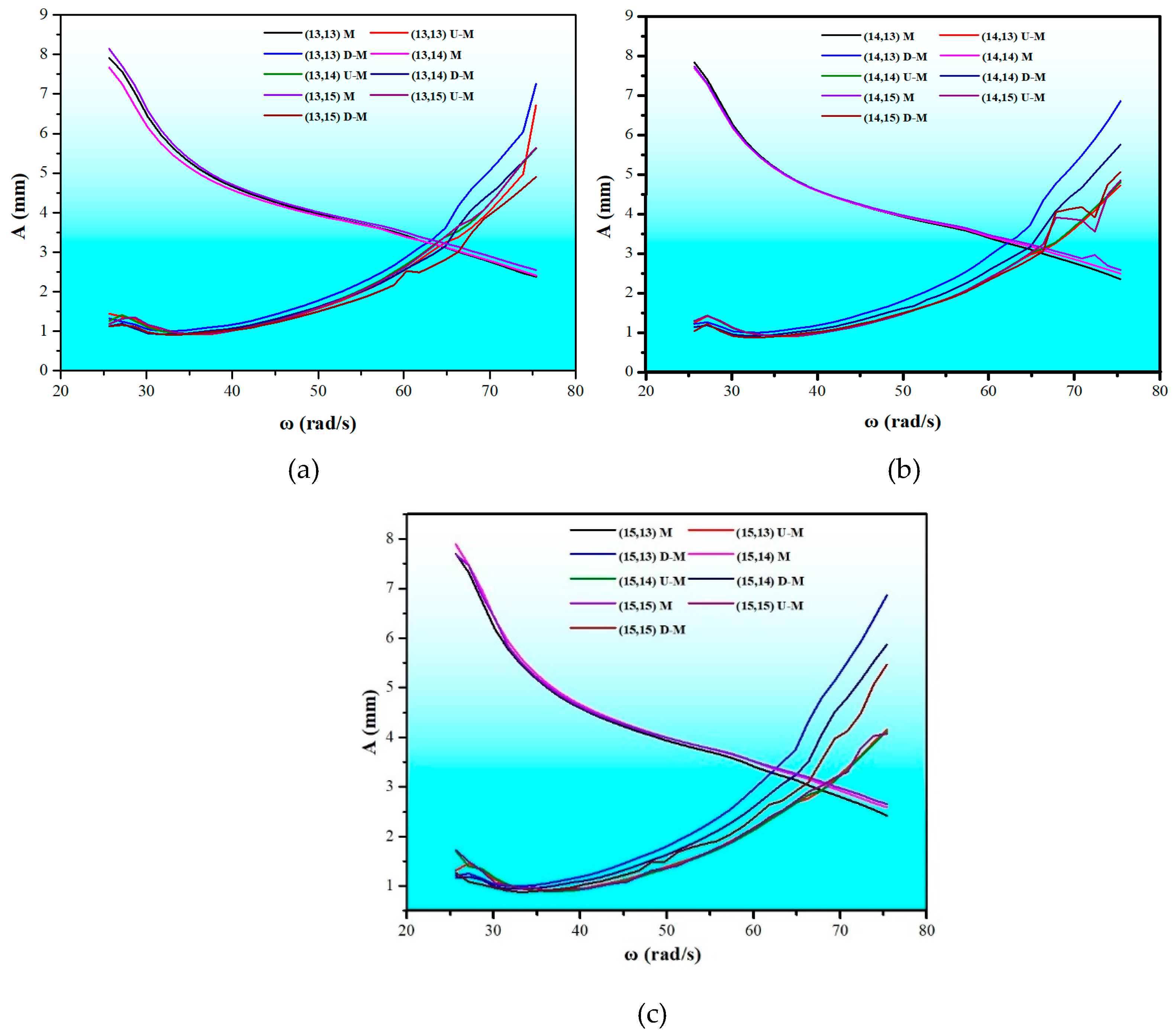
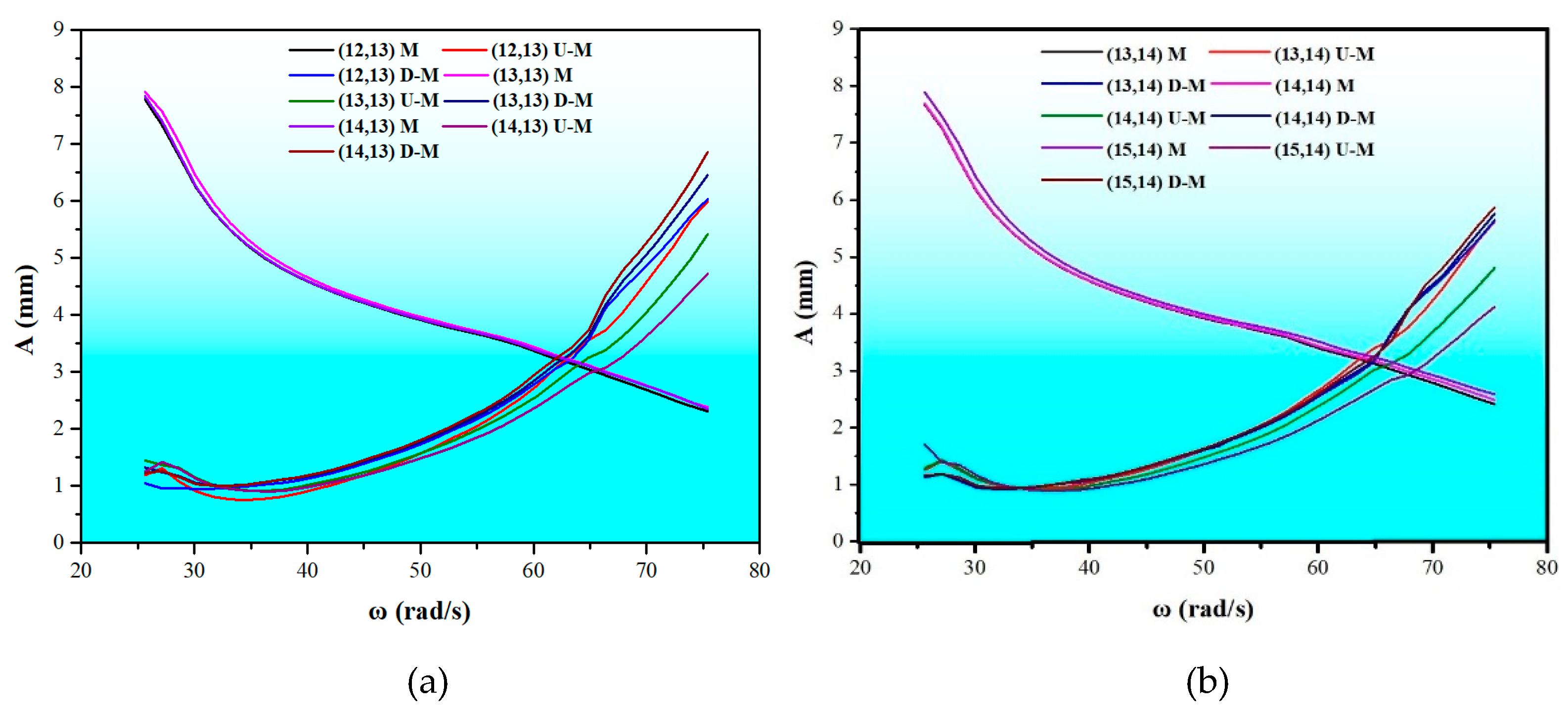
4.2.1. K1 Was Constant, K2 Was Variable
4.2.2. K1 Was Variable, K2 Was Constant
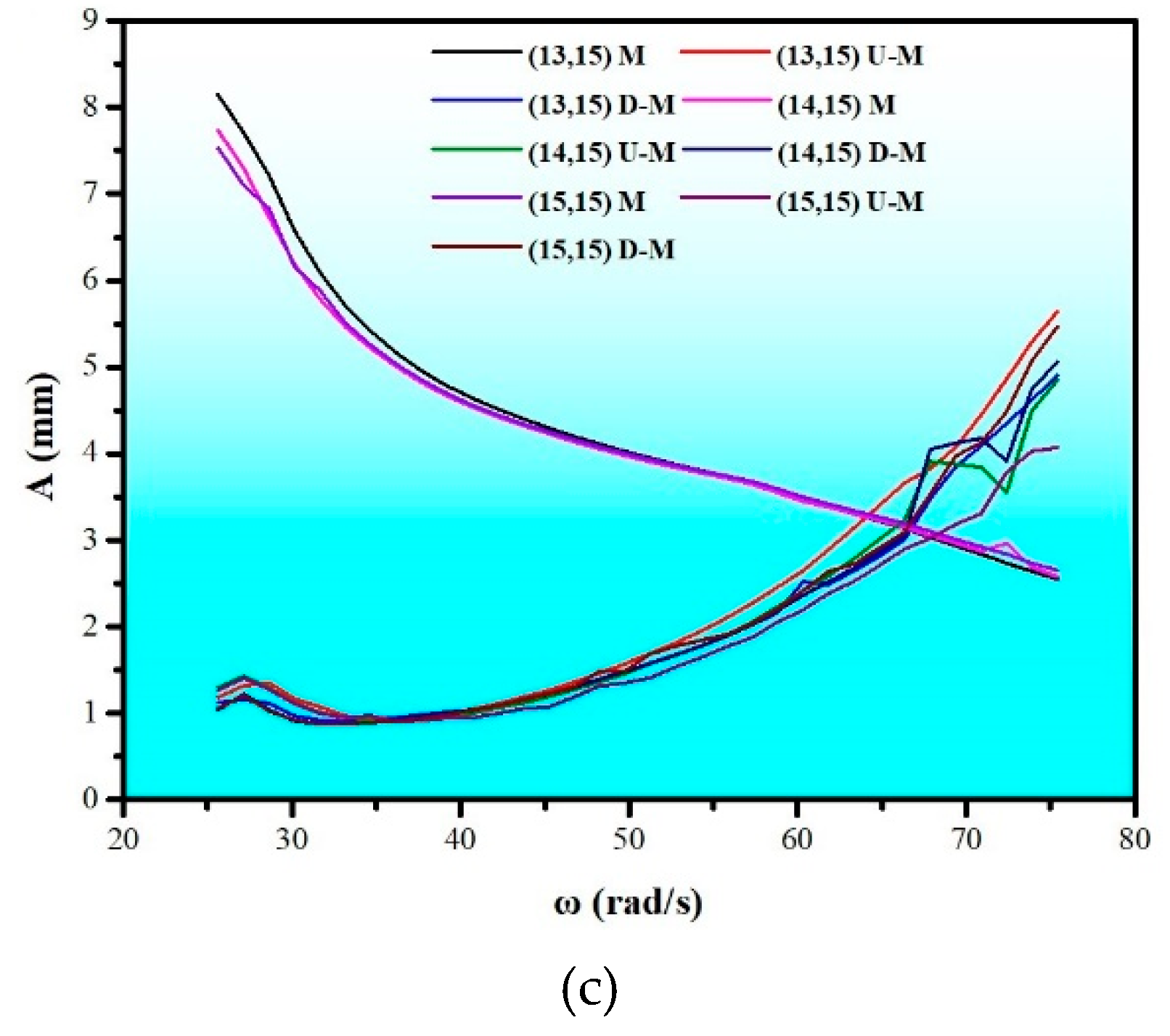
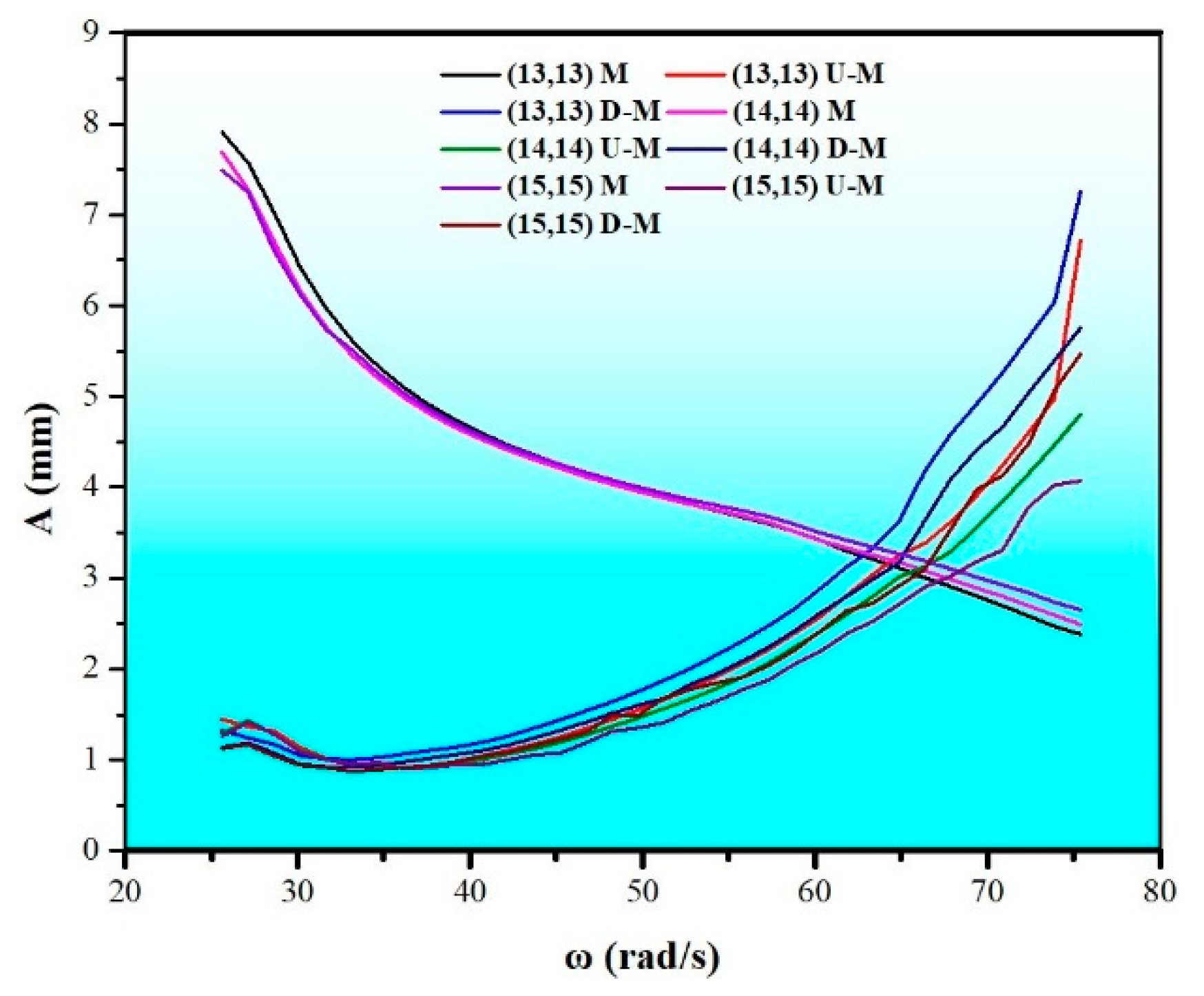
4.2.3. K1 and K2 Were Variable
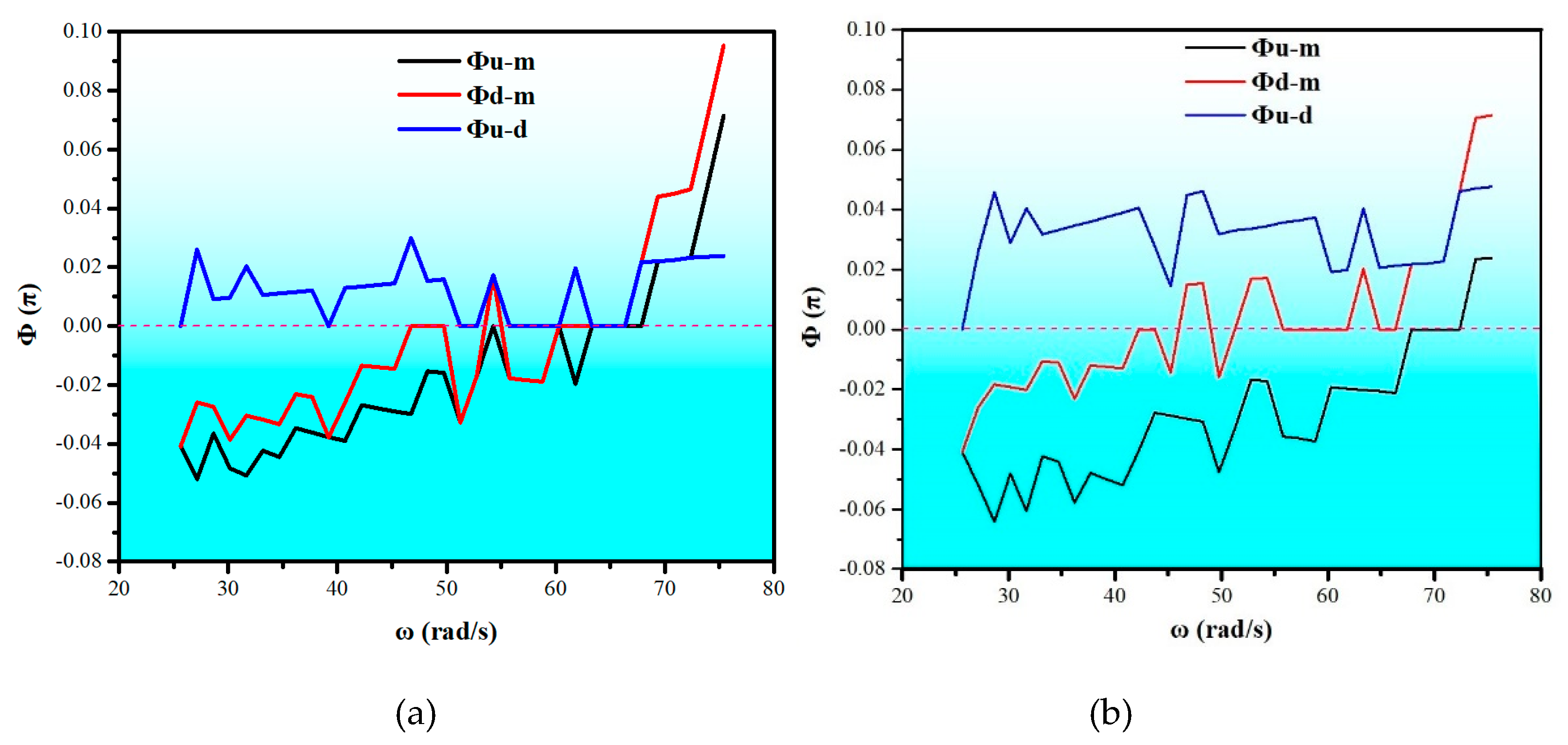
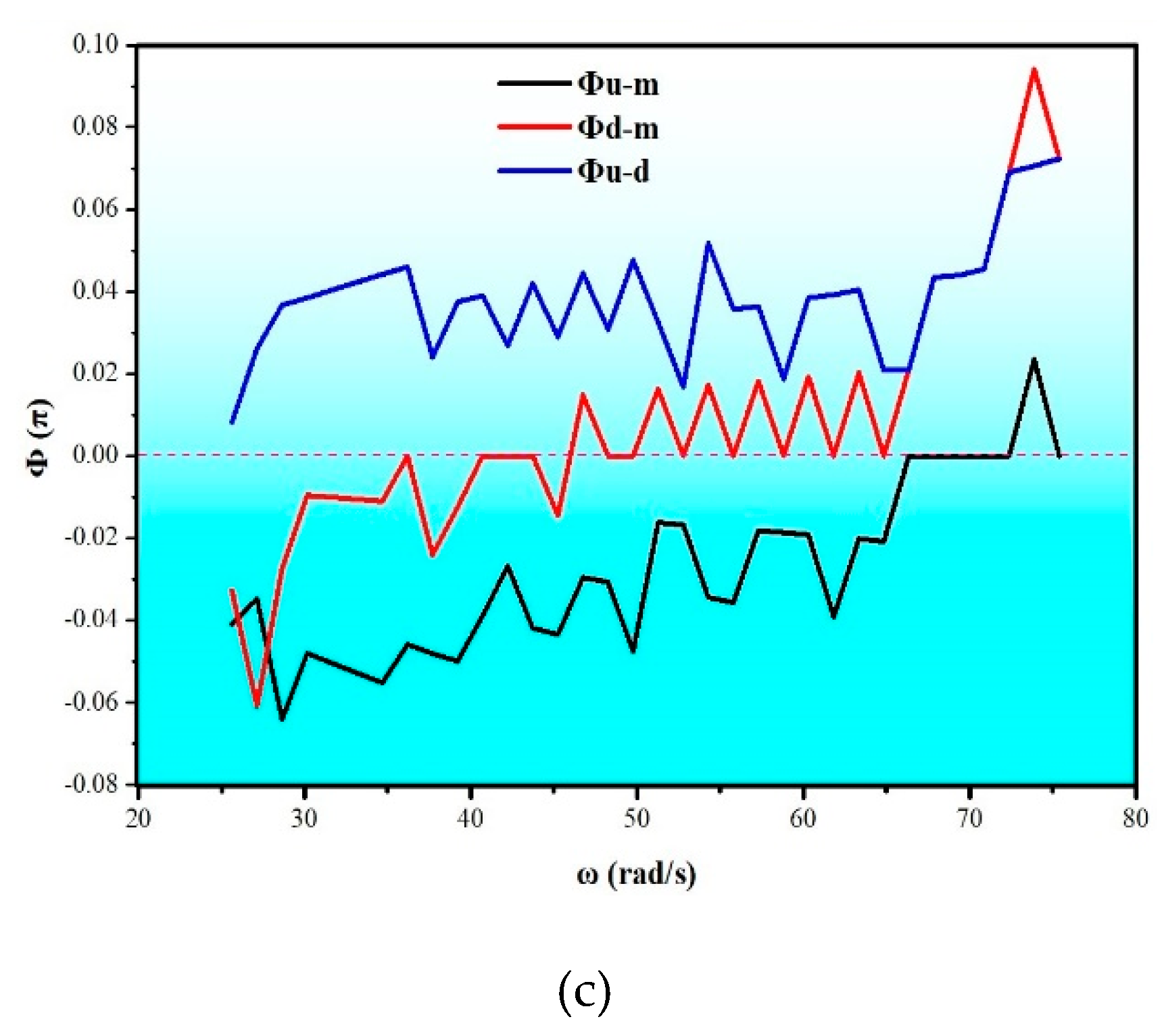
4.3. Phase–Frequency Characteristics
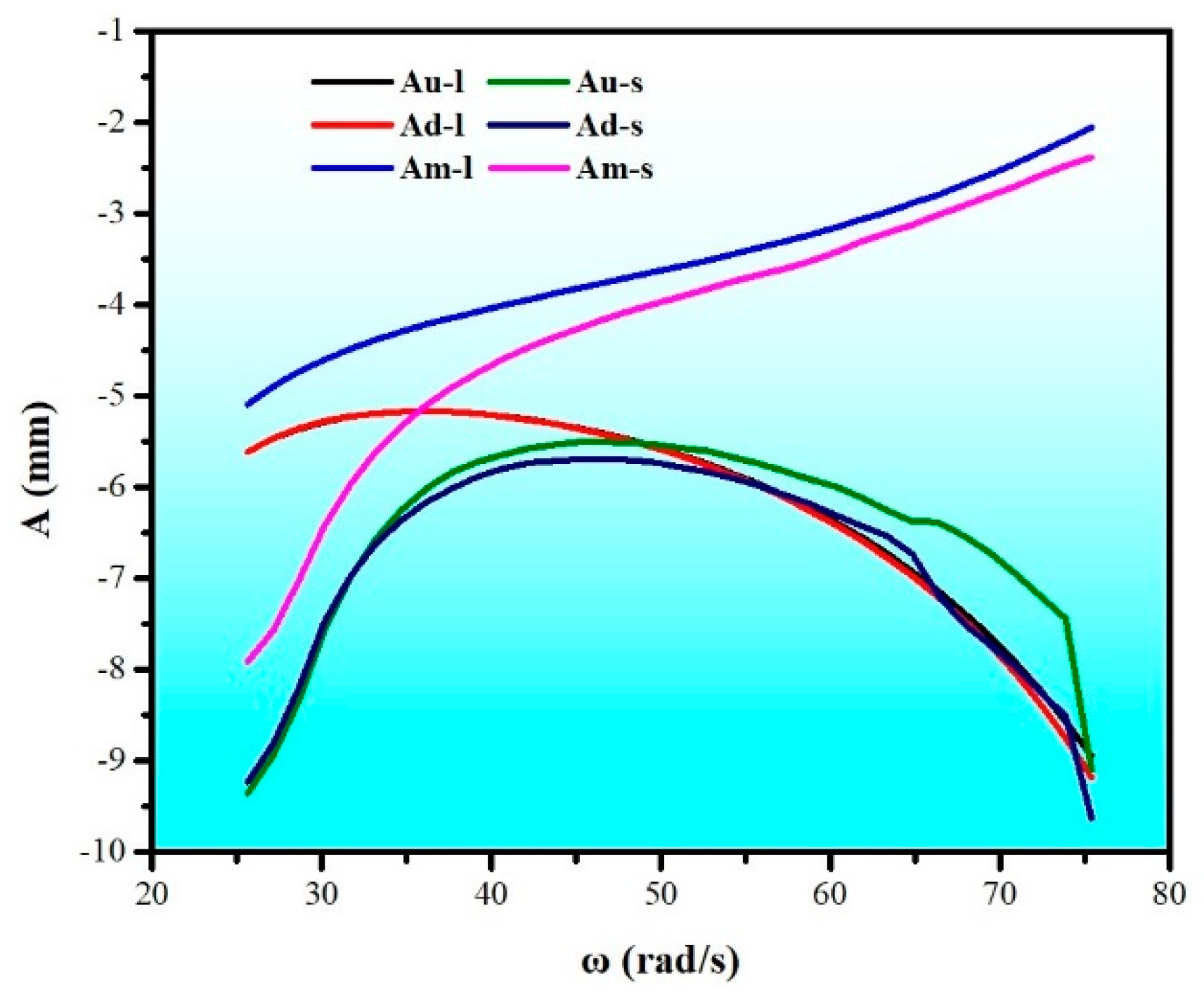
4.4. Comparison of Theoretical and Experimental Amplitude–Frequency Characteristics
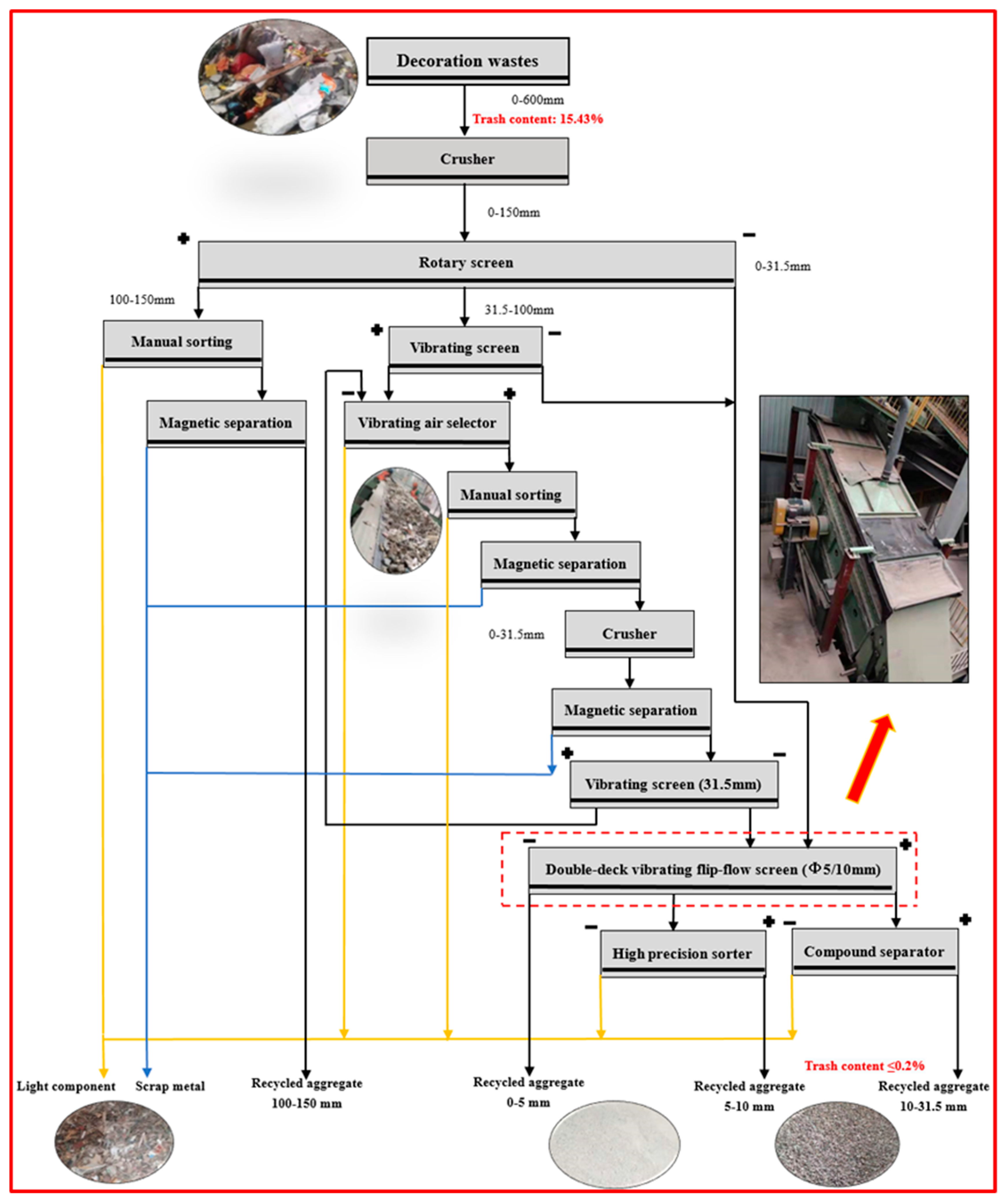
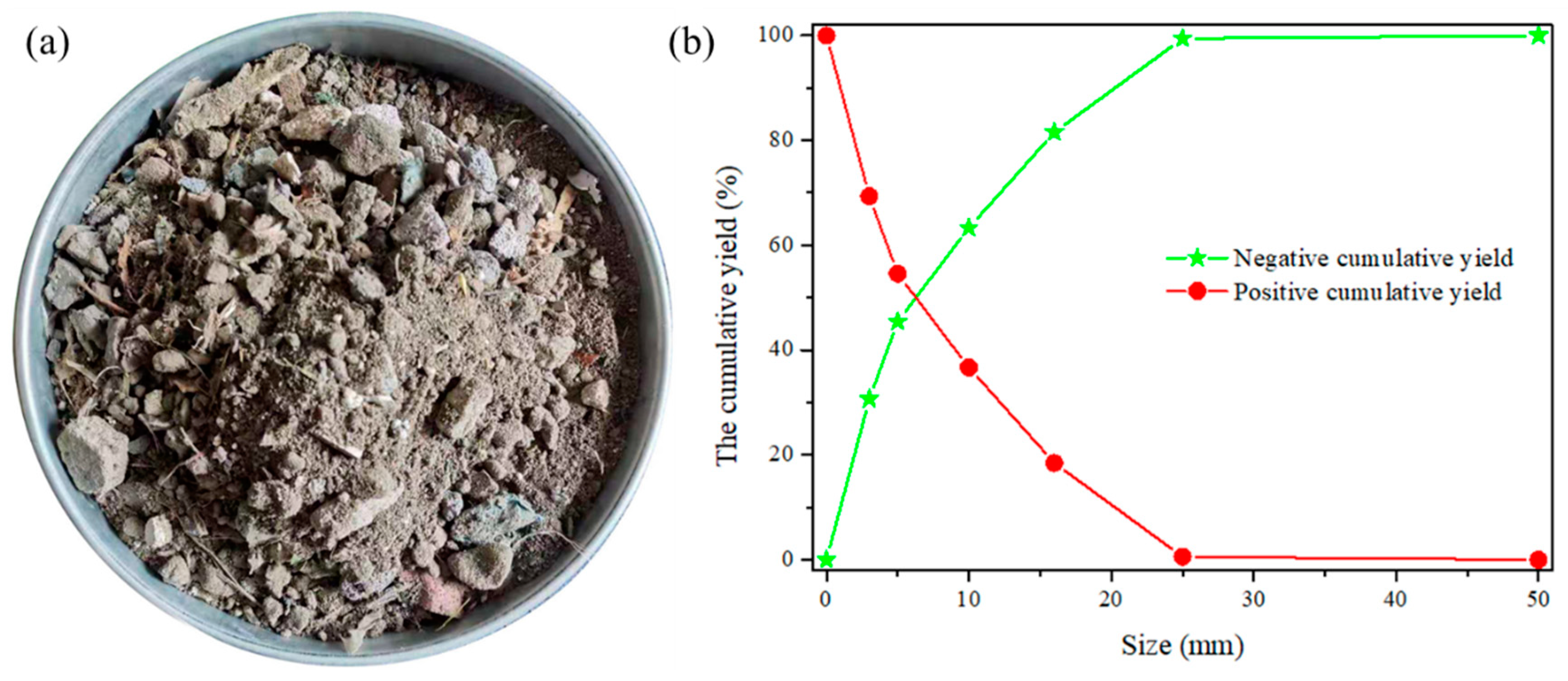
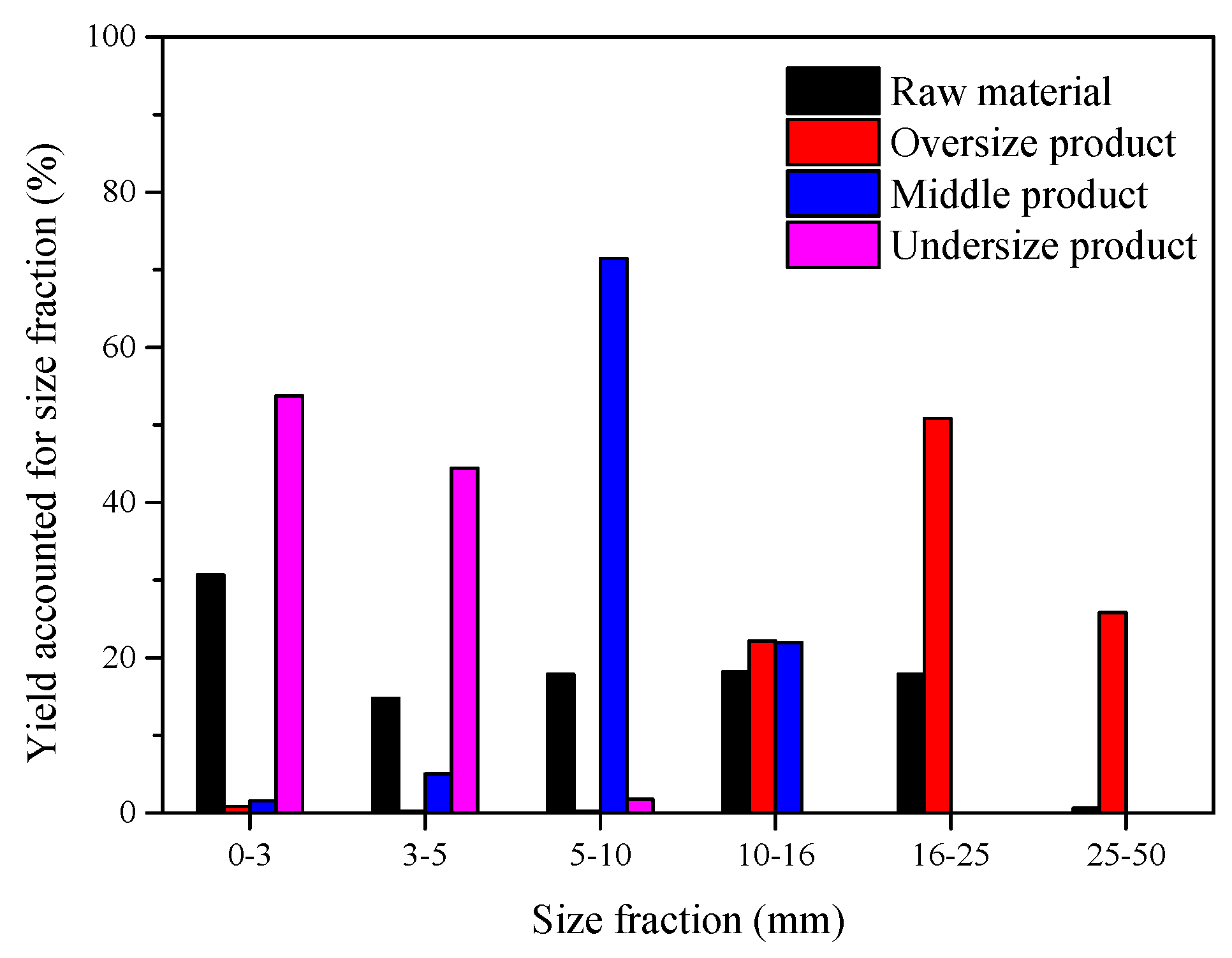
5. Screening Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| m1 | the mass of the upper floating screen frame and half of the screen plate of the upper floating screen frame, kg. |
| m2 | the mass of the lower floating screen frame and half of the screen plate of the lower floating screen frame, kg. |
| m3 | the mass of the double-deck vibrating flip-flow screen box side plates, fixed beams, vibrator, strengthening beams, half of the upper and lower floating screen frame plates, kg. |
| K1x | stiffness of the upper floating screen in the x direction, N/m. |
| K2x | stiffness of the lower floating screen in the x direction, N/m. |
| K3x | stiffness of the main screen frame in the x direction, N/m. |
| K1 | stiffness of the upper floating screen in the y direction, N/m. |
| K2 | stiffness of the lower floating screen in the y direction, N/m. |
| K3 | stiffness of the main screen frame in the y direction, N/m. |
| a | distance between the center of the right spring of the upper floating screen frame and the center of the main screen frame in x direction, mm. |
| b | distance between the center of the left spring of the upper floating screen frame and the center of the main screen frame in x direction, mm. |
| d | distance between the center of the left spring of the lower floating screen frame and the center of the main screen frame in the x direction, mm. |
| e | distance between the center of the right spring of the lower floating screen frame and the center of the main screen frame in the x direction, mm. |
| f | distance between the center of the left spring of the main screen frame and the center of the main screen frame in the x direction, mm. |
| g | distance between the center of the right spring of the main screen frame and the center of the main screen frame in the x direction, mm. |
| h1 | distance between the center of the upper floating screen frame and the center of the main screen frame in the y direction, mm. |
| h2 | distance between the center of the lower floating screen frame and the center of the main screen frame in the y direction, mm. |
| h3 | distance between the center of the spring in the x direction of the main screen frame and the center of the main screen frame in the y direction, mm. |
| lx | distance between the vibration exciter center and main screen center in x direction, mm. |
| ly | distance between the vibration exciter center and main screen center in y direction, mm. |
References
- Sun, P.; Zhang, N.; Zuo, J.; Mao, R.; Gao, X.; Duan, H. Characterizing the generation and flows of building interior decoration and renovation waste: A case study in Shenzhen City. J. Clean. Prod. 2020, 260, 121077. [Google Scholar] [CrossRef]
- Ajayi, S.O.; Oyedele, L.O. Policy imperatives for diverting construction waste from landfill: Experts’ recommendations for UK policy expansion. J. Clean. Prod. 2017, 147, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Hendrickson, C.; Horvath, A. Resource use and environmental emissions of U.S. construction sectors. J. Constr. Eng. Manag. 2000, 126, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Gálvez-Martos, J.; Styles, D.; Schoenberger, H.; Zeschmar-Lahl, B. Construction and demolition waste best management practice in Europe. Resour. Conserv. Recycl. 2018, 136, 166–178. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Gong, W.; Tam, V.W.; Illankoon, I.C.S. Conceptual framework for renovation waste management based on renovation waste generation rates in residential buildings: An empirical study in China. J. Clean. Prod. 2019, 228, 284–293. [Google Scholar] [CrossRef]
- Fatta, D.; Papadopoulos, A.; Avramikos, E.; Sgourou, E.; Moustakas, K.; Kourmoussis, F.; Mentzis, A.; Loizidou, M. Generation and management of construction and demolition waste in Greece—An existing challenge. Resour. Conserv. Recycl. 2003, 40, 81–91. [Google Scholar] [CrossRef]
- Gyurkó, Z.; Jankus, B.; Fenyvesi, O.; Nemes, R. Sustainable applications for utilization the construction waste of aerated concrete. J. Clean. Prod. 2019, 230, 430–444. [Google Scholar] [CrossRef]
- Huang, B.; Wang, X.; Kua, H.; Geng, Y.; Bleischwitz, R.; Ren, J. Construction and demolition waste management in China through the 3R principle. Resour. Conserv. Recycl. 2018, 129, 36–44. [Google Scholar] [CrossRef]
- Davis, P.; Aziz, F.; Newaz, M.; LauraSimon, W. The classification of construction waste material using a deep convolutional neural network. Autom. Constr. 2021, 122, 103481. [Google Scholar] [CrossRef]
- Directive, E.C. Directive 2008/98/EC of the European Parliament and of the Council of 19 November 2008 on waste and repealing certain Directives. Off. J. Eur. Union 2018, 312, 3–30. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010; p. 533. [Google Scholar]
- Gong, S.; Oberst, S.; Wang, X. An experimentally validated rubber shear spring model for vibrating flip-flow screens. Mech. Syst. Signal Process. 2020, 139, 106619. [Google Scholar] [CrossRef]
- Yu, C.; Wang, X.; Pang, K.; Zhao, G.; Sun, W. Dynamic Characteristics of a Vibrating Flip-Flow Screen and Analysis for Screening 3 mm Iron Ore. Shock. Vib. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Z.; Wu, J.; Zou, M.; Zhao, W.; Qiu, W. Design and Analysis of a Kind of Centralized Forced Flip-Flow Screen. In Proceedings of the 8th International Conference on Sustainable Development in the Minerals Industry, Beijing China, 25–29 January 2017; pp. 227–231. [Google Scholar]
- Chen, Z.; Tong, X.; Li, Z. Numerical Investigation on the Sieving Performance of Elliptical Vibrating Screen. Processes 2020, 8, 1151. [Google Scholar] [CrossRef]
- Jiang, H.; Zhao, Y.; Duan, C.; Yang, X.; Liu, C.; Wu, J.; Qiao, J.; Diao, H. Kinematics of variable-amplitude screen and analysis of particle behavior during the process of coal screening. Powder Technol. 2017, 306, 88–95. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, C.; Fan, M.; Wei, L. Research on acceleration of elastic flip–flow screen surface. Int. J. Miner. Process. 2000, 59, 267–274. [Google Scholar] [CrossRef]
- Wang, W.; Duan, C.; Jiang, H.; Yu, S.; Zhou, Z.; Qiao, J.; Zhao, Y.; Pan, M. Mechanism of overcoming plugging and optimization of parameters for rigid-flexible coupled elastic screening of moist fine coal. Powder Technol. 2020, 376, 113–125. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, X.; Niu, L.; Xiong, X.; Dong, Z.; Tang, J. Research on Sieving Performance of Flip-Flow Screen Using Two-Way Particles-Screen Panels Coupling Strategy. IEEE Access 2019, 7, 124461–124473. [Google Scholar] [CrossRef]
- Xiong, X.; Niu, L.; Gu, C.; Wang, Y. Vibration characteristics of an inclined flip-flow screen panel in banana flip-flow screens. J. Sound Vib. 2017, 411, 108–128. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Yu, C.; Liu, S.; Zhou, J.; Zhu, G. Research on Static and Dynamic Characteristics of Shear Spring of the Vibrating Flip-Flow Screen. Symmetry 2020, 12, 1644. [Google Scholar] [CrossRef]
- Gong, X.S.; Wang, S. Oberst, Non-linear Analysis of Vibrating Flip-flow Screens. In Proceedings of the MATEC Web of Conferences, Gdynia, Poland, 29 October 2018; Volume 221, p. 04007. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. Modern Coal Preparation Screening and Dewatering Equipment; China Coal Industry Publishing House: Beijing, China, 2014; p. 44. [Google Scholar]




| Symbol | Item | Value |
|---|---|---|
| m | The total mass of the exciter eccentric block (kg) | 345.04 |
| r | Eccentric distance (mm) | 12.18 |
| B | Width of plate (mm) | 1800 |
| L | Length of plate (mm) | 6100 |
| m1 | Upper floating screen frame mass (kg) | 1608.25 |
| m2 | Lower floating screen frame mass (kg) | 1622.56 |
| m3 | Main screen frame mass (kg) | 7339.42 |
| P | Motor power (kw) | 22 |
| k | Stiffness of shear spring (N/mm) | 220 |
| n | The number of shear spring groups | 12–15 |
| Excitation frequency rad/s | 75 | |
| K3 | Stiffness of vibration isolation springs (N/m) | 5,231,730 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Wang, X.; Lin, D.; Xu, N.; Yu, C.; Geng, R. Study of Double-Deck Vibrating Flip-Flow Screen Based on Dynamic Stiffness Characteristics of Shear Springs. Minerals 2021, 11, 928. https://doi.org/10.3390/min11090928
Zhao G, Wang X, Lin D, Xu N, Yu C, Geng R. Study of Double-Deck Vibrating Flip-Flow Screen Based on Dynamic Stiffness Characteristics of Shear Springs. Minerals. 2021; 11(9):928. https://doi.org/10.3390/min11090928
Chicago/Turabian StyleZhao, Guofeng, Xinwen Wang, Dongdong Lin, Ningning Xu, Chi Yu, and Runhui Geng. 2021. "Study of Double-Deck Vibrating Flip-Flow Screen Based on Dynamic Stiffness Characteristics of Shear Springs" Minerals 11, no. 9: 928. https://doi.org/10.3390/min11090928
APA StyleZhao, G., Wang, X., Lin, D., Xu, N., Yu, C., & Geng, R. (2021). Study of Double-Deck Vibrating Flip-Flow Screen Based on Dynamic Stiffness Characteristics of Shear Springs. Minerals, 11(9), 928. https://doi.org/10.3390/min11090928





