Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn
Abstract
:1. Introduction
2. Materials and Methods
2.1. Background of the Method
2.2. Method Description
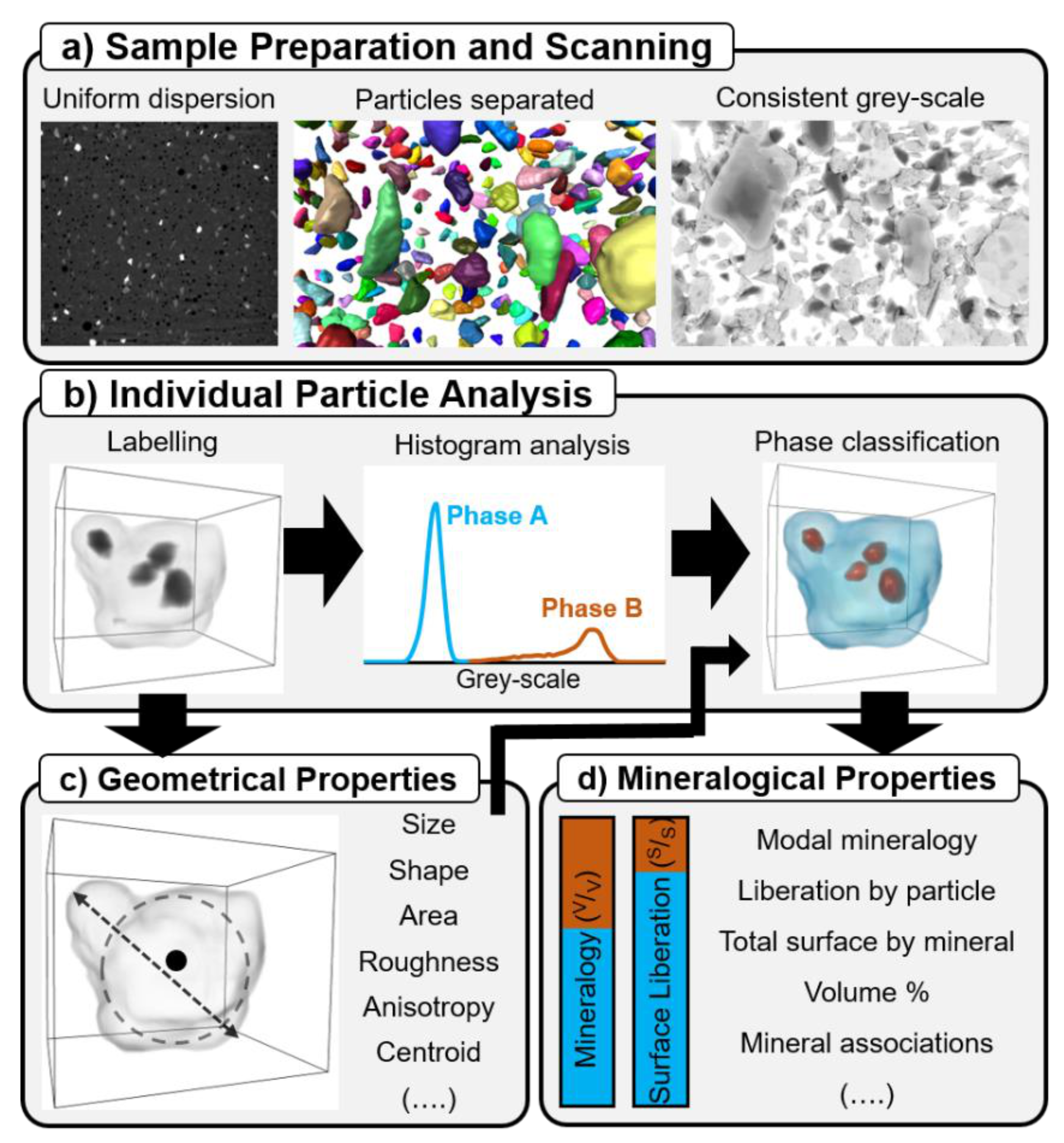
2.2.1. Sample Preparation and Scanning
2.2.2. Individual Particle Analysis
2.3. Mineralogical Validation
2.4. Method Demonstration
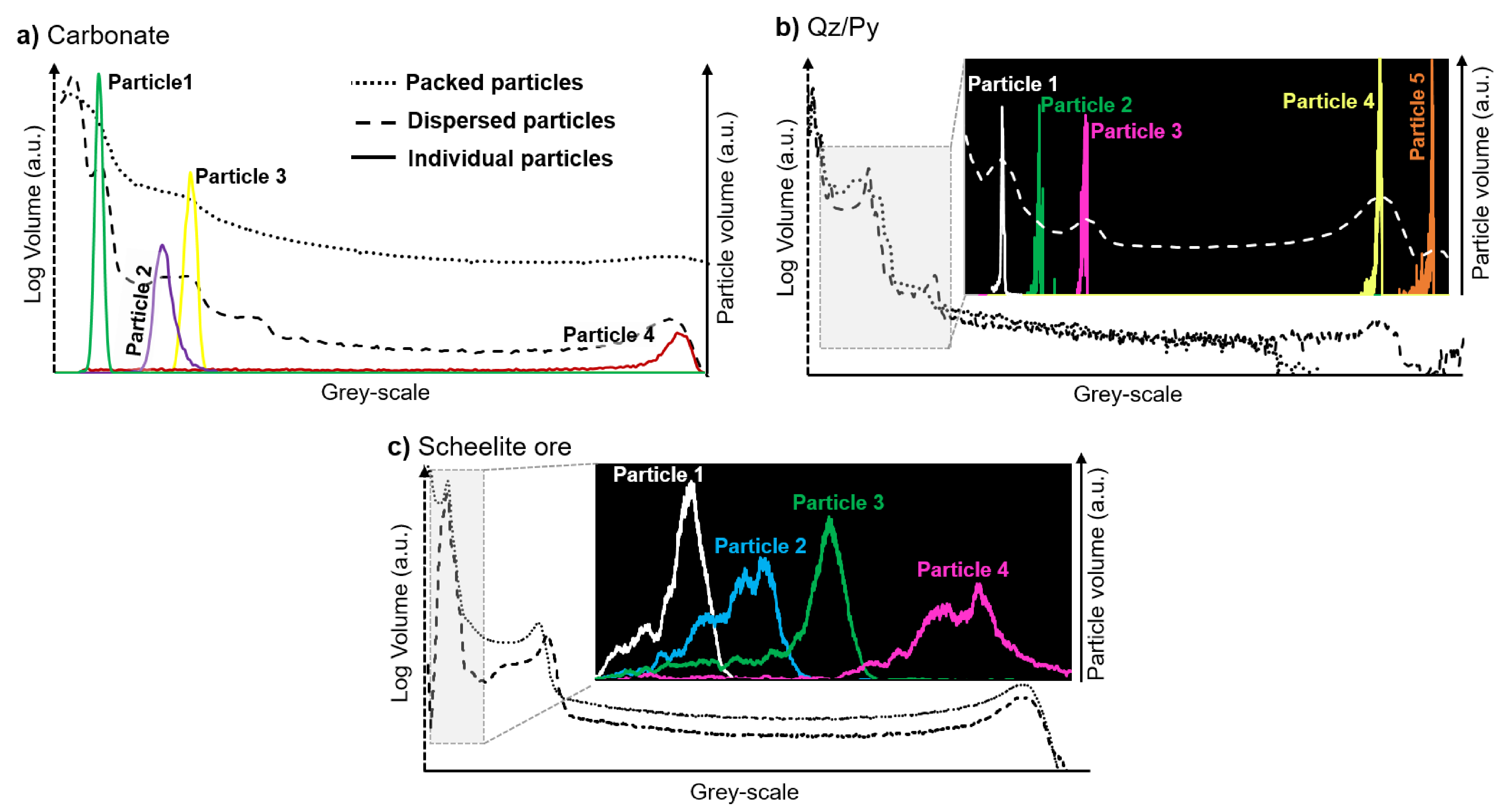
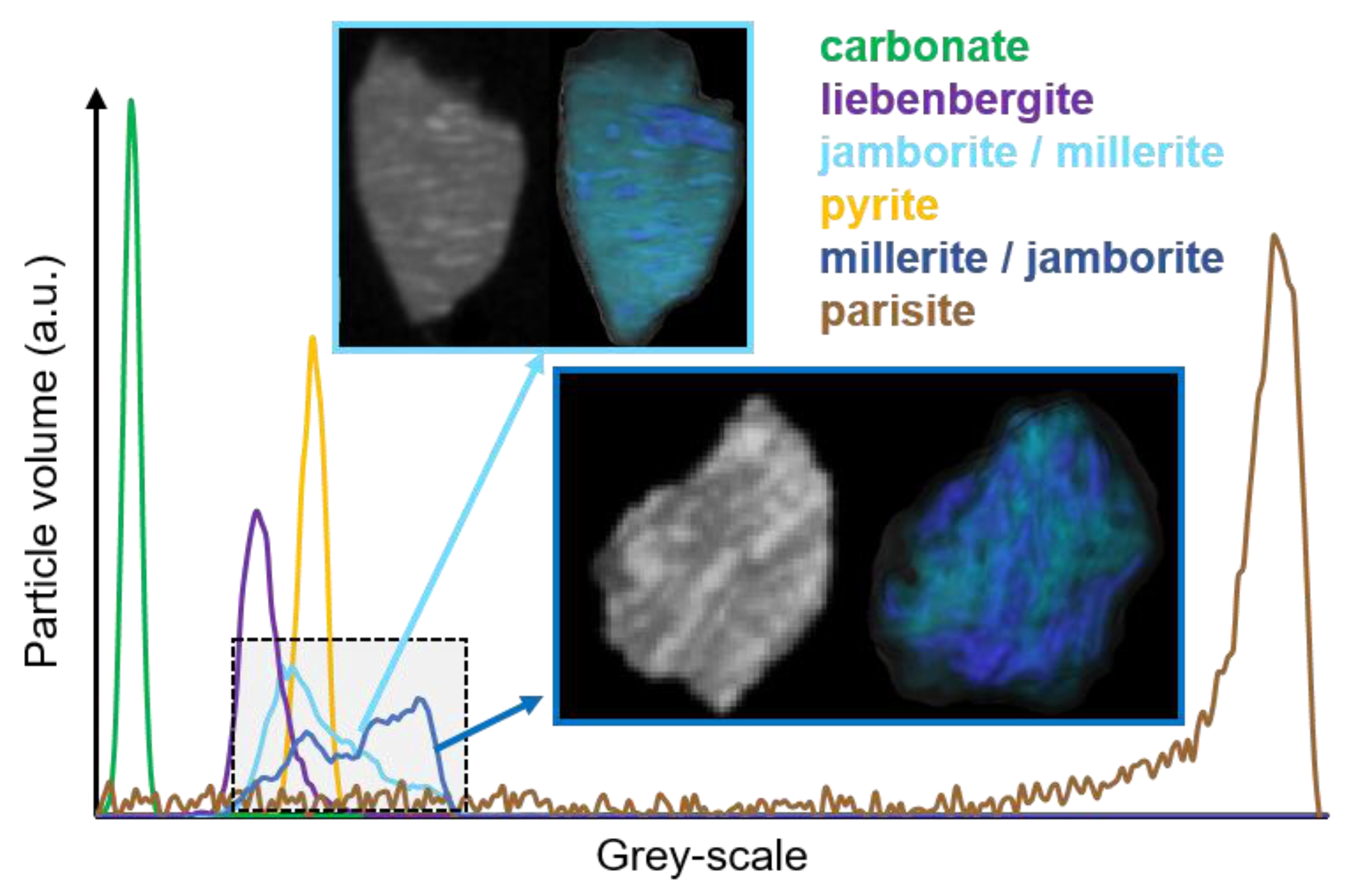
2.4.1. Carbonate Sample
2.4.2. Qz/Py Sample
2.4.3. Scheelite Ore
3. Results
3.1. Sample Preparation
3.2. Phase Classification in Individual Particles
3.2.1. Carbonate Sample
3.2.2. Qz/Py Sample
3.2.3. Scheelite Ore Sample
4. Discussion
4.1. Sample Preparation
4.2. Individual Particle Analysis
4.3. Phase Classification
4.4. Applications and Further Developments
- (1)
- To develop a systematic sample preparation procedure where the size of the spacer and the embedding material is determined by the size fraction of the sample’s particles.
- (2)
- To build a database for the hierarchical implementation of the selective criteria that can be used to classify a mineral, a group of minerals and/or the specific minerals and microstructures of a particular deposit. This could include developing a database of reference peak positions corresponding to a mineral. For instance, 2D/3D correlative methods could be used to classify specific phases in the 3D image of a reference material and stored as a database to be called every time another system with a similar composition is analyzed.
- (3)
- To automate the phase classification, by applying a set of defined criteria to all the particles.
- (4)
- To derive a particle/histogram-based method to quantify the mineralogical information contained in the histograms of the individual particles, which can be extrapolated to all particles in a sample. If these four developments can be realized, MSPaCMAn could be the foundation of semi-automated quantitative 3D mineral characterization methods.
5. Conclusions
6. Patents
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Role of Critical Minerals in Clean Energy Transitions; International Energy Agency: Paris, France. 2021. Available online: https://iea.blob.core.windows.net/assets/24d5dfbb-a77a-4647-abcc-667867207f74/TheRoleofCriticalMineralsinCleanEnergyTransitions.pdf (accessed on 2 August 2021).
- Ueda, T.; Oki, T.; Koyanaka, S. Experimental analysis of mineral liberation and stereological bias based on X-ray computed tomography and artificial binary particles. Adv. Powder Technol. 2018, 29, 462–470. [Google Scholar] [CrossRef]
- Reyes, F.; Lin, Q.; Cilliers, J.J.; Neethling, S.J. Quantifying mineral liberation by particle grade and surface exposure using X-ray microCT. Miner. Eng. 2018, 125, 75–82. [Google Scholar] [CrossRef]
- Blannin, R.; Frenzel, M.; Tuşa, L.; Birtel, S.; Ivăşcanu, P.; Baker, T.; Gutzmer, J. Uncertainties in quantitative mineralogical studies using scanning electron microscope-based image analysis. Miner. Eng. 2021, 167, 106836. [Google Scholar] [CrossRef]
- Pereira, L.; Frenzel, M.; Khodadadzadeh, M.; Tolosana-Delgado, R.; Gutzmer, J. A self-adaptive particle-tracking method for minerals processing. J. Clean. Prod. 2021, 279, 123711. [Google Scholar] [CrossRef]
- Schach, E.; Buchmann, M.; Tolosana-Delgado, R.; Leißner, T.; Kern, M.; van den Gerald Boogaart, K.; Rudolph, M.; Peuker, U.A. Multidimensional characterization of separation processes—Part 1: Introducing kernel methods and entropy in the context of mineral processing using SEM-based image analysis. Miner. Eng. 2019, 137, 78–86. [Google Scholar] [CrossRef]
- Parian, M.; Lamberg, P.; Rosenkranz, J. Developing a particle-based process model for unit operations of mineral processing—WLIMS. Int. J. Miner. Process. 2016, 154, 53–65. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Leißner, T.; Kern, M.; Mütze, T.; Rudolph, M.; Peuker, U.A.; Tolosana-Delgado, R. Multidimensional characterization of separation processes—Part 2: Comparability of separation efficiency. Miner. Eng. 2020, 150, 106284. [Google Scholar] [CrossRef]
- Furat, O.; Leißner, T.; Bachmann, K.; Gutzmer, J.; Peuker, U.; Schmidt, V. Stochastic Modeling of Multidimensional Particle Properties Using Parametric Copulas. Microsc. Microanal. 2019, 25, 720–734. [Google Scholar] [CrossRef] [Green Version]
- Hoang, D.H.; Kupka, N.; Peuker, U.A.; Rudolph, M. Flotation study of fine grained carbonaceous sedimentary apatite ore—Challenges in process mineralogy and impact of hydrodynamics. Miner. Eng. 2018, 121, 196–204. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Tolosana-Delgado, R.; Leißner, T.; Astoveza, J.; Kern, M.; Möckel, R.; Ebert, D.; Rudolph, M.; van den Boogaart, K.; et al. Evaluation of Magnetic Separation Efficiency on a Cassiterite-Bearing Skarn Ore by Means of Integrative SEM-Based Image and XRF–XRD Data Analysis. Minerals 2018, 8, 390. [Google Scholar] [CrossRef] [Green Version]
- Guntoro, P.I.; Ghorbani, Y.; Koch, P.-H.; Rosenkranz, J. X-ray Microcomputed Tomography (µCT) for Mineral Characterization: A Review of Data Analysis Methods. Minerals 2019, 9, 183. [Google Scholar] [CrossRef] [Green Version]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S.R. X-ray computed tomography. Nat. Rev. Methods Primers 2021, 51, 1–21. [Google Scholar] [CrossRef]
- Reyes, F.; Lin, Q.; Udoudo, O.; Dodds, C.; Lee, P.D.; Neethling, S.J. Calibrated X-ray micro-tomography for mineral ore quantification. Miner. Eng. 2017, 110, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.D.; Lin, C.L. X-ray tomography for mineral processing technology 3D particle characterization from mine to mill. Miner. Metall. Process. 2018, 35, 1–12. [Google Scholar] [CrossRef]
- Miller, J.D.; Lin, C.-L.; Hupka, L.; Al-Wakeel, M.I. Liberation-limited grade/recovery curves from X-ray micro CT analysis of feed material for the evaluation of separation efficiency. Int. J. Miner. Process. 2009, 93, 48–53. [Google Scholar] [CrossRef]
- Furat, O.; Leißner, T.; Ditscherlein, R.; Šedivý, O.; Weber, M.; Bachmann, K.; Gutzmer, J.; Peuker, U.; Schmidt, V. Description of Ore Particles from X-Ray Microtomography (XMT) Images, Supported by Scanning Electron Microscope (SEM)-Based Image Analysis. Microsc. Microanal. 2018, 24, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lin, C.L.; Miller, J.D. Quantitative analysis of exposed grain surface area for multiphase particles using X-ray microtomography. Powder Technol. 2017, 308, 368–377. [Google Scholar] [CrossRef]
- Guntoro, P.I.; Ghorbani, Y.; Parian, M.; Butcher, A.R.; Kuva, J.; Rosenkranz, J. Development and experimental validation of a texture-based 3D liberation model. Miner. Eng. 2021, 164, 106828. [Google Scholar] [CrossRef]
- Bauer, C.; Wagner, R.; Orberger, B.; Firsching, M.; Ennen, A.; Garcia Pina, C.; Wagner, C.; Honarmand, M.; Nabatian, G.; Monsef, I. Potential of Dual and Multi Energy XRT and CT Analyses on Iron Formations. Sensors 2021, 21, 2455. [Google Scholar] [CrossRef]
- Boas, F.E.; Fleischmann, D. CT artifacts: Causes and reduction techniques. Imaging Med. 2012, 4, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Neethling, S.J.; Dobson, K.J.; Courtois, L.; Lee, P.D. Quantifying and minimising systematic and random errors in X-ray micro-tomography based volume measurements. Comput. Geosci. 2015, 77, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Godinho, J.R.A.; Kern, M.; Renno, A.D.; Gutzmer, J. Volume quantification in interphase voxels of ore minerals using 3D imaging. Miner. Eng. 2019, 144, 106016. [Google Scholar] [CrossRef]
- Pankhurst, M.J.; Fowler, R.; Courtois, L.; Nonni, S.; Zuddas, F.; Atwood, R.C.; Davis, G.R.; Lee, P.D. Enabling three-dimensional densitometric measurements using laboratory source X-ray micro-computed tomography. SoftwareX 2018, 7, 115–121. [Google Scholar] [CrossRef]
- Voigt, M.; Miller, J.A.; Mainza, A.N.; Bam, L.C.; Becker, M. The Robustness of the Gray Level Co-Occurrence Matrices and X-Ray Computed Tomography Method for the Quantification of 3D Mineral Texture. Minerals 2020, 10, 334. [Google Scholar] [CrossRef] [Green Version]
- Godinho, J.R.A.; Westaway-Heaven, G.; Boone, M.A.; Renno, A.D. Spectral Tomography for 3D Element Detection and Mineral Analysis. Minerals 2021, 11, 598. [Google Scholar] [CrossRef]
- Ditscherlein, R.; Leißner, T.; Peuker, U.A. Preparation techniques for micron-sized particulate samples in X-ray microtomography. Powder Technol. 2020, 360, 989–997. [Google Scholar] [CrossRef]
- Ditscherlein, R.; Furat, O.; de Langlard, M.; Martins de Souza E Silva, J.; Sygusch, J.; Rudolph, M.; Leißner, T.; Schmidt, V.; Peuker, U.A. Multiscale Tomographic Analysis for Micron-Sized Particulate Samples. Microsc. Microanal. 2020, 26, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Dougherty, E.R. Mathematical Morphology in Image Processing, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781351830508. [Google Scholar]
- Bam, L.C.; Miller, J.A.; Becker, M.; De Beer, F.C.; Basson, I. (Eds.) X-ray Computed Tomography—Determination of Rapid Scanning Parameters for Geometallurgical Analysis of Iron Ore. In Proceedings of the Third ausimm International Geometallurgy Conference, Perth, Australia, 15–16 June 2016. [Google Scholar]
- Evans, C.L.; Napier-Munn, T.J. Estimating error in measurements of mineral grain size distribution. Miner. Eng. 2013, 52, 198–203. [Google Scholar] [CrossRef]
- Godinho, J.R.A.; Pereira, L. A Method and Device for 3D Analyzes of a Particulate Material. EP 21 158 241.6. 16 February 2021. [Google Scholar]
- Videla, A.R.; Lin, C.L.; Miller, J.D. 3D characterization of individual multiphase particles in packed particle beds by X-ray microtomography (XMT). Int. J. Miner. Process. 2007, 84, 321–326. [Google Scholar] [CrossRef]
- Da Wang, Y.; Shabaninejad, M.; Armstrong, R.T.; Mostaghimi, P. Physical Accuracy of Deep Neural Networks for 2D and 3D Multi-Mineral Segmentation of Rock micro-CT Images. arXiv 2002, arXiv:2002.05322v2. [Google Scholar]
- Alam, M.F.; Haque, A. A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils. Materials 2017, 10, 1195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bam, L.; Miller, J.; Becker, M. A Mineral X-ray Linear Attenuation Coefficient Tool (MXLAC) to Assess Mineralogical Differentiation for X-ray Computed Tomography Scanning. Minerals 2020, 10, 441. [Google Scholar] [CrossRef]
- Schulz, B.; Sandmann, D.; Gilbricht, S. SEM-Based Automated Mineralogy and Its Application in Geo- and Material Sciences. Minerals 2020, 10, 1004. [Google Scholar] [CrossRef]
- Sittner, J.; Godinho, J.R.A.; Renno, A.D.; Cnudde, V.; Boone, M.; de Schryver, T.; van Loo, D.; Merkulova, M.; Roine, A.; Liipo, J. Spectral X-ray computed micro tomography: 3-dimensional chemical imaging. X-ray Spectrom. 2021, 50, 92–105. [Google Scholar] [CrossRef]
- Warr, R.; Ametova, E.; Cernik, R.J.; Fardell, G.; Handschuh, S.; Jørgensen, J.S.; Papoutsellis, E.; Pasca, E.; Withers, P.J. Enhanced hyperspectral tomography for bioimaging by spatiospectral reconstruction. arXiv 2021, arXiv:2103.04796v1. [Google Scholar]
- Samson, I.M.; Wood, S.A.; Finucane, K. Fluid Inclusion Characteristics and Genesis of the Fluorite-Parisite Mineralization in the Snowbird Deposit, Montana. Econ. Geol. 2004, 99, 1727–1744. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Wang, Y.; Lin, C.L.; Miller, J.D. 3D image segmentation for analysis of multisize particles in a packed particle bed. Powder Technol. 2016, 301, 160–168. [Google Scholar] [CrossRef]

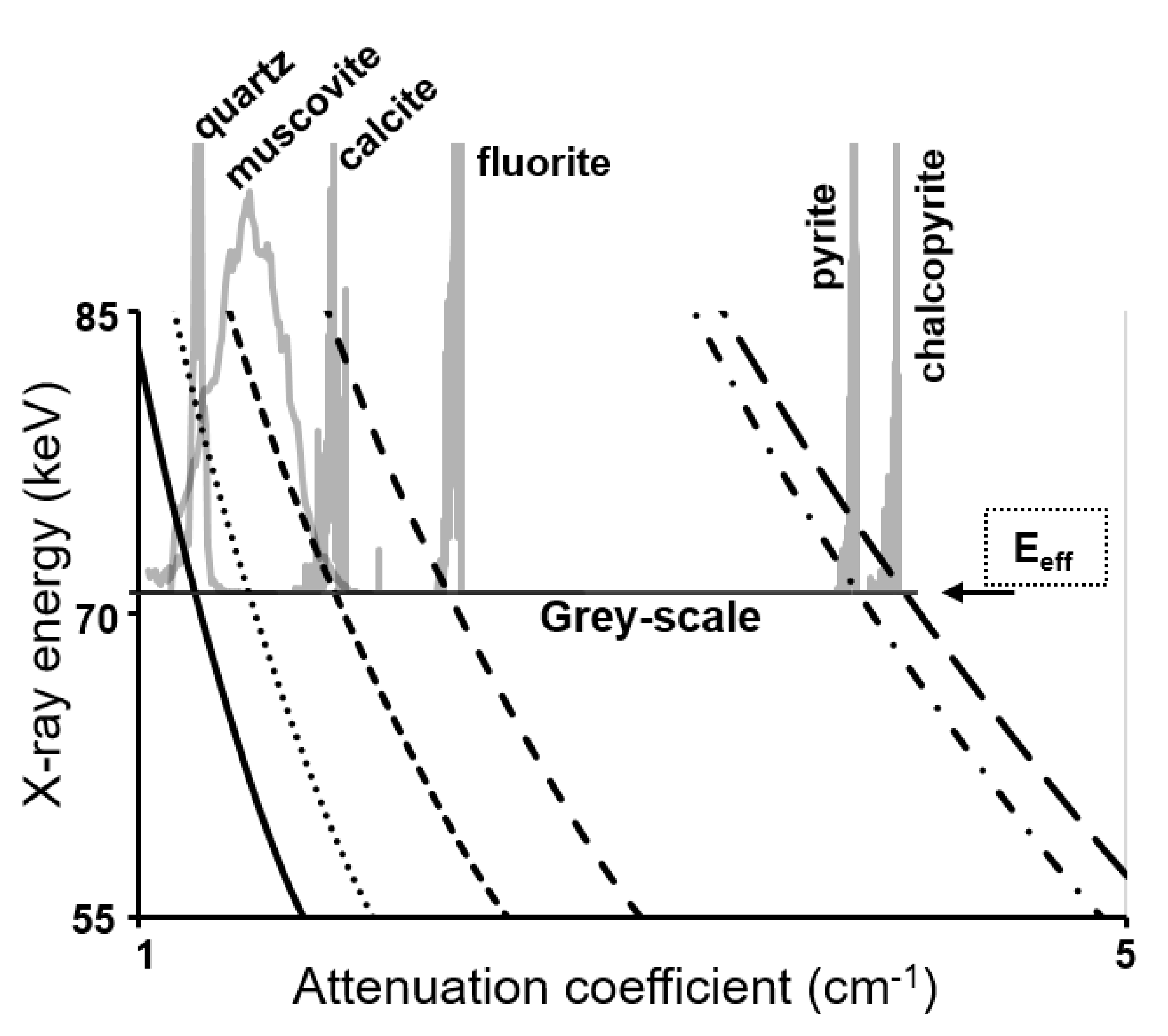
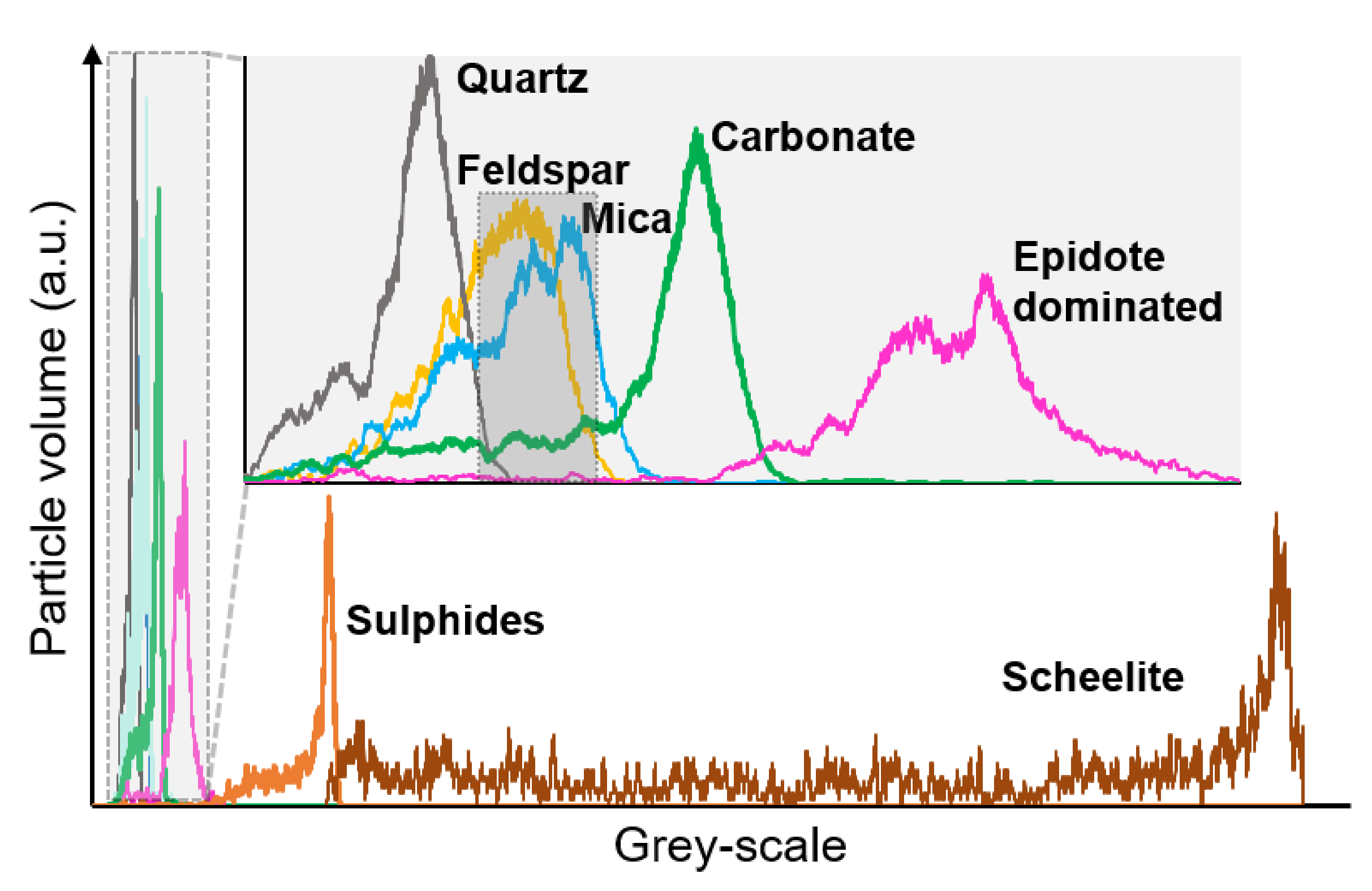


| Material | Main Minerals | Sample Size (µm) | Particles Size Fractions (mass ratios) | # Particles/Volume (particles·mm−3) | ParVox |
|---|---|---|---|---|---|
| Carbonate | Parisite Millerite Pyrite Liebenbergite Jamborite Carbonate | 100–500 | Material 13%; Sugar: 71–160 µm (50%), 160–300 µm (37%) | 20.3 | 25 |
| Qz/Py | Chalcopyrite Pyrite Fluorite/Epidote Calcite Muscovite Quartz | 315–425 | Material 12%; Sugar: <71 µm (44 %), 160–315 µm (22%); Graphite: 5–10 µm (22%) | 6.7 | 36 |
| Scheelite ore | Scheelite Sulphides Epidote/Chlorite Calcite Mica Feldspar Quartz | 150–200 | Material 14%; PMMA: <71 µm (15 %), 160–71 µm (32%), 315–160 µm (32%); Graphite: 5–10µm (8%) | 14.7 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godinho, J.R.A.; Grilo, B.L.D.; Hellmuth, F.; Siddique, A. Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn. Minerals 2021, 11, 947. https://doi.org/10.3390/min11090947
Godinho JRA, Grilo BLD, Hellmuth F, Siddique A. Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn. Minerals. 2021; 11(9):947. https://doi.org/10.3390/min11090947
Chicago/Turabian StyleGodinho, Jose R. A., Barbara L. D. Grilo, Friedrich Hellmuth, and Asim Siddique. 2021. "Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn" Minerals 11, no. 9: 947. https://doi.org/10.3390/min11090947
APA StyleGodinho, J. R. A., Grilo, B. L. D., Hellmuth, F., & Siddique, A. (2021). Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn. Minerals, 11(9), 947. https://doi.org/10.3390/min11090947







