Chemical Dissolution of Chalcopyrite Concentrate in Choline Chloride Ethylene Glycol Deep Eutectic Solvent
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mineral Characterization
2.2. Solvent Preparation and Characterization
2.3. Dissolution Conditions
2.4. Analytical Methods
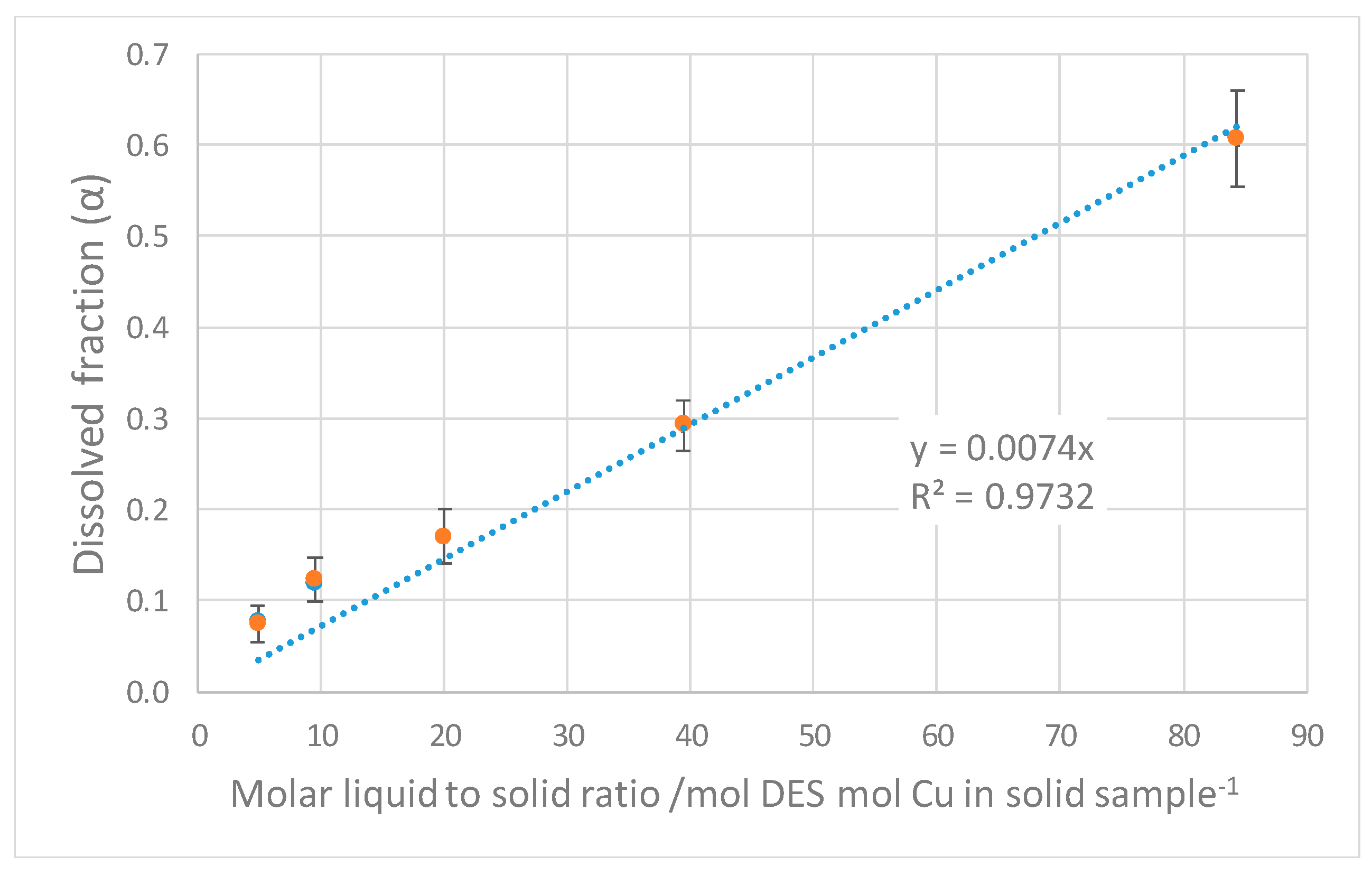
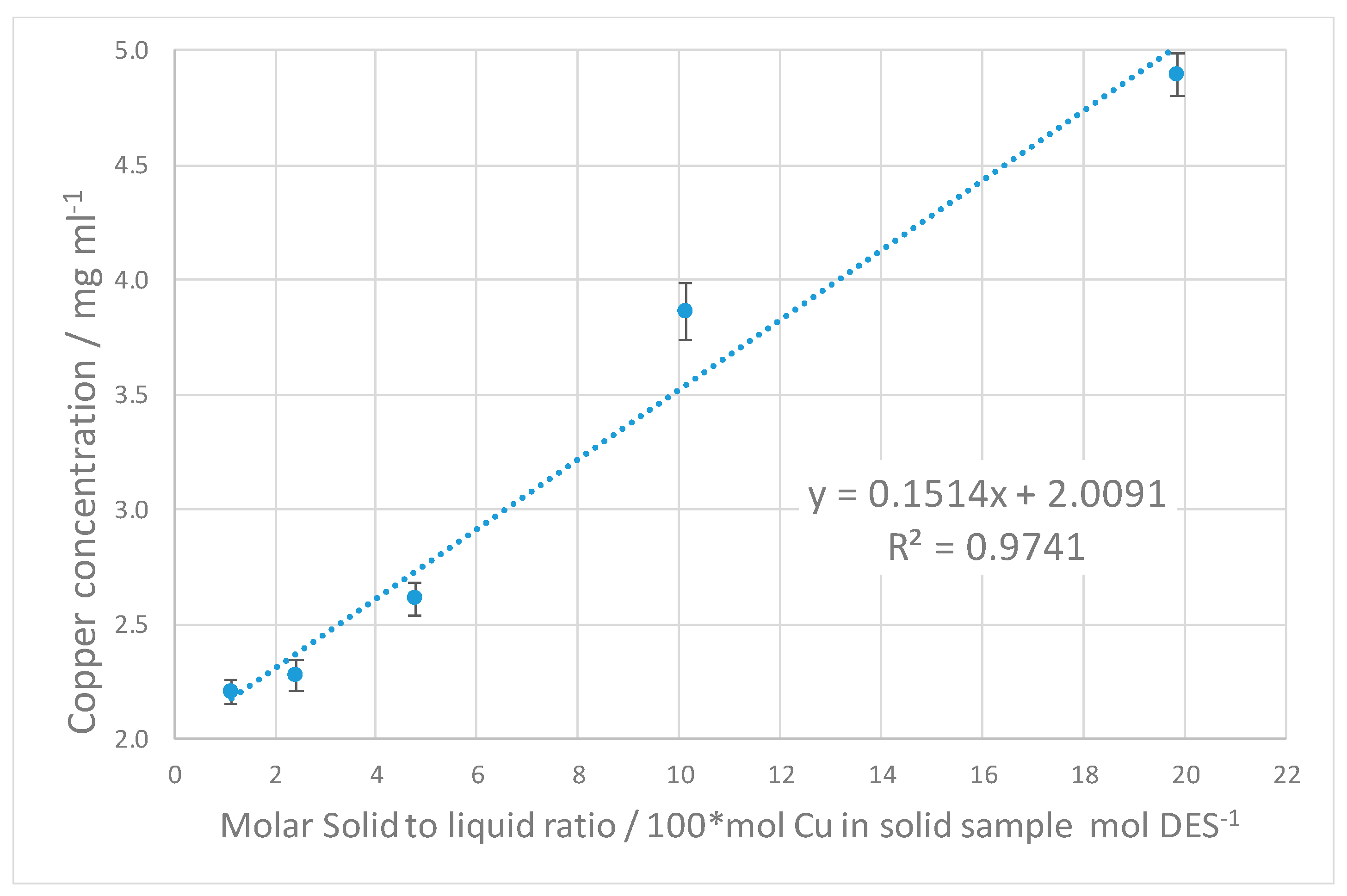
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

- The models are applicable for mono-sized particles or particles on a narrow size range. In this particular case of study, the particles come from a froth flotation process fulfilling this requirement
- The model does not consider the operative variables as stirring conditions, temperature, and chemical changes in the solvent in a straightforward way. All these factors affect the constant kD.
- The model does not allow to evaluate directly the ligand effect of the solvent, which must be relevant in this case
References
- Chen, J.; Wang, Z.; Wu, Y.; Li, L.; Li, B.; Pan, D.; Zuo, T. Environmental benefits of secondary copper from primary copper based on life cycle assessment in China. Resour. Conserv. Recycl. 2019, 146, 35–44. [Google Scholar] [CrossRef]
- Schipper, B.W.; Lin, H.C.; Meloni, M.A.; Wansleeben, K.; Heijungs, R.; van der Voet, E. Estimating global copper demand until 2100 with regression and stock dynamics. Resour. Conserv. Recycl. 2018, 132, 28–36. [Google Scholar] [CrossRef]
- Crundwell, F.K. The dissolution and leaching of minerals: Mechanisms, myths and misunderstandings. Hydrometallurgy 2013, 139, 132–148. [Google Scholar] [CrossRef]
- Córdoba, E.M.; Muñoz, J.A.; Blázquez, M.L.; González, F.; Ballester, A. Leaching of chalcopyrite with ferric ion. Part II: Effect of redox potential. Hydrometallurgy 2008, 93, 88–96. [Google Scholar] [CrossRef]
- Holmes, P.R.; Crundwell, F.K. Polysulfides do not cause passivation: Results from the dissolution of pyrite and implications for other sulfide minerals. Hydrometallurgy 2013, 139, 101–110. [Google Scholar] [CrossRef]
- Jorjani, E.; Ghahreman, A. Challenges with elemental sulfur removal during the leaching of copper and zinc sulfides, and from the residues: A review. Hydrometallurgy 2017, 171, 333–343. [Google Scholar] [CrossRef]
- Shin, D.; Ahn, J.; Lee, J. Kinetic study of copper leaching from chalcopyrite concentrate in alkaline glycine solution. Hydrometallurgy 2019, 183, 71–78. [Google Scholar] [CrossRef]
- Crundwell, F.K. The mechanism of dissolution of minerals in acidic and alkaline solutions: Part IV—Equilibrium and near-equilibrium behaviour. Hydrometallurgy 2015, 153, 46–57. [Google Scholar] [CrossRef]
- Crundwell, F.K. The mechanism of dissolution of minerals in acidic and alkaline solutions: Part I—A new theory of non-oxidation dissolution. Hydrometallurgy 2014, 149, 252–264. [Google Scholar] [CrossRef]
- Binnemans, K.; Jones, P.T. Solvometallurgy: An emerging branch of extractive metallurgy. J. Sustain. Metall. 2017, 3, 570–600. [Google Scholar] [CrossRef] [Green Version]
- Abbott, A.P.; Frisch, G.; Gurman, S.J.; Hillman, A.R.; Hartley, J.; Holyoak, F.; Ryder, K.S. Ionometallurgy: Designer redox properties for metal processing. Chem. Commun. 2011, 47, 10031–10033. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.L.; Abbott, A.P.; Ryder, K.S. Deep Eutectic Solvents (DESs) and their applications. Chem. Rev. 2014, 114, 11060–11082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carlesi, C.; Cortes, E.; Dibernardi, G.; Morales, J.; Muñoz, E. Ionic liquids as additives for acid leaching of copper from sulfidic ores. Hydrometallurgy 2016, 161, 29–33. [Google Scholar] [CrossRef]
- Dong, T.; Hua, Y.; Zhang, Q.; Zhou, D. Leaching of chalcopyrite with Brønsted acidic ionic liquid. Hydrometallurgy 2009, 99, 33–38. [Google Scholar] [CrossRef]
- Whitehead, J.A.; Zhang, J.; Pereira, N.; McCluskey, A.; Lawrance, G.A. Application of 1-alkyl-3-methyl-imidazolium ionic liquids in the oxidative leaching of sulphidic copper, gold and silver ores. Hydrometallurgy 2007, 88, 109–120. [Google Scholar] [CrossRef]
- Jenkin, G.R.T.; Al-Bassam, A.Z.M.; Harris, R.C.; Abbott, A.P.; Smith, D.J.; Holwell, D.A.; Chapman, R.J.; Stanley, C.J. The application of deep eutectic solvent ionic liquids for environmentally-friendly dissolution and recovery of precious metals. Miner. Eng. 2016, 87, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Anggara, S.; Bevan, F.; Harris, R.C.; Hartley, J.M.; Frisch, G.; Jenkin, G.R.T.; Abbott, A.P. Direct extraction of copper from copper sulfide minerals using deep eutectic solvents. Green Chem. 2019, 21, 6502–6512. [Google Scholar] [CrossRef]
- Hammond, O. Deep Eutectic Solvent: Sructure, Solvation and Synhesis. Ph.D. Thesis, University of Bath, Bath, UK, 2019. [Google Scholar]
- Xie, Y.; Dong, H.; Zhang, S.; Lu, X.; Ji, X. Effect of water on the density, viscosity, and CO2 solubility in choline chloride/urea. J. Chem. Eng. Data 2014, 59, 3344–3352. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, D.; Chen, W.; Fu, L.; Mu, T. Water absorption by deep eutectic solvents. Phys. Chem. Chem. Phys. 2019, 21, 2601–2610. [Google Scholar] [CrossRef]
- Carlesi, C.; Guajardo, N.; Schrebler, R.; Vasquez-Sandoval, D. Greener gas capture in deep eutectic solvents aqueous solutions: Performance in a dynamic condition. J. Clean. Prod. 2019, 240, 118240. [Google Scholar] [CrossRef]
- Abbott, A.P.; Alabdullah, S.S.M.; Al-Murshedi, A.Y.M.; Ryder, K.S. Brønsted acidity in deep eutectic solvents and ionic liquids. Faraday Discuss. 2018, 206, 365–377. [Google Scholar] [CrossRef]
- Skulcova, A.; Russ, A.; Jablonsky, M.; Sima, J. The pH behavior of seventeen deep eutectic solvents. BioResources 2019, 13, 5042–5051. [Google Scholar] [CrossRef]
- Abbott, A.P.; Capper, G.; Davies, D.L.; McKenzie, K.J.; Obi, S.U. Solubility of metal oxides in deep eutectic solvents based on choline chloride. J. Chem. Eng. Data 2006, 51, 1280–1282. [Google Scholar] [CrossRef]
- Greenz, T.A.; Valverde, P.; Roy, S. Anodic reactions and the corrosion of copper in deep eutectic solvents. J. Electrochem. Soc. 2018, 165, D313–D320. [Google Scholar] [CrossRef]
- Tang, J.; Xu, C.; Zhu, X.; Liu, H.; Wang, X.; Huang, M.; Hua, Y.; Zhang, Q.; Li, Y. Anodic dissolution of copper in choline chloride-urea deep eutectic solvent. J. Electrochem. Soc. 2018, 165, E406–E411. [Google Scholar] [CrossRef]
- Doche, M.L.; Mandroyan, A.; Mourad-Mahmoud, M.; Moutarlier, V.; Hihn, J.Y. An ultrasonic-assisted process for copper recovery in a DES solvent: Leaching and re-depositation. Chem. Eng. Process. Process Intensif. 2017, 121, 90–96. [Google Scholar] [CrossRef]
- De Vreese, P.; Brooks, N.R.; van Hecke, K.; van Meervelt, L.; Matthijs, E.; Binnemans, K.; van Deun, R. Speciation of copper(II) complexes in an ionic liquid based on choline chloride and in choline chloride/water mixtures. Inorg. Chem. 2012, 51, 4972–4981. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Cao, Y.; Harjanto, S.; Shibayama, A.; Naitoh, I.; Nanami, T.; Kasahara, K.; Okumura, Y.; Fujita, T. Kinetic study on the leaching of Pt, Pd and Rh from automotive catalyst residue by using chloride solutions. Mat. Transact. 2015, 47, 2015–2024. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.V.; Khaddour, I.A.; Gupta, V.K. A pseudo second-order kinetic expression for dissolution kinetic profiles of solids in solutions. Ind. Eng. Chem. Res. 2010, 49, 7257–7262. [Google Scholar] [CrossRef]
- Kuzmina, O.; Symianakis, E.; Godfrey, D.; Albrecht, T.; Welton, T. Ionic liquids for metal extraction from chalcopyrite: Solid, liquid and gas phase studies. Phys. Chem. Chem. Phys. 2017, 19, 21556–21564. [Google Scholar] [CrossRef] [PubMed]
- Havlik, T. Microwave leaching of chalcopyrite—Possible improvement in hydrometallurgy. Metall 2010, 64, 236–239. [Google Scholar]
- Abbott, A.P.; El Ttaib, K.; Frisch, G.; Mckenzie, K.J.; Ryder, K.S. Electrodeposition of copper composites from deep eutectic solvents based on choline chloride. Phys. Chem. Chem. Phys. 2009, 11, 4269–4277. [Google Scholar] [CrossRef] [PubMed]




| Sulfides | Oxides | ||||
|---|---|---|---|---|---|
| Component | Chemical Formulae | wt (%) | Component | Chemical Formulae | wt (%) |
| Chalcopyrite | CuFeS2 | 72.182 | Magnetite/Hematite/Goethite | Fe3O4/Fe2O3/FeO(OH) | 0.137 |
| Bornite | Cu5FeS4 | 0.574 | Alumo-goethite/Harrisonite | Fe(Al)O(OH)/CaFe6(SiO4)2(PO4)2 | 0.020 |
| Covellite | CuS | 0.143 | Rutile | TiO2 | 0.479 |
| Chalcocite | Cu2S/Cu5S2 | 0.131 | Ilmenite | FeTiO3 | 0.024 |
| Enargite | Cu3AsS4 | 0.251 | Total Oxides | 0.660 | |
| Tennantite | Cu11FeAs4S13 | 3.509 | |||
| Pyrite | FeS2 | 9.994 | |||
| Sphalerite | Zn0.9Fe0.05S | 0.369 | |||
| Arsenopyrite | FeAsS | 0.004 | |||
| Molybdenite | MoS2 | 1.568 | |||
| Other Sulfides | 0.154 | ||||
| Total Sulfides | 88.879 | ||||
| Component | Weight Percentage (%) |
|---|---|
| Quartz | 2.243 |
| K-Feldspar | 1.805 |
| Albite | 0.711 |
| Zoisite | 0.002 |
| Tourmaline | 0.420 |
| Amphiboles | 0.025 |
| Muscovite | 3.637 |
| Biotite | 0.432 |
| Kaolinite | 0.226 |
| Montmorillonite | 0.057 |
| Other clays | 0.011 |
| Chlorites | 0.214 |
| Zircon | 0.057 |
| Titanite | 0.001 |
| Calcite | 0.036 |
| Dolomite | 0.065 |
| Mn-siderite | 0.393 |
| Anhydrite | 0.018 |
| Jarosite | 0.002 |
| Other sulfates | 0.005 |
| Apatite | 0.091 |
| Other phosphates | 0.007 |
| Others minor components | 0.004 |
| Total gangue | 10.462 |
| Temperature (°C) | 19.5 | 50 | 80 | 90 |
|---|---|---|---|---|
| Slope of linear regression | 0.875 | 0.563 | 0.405 | 0.377 |
| Intercept of linear regression | 10.93 | 7.95 | 6.40 | 6.28 |
| Maximum dissolution fraction [αs] | 0.0915 | 0.126 | 0.156 | 0.159 |
| Apparent kinetic constant [k] (s−1) | 0.208 | 0.235 | 0.263 | 0.277 |
| Coefficient of correlation [R2] | 0.929 | 0.994 | 0.976 | 0.979 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlesi, C.; Harris, R.C.; Abbott, A.P.; Jenkin, G.R.T. Chemical Dissolution of Chalcopyrite Concentrate in Choline Chloride Ethylene Glycol Deep Eutectic Solvent. Minerals 2022, 12, 65. https://doi.org/10.3390/min12010065
Carlesi C, Harris RC, Abbott AP, Jenkin GRT. Chemical Dissolution of Chalcopyrite Concentrate in Choline Chloride Ethylene Glycol Deep Eutectic Solvent. Minerals. 2022; 12(1):65. https://doi.org/10.3390/min12010065
Chicago/Turabian StyleCarlesi, Carlos, Robert C. Harris, Andrew P. Abbott, and Gawen R. T. Jenkin. 2022. "Chemical Dissolution of Chalcopyrite Concentrate in Choline Chloride Ethylene Glycol Deep Eutectic Solvent" Minerals 12, no. 1: 65. https://doi.org/10.3390/min12010065
APA StyleCarlesi, C., Harris, R. C., Abbott, A. P., & Jenkin, G. R. T. (2022). Chemical Dissolution of Chalcopyrite Concentrate in Choline Chloride Ethylene Glycol Deep Eutectic Solvent. Minerals, 12(1), 65. https://doi.org/10.3390/min12010065






