Shape from Shading-Based Study of Silica Fusion Characterization Problems
Abstract
:1. Introduction
2. Related Works
3. Model
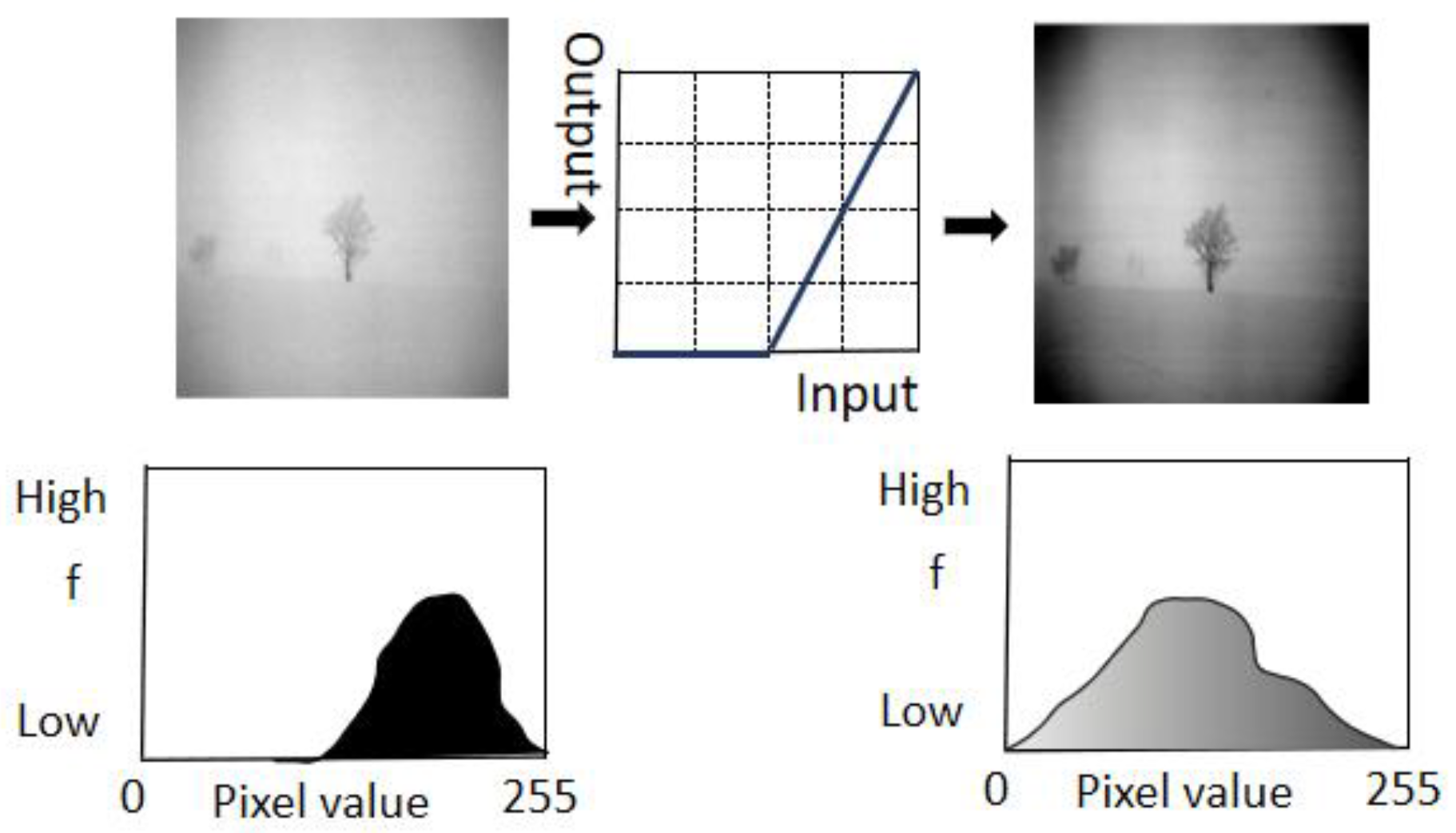
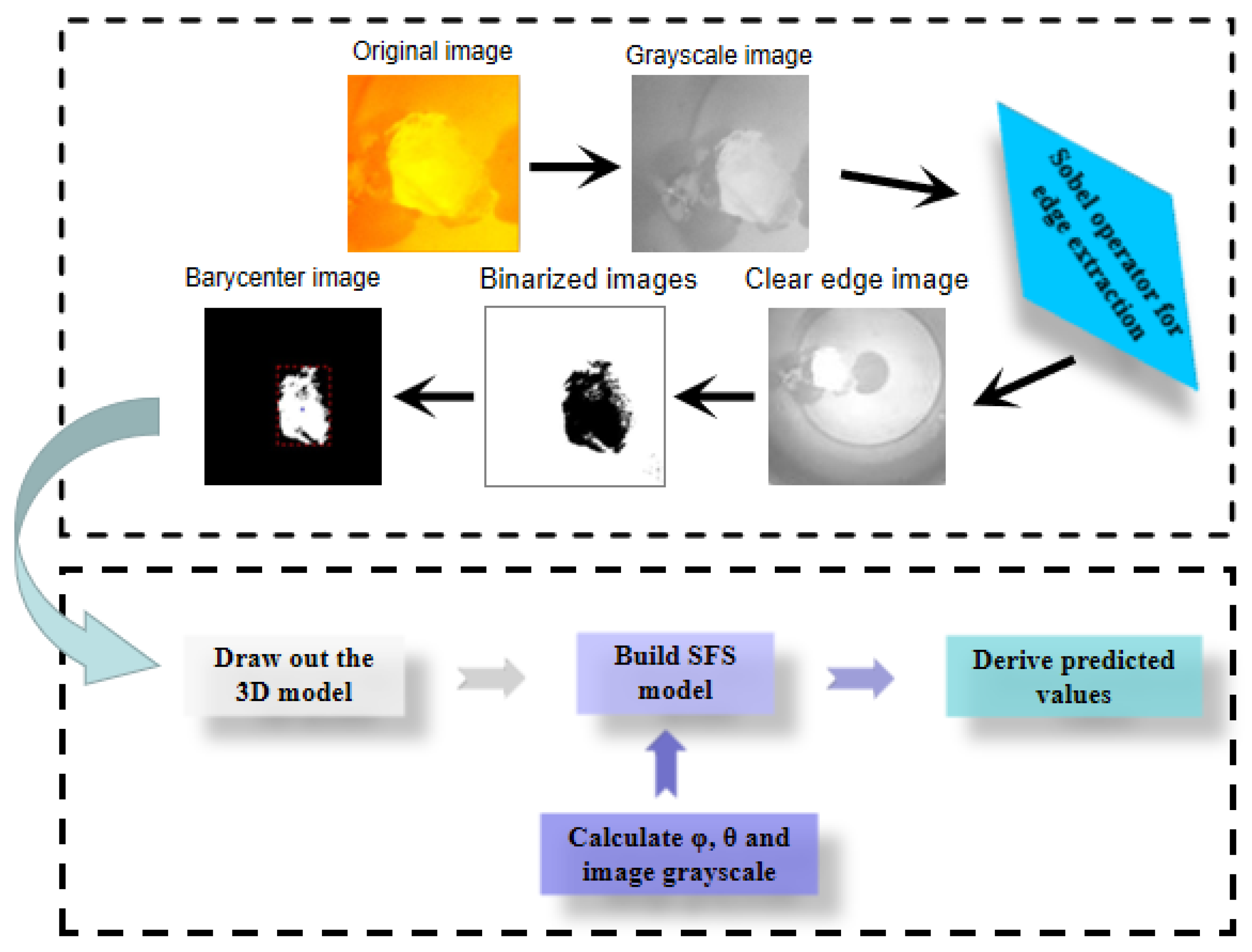
3.1. Image Pre-Processing
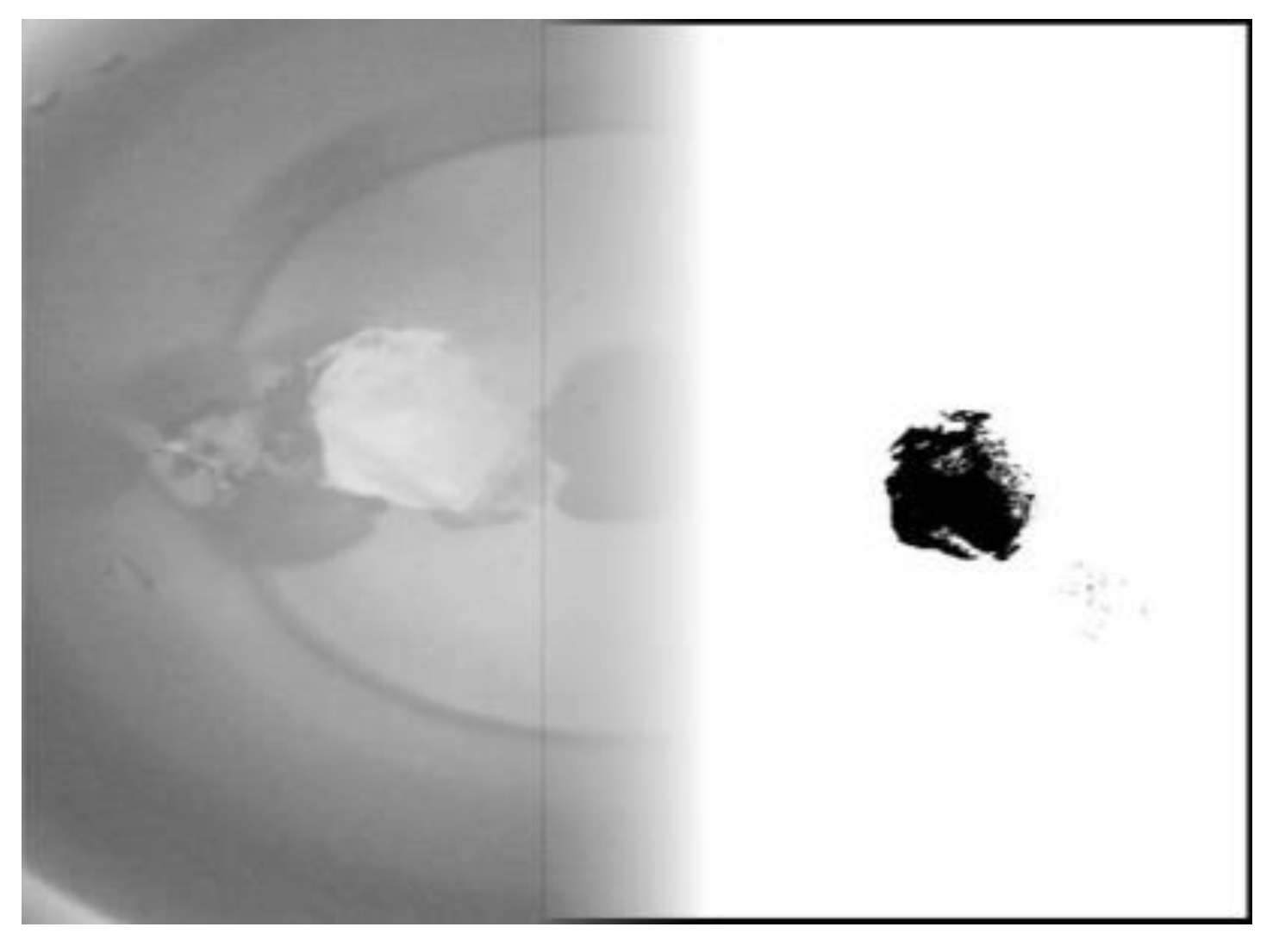
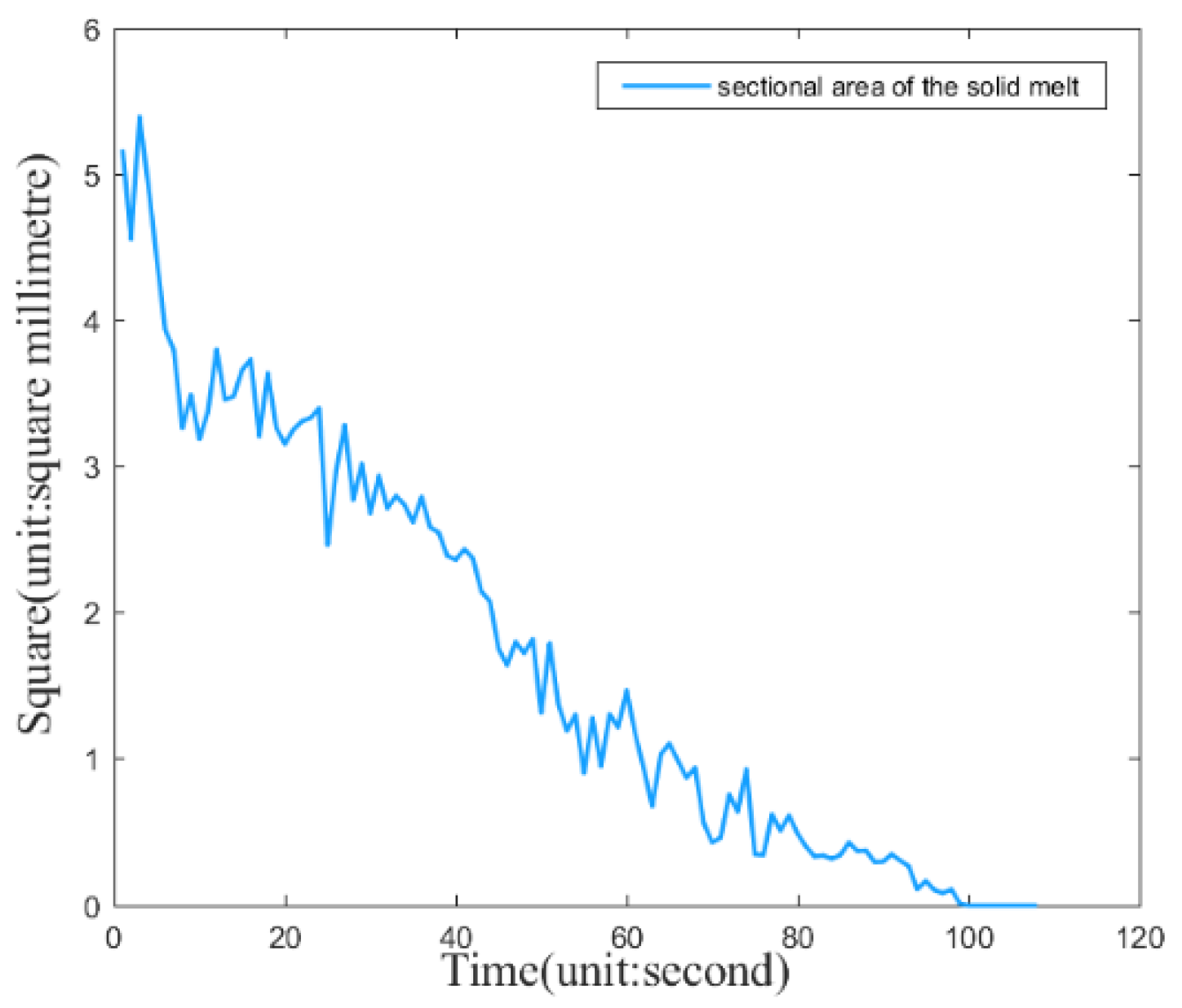
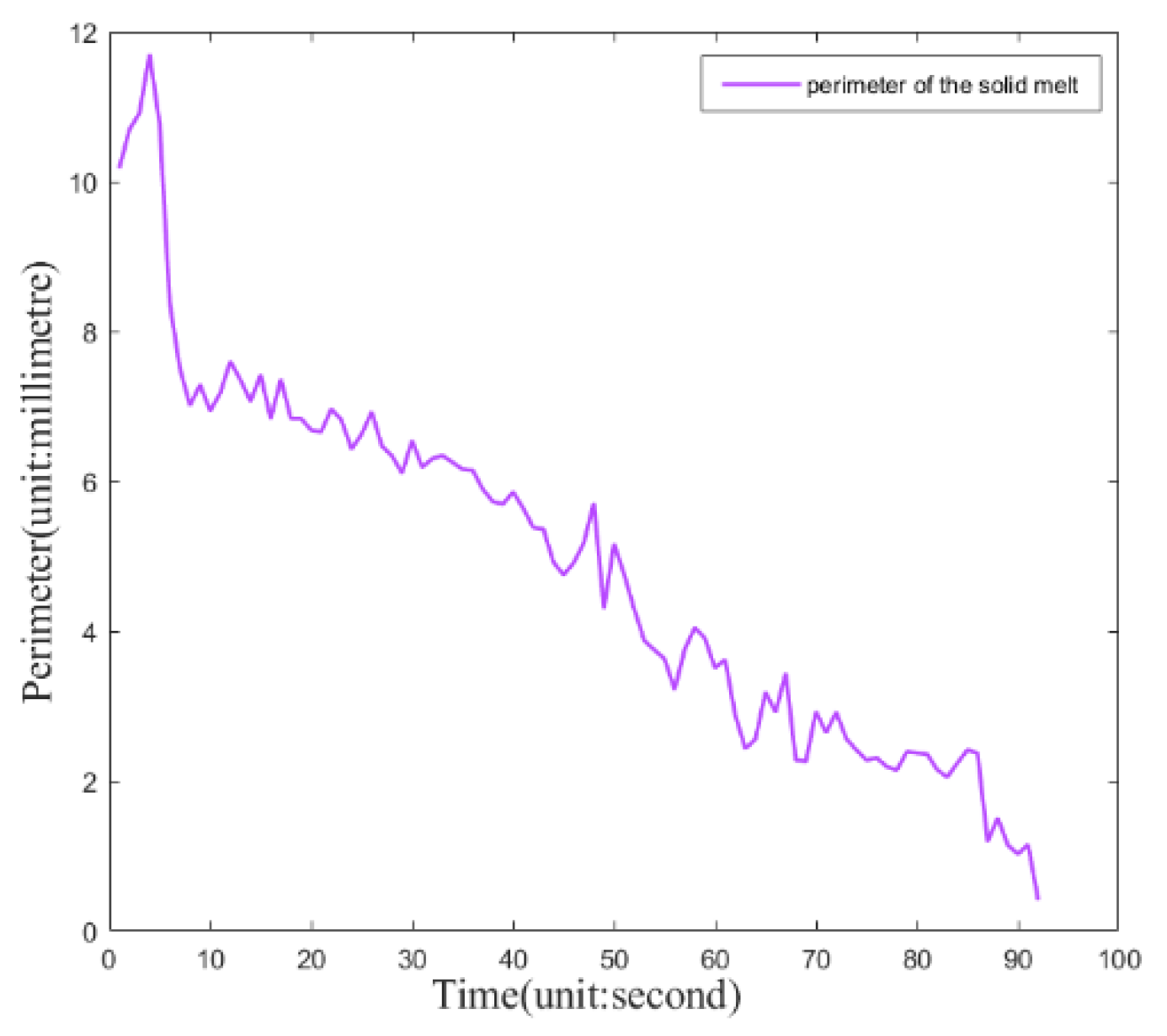
3.2. Indicators of the Trajectory and Edge Profile Characteristics of the Silicon Dioxide Plasmas
3.3. Theoretical Knowledge of the SFS Model
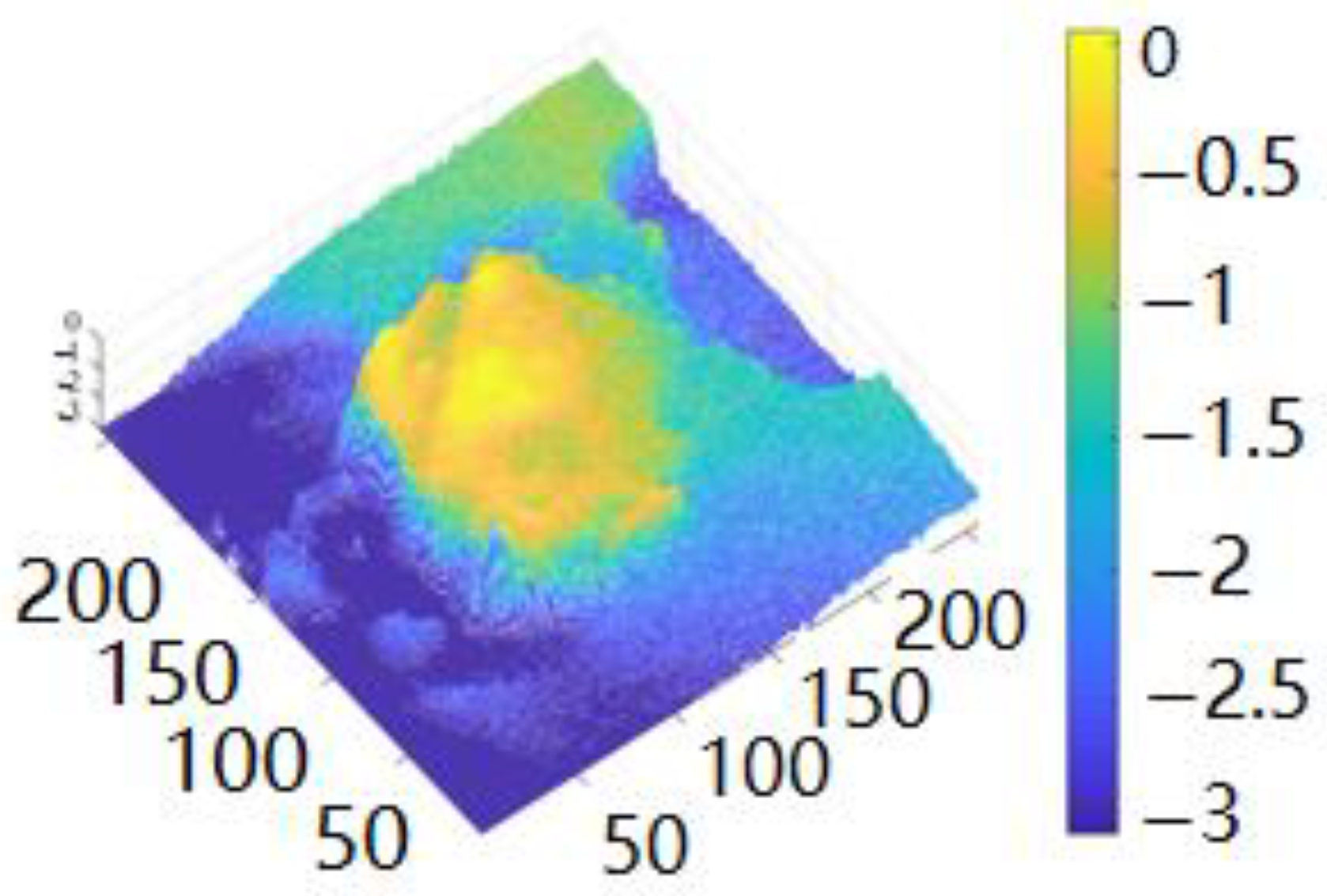
3.4. SFS Model Building
4. Model Analysis
5. Model Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bose, B.; Davis, C.R.; Erk, K.A. Microstructural refinement of cement paste internally cured by polyacrylamide composite hydrogel particles containing silica fume and nanosilica. Cem. Concr. Res. 2021, 143, 106400. [Google Scholar] [CrossRef]
- Iyer, K.A.; Hu, Y.; Klose, T.; Murayama, T.; Samso, M. Structural characterization of MH/CCD NTD mutations in skeletal ryanodine receptor by cryo-EM. Biophys. J. 2022, 121, 91a–92a. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.Q.; Han, Y.; Liu, W.X.; Yang, A.M.; Li, F.; Li, D.L. Dynamic Compensation Model of BF Slag Homogenization Thermal Based on Advanced Deep Learning Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 4107–4116. [Google Scholar] [CrossRef]
- Gao, P.; Song, Y.; Song, M.; Qian, P.; Su, Y. Extract nanoporous gold ligaments from SEM images by combining fully convolutional network and Sobel operator edge detection algorithm. Scr. Mater. 2022, 213, 114627. [Google Scholar] [CrossRef]
- Yang, A.; Li, S.; Lin, H.; Jin, D. Edge extraction of mineralogical phase based on fractal theory. Chaos Solitons Fractals Interdiscip. J. Nonlinear Sci. Nonequilibrium Complex Phenom. 2018, 117, 215221. [Google Scholar]
- Lester, C.; Geonzon, S.M. Accuracy improvement of centroid coordinates and particle identification in particle tracking technique. J. Biorheol. 2019, 33, 2–7. [Google Scholar]
- Yang, X.; Lu, D.; Zhu, B.; Sun, Z.; Li, G.; Li, J.; Liu, Q.; Jiang, G. Phase transformation of silica particles in coal and biomass combustion processes. Environ. Pollut. 2022, 292, 118312. [Google Scholar] [CrossRef]
- Cao, Y.-L. Research on the Bimetallic Composite Roll Produced by the Electroslag Cladding Method; Northeastern University: Boston, MA, USA, 2018. [Google Scholar] [CrossRef]
- Wang, D.-q.; Ma, Z.-j.; Chen, H.; Wang, W.; Zhu, W.C. Thermodynamic analysis of reducing MgO content in slag for blast furnace A in Shougang. China Metall. 2018, 28, issn1006–issn9356. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.; Yang, X.-L.; Liu, W.-X. Dynamic Prediction Research of Silicon Content in Hot Metal Driven by Big Data in Blast Furnace Smelting Process under Hadoop Cloud Platform. Complexity 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Peng, H.; Zhang, L.; Hu, Y.; Su, H. Neural fuzzy approximation enhanced autonomous tracking control of the wheel-legged robot under uncertain physical interaction. Neurocomputing 2020, 410, 342–353. [Google Scholar] [CrossRef]
- Narlagiri, L.M.; Rao, S.V. Correction to: Identification of metals and alloys using color CCD images of laser-induced breakdown emissions coupled with machine learning. Appl. Phys. B 2020, 126, 1. [Google Scholar] [CrossRef]
- Arora, S.; Chaudhary, N. Gray Image and Colour Image Security using AES Algorithm. IOP Conf.Ser. Mater. Sci. Eng. 2022, 1224, 12024. [Google Scholar] [CrossRef]
- Putriany, D.M.; Rachmawati, E.; Sthevanie, F. Indones-ian Ethnicity Recognition Based on Face Image Using Gray Level Co-occurrence Matrix and Color Histogram. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1077, 12040. [Google Scholar] [CrossRef]
- Chatterjee, J.; Bhattacharyya, R.; Maulik, A.; Palodhi, K. Application of Machine Learning on sequential deconvolution and convolution techniques for analysis of images from Nuclear Track Detectors (NTDs). Radiat. Meas. 2021, 144, 106581. [Google Scholar] [CrossRef]
- Asha, J.; Kamalraj, S. High-capacity reversible data hiding using quotient multi pixel value differencing scheme in encrypted images by fuzzy based encryption. Multimed. Tools Appl. 2021, 80, 1–27. [Google Scholar]
- Jacobs, B.A.; Celik, T. Unsupervised document image binarization using a system of nonlinear partial differential equations. Appl. Math. Comput. 2022, 418, 126806. [Google Scholar] [CrossRef]
- Mendonça, L.S.M.; Braun, P.X.; Martin, S.M.; Hüther, A.; Mehta, N.; Zhao, Y.; Abu-Qamar, O.; Konstantinou, E.K.; Regatieri, C.V.S.; Witkin, A.J.; et al. Repeatability and Reproducibility of Photoreceptor Density Measurement in the Macula Using the Spectralis High Magnification Module. Ophthalmol. Retin. 2020, 4, 1083–1092. [Google Scholar] [CrossRef] [PubMed]
- Sarki, R.; Ahmed, K.; Wang, H.; Zhang, Y.; Ma, J.; Wang, K. Image Preprocessing in Classification and Identification of Diabetic Eye Diseases. Data Sci. Eng. 2021, 6, 11–17. [Google Scholar] [CrossRef]
- Ravivarma, G.; Gavaskar, K.; Malathi, D.; Asha, K.G.; Aarthi, S. Implementation of Sobel operator based image edge detection on FPGA. Mater. Today Proc. 2021, 45, 2401–2407. [Google Scholar] [CrossRef]
- Vafa, A.P.; Karimi, P.; Khavasi, A. Analog optical edge detection by spatial high-pass filtering using litho-graphyfree structures. Opt. Commun. 2021, 495, 127084. [Google Scholar] [CrossRef]
- Ortega, P.P.P.; Ortiz, O.R.D.; Marin, R.A.M. Hyperbolic Center of Mass for a System of Particles in a Two-Dimensional Space with Constant Negative Curvature: An Application to the Curved 2-Body Problem. Mathematics 2021, 9, 531. [Google Scholar] [CrossRef]
- Girdhar, G.L.; Ravi, K.S.P. An efficient distance estimation and centroid selection based on k-means clustering for small and large dataset. Int. J. Adv. Technol. Eng. Explor. 2020, 7, 234–240. [Google Scholar]
- Chaurasia, V.; Pandey, M.K.; Pal, S. Prediction of Presence of Breast Cancer Disease in the Patient using Machine Learning Algorithms and SFS. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1099, 12003. [Google Scholar] [CrossRef]
- Toda, A.; Taguchi, K.; Nozaki, K. Fast limiting behavior of the melting kinetics of polyethylene crystals examined by fast-scan calorimetry. Thermochim. Acta 2019, 677, 211–216. [Google Scholar] [CrossRef]
- Mahrous, A.; Elgreatly, A.; Qian, F.; Schneider, G.B. A comparison of pre-clinical instructional technologies: Natural teeth, 3D models, 3D printing, and augmented reality. J. Dent. Educ. 2021, 85, 1795–1801. [Google Scholar] [CrossRef]
- Sahlstrom, T.; Pulkkinen, A.; Leskinen, J.; Tarvainen, T. Computationally Efficient Forward Operator for Photoacoustic Tomography Based on Coordinate Transformations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021, 68, 2172–2182. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, W.; Cho, H. Lambertian Extraction of Light from Organic Light-Emitting Devices Using Randomly Dispersed Sub-Wavelength Pillar Arrays. J. Nanosci. Nanotechnol. 2021, 21, 3909–3913. [Google Scholar] [CrossRef]
- Kang, K.; Kushnarev, S.; Pin, W.W.; Ortiz, O.; Shihang, J.C. Impact of Virtual Reality on the Visualization of Partial Derivatives in a Multivariable Calculus Class. IEEE Access 2020, 8, 58940–58947. [Google Scholar] [CrossRef]
- Davids, P.S. Normal vector approach to Fourier modal scattering from planar periodic photonic structures. Photonics Nanostructures Fundam. Appl. 2021, 43, 100864. [Google Scholar] [CrossRef]
- Brambach, M.; Ernst, A.; Nolbrant, S.; Drouin-Ouellet, J.; Kirkeby, A.; Parmar, M.; Olariu, V. Neural tube patterning: From a minimal model for rostrocaudal patterning toward an integrated 3D model. iScience 2021, 24, 102559. [Google Scholar] [CrossRef]





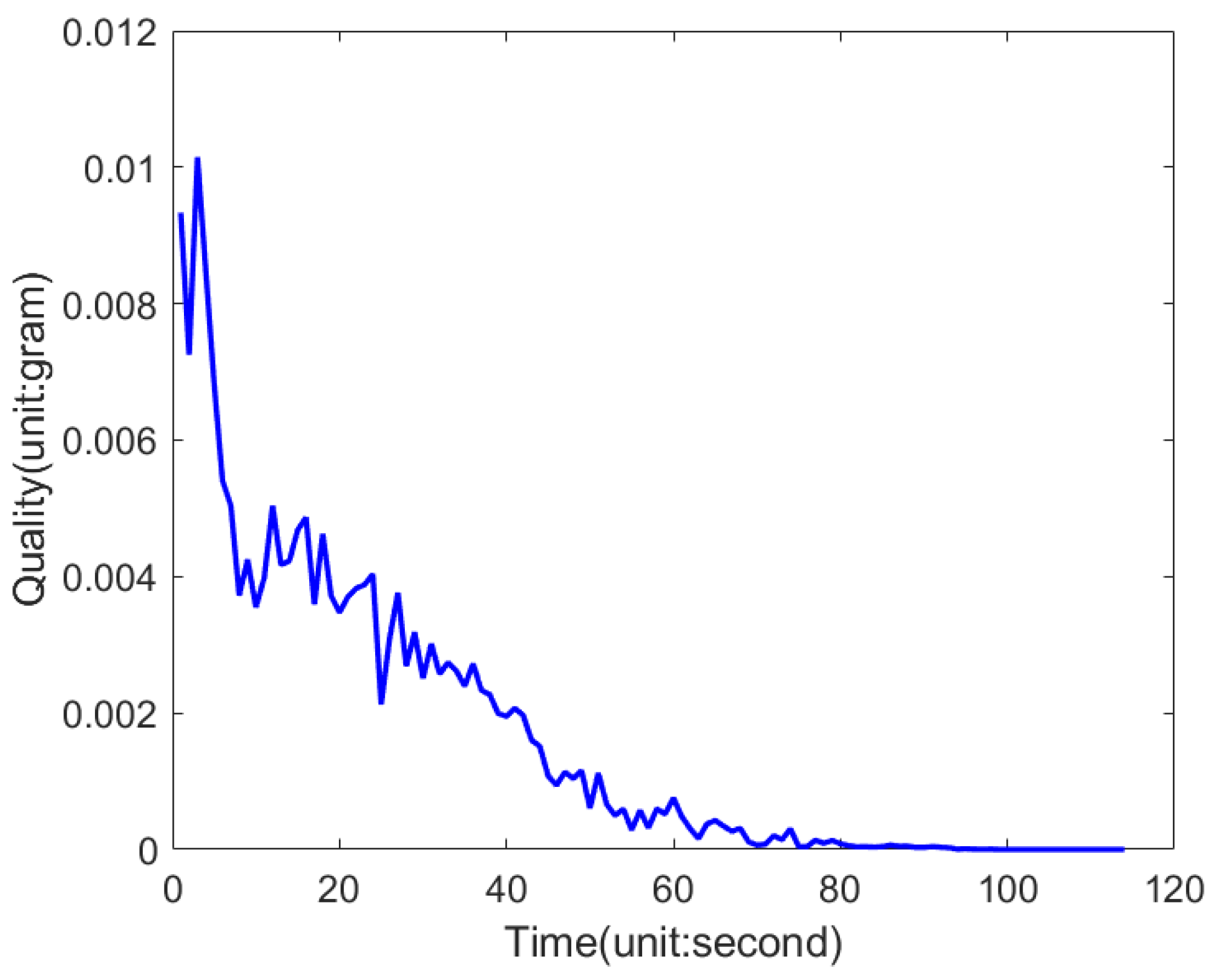
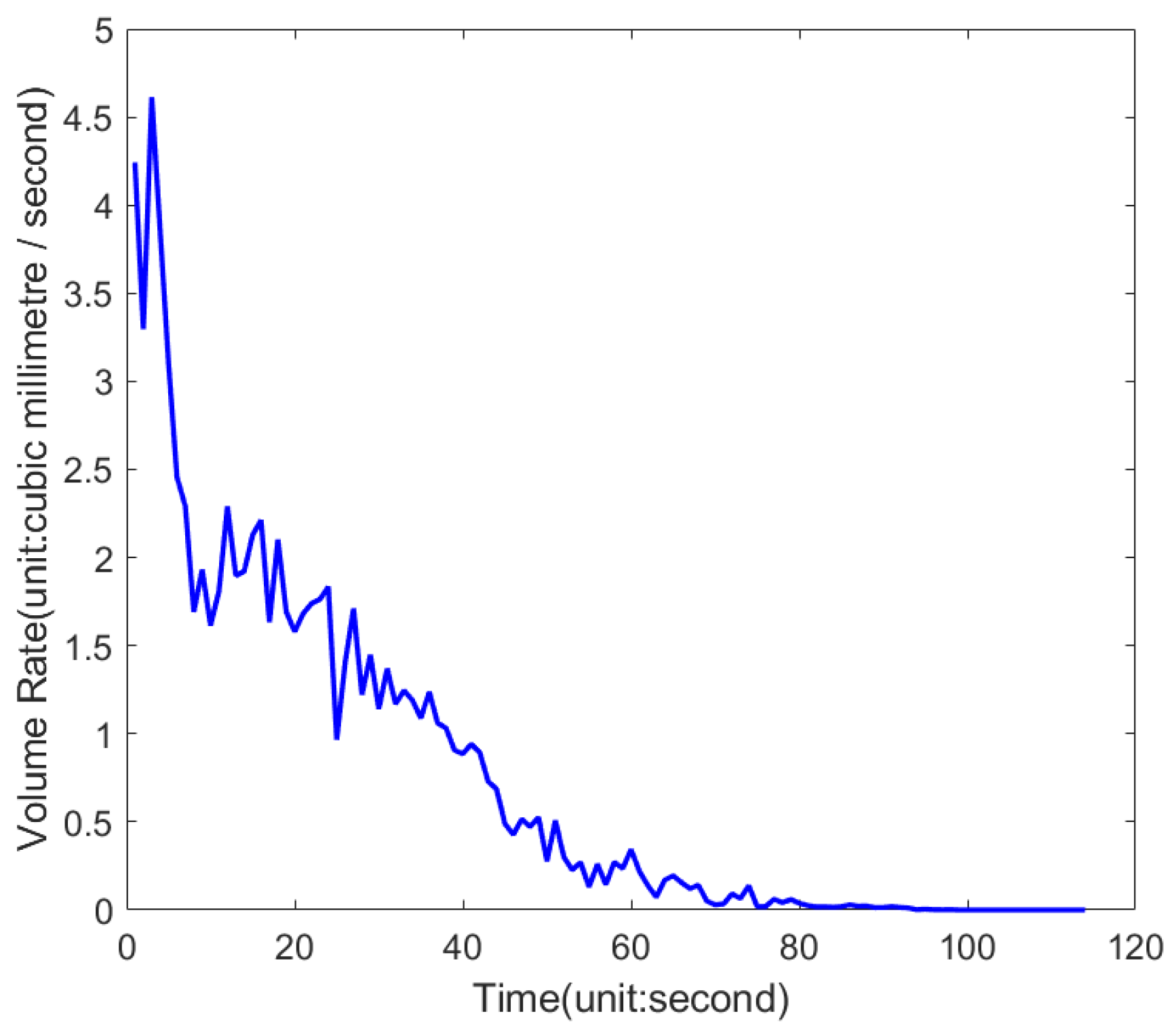

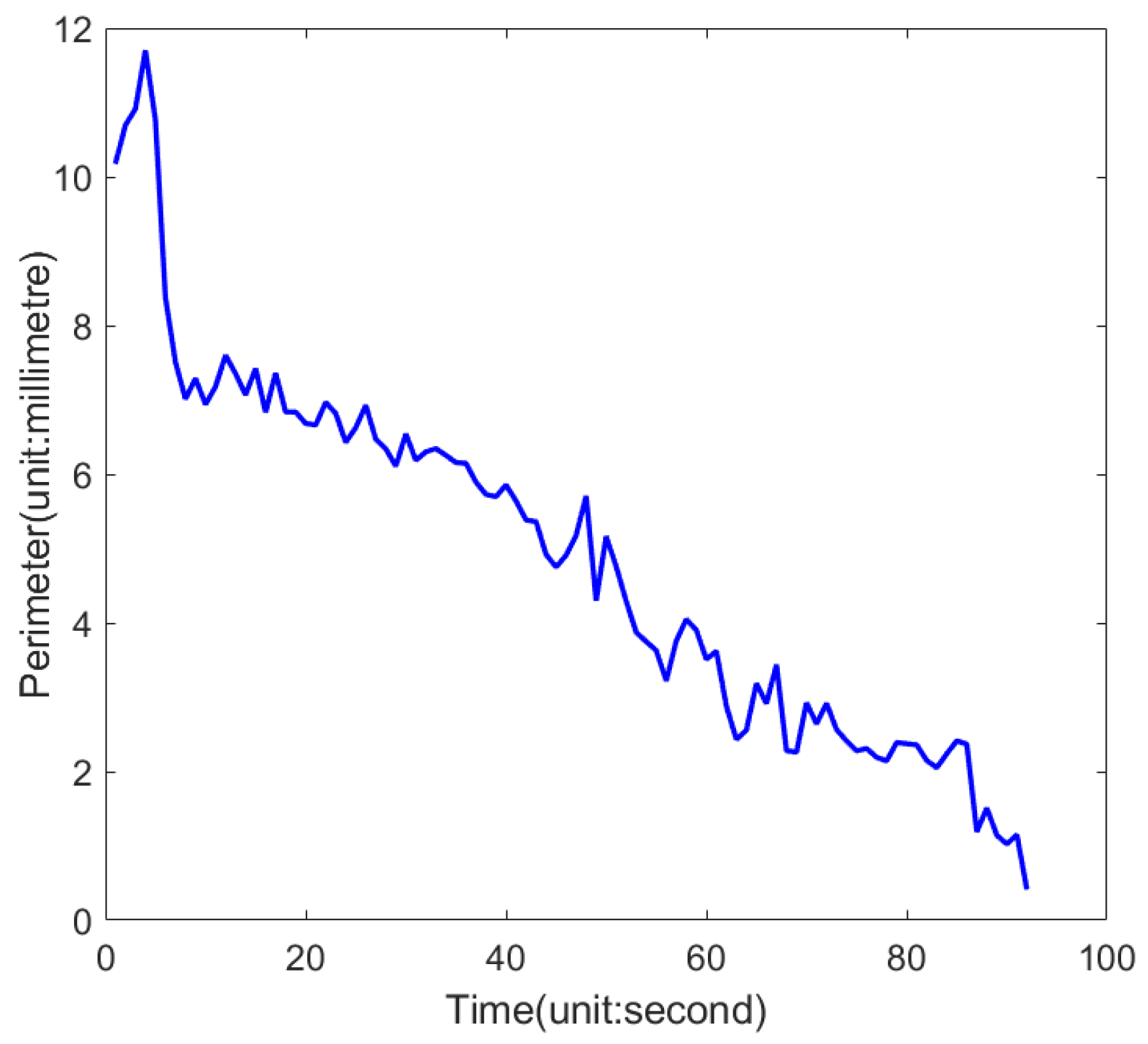

| Moment | Coordinate Points | Moment | Coordinate Points |
|---|---|---|---|
| 1 | (225, 202) | 25 | (209, 223) |
| 2 | (224, 205) | 26 | (208, 212) |
| 3 | (217, 226) | 27 | (191, 232) |
| 4 | (220, 225) | 28 | (176, 246) |
| 5 | (213, 244) | 29 | (171, 241) |
| 6 | (236, 235) | 30 | (166, 242) |
| 7 | (221, 239) | 31 | (164, 245) |
| 8 | (218, 235) | 32 | (161, 243) |
| 9 | (215, 235) | 33 | (165, 244) |
| 10 | (214, 234) | 34 | (168, 240) |
| 11 | (214, 237) | 35 | (176, 244) |
| 12 | (209, 239) | 36 | (169, 239) |
| 13 | (208, 236) | 37 | (198, 233) |
| 14 | (204, 233) | 38 | (193, 234) |
| 15 | (197, 237) | 39 | (195, 228) |
| 16 | (281, 225) | 40 | (190, 236) |
| 17 | (203, 239) | 41 | (171, 245) |
| 18 | (200, 237) | 42 | (164, 240) |
| 19 | (199, 237) | 43 | (156, 245) |
| 20 | (195, 234) | 44 | (142, 250) |
| 21 | (198, 233) | 45 | (139, 253) |
| 22 | (190, 237) | 46 | (140, 249) |
| 23 | (191, 234) | 47 | (136, 253) |
| 24 | (202, 231) | 48 | (126, 265) |
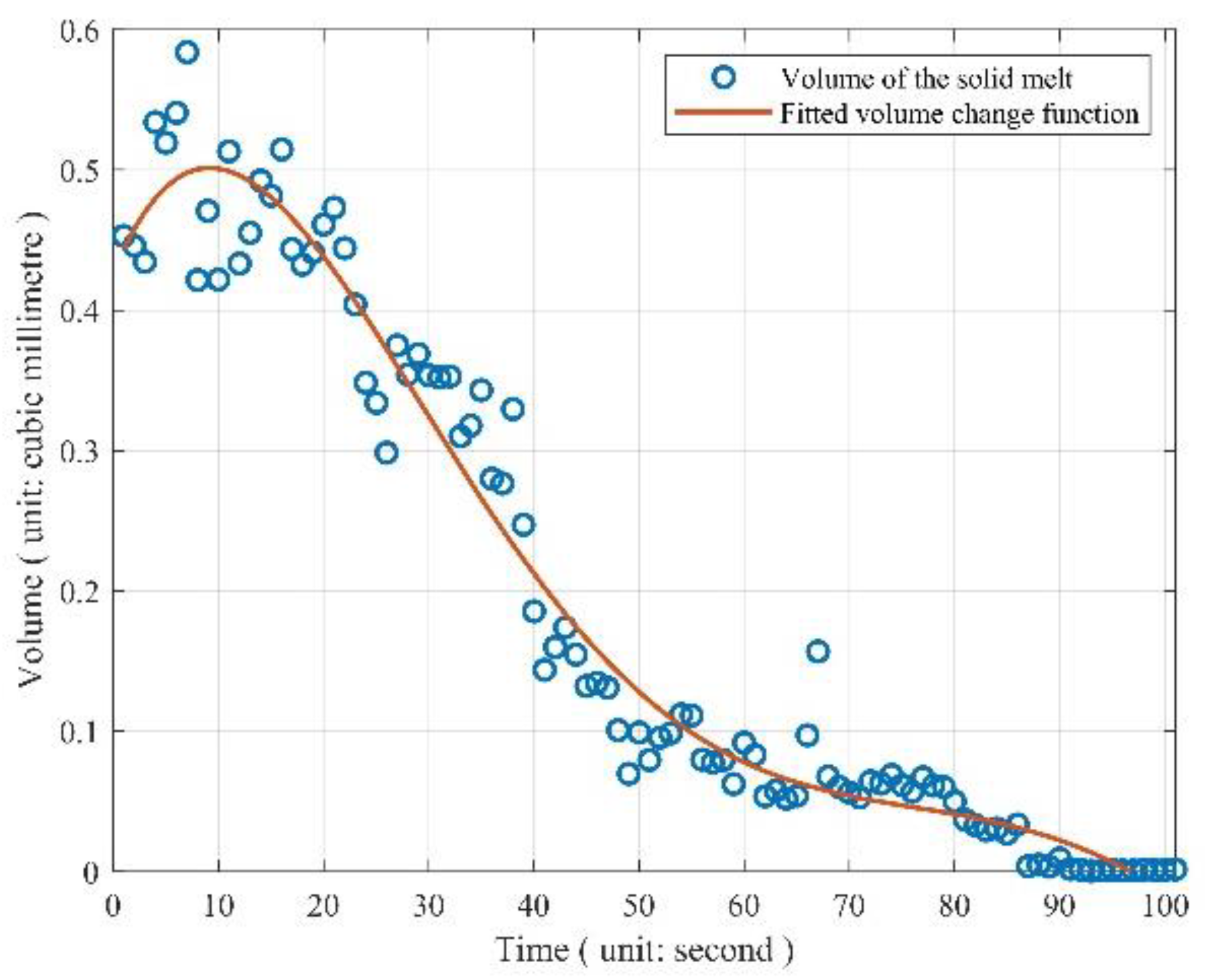
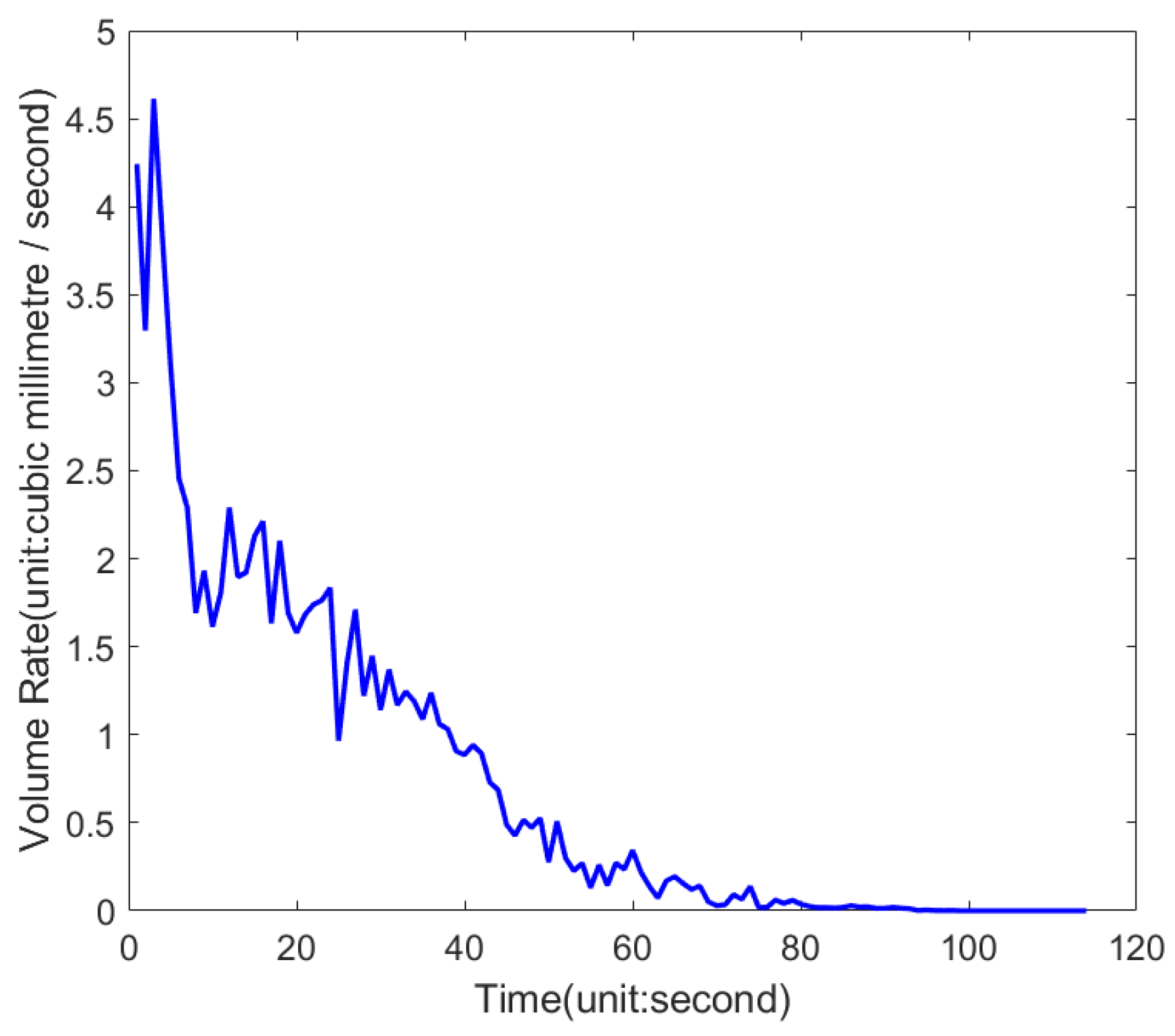
| Moment | Volume (mm3) | Rate (mm3/s) | Moment | Volume (mm3) | Rate (mm3/s) |
|---|---|---|---|---|---|
| 1 | 4.24 | 0.95 | 25 | 0.97 | 0.44 |
| 2 | 3.30 | 1.32 | 26 | 1.40 | 0.31 |
| 3 | 4.61 | 0.76 | 27 | 1.71 | 0.49 |
| 4 | 3.85 | 0.75 | 28 | 1.22 | 0.23 |
| 5 | 3.10 | 0.65 | 29 | 1.45 | 0.31 |
| 6 | 2.46 | 0.17 | 30 | 1.14 | 0.23 |
| 7 | 2.29 | 0.60 | 31 | 1.37 | 0.20 |
| 8 | 1.69 | 0.24 | 32 | 1.17 | 0.08 |
| 9 | 1.93 | 0.32 | 33 | 1.25 | 0.06 |
| 10 | 1.61 | 0.20 | 34 | 1.19 | 0.10 |
| 11 | 1.81 | 0.48 | 35 | 1.09 | 0.15 |
| 12 | 2.29 | 0.39 | 36 | 1.24 | 0.18 |
| 13 | 1.90 | 0.02 | 37 | 1.06 | 0.03 |
| 14 | 1.92 | 0.21 | 38 | 1.03 | 0.13 |
| 15 | 2.13 | 0.08 | 39 | 0.91 | 0.02 |
| 16 | 2.21 | 0.58 | 40 | 0.89 | 0.05 |
| 17 | 1.63 | 0.47 | 41 | 0.94 | 0.04 |
| 18 | 2.10 | 0.41 | 42 | 0.89 | 0.16 |
| 19 | 1.69 | 0.11 | 43 | 0.73 | 0.04 |
| 20 | 1.58 | 0.10 | 44 | 0.69 | 0.20 |
| 21 | 1.68 | 0.06 | 45 | 0.49 | 0.06 |
| 22 | 1.74 | 0.02 | 46 | 0.43 | 0.09 |
| 23 | 1.76 | 0.07 | 47 | 0.52 | 0.04 |
| 24 | 1.83 | 0.87 | 48 | 0.47 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, A.; Wang, L.-J.; Ma, W.-N.; Tang, M.; Chen, J. Shape from Shading-Based Study of Silica Fusion Characterization Problems. Minerals 2022, 12, 1286. https://doi.org/10.3390/min12101286
Yang A, Wang L-J, Ma W-N, Tang M, Chen J. Shape from Shading-Based Study of Silica Fusion Characterization Problems. Minerals. 2022; 12(10):1286. https://doi.org/10.3390/min12101286
Chicago/Turabian StyleYang, Aimin, Li-Jing Wang, Wei-Ning Ma, Mei Tang, and Jing Chen. 2022. "Shape from Shading-Based Study of Silica Fusion Characterization Problems" Minerals 12, no. 10: 1286. https://doi.org/10.3390/min12101286
APA StyleYang, A., Wang, L.-J., Ma, W.-N., Tang, M., & Chen, J. (2022). Shape from Shading-Based Study of Silica Fusion Characterization Problems. Minerals, 12(10), 1286. https://doi.org/10.3390/min12101286






