Flotation Performance and Gas Dispersion Properties in a Laboratory Flotation Cell
Abstract
:1. Introduction
2. Experimental Work
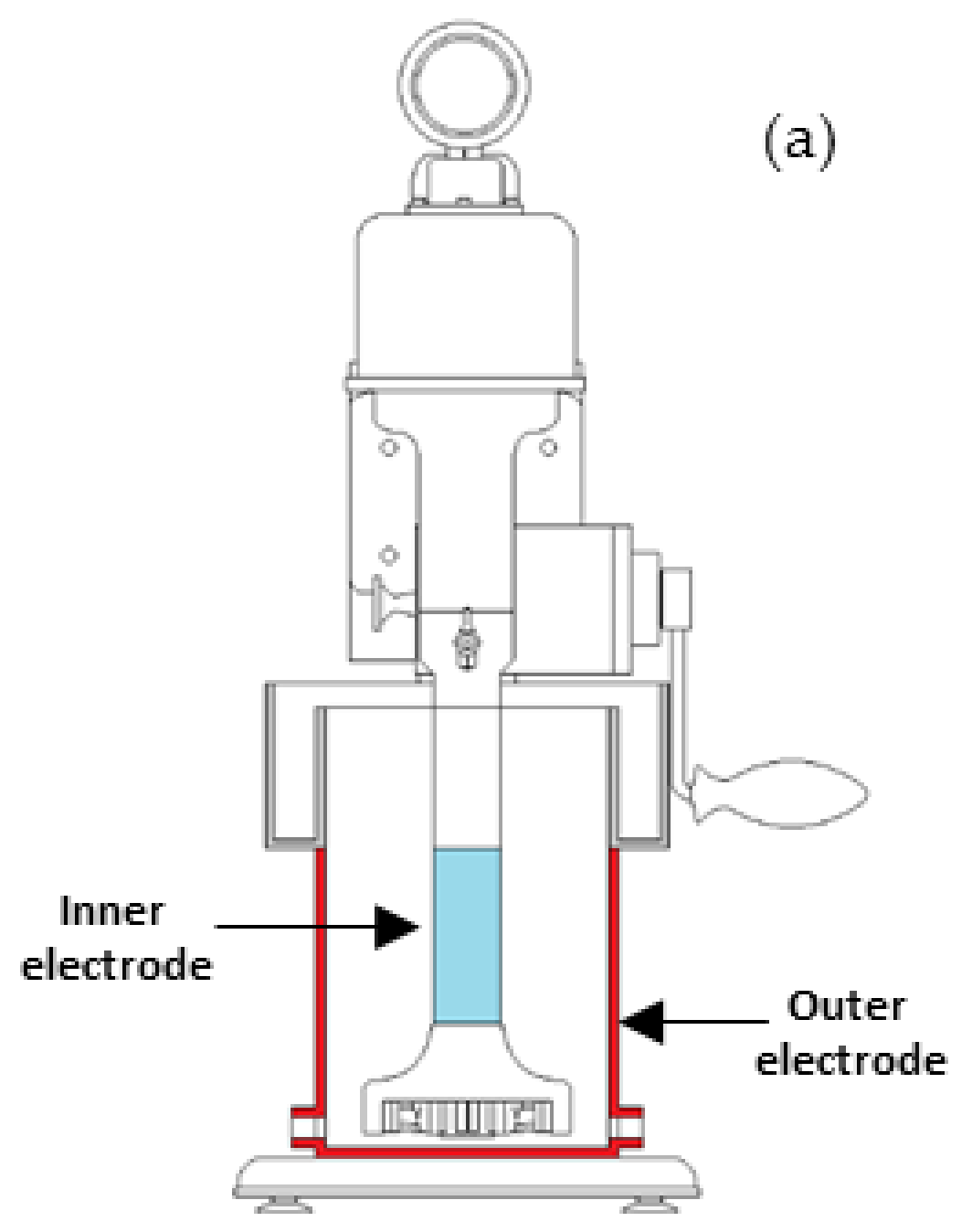
2.1. Gas Holdup Measurement
2.2. Experimental
2.2.1. Gas Dispersion Testing
2.2.2. Metallurgical Performance Testing
3. Results
3.1. Gas Dispersion Testing
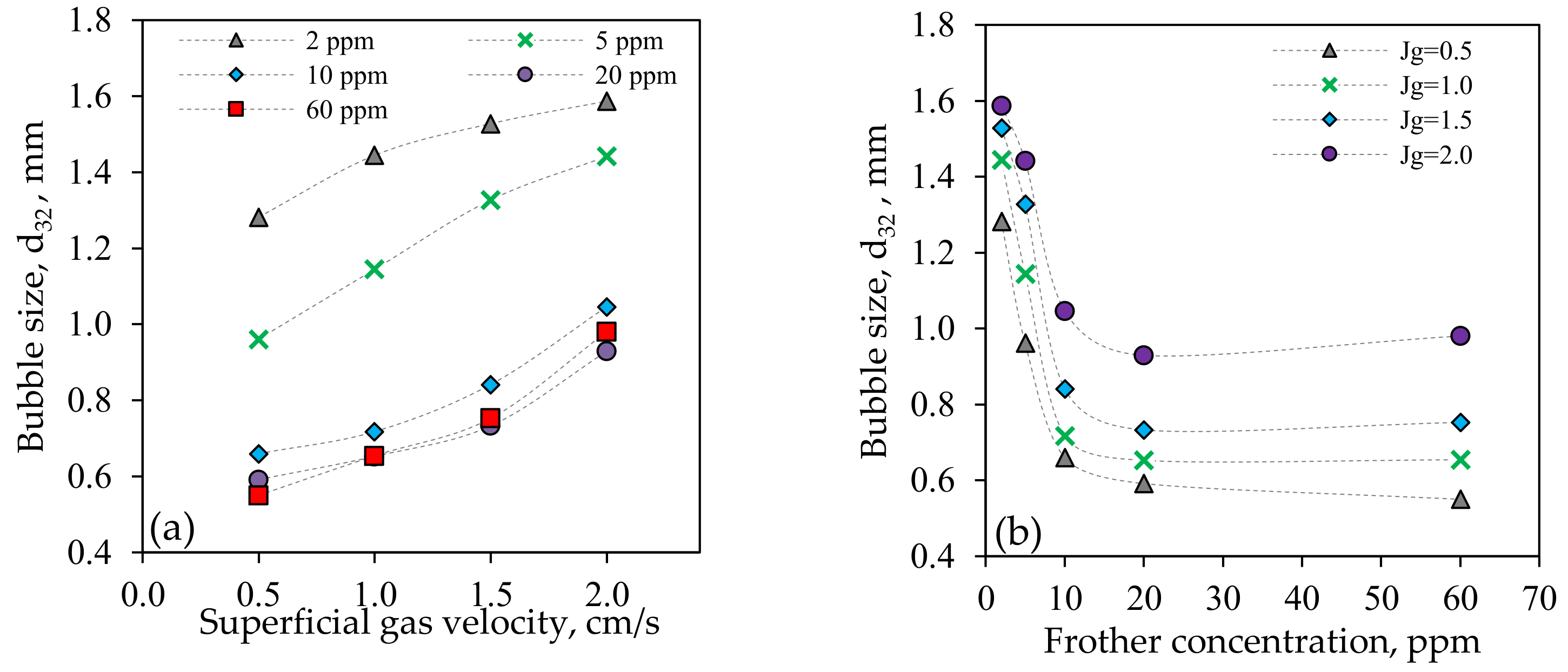
3.1.1. Bubble Size (d32)
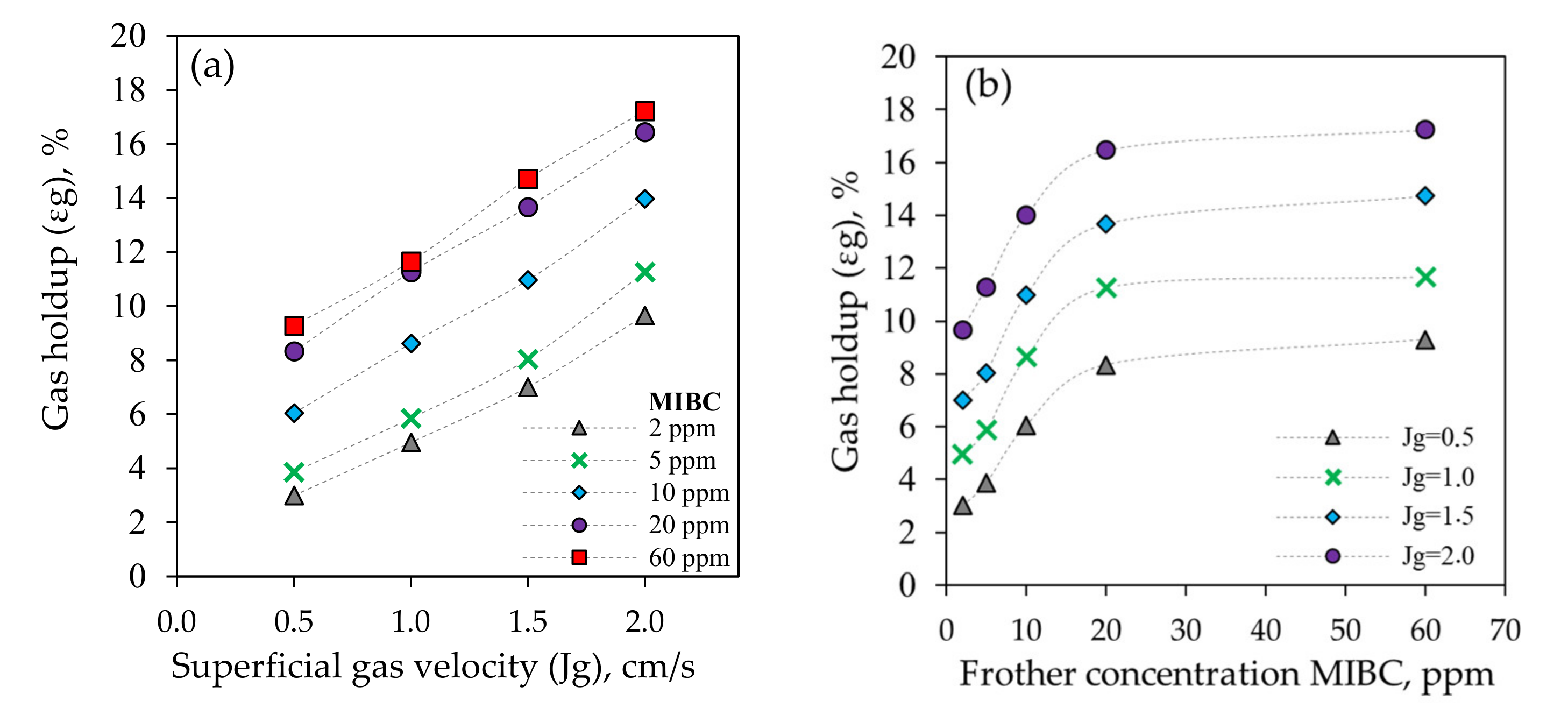
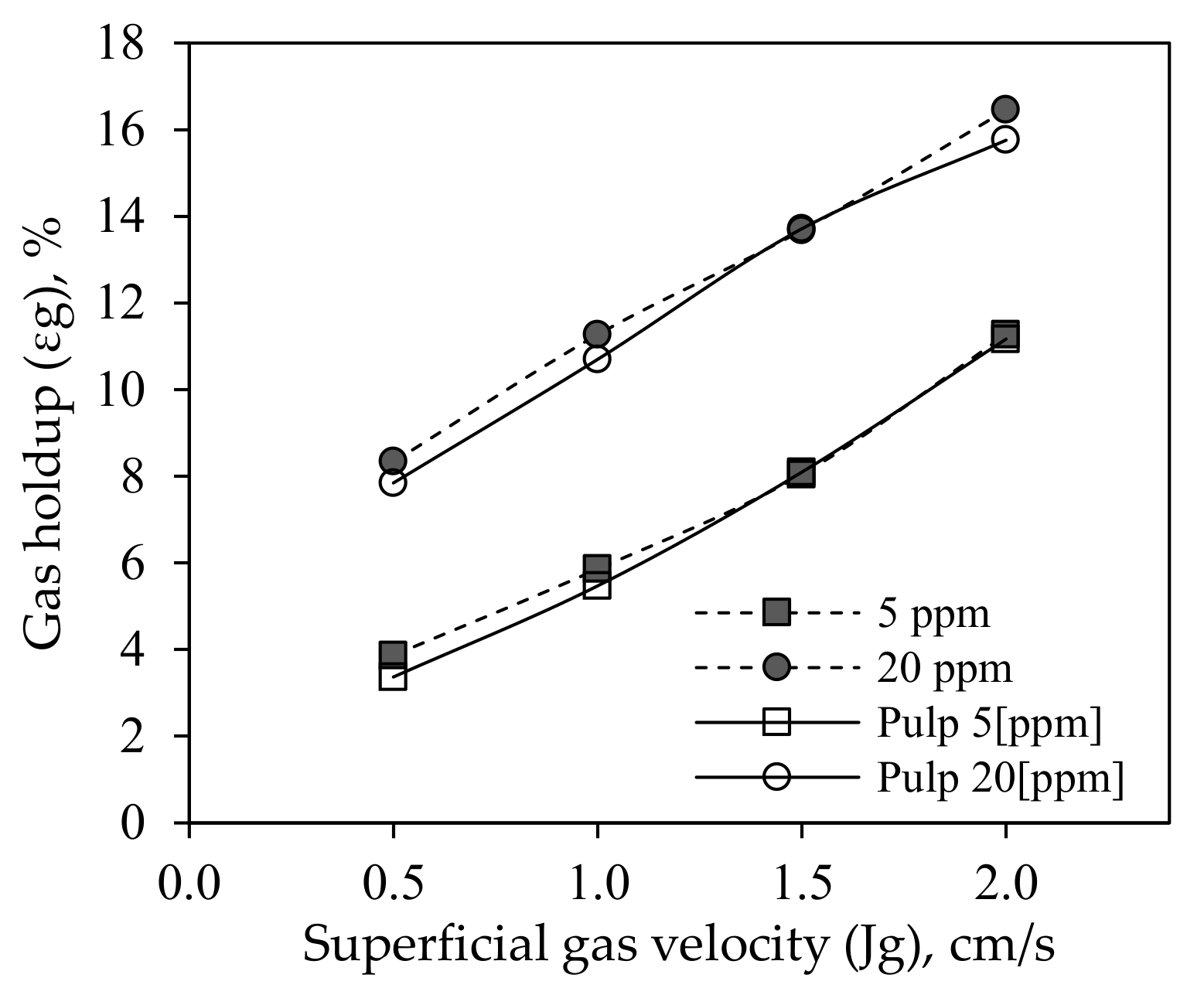
3.1.2. Gas Holdup (εg)
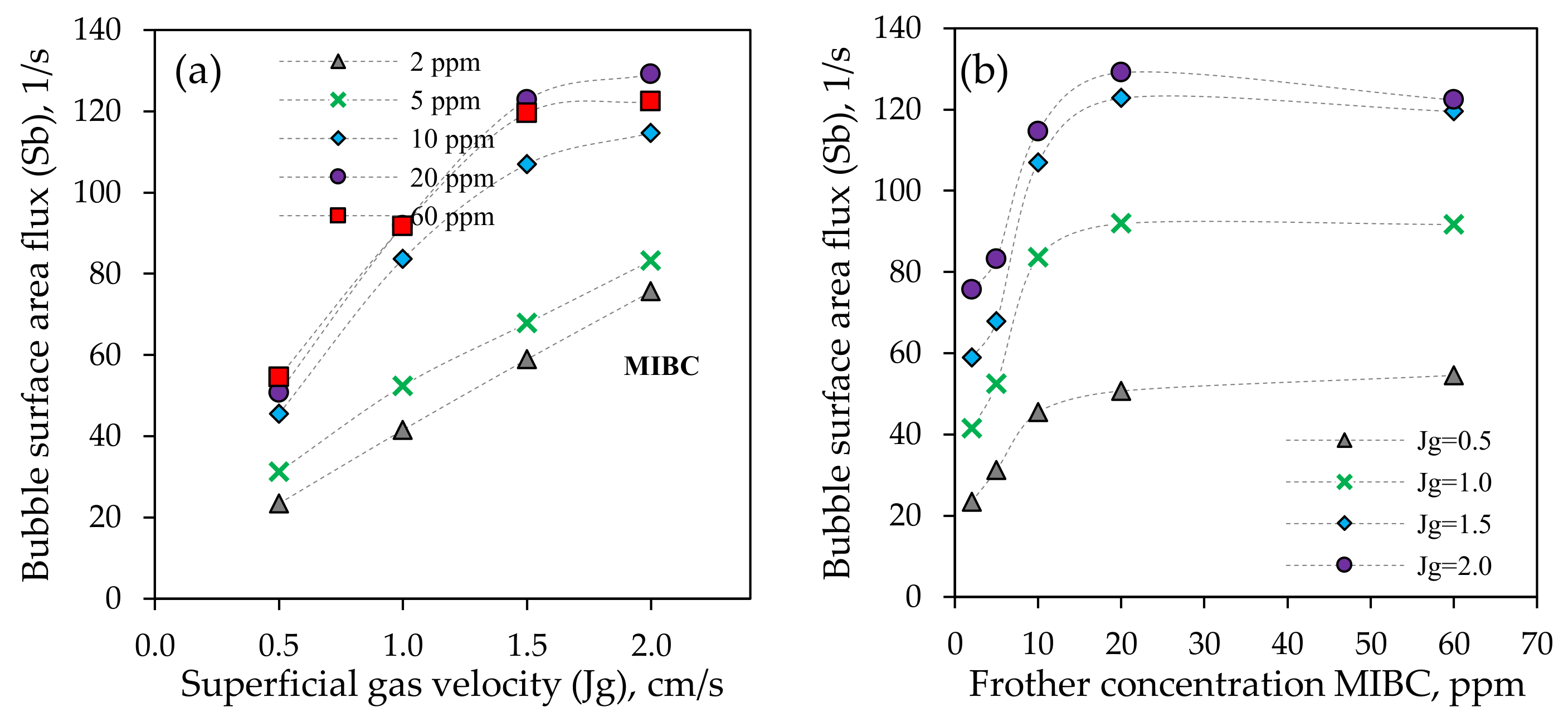
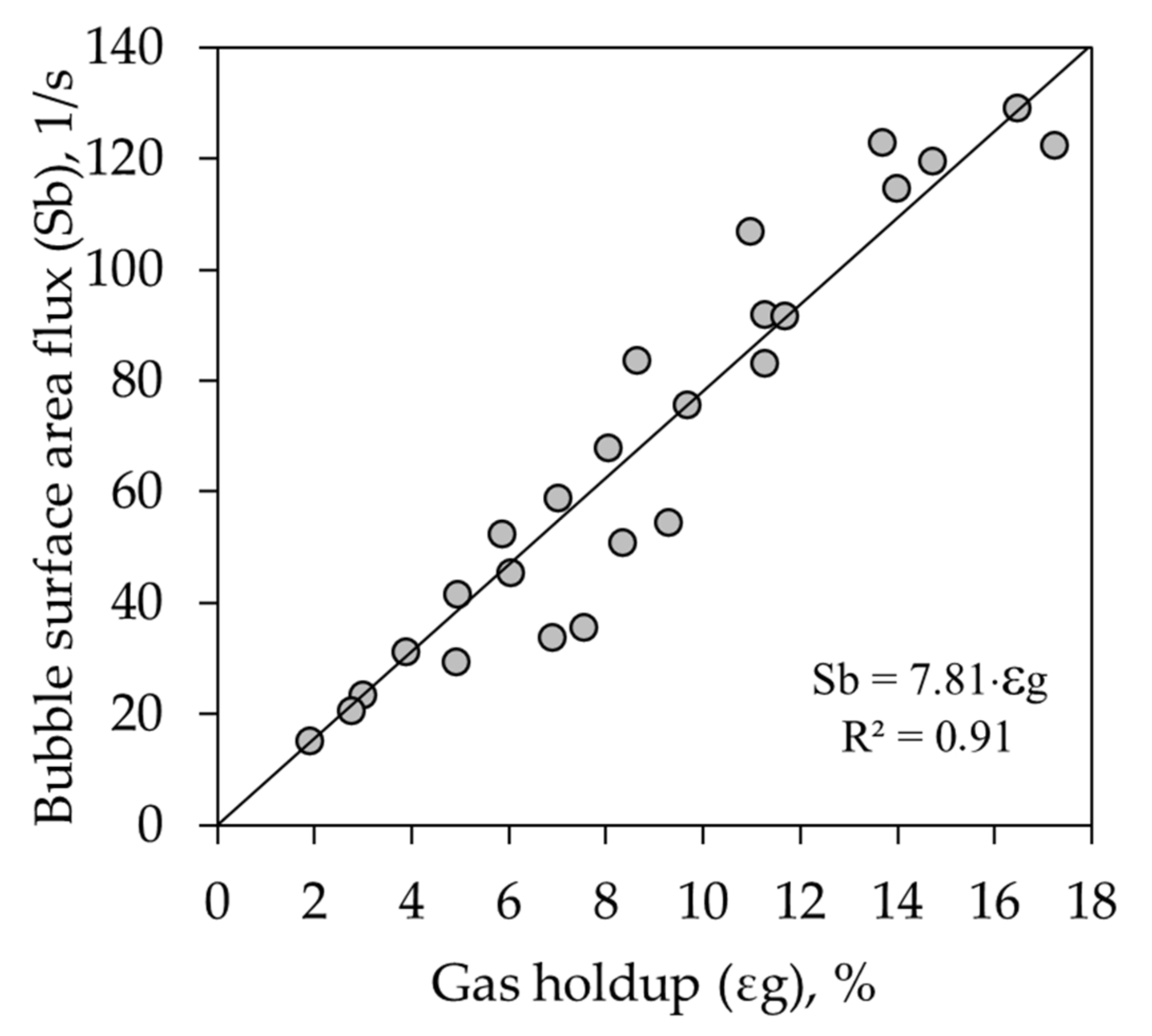
3.1.3. Bubble Surface Area Flux (Sb)
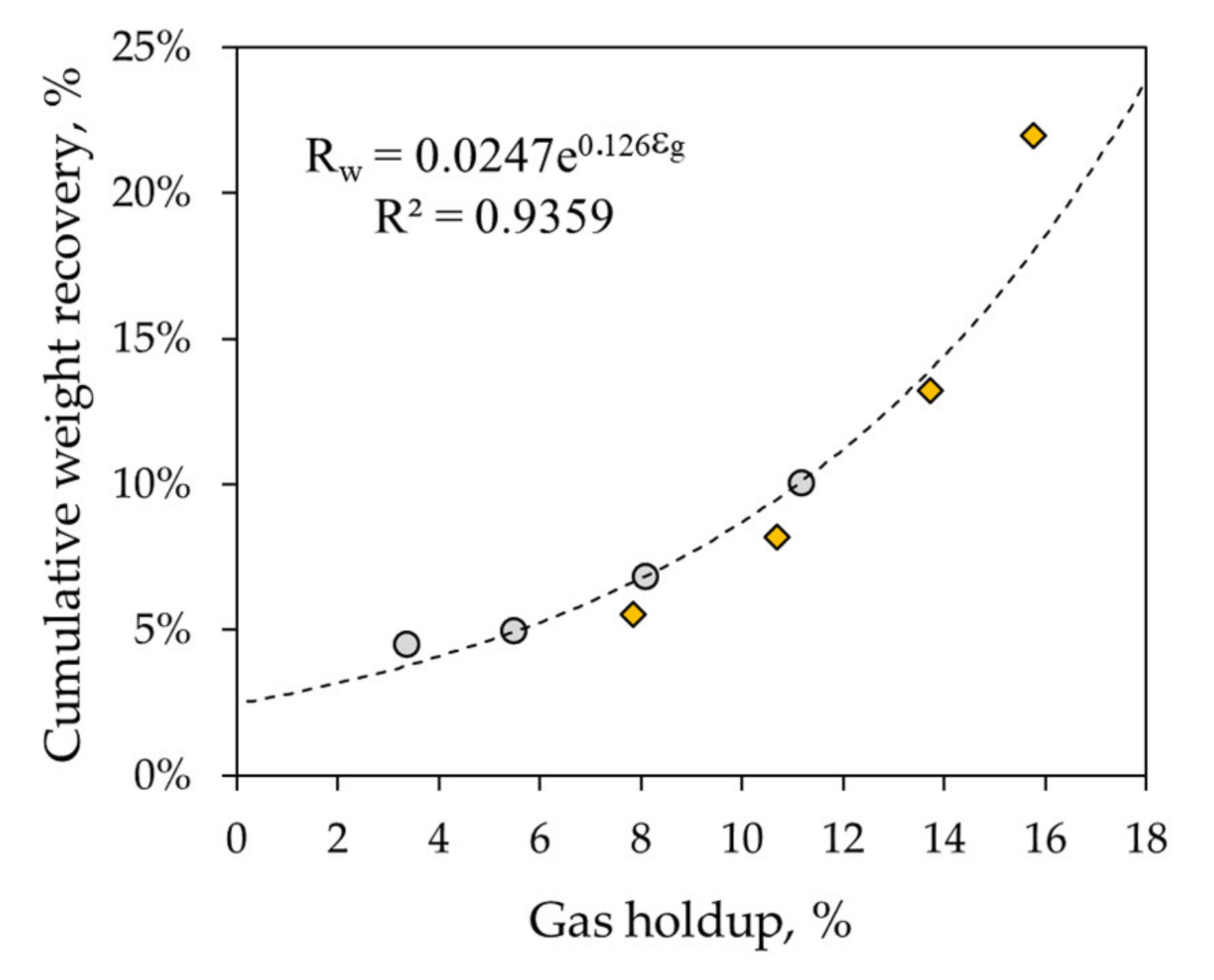
3.1.4. Water Recovery
3.2. Metallurgical Performance Testing
3.2.1. Gas Holdup in Two and Three-Phase System
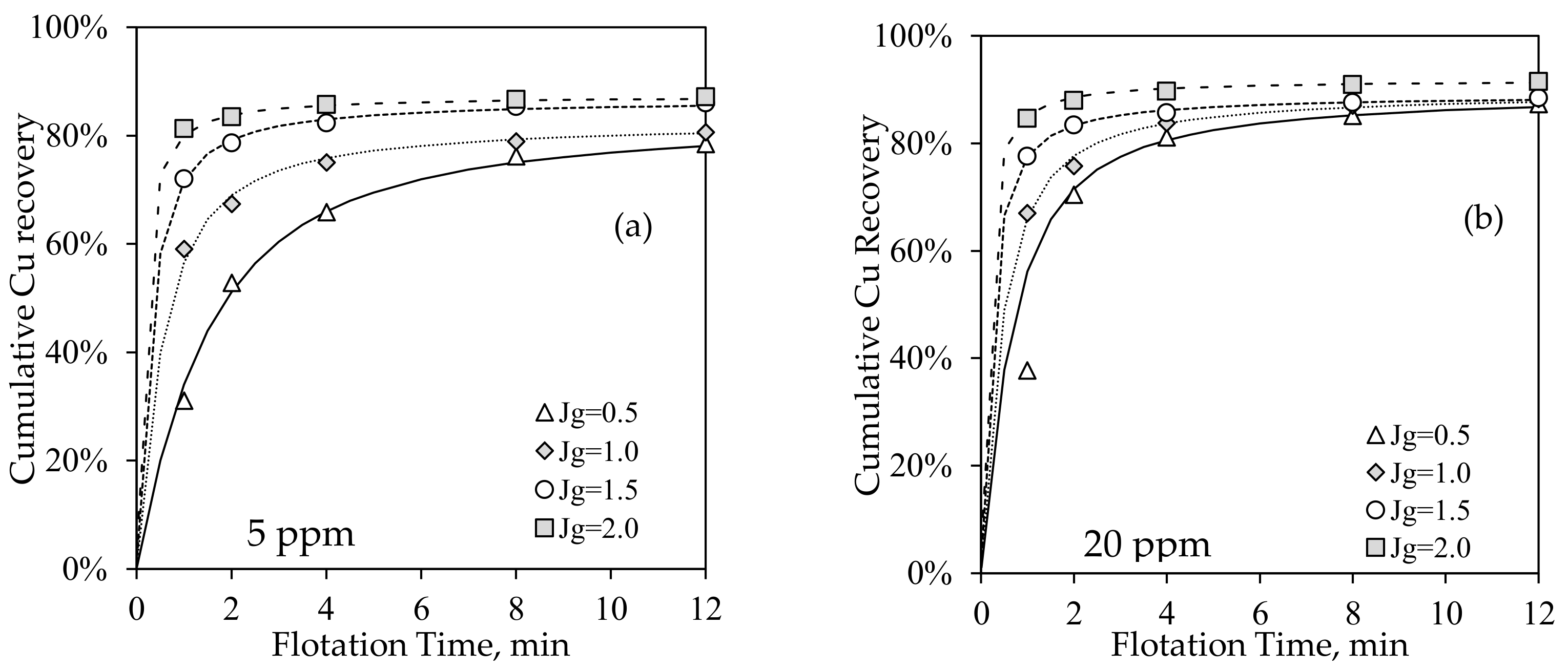
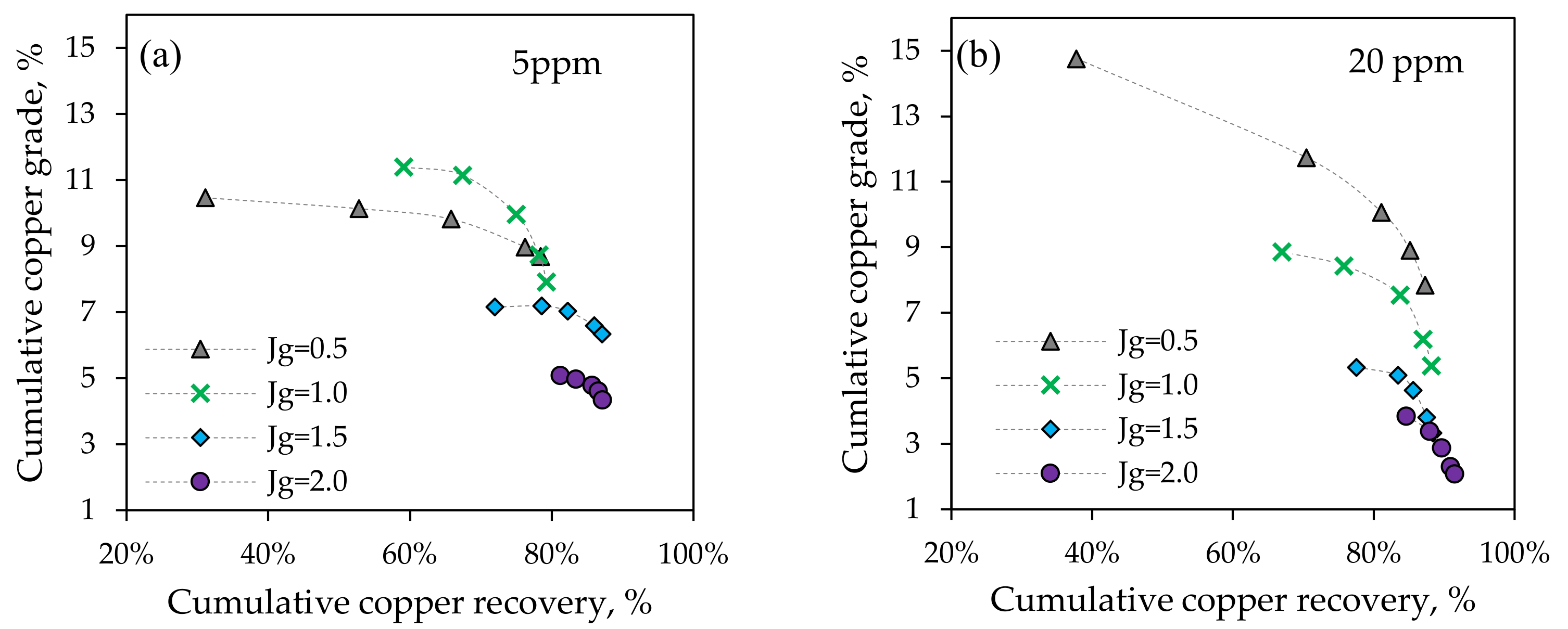
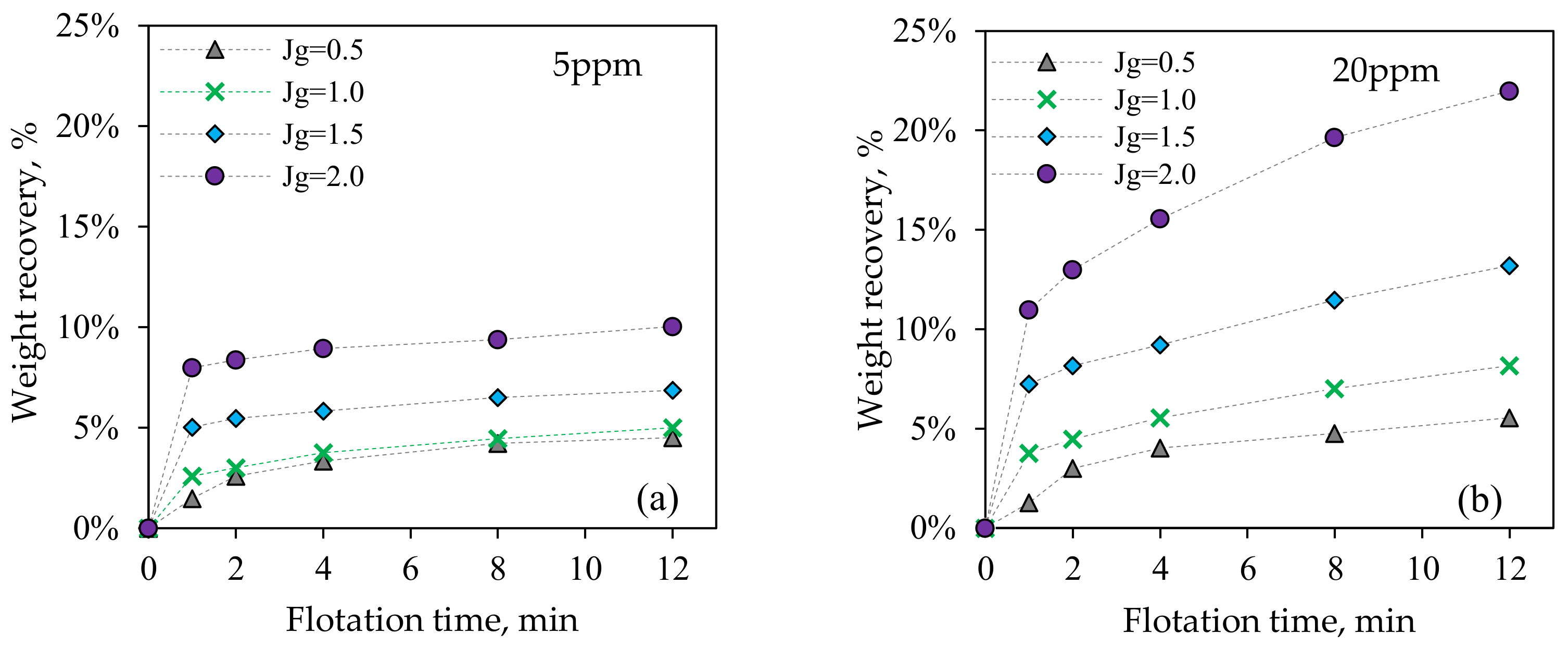
3.2.2. Batch Flotation Tests
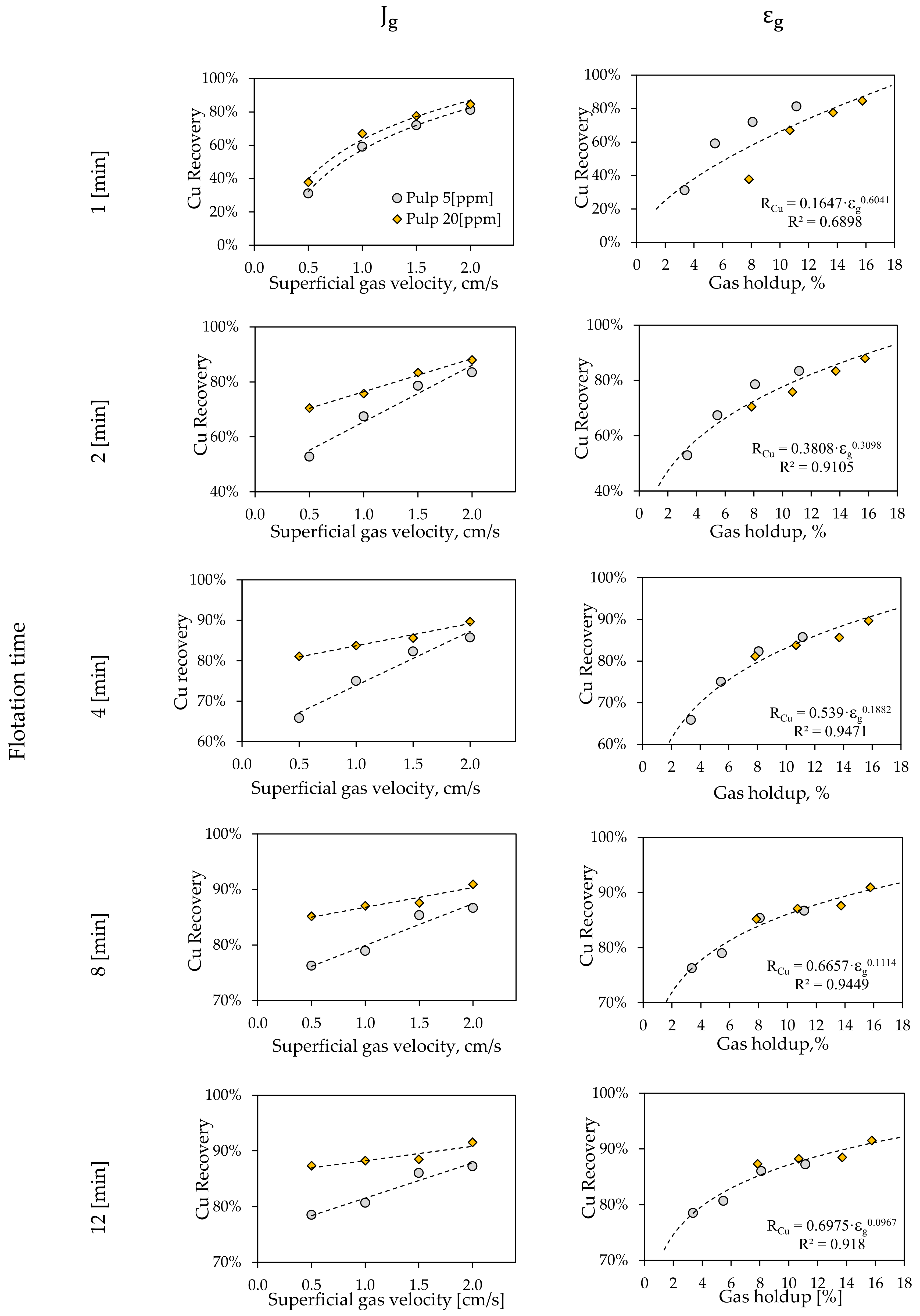
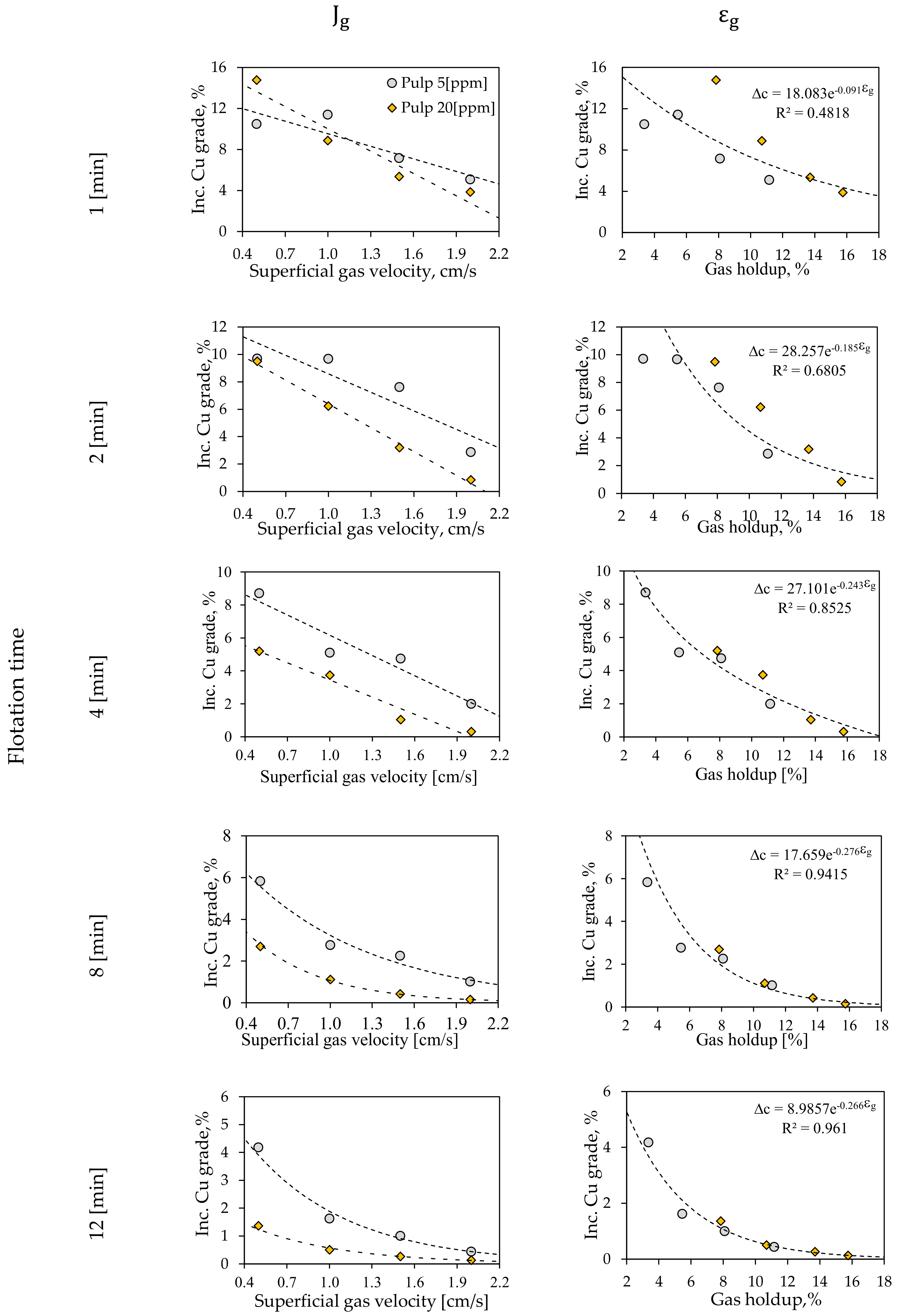
3.2.3. Froth Flotation Kinetics Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klimpel, R.R.; Dhansen, R.; Fee, B.S. Selection of flotation reagents for mineral flotation. In Design and Installation of Concentration and Dewatering Circuit; Mular, A.L., Anderson, M.A., Eds.; Society of Mining Engineers: Englewood, CO, USA, 1986; Volume 26, pp. 384–404. [Google Scholar]
- Lynch, A.J.; Elber, L. Modelling and control of mineral processing plants. In Proceedings of the IFAC Mining, Mineral, and Metal Processing, Montreal, QC, Canada, 18–20 August 1980; pp. 25–32. [Google Scholar]
- Gomez-Flores, A.; Heyes, G.; Ilyas, S.; Kim, H. Prediction of grade and recovery in flotation from physicochemical and operational aspects using machine learning models. Miner. Eng. 2022, 183, 107627. [Google Scholar] [CrossRef]
- Hadler, K.; Cilliers, J.J. The relationship between the peak in air recovery and flotation bank performance. Miner. Eng. 2009, 22, 451–455. [Google Scholar] [CrossRef]
- Hadler, K.; Greyling, M.; Plint, N.; Cilliers, J.J. The effect of froth depth on air recovery and flotation performance. Miner. Eng. 2012, 36–38, 248–253. [Google Scholar] [CrossRef]
- Finch, J.A.; Xiao, J.; Hardie, C.; Gomez, C.O. Gas Dispersion Properties: Bubble surface area flux and gas hold-up. Miner. Eng. 2000, 13, 365–372. [Google Scholar] [CrossRef]
- Finch, J.; Dobby, G. Column Flotation; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
- Cappuccitti, F.; Finch, J.A. Development of new frothers through hydrodynamic characterization. Miner. Eng. 2008, 21, 944–948. [Google Scholar] [CrossRef]
- Azgomi, F.; Gomez, C.O.; Finch, J.A. Correspondence of gas holdup and bubble size in presence of different frothers. Int. J. Miner. Process. 2007, 83, 1–11. [Google Scholar] [CrossRef]
- Quinn, J.J.; Kracht, W.; Gomez, C.O.; Gagnon, C.; Finch, J.A. Comparing the effect of salts and frother (MIBC) on gas dispersion and froth properties. Miner. Eng. 2007, 20, 1296–1302. [Google Scholar] [CrossRef]
- Massinaei, M.; Kolahdoozan, M.; Noaparast, M.; Oliazadeh, M.; Yianatos, J.; Shamsadini, R.; Yarahmadi, M. Hydrodynamic and kinetic characterization of industrial columns in rougher circuit. Miner. Eng. 2009, 22, 357–365. [Google Scholar] [CrossRef]
- Matiolo, E.; Testa, F.; Yianatos, J.; Rubio, J. On the gas dispersion measurements in the collection zone of flotation columns. Int. J. Miner. Process. 2011, 99, 78–83. [Google Scholar] [CrossRef]
- López-Saucedo, F.; Uribe-Salas, A.; Pérez-Garibay, R.; Magallanes-Hernández, L. Gas dispersion in column flotation and its effect on recovery and grade. Can. J. Metall. Mater. Sci. 2012, 51, 111–117. [Google Scholar] [CrossRef]
- Vazirizadeh, A.; Bouchard, J.; del Villar, R.; Ghasemzadeh Barvarz, M.; Duchesne, C. On the relationship between hydrodynamic characteristics and the kinetics of flotation. Part II: Model validation. Miner. Eng. 2015, 74, 198–206. [Google Scholar] [CrossRef]
- Gomez, C.O.; Cortés-López, F.; Finch, J.A. Industrial testing of a gas holdup sensor for flotation systems. Miner. Eng. 2003, 16, 493–501. [Google Scholar] [CrossRef]
- Amenlunxen, P.; Rothman, P. The on-line determination of bubble surface area flux using the CIDRA GH-100 sonar gas holdup meter. IFAC Proc. 2009, 42, 156–160. [Google Scholar] [CrossRef] [Green Version]
- Maldonado, M.; Gomez, C.O. A new approach to measure gas holdup in industrial flotation machines Part I: Demonstration of working principle. Miner. Eng. 2018, 118, 1–8. [Google Scholar] [CrossRef]
- Ramos, I.; Maldonado, M.; Meriño, D.; Bustos, P.; Henriquez, F.; Morales, M. A new approach to measure gas holdup in industrial flotation machines Part III: Industrial prototype design and assessment. Miner. Eng. 2022, 180, 107490. [Google Scholar] [CrossRef]
- Dahlke, R.; Gomez, C.; Finch, J.A. Operating range of a flotation cell determined from gas holdup vs. gas rate. Miner. Eng. 2005, 18, 977–980. [Google Scholar] [CrossRef]
- Vinnett, L.; Yianatos, Y.; Alvarez, M. Gas dispersion measurements in mechanical flotation cells: Industrial experience in Chilean concentrators. Miner. Eng. 2014, 57, 12–15. [Google Scholar] [CrossRef]
- Gorain, B.K.; Franzidis, J.P.; Manlapig, E.V. Studies on impeller type, impeller speed and air flow rate in an industrial: Scale flotation cell. Part 4: Effect of bubble surface area flux on flotation kinetics. Miner. Eng. 1997, 10, 367–379. [Google Scholar] [CrossRef]
- Gorain, B.K.; Franzidis, J.P.; Manlapig, E.V. Studies on impeller type, impeller speed and air flow rate in an industrial scale flotation cell. Part 5: Validation of k-Sb relationship and effect of froth depth. Miner. Eng. 1998, 11, 615–626. [Google Scholar] [CrossRef]
- Kracht, W.; Vallebuona, G.; Casali, A. Rate constant modelling for batch flotation, as a function of gas dispersion properties. Miner. Eng. 2005, 18, 1067–1076. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. CDF model of a self-aerating flotation cell. Int. J. Miner. Process. 2007, 85, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Maldonado, M.; Pinto, A.; Gomez, C.O.; Becerra-Yoma, N. Electrode arrangements for continuous measurement of dispersion conductivity in lab flotation cells. Miner. Eng. 2017, 111, 1–4. [Google Scholar] [CrossRef]
- Maldonado, M.; Pinto, A.; Magne, L.; Gomez, C.O.; Finch, J.A. Gas hold-up estimation using Maxwell equation in flotation systems: Revisited. Miner. Eng. 2016, 98, 9–13. [Google Scholar] [CrossRef]
- Gontijo, C.; Fornasiero, D.; Ralston, J. The limits of fine and coarse particle flotation. Can. J. Chem. Eng. 2007, 85, 739–747. [Google Scholar] [CrossRef]
- Gomez-Flores, A.; Heyes, G.; Ilyas, S.; Kim, H. Effects of artificial impeller blade wear on bubble—particle interactions using CFD (k − ε and LES), PIV, and 3D printing. Miner. Eng. 2022, 186, 107766. [Google Scholar] [CrossRef]
- Grandón, F.; Alvarez, J.; Gómez, C. Frother dosage in laboratory flotation testing. In Proceedings of the 11th International Mineral Processing Conference (2015 Procemin), Santiago, Chile, 21–23 October 2015; pp. 1–11. [Google Scholar]
- Laskowski, J.S. Testing flotation frothers. Physicochem. Probl. Miner. Process. 2004, 38, 13–22. [Google Scholar]
- Moyo, P.; Gomez, C.O.; Finch, J.A. Characterizing frothers using water carrying rate. Can. Metall. Q. 2007, 46, 215–220. [Google Scholar] [CrossRef]
- Martinez, J.; Maldonado, M.; Gutierrez, L. A method to predict water recovery to predict water recovery rate in the collection and froth zone of flotation systems. Minerals 2020, 10, 630. [Google Scholar] [CrossRef]
- Smith, P.G.; Warren, L.J. Entrainment of Particles into Flotation Froths. Miner. Process. Extr. Metall. Rev. 1989, 5, 123–145. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K.; Bradshaw, D. A review of entrainment: Mechanisms, contributing factor and modelling in flotation. Miner. Eng. 2015, 70, 77–91. [Google Scholar] [CrossRef]
- Runge, K.C. Laboratory Flotation Testing—An Essential Tool for Ore Characterisation. In Flotation Plan Optimation: A Metallurgical Guide to Identifying and Solving Problems in Flotation Plants; Greet, C.J., Ed.; Ausimm the Minerals Institute: Carlon, VIC, Australia, 2010; Chapter 9; pp. 155–173. [Google Scholar]
- Geldenhuys, S.; McFadzean, B. The effect of pulp bubble size on the dynamic froth stability measurement. Miner. Eng. 2019, 131, 164–169. [Google Scholar] [CrossRef]
- McFadzean, B.; Marozva, T.; Wiese, J. Flotation frother mixtures: Decoupling the sub-processes of froth stability, froth recovery and entrainment. Miner. Eng. 2016, 85, 72–79. [Google Scholar] [CrossRef]



| Levels | |||||||
|---|---|---|---|---|---|---|---|
| Manipulated Variables | Testing Number | Units | − − | − | 0 | + | + + |
| Water solution rate | 1 | L/min | 2 | ||||
| Superficial gas velocity (Jg) | 4 | cm/s | 0.5 | 1 | 1.5 | 2 | |
| Froth level | 1 | cm | 2 | ||||
| Frother concentration | 5 | ppm | 2 | 5 | 10 | 20 | 60 |
| Rotor speed | 1 | rpm | 1000 | ||||
| Frother Type | 1 | MIBC | |||||
| Total number of tests | 20 |
| 5 [ppm] | 20 [ppm] | Average | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Element | Jg = 0.5 cm/s | Jg = 1.0 | Jg = 1.5 | Jg = 2.0 | Jg = 0.5 | Jg = 1.0 | Jg = 1.5 | Jg = 2.0 | |
| CuT [%] | 0.50 | 0.49 | 0.50 | 0.50 | 0.51 | 0.50 | 0.51 | 0.50 | 0.50 |
| Fe [%] | 5.20 | 5.06 | 5.29 | 5.27 | 5.33 | 5.16 | 5.19 | 5.20 | 5.20 |
| Levels | |||||||
|---|---|---|---|---|---|---|---|
| Manipulated Variables | Testing Number | Units | − − | − | 0 | + | ++ |
| Feed rate (pulp) | 1 | L/min | Batch | ||||
| Superficial gas velocity (Jg) | 4 | cm/s | 0.5 | 1 | 1.5 | 2 | |
| Froth level | 1 | cm | 2 | ||||
| Frother concentration | 2 | ppm | 5 | 20 | |||
| Rotor speed | 1 | rpm | 1000 | ||||
| Percent solids | 1 | % | 28–31 | ||||
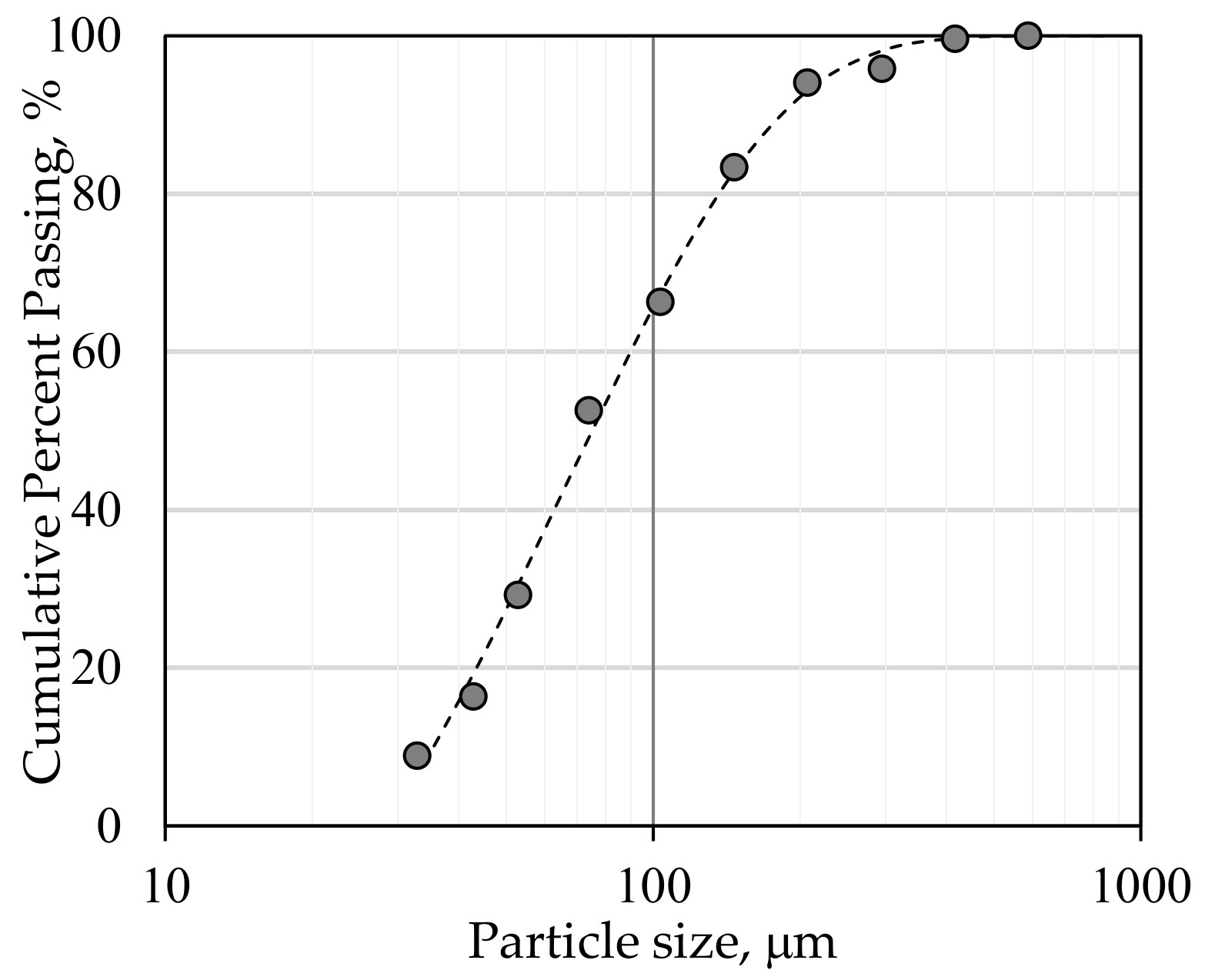
| P80 | 1 | μm | 137 | ||||
| Copper feed grade (%CuT) | 1 | % | 0.5 | ||||
| Frother Type | 1 | MIBC * | |||||
| Collector Type | 1 | SIBX * | |||||
| Collector Concentration | 1 | g/t | 20 | ||||
| pH | 1 | − | 10 | ||||
| Flotation time | min | 1 | 2 | 4 | 8 | 12 | |
| Total number of tests | 8 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Femenias, F.; Maldonado, M.; Miranda, N.; Gutierrez, L. Flotation Performance and Gas Dispersion Properties in a Laboratory Flotation Cell. Minerals 2022, 12, 1351. https://doi.org/10.3390/min12111351
Femenias F, Maldonado M, Miranda N, Gutierrez L. Flotation Performance and Gas Dispersion Properties in a Laboratory Flotation Cell. Minerals. 2022; 12(11):1351. https://doi.org/10.3390/min12111351
Chicago/Turabian StyleFemenias, Francisco, Miguel Maldonado, Nicolas Miranda, and Leopoldo Gutierrez. 2022. "Flotation Performance and Gas Dispersion Properties in a Laboratory Flotation Cell" Minerals 12, no. 11: 1351. https://doi.org/10.3390/min12111351
APA StyleFemenias, F., Maldonado, M., Miranda, N., & Gutierrez, L. (2022). Flotation Performance and Gas Dispersion Properties in a Laboratory Flotation Cell. Minerals, 12(11), 1351. https://doi.org/10.3390/min12111351







