Evaluation of Operating Performance of Backfilling Hydraulic Support Using Six Hybrid Machine Learning Models

Abstract

Previously conducted studies have established that surface subsidence is typically avoided by filling coal mined-out areas with solid waste. Backfilling hydraulic supports are critically important devices in solid backfill mining, whose operating performance can directly affect backfill mining efficiency. To accurately evaluate the operating performance, this paper proposes hybrid machine learning models for the operating states. An analysis of the factors that influence operating performance provides eight indices for evaluating backfilling hydraulic supports. Based on the data obtained from the Creo simulation model and field measurement, six hybrid models were constructed by combining swarm intelligent algorithms and support vector machines (SVM). Models of the SVM optimized by the modified sparrow search algorithm have shown improved convergence performance. The results show that the modified model has a prediction accuracy of 95.52%. The related evaluation results fit well with the actual support intervals of the backfilling hydraulic support.

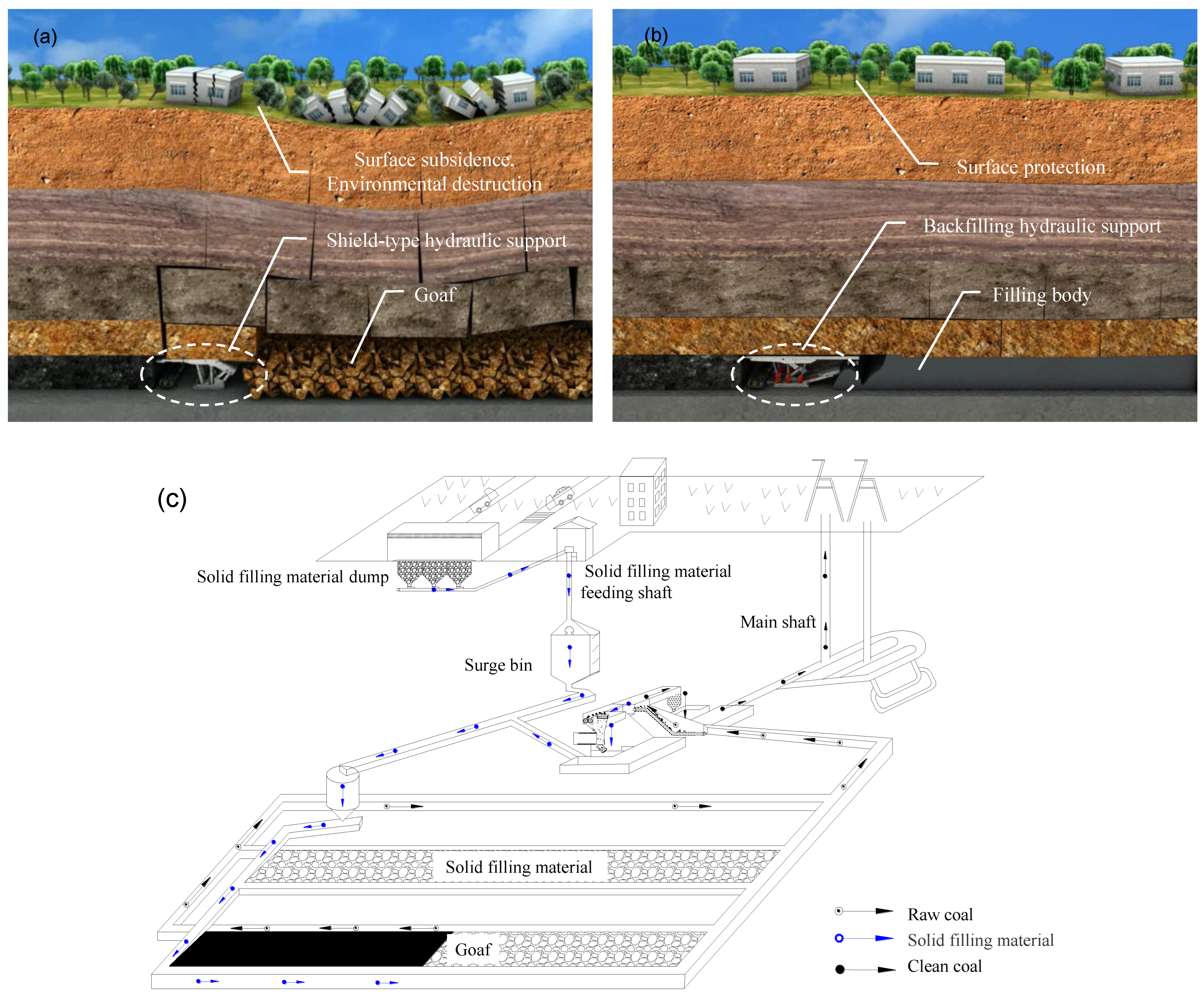
1. Introduction

China is currently the largest producer of coal in the world [1], and 90% of this coal is mined from underground [2]. However, the caving method for underground mining may result in ecological damage, such as surface subsidence and building damage [3,4,5], as shown in Figure 1a. In order to preserve the ecological balance of mined areas, filling methods are preferred [6]. For example, caulking of gobs and filling cave-in voids with fine-grained binder mixtures based on tailings or other mining waste is practiced in Poland [7] and India [8], in order to restrain the deformation of rock mass. In Russia, the use of stowing during the development of salt deposits, along with the adoption of waste-free production, makes mining operations safer [9,10]. German scholars found that the nanomodified backfill based on the water-soluble ores can increase the strength properties of artificial mass while reducing binder consumption [11]. Meanwhile, solid filling using coarse-grained gangue has been applied in China [12], as the high filling rate can ensure safe coal mining under buildings, railways, and water bodies [13]. All the above filling methods have been adopted widely, among which solid filling has higher filling rate and better control effect on the rock strata, while paste filling has higher efficiency and better economy.

As shown in Figure 1b, using solid backfill mining, goafs can be filled to avoid ground depression. As shown in Figure 1c, the solid backfilling material is transported as follows: solid filling material dump → solid filling material feeding shaft → surge bin (underground) → goaf (the blue route in Figure 1c). In addition to supporting the roof, the backfilling hydraulic support can also compress the solid backfilling material [14]. After the solid backfilling material falls from the scraper conveyor (part 5 in Figure 2), the tamping structure at the back of the backfilling hydraulic support (part 6 in Figure 2) compacts so that complete contact with the roof is realized [12]. Therefore, the backfilling hydraulic support serves as a key piece of equipment [15]. Different operating states of the hydraulic supports can directly affect the supporting performance and degree of tamping of the filling body. Therefore, it is necessary to evaluate the operating performance of backfilling hydraulic supports, including structural characteristics, tamping characteristics, and support characteristics, and identify the favorable operating interval for filling performance.

Previously conducted studies have established that simulation, experiments, and comprehensive evaluation is used for investigating operating state of hydraulic supports. For example, [16] measured both the posture and straightness of hydraulic supports with a point cloud, which is of considerable significance to unassisted measurement. Dynamic simulation can be used to analyze the stability of backfilling hydraulic supports, which can provide a basis for the optimization design and stability evaluation of backfilling hydraulic supports [17]. Ren et al. [18] conducted a dynamic impact test on hydraulic supports based on a physical model, and monitored and evaluated the impact resistance performance. To evaluate the reliability of backfilling hydraulic supports, [15] comprehensively evaluated hydraulic supports by combining the entropy weight method and single-objective optimization strategy. Despite extensive research, the following problems still exist. Firstly, there are few machine learning methods used in the research of backfilling hydraulic support. Secondly, scholars mainly focused on the mechanical properties of hydraulic supports but rarely considered the structural properties.

Analyzing the above, it can be noted that applying machine learning methods to the research of traditional backfilling hydraulic support is a very topical issue. Therefore, the purpose of this study is to evaluate the operating performance of backfilling hydraulic supports by combining the swarm intelligence optimization algorithm and support vector machine, and to achieve this, it is necessary to solve the following tasks: (1) select and determine the evaluation indices of backfilling hydraulic support; (2) train the machine learning model and apply it to the evaluation of backfilling hydraulic support; (3) evaluate the performance of the machine learning model.

Accordingly, this study proposed six hybrid machine learning models and selected eight indices for evaluating the operating performance of backfilling hydraulic supports. Moreover, the generalization capability of the hybrid models was evaluated in terms of several indices, including accuracy, precision ratio (P), recall rate (R), and F₁ score. The present study can provide important reference for evaluating the operating performance of backfilling hydraulic supports.

2. Establishment of Evaluation Indices and Materials

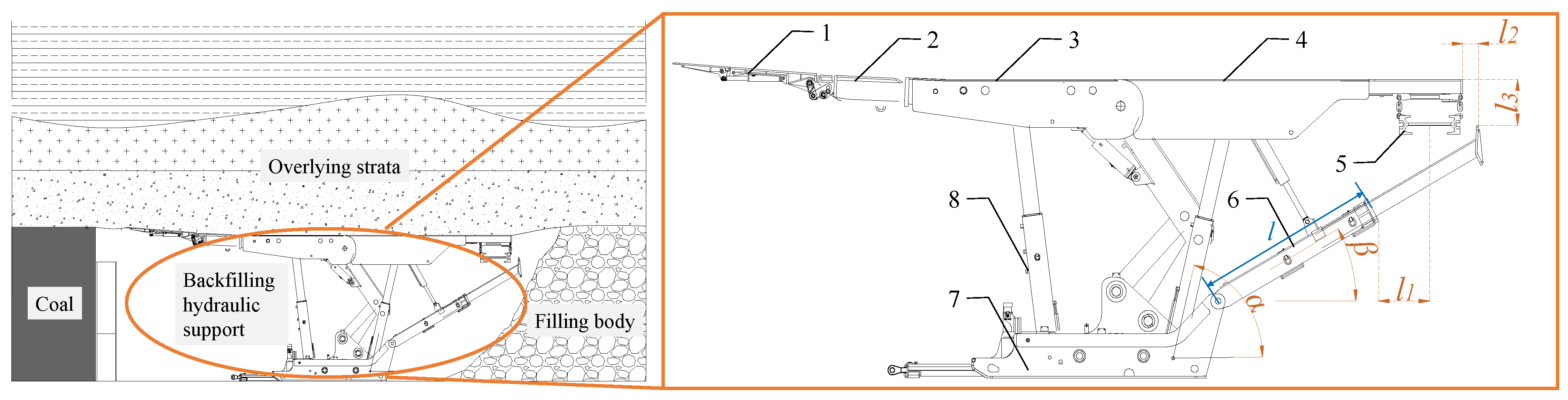
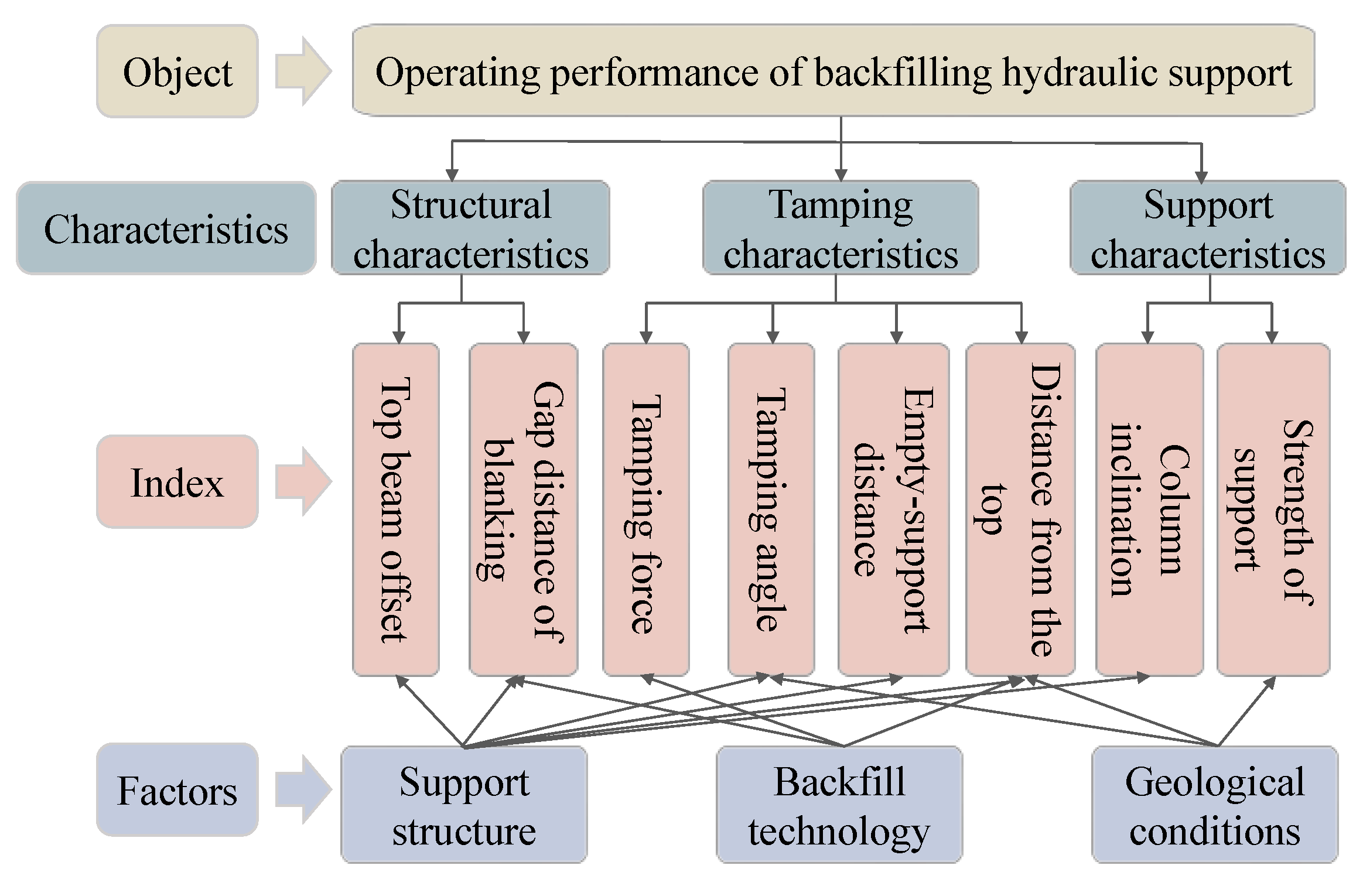
2.1. Determination of Evaluation Indices of the Operating Performances of Backfilling Hydraulic Supports

For backfilling hydraulic support, operating performances refer to dynamic operating characteristics in maintaining backfilling mining space. Hydraulic supports with different heights show different operating states. Scholars have proposed that the filling characteristics of hydraulic supports include the distance from the top, the tamping force, the strength of support, and the adaptivity to geological conditions [15]. On that basis, this study started from three main influencing factors—support structure, geological condition, and backfill technology—and summarized eight indices for evaluating the operating performances: the top beam offset, gap distance of blanking, tamping force, tamping angle, empty-support distance, distance from the top, column inclination, and strength of support. Figure 2 shows the various indices in detail.

The eight operating performance indices include the effects of support structure, geological conditions, and backfill technology on the supporting state of backfilling hydraulic supports [12]. To be specific, the support structure can affect the top beam offset, gap distance of blanking, tamping angle, empty support distance, distance from the top, and column inclination, due to the relationship of the different sizes of various components. The backfill technology can change the degree of inclination of the gravity center of the scraper conveyor and hence affect the gap distance of blanking. The blanking degree can affect both distance from the top and tamping force. With regard to geological conditions, the tamping angle, distance from the top, and strength of support can be affected by the roof settling condition. Figure 3 illustrates the effects of different factors on each index.

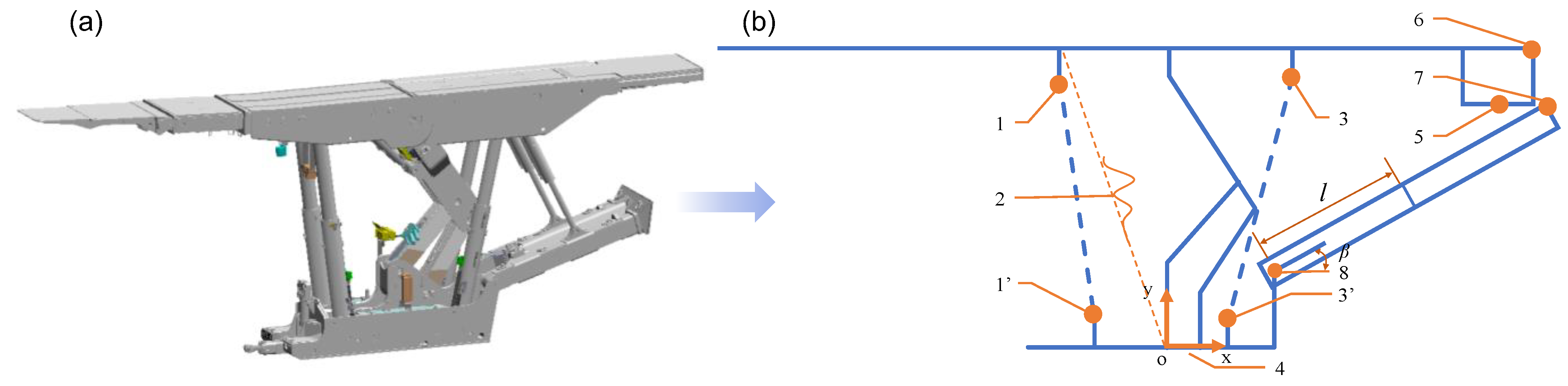
2.2. Acquisition of Operating Performance Indices and Preparation of Datasets

This study selected 4-column backfilling hydraulic supports with a supporting interval of 2900–4800 mm, and attempted the applications in the solid backfill working face with a coal seam thickness of 4.1~4.6 m.

Table 1. Parameters of filling hydraulic support.

Objects	Parameters	Objects	Parameters
Height (mm)	2900~4800	Initial support force (kN)	3870
Width (mm)	1430~1600	Working resistance (kN)	5160
Step distance (mm)	630	Support strength (MPa)	0.57
Center distance (mm)	1500	Floor specific pressure (MPa)	2.98

list the parameters of the backfilling hydraulic support.

The operating performance indices of hydraulic supports can mainly be obtained via simulation and field measurement. As shown in Figure 4, the monitoring points were set in the simulation model established by Creo software, and a servo motor was added to the model for motion simulation to record the values of various indices during the motion process. The operating performance indices can be obtained by calculating the coordinates between multiple monitoring points, as shown in

Table 2. The statistical parameters for the dataset.

Indices	Calculation Method	Minimum	Maximum	Unit	Source
Top beam offset	X6-X06	0	216.4	mm	Simulation model
Gap distance of blanking	X5-X8-l*cos(β)	120	1310.9	mm
Empty support distance	X7-X6	69.3	1202.9	mm
Distance from the top	Y6-Y7	370.7	629.3	mm
Front column inclination	arctan(|(Y1-Y1’)/(X1-X1’)|)	70.2	76.5	°
Rear column inclination	arctan(|(Y3-Y3’)/(X3-X3’)|)	73.7	83.8	°
Tamping angle	arctan(Y7/X7)	13.2	37.3	°
Tamping force	-	695	762	kN	Field measurement
Strength of support	-	26	47	Mpa

. In addition, the tamping force and support strength are obtained from the oil cylinder of the hydraulic support via field measurement.

A total of 334 sets of data were collected to train and test six hybrid models. Next, the data can be divided into the training set and the test set according in the ratio 8:2; to be specific, the training set includes 267 sets of data, and the test set includes 67 groups of data. Table 2 summarizes the data statistics for the entire dataset.

3. X₀₆—Initial abscissa of monitoring point 63. Methodology

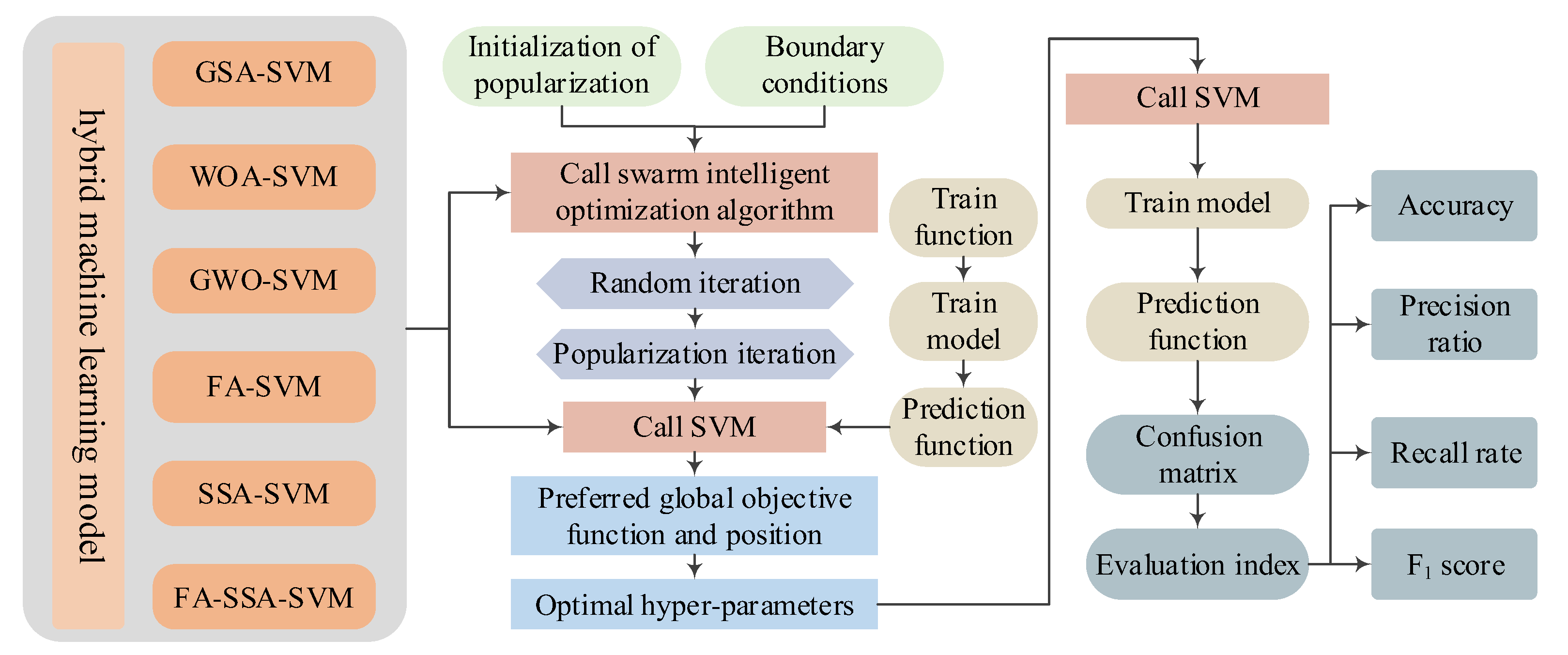
3.1. Principle of Hybrid Machine Learning Models

In this study, six swarm intelligent optimization algorithms and SVM were included in the hybrid models, as described in Section 3.2 and Section 3.3. Figure 5 displays the combination modes of swarm intelligent optimization algorithms and SVM. SVM was used for establishing the relationships between the operating performances of hydraulic supports and the eight indices, while swarm intelligent optimization algorithms were used for optimizing the SVM hyperparameters.

3.2. Support Vector Machine

SVM is a machine learning method established on the basis of statistical theory [19,20], which involves establishing an interval zone among different data for classification. For high-dimensional data, the data can be mapped to a high-dimensional space by the defined kernel function and then classified. As shown in Figure 6, a hyperplane y = w^TΦ(x) + b can be established, in which w and b denote the normal vector and offset, respectively. By calculating the distance between support vectors and the hyperplane, the following basic equation can be derived:

$$\begin{array}{l}\min \frac{1}{2}{\Vert w\Vert }^2+C{\displaystyle \sum _{i=1}^m\epsilon }\\ s.t.,\{\begin{array}{l}{y}_i(w^T\cdot \varphi (x_i)+b)\ge 1-\epsilon \\ \epsilon \ge 0\end{array}\end{array}$$

(1)

where C denotes the penalty parameter and ε denotes the relaxation factor. In applications, a fully linear separable hyperplane can hardly be determined for classifying the data samples. It is therefore necessary to control the width of the interval zone in the form of a slack variable.

The above problem can be regarded a constrained convex quadratic programming problem. The Lagrangian multiplier α can be introduced, and the constraint conditions can be fused into the objective function by the Lagrangian function to solve the dual problem:

$$\begin{array}{l}\max \left[-\frac{1}{2}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m({\alpha }_i-{\alpha }_i{}^{\ast })({\alpha }_j-{\alpha }_j{}^{\ast })\varphi (x_i)\cdot \varphi (x_j)+{\displaystyle \sum _{i=1}^m({\alpha }_i-{\alpha }_i{}^{\ast })y_i-{\displaystyle \sum _{i=1}^m({\alpha }_i+{\alpha }_i{}^{\ast })\epsilon }}}}\right]\\ s.t.,{\displaystyle \sum _{i=1}^m({\alpha }_i-{\alpha }_i{}^{\ast })=0,}0\le {\alpha }_i\le C,0\le {\alpha }_i{}^{\ast }\le C\end{array}$$

(2)

The key function of SVM is to deal with nonlinear problems, which determines the mapping relationship of the training samples from the original space to the high-dimensional space. In this study, the radial basis function (RBF) was used and can be written as:

$$K(x_i,x_j)=\exp \left(-g{\Vert x_i-x_j\Vert }^2\right)$$

(3)

where g denotes the parameter of the RBF.

Based on the above analysis, two hyper-parameters (C and g) determine the generalization capability of SVM, which should be optimized. Next, six swarm intelligent optimization algorithms were introduced for the optimization of the SVM hyperparameters.

3.3. Hybrid Machine Learning Models

3.3.1. SVM Models Optimized by a Single Swarm Optimization Algorithm

(1)

SVM optimized by gravity search algorithm (GSA-SVM)

GSA is an optimization algorithm based on the law of universal gravitation and Newton’s second law [21]. In this paper, 30 particles are set and they move constantly in the searching space, and accelerations, velocities, and hyperparameters of SVM can be updated for optimization. With the optimum hyperparameters, SVM can get better classification results.

(2)

SVM optimized by whale optimization algorithm (WOA-SVM)

WOA achieves optimization search by simulating the swarm search of humpback whales, and how they encircle, chase, and attack prey [22]. The unique foraging method of whales can be divided into two phases—upward spiral motion and dual circulation. In this analysis, the number of whales were set to 30 and subjected to 100 iterations to optimize SVM.

(3)

SVM optimized by gray wolf optimization algorithm (GWO-SVM)

Using GWO, the wolf pack can be classified into four levels [23]. High-level gray wolves can dominate low-level wolves. The wolf pack can move close to the prey according to the relationship between the gray wolf’s adaptive values and various levels to finish the optimization process. From the 100 iterations, the best wolf can be selected from among the 30 considered initially, and this represents the best parameters of the SVM.

(4)

SVM optimized by firefly algorithm (FA-SVM)

FA can achieve the optimization of position by simulating the process whereby fireflies move towards the individual with the greatest brightness in the neighborhood [24]. The attraction among fireflies can be attributed to two factors—brightness and degree of attraction. The fluorescent brightness of a firefly depends on the target value at the position. A higher degree of brightness is indicative of a more favorable target value at the position. The attraction degree is related to brightness. A brighter firefly possesses greater attraction, which can attract the other individuals. In this study, the number of fireflies is set to 30, and the optimal SVM hyperparameters can be obtained after 100 iterations.

(5)

SVM optimized by sparrow search algorithm (SSA-SVM)

SSA is a swarm intelligent optimization algorithm that simulates the sparrow’s preying process [25]. Sparrow groups can be classified into three types—finders, newcomers, and guards. Finders are responsible for leading the group in the search for food. The newcomers can provide the foraging direction and be transformed into finders. Guards are responsible for vigilance. Through 100 iterations, the best location of the sparrow can be selected from among the 30 sparrows that were set initially, which represents the best parameters of SVM.

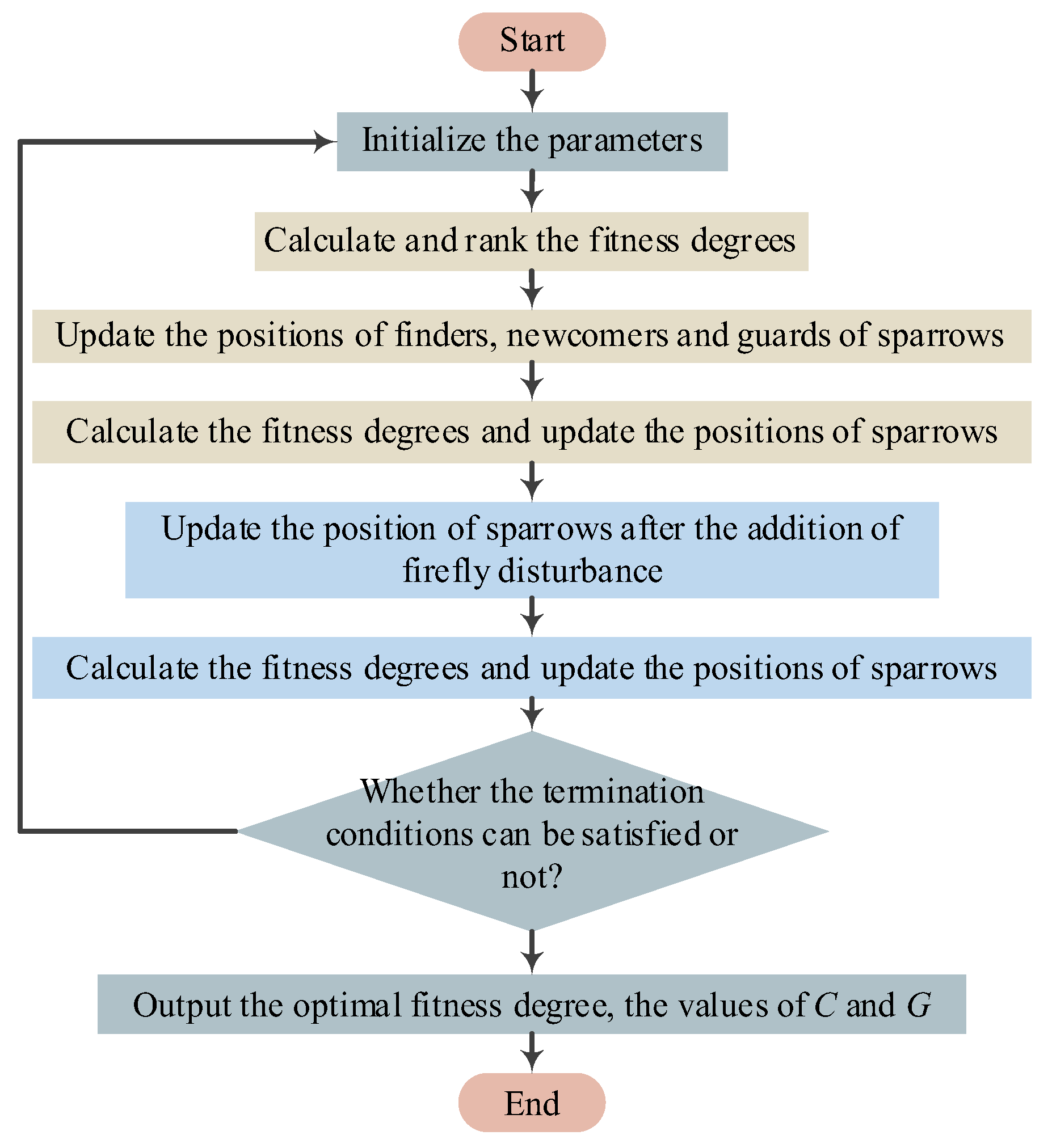
3.3.2. Model of Improved Optimization Algorithm—SVM Optimized by Firefly-Disturbed SSA (FA-SSA-SVM)

According to previous experimental data, SSA shows relatively slow convergence rate in spite of high precision [26,27]; moreover, SSA may easily be trapped into a local optimal solution range because of early-maturing [28]. FA has a relatively simple algorithm structure and fast convergence rate [29,30]. Accordingly, by combining the advantages of FA and SSA, FA was introduced for the improvement of SSA. Figure 7 illustrates the principle of firefly-disturbed SSA. After food searching by sparrows, firefly can impose disturbance on the fitness degree, and then seek the firefly individual with strongest attraction according to its movement logistics for position updating. Accordingly, the optimization ability of SSA can be enhanced.

4. Results and Discussion

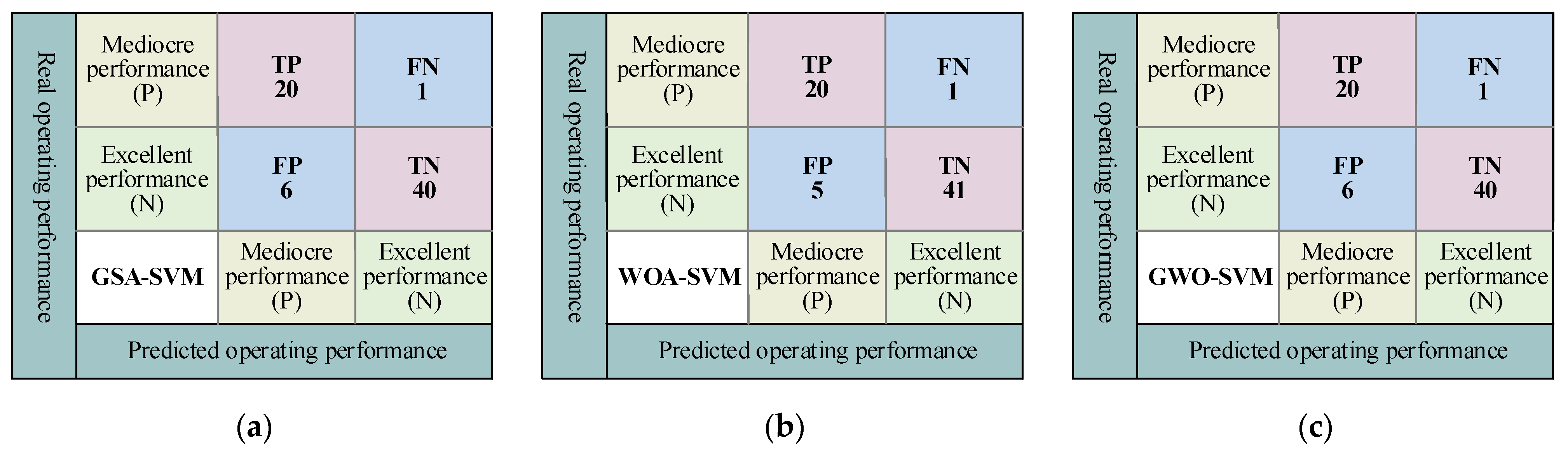
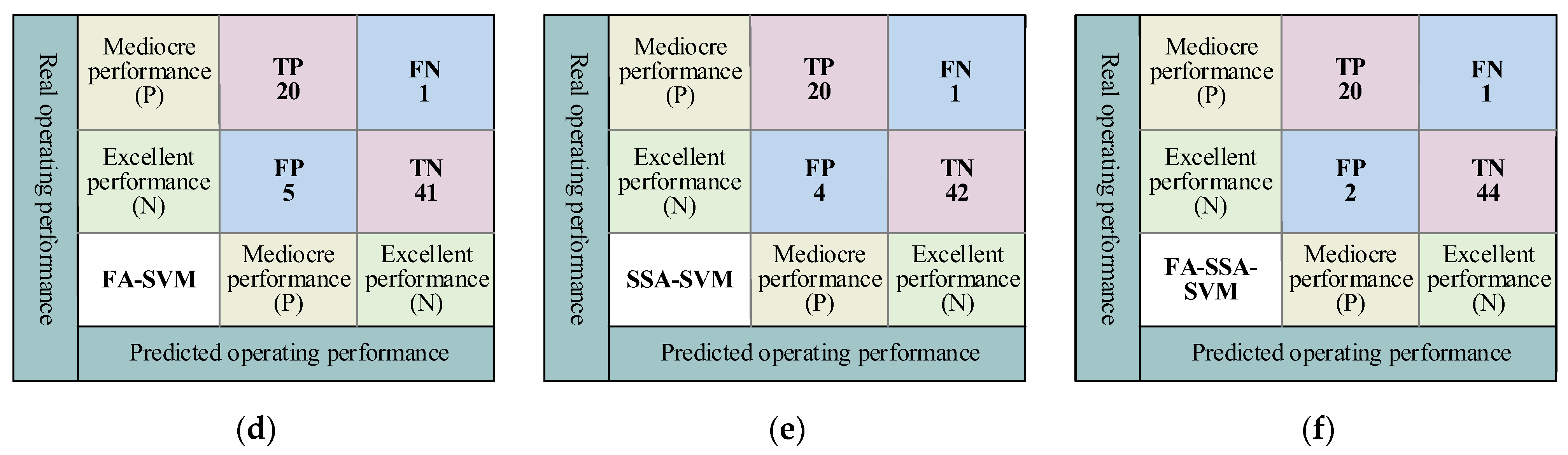
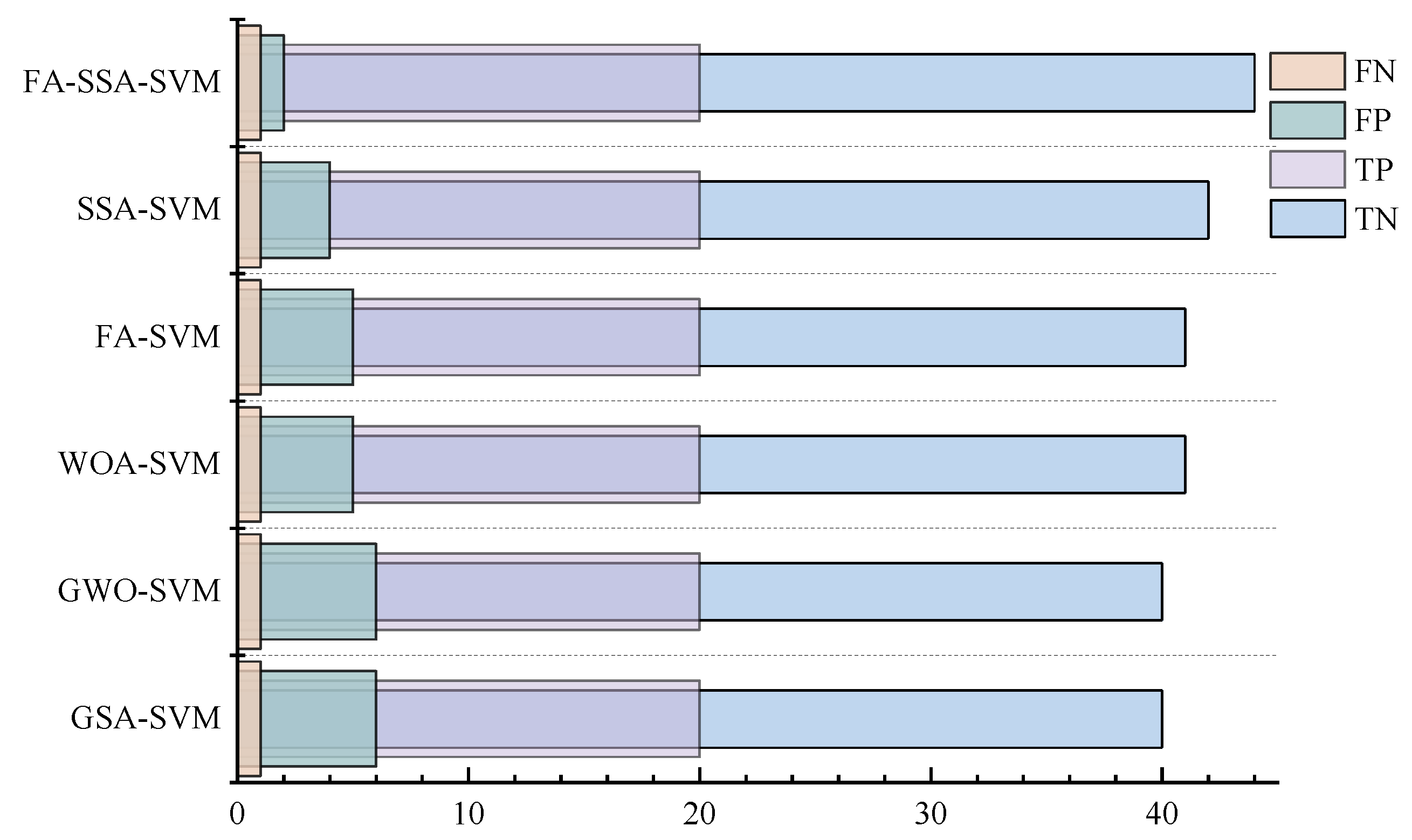
4.1. Model Validation Evaluation and Contrast Analysis

The model was then validated and evaluated to examine the generality. In this study, in order to explore the effects of classification accuracy and data imbalance, four evaluation indices (accuracy, P, R, and F₁ score) [31,32] for SVM classification evaluation can be selected based on the confusion matrix generated in prediction. In addition, the convergence of various models is evaluated by the convergence curve.

These four classification evaluation indices were calculated based on True Positives (TP), False Negatives (FN), False Positives (FP), and True Negatives (TN) in the confusion matrix [33]; their definitions are listed in

Table 3. The meaning of confusion matrix.

Index	Meaning
TP	The positive sample is predicted to be positive.
FN	The positive sample is predicted to be negative.
FP	The negative samples are predicted to be positive.
TN	The negative samples are predicted to be negative.

. According to the definitions of the confusion matrix, the appropriate support interval of the supports can be regarded as favorable performance, i.e., the negative sample; otherwise, the support interval outside the appropriate range can be regarded as general performance, i.e., the positive sample.

The classification accuracy is defined as the proportion of accurately-classified samples in the total samples:

$$\mathrm{accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FN}+\mathrm{FP}+\mathrm{TN}}$$

(4)

The recall ratio is defined as the proportion of accurately-predicted samples in actually positive samples:

$$\mathrm{R}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$

(5)

The precision ratio is defined as the proportion of accurately-predicted samples in the samples that were predicted as positive:

$$\mathrm{P}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}$$

(6)

F₁ scores are defined as the harmonic mean of the recall rate and the precision ratio:

$$\frac{2}{\mathrm{F}1}=\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{P}}$$

(7)

$$\mathrm{F}1=2\times \frac{\mathrm{P}\times \mathrm{R}}{\mathrm{P}+\mathrm{R}}=\frac{2\mathrm{TP}}{2\mathrm{TP}+\mathrm{FP}+\mathrm{FN}}$$

(8)

Figure 8 and Figure 9 show the confusion matrices of different models and their comparison, respectively. Using the various models, the TP and FN samples were similar, while FP and TN samples differed greatly. FA-SSA-SVM had the smallest FP and the largest TN. The advantage of FA-SSA-SVM lies in the fact that it was comfortably able to avoid the error prediction (i.e., negative was mis-predicted as positive, FP), and it also achieved correct prediction (i.e., negative was predicted as negative, TN).

Figure 10 lists the evaluation indices of the different models and their comparison. Various models differed slightly in the values of R but greatly in the values of accuracy, P and F₁ score. As shown in Figure 10, through overall consideration, FA-SSA-SVM ranked the first in terms of classification ability, followed by SSA-SVM, WOA-SVM, FA-SVM, and finally by GWO-SVM and GSA-SVM, (i.e., FA-SSA-SVM > SSA-SVM > FA-SVM = WOA-SVM > GWO-SVM = GSA-SVM).

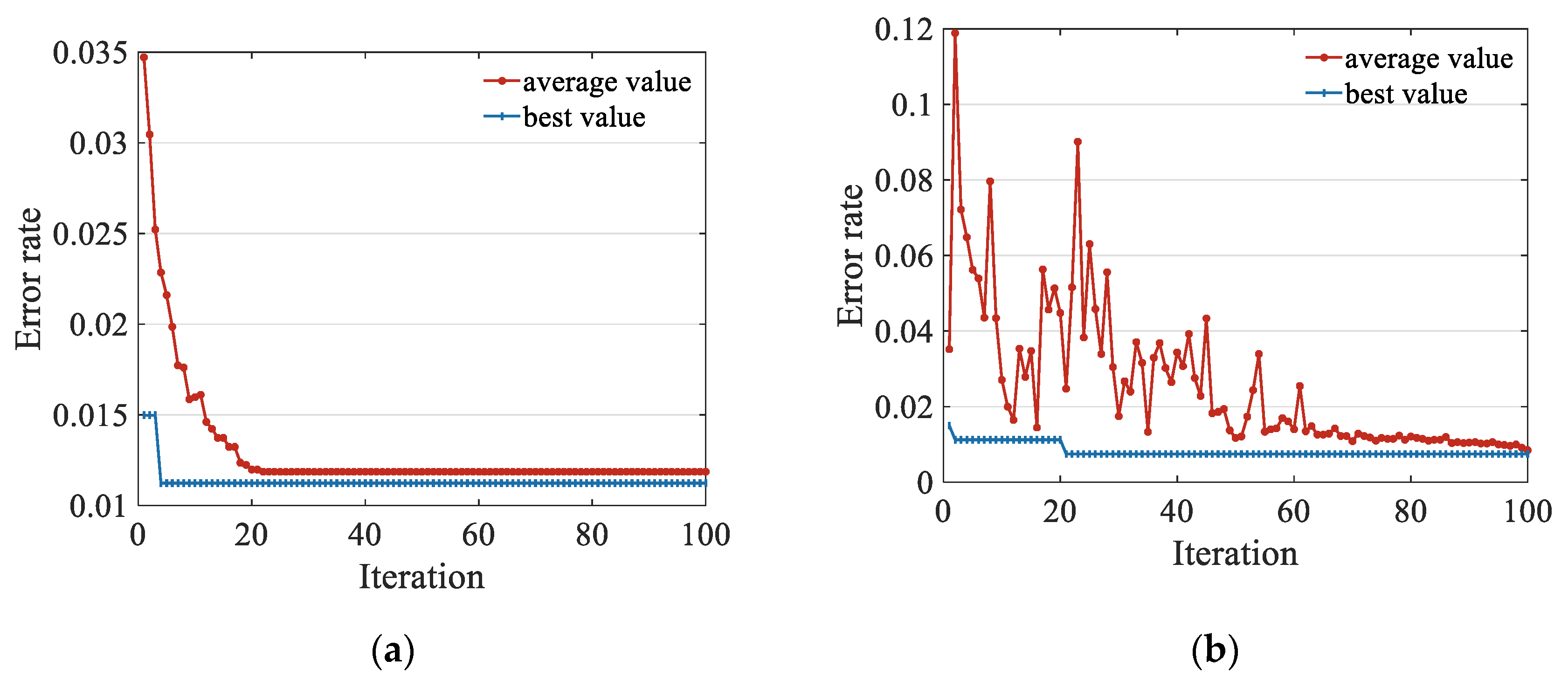
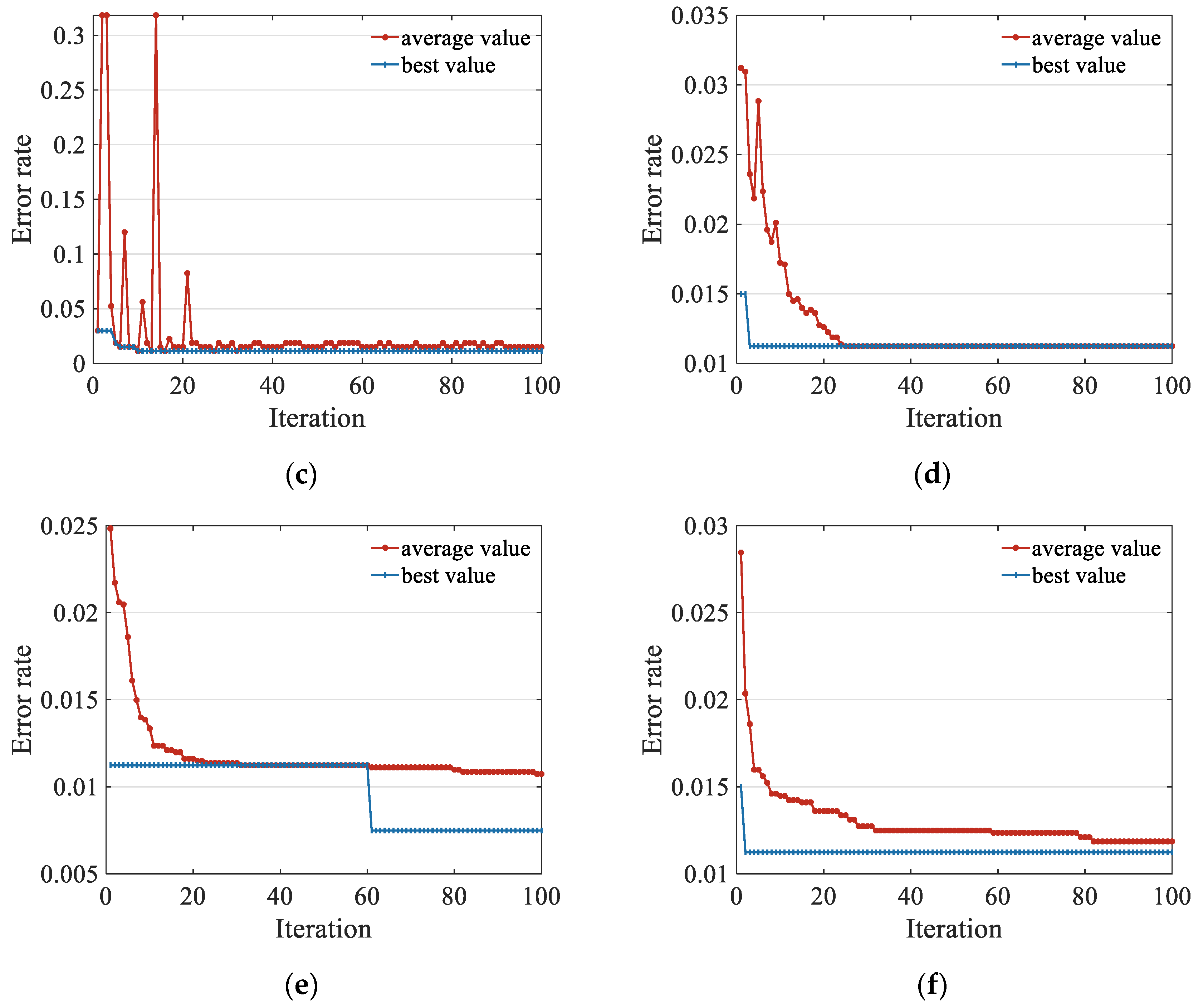
4.2. Convergence Analysis of the Models

In addition to the evaluation index based on the confusion matrix, the convergence of the model was also compared. Figure 11 shows the convergence of the six hybrid models. Each model takes the predicted minimum error rate as the value of the objective function. The optimal value of the objective function in each iteration and the average value of the population were obtained. It can be found that the convergence was faster in GSA-SVM and FA-SVM, and the average value fluctuated greatly in the iterative process of WOA-SVM and GWO-SVM, while the other models were less volatile. In addition, SSA-SVM converged slowly, but it effectively minimized the objective function. The improved FA-SSA-SVM integrated the advantages of FA and SSA, which meant that it moved fast to attain the highest accuracy.

Overall, the FA-SSA-SVM model performed best both in model classification ability and convergence performance, and the related prediction results were most consistent with actual appropriate support intervals.

5. Conclusions

In this study, a systematic comparative analysis and verification of six hybrid models for evaluating the operating performance of backfilling hydraulic supports has been made. These hybrid models were obtained by combining swarm intelligence optimization algorithms with SVM. At the same time, the performance of these hybrid models was evaluated by the accuracy, P, R, F₁ score, and convergence curve. The following conclusions can be obtained:

(1)

The calculation and acquisition methods for the operating performance indices are determined. The six SVM-based hybrid models proposed in this paper show a good potential for evaluating the operating performance of backfilling hydraulic supports.

(2)

In terms of evaluation indices, the FA-modified SSA-SVM shows the best accuracy (95.52%), precision ratio (95.65%), and F₁ score (95.447), and the six hybrid models can be arranged in the order of their evaluation performance from high to low as FA-SSA-SVM, SSA-SVM, FA-SVM, WOA-SVM, GWO-SVM, and GSA-SVM.

(3)

FA-SSA-SVM and GSA-SVM give the fastest and smoothest convergence. Overall, the FA-modified SSA-SVM showed the best evaluation capability and convergence performance, and the related prediction results are most consistent with the actual appropriate support interval.