Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation
Abstract
:1. Introduction
2. True Triaxial Model Test
2.1. Test System
2.2. Specimen Preparation
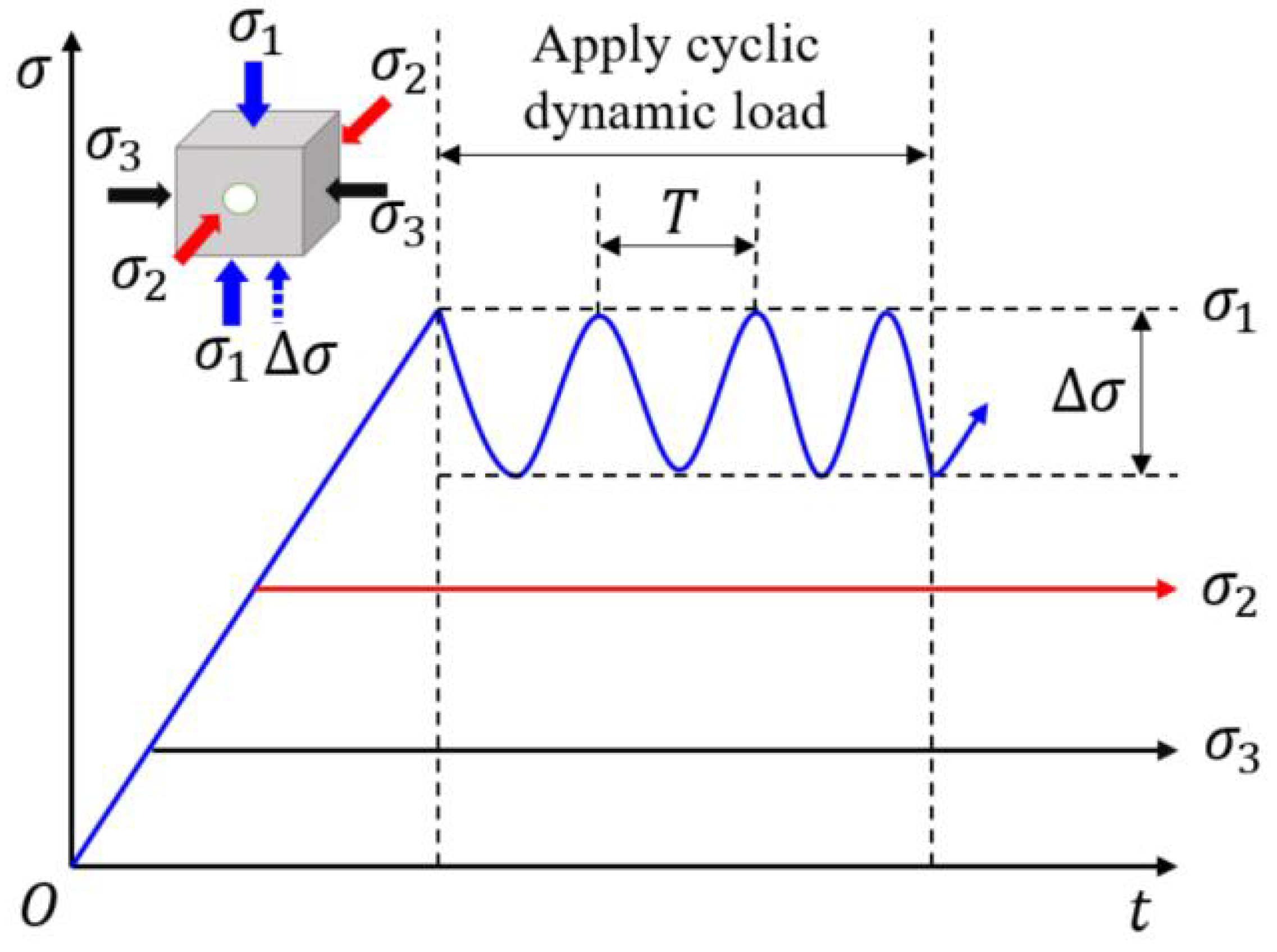
2.3. Experimental Protocol
3. Influence of Cyclic Dynamic Load Amplitude on Failure Characteristics of Surrounding Rock
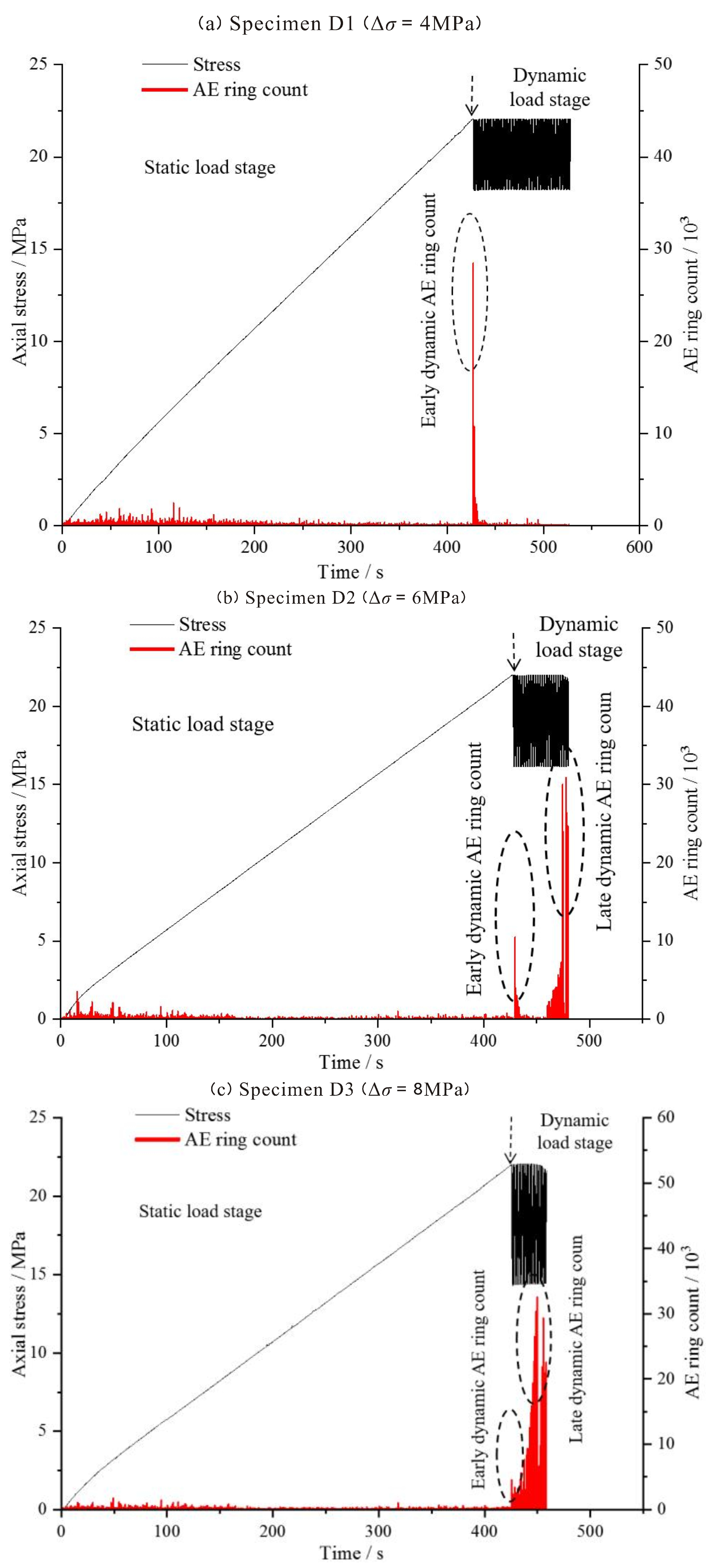
3.1. AE Characteristics
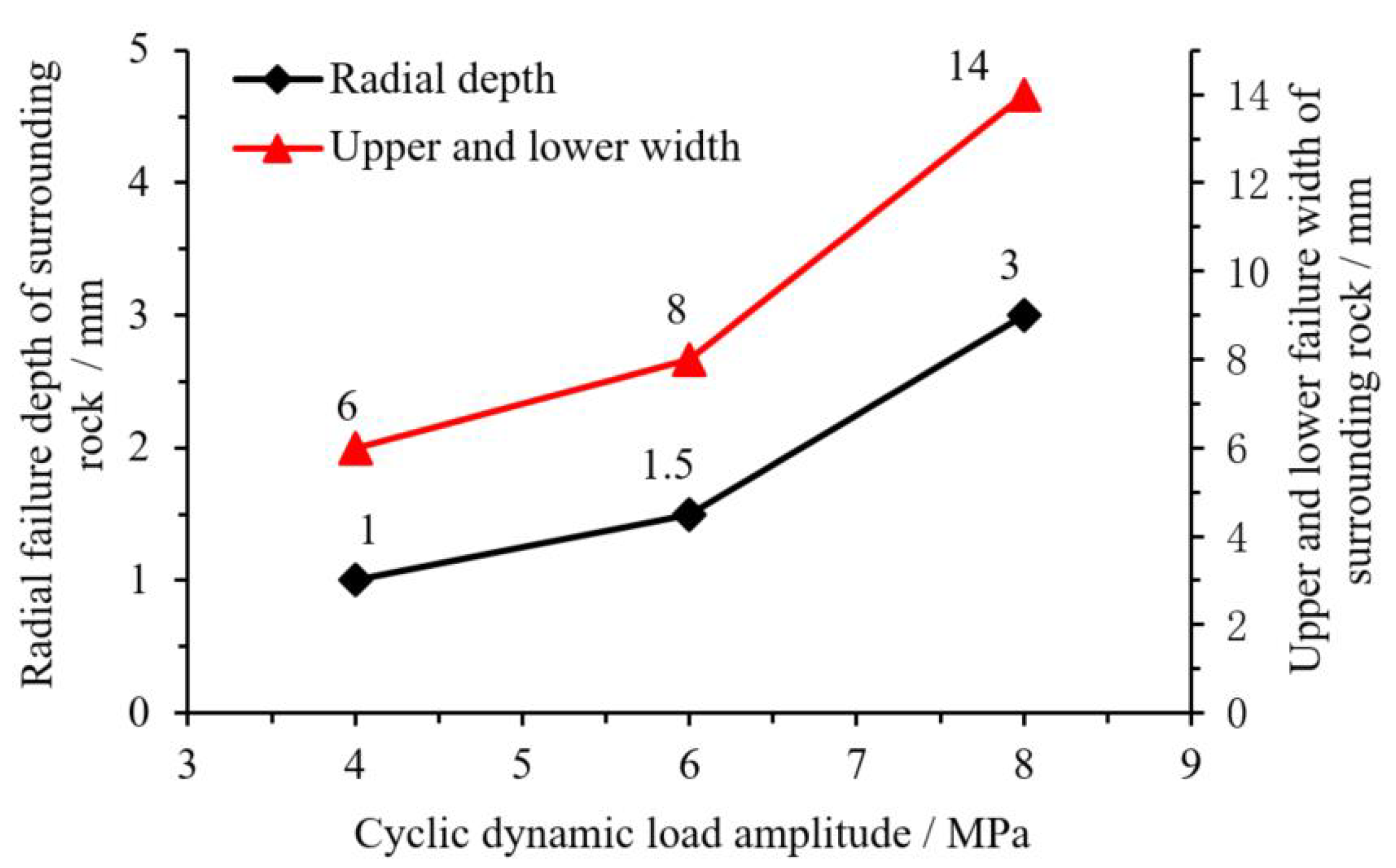
3.2. Ultimate Failure Modes of Surrounding Rocks
4. Influence of Intermediate Principal Stress on Failure Characteristics of Surrounding Rock under Cyclic Dynamic Loading
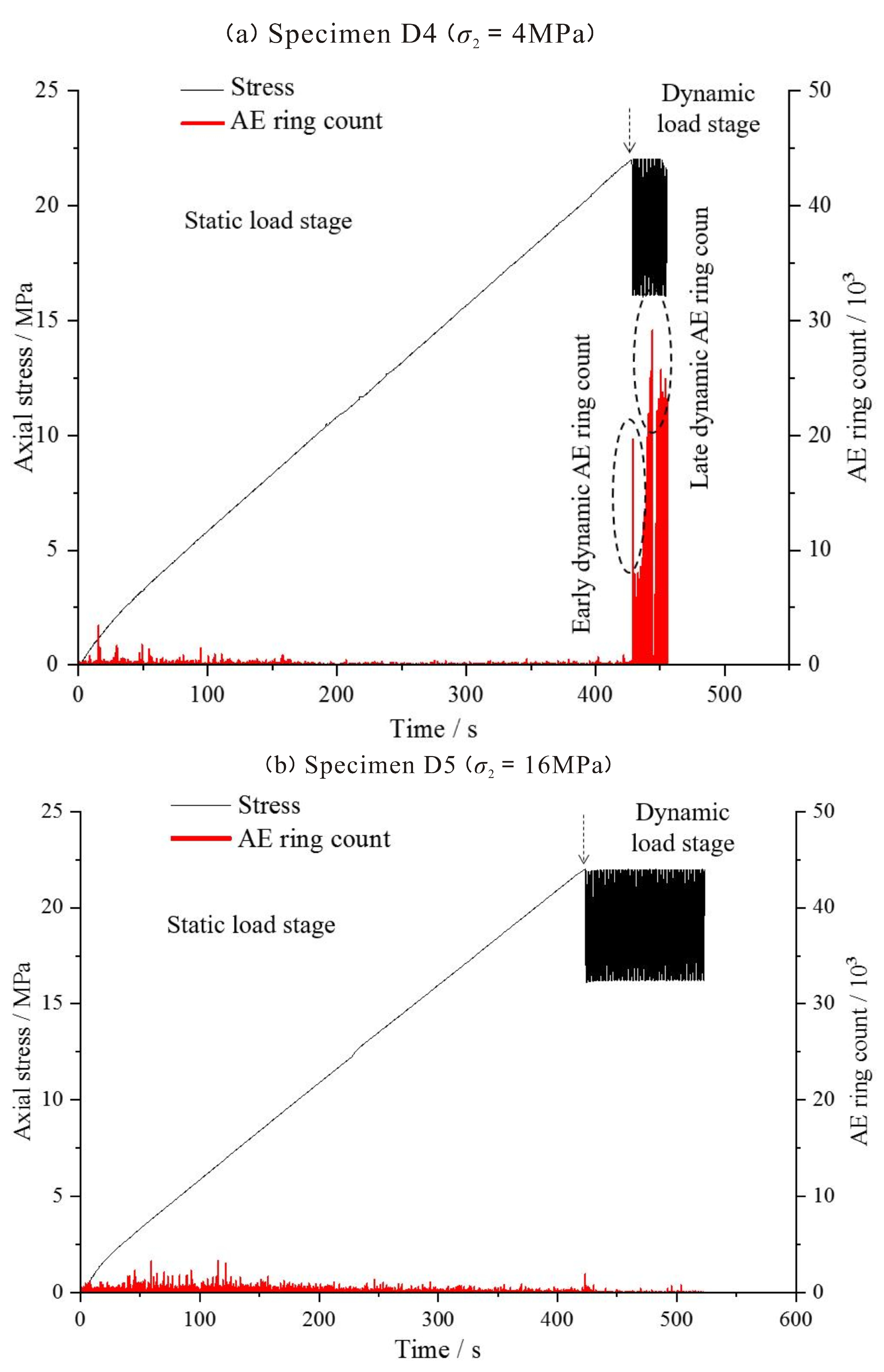
4.1. AE Characteristics
4.2. Ultimate Failure Modes of Surrounding Rocks
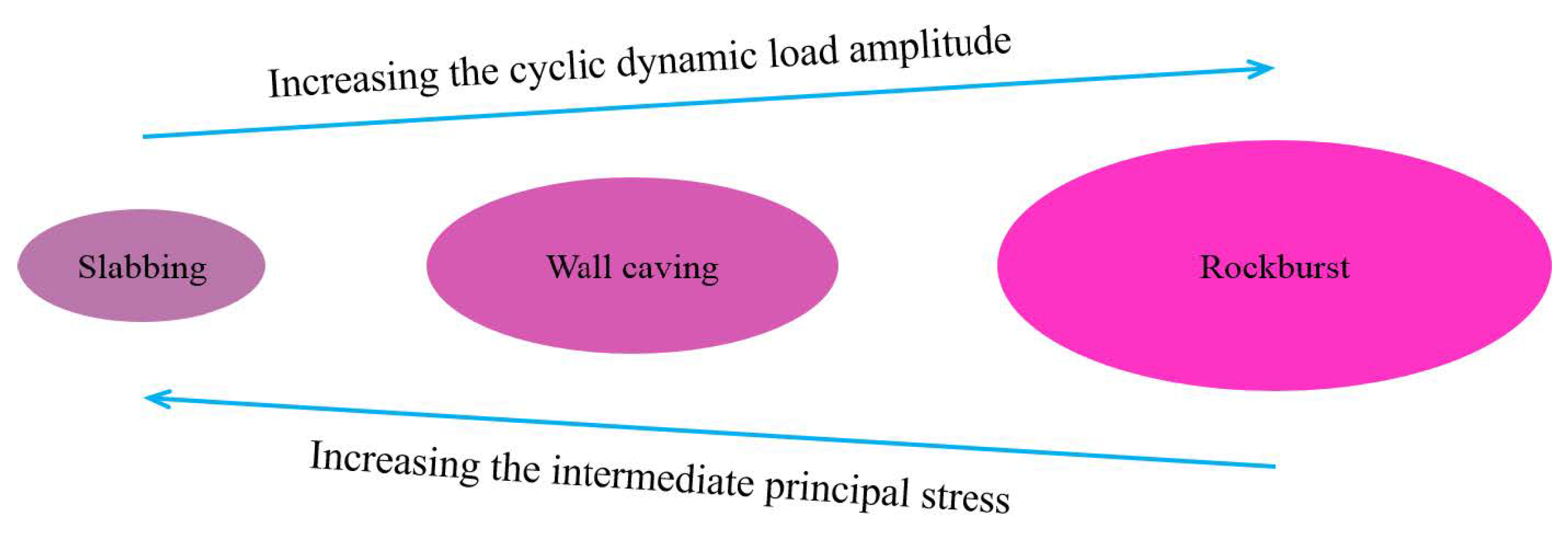
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Acoustic emission; |
| PDT | Peak definition time; |
| HDT | Hit definition time; |
| HLT | Hit lockout time; |
References
- Zhang, J.Z.; Zhou, X.P.; Zhou, L.S.; Berto, F. Progressive failure of brittle rocks with non-isometric flaws: Insights from acousto-optic-mechanical (AOM) data. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1787–1802. [Google Scholar] [CrossRef]
- Zhang, J.Z. A Study of the Failure Process in Brittle Awed Rocks and Geophysical Failure Forecast by Integrated Acousto-Optical Data. Ph.D. Thesis, Chongqing University, Chongqing, China, 2020. [Google Scholar]
- Zhang, J.Z.; Zhou, X.P. Forecasting catastrophic rupture in brittle rocks using precursory AE time series. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019276. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Zhou, X.P. AE event rate characteristics of flawed granite: From damage stress to ultimate failure. Geophys. J. Int. 2020, 222, 795–814. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhang, J.Z.; Qian, Q.H.; Niu, Y. Experimental investigation of progressive cracking processes in granite under uniaxial loading using digital imaging and ae techniques. J. Struct. Geol. 2019, 126, 129–145. [Google Scholar] [CrossRef]
- Li, L.P.; Hu, J.; Li, S.C.; Qin, C.S.; Liu, H.L.; Chen, D.Y.; Wang, J. Development of a novel triaxial rock testing method based on biaxial test apparatus and its application. Rock Mech. Rock Eng. 2021, 54, 1597–1607. [Google Scholar] [CrossRef]
- Li, L.P.; Shang, C.S.; Chu, K.W.; Zhou, Z.Q.; Song, S.G.; Liu, Z.H.; Chen, Y.H. Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel. Tunn. Undergr. Space Technol. 2021, 109, 103756. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhang, J.Z. Damage progression and acoustic emission in brittle failure of granite and sandstone. Int. J. Rock Mech. Min. Sci. 2021, 143, 104789. [Google Scholar] [CrossRef]
- Fan, Y.; Jiang, L.; Lu, W.B.; Zhou, Y.H.; Zhao, C.J.; Yan, P. Strain energy characteristics of surrounding rock under blasting load and transient release of geostress during excavation of circular tunnel. Chin. J. Rock Mech. Eng. 2017, 36, 1855–1866. [Google Scholar]
- Thongraksa, A.; Punya-in, Y.; Jongpradist, P.; Kim, H.M.; Jamsawang, P. Failure behaviors of rock masses around highly pressurized cavern: Initiation and modes of failure. Tunn. Undergr. Space Technol. 2021, 115, 104058. [Google Scholar] [CrossRef]
- Barla, M. Numerical simulation of the swelling behaviour around tunnels based on special triaxial tests. Tunn. Undergr. Space Technol. 2008, 23, 508–521. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, S.W.; Tang, C.A.; Zhu, W.C. Numerical simulation of the failure mechanism of circular tunnels in transversely isotropic rock masses. Tunn. Undergr. Space Technol. 2012, 32, 231–244. [Google Scholar] [CrossRef]
- Li, S.J.; Feng, X.T.; Li, Z.H.; Chen, B.R.; Jiang, Q.; Wu, S.Y.; Hu, B.; Xu, J.S. In situ experiments on width and evolution characteristics of excavation damaged zone in deeply buried tunnels. Sci. China Technol. Sci. 2011, 54, 167–174. [Google Scholar] [CrossRef]
- Feng, X.T.; Chen, B.R.; Ming, H.J.; Wu, S.Y.; Xiao, Y.X.; Feng, G.L.; Zhou, H.; Qiu, S.L. Evolution law and mechanism of rock bursts in deep tunnels: Immediate rockburst. Chin. J. Rock Mech. Eng. 2012, 31, 433–444. [Google Scholar]
- Dai, B.; Luo, X.Y.; Chen, L.; Tian, Y.K.; Zhang, Z.J.; Chen, Y.; Shan, Q.W. Analysis of the damage characteristics and energy dissipation of rocks with a vertical hole under cyclic impact loads. Adv. Civ. Eng. 2020, 2020, 13. [Google Scholar] [CrossRef]
- Cheon, D.S.; Jeon, S.; Park, C.; Song, W.K.; Park, E.S. Characterization of brittle failure using physical model experiments under polyaxial stress conditions. Int. J. Rock Mech. Min. Sci. 2011, 48, 152–160. [Google Scholar] [CrossRef]
- Hu, X.C.; Su, G.S.; Chen, G.Y.; Mei, S.M.; Feng, X.T.; Mei, G.X.; Huang, X.H. Experiment on rockburst process of borehole and its acoustic emission characteristics. Rock Mech. Rock Eng. 2019, 52, 783–802. [Google Scholar] [CrossRef]
- Dresen, G.; Stanchits, S.; Rybacki, E. Borehole breakout evolution through acoustic emission location analysis. Int. J. Rock Mech. Min. Sci. 2010, 47, 426–435. [Google Scholar] [CrossRef]
- Zhao, H.G.; Liu, C.; Huang, G.; Yu, B.C.; Liu, Y.B.; Song, Z.L. Experimental investigation on rockburst process and failure characteristics in trapezoidal tunnel under different lateral stresses. Constr. Build Mater. 2020, 259, 119530. [Google Scholar] [CrossRef]
- Hou, G.Y.; Jing, H.Y.; Liang, J.P.; Tan, J.P.; Zhang, Y.K.; Yang, X.; Xie, X. Experimental study on surrounding rock deformation and acoustic emission characteristics of rectangular roadway under different loads. Rock Soil Mech. 2020, 41, 1818–1828. [Google Scholar]
- Zhu, G.Q.; Feng, X.T.; Zhou, Y.Y.; Li, Z.W.; Fu, L.J.; Xiong, Y.R. Physical model experimental study on spalling failure around a tunnel insynthetic marble. Rock Mech. Rock Eng. 2020, 53, 909–926. [Google Scholar] [CrossRef]
- Kamata, H.; Mashimo, H. Centrifuge model test of tunnel face reinforcement by bolting. Tunn. Undergr. Space Technol. 2003, 18, 205–212. [Google Scholar] [CrossRef]
- Sagong, M.; Park, D.; Yoo, J.; Lee, J.S. Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression. Int. J. Rock Mech. Min. Sci. 2011, 48, 1055–1067. [Google Scholar] [CrossRef]
- Hidalgo, K.P.; Nordlund, E. Failure process analysis of spalling failure—Comparison of laboratory test and numerical modelling data. Tunn. Undergr. Space Technol. 2012, 32, 66–77. [Google Scholar] [CrossRef]
- Zhong, Z.B.; Deng, R.G.; Lv, L.; Fu, X.M.; Yu, J. Fracture mechanism of naturally cracked rock around an inverted u-shaped opening in a biaxial compression test. Int. J. Rock Mech. Min. Sci. 2018, 103, 242–253. [Google Scholar] [CrossRef]
- Mishra, S.; Kumar, A.; Rao, K.; Gupta, N. Experimental and numerical investigation of the dynamic response of tunnel in soft rocks. Structures 2021, 29, 2162–2173. [Google Scholar] [CrossRef]
- Luo, D.; Su, G.; Zhang, G. True-triaxial experimental study on mechan-ical behaviours and acoustic emission characteristics of dynamicallyinduced rock failure. Rock Mech. Rock Eng. 2020, 53, 1205–1223. [Google Scholar] [CrossRef]
- Gong, F.Q.; Luo, Y.; Li, X.B.; Si, X.F.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Si, X.F.; Huang, L.Q.; Gong, F.Q.; Liu, X.L.; Li, X.B. Experimental investigation on influence of loading rate on rockburst in deepcircular tunnel under true-triaxial stress condition. J. Cent. South Univ. 2020, 27, 2914–2929. [Google Scholar] [CrossRef]
- Luo, Y.; Gong, F.Q.; Li, X.B.; Wang, S.Y. Experimental simulation inves-tigation of influence of depth on spalling characteristics in circular hardrock tunnel. J. Cent. South Univ. 2020, 27, 891–910. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Li, F.; Duan, K.; Yu, G.Y.; Cheng, L.; Guo, X. Experimental investigation on splitting failure of high sidewall cavern under three-dimensional high in-situ stress. Tunn. Undergr. Space Technol. 2021, 108, 103725. [Google Scholar] [CrossRef]
- Zhang, S.R.; Sun, B.; Wang, C.; Yan, L. Influence of intermediate principal stress on failure mechanism of hard rock with a pre-existing circular opening. J. Cent. South Univ. 2014, 21, 1571–1582. [Google Scholar] [CrossRef]
- Mei, S.M.; HU, X.C.; Su, G.S.; Chen, G.Y. Model test study of the influence of intermediate principal stress on rockburst in tunnel. Rock Soil Mech. 2019, 40, 3959–3968. [Google Scholar]
- Aggelis, D.; Mpalaskas, A.; Matikas, T. Investigation of different fracture modes in cement-based materials by acoustic emission. Cem. Concr. Res. 2013, 48, 1–8. [Google Scholar] [CrossRef]






| Type | /MPa | /MPa | /(g·cm−3) | E/GPa |
|---|---|---|---|---|
| Model material | 21.1 | 2.2 | 1.96 | 26.57 |
| Static Load | Cyclic Dynamic Load | ||||
|---|---|---|---|---|---|
| No. | /MPa | /MPa | /MPa | /MPa | f/Hz |
| D1 | 22 | 8 | 2 | 4 | 1 |
| D2 | 22 | 8 | 2 | 6 | 1 |
| D3 | 22 | 8 | 2 | 8 | 1 |
| D4 | 22 | 4 | 2 | 6 | 1 |
| D5 | 22 | 16 | 2 | 6 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Gao, P.; Cao, Y.; Gong, W.; Zhang, S.; Zhang, J. Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation. Minerals 2022, 12, 134. https://doi.org/10.3390/min12020134
Li B, Gao P, Cao Y, Gong W, Zhang S, Zhang J. Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation. Minerals. 2022; 12(2):134. https://doi.org/10.3390/min12020134
Chicago/Turabian StyleLi, Binglei, Pengfei Gao, Yangbing Cao, Weiguo Gong, Sui Zhang, and Jianzhi Zhang. 2022. "Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation" Minerals 12, no. 2: 134. https://doi.org/10.3390/min12020134
APA StyleLi, B., Gao, P., Cao, Y., Gong, W., Zhang, S., & Zhang, J. (2022). Damage and Failure Characteristics of Surrounding Rock in Deep Circular Cavern under Cyclic Dynamic Load: A True Triaxial Experiment Investigation. Minerals, 12(2), 134. https://doi.org/10.3390/min12020134







