Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experiment Methods
2.2.1. Experimental Design
2.2.2. Testing Procedure
3. Results
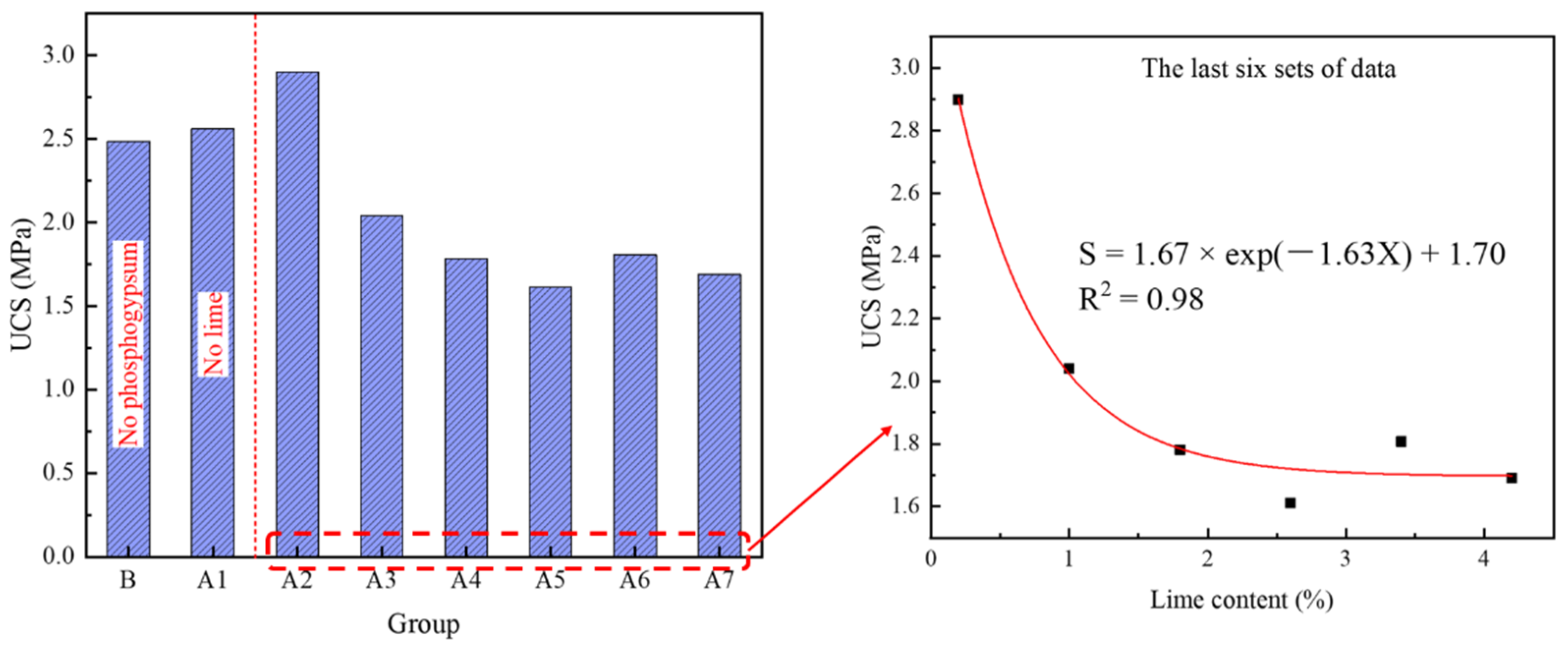
3.1. Strength Attributes
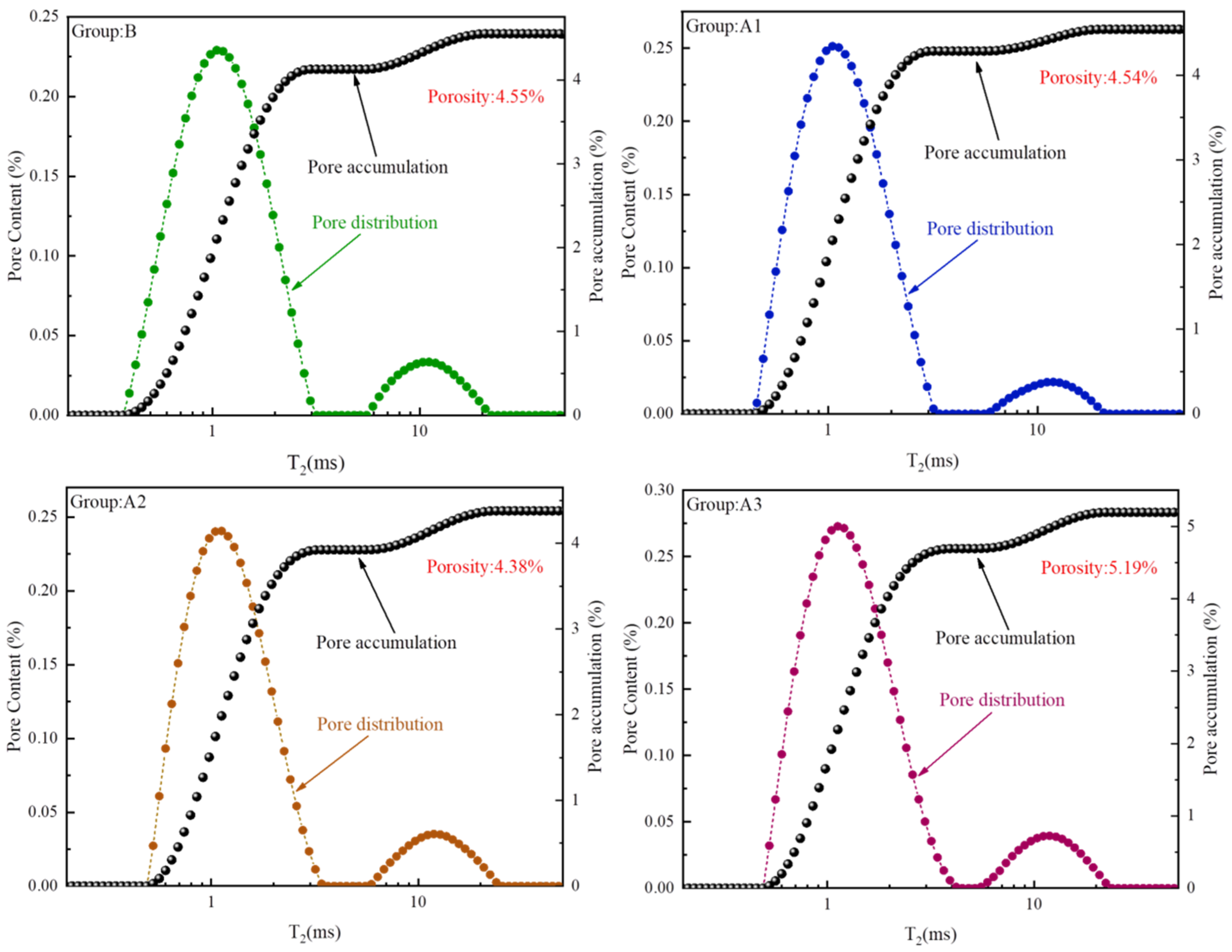
3.2. NMR Characteristics
3.3. SEM Characteristics
4. Discussion and Analysis
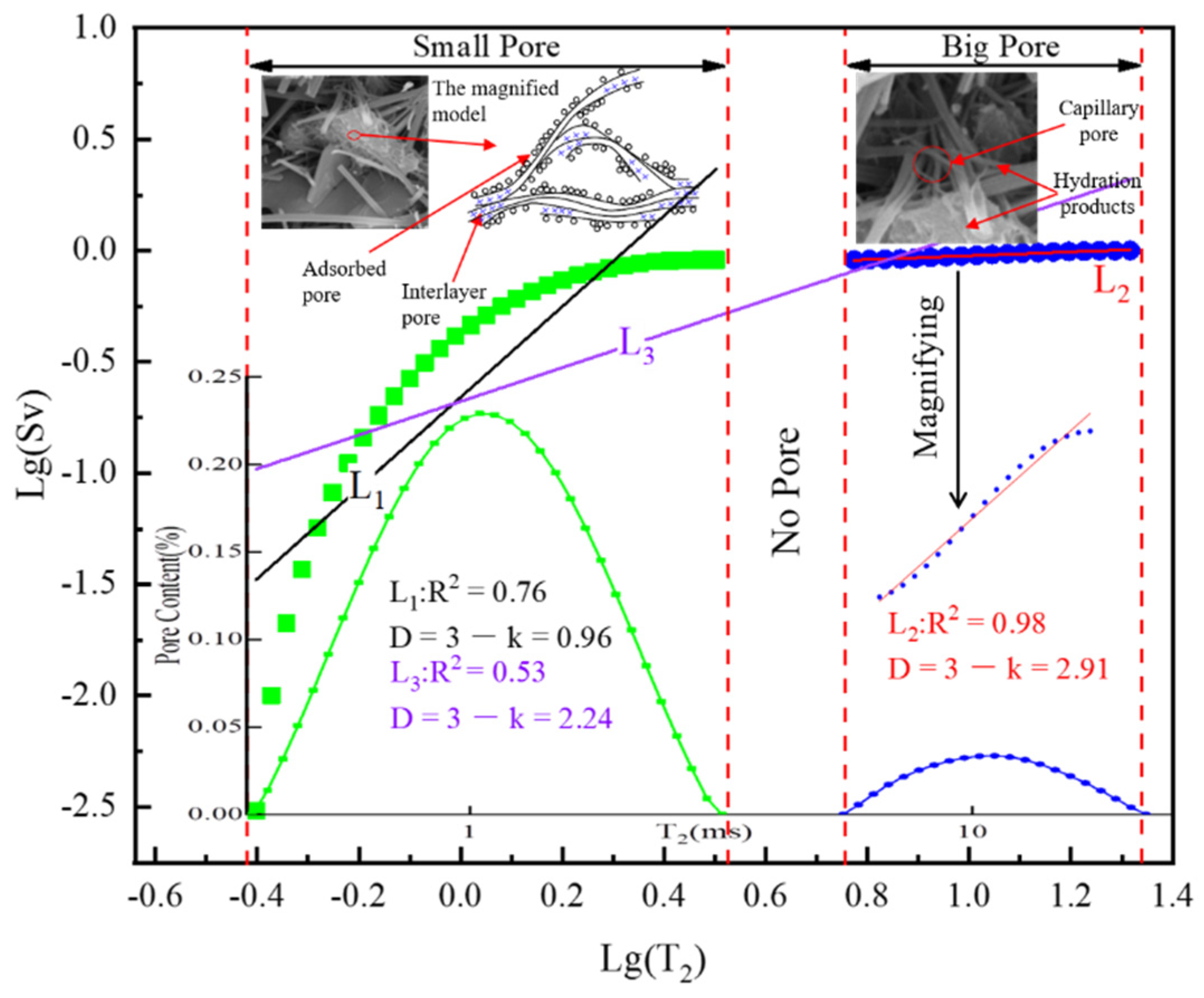
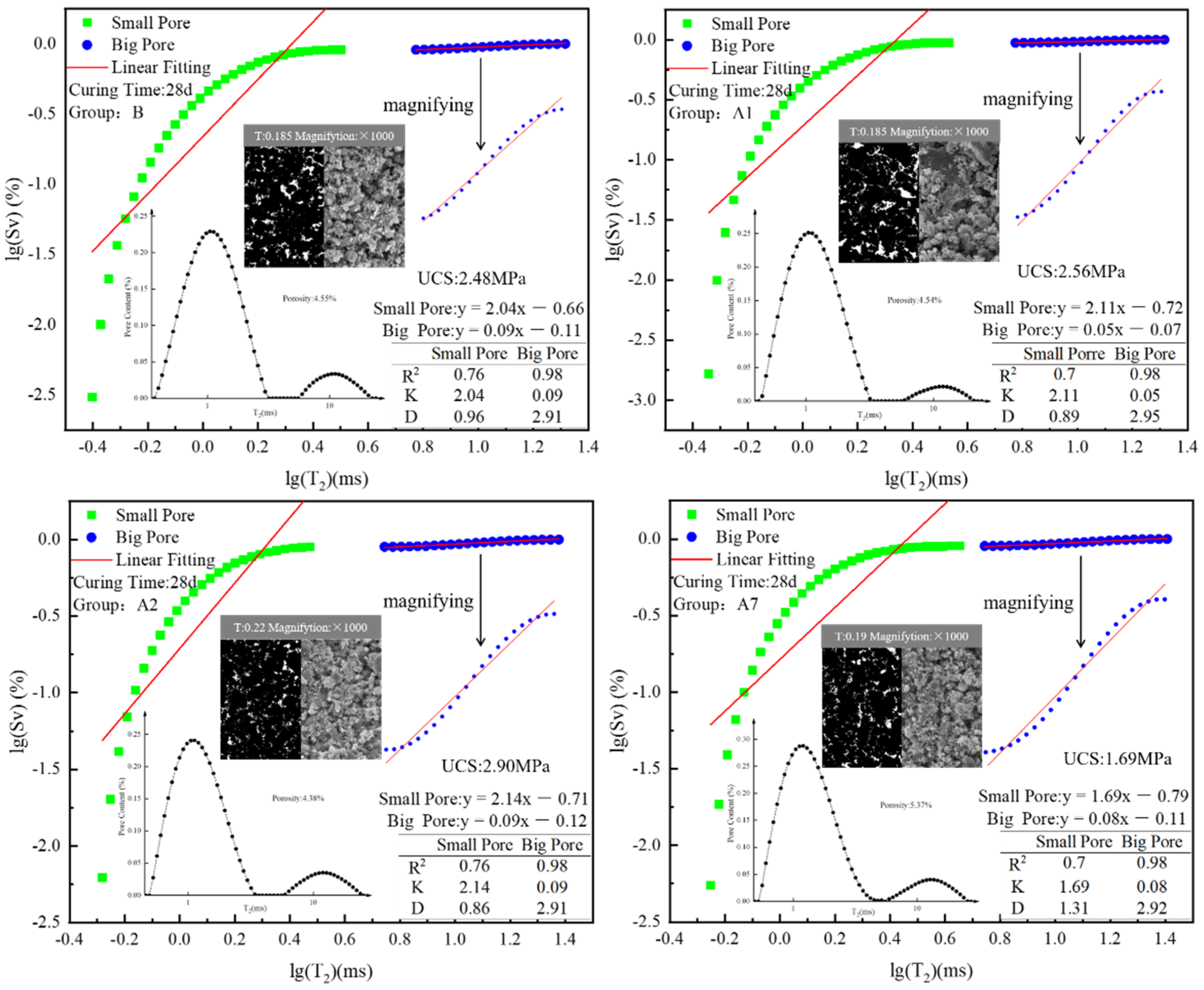
4.1. Fractal Characteristics of NMR
4.1.1. Fractal Function of NMR
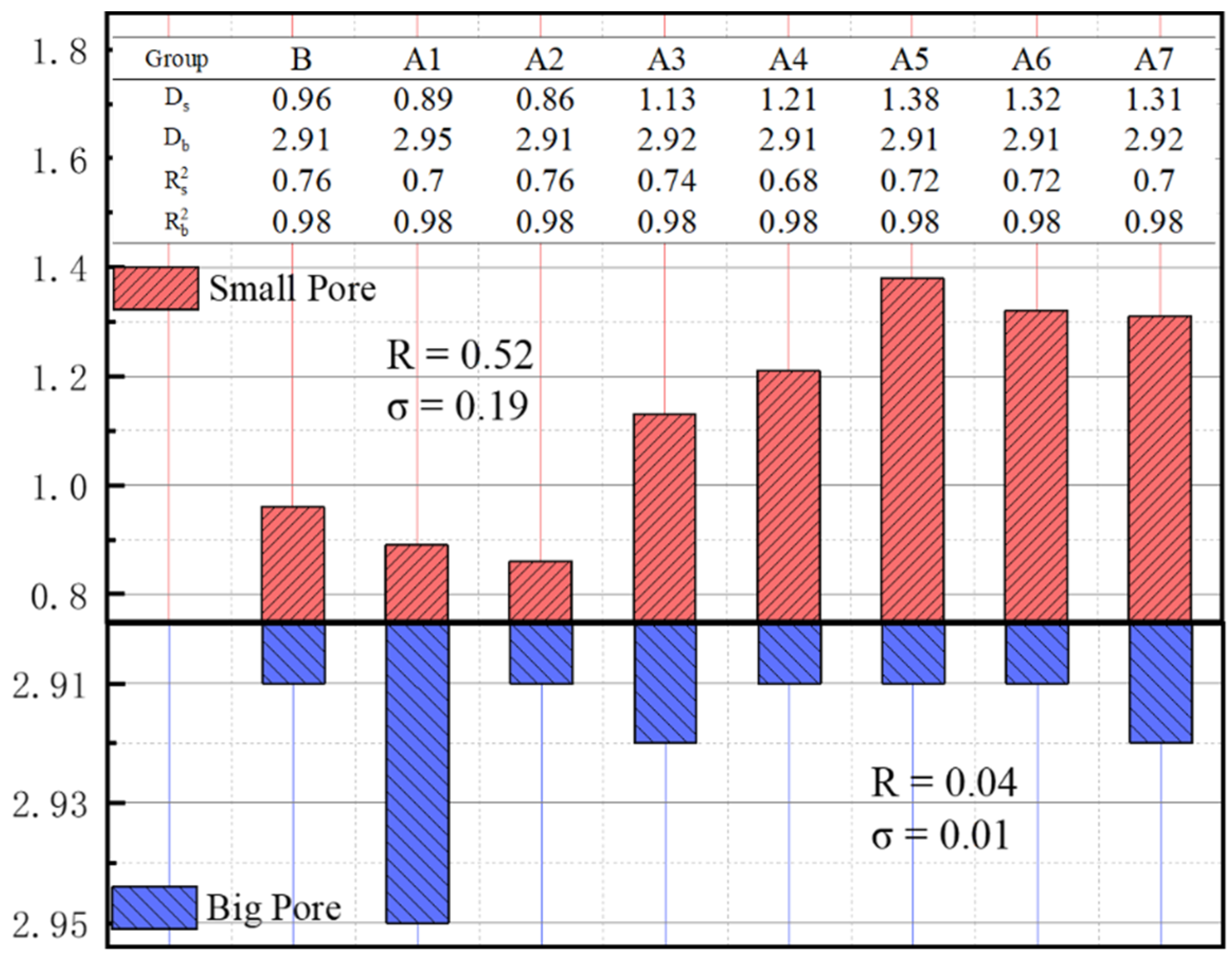
4.1.2. NMR-FT Characteristic Analysis of LMPGCB
4.2. Fractal Characteristics of SEM
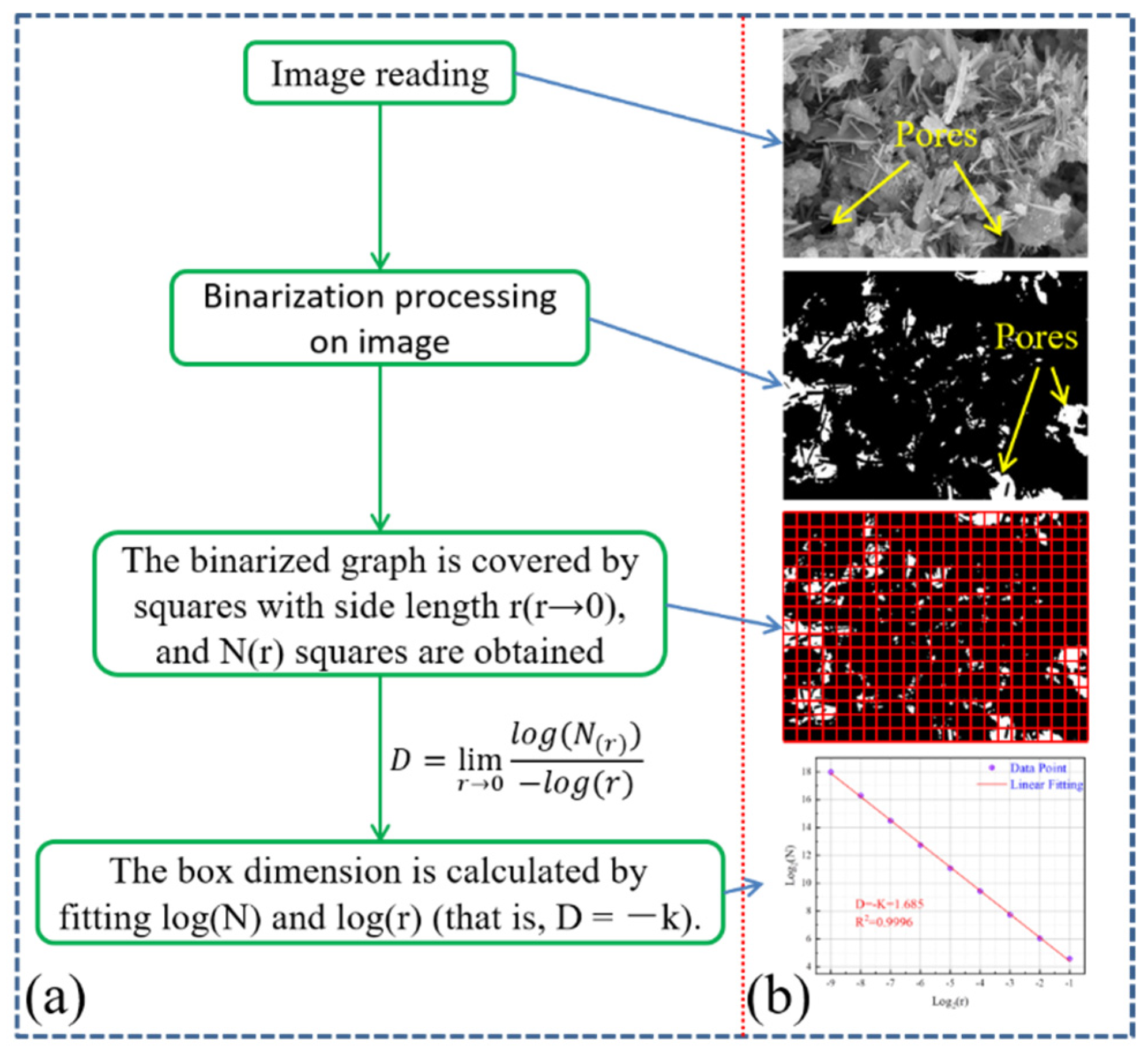
4.2.1. Fractal Principle of SEM
4.2.2. SEM-FT Characteristic Analysis of LMPGCB
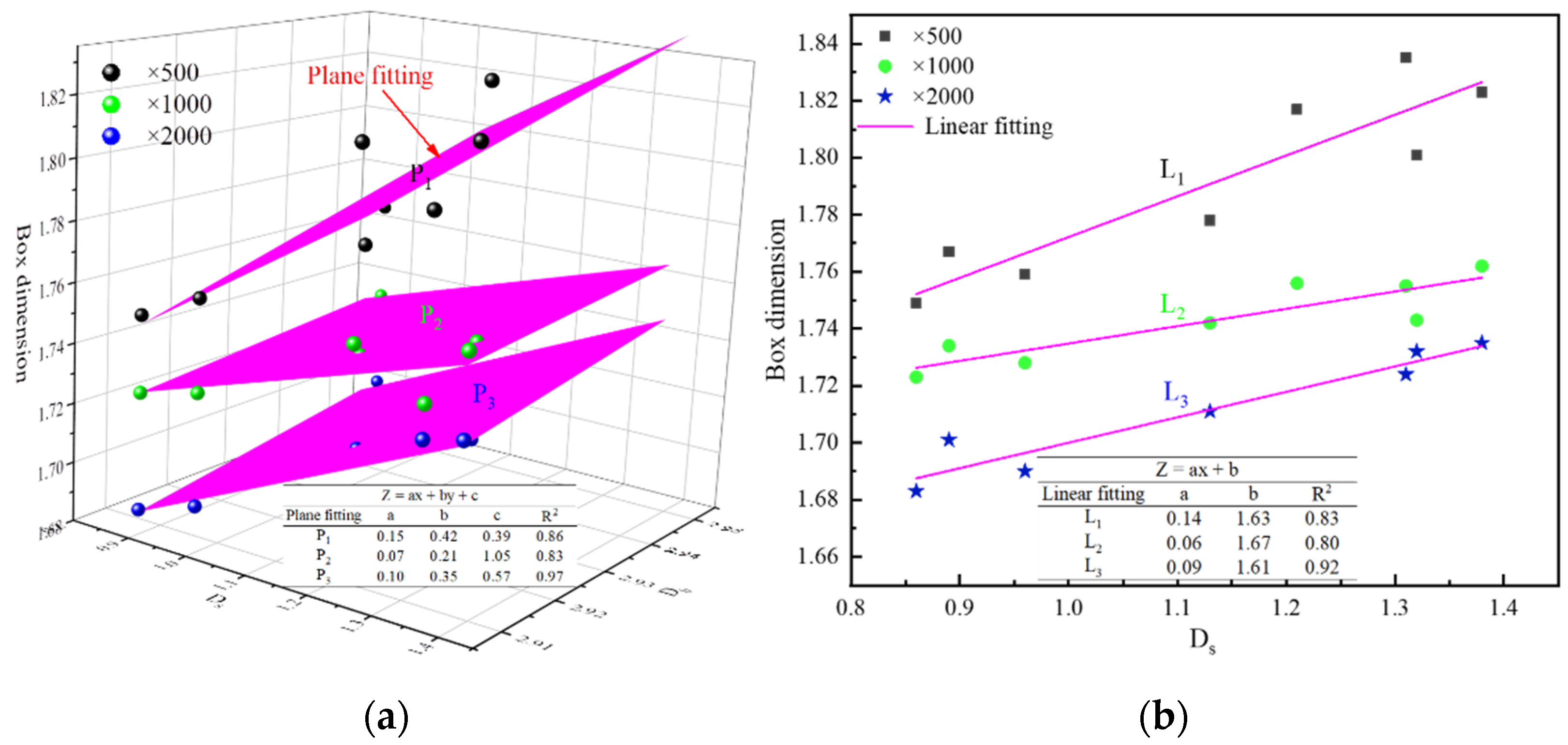
4.3. Dimensions Relationship
4.4. Relationship Model Construction of Macro-Meso Parameters
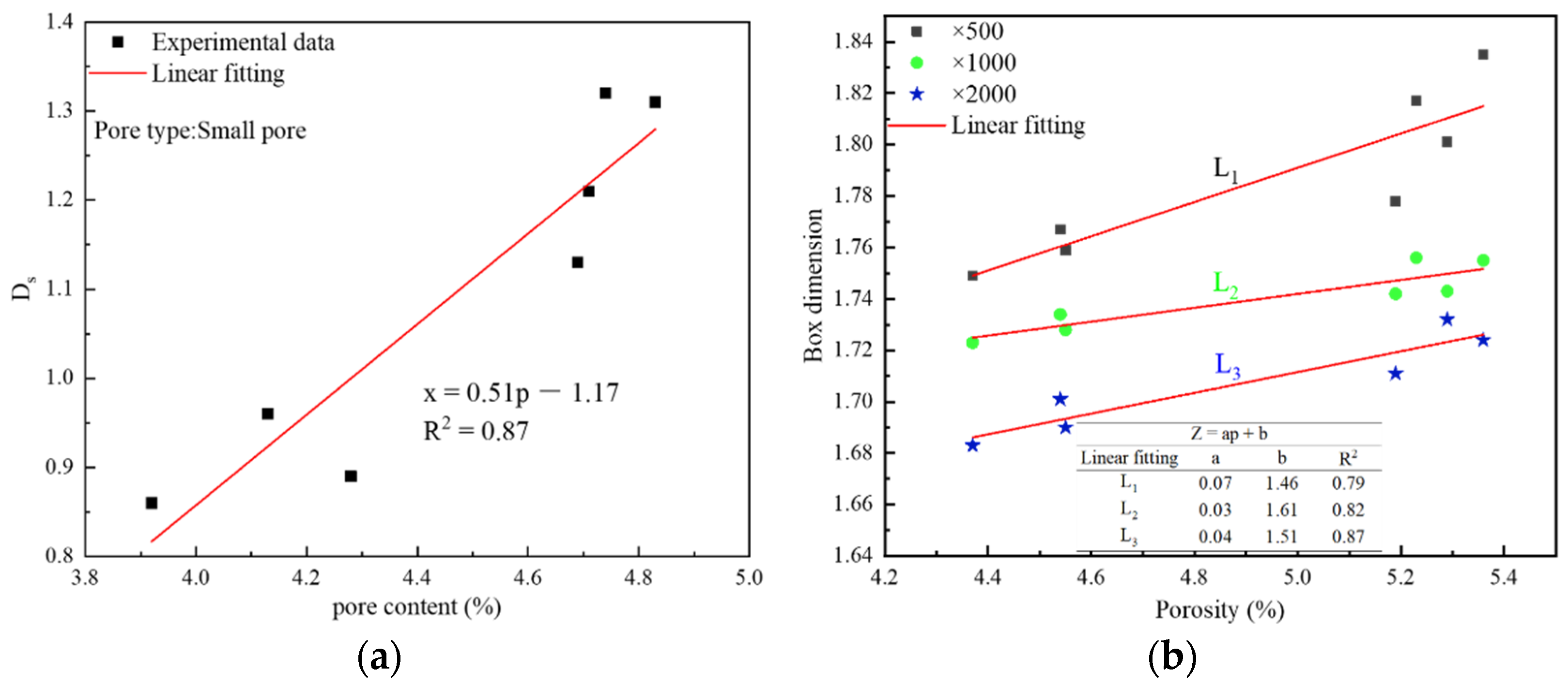
4.4.1. The Relationship between Strength and Pore Content
4.4.2. The Relationship between Dimension and Pore Content
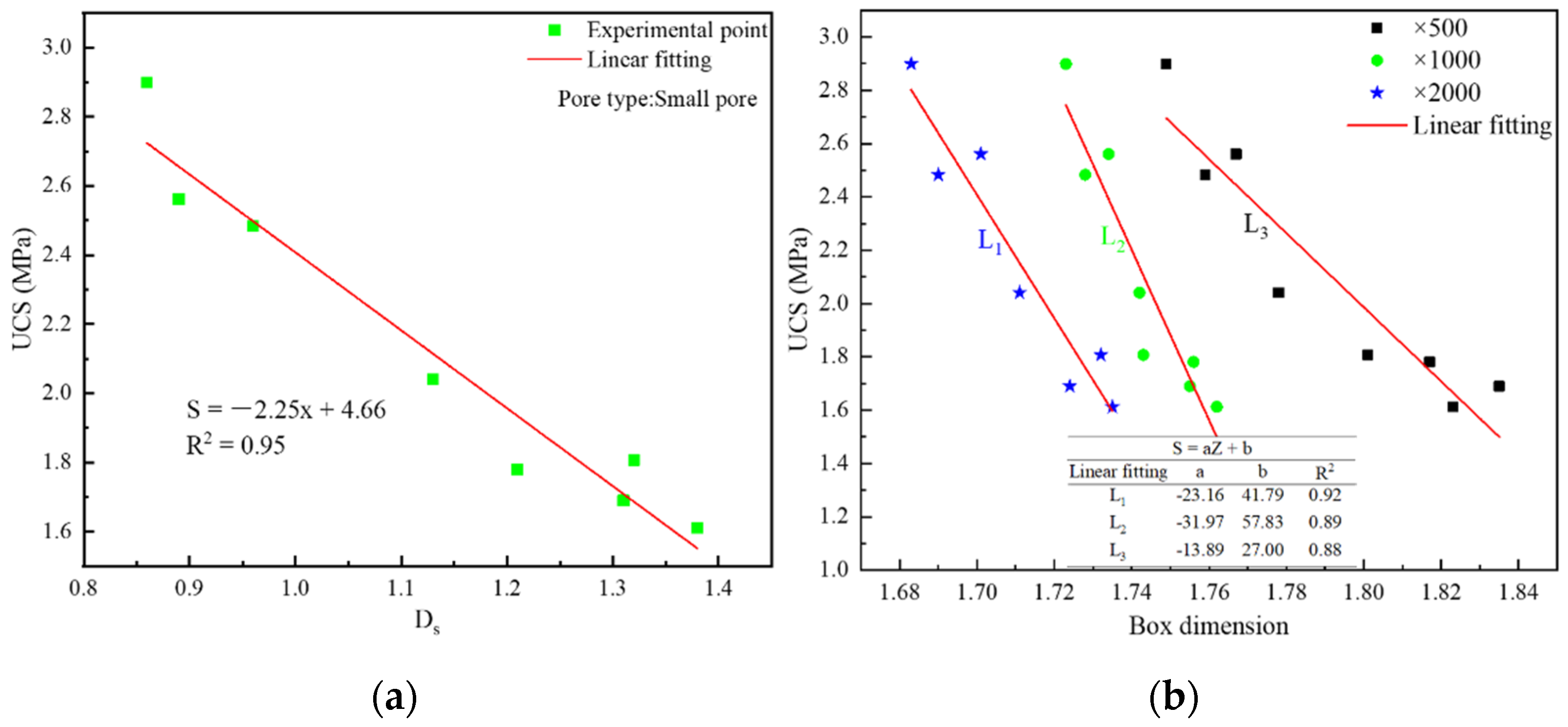
4.4.3. The Relationship between Dimension and Strength
5. Conclusions
- (1)
- The NMR-FT fractal effect of various types of pores is good, but the overall fractal effect is poor. The model of the dimension of the small pores is strong. The fractal dimension of the small pore is between 0.86–1.38 (the overall trend decreases first and then increases).
- (2)
- The SEM-FT box dimension is 1.749–1.835 at ×500 magnification, 1.723–1.762 at ×1000 magnification, and 1.683–1.735 at ×2000 magnification, whose overall trend also decreased first and then increased. With the increase of magnification, the box dimension decreases.
- (3)
- By developing the relationship between NMR-FT fractal dimension and the SEM-FT box dimension, it is seen that there is a direct linear relationship between the SEM-FT box dimension and the NMR-FT fractal dimension of small pores. The relationship between the SEM-FT box dimension and the NMR-FT fractal dimension conforms to plane relationship.
- (4)
- By constructing the functional relationship model between dimension and pore content and strength, it is shown that there is a linearly increasing relationship between dimension and pore content and a linear decreasing relationship between dimension and strength.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Zhu, J.; He, F.; Jiang, Y.D. Compressibility and fractal dimension analysis in the bituminous coal specimens. AIP Adv. 2018, 8, 075118. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.B.; Liu, D.M. Comparison of low-field NMR and mercury intrusion porosimetry in characterizing pore size distributions of coals. Fuel 2012, 95, 152–158. [Google Scholar] [CrossRef]
- Guo, Y.H.; Ding, H.Y.; Zhang, P.Y.; Zhang, L. Pore Structure Characteristics of SAP Concrete Based on Mercury Intrusion Test. J. Build. Mater. 2018, 21, 138–142. [Google Scholar] [CrossRef]
- Liu, H.B.; Ju, Y.; Tian, K.P.; Liu, J.H.; Wang, L.; Zhang, Q.G.; Liu, P. Investigate on Pore Structure Characteristics of Reactive Powder Concrete after High Temperatures. Appl. Mech. Mater. 2012, 174, 1010–1014. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, J.; Yang, D.; Kuang, Y.; Xiao, H.; Zheng, M.; Wang, X. Study on the Relationship between Pore Structure and Uniaxial Compressive Strength of Cemented Paste Backfill by Using Air-Entraining Agent. Adv. Civ. Eng. 2021, 2021, 6694744. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, F.; Ren, Q.; Kuang, Y.; Zhou, T.; Luo, Z. Microscopic characterization and strength characteristics of cemented backfill under different humidity curing conditions. R. Soc. Open Sci. 2019, 6, 191227. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.J.; Zhao, L.H. Creation and Application of the Fractal Theory. J. Liaoning Inst. Technol. 2005, 25, 113–117. [Google Scholar]
- Guo, W.; Qin, H.; Chen, H.; Sun, W. Fractal theory and its application in the study of concrete materials. J. Silic. 2010, 38, 1362–1368. [Google Scholar]
- Deng, H.; Duan, T.; Tian, G.; Liu, Y.; Zhang, W. Research on Strength Prediction Model and Microscopic Analysis of Mechanical Characteristics of Cemented Tailings Backfill under Fractal Theory. Minerals 2021, 11, 886. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, F.; Kuang, Y.; Yang, D.; Zheng, M.; Zhao, L. Microscopic characteristics of the action of an air entraining agent on cemented paste backfill pores. Alex. Eng. J. 2020, 59, 1583–1593. [Google Scholar] [CrossRef]
- Yuan, Y.J.; Rezaee, R.Z. Fractal analysis of the pore structure for clay bound water and potential gas storage in shales based on NMR and N2 gas adsorption. J. Pet. Sci. Eng. 2019, 177, 756–765. [Google Scholar] [CrossRef]
- Deng, H.; Tian, G.; Yu, S.; Jiang, Z.; Zhong, Z.; Zhang, Y. Research on Strength Prediction Model of Sand-Like Material Based on Nuclear Magnetic Resonance and Fractal Theory. Appl. Sci. 2020, 10, 6601. [Google Scholar] [CrossRef]
- Hu, J.H.; Ren, Q.F.; Yang, D.J.; Shang, J.L.; Ding, X.T.; Luo, Z.Q. Cross-scale characteristics of backfill material using NMR and fractal theory. Trans. Nonferr. Met. Soc. China 2020, 30, 1347–1363. [Google Scholar] [CrossRef]
- Hu, J.H.; Ren, Q.F.; Ding, X.T.; Jiang, Q. Trans-scale relationship analysis between the pore structure and macro parameters of backfill and slurry. R. Soc. Open Sci. 2019, 6, 190389. [Google Scholar] [CrossRef] [Green Version]
- Lü, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar] [CrossRef]
- Wang, Y.X.; Shi, X.S.; Ji, F.; Gu, H.D.; Ding, J.W. Fractal characteristics of natural Sedimentary Diatomaceous earth based on SEM images. Hydro-Sci. Eng. 2017, 5, 96–102. [Google Scholar]
- Zhang, C.M.; Chen, Z.B.; Zhang, Z.S.; Li, J.; Linghu, S.; Sun, B.X. Study on pore fractal structure of reservoir rock based on NMR T2 spectrum distribution. J. Oil Gas Technol. 2007, 29, 80–86. [Google Scholar]
- He, C.Y.; Yuan, W.; Tan, K.F. Study on property of cementitious binder consisting of phosphogypsum-flyash-lime-cement. New Build. Mater. 2009, 8, 1–3. [Google Scholar]
- Ba, T.B.; Xu, Y.Z.; Lu, W.Y.; Wang, L.N.; Shi, Z.G. Experimental study on the lime neutralizing pretreatment of phosphogypsum. New Build. Mater. 2018, 2, 96–99. [Google Scholar]
- Li, J.L.; Kaunda, R.B.; Zhou, K.P. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Liu, L.; Fang, Z.; Qi, C.; Zhang, B.; Guo, L.; Song, K.I. Experimental investigation on the relationship between pore characteristics and unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 179, 254–264. [Google Scholar] [CrossRef]
- Zhou, K.P.; Li, J.L.; Xu, Y.J.; Zhang, Y.M. Measurement of rock pore structure based on NMR technology. J. Cent. South Univ. (Sci. Technol.) 2012, 43, 4796–4800. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete; China Electric Power Press: Beijing, China, 2008. [Google Scholar]
- Hu, J.; Jiang, Q.; Ren, Q.; Ding, X.T. Cross scale correlation characteristics of pore structure and meso parameters of filling body. Trans. Nonferr. Met. Soc. China 2018, 28, 2154–2163. [Google Scholar]
- Sun, B.L. Fraetal Dimension and Its Metrical Methods. J. Northeast. For. Univ. 2004, 32, 116–119. [Google Scholar]
- Tan, M.Y.; Zhang, X.X.; Xiang, L.X.; Yu, X. Research progress of phosphorus gypsum as cement retarder. Inorg. Chem. Ind. 2016, 48, 4–6. [Google Scholar]
- Yang, Q.Q.; Xu, S.L.; Qiang, F.Z.; Cai, R.L. Study on fractal dimension of SEM images of solid propellant. Chem. Propellants Polymer. Mater. 2021, 19, 63–67. [Google Scholar]
- Jiang, N. The Historical Evolution of the Concept of Box Dimension. Stud. Dialectics Nat. 2020, 36, 84–90. [Google Scholar]
- Yu, Z.L.; Zhao, L.J.; Meng, F.H. Calculating SEM fractal dimension of concrete by MATLAB. Cem. Eng. 2014, 5, 59–62. [Google Scholar]
- Shi, Y.; Quan, S.H.; Li, Z.J.; Zhang, L.Y. Effect on Fractal Dimension of SEM Images. J. Huangshi Inst. Technol. 2007, 23, 23–26. [Google Scholar]
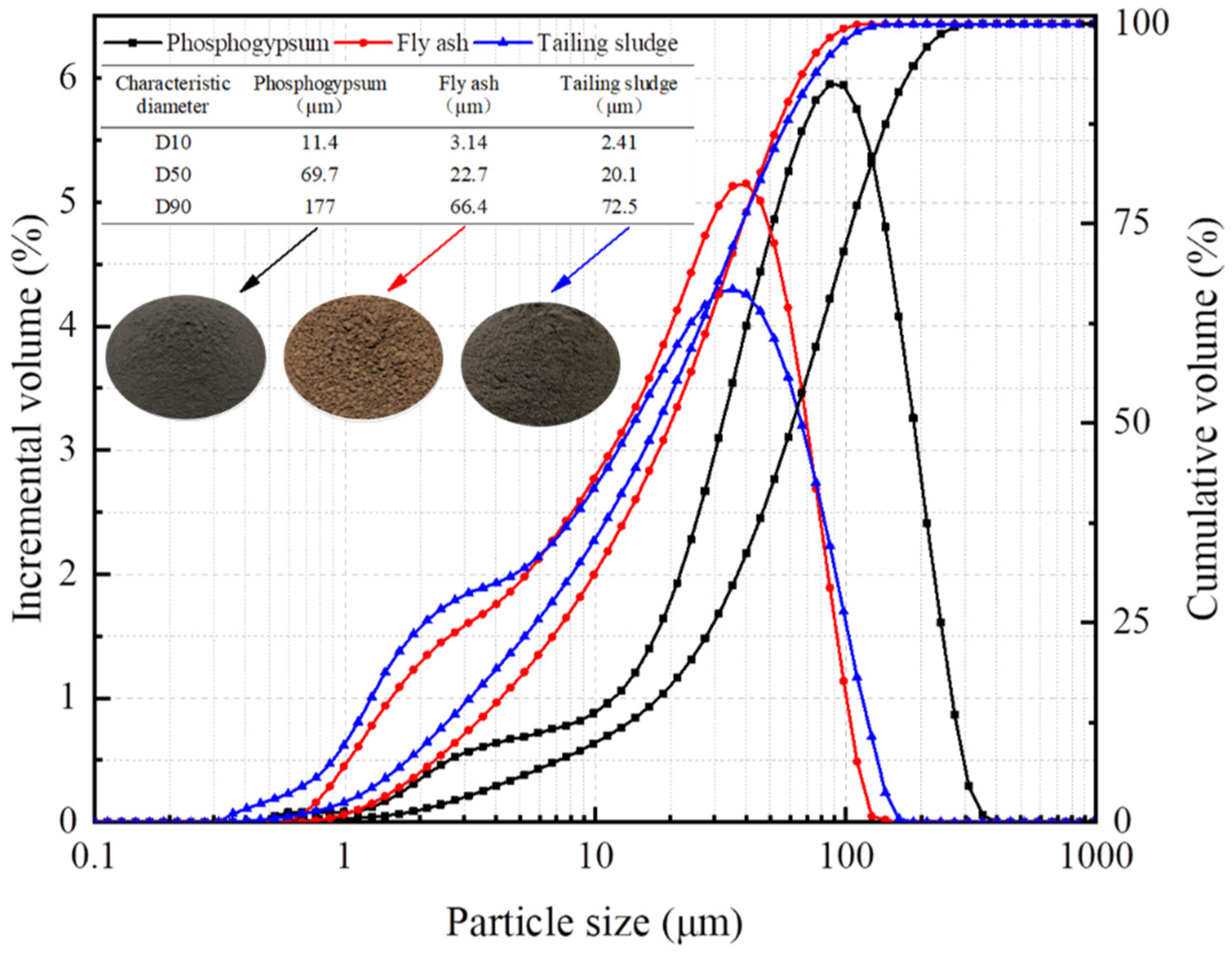







| Particle Size/mm | Mass Fraction/% | Mass Accumulation/% |
|---|---|---|
| 0.28–1.25 | 26 | 26 |
| 1.25–2 | 27 | 53 |
| 2–3 | 20 | 73 |
| 3–4 | 17 | 90 |
| 4–5 | 10 | 100 |
| Sample | Apparent Density/(kg∙m−3) | Packing Density/(kg∙m−3) | Surface Moisture Content/% |
|---|---|---|---|
| Tailings | 2626 | 1464 | 0.120 |
| Tailing sludge | 2653 | 923 | 0.974 |
| Fly ash | 1990 | 650 | 0.049 |
| Phosphogypsum | 1992 | 850 | 8.11 |
| Sample | Mass Fraction/% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hydroxyllapatite | Quartz | Hematite | Albite | Plagioclase | Muscovite | Illite | Dolomite | Plaster | Amphibole | Calcite | |
| Tailings | 10.15 | 6.91 | 12.75 | - | - | - | - | 69.65 | 0.2 | - | 0.34 |
| Fly ash | - | 61.55 | 1.46 | 15.99 | - | 20.99 | - | - | - | - | - |
| Phosphogypsum | - | 1.35 | - | - | - | - | 4.05 | - | 94.02 | 0.59 | - |
| Tailing sludge | 60.94 | 2.24 | - | 8.38 | 11.42 | - | 9.76 | 6.30 | 0.34 | - | 0.61 |
| Group | Phosphogypsum Content/% | Lime Content/% | Mass Percentage | Cement Tailings Ratio |
|---|---|---|---|---|
| B | 0 | 0 | 80% | 1:6 |
| A1 | 20 | 0 | ||
| A2 | 20 | 0.2 | ||
| A3 | 20 | 1 | ||
| A4 | 20 | 1.8 | ||
| A5 | 20 | 2.6 | ||
| A6 | 20 | 3.4 | ||
| A7 | 20 | 4.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Hu, J.; Yang, Y.; Xiao, H.; Ma, F. Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory. Minerals 2022, 12, 403. https://doi.org/10.3390/min12040403
Zhao F, Hu J, Yang Y, Xiao H, Ma F. Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory. Minerals. 2022; 12(4):403. https://doi.org/10.3390/min12040403
Chicago/Turabian StyleZhao, Fengwen, Jianhua Hu, Yinan Yang, Hongxing Xiao, and Fengcheng Ma. 2022. "Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory" Minerals 12, no. 4: 403. https://doi.org/10.3390/min12040403
APA StyleZhao, F., Hu, J., Yang, Y., Xiao, H., & Ma, F. (2022). Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory. Minerals, 12(4), 403. https://doi.org/10.3390/min12040403







