Dissolution of Magnetite and Hematite in Mixtures of Oxalic and Nitric Acid: Mechanisms and Kinetics
Abstract
:1. Introduction
2. Theory
2.1. Dissolution of Iron Oxides in Oxalic Acid
2.2. Dissolution of Iron Oxides in Nitric Acid
2.3. Reaction of Oxalic Acid with Nitric Acid
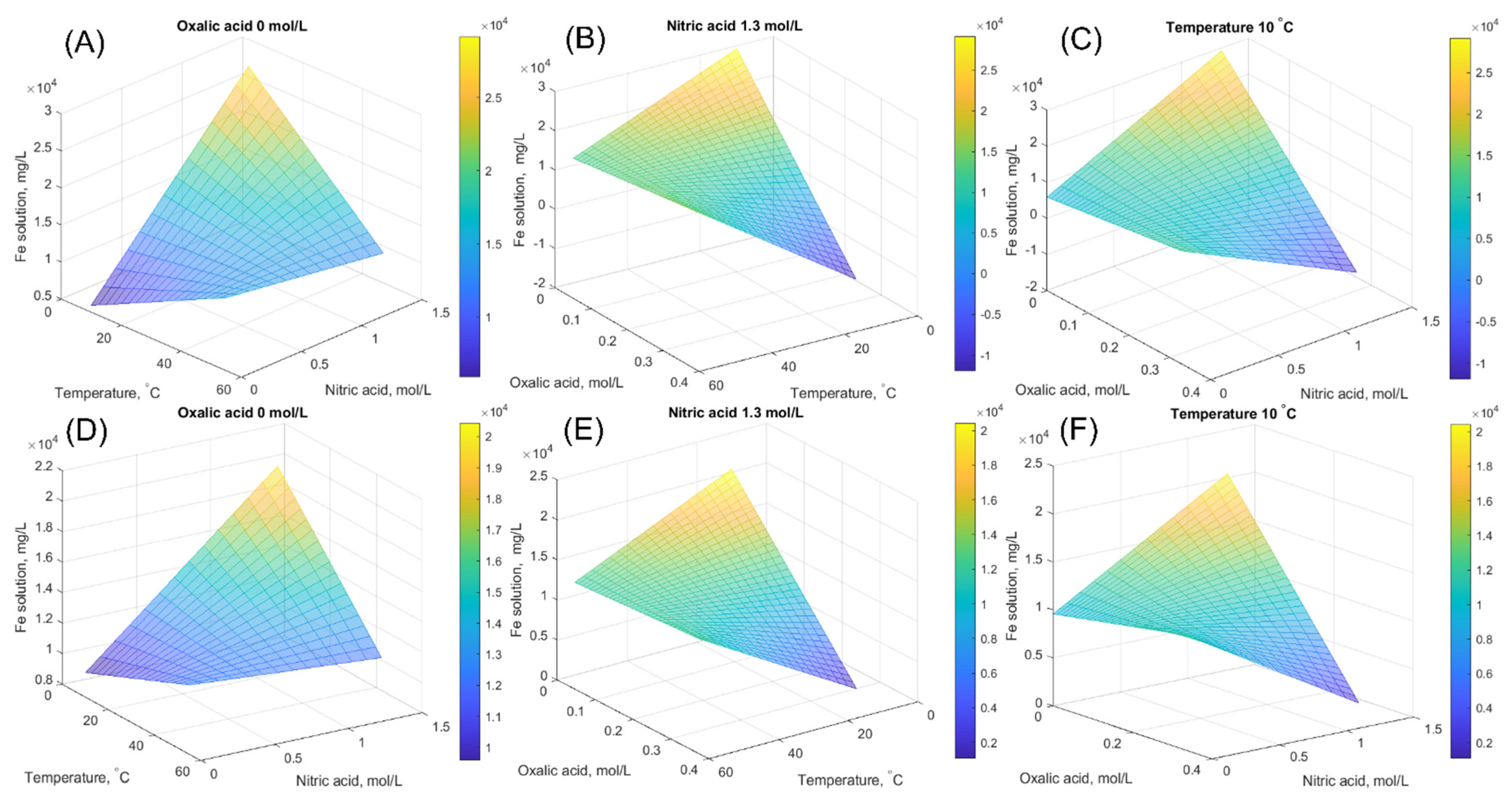
2.4. Modelling of Iron Oxide Solubility
2.5. Kinetic Modelling
3. Materials and Methods
3.1. Chemicals
3.2. Analysis
3.3. Dissolution Experiments
4. Results and Discussion
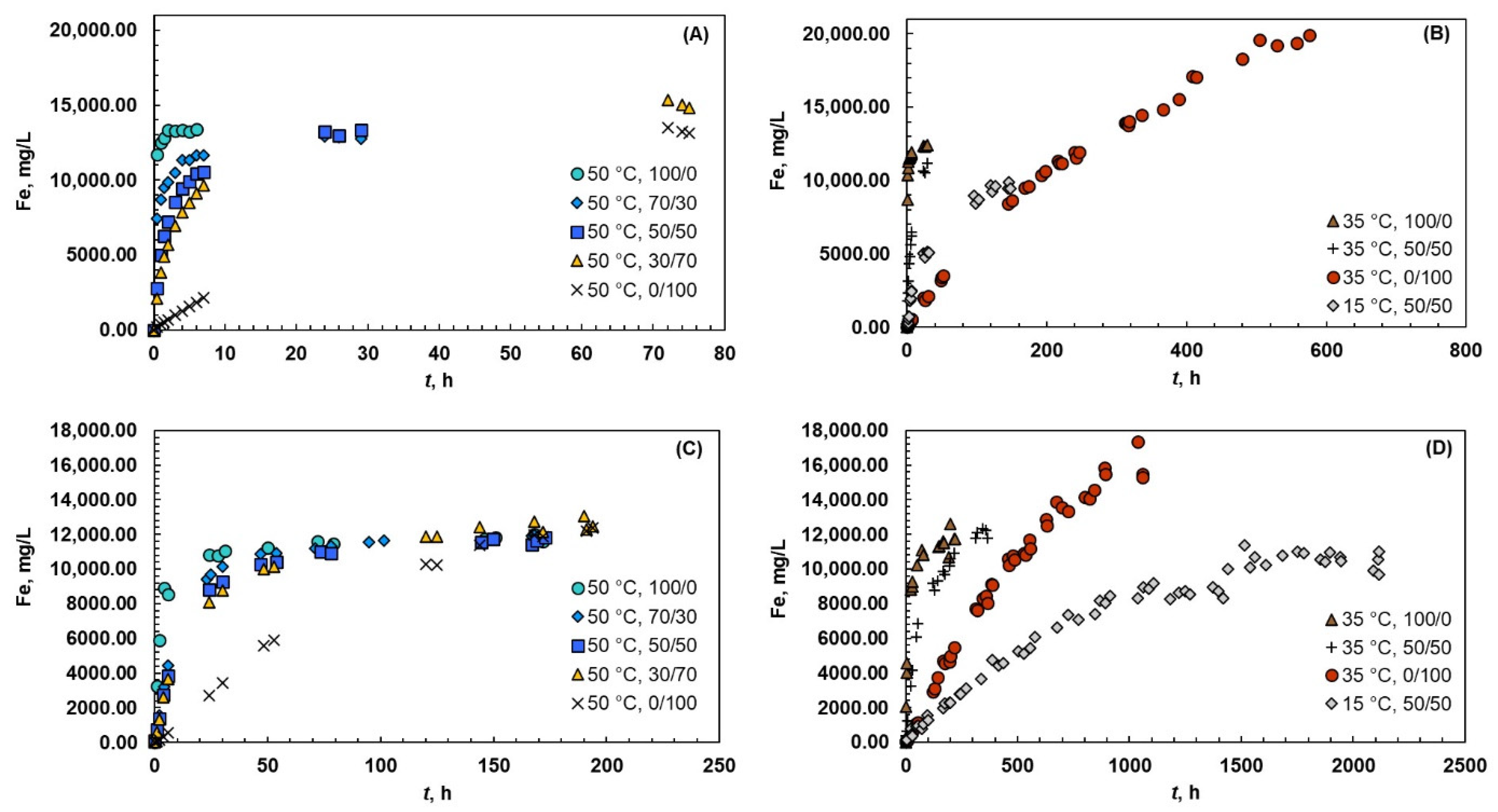
4.1. Effect of Acid System and Reaction Temperature on Solubility
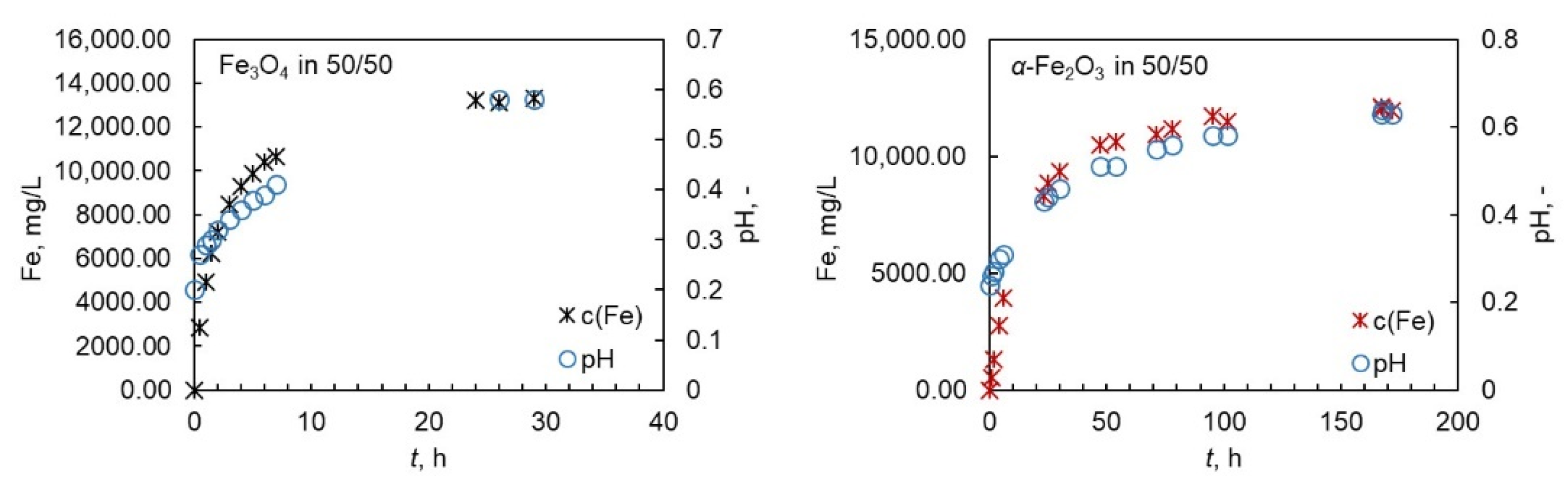
4.2. Behavior of pH during the Experiments
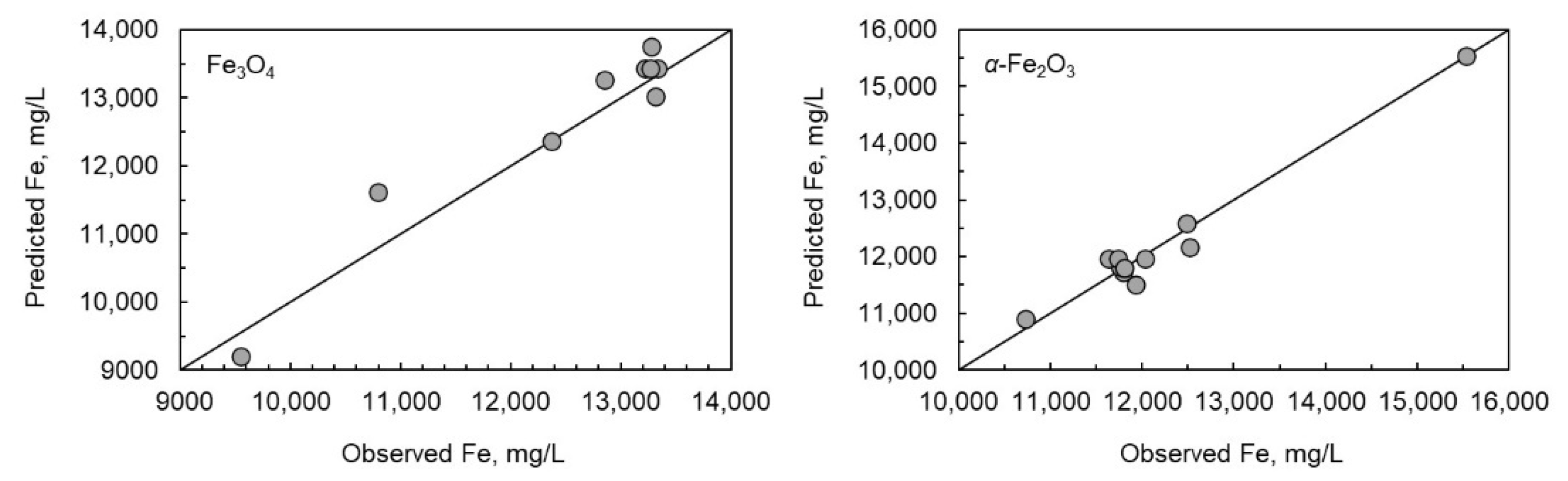
4.3. Statistical Analysis of Thermodynamic Data
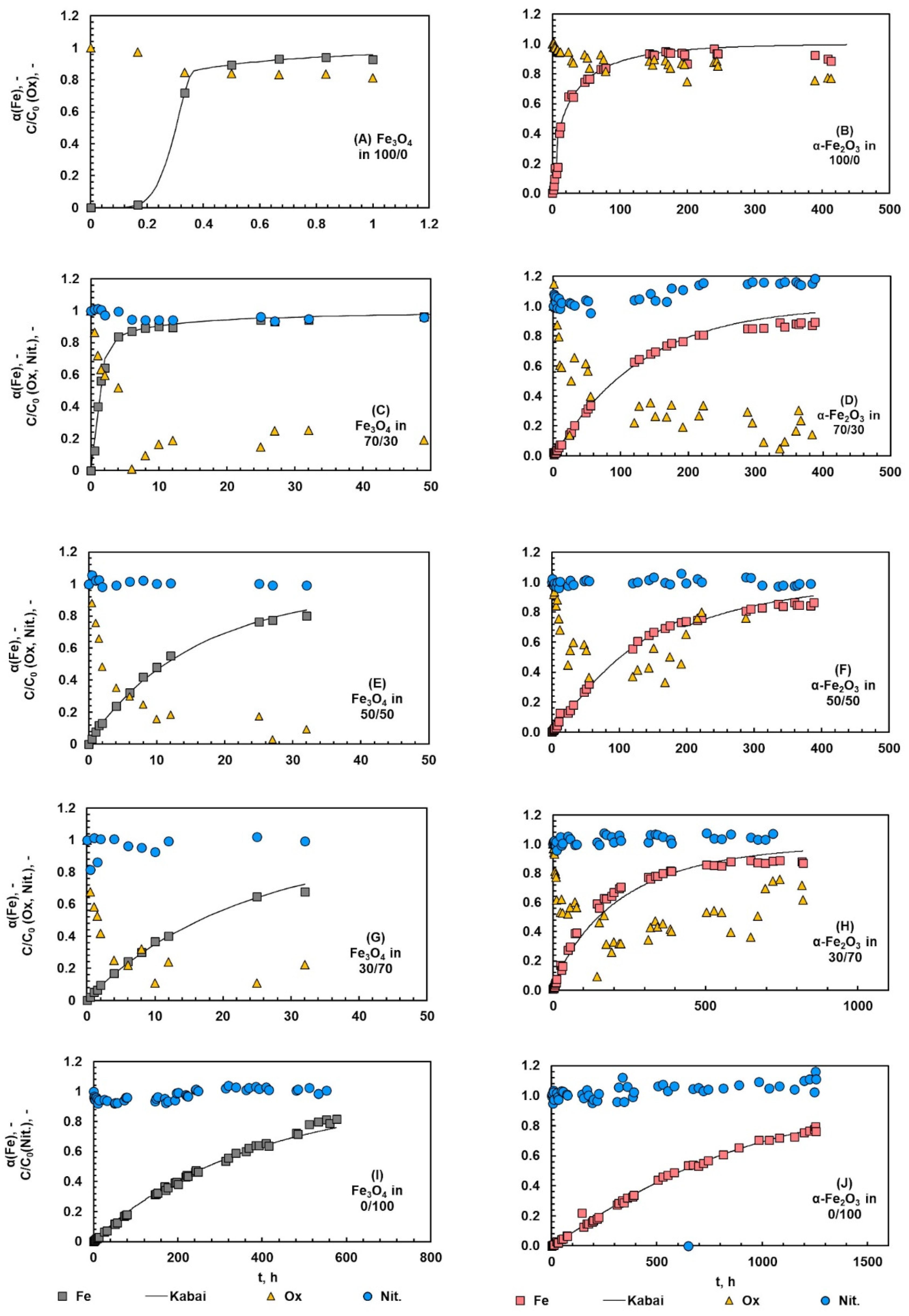
4.4. Kinetics of Dissolution
4.5. Solid Phase after Dissolution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, Y.; Wang, W.; Xu, J.; Ding, J.; Wang, Q.; Wang, A. Solid-phase oxalic acid leaching of natural red palygorskite-rich clay: A solvent-free way to change color and properties. Appl. Clay Sci. 2020, 198, 105848. [Google Scholar] [CrossRef]
- Tanvar, H.; Mishra, B. Hydrometallurgical recycling of red mud to produce materials for industrial applications: Alkali separation, iron leaching and extraction. Metall. Mater. Trans. B 2021, 52B, 3543–3557. [Google Scholar] [CrossRef]
- Turan, M.D.; Sarı, Z.A.; Erdemoğlu, M. Copper enrichment in solid with selective reverse leaching with oxalic acid. J. Sustain. Metall. 2020, 6, 428–436. [Google Scholar] [CrossRef]
- Yang, C.-Q.; Li, S.-Q. Kinetics of iron removal from quartz under ultrasound-assisted leaching. High Temp. Mater. Process. 2020, 39, 395–404. [Google Scholar] [CrossRef]
- Cornell, R.M.; Schwertmann, U. The Iron Oxides, 2nd ed.; Wiley-VHC: Weinheim, Germany, 2003. [Google Scholar]
- Smith, J.; Sheridan, C.; van Dyk, L.; Naik, S.; Plint, N.; Turrer, H.D.G. Optimal ceramic filtration operating conditions for an iron ore concentrate. Miner. Eng. 2018, 115, 1–3. [Google Scholar] [CrossRef]
- Kim, H.R.; Park, J.K.; Lee, S.I.; Oh, W.; Kim, J.; Kim, C.; Lee, B.-C. Kinetics of Reductive Dissolution of a Magnetite Specimen Using Oxalic Acid. Processes 2022, 10, 696. [Google Scholar] [CrossRef]
- Markus, H.; Fugleberg, S.; Valtakari, D.; Salmi, T.; Murzin, D.Y.; Lahtinen, M. Reduction of ferric to ferrous with sphalerite concentrate, kinetic modelling. Hydrometallurgy 2004, 73, 269–282. [Google Scholar] [CrossRef]
- Prater, J.D.; Queneau, P.B.; Hudson, T.J. Nitric acid route to processing copper concentrates. Transactions 1973, 254, 117–122. [Google Scholar]
- Van Weert, G.; Shang, Y. Iron control in nitrate hydrometallurgy by (auto) decomposition of iron (II) nitrate. Hydrometallurgy 1993, 33, 255–271. [Google Scholar] [CrossRef]
- Bas, A.D.; Devaci, H.; Yazici, E.Y. Treatment of manufacturing scrap TV boards by nitric acid leaching. Sep. Purif. Technol. 2014, 130, 151–159. [Google Scholar] [CrossRef]
- Salmimies, R.; Mannila, M.; Kallas, J.; Häkkinen, A. Acidic dissolution of magnetite: Experimental study on the effects of acid concentration and temperature. Clays Clay Miner. 2011, 59, 136–146. [Google Scholar] [CrossRef]
- Ambikadevi, V.R.; Lalithambika, M. Effect of organic acids on ferric iron removal from iron-stained kaolinite. Appl. Clay Sci. 2000, 16, 133–145. [Google Scholar] [CrossRef]
- Salmimies, R.; Vehmaanperä, P.; Häkkinen, A. Acidic dissolution of magnetite in mixtures of oxalic and sulfuric acid. Hydrometallurgy 2016, 163, 91–98. [Google Scholar] [CrossRef]
- Vehmaanperä, P.; Salmimies, R.; Häkkinen, A. Thermodynamic and kinetic studies of dissolution of hematite in mixtures of oxalic and sulfuric acid. Mining Metall. Explor. 2021, 38, 69–80. [Google Scholar] [CrossRef]
- Pimienta, V.; Lavabre, D.; Levy, G.; Micheau, J.C. Kinetic Modeling of the KMNO4/H2C2O4/H2SO4 Reaction: Origin of the Bistability in a CSTR. J. Phys. Chem. 1995, 99, 14365–14371. [Google Scholar] [CrossRef]
- Riemenschneider, W.; Tanifuji, M. Oxalic acid. In Ullmann’s Encyclopedia of Industrial Chemistry. Electronic Release; Organic Chemicals; Wiley-VHC: Weinheim, Germany, 2012; pp. 529–549. [Google Scholar]
- Panias, D.; Taxiarchou, M.; Douni, I.; Paspaliaris, I.; Kontopoulos, A. Thermodynamic analysis of the reactions of iron oxides: Dissolution in oxalic acid. Can. Metall. Q. 1996, 35, 363–373. [Google Scholar] [CrossRef]
- Baumgartner, E.; Blesa, M.A.; Marinovich, H.; Maroto, A.J.G. Heterogeneous electron transfer as a pathway in the dissolution of magnetite in oxalic acid solutions. Inorg. Chem. 1993, 22, 2224–2226. [Google Scholar] [CrossRef]
- Panias, D.; Taxiarchou, M.; Paspaliaris, I.; Kontopoulos, A. Mechanisms of dissolution of iron oxides in aqueous oxalic acid solutions. Hydrometallurgy 1996, 42, 257–265. [Google Scholar] [CrossRef]
- Lee, S.O.; Tran, T.; Park, Y.Y.; Kim, S.J.; Kim, M.J. Study on the kinetics of iron oxide leaching by oxalic acid. Int. J. Miner. Process. 2006, 80, 144–152. [Google Scholar] [CrossRef]
- Vehmaanperä, P.; Gong, B.; Sit, P.H.-L.; Salmimies, R.; Barbiellini, B.; Häkkinen, A. Formation of humboldtine during the dissolution of hematite in oxalic acid- Density functional theory (DFT) calculations and experimental verification. Clays Clay Miner. 2021, 69, 655–662. [Google Scholar] [CrossRef]
- Kaya, M.; Hussaini, S.; Kursunoglu, S. Critical review on secondary zinc resources and their recycling technologies. Hydrometallurgy 2018, 195, 105362. [Google Scholar] [CrossRef]
- Gordon, A.J.; Ford, R.A. Chemist’s Companion—A Handbook of Practical Data, Techniques, and References—1.9.3.2 Dissociation Constants of Common Acids in Water; John Wiley & Sons: Hoboken, NJ, USA, 1972; p. 59. [Google Scholar]
- Stumm, W.; Furrer, G. The dissolution of oxides an aluminum silicate: Examples of surface-coordination-controlled kinetics. In Aquatic Surface Chemistry; Stumm, W., Ed.; John Wiley & Sons: New York, NY, USA, 1987; pp. 197–219. [Google Scholar]
- Ma, B.; Wang, C.; Yang, W.; Yang, B.; Zhang, Y. Selective pressure leaching of Fe(II)-rich limonitic laterite ores from Indonesia using nitric acid. Miner. Eng. 2013, 45, 151–158. [Google Scholar] [CrossRef]
- Droppert, D.J.; Shang, Y. The leaching behaviour of nickeliferous pyrrhotite concentrate in hot nitric acid. Hydrometallurgy 1995, 39, 169–182. [Google Scholar] [CrossRef]
- Thermoddem. Thermochemical and Mineralogical Tables for Geochemical Modeling. Available online: http://thermoddem.brgm.fr/databases (accessed on 27 February 2019).
- Mason, C.; Brown, T.L.; Buchanan, D.; Maher, C.J.; Morris, D.; Taylor, R.J. The decomposition of oxalic acid in nitric acid. J. Solut. Chem. 2016, 45, 325–333. [Google Scholar] [CrossRef]
- Volkan, A.; Oktay, B. Removal of Fe from kaolin by chemical leaching and bioleaching. Clays Clay Miner. 2009, 57, 787–794. [Google Scholar]
- Beolchini, F.; Petrangeli Papini, M.; Toro, L.; Trifoni, M.; Vegliò, F. Acid leaching of manganiferous ores by sucrose: Kinetic modelling and related statistical analysis. Miner. Eng. 2001, 14, 175–184. [Google Scholar] [CrossRef]
- Salmimies, R.; Huhtanen, M.; Kallas, J.; Häkkinen, A. The solubility of two magnetite powders in oxalic acid—Applicability of empirical modelling. J. Powder Technol. 2013, 2013, 164239. [Google Scholar] [CrossRef] [Green Version]
- Brown, L.; Donev, A.N.; Bisset, A.C. General blending models for data from mixture experiments. Technometrics 2015, 57, 449–456. [Google Scholar] [CrossRef]
- Sinha, B.K.; Mandl, N.K.; Pal, M.; Das, P. Optimal Mixture Experiments; Springer eBooks: New Delhi, India, 2014. [Google Scholar]
- Castro Dantas, T.N.; Dantos Neto, A.A.; Moura, M.C.P.A.; Barros Neto, E.L.; Forte, K.L.; Leite, R.H.L. Heavy metals extraction by microemulsions. Water Res. 2003, 37, 2709–2717. [Google Scholar] [CrossRef]
- Kabai, J. Determination of specific activation energies of metal oxides and metal oxide hydrates by measurement of the rate of dissolution. Acta Chim. Acad. Sci. Hung. 1973, 78, 57–73. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Ruan, H.D.; Gilkes, R.J. Acidic dissolution of synthetic aluminous goethite before and after transformation to hematite by heating. Clay Miner. 1995, 30, 55–65. [Google Scholar] [CrossRef]
- Schwertmann, U.; Cambier, P.; Murad, E. 1985. Properties of goethites of varying crystallinity. Clays Clay Miner. 1985, 33, 369–378. [Google Scholar] [CrossRef]
- Schwertmann, U.; Latham, M. Properties of iron oxides in some New Caledonia, oxisoils. Geoderma 1986, 39, 105–123. [Google Scholar] [CrossRef]
- Costa, P.; Lobo, J.M.S. Modeling and comparison of dissolution profiles. Eur. J. Pharm. Sci. 2001, 13, 123–133. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-State Kinetic Models: Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Salmimies, R.; Mannila, M.; Kallas, J.; Häkkinen, A. Acidic dissolution of hematite: Kinetic and thermodynamic investigations with oxalic acid. Int. J. Miner. Process. 2012, 110–111, 121–125. [Google Scholar] [CrossRef]
- Taxiarchou, M.; Panias, D.; Douni, I.; Paspaliaris, I.; Kontopoulos, A. Dissolution of magnetite in acidic oxalate solutions. Miner. Process Ext. Metall. 1998, 107, 37–41. [Google Scholar]
- Sasaki, K.J.; Ootsuka, K.; Tozawa, K. Solubility of goethite into sulphuric acid Solutions from 70 °C to 110 °C. Shigen-To-Sozai 1995, 111, 505–511. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Papangelakis, V.G.; Alam, M.S.; Singh, G. Solubility of hematite in H2SO4 solutions at 230–270 °C. Can. Metall. Q. 2003, 42, 199–207. [Google Scholar] [CrossRef]
- Lee, S.O. Dissolution of Iron Oxides by Oxalic Acid. Ph.D. Thesis, The University of New South Wales, Sydney, Australia, September 2005. [Google Scholar]
- Martínez-Luévanos, A.; Rodríguez-Delgado, M.G.; Uribe-Salas, A.; Carrillo-Pedroza, F.R.; Osuna-Alarcón, J.G. Leaching kinetics of iron from low grade kaolin by oxalic acid solutions. Appl. Clay Sci. 2011, 51, 473–477. [Google Scholar] [CrossRef]
- Sidhu, P.S.; Gilkes, R.J.; Cornell, R.M.; Posner, A.M.; Quirk, J.P. Dissolution of iron oxides and oxyhydroxides in hydrochloric and perchloric acids. Clays Clay Miner. 1981, 29, 269–276. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Wang, Y.; Zhao, J.; Chen, X.; Dai, Y.; Yao, Y. Enhanced electrochemical properties of iron oxalate with more stable Li+ ions diffusion channels by controlling polymorphic structure. Chem. Eng. J. 2020, 384, 123281. [Google Scholar] [CrossRef]




| Ox/HNO3 | c(Ox), mol/L | c(HNO3), mol/L |
|---|---|---|
| 100/0 | 0.330 | 0 |
| 70/30 | 0.231 | 0.39 |
| 50/50 | 0.165 | 0.65 |
| 30/70 | 0.099 | 0.91 |
| 0/100 | 0 | 1.3 |
| Term | p-Value (Magnetite) | p-Value (Hematite) |
|---|---|---|
| T | 0.6082 | 0.8755 |
| [Ox] | 0.0246 | 0.0002 |
| [HNO3] | 0.0002 | 0.00001 |
| T∙[HNO3] | 0.0113 | 0.0055 |
| [Ox]∙[HNO3] | 0.0031 | 0.0012 |
| T∙[Ox]∙[HNO3] | 0.0057 | 0.0026 |
| Magnetite | Ox/HNO3 | Part | Controlling Step | a, - | k, s−1 | R2, - |
| 100/0 | I | Chemical reaction | 6.055 | 8.66·10−4 | 1.00 | |
| II | Diffusion | 0.478 | 3.03·10−3 | 0.97 | ||
| 70/30 | I | Chemical reaction | 1.514 | 1.57·10−4 | 0.97 | |
| II | Diffusion | 0.281 | 5.85·10−4 | 0.99 | ||
| 50/50 | - | Diffusion | 0.919 | 1.66·10−5 | 0.99 | |
| 30/70 | - | Diffusion | 0.947 | 1.14·10−5 | 1.00 | |
| 0/100 | - | Diffusion | 0.947 | 7.02·10−7 | 1.00 | |
| Hematite | Ox/HNO3 | Part | Controlling Step | a, - | k, s−1 | R2, - |
| 100/0 | I | Chemical reaction | 1.194 | 1.28·10−5 | 0.98 | |
| II | Diffusion | 0.593 | 9.94·10−6 | 0.99 | ||
| 70/30 | - | Diffusion | 0.964 | 1.90·10−6 | 1.00 | |
| 50/50 | - | Diffusion | 0.999 | 1.71·10−6 | 0.99 | |
| 30/70 | - | Diffusion | 0.865 | 1.24·10−6 | 0.98 | |
| 0/100 | - | Chemical reaction | 1.105 | 3.22·10−7 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vehmaanperä, P.; Sihvonen, T.; Salmimies, R.; Häkkinen, A. Dissolution of Magnetite and Hematite in Mixtures of Oxalic and Nitric Acid: Mechanisms and Kinetics. Minerals 2022, 12, 560. https://doi.org/10.3390/min12050560
Vehmaanperä P, Sihvonen T, Salmimies R, Häkkinen A. Dissolution of Magnetite and Hematite in Mixtures of Oxalic and Nitric Acid: Mechanisms and Kinetics. Minerals. 2022; 12(5):560. https://doi.org/10.3390/min12050560
Chicago/Turabian StyleVehmaanperä, Paula, Tuomas Sihvonen, Riina Salmimies, and Antti Häkkinen. 2022. "Dissolution of Magnetite and Hematite in Mixtures of Oxalic and Nitric Acid: Mechanisms and Kinetics" Minerals 12, no. 5: 560. https://doi.org/10.3390/min12050560
APA StyleVehmaanperä, P., Sihvonen, T., Salmimies, R., & Häkkinen, A. (2022). Dissolution of Magnetite and Hematite in Mixtures of Oxalic and Nitric Acid: Mechanisms and Kinetics. Minerals, 12(5), 560. https://doi.org/10.3390/min12050560






