3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks
Abstract
:1. Introduction
2. Methodology
2.1. Forward Modeling
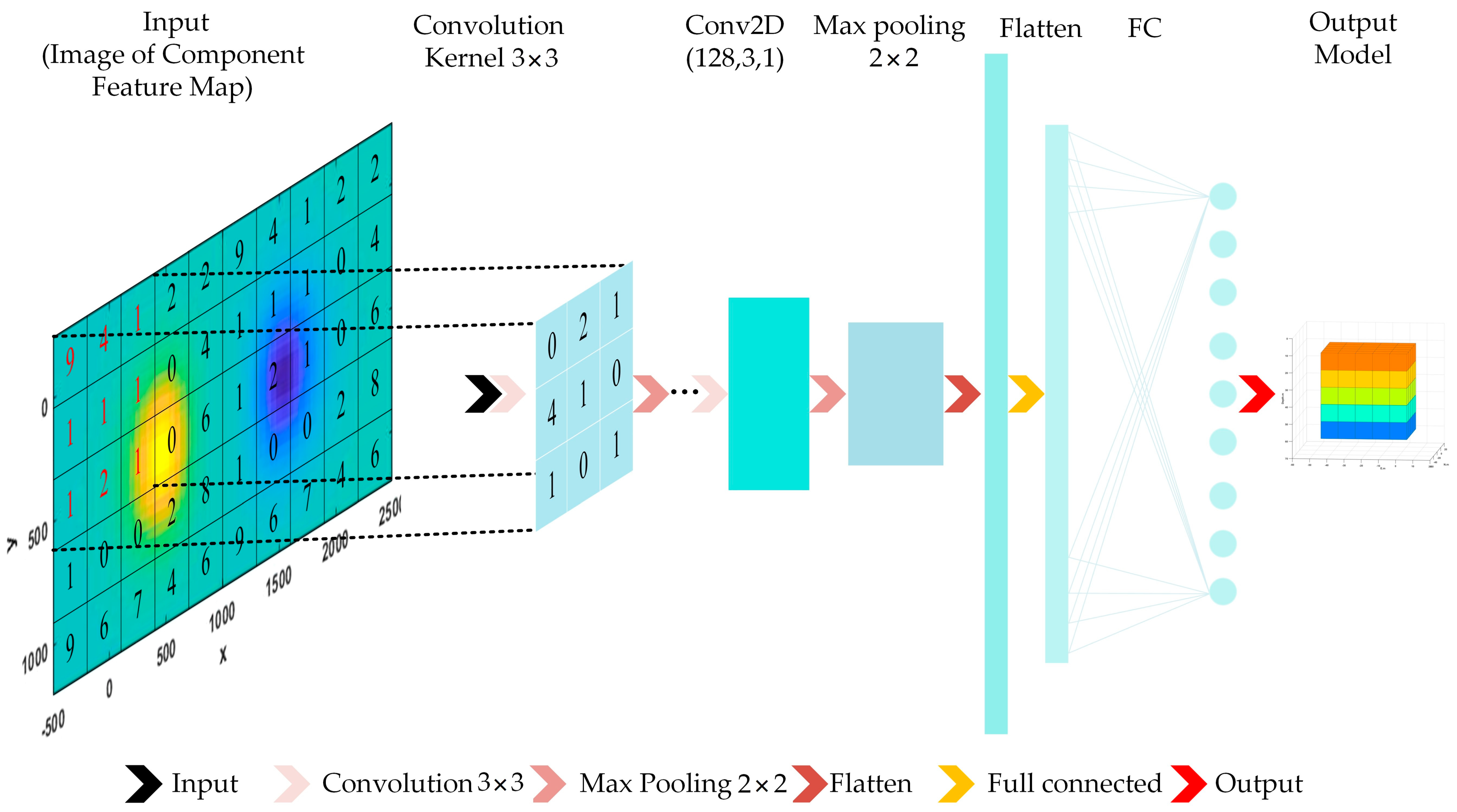
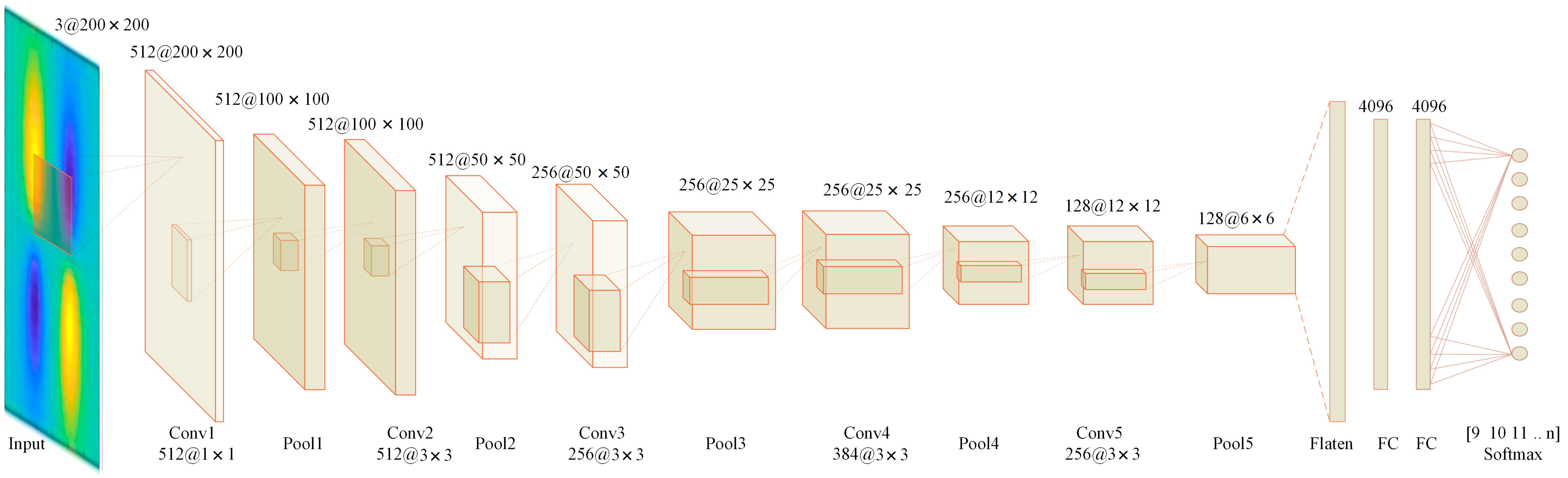
2.2. CNN
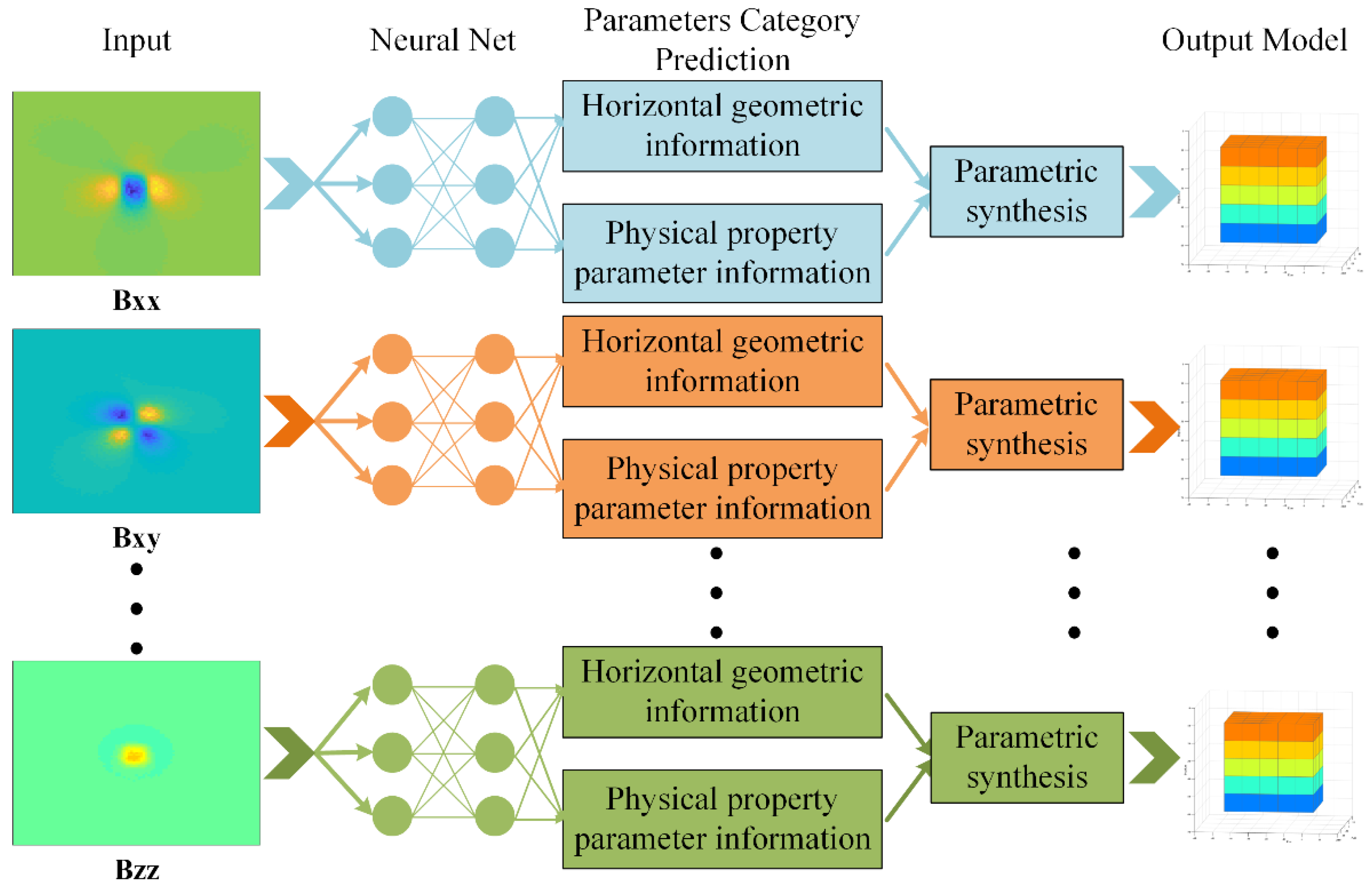
2.3. The Overall Research Framework
3. Method
3.1. Forward Model
3.2. Sample Generation Algorithms
| Algorithm 1. Sample Produce | |
| 1: | Procedure Sample (Tag_Station, Shape, Depth, Magnetic, Tag_I, Tag_D …) |
| 2: | e.g., Produce Tag_I |
| 3: | Initialize: Tag_I ← [52 54 56 … 72] ∈ [52 72]; Species = 5; |
| 4: | Tag_Station ← [0 1 2 … 8]; Number > 8000; |
| 5: | Shape ← [Ball Rectangle Rectangle_2A Rectangle_2B …]; |
| 6: | Depth ← [40 120 … 360]; |
| 7: | Magnetic ← 0.1 + 0.6(0.6 − 0.1) × rand(m,1) Magnetic ∈ [0.1 0.6] |
| 8: | Tag_D ← −10 + 10(10 + 10) × rand(n,1) Tag_D ∈ [−10 10] |
| 9: | Components ← [Bxx Bxy Bxz Byy Byz Bzz]; |
| 10: | Pi ← {Tag_Station, Shape, Depth, …} |
| 11: | while k1 < Number/Species do |
| 12: | while k2 < Number/Species do |
| 13: | Sample_Tag_I(i) ← Mag_Tensor_Forword(P{k1,k2}, Components, …) |
| 14: | Tag_Record(i) ← [P{k1,k2}, …] |
| 15: | … |
| 16: | end While |
| 17: | end While |
| 18: | save Sample_Tage_I |
| 19: | saveTag_Record |
| 20: | endprocedure |
3.3. Network Training and Prediction
3.4. Parametric Synthesis
3.5. Analysis of Factorsaffecting Prediction Accuracy
3.5.1. The Number of Training Samples
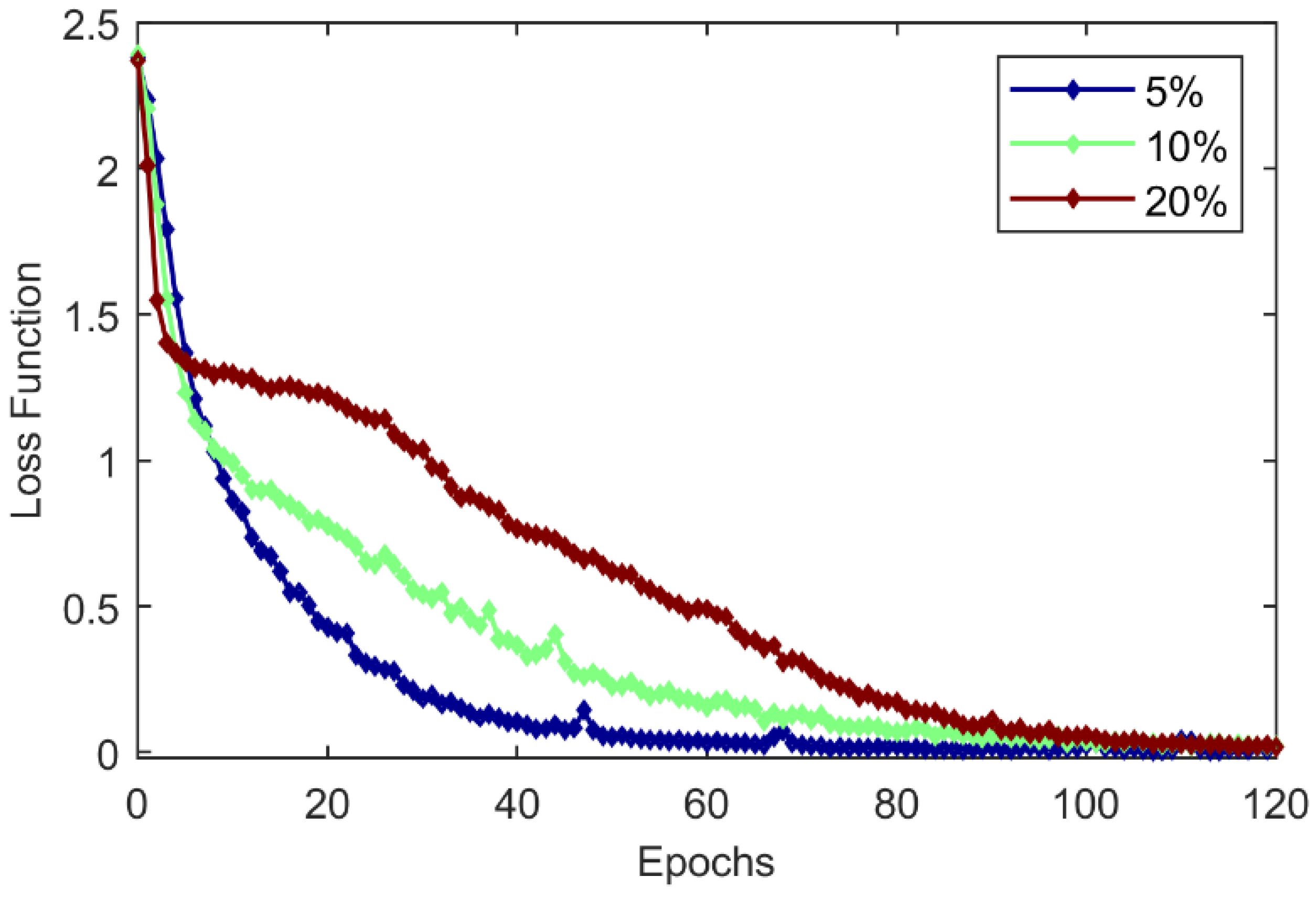
3.5.2. Sample Noise Levels
3.5.3. MGT Joint Inversion
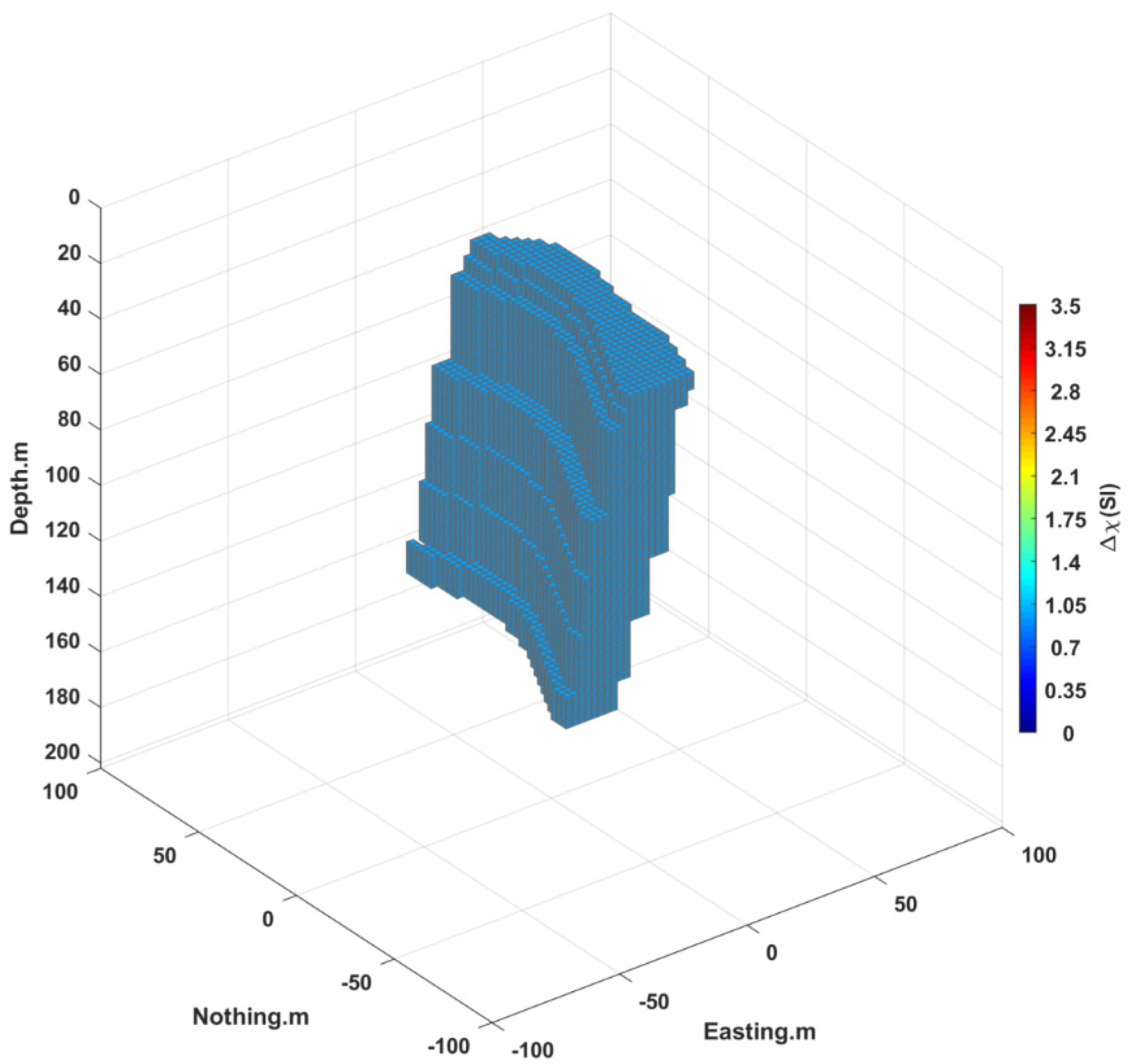
4. Application to Field Data: Tallawang Magnetite Silica, Australia
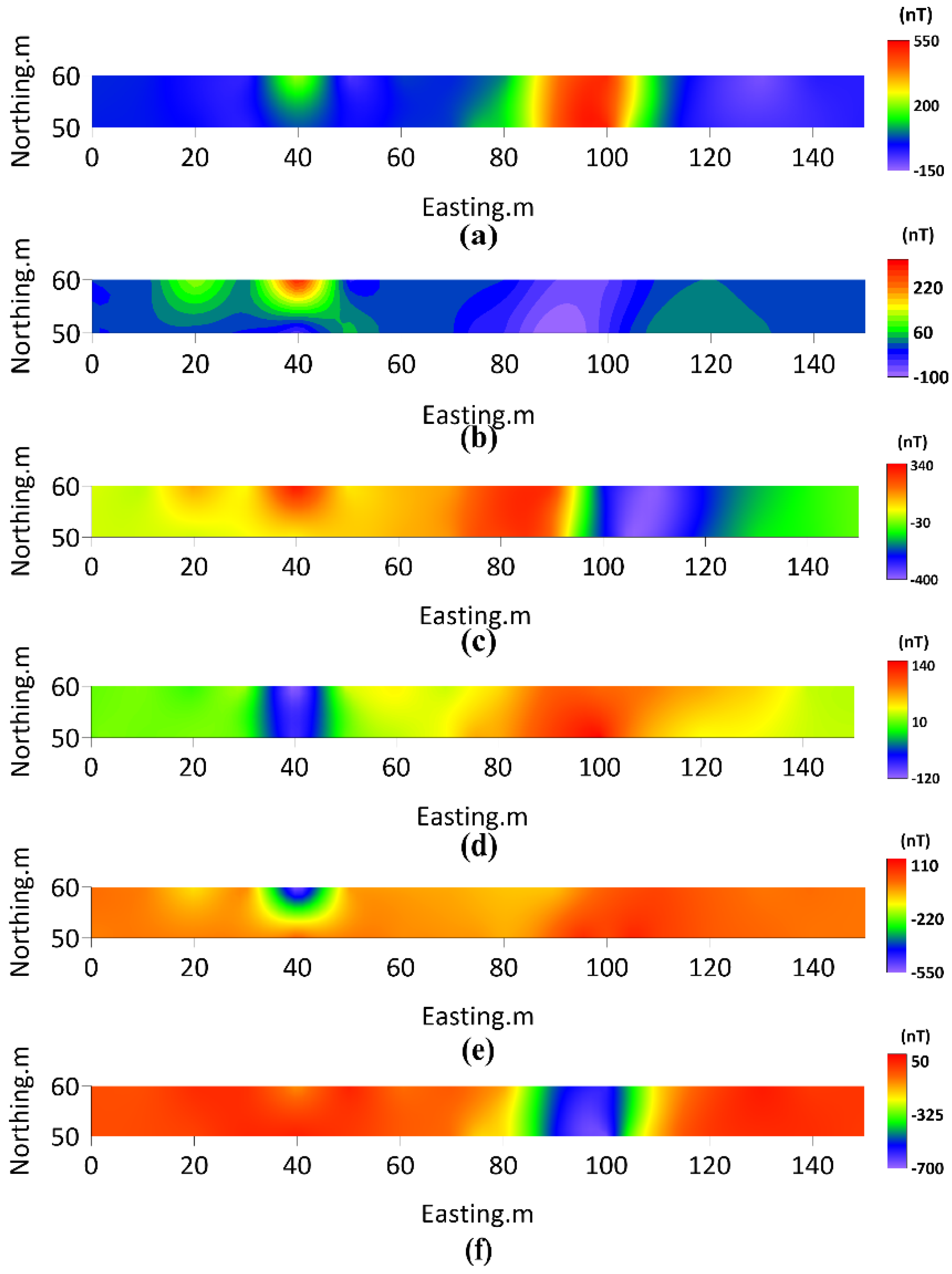
4.1. Geologic Background
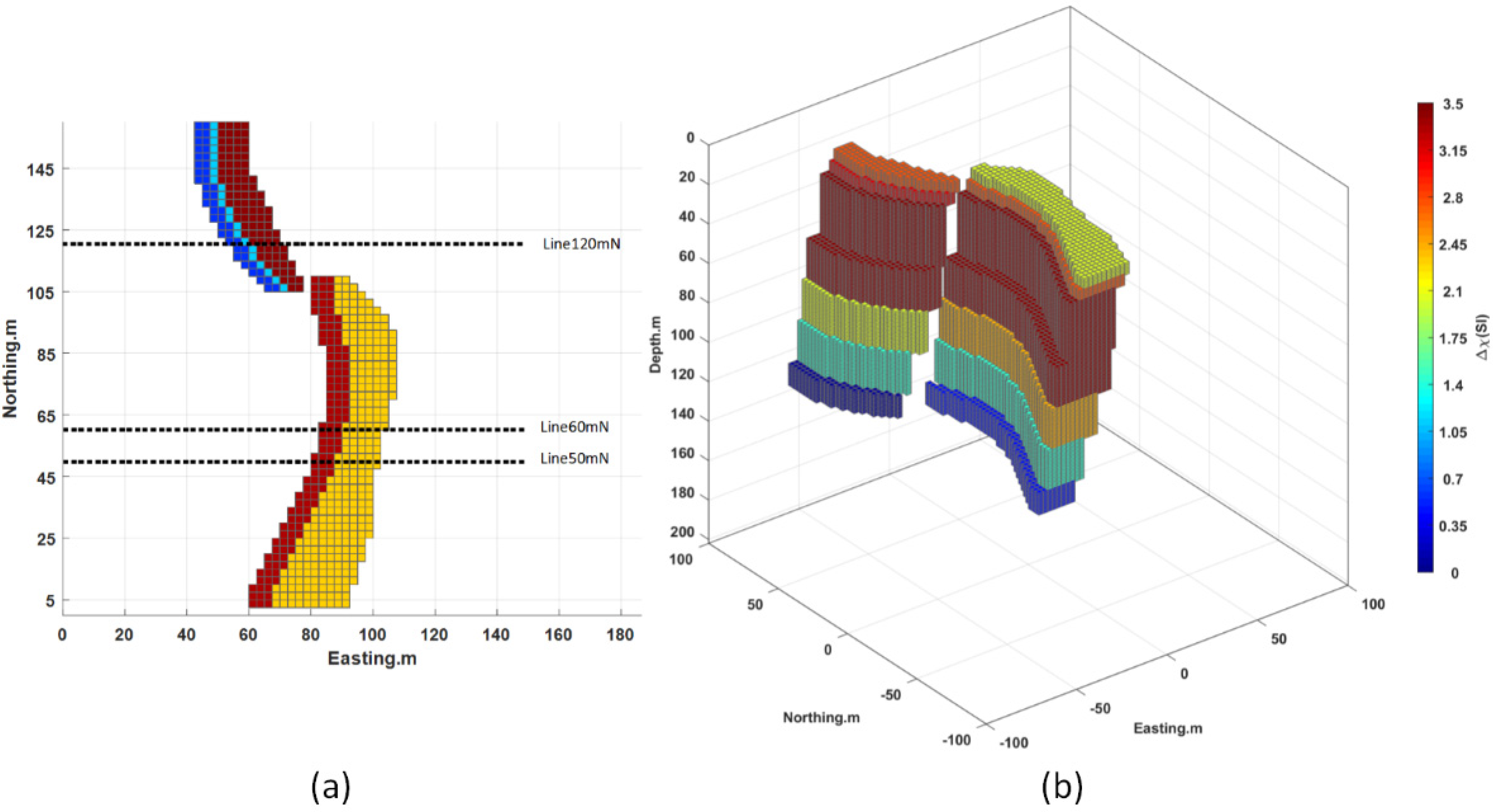
4.2. Parameter Prediction
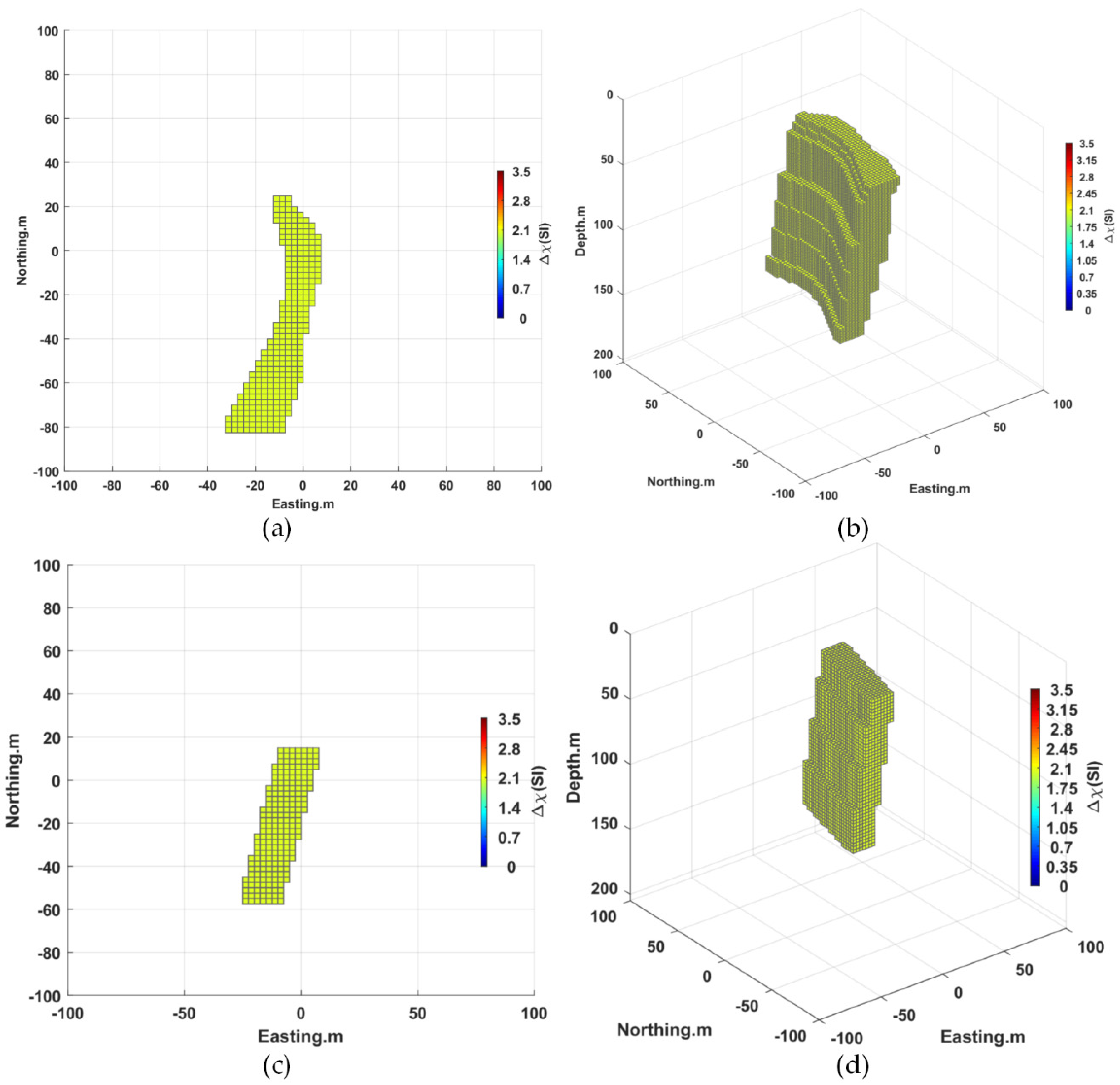
4.3. The Effect of the Source Body Parameters on Predictions
5. Conclusions
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Christensen, A.; Rajagopalan, S.J.P. The magnetic vector and gradient tensor in mineral and oil exploration. Preview 2000, 84, 77. [Google Scholar]
- Schmidt, P.; Clark, D.A. Advantages of measuring the magnetic gradient tensor. Preview 2000, 85, 26–30. [Google Scholar]
- Heath, P.; Heinson, G.; Greenhalgh, S. Some comments on potential field tensor data. Explor. Geophys. 2003, 34, 57–62. [Google Scholar] [CrossRef]
- Schmidt, P.; Clark, D.; Leslie, K.; Bick, M.; Tilbrook, D.; Foley, C. GETMAG—A SQUID magnetic tensor gradiometer for mineral and oil exploration. Explor. Geophys. 2004, 35, 297–305. [Google Scholar] [CrossRef]
- Schmidt, P.W.; Clark, D.A. The calculation of magnetic components and moments from TMI: A case study from the Tuckers igneous complex, Queensland. Explor. Geophys. 1998, 29, 609–614. [Google Scholar] [CrossRef]
- Stolz, R.; Zakosarenko, V.; Schulz, M.; Chwala, A.; Fritzsch, L.; Meyer, H.-G.; Köstlin, E.O. Magnetic full-tensor SQUID gradiometer system for geophysical applications. Lead. Edge 2006, 25, 178–180. [Google Scholar] [CrossRef]
- Schmidt, P.W.; Clark, D.A. The magnetic gradient tensor: Its properties and uses in source characterization. Lead. Edge 2006, 25, 75–78. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Stolz, R.; Chwala, A.; Schulz, M. SQUID technology for geophysical exploration. Phys. Status Solidi (C) 2005, 2, 1504–1509. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Frahm, C.P. Inversion of the magnetic field gradient equation for a magnetic dipole field. NCSL Informal Rep. 1972, 135–172. [Google Scholar]
- Wynn, W.; Frahm, C.; Carroll, P.; Clark, R.; Wellhoner, J.; Wynn, M. Advanced superconducting gradiometer/Magnetometer arrays and a novel signal processing technique. IEEE Trans. Magn. 1975, 11, 701–707. [Google Scholar] [CrossRef]
- Zhang, C.; Mushayandebvu, M.F.; Reid, A.B.; Fairhead, J.D.; Odegard, M. Euler deconvolution of gravity tensor gradient data. Geophysics 2000, 65, 512–520. [Google Scholar] [CrossRef] [Green Version]
- Zhdanov, M.S. Geophysical Inverse Theory and Regularization Problems; Elsevier: Amsterdam, The Netherlands, 2002; Volume 36. [Google Scholar]
- Zhdanov, M.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Zhdanov, M.; Liu, X.; Wilson, G. Potential field migration for rapid 3D imaging of entire gravity gradiometry surveys. First Break 2010, 28, 47–51. [Google Scholar] [CrossRef]
- Cai, H. Migration and Inversion of Magnetic and Magnetic Gradiometry Data. Master’s Thesis, The University of Utah, Salt Lake City, UT, USA, 2012. [Google Scholar]
- Sun, J.; Li, Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering. Geophysics 2015, 80, ID1–ID18. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Lin, W. Adaptive multinary inversion of gravity and gravity gradiometry data. Geophysics 2017, 82, G101–G114. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Zhang, H.; Geng, M.; Zuo, B. 3D Magnetization Vector Inversion of Magnetic Data: Improving and Comparing Methods. Pure Appl. Geophys. 2017, 174, 4421–4444. [Google Scholar] [CrossRef]
- Geng, M.; Hu, X.; Zhang, H.; Liu, S. 3D inversion of potential field data using a marginalizing probabilistic method. Geophysics 2018, 83, G93–G106. [Google Scholar] [CrossRef]
- Raiche, A. A pattern recognition approach to geophysical inversion using neural nets. Geophys. J. Int. 1991, 105, 629–648. [Google Scholar] [CrossRef] [Green Version]
- Spichak, V.; Popova, I. Artificial neural network inversion of magnetotelluric data in terms of three-dimensional earth macroparameters. Geophys. J. Int. 2000, 142, 15–26. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Joint inversion of multiple geophysical and petrophysical data using generalized fuzzy clustering algorithms. Geophys. J. Int. 2016, 208, 1201–1216. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, S. Identification of different geologic units using fuzzy constrained resistivity tomography. J. Appl. Geophys. 2018, 148, 127–138. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef] [Green Version]
- Noh, K.; Yoon, D.; Byun, J. Imaging subsurface resistivity structure from airborne electromagnetic induction data using deep neural network. Explor. Geophys. 2020, 51, 214–220. [Google Scholar] [CrossRef]
- Liu, B.; Guo, Q.; Li, S.; Liu, B.; Ren, Y.; Pang, Y.; Guo, X.; Liu, L.; Jiang, P. Deep Learning Inversion of Electrical Resistivity Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5715–5728. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Hu, X.; Liu, S.; Jie, Q.; Wang, H.; Chen, Q. 3-D Gravity Inversion Based on Deep Convolution Neural Networks. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3001305. [Google Scholar] [CrossRef]
- Nurindrawati, F.; Sun, J. Predicting Magnetization Directions Using Convolutional Neural Networks. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019675. [Google Scholar] [CrossRef]
- Li, R.; Yu, N.; Wang, X.; Liu, Y.; Cai, Z.; Wang, E. Model-Based Synthetic Geoelectric Sampling for Magnetotelluric Inversion With Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2020, 60, 4500514. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Hu, X.; Fu, L.; Qu, J.; Wang, H.; Cheng, Q. Inversion of magnetic data using deep neural networks. Phys. Earth Planet. Inter. 2021, 311, 106653. [Google Scholar] [CrossRef]
- He, S.; Cai, H.; Liu, S.; Xie, J.; Hu, X. Recovering 3D Basement Relief Using Gravity Data Through Convolutional Neural Networks. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022611. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. NIPS 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Li, K.; Chen, L.-W.; Chen, Q.-R.; Dai, S.-K.; Zhang, Q.-J.; Zhao, D.-D.; Ling, J.-X. Fast 3D forward modeling of the magnetic field and gradient tensor on an undulated surface. Appl. Geophys. 2018, 15, 500–512. [Google Scholar] [CrossRef]
- Gao, X.; Sun, S. Comment on “3DINVER. M: A MATLAB program to invert the gravity anomaly over a 3D horizontal density interface by Parker-Oldenburg’s algorithm”. Comput. Geosci. 2019, 127, 133–137. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, C.; Tang, J.; Chen, H.; Hu, S.; Zhou, C.; Xiao, X. Closed-form formula of magnetic gradient tensor for a homogeneous polyhedral magnetic target: A tetrahedral grid example. Geophysics 2017, 82, WB21–WB28. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Beiki, M.; Clark, D.A.; Austin, J.R.; Foss, C.A. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data. Geophysics 2012, 77, J23–J37. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional Sturm-Liouville eigen-problems: Theory and numerical approximation. J. Comput. Phys. 2013, 252, 495–517. [Google Scholar] [CrossRef]
- Chen, X.; Duan, J.; Karniadakis, G.E. Learning and meta-learning of stochastic advection–diffusion–reaction systems from sparse measurements. Eur. J. Appl. Math. 2021, 32, 397–420. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Karniadakis, G.E. DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. arXiv 2019, arXiv:1910.03193. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of back-propagation learning. In From Natural to Artificial Neural Computation; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learn (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited On 2012, 14, 2. [Google Scholar]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M.; Recognition, P. Bag of Tricks for Image Classification with Convolutional Neural Networks. arXiv 2019, arXiv:1812.01187. [Google Scholar]
- Wiegert, R.; Oeschger, J. Generalized Magnetic Gradient Contraction Based Method for Detection, Localization and Discrimination of Underwater Mines and Unexploded Ordnance. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; Volume 1322, pp. 1325–1332. [Google Scholar]
- Blakely, R.J.; Simpson, R.W. Approximating edges of source bodies from magnetic or gravity anomalies. Geophysics 1986, 51, 1494–1498. [Google Scholar] [CrossRef]
- Wijns, C.; Perez, C.; Kowalczyk, P. Theta map: Edge detection in magnetic data. Geophysics 2005, 70, L39–L43. [Google Scholar] [CrossRef]
- Pilkington, M.; Tschirhart, V. Practical considerations in the use of edge detectors for geologic mapping using magnetic data. Geophysics 2017, 82, J1–J8. [Google Scholar] [CrossRef]
- Seccombe, P.K.; Offler, R.; Ayshford, S. Origin of the Magnetite Skarn at Tallawang, NSW Preliminary Sulfur Isotope Results. In Research Report 1995–2000; IAEA: Vienna, Austria, 2000. [Google Scholar]
- Offler, R.; Seccombe, S.A.P. Geology and origin of the Tallawang magnetite skarn, Gulgong, NSW. In Proceedings of the 3rd National Conference of the Specialist Group in Economic Geology, Launceston, Australia, 10–14 November 1997. [Google Scholar]
- Ayshford, S.; Offler, R.; Seccombe, P. Geology and origin of the Tallawang magnetite skarn, Gulgong, NSW. Geol. Soc. Aust.-Abstr. 1997, 44, 5. [Google Scholar]
- Foster, D.A.; Gray, D.R. Evolution and Structure of the Lachlan Fold Belt (Orogen) of Eastern Australia. Annu. Rev. Earth Planet. Sci. 2000, 28, 47–80. [Google Scholar] [CrossRef]
- Collins, W.; Vernon, R. Palaeozoic arc growth, deformation and migration across the Lachlan Fold Belt, southeastern Australia. Tectonophysics 1992, 214, 381–400. [Google Scholar] [CrossRef]
- Lu, J.; Seccombe, P.; Foster, D.; Andrew, A. Timing of mineralization and source of fluids in a slate-belt auriferous vein system, Hill End goldfield, NSW, Australia: Evidence from 40Ar39Ar dating and O- and H-isotopes. Lithos 1996, 38, 147–165. [Google Scholar] [CrossRef]
- Powell, C.M.; Edgecombe, D.R.; Henry, N.M.; Jones, J.G. Timing of regional deformation of the hill end trough: A reassessment. J. Geol. Soc. Aust. 1976, 23, 407–421. [Google Scholar] [CrossRef]
- Packham, G.H. Radiometric evidence for Middle Devonian inversion of the Hill End Trough, northeast Lachlan Fold Belt. Aust. J. Earth Sci. 1999, 46, 23–33. [Google Scholar] [CrossRef]
- Colquhoun, G.P. Siliciclastic sedimentation on a storm- and tide-influenced shelf and shoreline: The Early Devonian Roxburgh Formation, NE Lachlan Fold Belt, southeastern Australia. Sediment. Geol. 1995, 97, 69–98. [Google Scholar] [CrossRef]

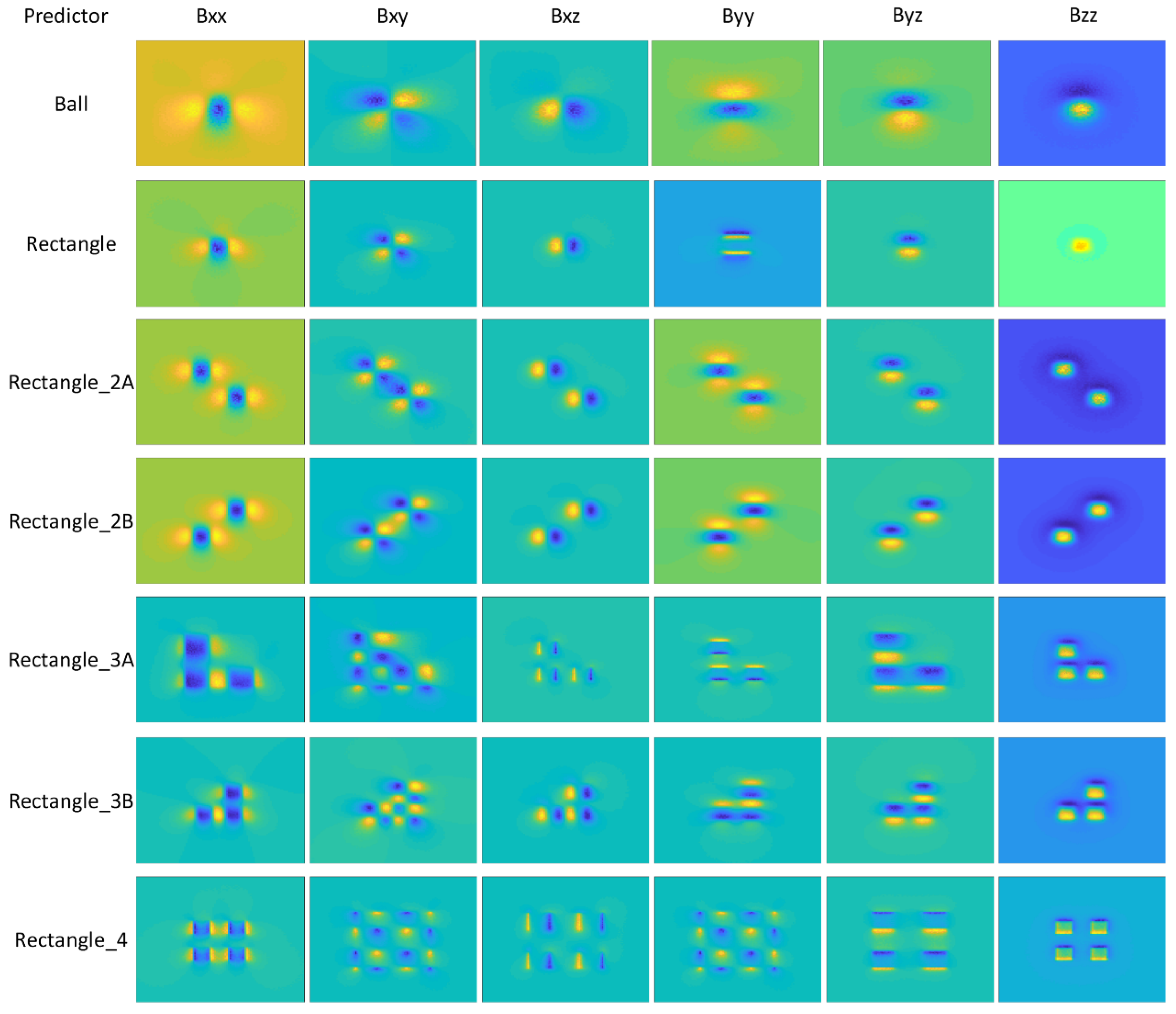
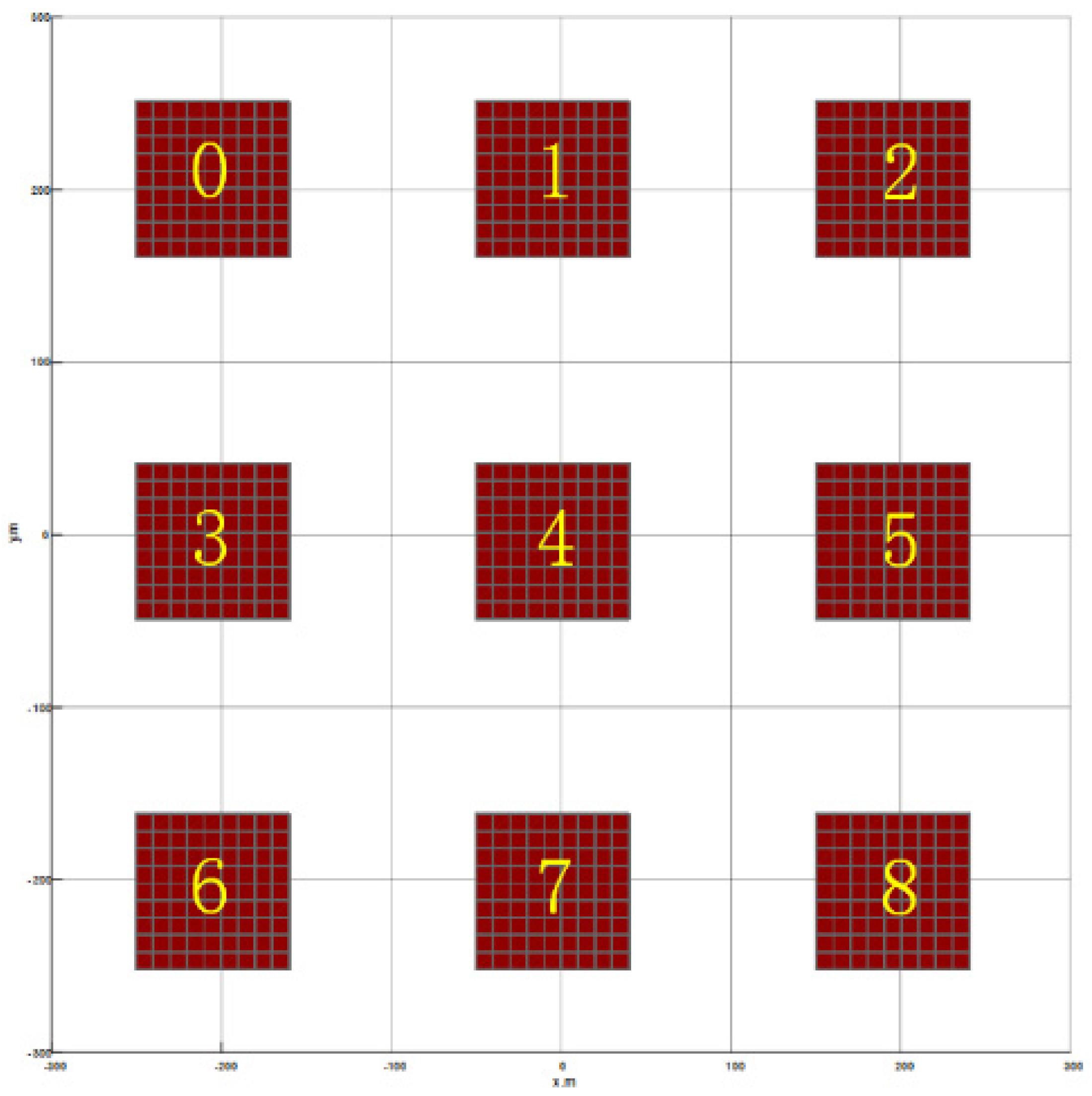
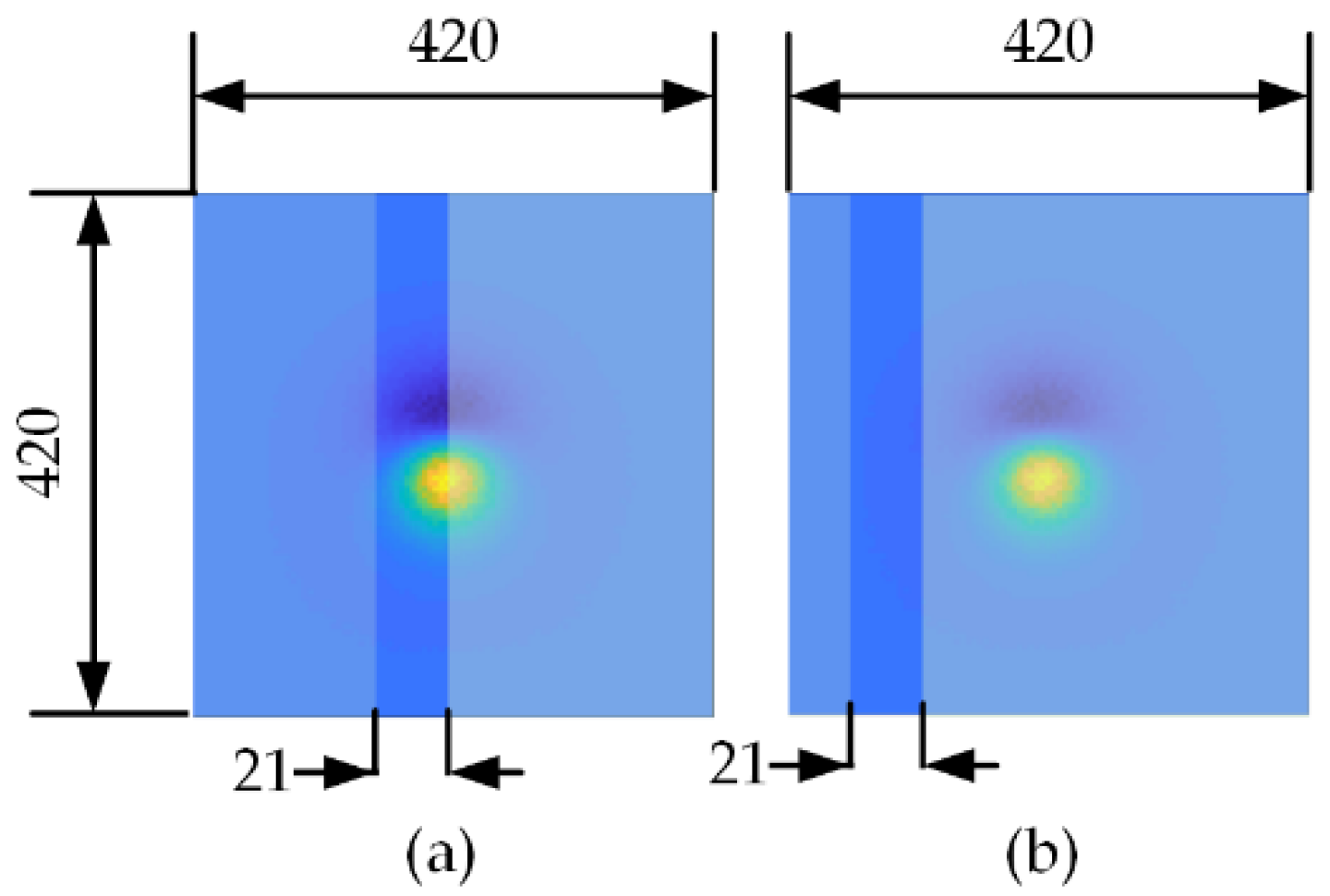
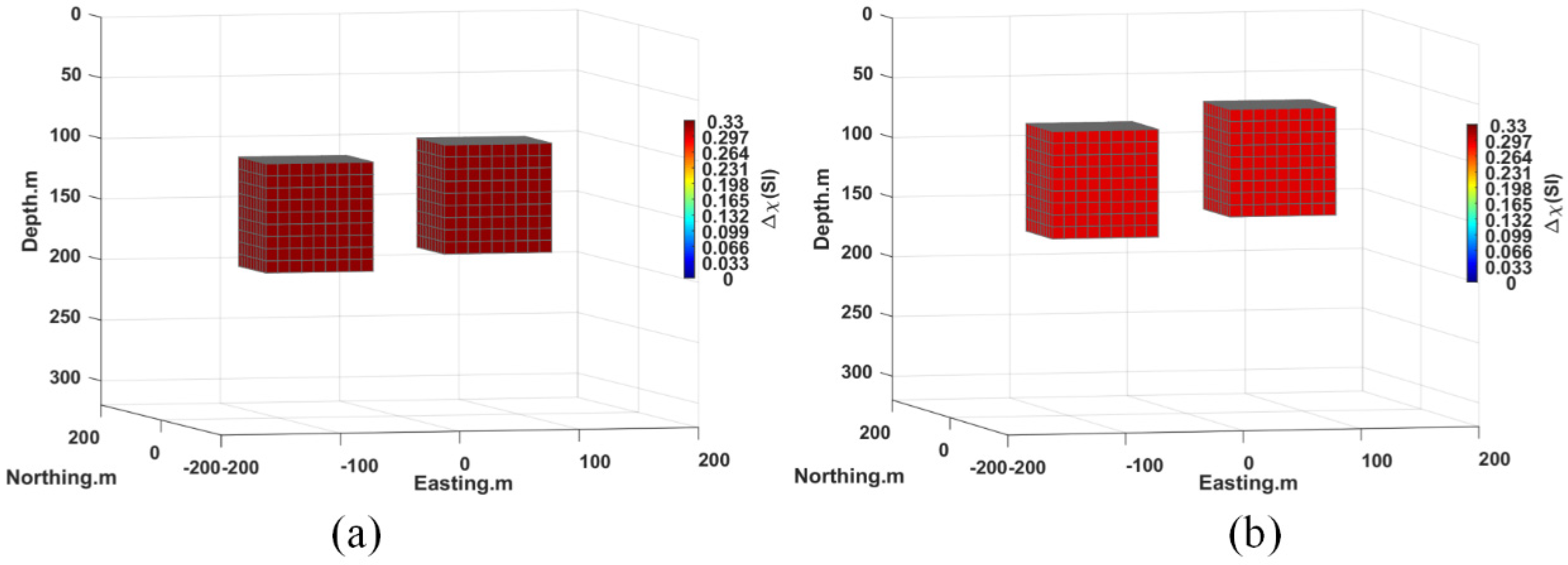
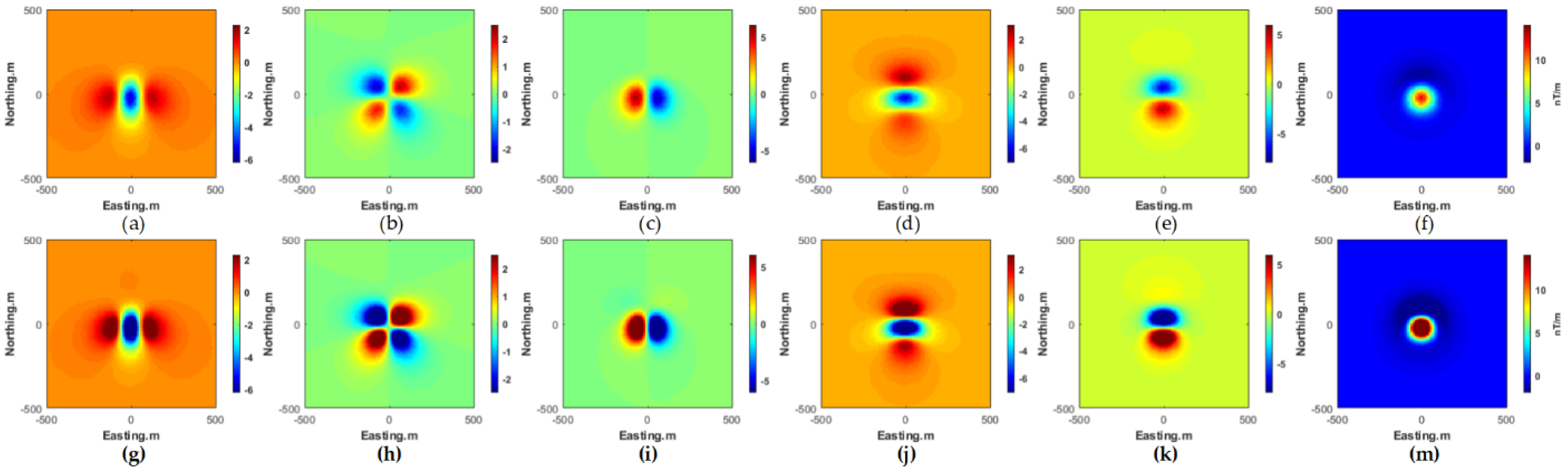
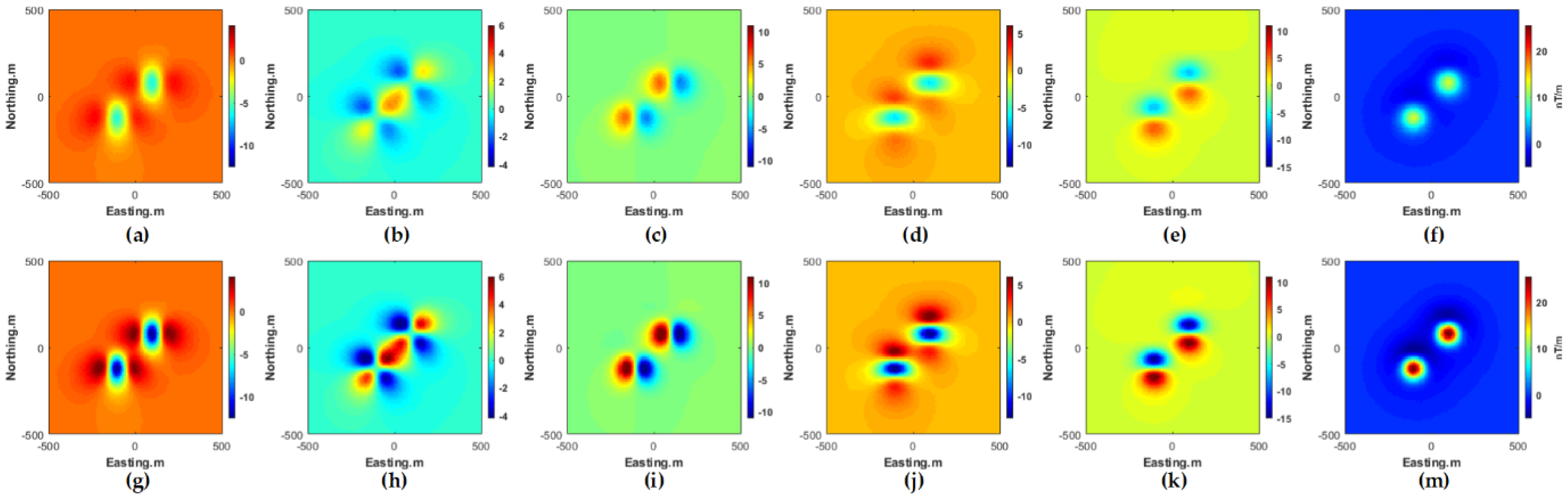
| Shape | Tag Name | Horizontal Position | Depth (m) | D | I | Magnetic Su-Sceptibility(SI) |
|---|---|---|---|---|---|---|
 | Ball | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle_2A | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle_2B | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle_3A | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle_3B | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
 | Rectangle_4 | (0,8) | (40,360) | (−10,10) | (52,72) | (0.1,0.6) |
| Predictor | Bxx | Bxy | Bxz | Byy | Byz | Bzz |
|---|---|---|---|---|---|---|
| Horizontal Position | 100% | 100% | 100% | 100% | 100% | 100% |
| Shape | 100% | 100% | 100% | 100% | 100% | 100% |
| Depth | 93.1% | 96.2% | 94.1% | 99.9% | 98.9% | 95.8% |
| D | 93.6% | 92.2% | 91.1% | 99.9% | 97.9% | 94.2% |
| I | 99.9% | 99.4% | 98.7% | 99.9% | 99.8% | 99.4% |
| Magnetic Sus-ceptibility(SI) | 91.4% | 90.2% | 92.7% | 91.1% | 90.5% | 93.3% |
| Predictor | Bxx | Bxy | Bxz | Byy | Byz | Bzz |
|---|---|---|---|---|---|---|
| Horizontal Position | 100% | 100% | 100% | 100% | 100% | 100% |
| Shape | 100% | 100% | 100% | 100% | 100% | 100% |
| Depth | 99.1% | 99.2% | 99.1% | 99.9% | 99.3% | 99.9% |
| D | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% |
| I | 99.6% | 99.4% | 99.7% | 99.9% | 99.4% | 99.3% |
| Magnetic Sus-ceptibility(SI) | 99.3% | 99.7% | 99.3% | 99.9% | 99.8% | 99.1% |
| Predictor | Input Model | Magnetic Tensor Gradient Prediction | |||||
|---|---|---|---|---|---|---|---|
| Bxx | Bxy | Bxz | Byy | Byz | Bzz | ||
| Horizontal Position | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Shape | Rectangle | Rectangle | Rectangle | Rectangle | Rectangle | Rectangle | Rectangle |
| Depth | 150 | 120 | 120 | 120 | 120 | 120 | 120 |
| D | −2° | −2° | −2° | −2° | −2° | −2° | −2° |
| I | 58° | 58° | 58° | 58° | 58° | 58° | 58° |
| Magnetic Sus- ceptibility(SI) | 0.6 | 0.5 | 0.6 | 0.6 | 0.5 | 0.6 | 0.6 |
| Predictor | Input Model | Magnetic Tensor Gradient Prediction | |||||
|---|---|---|---|---|---|---|---|
| Bxx | Bxy | Bxz | Byy | Byz | Bzz | ||
| Horizontal Position | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Shape | Rectan gle_2B | Rectan gle_2B | Rectan gle_2B | Rectan gle_2B | Rectan gle_2B | Rectan gle_2B | Rectan gle_2B |
| Depth | 150 | 120 | 120 | 120 | 120 | 120 | 120 |
| D | −2° | −2° | −2° | −2° | −2° | −2° | −2° |
| I | 58° | 58° | 58° | 58° | 58° | 58° | 58° |
| Magnetic Sus- ceptibility(SI) | 0.33 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Error Pattern | Bxx | Bxy | Bxz | Byy | Byz | Bzz |
|---|---|---|---|---|---|---|
| Misfit | 0.0707 | 0.0580 | 0.0354 | 0.0637 | 0.0346 | 0.2676 |
| MSE | 197.54 | 259.04 | 151.25 | 190.98 | 147.95 | 180.38 |
| Error Pattern | Bxx | Bxy | Bxz | Byy | Byz | Bzz |
|---|---|---|---|---|---|---|
| Misfit | 0.1017 | 0.0737 | 0.0580 | 0.0669 | 0.0601 | 0.1212 |
| MSE | 622.11 | 498.66 | 310.91 | 482.59 | 333.51 | 591.29 |
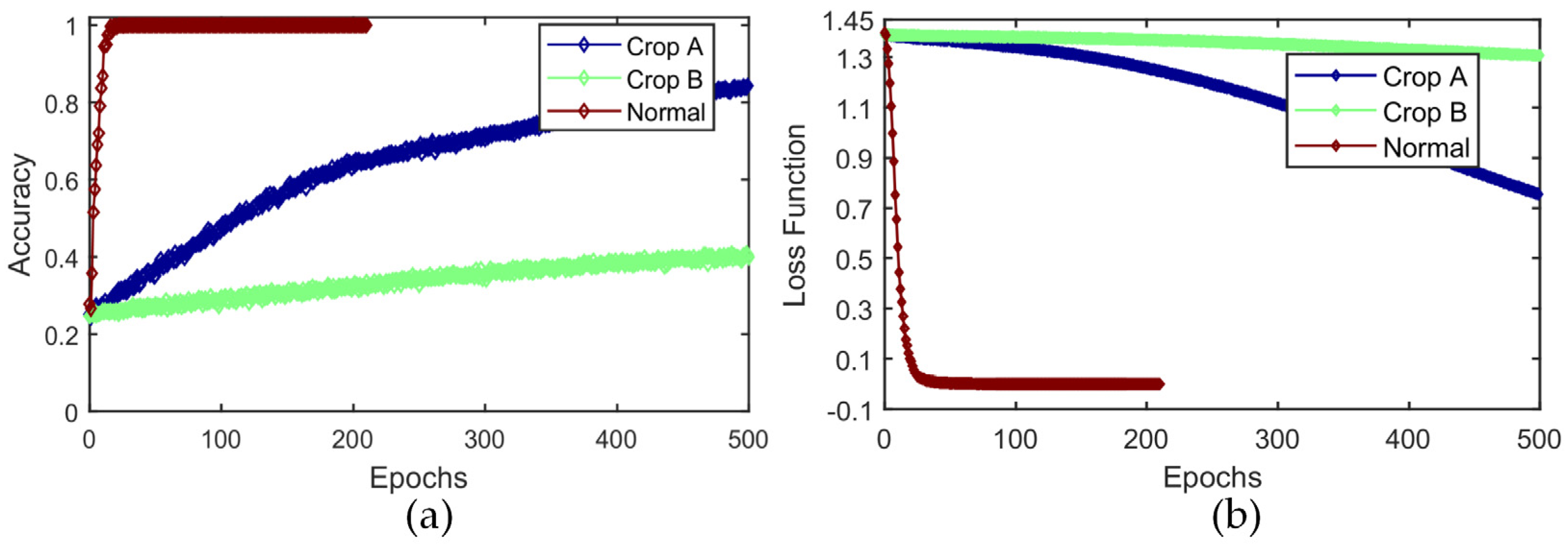
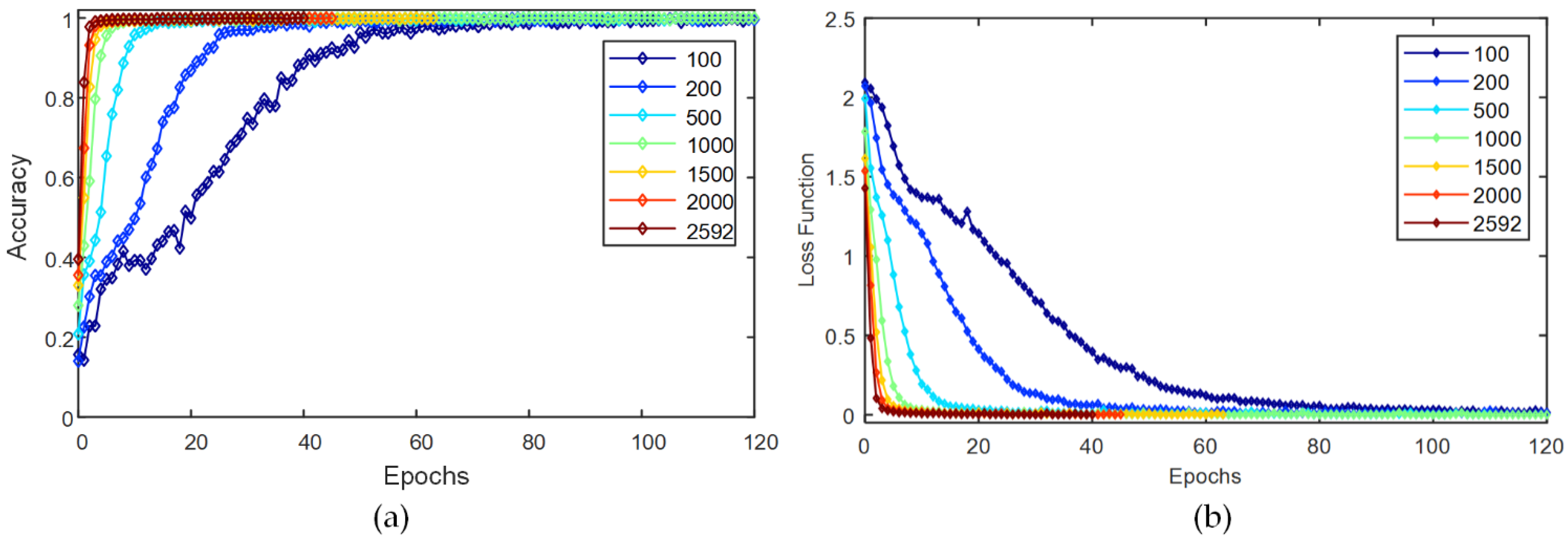
| Sample Numbers | T_ Epoch(s) 1 | Epoch_Num 2 | T_Sum(s) 3 | Test Accuracy |
|---|---|---|---|---|
| 100 | 4 | 44 | 176 | 97.3% |
| 200 | 9 | 24 | 216 | 99.5% |
| 500 | 18 | 10 | 180 | 99.8% |
| 1000 | 35 | 5 | 175 | 99.9% |
| 1500 | 66 | 4 | 264 | 100% |
| 2000 | 88 | 3 | 264 | 100% |
| 2592 | 114 | 3 | 342 | 100% |
| Component Name | … | 58 | 60 | 62 | 64 | 66 | … |
|---|---|---|---|---|---|---|---|
| Bt | … | 1.48 × 10−8 | 1.26 × 10−7 | 9.91 × 10−1 | 1.46 × 10−13 | 1.76 × 10−4 | … |
| Bxx | … | 2.09 × 10−14 | 9.57× 10−18 | 9.99 × 10−1 | 1.61 × 10−31 | 3.67× 10−4 | … |
| Bxy | … | 4.28 × 10−13 | 9.91× 10−16 | 9.99 × 10−1 | 2.63 × 10−28 | 3.91 × 10−4 | … |
| Bxz | … | 1.11 × 10−18 | 4.87 × 10−11 | 9.54 × 10−1 | 2.87 × 10−24 | 2.59 × 10−8 | … |
| Byy | … | 3.05 × 10−13 | 2.19 × 10−13 | 9.99 × 10−1 | 1.65 × 10−25 | 3.16 × 10−5 | … |
| Byz | … | 4.06 × 10−15 | 3.95 × 10−13 | 9.99 × 10−1 | 7.01 × 10−23 | 7.64 × 10−6 | … |
| Bzz | … | 1.74 × 10−10 | 1.77 × 10−10 | 9.99 × 10−1 | 2.02 × 10−18 | 7.53 × 10−5 | … |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Hu, X.; Cai, H.; Liu, S.; Peng, R.; Liu, Y.; Han, B. 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals 2022, 12, 566. https://doi.org/10.3390/min12050566
Deng H, Hu X, Cai H, Liu S, Peng R, Liu Y, Han B. 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals. 2022; 12(5):566. https://doi.org/10.3390/min12050566
Chicago/Turabian StyleDeng, Hua, Xiangyun Hu, Hongzhu Cai, Shuang Liu, Ronghua Peng, Yajun Liu, and Bo Han. 2022. "3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks" Minerals 12, no. 5: 566. https://doi.org/10.3390/min12050566
APA StyleDeng, H., Hu, X., Cai, H., Liu, S., Peng, R., Liu, Y., & Han, B. (2022). 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals, 12(5), 566. https://doi.org/10.3390/min12050566






