Feasibility of Broken Ore Flow Simulation in Block Caving Mining Method Using Attribute Stochastic Medium Theory
Abstract
:1. Introduction
1.1. Research Background
1.2. Related Works
2. Methods
2.1. Block Discreteness and Attribute Modeling
2.2. Attribute Stochastic Medium Theory
2.2.1. Modeling Technique of Combining Stochastic Media Theory and Attribute Blocks
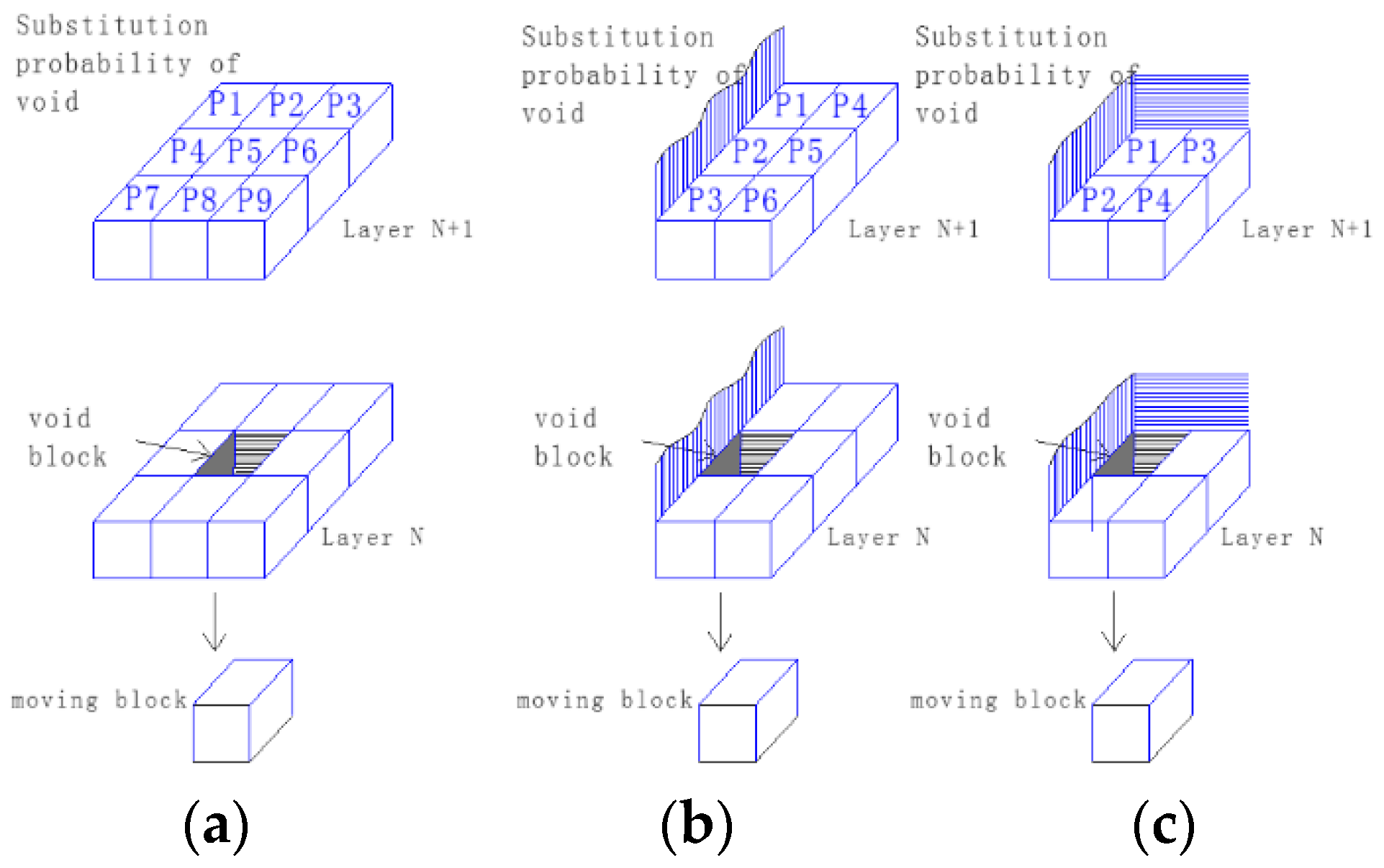
2.2.2. Probability Model of Void Block Transfer in Stochastic Media Theory
2.3. Flow Algorithms of Caved Ore-Rock Blocks Based on Attribute Stochastic Medium Theory
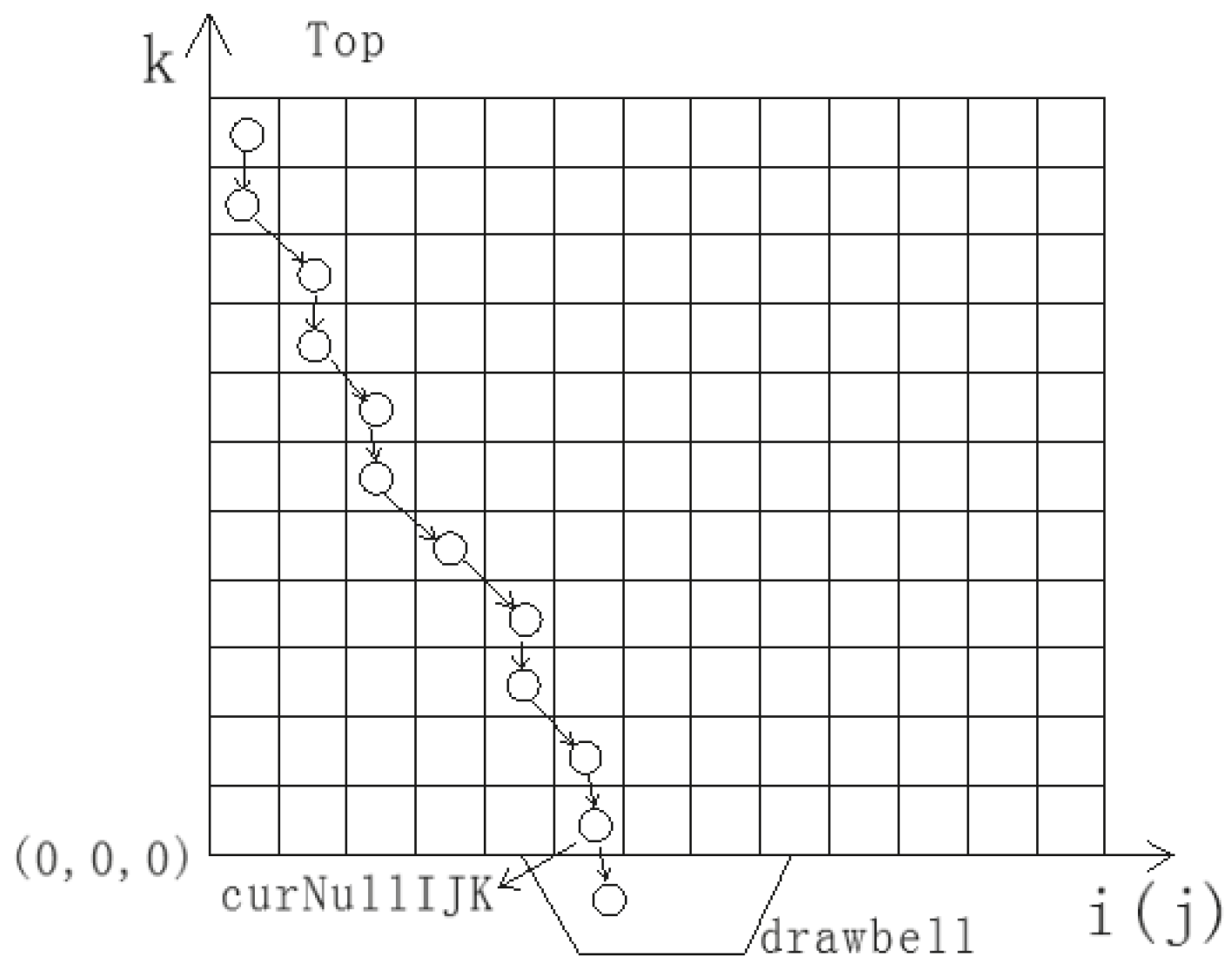
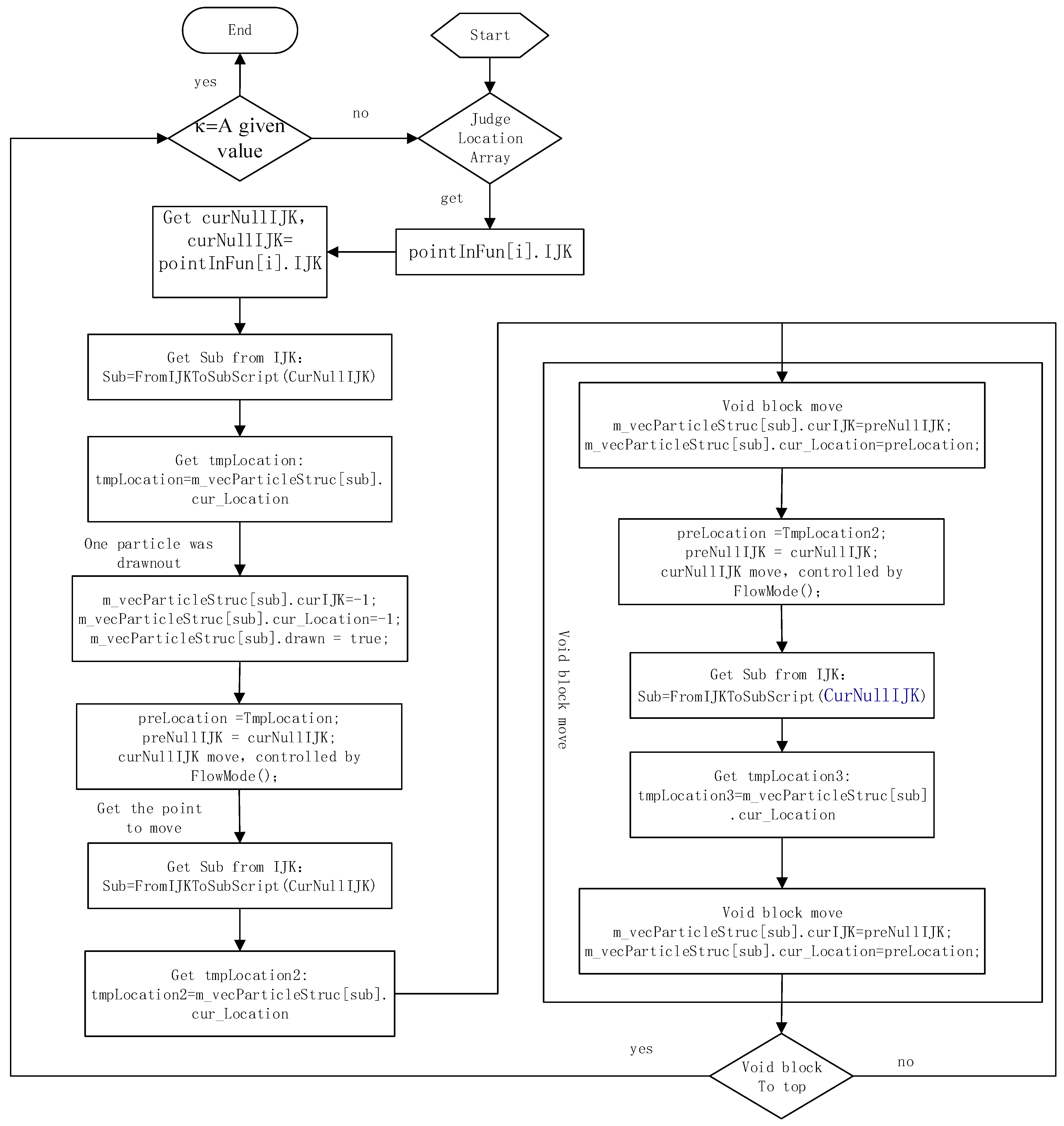
2.3.1. Data Structure Design and Simulation Process
Design of Flow Particle Structure
Flow Model of Particle and Simulation Process
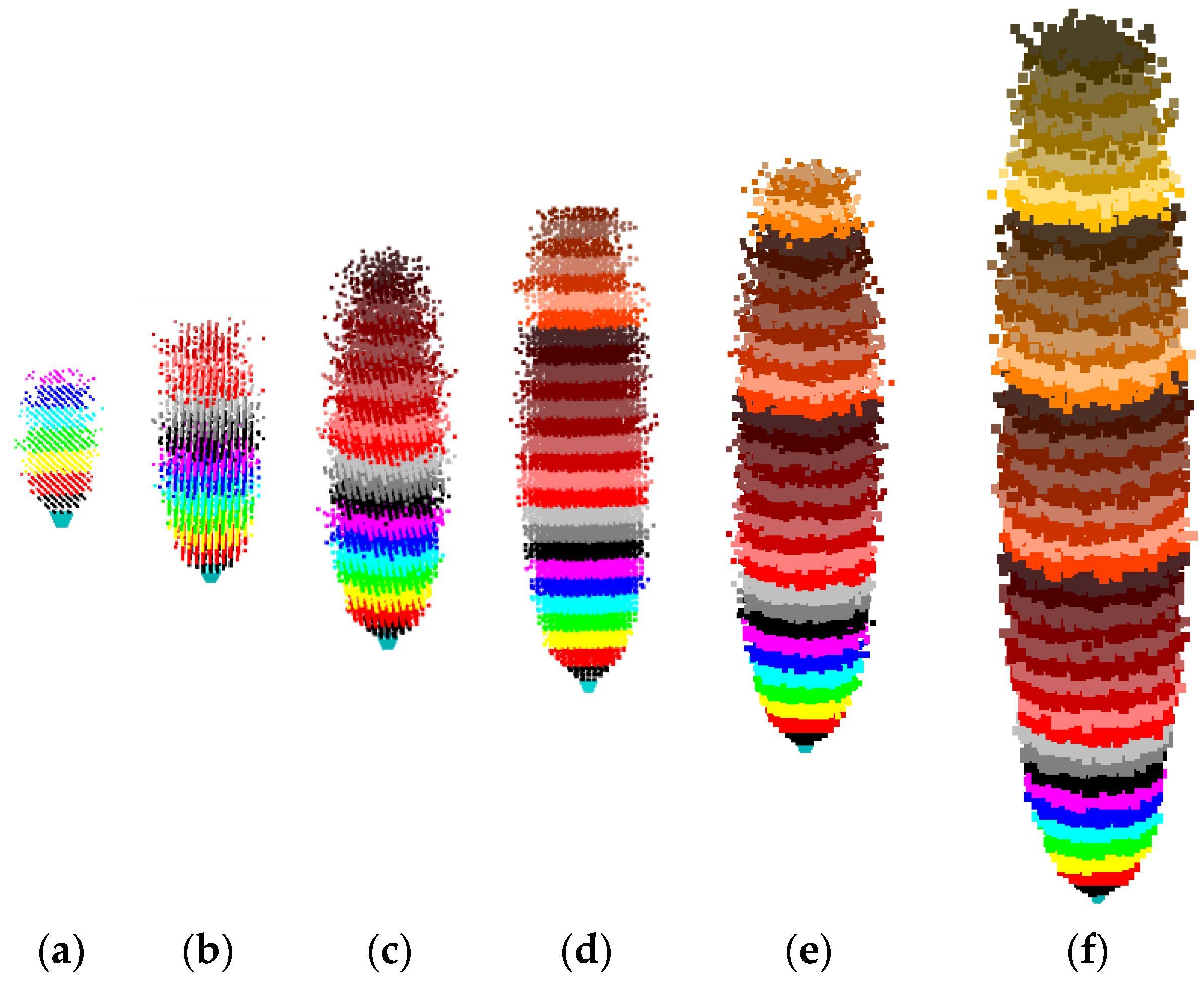
2.3.2. Block Flow Characteristics under Different Block Size Conditions
2.4. System Development
3. Results
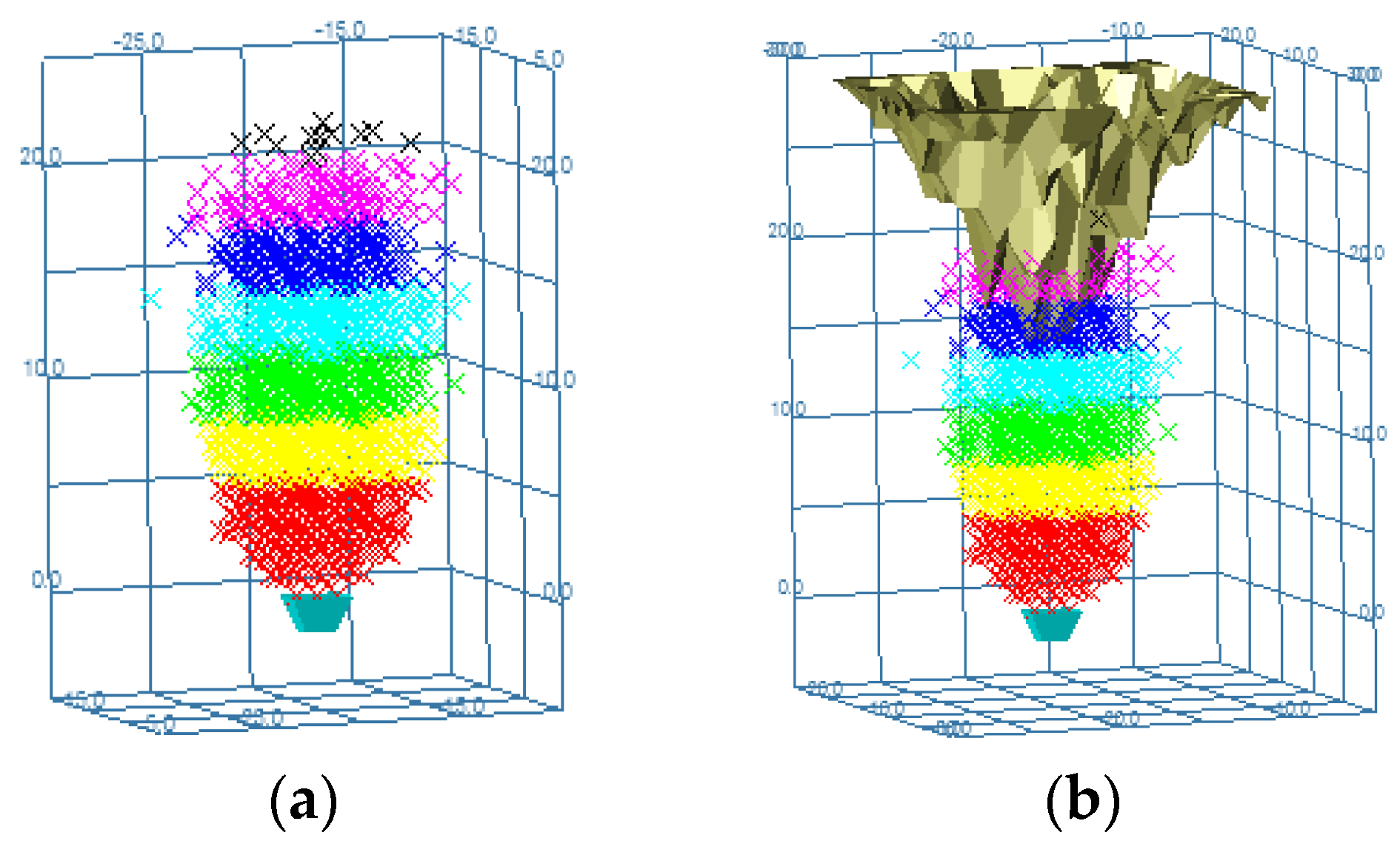
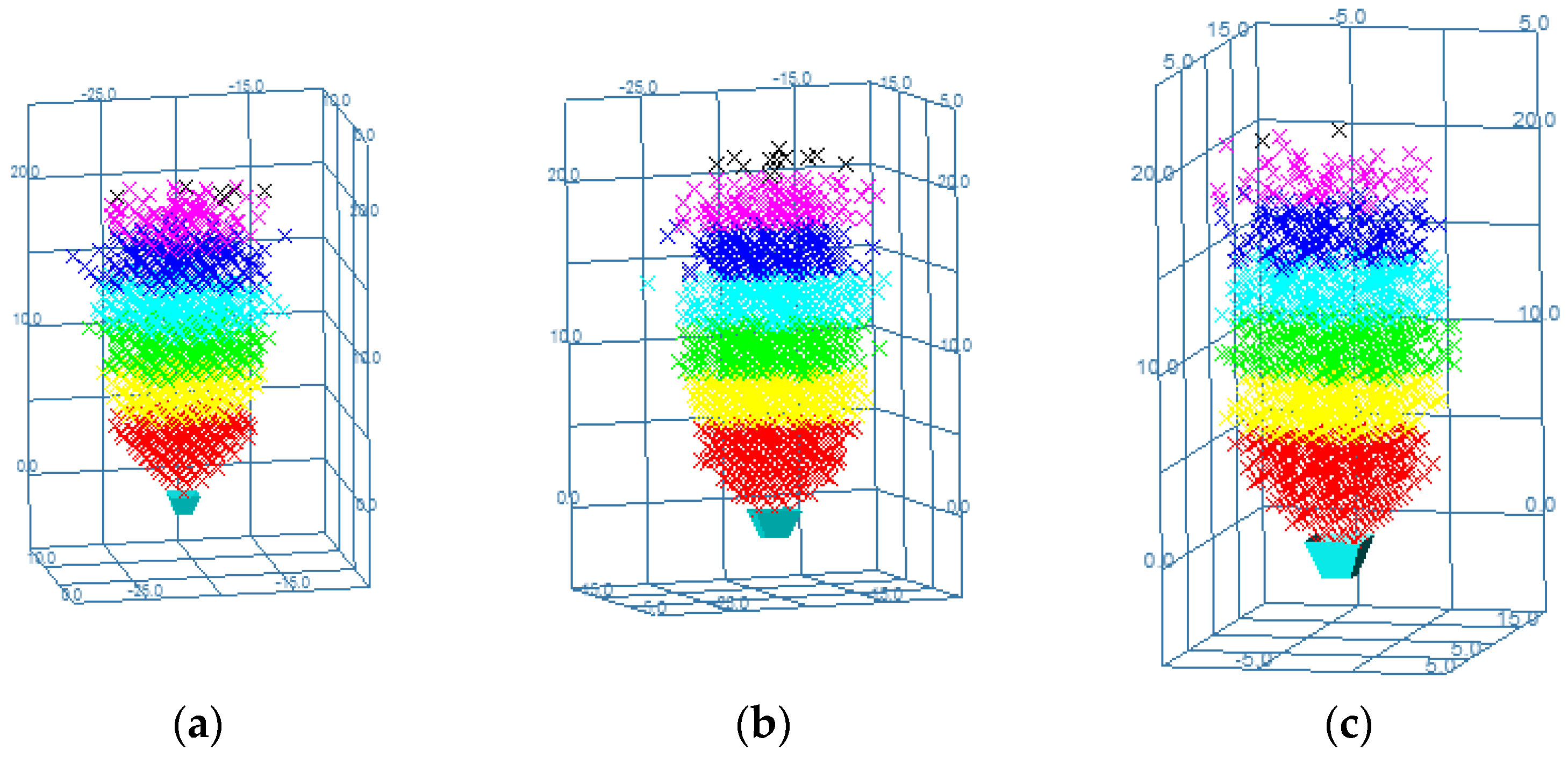
3.1. Mineral-Rock Flow in Fixed Target Drawing Heap
3.2. Mineral-Rock Flow at Different Drawing Heights
3.3. Mineral-Rock Flow under Different Fragmentation Conditions
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, E.T. Block Caving Geomechanics; Julius Kruttschnitt Mineral Research Centre, University of Queensland: Brisbane, QLD, Australia, 2002. [Google Scholar]
- Xing-long, F. Study on Digital Assessment and Simulation Technology at Rock Mass Engineering Quality of Block Caving; Central South University: Changsha, China, 2010. [Google Scholar]
- Laubscher, D.H. Caving mining-the state of art. Underground Mining Methods: Engineering Fundamentals and International Case Histories; Society for Mining, Metallurgy and Exploration: Littleton, CO, USA, 2001. [Google Scholar]
- Kacmar, L. Theoretical aspects of new options of sublevel caving methods. Acta Montan. Slovaca 2008, 13, 448–453. [Google Scholar]
- Morner, N.A.; Sjoberg, R. Merging the concepts of pseudokarst and paleoseismicity in Sweden: A unified theory on the formation of fractures, fracture caves, and angular block heaps. Int. J. Speleol. 2018, 47, 393–405. [Google Scholar] [CrossRef]
- Nezhadshahmohammad, F.; Aghababaei, H.; Pourrahimian, Y. Conditional draw control system in block-cave production scheduling using mathematical programming. Int. J. Min. Reclam. Environ. 2019, 33, 223–246. [Google Scholar] [CrossRef]
- Power, G.R. Modeling Granular Flow in Caving Mines: Large Scale Physical Models and Full Scale Experiments. Ph.D. Thesis, University of Queensland, Brisbane, QLD, Australia, 2004. [Google Scholar]
- Brunton, I.D.; Fraser, S.J.; Hodgkinson, J.H.; Stewart, P.C. Parameters influencing full scale sublevel caving material recovery at the Ridgeway gold mine. Int. J. Rock Mech. Min. Sci. 2010, 47, 647–656. [Google Scholar] [CrossRef]
- Castro, R.; Trueman, R.; Halim, A. A study of isolated draw zones in block caving mines by means of a large 3D physical model. Int. J. Rock Mech. Min. Sci. 2007, 44, 860–870. [Google Scholar] [CrossRef] [Green Version]
- Trueman, R.; Castro, R.; Halim, A. Study of multiple draw-zone interaction in block caving mines by means of a large 3D physical model. Int. J. Rock Mech. Min. Sci. 2008, 45, 1044–1051. [Google Scholar] [CrossRef] [Green Version]
- Melo, F.; Vivanco, F.; Fuentes, C.; Apablaza, V. Kinematic model for quasi static granular displacements in block caving: Dilatancy effects on drawbody shapes. Int. J. Rock Mech. Min. Sci. 2008, 45, 248–259. [Google Scholar] [CrossRef]
- Melo, F.; Vivanco, F.; Fuentes, C. Calculated isolated extracted and movement zones compared to scaled models for block caving. Int. J. Rock Mech. Min. Sci. 2009, 46, 731–737. [Google Scholar] [CrossRef]
- Zhang, X.; Tao, G.; Zhu, Z. Laboratory study of the influence of dip and ore width on gravity flow during longitudinal sublevel caving. Int. J. Rock Mech. Min. Sci. 2018, 103, 179–185. [Google Scholar] [CrossRef]
- Jia, Q.; Tao, G.; Liu, Y.; Wang, S. Laboratory study on three-dimensional characteristics of gravity flow during longitudinal sublevel caving. Int. J. Rock Mech. Min. Sci. 2021, 144, 9. [Google Scholar] [CrossRef]
- Sanchez, V.S.; Castro, R.L.; Palma, S. Gravity flow characterization of fine granular material for Block Caving. Int. J. Rock Mech. Min. Sci. 2019, 114, 24–32. [Google Scholar] [CrossRef]
- Diering, T. PC-BC: A block cavedesign and draw control system. In Proceedings of MassMin2000; The Australasian Institute of Mining and Metallurgy: Brisbane, QLD, Australia, 2000. [Google Scholar]
- Huang, M.Q.; Wang, Y.M.; Gao, Q. Three-dimensional Simulation of Hopper Ore Drawing Regularity in Natural Caving. Met. Mine 2018, 501, 151–155. [Google Scholar]
- Rafiee, R.; Ataei, M.; KhalooKakaie, R.; Jalali, S.E.; Sereshki, F.; Noroozi, M. Numerical modeling of influence parameters in cavabililty of rock mass in block caving mines. Int. J. Rock Mech. Min. Sci. 2018, 105, 22–27. [Google Scholar] [CrossRef]
- Castro, R.L.; Gonzalez, F.; Arancibia, E. Development of a gravity flow numerical model for the evaluation of drawpoint spacing for block/panel caving. J. S. Afr. Inst. Min. Metall. 2009, 109, 393–400. [Google Scholar]
- Sanchez, K.S.; Palma, S.; Castro, R.L. Numerical Modelling of Water Flow Through Granular Material for Isolated and Simultaneous Extractions in Block Caving. Rock Mech. Rock Eng. 2019, 52, 133–147. [Google Scholar] [CrossRef]
- Woo, K.S.; Eberhardt, E.; Rabus, B.; Stead, D.; Vyazmensky, A. Integration of field characterisation, mine production and InSAR monitoring data to constrain and calibrate 3-D numerical modelling of block caving-induced subsidence. Int. J. Rock Mech. Min. Sci. 2012, 53, 166–178. [Google Scholar] [CrossRef]
- Li-guan, W.; Xin, C. Advancing technologies for digital mine. Chin. J. Nonferrous Met. 2016, 26, 1693–1710. [Google Scholar]
- Zhong, D.-Y.; Wang, L.-G.; Jia, M.-T.; Bi, L.; Zhang, J. Orebody Modeling from Non-Parallel Cross Sections with Geometry Constraints. Minerals 2019, 9, 229. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhong, D.; Wu, Z.; Wang, L.; Tang, Q. Local Dynamic Updating Method of Orebody Model Based on Mesh Reconstruction and Mesh Deformation. Minerals 2021, 11, 232. [Google Scholar] [CrossRef]
- Zhong, D.-Y.; Wang, L.-G.; Bi, L.; Jia, M.-T. Implicit modeling of complex orebody with constraints of geological rules. Trans. Nonferrous Met. Soc. China 2019, 29, 2392–2399. [Google Scholar] [CrossRef]
- Zhong, D.-Y.; Wang, L.-G.; Bi, L. Implicit surface reconstruction based on generalized radial basis functions interpolant with distinct constraints. Appl. Math. Model. 2019, 71, 408–420. [Google Scholar] [CrossRef]
- Gang-hai, H.; Yu-yong, J.; Xiu-li, Z. Visual modeling for 3D spherical particle for geological body model of rock engineering. Chin. J. Geotech. Eng. 2014, 36, 782–787. [Google Scholar]
- Han, K.; Feng, Y.T.; Owen, D.R.J. Sphere packing with a geometric based compression algorithm. Powder Technol. 2005, 155, 33–41. [Google Scholar] [CrossRef]
- Liu, J.; Geng, Q.D. Three-dimensional particles generation algorithm. J. Dalian Univ. Technol. 2011, 51, 236–243. [Google Scholar]
- Bi, L.; Wang, L.G.; Chen, J.H.; Feng, X.L. Study of Octree-Based Block Model of Complex Geological Bodies. J. China Univ. Min. Technol. 2008, 37, 532–537. [Google Scholar]
- Beck, D.A.; Sharrock, G.; Capes, G. A Coupled DFE-Newtonian Cellular Automata Cave Initiation, Propagation And Induced Seismicity. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Castro, R.; Gómez, R.; Arancibia, L. Fine material migration modelled by cellular automata. Granul. Matter 2021, 24, 14. [Google Scholar] [CrossRef]
- Gibson, W. Stochastic Models for Gravity Flow: Numerical Considerations. In Proceedings of the 3rd International Symposium on Block and Sublevel Caving, Santiago, Chile, 5–6 June 2014; Volume 1. [Google Scholar]
- Litwiniszyn, J. Application of the equation of stochastic processes to mechanics of loose bodies. Arch. Mech. 1956, 8, 393–411. [Google Scholar]
- Bin, Y.; Di-jie, Z.; Zhong-hui, C. Top-coal drawing law of LTCC mining based on stochastic medium theory. J. China Coal Soc. 2017, 42, 1366–1371. [Google Scholar]
- Bo, L.; Weihong, Y.; Gong, Z.; Lei, G. A prediction model based on stochastic medium theory for ground surface settlement induced by non-uniform tunnel deformation. Chin. J. Rock Mech. Eng. 2018, 37, 1943–1952. [Google Scholar]
- Bao-chen, L.; Hua-yang, D. Research Development and Origin of Probability Integral Method. Coal Min. Technol. 2016, 21, 1–3. [Google Scholar]
- Ren, F.Y. Stochastic Medium Theory for Ore Draw and Its Application; Metallurgical Industry Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Zhong-hua, Z.; Jie, H.; Gan-qiang, T. Flow simulation of ore and rock and optimization of structure parameter of oredrawing of high stage block caving under multi funnel. J. Chongqing Univ. 2017, 4, 49–59. [Google Scholar]
- Zhong-hua, Z.; Bi-bo, D.; Gan-qiang, T. Preliminary optimization of ore drawing scheme of block caving. J. Chongqing Univ. 2018, 41, 75–85. [Google Scholar]
- Jolley, D. Computer simulation of the movement of ore and waste in an underground mining pillar. Can. Min. Met. 1968, 67, 854–859. [Google Scholar]
- Zhu, Z.H. Study on Key Technologies of Drawing Control Optimization and Intelligent Management of Block Caving; School of Resources and Safety Engineering, Central South University: Changsha, China, 2015. [Google Scholar]





| Draw-Out Index κ (%) | 3 | 5 | 10 | 15 | 16.4 |
|---|---|---|---|---|---|
| Cu grade of IEZ (%) | 0.51 | 0.49 | 0.49 | 0.53 | 0.51 |
| Long Half Axis of IEZ (m) | 7.5 | 9.56 | 13.2 | 15.5 | 16.1 |
| Short Half Axis of IEZ (m) | 4.8 | 5.55 | 6.7 | 7.5 | 8.0 |
| Eccentricity | 0.76 | 0.81 | 0.86 | 0.87 | 0.87 |
| Remnants volume (m3) | 11,646 | 11,407 | 10,820 | 10,212 | 10,032 |
| Average Depth of Depression Pit (m) | 0.75 | 1.48 | 2.95 | 4.47 | 5.91 |
| Drawing Height (m) | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 300 |
|---|---|---|---|---|---|---|---|---|
| Length of Long Half Axis (m) | 10.56 | 21.34 | 31.75 | 42.05 | 52.78 | 74.68 | 106.6 | 157.5 |
| Length of Short Half Axis (m) | 6.3 | 8.7 | 11.7 | 12.6 | 14.1 | 16.4 | 19.5 | 20.4 |
| Eccentricity | 0.80 | 0.91 | 0.93 | 0.95 | 0.96 | 0.98 | 0.98 | 0.99 |
| Cu (%) | 0.51 | 0.54 | 0.55 | 0.52 | 0.51 | 0.49 | 0.50 | 0.47 |
| Block Index β | Cu Grade of IEZ (%) | Length of Short Half Axis (m) | Eccentricity of IEZ | Average Depth of Depression Pit (m) |
|---|---|---|---|---|
| 1 | 0.50 | 6.3 | 0.84 | 2.93 |
| 2 | 0.49 | 6.5 | 0.83 | 2.95 |
| 3 | 0.51 | 7.5 | 0.8 | 2.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, B.; Zhao, X.; Zhu, Z.; Tao, G.; Yin, G. Feasibility of Broken Ore Flow Simulation in Block Caving Mining Method Using Attribute Stochastic Medium Theory. Minerals 2022, 12, 576. https://doi.org/10.3390/min12050576
Dai B, Zhao X, Zhu Z, Tao G, Yin G. Feasibility of Broken Ore Flow Simulation in Block Caving Mining Method Using Attribute Stochastic Medium Theory. Minerals. 2022; 12(5):576. https://doi.org/10.3390/min12050576
Chicago/Turabian StyleDai, Bibo, Xingdong Zhao, Zhonghua Zhu, Ganqiang Tao, and Gui Yin. 2022. "Feasibility of Broken Ore Flow Simulation in Block Caving Mining Method Using Attribute Stochastic Medium Theory" Minerals 12, no. 5: 576. https://doi.org/10.3390/min12050576
APA StyleDai, B., Zhao, X., Zhu, Z., Tao, G., & Yin, G. (2022). Feasibility of Broken Ore Flow Simulation in Block Caving Mining Method Using Attribute Stochastic Medium Theory. Minerals, 12(5), 576. https://doi.org/10.3390/min12050576






