Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines
Abstract
:1. Introduction
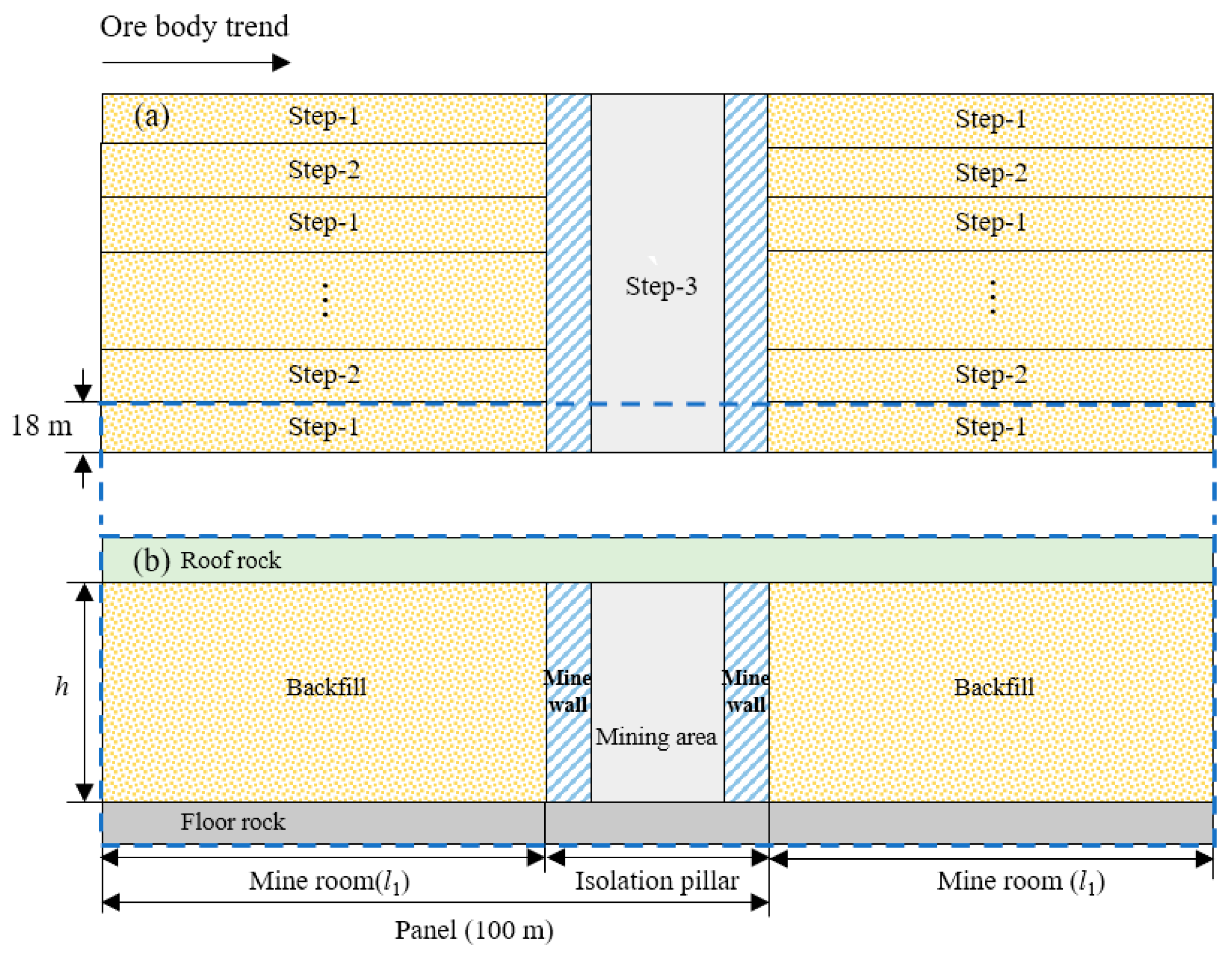
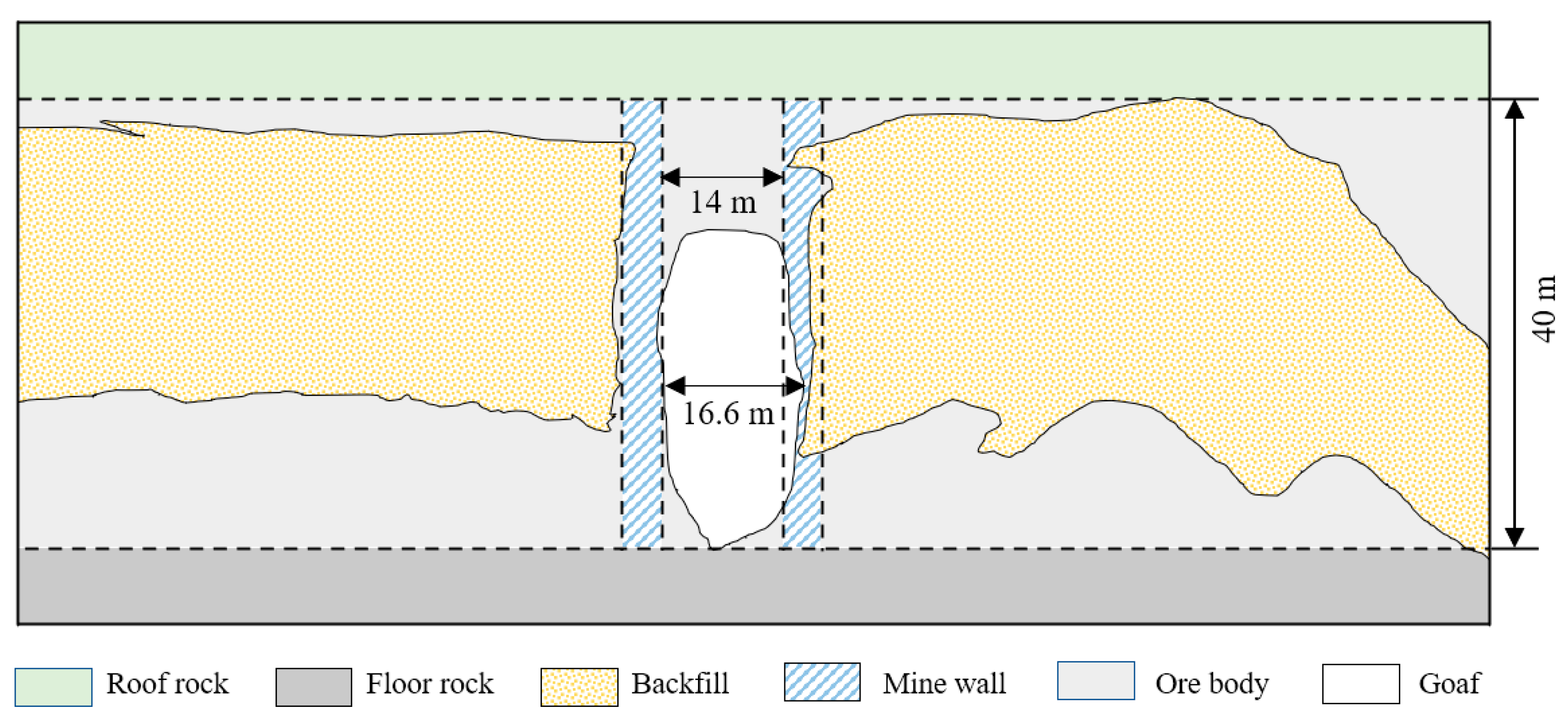
2. Project Overview
3. Analysis of Mine Wall Safety Factor
3.1. Mine Wall Mechanics Model
3.2. Compression Safety Factor
3.3. Shear Safety Factor
3.4. Overturning Safety Factor
3.5. Comprehensive Safety Factor
4. Analysis of Factors Affecting Mine Wall Stability
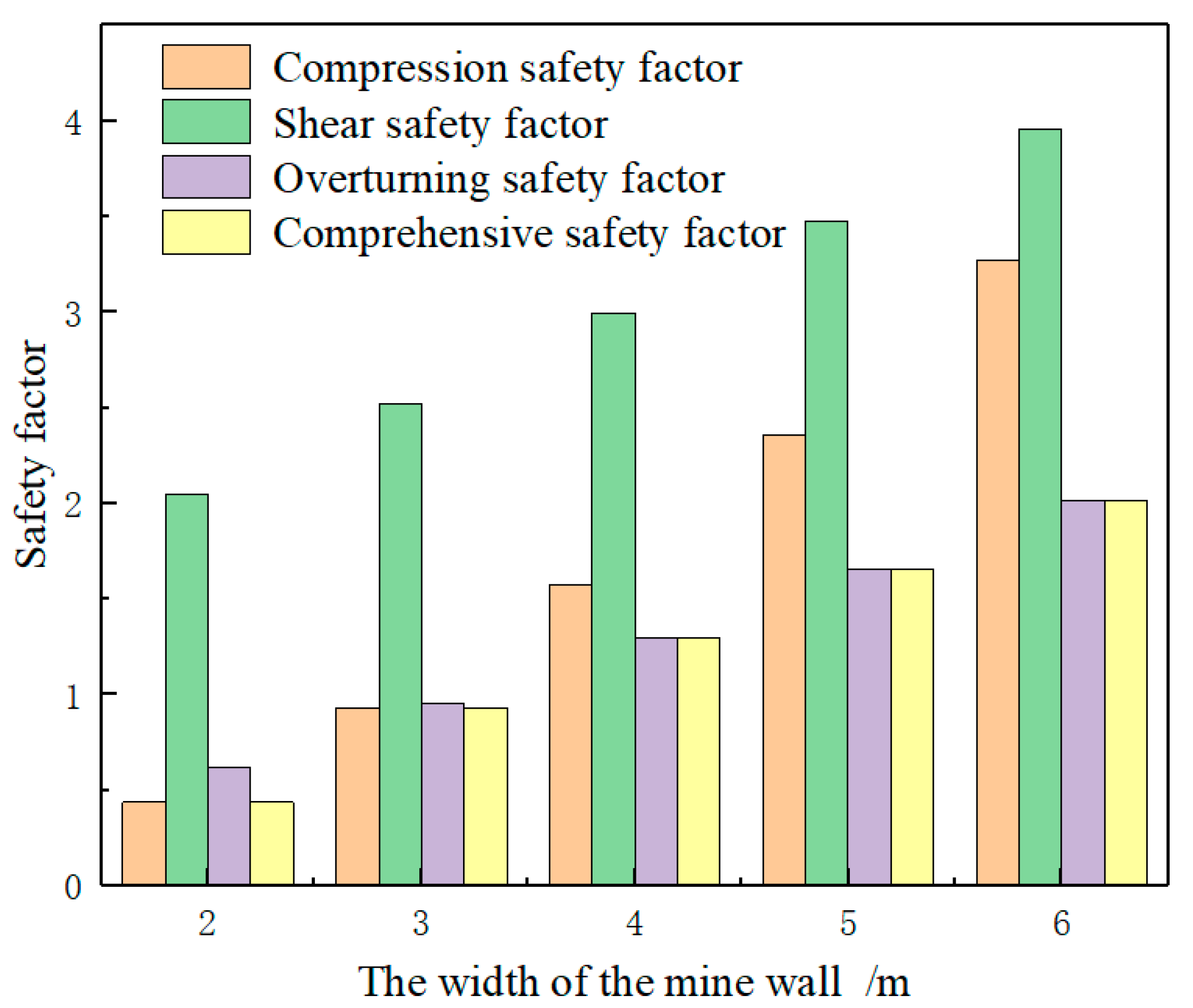
4.1. Quantitative Relationship between Mine Wall Safety Factor and the Width of the Mine Wall
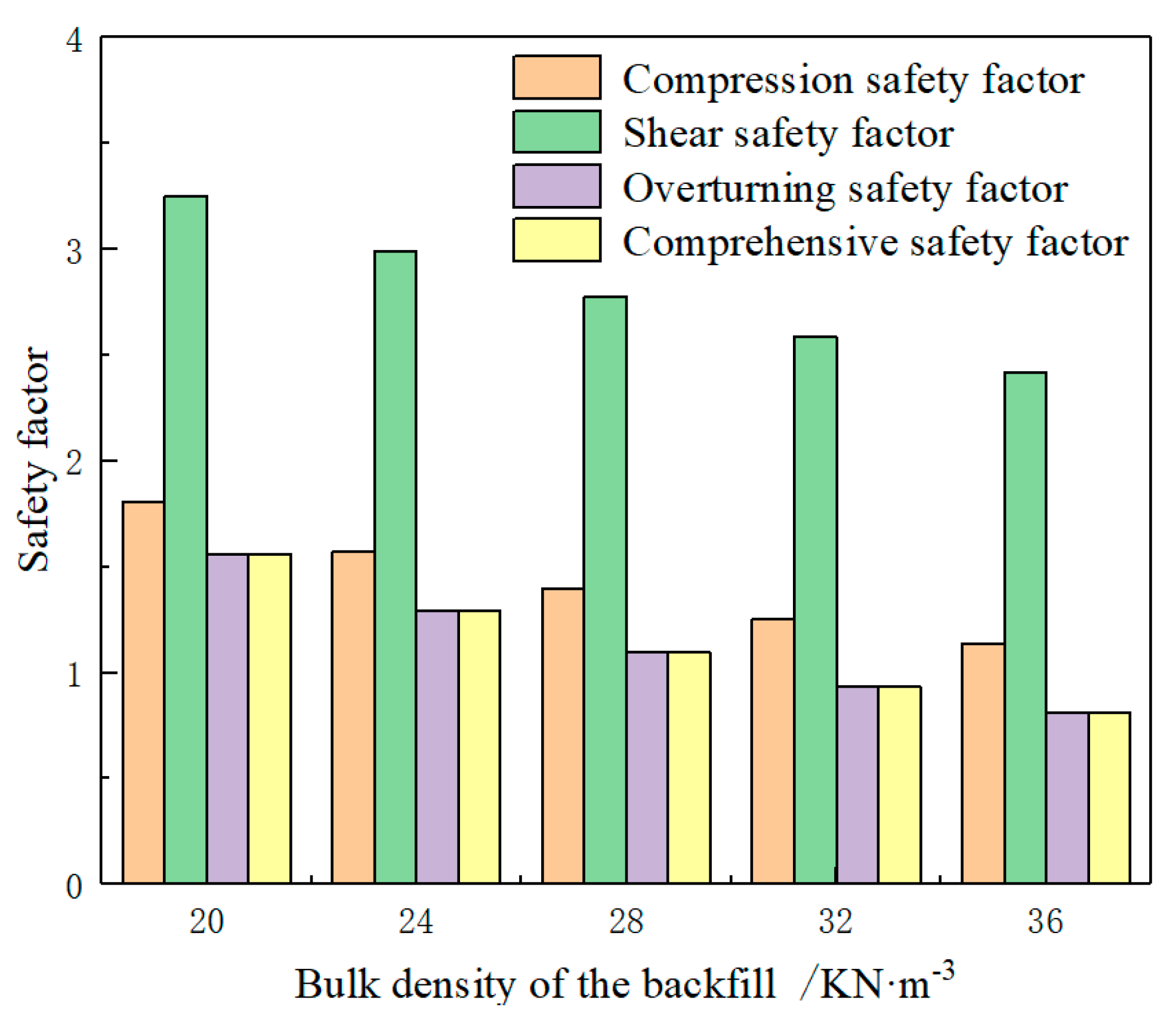
4.2. Quantitative Relationship between Safety Factor of Mine Wall and Bulk Density of the Backfill
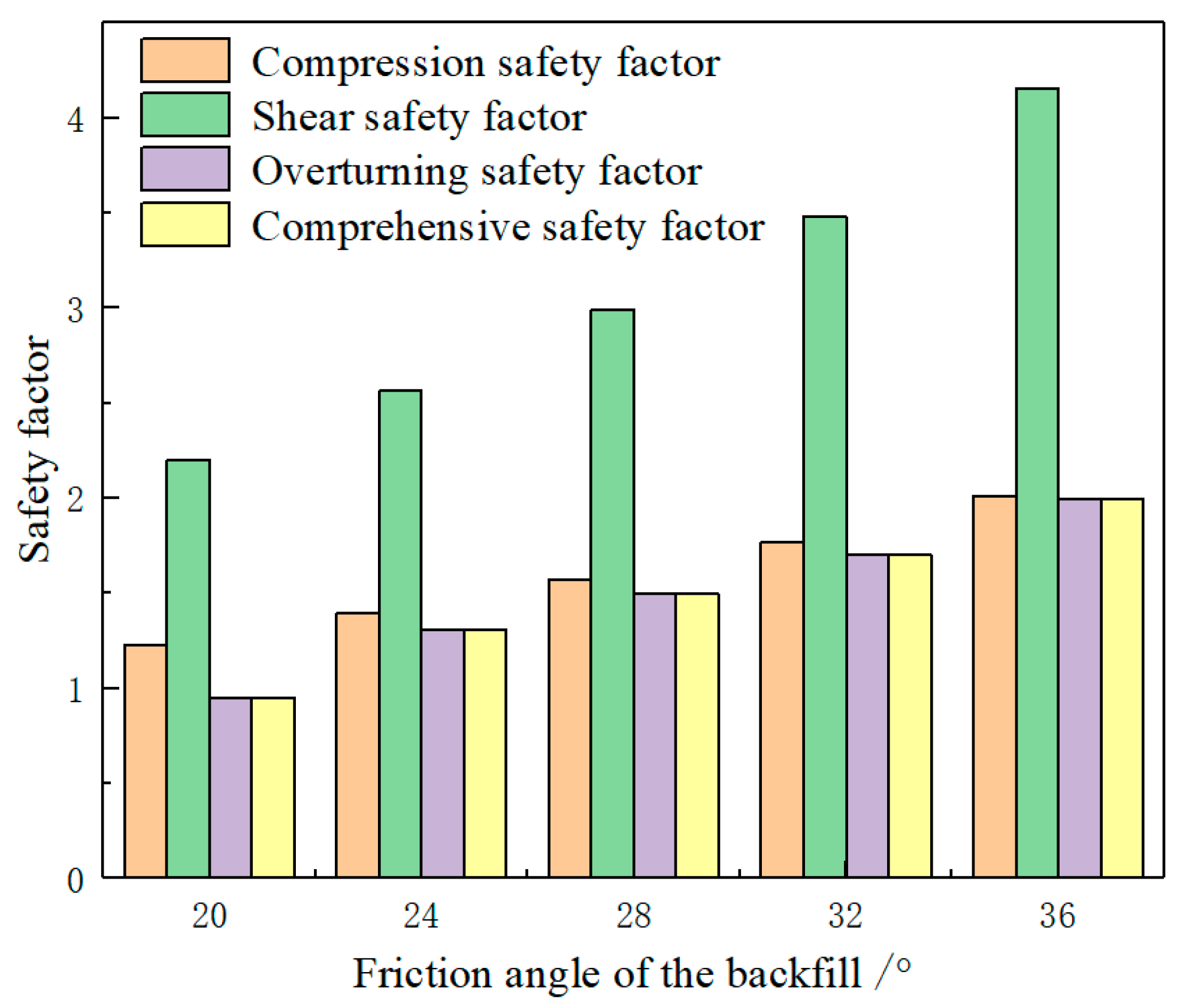
4.3. Quantitative Relationship between the Mine Wall Safety Factor and the Friction of the Backfill
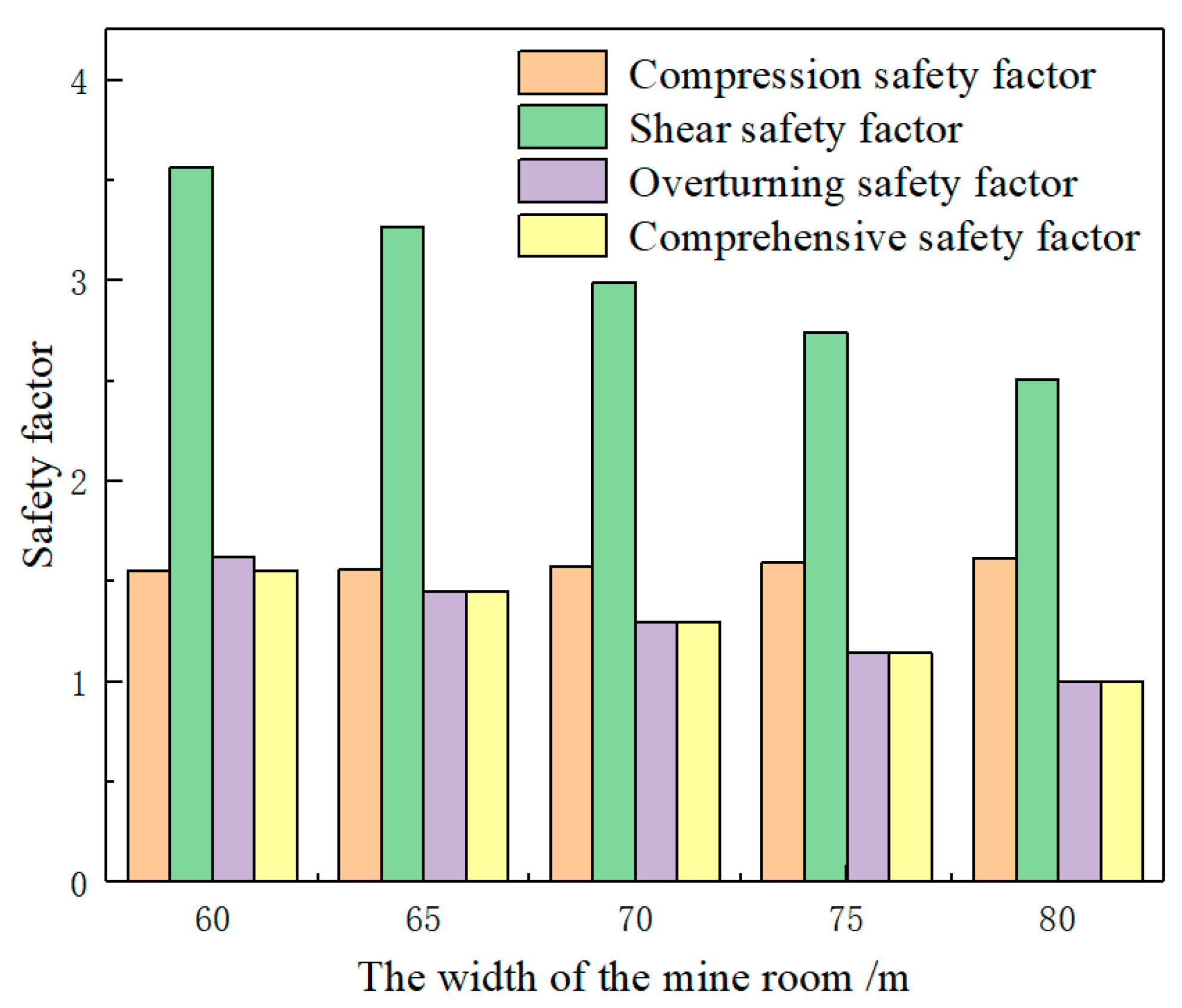
4.4. Quantitative Relationship between Mine Wall Safety Factor and the Width of the Mine Room
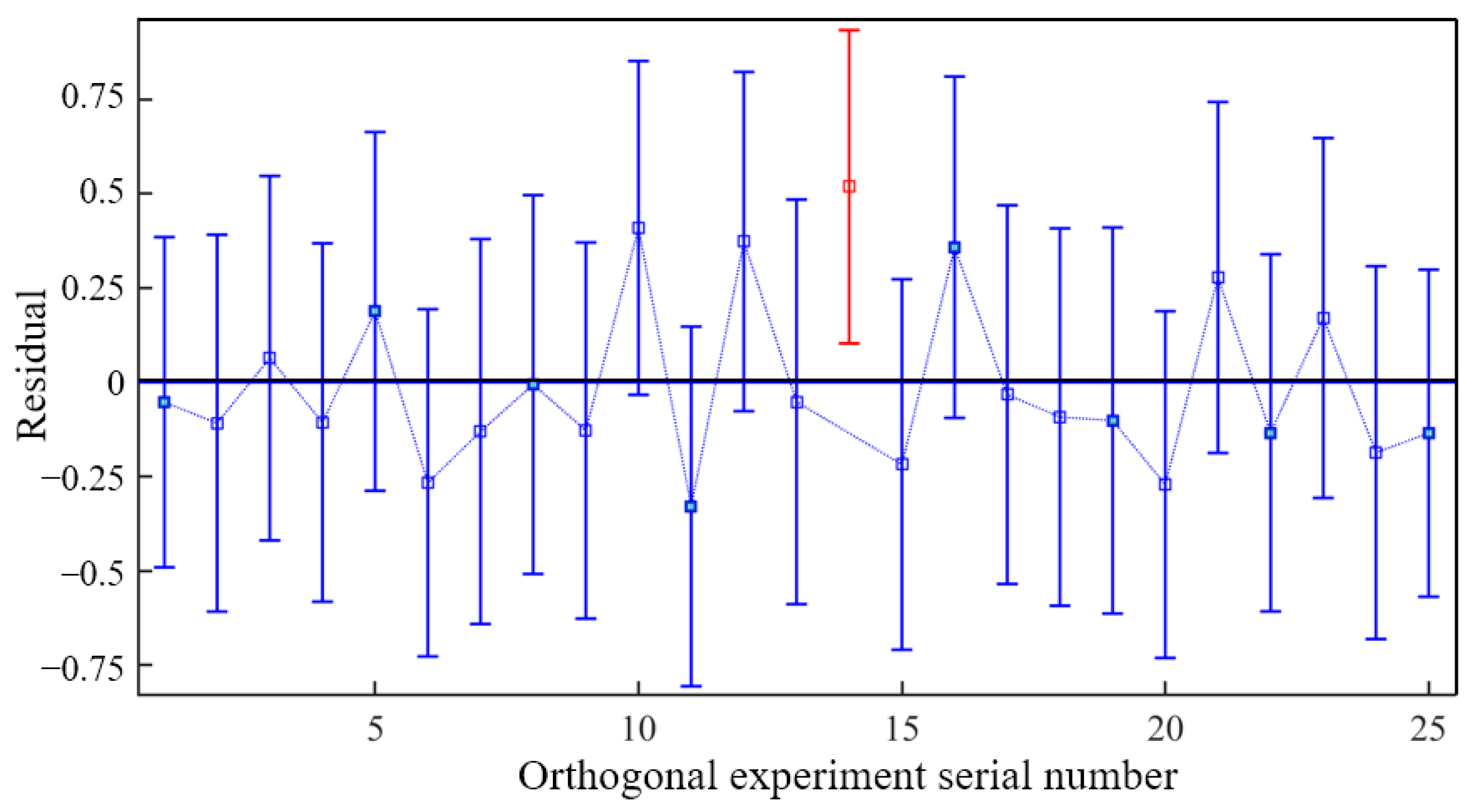
4.5. Multi-Factor Analysis of Mine Wall Safety Factor
5. Engineering Examples
6. Conclusions
- The important factors affecting the stability of the mine wall are the width of the mine wall, the bulk density of the backfill, the friction angle of the filling body and the width of the mine room. Among them, the width of the mine wall mainly affects the bearing strength and the stress distribution state of the mine wall. The bulk density of the backfill and the friction angle mainly affect the lateral load of the mine wall, and the width of the mine room affects both the vertical load and the lateral load of the mine wall.
- The main forms of mine wall failure are brittle compression failure and overturning failure. Increasing the width of the mine wall can significantly improve the mine wall compression safety factor. Reducing the bulk density of the backfill and increasing the friction angle of the backfill can improve the mine wall overturning safety factor. The increase of the mine width increases the compression safety factor and reduces the overturning safety factor of the mine wall.
- According to the regression equation calculation, the comprehensive safety factor of the 52-line G5 mine wall is about 1.4, which is close to the theoretical equation and the actual situation of engineering exploration. It provides ideas for the optimization of mine wall design and filling scheme in the process of deep isolation pillar mining.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, R.; Mandal, P.K.; Singh, A.K.; Kumar, R.; Sinha, A. Coal pillar extraction at deep cover: With special reference to Indian coalfields. Int. J. Coal Geol. 2011, 86, 276–288. [Google Scholar] [CrossRef]
- Wagner, H. Deep mining: A rock engineering challenge. Rock Mech. Rock Eng. 2019, 52, 1417–1446. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.J.; Li, L.Y.; Wang, L.; Qi, L.L. The current situation and prevention and control countermeasures for typical dynamic disasters in kilometer-deep mines in China. Saf. Sci. 2019, 115, 229–236. [Google Scholar] [CrossRef]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Dong, L.J.; Hu, Q.C.; Tong, X.J.; Liu, Y.F. Velocity-free MS/AE source location method for three-dimensional hole-containing structures. Engineering 2020, 6, 827–834. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A. Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner. Eng. 2019, 144, 106025. [Google Scholar] [CrossRef]
- Fall, M.; Célestin, J.C.; Pokharel, M.; Touré, M. A contribution to understanding the effects of curing temperature on the mechanical properties of mine cemented tailings backfill. Eng. Geol. 2010, 114, 397–413. [Google Scholar] [CrossRef]
- Lei, Z.; Rougier, E.; Knight, E.E.; Munjiza, A. A framework for grand scale parallelization of the combined finite discrete element method in 2d. Comput. Part. Mech. 2014, 1, 307–319. [Google Scholar] [CrossRef] [Green Version]
- Das, A.J.; Mandal, P.K.; Bhattacharjee, R.; Tiwari, S.; Kushwaha, A.; Roy, L.B. Evaluation of stability of underground workings for exploitation of an inclined coal seam by the ubiquitous joint model. Int. J. Rock Mech. Min. Sci. 2017, 93, 101–114. [Google Scholar] [CrossRef]
- Basarir, H.; Sun, Y.; Li, G. Gateway stability analysis by global-local modeling approach. Int. J. Rock Mech. Min. Sci. 2019, 113, 31–40. [Google Scholar] [CrossRef]
- Ibishi, G. Stability assessment of post pillars in cut-and-fill stoping method at trepça underground mine. Geomech. Eng. 2019, 28, 463–475. [Google Scholar]
- Zhang, G.C.; Chen, L.J.; Wen, Z.J.; Chen, M.; Tao, G.Z.; Li, Y.; Zuo, H. Squeezing failure behavior of roof-coal masses in a gob-side entry driven under unstable overlying strata. Energy Sci. Eng. 2020, 8, 2443–2456. [Google Scholar] [CrossRef]
- Wei, G.; Ge, M.M. Stability of a coal pillar for strip mining based on an elastic-plastic analysis. Int. J. Rock Mech. Min. Sci. 2016, 100, 23–28. [Google Scholar]
- Huang, Z.G.; Dai, X.G.; Dong, L.J. Buckling failures of reserved thin pillars under the combined action of in-plane and lateral hydrostatic compressive forces. Comput. Geotech. 2017, 87, 128–138. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Li, H.Z.; Guo, G.L.; Liu, X.P. Stability analysis of hyperbolic coal pillars with peeling and high temperature effects. Energy Explor. Exploit. 2020, 38, 1574–1588. [Google Scholar] [CrossRef]
- Wang, X.R.; Guan, K.; Yang, T.H.; Liu, X.G. Instability mechanism of pillar burst in asymmetric mining based on cusp catastrophe model. Rock Mech. Rock Eng. 2021, 54, 1463–1479. [Google Scholar] [CrossRef]
- Idris, M.A.; Saiang, D.; Nordlund, E. Stochastic assessment of pillar stability at Laisvall mine using artificial neural network. Tunn. Undergr. Space Technol. 2015, 49, 307–319. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.X.; Luo, T.; Li, X.; Li, X.B.; Huai, Z.; Wang, S.F. Construction of reasonable pillar group for undersea mining in metal mine. Trans. Nonferrous Met. Soc. China 2018, 28, 757–765. [Google Scholar] [CrossRef]
- Ding, H.X.; Li, G.H.; Dong, X.; Lin, Y. Prediction of pillar stability for underground mines using the stochastic gradient boosting technique. IEEE Access 2018, 6, 69253–69264. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Deng, K.Z.; Zhu, C.G.; Xing, Z.Q. Analysis of stability of coal pillars with multi-coal seam strip mining. Trans. Nonferrous Met. Soc. China 2011, 21, s549–s555. [Google Scholar] [CrossRef]
- Zhang, P.; Heasley, K.A. Elimination of boundary effect for laminated overburden model in pillar stability analysis. J. Cent. South Univ. 2016, 23, 1468–1473. [Google Scholar] [CrossRef]
- Yang, R.S.; Zhu, Y.; Li, Y.L.; Li, W.Y.; Lin, H. Coal pillar size design and surrounding rock control techniques in deep longwall entry. Arab. J. Geosci. 2020, 13, 453. [Google Scholar] [CrossRef]
- Chen, S.M.; Wu, A.X.; Wang, Y.M.; Chen, X. Analysis of influencing factors of pillar stability and its application in deep mining. J. Cent. South Univ. 2018, 49, 2050–2057. [Google Scholar]
- Li, C.; Zhou, J.; Armaghani, D.J.; Li, X. Stability analysis of underground mine hard rock pillars via combination of finite difference methods, neural networks, and Monte Carlo simulation techniques. Undergr. Space 2021, 6, 379–395. [Google Scholar] [CrossRef]
- Zhu, C.M.; Zhang, W.P. Structural Mechanics; Higher Education Press: Beijing, China, 2009; Volume 1, pp. 168–194. [Google Scholar]
- Zhao, W.; Cao, P.; Zhang, G. Rock Mechanics; Central South University Press: Changsha, China, 2010; pp. 162–166. [Google Scholar]
- Jiang, L.C.; Wang, Y.D. Comprehensive safety factor of residual mining pillar under complex loads. J. Cent. South Univ. 2018, 49, 1511–1518. [Google Scholar]
- Dong, L.J.; Chen, Y.C.; Sun, D.Y.; Zhang, Y.H. Implications for rock instability precursors and principal stress direction from rock acoustic experiments. Int. J. Min. Sci. Technol. 2021, 31, 789–798. [Google Scholar] [CrossRef]
- Ji, W.D. Mine Rock Mechanics; Metallurgical Industry Press: Beijing, China, 1991; pp. 36–41. [Google Scholar]
- Guo, J.; Zhao, Y.; Zhang, W.X.; Dai, X.G.; Xie, X.B. Stress analysis of mine wall in panel barrier pillar-stope under multi-directional loads. J. Cent. South Univ. 2018, 49, 3020–3028. [Google Scholar]
- Jiang, L.C.; Su, Y. Theoretical model and application of critical blasting vibration velocity for instability of cemented backfill pillar. Chin. J. Nonferrous Met. 2019, 29, 2663–2670. [Google Scholar]
- Cao, S.; Du, C.F.; Tan, Y.Y.; Fu, J.X. Mechanical model analysis of consolidated filling pillar using stage-delayed backfill in metal mines. Rock Soil Mech. 2015, 36, 2370–2376. [Google Scholar]
- Bieniawski, Z.T.; Van Heerden, W.L. The significance of in situ tests on large rock specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 101–113. [Google Scholar] [CrossRef]
- Dong, L.J.; Tong, X.J.; Hu, Q.C.; Tao, Q. Empty region identification method and experimental verification for the two-dimensional complex structure. Int. J. Rock Mech. Min. Sci. 2021, 147, 104885. [Google Scholar] [CrossRef]
- Dong, L.J.; Tong, X.J.; Ma, J. Quantitative investigation of tomographic effects in abnormal regions of complex structures. Engineering 2021, 7, 1011–1022. [Google Scholar] [CrossRef]
- Guo, J.; Feng, Y.F. Cusp catastrophe theory analysis and width optimization on instability of pillar in deep mining. J. Saf. Sci. Technol. 2017, 13, 111–116. [Google Scholar]
- Xue, B.X.; Li, D.X.; Kong, L.Y. Stability analysis model of ore wall based on elastic thin plate theory and its application. J. Min. Saf. Eng. 2020, 37, 698–706. [Google Scholar]

| Name | Bulk Density /KN·m−3 | Poisson | Cohesion/Mpa | Friction/° |
|---|---|---|---|---|
| Roof rock | 27.1 | 0.2087 | 36.50 | 35.3 |
| Mine wall | 32.2 | 0.3124 | 21.43 | 50.21 |
| Test Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 60 | 2 | 20 | 20 | 0.3870 | 1.9867 | 0.7080 | 0.6863 |
| 2 | 60 | 3 | 28 | 32 | 0.7225 | 2.5390 | 0.8276 | 0.7225 |
| 3 | 60 | 4 | 36 | 24 | 1.9760 | 4.9425 | 2.2466 | 1.9760 |
| 4 | 60 | 5 | 24 | 36 | 1.5123 | 2.7669 | 1.0465 | 1.0465 |
| 5 | 60 | 6 | 32 | 28 | 3.2470 | 4.9980 | 2.4223 | 2.4223 |
| 6 | 65 | 2 | 36 | 32 | 0.4456 | 2.6540 | 0.6855 | 0.4456 |
| 7 | 65 | 3 | 24 | 24 | 0.8124 | 2.3587 | 0.9161 | 0.8124 |
| 8 | 65 | 4 | 32 | 36 | 1.2796 | 3.0240 | 1.0286 | 1.0286 |
| 9 | 65 | 5 | 20 | 28 | 1.6343 | 2.5561 | 1.1373 | 1.1373 |
| 10 | 65 | 6 | 28 | 20 | 3.6705 | 4.7018 | 2.7559 | 2.7559 |
| 11 | 70 | 2 | 32 | 24 | 0.4952 | 2.3765 | 0.7222 | 0.4952 |
| 12 | 70 | 3 | 20 | 36 | 0.5020 | 1.4942 | 0.4386 | 0.4386 |
| 13 | 70 | 4 | 28 | 28 | 1.3959 | 2.7750 | 1.0948 | 1.0948 |
| 14 | 70 | 5 | 36 | 20 | 3.3561 | 5.2323 | 2.7465 | 2.7465 |
| 15 | 70 | 6 | 24 | 32 | 2.3529 | 2.9248 | 1.2510 | 1.2510 |
| 16 | 75 | 2 | 28 | 36 | 0.3050 | 1.5236 | 0.3536 | 0.3050 |
| 17 | 75 | 3 | 36 | 28 | 1.0779 | 2.9706 | 0.9955 | 0.9955 |
| 18 | 75 | 4 | 24 | 20 | 1.6238 | 2.5372 | 1.1667 | 1.1667 |
| 19 | 75 | 5 | 32 | 32 | 2.1605 | 3.2314 | 1.2491 | 1.2491 |
| 20 | 75 | 6 | 20 | 24 | 2.6039 | 2.6640 | 1.3099 | 1.3099 |
| 21 | 80 | 2 | 24 | 28 | 0.3370 | 1.3522 | 0.3552 | 0.3370 |
| 22 | 80 | 3 | 32 | 20 | 1.2449 | 2.6173 | 1.0063 | 1.0063 |
| 23 | 80 | 4 | 20 | 32 | 0.9804 | 1.6180 | 0.5517 | 0.5517 |
| 24 | 80 | 5 | 28 | 24 | 2.4243 | 2.9227 | 1.2762 | 1.2762 |
| 25 | 80 | 6 | 36 | 36 | 3.2303 | 3.8513 | 1.4194 | 1.4194 |
| K1 | 1.3707 | 0.4538 | 0.8248 | 1.6723 |
| K2 | 1.2360 | 0.7951 | 0.9227 | 1.1739 |
| K3 | 1.2052 | 1.1636 | 1.2309 | 1.1974 |
| K4 | 1.0052 | 1.4911 | 1.2403 | 0.8440 |
| K5 | 0.9181 | 1.8317 | 1.5166 | 0.8476 |
| R | 0.4526 | 1.3779 | 0.6918 | 0.8284 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Cheng, X.; Lu, J.; Zhao, Y.; Xie, X. Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines. Minerals 2022, 12, 623. https://doi.org/10.3390/min12050623
Guo J, Cheng X, Lu J, Zhao Y, Xie X. Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines. Minerals. 2022; 12(5):623. https://doi.org/10.3390/min12050623
Chicago/Turabian StyleGuo, Jiang, Xin Cheng, Junji Lu, Yan Zhao, and Xuebin Xie. 2022. "Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines" Minerals 12, no. 5: 623. https://doi.org/10.3390/min12050623
APA StyleGuo, J., Cheng, X., Lu, J., Zhao, Y., & Xie, X. (2022). Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines. Minerals, 12(5), 623. https://doi.org/10.3390/min12050623






