Temperature Variation Characteristics and Model Optimization of Flocculation Sedimentation of Overflow Ultra-Fine Iron Tailings

Abstract

In order to study the effect of temperature on the settling characteristics of overflow ultra-fine iron tailings, the settling velocity of overflow ultra-fine iron tailings at eight different temperatures at 10–80 °C was experimentally studied. The results show that, with the increase in slurry temperature, the flocculation settling velocity of overflow ultra-fine iron tailings increases first and then decreases. That is, when the temperature is less than 60 °C, the settling velocity of flocs increases with the increase in temperature. When the temperature is 60 °C, the settling velocity reaches the maximum 5.66 mm/s. When the temperature is more than 60 °C, the settling velocity of tailings flocs gradually decreases. In addition, with the increase in the test temperature, when the temperature is less than 60 °C, the particle size, fractal dimension, and density of tailings flocculant gradually increase, the gap of flocculant structure gradually decreases, and the floc structure becomes denser. When the temperature is higher than 60 °C, the particle size, fractal dimension, and density of flocs gradually decrease, and the gap between flocs is larger than that at 60 °C. On this basis, the temperature model of overflow ultra-fine iron tailings is established according to the analysis of particle settling process, and the settling model was optimized according to different settling areas. The mean absolute error between the optimized settling velocity and the actual velocity is 0.007, the root mean square error is 0.002, and the error is small. The theoretical calculation results are in good agreement with the experimental data, and the optimized flocculation settling model has an important role in promoting the theoretical study of the flocculation settling of such ultra-fine iron mineral particles, and can be used to guide the sedimentation and separation system to achieve good sedimentation treatment effect under the best working conditions as required.

1. Introduction

With the increasing constraints and control of resources and environment, the use of mine tailings instead of natural river sand is gradually becoming a new consensus in the construction industry. Because of the differences between tailings and river sand in mineral composition and grain size composition, in the actual utilization process, it is usually necessary to use a fine screen or cyclone equipment to remove ultra-fine particles in tailings [1,2,3]. With the dilution and complexity of mineral resources increasing, fine grinding leads to the increasing content of ultra-fine particles in tailings. At about 50%, the content of this part of particles in some tailings can reach about 70% [4,5]. Compared with the whole tailings, the particle size composition of ultra-fine iron tailings has changed greatly, which makes its settlement performance different. Moreover, the water temperature varies greatly in different regions and seasons, which will affect the settling efficiency of tailings. Because the settling separation system for tailings settlement is usually located outdoors, the environmental temperature changes greatly in one year, and the settling effect of the settling separation system will be affected by the environmental temperature [6,7,8,9]. The influence of water temperature on the settling velocity of tailings particles is an indispensable factor to ensure good sedimentation treatment effect.

In order to realize the rapid flocculation settlement of tailings, scholars explored the influence of mortar concentration, flocculant type, dosage, and slurry environment on the settling velocity of tailings, and achieved rich results [10,11,12]. However, the effect of temperature on settling velocity cannot be ignored either. For mining areas with middle and high latitudes, the temperature changes obviously in different seasons, even at different time periods of the day [13,14,15,16]. For example, Jiashi Copper Mine, located in the west of Xinjiang Autonomous Region of China, has a large temperature change. The highest temperature in summer can reach 45 °C and the lowest temperature in winter can reach 22 °C. The daily temperature difference is generally above 12 °C, up to 40 °C, and the temperature has a great impact on the operation in the mining area [17]. Temperature has an important influence on the dissolution and performance of reagent in tailings water. When the temperature is low, the thermal movement and hydrolysis reaction of molecules become slower, which increases the movement resistance of particles, resulting in smaller particles and lower compactness of flocs. The resistance of floc settling in tailings water is higher and the settling velocity is slower [18]. Raising the water temperature within a certain range will help the flocculant to decompose and interact with the ore particles to form larger and more compact flocs, which will make the ore particles flocculate and settle faster [19]. However, when the water temperature is too high, the molecular thermal motion is enhanced, which makes the reaction speed between flocculants and ore particles too fast, which is not conducive to the formation of large and dense flocs, and the flocs generated by flocculation are smaller, so the settling velocity is reduced [20]. Zhen F et al. [21] and Lau Y et al. [22] conducted flocculation and sedimentation tests of kaolin at different temperatures, and considered that, with the increase in temperature, the sedimentation rate of kaolin showed an upward trend. Chen X [23] and Wan Y et al. [24] studied the settling velocity of fine sediment in the Yangtze River Estuary at different temperatures, and concluded that the settling velocity would increase with the increase in temperature, but the influence degree was different in different stages. Guo X et al. [25] conducted flocculation and sedimentation tests of acidic copper-bearing slurry at different temperatures, and considered that, when the slurry temperature is 20–60 °C, it has a great impact on the slurry settling velocity. The higher the slurry temperature is, the faster the settling velocity is. When the pulp temperature exceeds 60 °C, the flocculant will be degraded by increasing the temperature, which will adversely affect the flocculation and sedimentation of particles and reduce the settling velocity performance. Winkler MKH et al. [26] conducted a sedimentation test of sludge particles at different temperatures, and the sludge settling velocity depends on the temperature of sludge water. It is considered that, when the temperature is low, the small granular sludge will float in the liquid; when the temperature is high, the diameter and mass of the particles will increase significantly and the settling velocity will be accelerated. However, decreasing the temperature will reduce the density and size of sludge, resulting in the decrease in settling velocity. Hayet C et al. [27] conducted the temperature settling test of sludge and thought that high temperature could increase the settling velocity, but it would increase the turbidity of supernatant; low temperature can also increase the settling velocity, but its growth rate is smaller than high temperature, and the variation in sedimentation rate function with temperature is not linear. Yu Z et al. [28] simulated the water temperature distribution of Xiangxi Bay, a typical tributary of the Three Gorges Reservoir in China, by establishing a three-dimensional hydrodynamic water temperature model. By analyzing the relationship between water temperature and settling velocity of single spherical solid particles, it is found that temperature has a significant influence on the settling velocity of suspended particles. Although different experimental materials are used in the literature [29,30,31], similar conclusions are also obtained, that is, increasing the temperature within a certain range is helpful for flocculation and sedimentation.

At present, there is little research on the model of flocculation settlement of iron tailings caused by temperature. The purpose of this study is to analyze the structure of tailings floc at different temperatures and its influence on settling velocity through flocculation settling experiments of overflow ultra-fine tailings at different temperatures. According to the analysis of the particle settling process, the flocculation settling temperature model is established. By comparing with the actual settling velocity, the settling models at different settling times are optimized, thus providing a theoretical basis for flocculation settlement of ultra-fine iron tailings. In order to achieve a good sedimentation effect and ensure that the sedimentation and separation system is in the best working conditions, the temperature of the system can be adjusted in time to obtain satisfactory results.

2. Materials and Methods

2.1. Materials

2.1.1. Test Sample

The test samples were the overflow tailings of the iron ore cyclone classification of a concentrator in Tangshan. The samples were sampled by fractional sampling, and three representative samples were tested by ZSX Primus II X-ray fluorescence spectrometer. The difference in test results was small. The average of three groups of data was used as the chemical element of overflow ultra-fine iron tailings. The results are shown in

Table 1. Chemical element analysis of overflow ultra-fine iron tailings, %.

SiO2	Fe2O3	CaO	Al2O3	MgO	K2O	Na2O
63.320	12.150	8.326	7.353	3.881	1.925	0.975
TiO2	P2O5	SO3	MnO	Cl	Cr2O3	ZnO
0.744	0.727	0.389	0.140	0.027	0.025	0.017

.

In Table 1, the main components of the ultra-fine iron tailings are SiO₂, accounting for 63.320%, followed by Fe₂O₃, accounting for 12.150%, and CaO, Al₂O₃, MgO, K₂O, etc.; all sub-sections can be gathered as Materials and Experimental Analysis.

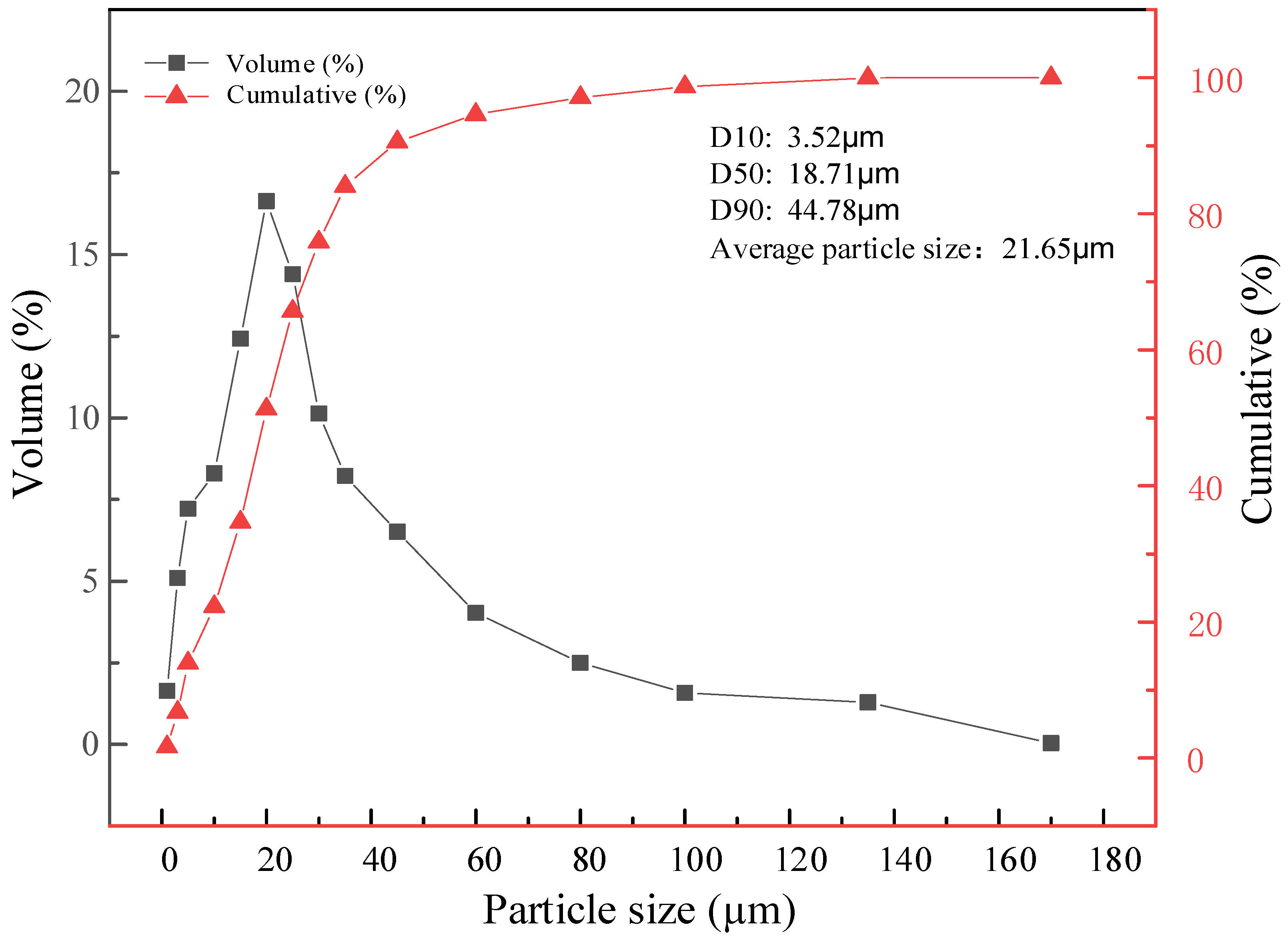
2.1.2. Particle Size Composition

Mastersizer 2000 laser particle size analyzer was used to analyze the particle size of the sample, and the results are shown in Figure 1.

Figure 1 shows that there is a large amount of fine particles in the tailings sample. The contents of samples with particle sizes of 1 µm, 30 µm, and 45 µm are 8.30%, 10.13%, and 6.51%, respectively. In the sample, the particle size of −3.52 µm accounts for 10% of the total sample size, the particle size of −18.71 µm accounts for 50%, the particle size of −44.78 µm accounts for 90%, and the average particle size of the sample is 21.65 µm, and the tailings belong to ultra-fine iron tailings.

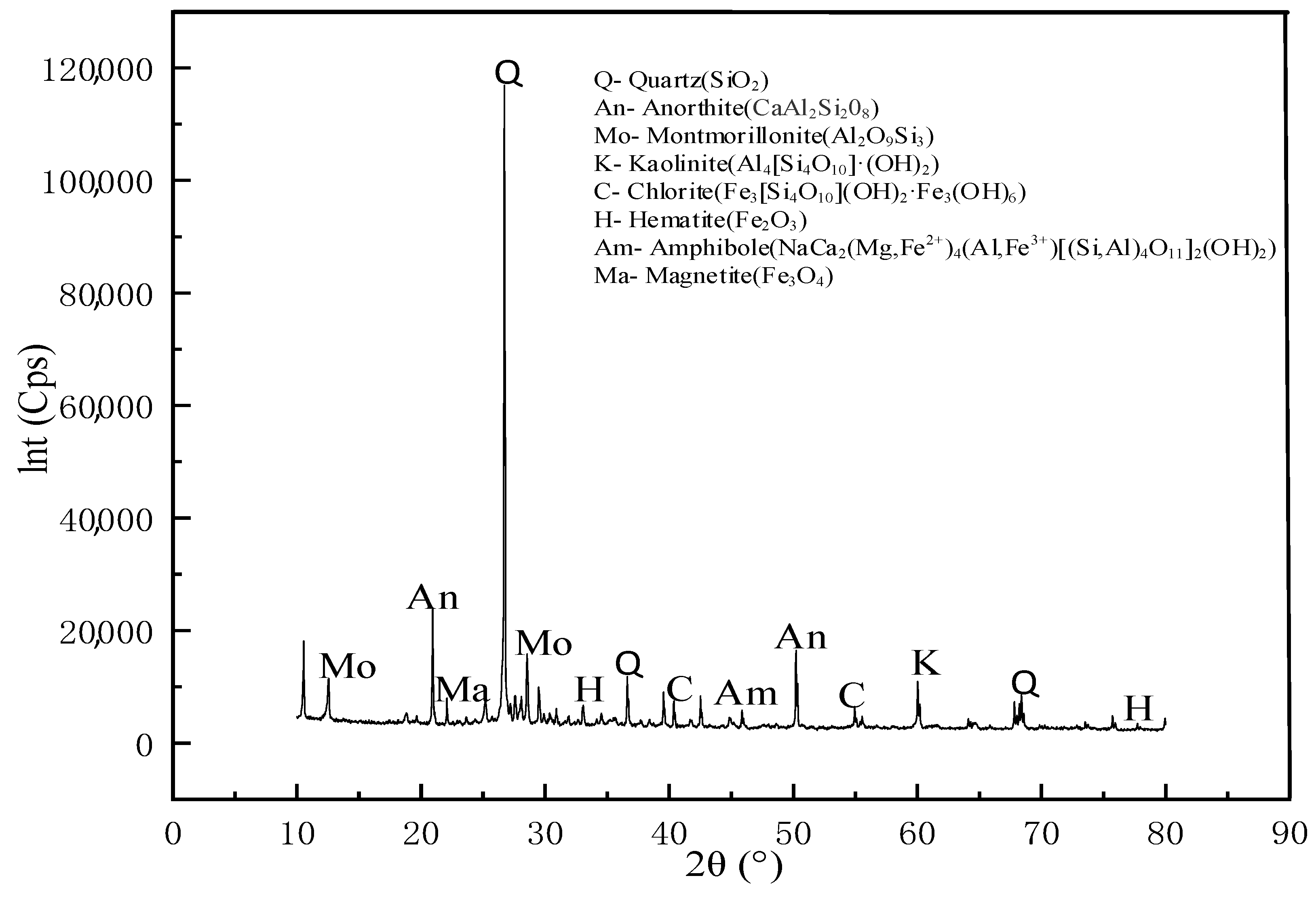
2.1.3. Mineral Composition

The mineral composition of the tailings was analyzed by D/MAX2500PC X-ray diffractometer, and the X-ray diffraction (XRD) analysis results are shown in Figure 2.

The main mineral components of the tailings sample are quartz, anorthite, montmorillonite, kaolinite, chlorite, hematite, amphibole, and magnetite, of which quartz, kaolinite, and montmorillonite belong to clay minerals, which are the main contributing minerals to the deterioration of the sedimentation performance of overflow ultra-fine tailings.

2.2. Flocculant

The flocculating agents used in the experiment are liquid ferric trichloride and solid polyaluminium chloride; ferric trichloride is an inorganic flocculant and polyaluminum chloride is a cationic inorganic polymer flocculant. The content of FeCl₃ is 30–44%, the content of FeCl₂ is ≤0.25%, and the content of Al₂O₃ is ≥28%.

2.3. Test Method

Determination of settling velocity: in order to simulate the actual production of enterprises and the needs of laboratory research, the test temperature was controlled at 10–80 °C, and 4.5 g ultra-fine iron tailings and 100 mL deionized water were used to prepare 4.5% slurry. The temperature of the constant temperature water bath was adjusted to the test temperature, and the water temperature was accurately measured with a thermometer, and the allowable error was 0.1 °C. The water was used at this temperature to prepare the slurry. The prepared pulp was mixed evenly, put it into a 100 mL measuring cylinder, and 30 mg/L ferric chloride and polyaluminium chloride flocculant was added in turn. The top of the measuring cylinder was covered with plastic film, and the measuring cylinder inverted 15 times repeatedly to fully mix the pulp and flocculant, trying to ensure a uniform speed during the inversion process. Then, the measuring cylinder was placed in a constant-temperature water bath pot. At this time, the whole test environment was kept at a constant temperature. During the whole process of sedimentation, the suspension temperature was always kept at the test temperature. It was left to stand, timed with a stopwatch, and the settlement surface height of the clarification layer was observed and recorded at different times.

The actual settling velocity was calculated according to Formula (1).

$$\mathrm{v}=\frac{\mathrm{H}}{\mathrm{t}}$$

(1)

where $\mathrm{v}$ is the settling velocity, mm/s; H is the height of clarification layer, mm; and t is settlement time, s.

2.4. Floc Structure Test

2.4.1. Floc Particle Size and Fractal Dimension Test

In the above-mentioned settling speed measuring method, 60 s after the beginning of pulp sedimentation, a sample at the 20 mL scale of the graduated cylinder was taken with a Babbitt dropper to prepare a floc structure analysis sample. The prepared flocs were observed under a microscope, and the collected images were processed by Image-Pro Plus 6.0 software. Opening the image of floc to be measured, the corresponding scale was selected for calibration, the parameters of floc diameter and area to be measured were selected, and the outline of floc was extracted. The extracted contour was labeled in red, and the software automatically converted the pixel length into the actual length and output it. The average particle size and area of flocs was calculated according to the particle size and area of each floc output by the software. The process is shown in Figure 3.

According to the flocculated particle size and area of the settled particle flocs obtained in the above steps, the fractal dimension [32] is calculated according to Formula (2).

$$\mathrm{lnS}=\mathrm{lnB}+\mathrm{DlnL}$$

(2)

where S is floc area, µm²; B is a proportional constant; L is the particle size of flocs, µm; and D is the fractal dimension.

2.4.2. Density Test

A 50 mL pycnometer was used to determine the density of the flocs. The following operation steps were conducted in accordance with the operating instructions of density measurement by pycnometer: (1) after drying, the pycnometer was filled with distilled water, and the body of the pycnometer was dried and its weight was measured as $g_1$; (2) the floc sample was freeze-dried with a freeze vacuum dryer, and its weight was measured as $g_2$ after drying; (3) the distilled water in the pycnometer was removed, and the dried floc sample was slowly poured into the bottle along the bottle wall, then the distilled water was filled up and the changes in bubbles on the sample surface were observed after a few minutes; the bottle body was wiped dry after the bubbles disappeared and its weight was measured as $g_3$. Then, the density $\mathsf{\rho }$ of floc was calculated [33] according to Formula (3).

$$\mathsf{\rho }=\frac{g_2}{g_1+g_2-g_3}{\mathsf{\rho }}_0$$

(3)

where $\mathsf{\rho }$ is the density of floc, g/cm³; ${\mathsf{\rho }}_0$ is the density of water, g/cm³; and $g$ is the weight, g.

2.4.3. SEM Test

The tailings floc samples at different temperatures were collected, and the floc samples, after freeze-vacuum drying, were sprayed with gold, and then observed and photographed on the electron microscope stage to obtain SEM images of floc. SEM equipment used in the experiment was Scios focused ion beam field emission scanning electron microscope with scanning time of 0.4 s, scanning thickness of 41.4 µm, and image size of 1536 × 1094.

2.5. Settlement Model

Particles settle down in a still liquid due to gravity, but this settling process is very complicated, and its settling performance will be affected by particle size, shape and density, liquid concentration, viscosity, and temperature. Many scholars at home and abroad have made in-depth research on the basic theory of flocculation and sedimentation of solid particles. For example, the Kozeni–Kaman equation [34] holds that the settling velocity depends on the liquid flow rate in the channel formed between flocs, while Navier–Stokes equation [35] is suitable for the case of low settling velocity. However, there is little research on the temperature model of particle flocculation settlement, so the temperature model of overflow ultra-fine tailings is established through the analysis of the particle settlement process.

Assuming that under the same test conditions and time, each particle is spherical and its diameter and density are equal, and the particles settle under the combined action of gravity, resistance, and buoyancy [36,37,38], the settling process of the particles and its stress situation are established as shown in Figure 4.

According to the research of Moshfegh et al. [39], combined with Figure 4, it can be known that various forces on particles are as follows:

$$\mathrm{Gravity}: {\mathrm{F}}_{\mathrm{g}}=\frac{\mathsf{\pi }}{6}{\mathrm{d}}_{\mathrm{t}}^3{\mathsf{\rho }}_{\mathrm{t}}g$$

(4)

$$\mathrm{Buoyancy}: {\mathrm{F}}_{\mathrm{b}}=\frac{\mathsf{\pi }}{6}{\mathrm{d}}_{\mathrm{t}}^3\mathsf{\rho }g$$

(5)

$$\mathrm{Obstruction}: {\mathrm{F}}_{\mathrm{d}}=\mathsf{\epsilon }\frac{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^2}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{2}$$

(6)

where ${\mathrm{d}}_{\mathrm{t}}$ is the diameter of particles, µm; ${\mathsf{\rho }}_{\mathrm{t}}$ is the density of particles, g/cm³; $\mathsf{\rho }$ is the density of pulp, g/cm³; $g$ is the acceleration of gravity, m/s²; $\mathsf{\epsilon }$ is the resistance coefficient when particles settle; and v is the descending speed of particles, mm/s.

According to Newton’s second law [40]:

$${\mathrm{F}}_{\mathrm{g}}-{\mathrm{F}}_{\mathrm{b}}-{\mathrm{F}}_{\mathrm{d}}=\mathrm{ma}$$

(7)

$$\mathrm{a}=\left(\frac{{\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }}{{\mathsf{\rho }}_{\mathrm{t}}}g\right)-\frac{3\mathsf{\epsilon }\mathsf{\rho }}{{4\mathrm{d}}_{\mathrm{t}}{\mathsf{\rho }}_{\mathrm{t}}}{\mathrm{v}}^2$$

(8)

Substitute (4)–(6) into (7) to obtain:

The sedimentation of particles in liquid includes accelerated sedimentation and uniform sedimentation. The fine tailings particles are small and the accelerated sedimentation period is negligible. At this time, the whole sedimentation process can be regarded as uniform sedimentation [41]. The acceleration of particles during uniform sedimentation is a = 0, so the settling velocity of particles can be obtained from Formula (8):

$${\mathrm{v}}_{\mathrm{t}}=\sqrt{\frac{4g{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)}{3\mathsf{\epsilon }\mathsf{\rho }}}$$

(9)

According to Formula (9), the settling velocity of the particles is inversely proportional to the resistance coefficient $\mathsf{\epsilon }$ when the particles settle, and the smaller the $\mathsf{\epsilon }$ is, the greater the velocity ${\mathrm{v}}_{\mathrm{t}}$ is. In addition, the resistance coefficient $\mathsf{\epsilon }$ is a function of Reynolds number ${\mathrm{Re}}_{\mathrm{t}}$ when the fluid moves relative to the particles [42], that is:

$${\mathsf{\epsilon }=\mathsf{\phi }(\mathrm{Re}}_{\mathrm{t}})$$

(10)

At the stage of uniform sedimentation, assuming that the particles are in the transition zone, Allen formula can be introduced [43] and the resistance coefficient $\mathsf{\epsilon }$ can be calculated according to Formula (11):

$$\mathsf{\epsilon }=\frac{18.5}{{\mathrm{Re}}_{\mathrm{t}}{}^{0.6}}$$

(11)

Substituting Equation (11) into Equation (9), the settling velocity of the particles is:

$${\mathrm{v}}_{\mathrm{t}}=0.27\sqrt{\frac{{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)g}{\mathsf{\rho }}{\mathrm{Re}}_{\mathrm{t}}{}^{0.6}}$$

(12)

In the process of particle settling, the fluid is almost in a static state, and the formula of Reynolds number ${\mathrm{Re}}_{\mathrm{t}}$ [44] is as shown in Formula (13):

$${\mathrm{Re}}_{\mathrm{t}}=\frac{{\mathsf{\rho }}_{\mathrm{t}}{\mathrm{d}}_{\mathrm{t}}{\mathrm{v}}_{\mathrm{t}}}{{\mathsf{\mu }}_{\mathrm{t}}}$$

(13)

In addition, in the actual settling process, liquid viscosity $\mathsf{\mu }$ is greatly affected by temperature, and, with the change in liquid temperature t, ${\mathsf{\mu }}_{\mathrm{t}}$ changes significantly [45]. The relationship between ${\mathsf{\mu }}_{\mathrm{t}}$ and t is shown in Formula (14):

$${\mathsf{\mu }}_{\mathrm{t}}=\frac{{\mathsf{\mu }}_0}{0.5+0.025\mathrm{t}}$$

(14)

where ${\mathsf{\mu }}_0$ is the viscosity of the slurry at 20 °C, Pa·s; ${\mathsf{\mu }}_{\mathrm{t}}$ is the viscosity of the slurry in the process of settling at any temperature, Pa·s; and t is the temperature of the slurry, °C.

Formula (14) is brought into the Formulas (12) and (13) to obtain the Formula (15):

$${\mathrm{v}}_{\mathrm{t}}=0.27\sqrt{\frac{{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)g}{\mathsf{\rho }}{\left[(0.5+0.025\mathrm{t})\frac{{\mathsf{\rho }}_{\mathrm{t}}{\mathrm{d}}_{\mathrm{t}}{\mathrm{v}}_{\mathrm{t}}}{{\mathsf{\mu }}_0}\right]}^{0.6}}$$

(15)

3. Results and Discussion

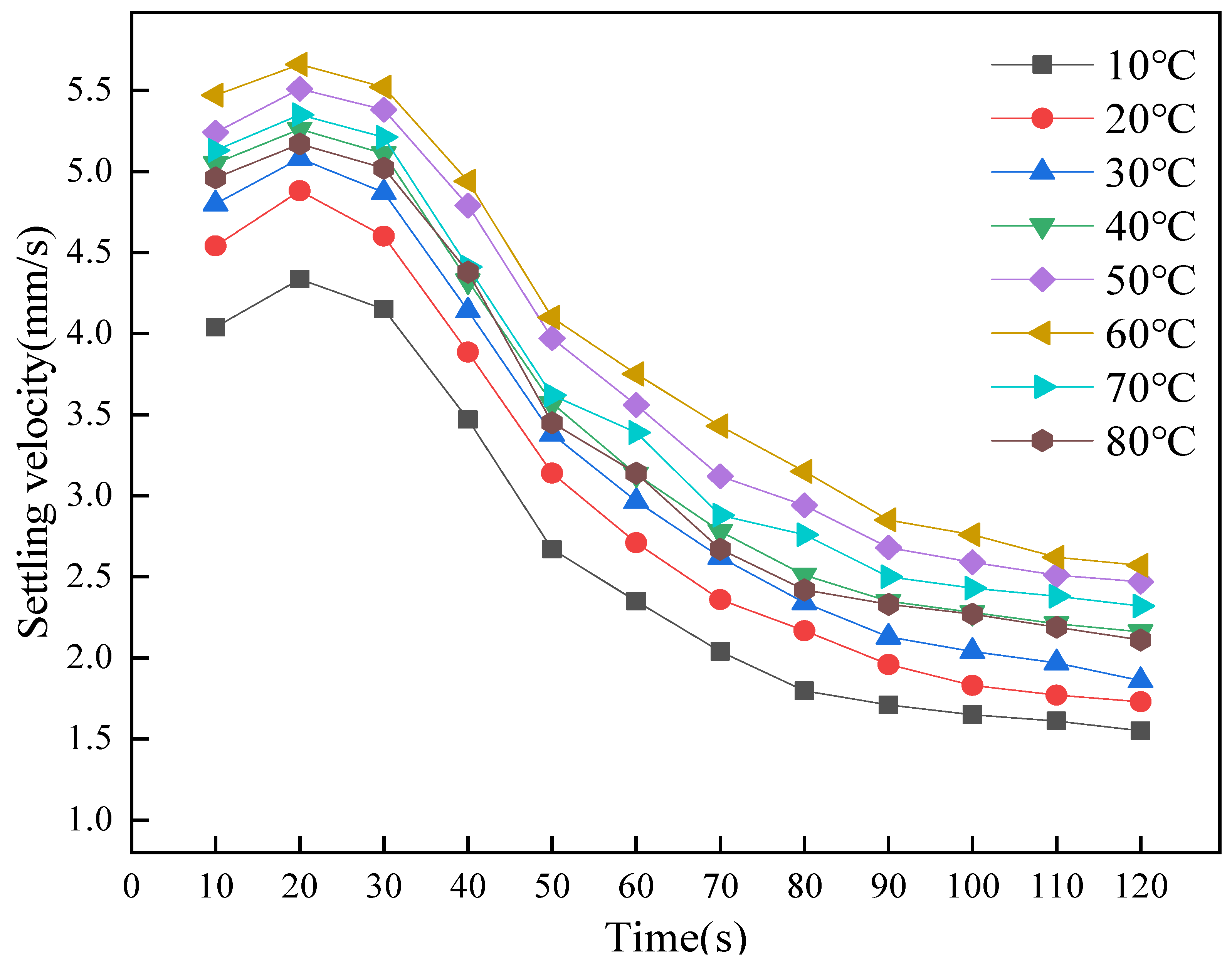
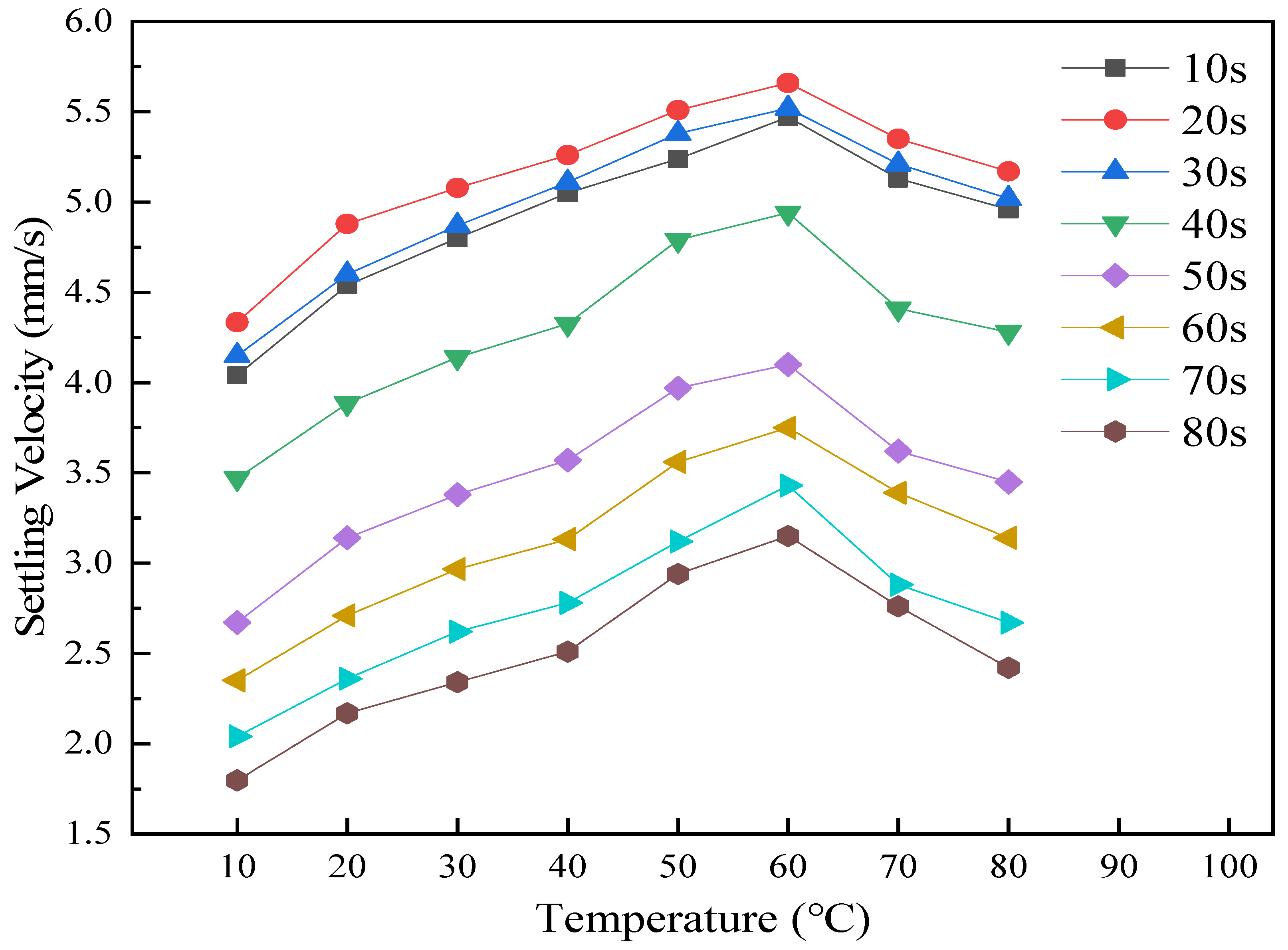
3.1. Flocculation Settlement Results

When the pulp pH was 7.5, the stage dosing was adopted. Firstly, 30 mg/L liquid ferric chloride was added and stirred for 10 s, and then 30 mg/L polyaluminium chloride was added and stirred for 10 s. The flocculation and sedimentation tests of ultra-fine iron tailings at eight different pulp temperatures (10–80 °C with the step of 10 °C) were carried out. The effect of temperature change on flocculation and settling velocity was investigated and the results are shown in Figure 5.

According to Figure 5, during the initial settlement, with the increase in the settling time, the settling velocity of the tailings floc particles first increased and then decreased. At the time of settling for 20 s, the settling velocity reached the maximum and the tailings floc particles completed the accelerated settling process at this stage; after that, with the increase in the settling time, the settling velocity gradually decreased. When the settling time was 120 s, the settling velocity changed little, indicating that the overflow ultrafine tailings settling had been completed when the settling time was 120 s. It can be seen that, with the increase in slurry temperature, the settling velocity of overflow superfine tailings gradually increases. When the settling time is 20 s, the settling velocity is 4.33 mm/s at a constant temperature of 10 °C, and the maximum settling velocity is 5.66 mm/s at a constant temperature of 60 °C. However, when the temperature exceeds 60 °C, the settling velocity of tailings gradually decreases. When the temperature increases from 60 °C to 70 °C and 80 °C, the settling velocity decreases from 5.66 mm/s to 5.35 mm/s and 5.17 mm/s.

The settling velocity of tailings with different settling time is analyzed, and the results are shown in Figure 4.

Figure 6 shows the relationship between the settling velocity of tailings and temperature at different settling times (10–80 s). The settling velocity of ultrafine tailings reaches the maximum when settling for 20 s, and then the settling velocity of ultrafine tailings gradually decreases with the increase in settling time. Under the same settling time, when the temperature is less than 60 °C, the settling velocity of ultrafine tailings increases with the increase in temperature, When the temperature is greater than 60 °C, the settling velocity decreases with the increase in temperature. When the settling time is 80 s and the temperature is less than 60 °C, the settling velocity increases from 1.8 mm/s at 10 °C to 2.17 mm/s, 2.34 mm/s, 2.51 mm/s, 2.94 mm/s, and 3.15 mm/s, and the settling velocity changes greatly with the increase in temperature. When the temperature is greater than 60 °C, the settling velocity decreases from 3.15 mm/s at 60 °C to 2.76 mm/s and 2.42 mm/s, and the settling velocity decreases with the increase in temperature.

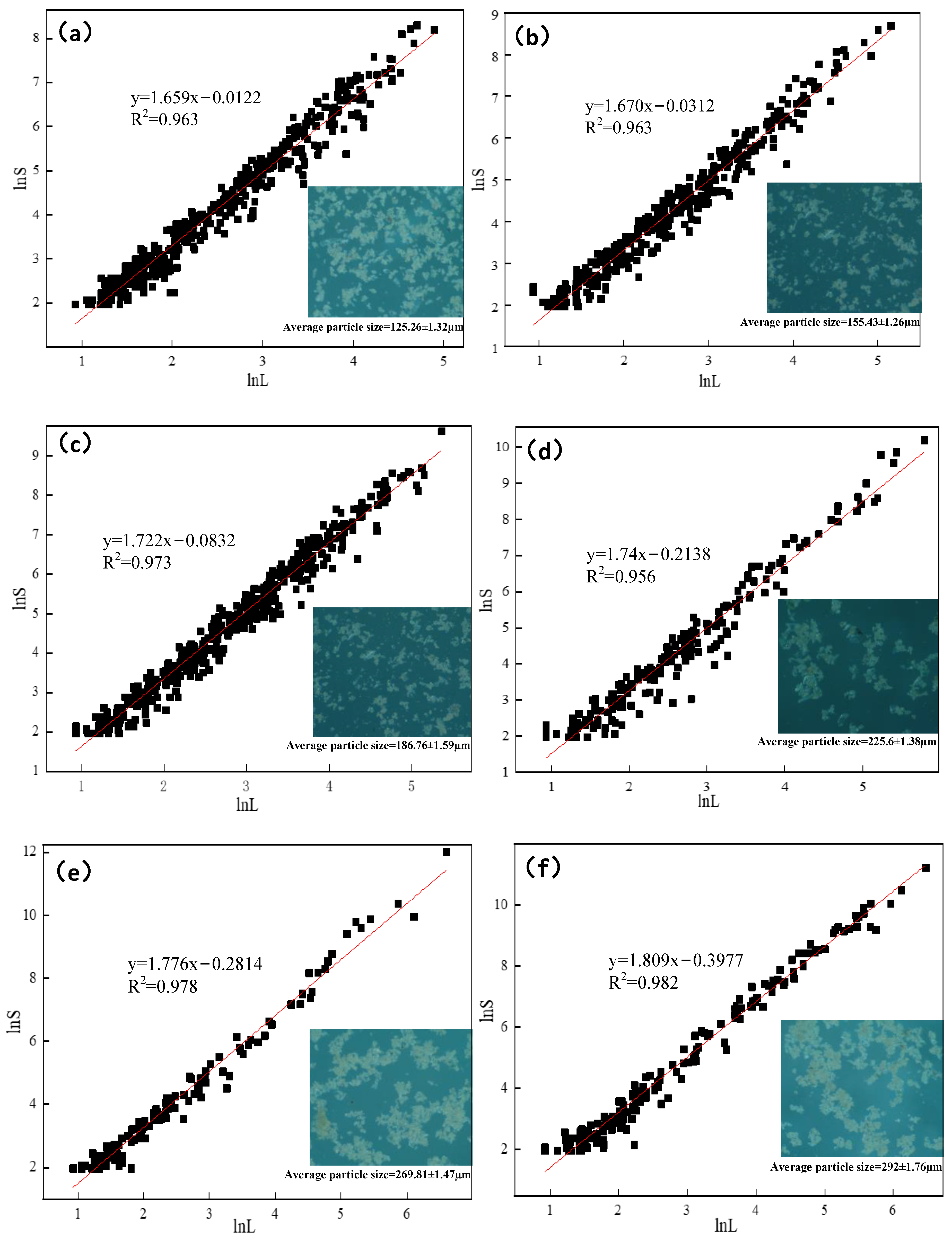
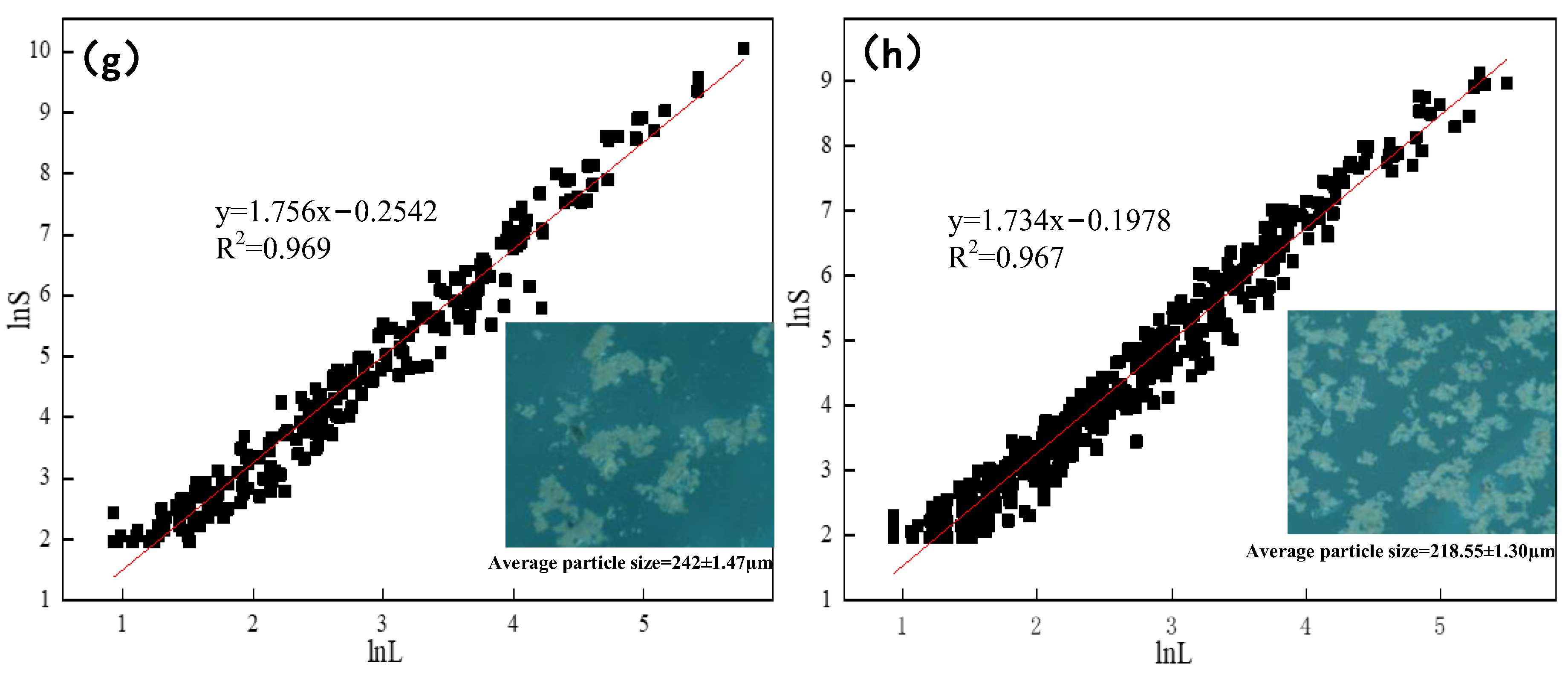
3.2. Floc Particle Size and Fractal Dimension Results

According to the above steps, the obtained floc samples are processed, and the collected floc images are processed by Image-Pro Plus 6.0 software, so that the particle size and area can be obtained. From the double logarithm curve of ln L−ln S, the slope of the curve is its fractal dimension. The average particle size and fractal dimension of tailings flocs at different temperatures are shown in Figure 7.

Figure 7 shows that, when the temperature is less than 60 °C, the average particle size and fractal dimension of tailings flocs increase with the increase in the test temperature. The average particle size of tailings flocs gradually increased from 125.26 µm at 10 °C to 155.43 µm, 186.76 µm, 225.6 µm, 269.81 µm, and 292 µm, and reached a maximum at 60 °C. The fractal dimension gradually increases from 1.659 at 10 °C to 1.670, 1.722, 1.740, 1.776, and 1.809, reaching a maximum value of 1.809 at 60 °C. When the temperature is greater than 60 °C, the average particle size and fractal dimension of tailings flocs decrease with the increase in the test temperature. The average particle size gradually decreased from 292 µm at 60 °C to 242 µm and 218.55 µm; the fractal dimension gradually decreased from 1.809 at 60 °C to 1.756 and 1.734.

3.3. Density Results

Through the density test, the solid density of the tailing floc sample is obtained, which is used as a quantitative indicator of the tailings floc structure. The results are shown in

Table 2. Solid density of tailings floc sample.

Temperature (°C)	10	20	30	40	50	60	70	80
Density (g/cm3)	2.422	2.468	2.491	2.543	3.057	3.186	2.854	2.507

.

From Table 2 we know that there are significant differences in the density of solids in tailings floc samples at different flocculation settling temperatures. When the temperature is less than 60 °C, the density of the sample increases with the increase in the test temperature. The minimum density is 2.422 g/cm³ at 10 °C, the maximum density is 3.186 g/cm³ at 60 °C, and the maximum density is 1.32 times the minimum density. When the temperature is greater than 60 °C, the density of the sample decreases with the increase in the test temperature, from 3.186 g/cm³ at 60 °C to 2.854 g/cm³ and 2.507 g/cm³.

3.4. SEM Results

Scanning electron microscopy (SEM) was used to test floc samples at different test temperatures. By analyzing the microstructure and morphology of eight samples, the flocculation and sedimentation characteristics of ultra-fine tailings at different temperatures were further explored. The results are shown in Figure 8.

According to Figure 8, at 10 °C, there are more coarse tailings particles (CTPs), and a small amount of tiny tailings particles (TTPs) are adsorbed on the CTPs to form larger flocs. The structure of the floc is loose, and the maximum gap of the flocculation structure is 89.94 μm and the minimum is 33.1 μm. The large flocculation gap leads to the difficulty of water separation between flocs, which affects the flocculation settling effect and makes the settling velocity smaller. As the temperature increases, the flocculation structure gap gradually decreases. When the temperature reaches 60 °C, a large number of TTPs are adsorbed on the CTPs and the flocculation structure gap becomes smaller, the maximum gap is 33.33 µm, the minimum is 9.09 µm, and there are many small gaps; the cohesion between the flocs increases, which makes the structure of the flocs more compact and promotes the settlement of tailings flocs. When the temperature is higher than 60 °C, the number of CTPs increases, and the TTPs are adsorbed on the coarse tailings particles, making the structure of the floc smaller. However, the gap is larger than that at 60 °C when the temperature reaches 80 °C, the maximum gap is 60.65 µm, and the minimum is 12.69 µm.

In summary, with the increase in temperature, when the temperature is less than 60 °C, the average particle size, fractal dimension, and density of tailings flocs increase rapidly, the flocculation structure gap gradually decreases, and the structure of flocs is more compact. When the temperature is higher than 60 °C, the average particle size, fractal dimension, and density gradually decrease, and the flocculation structure gap is larger than that at 60 °C.

4. Temperature Model of Flocculation and Sedimentation of Tailings Particles

4.1. Optimization of Mineral Particle Temperature Model

The ultra-fine minerals used in the experiment are different in size and shape in actual settlement, and the resistance is closely related to the flocculation degree, flocculant properties, pulp properties, and temperature of the minerals, and the forces in different settlement stages are also different. In the stage of rapid and uniform sedimentation, the resistance is small. As the sedimentation progresses, according to the force analysis in Figure 7, the lower flocs are continuously under compression, and its settlement resistance is obviously greater than the former, so, for these two stages, the established settling velocity model could be expanded.

It is assumed that the floc will settle rapidly in the first 20 s, and its resistance is small. The resistance at this stage is shown in Formula (16):

$${\mathrm{F}}_{\mathrm{d}}^{\prime }=\mathrm{A}\mathsf{\epsilon }\frac{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^2}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{2}$$

(16)

where A is the modified drag coefficient.

Substituting (16) into (6)–(9), the A value can be calculated according to (17):

$$\mathrm{A}=\frac{4g{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)}{{3\mathsf{\epsilon }\mathsf{\rho }\mathrm{v}}^2}$$

(17)

In 20–80 s, the floc is compressed, the water is squeezed out, the viscosity of floc increases, and the particles collide with each other, and the settlements among the particles interfere with each other, which leads to the increase in resistance. The resistance at this stage is shown in Formula (18):

$${\mathrm{F}}_{\mathrm{d}}^{″}=\mathrm{B}\mathsf{\epsilon }\frac{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^2}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{2}+\mathrm{C}$$

(18)

In the formula, B and C are the modified resistance coefficients, and B > A.

Substituting (18) into (6)–(9), B and C can be calculated according to (19):

$$\mathrm{B}\mathsf{\epsilon }\frac{3\mathsf{\pi }}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{{\mathrm{d}}_{\mathrm{t}}{\mathsf{\rho }}_{\mathrm{t}}}+\frac{6\mathrm{C}}{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^3{\mathsf{\rho }}_{\mathrm{t}}}=0$$

(19)

$$\mathrm{c}=\frac{{\mathrm{F}}_{\mathrm{d}}}{{\mathsf{\rho }\mathrm{d}}^2{\mathrm{v}}_0^2}$$

(20)

Substituting the diameter and density of flocs, pulp density, and resistance coefficient obtained from the test into Equations (17), (19) and (20), combined with (13) and (14), it can be calculated that A = 1.27, B = 5.75, and C = 0.14.

Therefore, the corrected resistance is shown in Equations (21) and (22):

$${\mathrm{F}}_{\mathrm{d}}^{\prime }=1.27\mathsf{\epsilon }\frac{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^2}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{2}$$

(21)

$${\mathrm{F}}_{\mathrm{d}}^{″}=5.75\mathsf{\epsilon }\frac{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}{}^2}{4}\frac{{\mathsf{\rho }\mathrm{v}}^2}{2}+0.14$$

(22)

Substituting Equations (21) and (22) into Equations (4)–(14), respectively, the settling velocity in 0–20 s and 20–80 s can be obtained. The settling velocities of the two stages after correction and expansion are shown in Equations (23) and (24):

$${\mathrm{v}}_{\mathrm{t}}^{\prime }=0.23\sqrt{\frac{{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)g}{\mathsf{\rho }}{\left[(0.5+0.025\mathrm{t})\frac{{\mathsf{\rho }}_{\mathrm{t}}{\mathrm{d}}_{\mathrm{t}}{\mathrm{v}}_{\mathrm{t}}}{{\mathsf{\mu }}_0}\right]}^{0.6}}$$

(23)

$${\mathrm{v}}_{\mathrm{t}}^{″}=\sqrt{(\frac{0.0125{\mathrm{d}}_{\mathrm{t}}\left({\mathsf{\rho }}_{\mathrm{t}}-\mathsf{\rho }\right)g}{\mathsf{\rho }}-\frac{0.0105}{{\mathsf{\pi }\mathrm{d}}_{\mathrm{t}}^2\mathsf{\rho }}){\lfloor \left(0.5+0.025\mathrm{t}\right)\frac{{\mathsf{\rho }}_{\mathrm{t}}{\mathrm{d}}_{\mathrm{t}}{\mathrm{v}}_{\mathrm{t}}}{{\mathsf{\mu }}_0}\rfloor }^{0.6}}$$

(24)

The optimized settling temperature model of ultra-fine tailings comprehensively considers the influence of floc particle size, shape, density, pulp density and viscosity, resistance coefficient, etc., which has a certain guiding role in studying the settling performance of similar ultra-fine mineral particles.

4.2. Experimental Verification of Flocculation Settlement Model of Ultra-Fine Minerals

In order to further verify the optimized settlement temperature model of ultra-fine tailings, the eight groups of data that settled for 80 s in this experiment were used as samples, and the theoretical settlement model and the optimized model were used to calculate the settling velocity of this group of experiments. The settling velocity obtained by the model was compared with the actual velocity, so as to analyze the rationality and accuracy of the model. The comparison results of settling velocity are shown in Figure 9.

Figure 9 reveals that the theoretical settlement temperature model velocity is far lower than the actual settling velocity and the optimized model velocity. Compared with the theoretical model, the settling velocity curve of ultra-fine tailings obtained by the optimized model is closer to the actual settling velocity curve, and the optimized model is closer to the actual value.

The error between the sedimentation velocity obtained by the two models and the actual velocity was analyzed, and the results are shown in

Table 3. Comparison of model errors.

Statistical Indicators	Theoretical Model Velocity	Modified Model Velocity
Mean absolute error	0.872	0.007
Root mean square error	0.794	0.002

.

Table 3 shows that the mean absolute error between the theoretical settlement temperature model velocity and the actual velocity is 0.872, and the root mean square error is 0.794, which is relatively large. However, after optimization, the mean absolute error between the model velocity and the actual velocity is 0.007, the root mean square error is 0.002, and the error is small. In general, the optimized settlement temperature model of ultra-fine tailings has a good validation for the settling velocity of ultra-fine mineral particles and has an important guiding role for mining operations at different temperatures.

4.3. Mechanism Analysis

The effect of temperature on flocculation and sedimentation of tailings particles can be explained by Brownian motion [46,47] and adsorption bridging theory [48,49,50]. It is generally considered that flocculation refers to adding flocculants to the liquid containing suspended particles. When particles move in the liquid, they will be collided by liquid molecules from all directions, and, in the process of collision, the adjacent particles of the adsorbed water film will be combined together to gather and become larger, forming flocs and promoting the sedimentation of particles in the liquid [51,52,53]. Flocculation caused by Brownian motion is called anisotropic flocculation.

In liquid, the Brownian motion of particles is usually expressed by the half-life (${\mathrm{t}}_{1/2}$) of particle concentration in liquid, that is, the time taken for ${\mathrm{c}}_{1/2}$ when the particle concentration in liquid is reduced from the initial value ${\mathrm{c}}_1$ to half [1]. Assuming that the particles in the liquid are uniform spheres, the formula (${\mathrm{t}}_{1/2}$) in Brownian motion can be derived according to Fick’s first law, as follows:

$${\mathrm{t}}_{1/2}=\frac{3\mathsf{\mu }}{{4\mathsf{\alpha }\mathrm{kTc}}_1}$$

(25)

where ${\mathrm{t}}_{1/2}$ is the half-life of the particle concentration in the liquid, s; $\mathsf{\mu }$ is the viscosity of the liquid, Pa·s; $\mathsf{\alpha }$ is the adhesion efficiency factor of collision and adhesion of particles in liquid; k is Boltzmann constant, J/K; T is the liquid temperature, °C; and ${\mathrm{c}}_1$ is the concentration of particles in the liquid, mg/L.

From Formula (25), we know that, with the increase in temperature, ${\mathrm{t}}_{1/2}$ decreases gradually, and the shorter the time required for the particles to reduce from the initial concentration, the more intense the molecular motion in the liquid, the greater the probability of particle collision and adhesion, and the more obvious the Brownian motion. When the temperature rises from 10 °C to 60 °C, the Brownian motion increases gradually, the flocculation effect of particles becomes more obvious, and the settling velocity also gradually increased. At the same time, with the increase in temperature, the thickness of the diffusion layer gradually increases and the molecular chain of flocculant is stretched, so that more tailings particles are adsorbed on the polymer chain and the adsorption bridging effect is obvious [54], and the best value is obtained when the sedimentation rate is 60 °C.

When the temperature rises continuously and exceeds 60 °C, the total thickness of the diffusion layer becomes very large, which makes the distance between the two tailings particles exceed the place where the polymer flocculant can extend. It is difficult for the polymer flocculant chain to link the tailings particles through the thick diffusion layer, which makes it difficult to bridge the adsorption between the particles and the flocculant [55]. Therefore, too high a temperature will reduce the settling velocity.

5. Conclusions

Through flocculation and sedimentation testing, the settling velocity of overflow ultra-fine iron tailings at different temperatures was obtained, and it can be known that temperature will have a significant impact on the flocculation and settling velocity of ultra-fine tailings. When the temperature is less than 60 °C, the flocculation and sedimentation velocity of tailings increases significantly with the increase in slurry temperature, reaching a maximum velocity of 5.66 mm/s at 60 °C. When the temperature is greater than 60 °C, the flocculation and sedimentation velocity of tailings gradually decreases.

With the increase in test temperature, when the temperature is less than 60 °C, the particle size, fractal dimension, and density of tailings floc gradually increase, the flocculation gap gradually decreases, the floc structure becomes denser, and the flocculation settling velocity is faster. When the temperature is higher than 60 °C, the particle size, fractal dimension, and density of flocs gradually decrease, and the gap between flocs is larger than that at 60 °C.

According to the different settling properties of ultra-fine tailings particles in different temperature areas, the theoretical settling model of flocculated particles is established, and the settling model is optimized based on the experimental data. The mean absolute error between the optimized model and the actual settling velocity is 0.088, and the root mean square error is 0.010, which is small and has a high agreement with the experimental data. The model has a certain theoretical value in the flocculation and sedimentation of ultra-fine mineral particles, and has an important guiding significance for the operation in mining areas in different temperature areas. According to the model, the system temperature can be adjusted appropriately in different temperature areas to make the precipitation separation system in the best working condition, and the satisfactory sedimentation effect can be obtained.