Evolution Characteristics of Overlying Strata Fractures in Paste Composite Filling Stope
Abstract
:1. Introduction
2. Methods
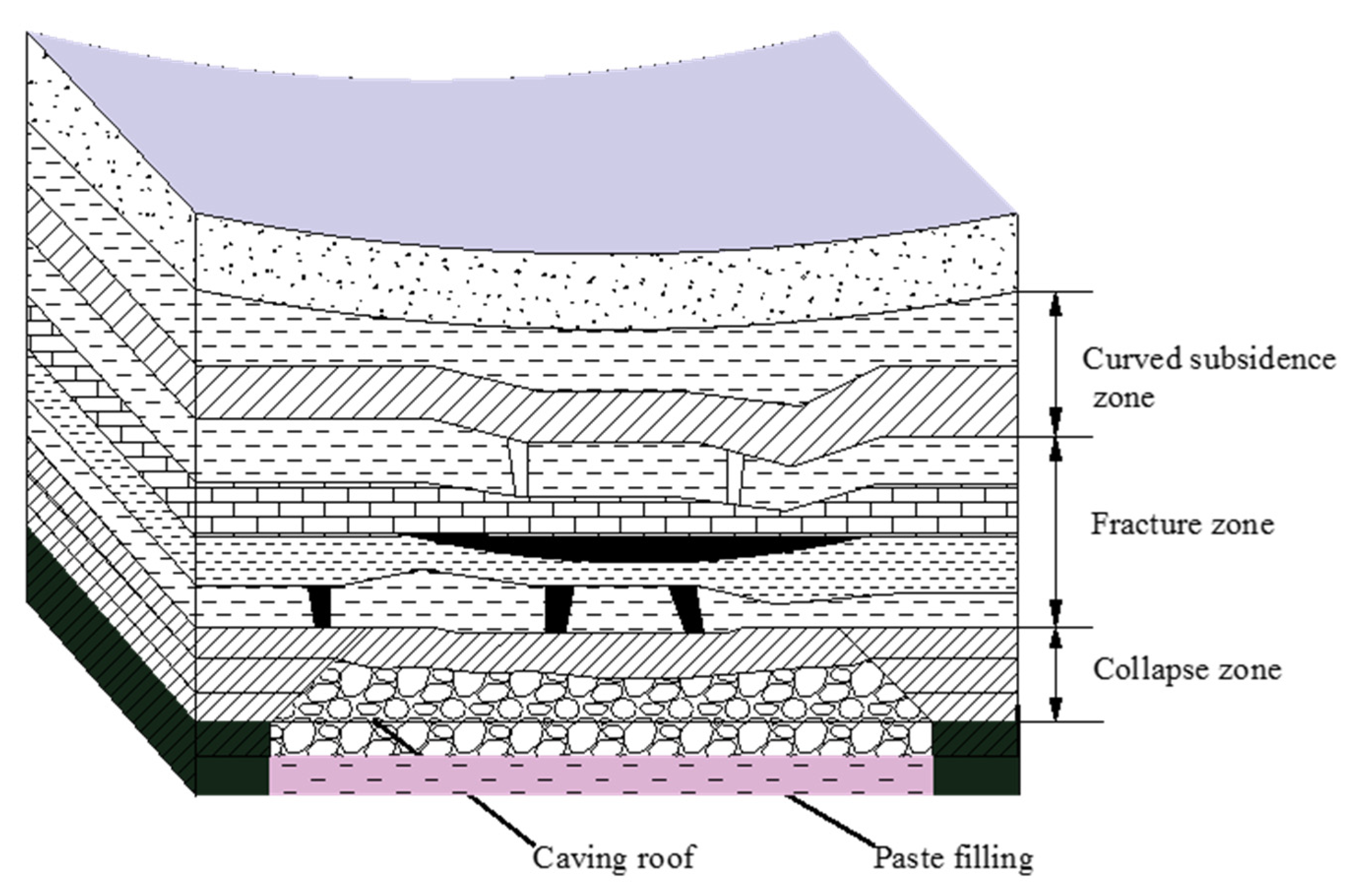
2.1. Engineering Background
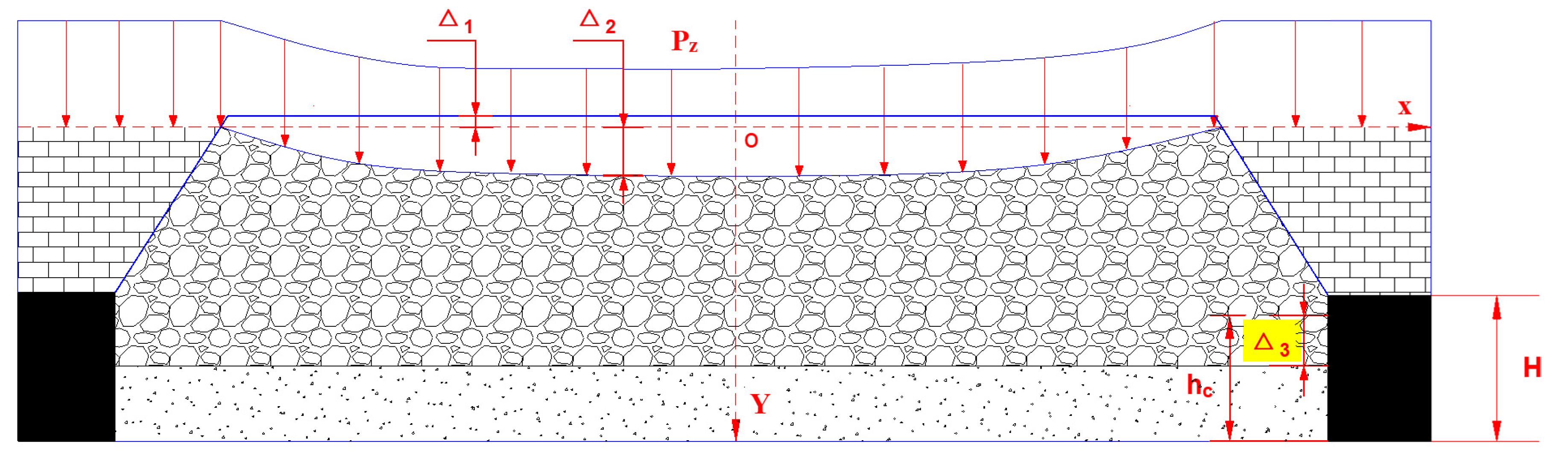
2.2. Theoretical Analysis

2.3. Physical Similarity Simulation Experiment
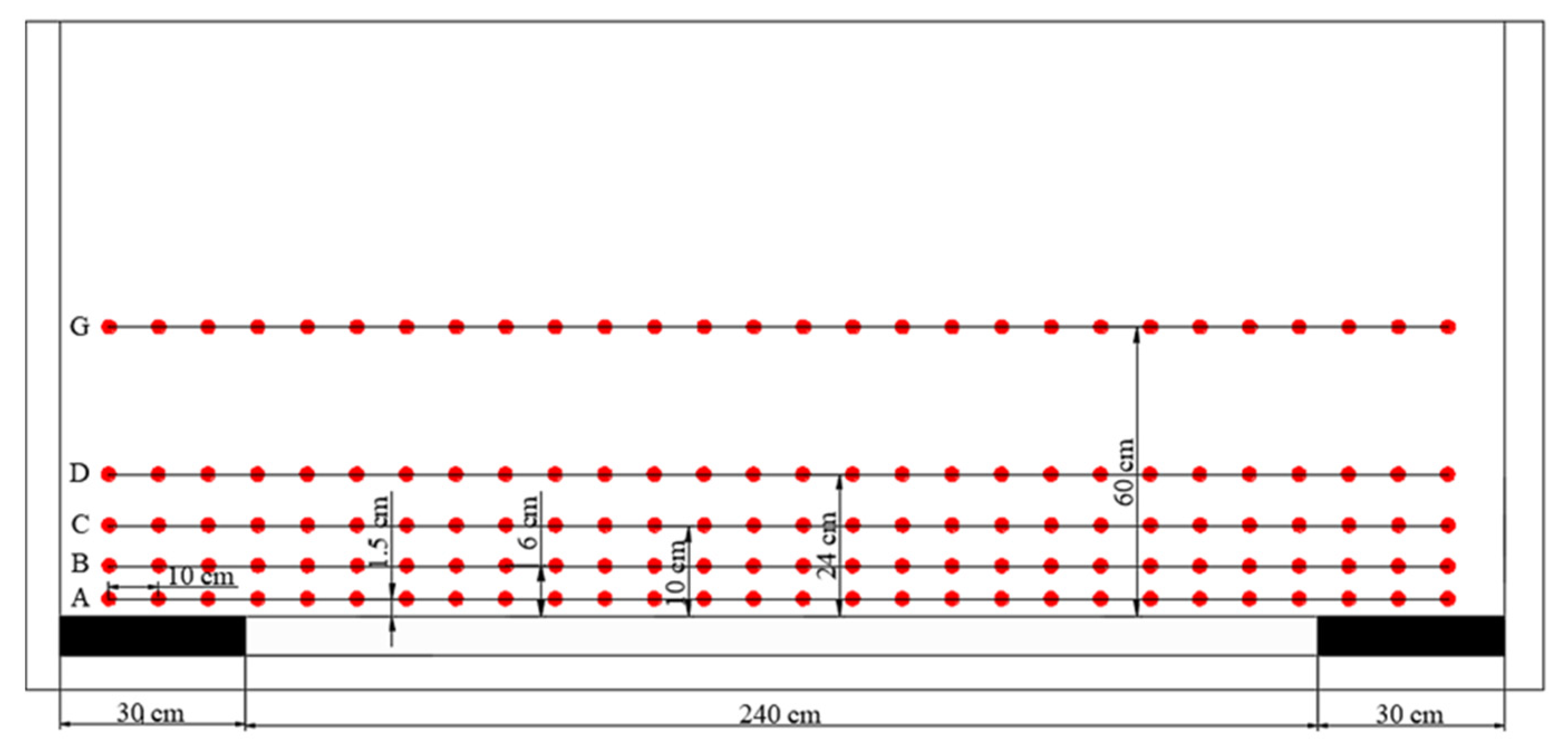
2.3.1. Model Establishment
2.3.2. Experimental Monitoring Scheme and Equipment
2.4. Computer Numerical Simulation Experiment
2.4.1. Model Establishment
2.4.2. Boundary Conditions and Model Excavation
3. Results and Discussion
3.1. Physical Similarity Simulation Experiment Results
3.2. Computer Numerical Simulation Results
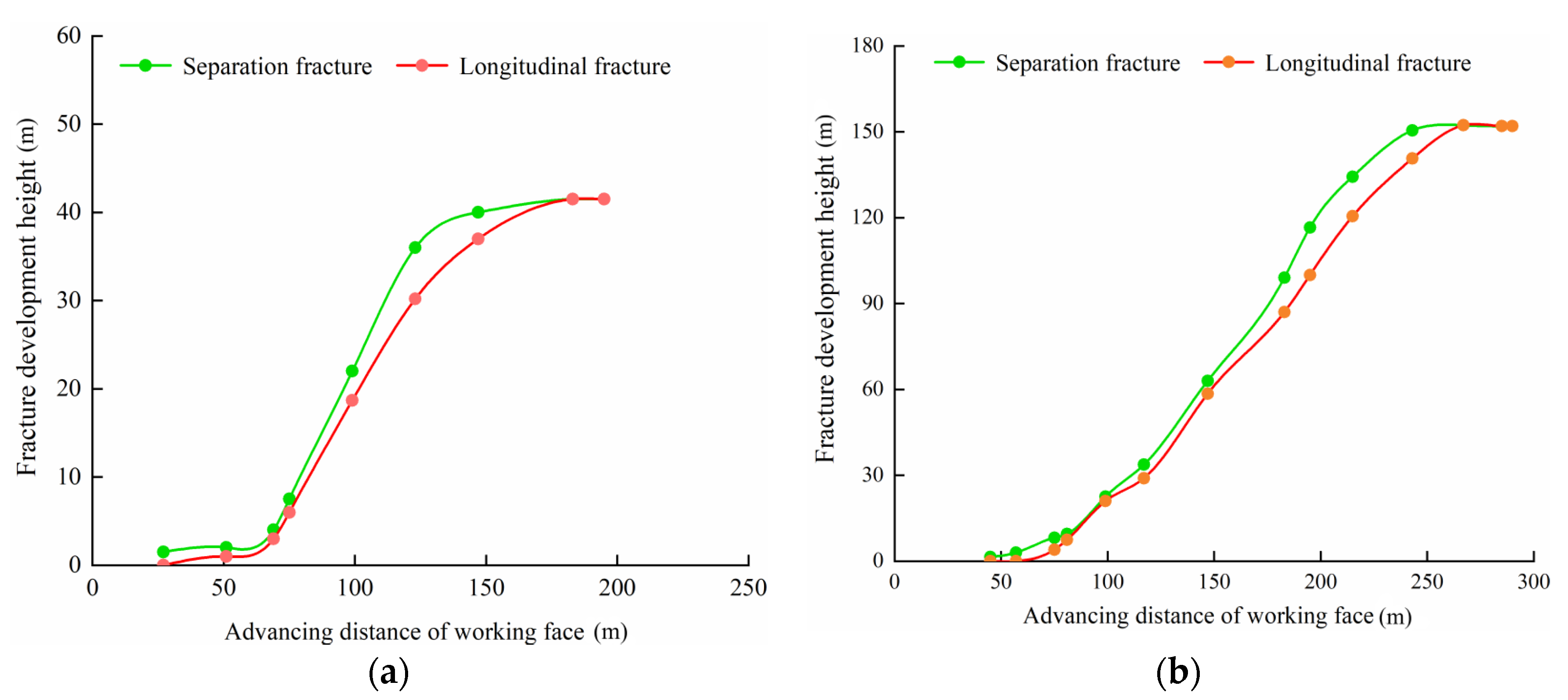
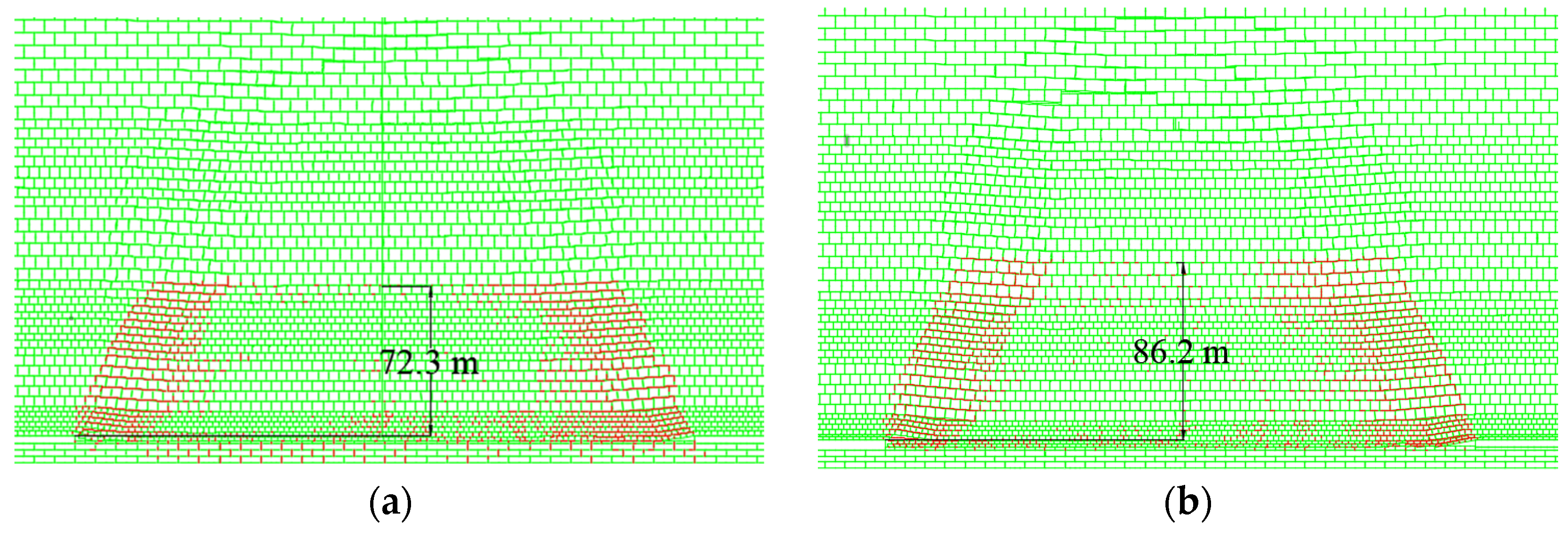
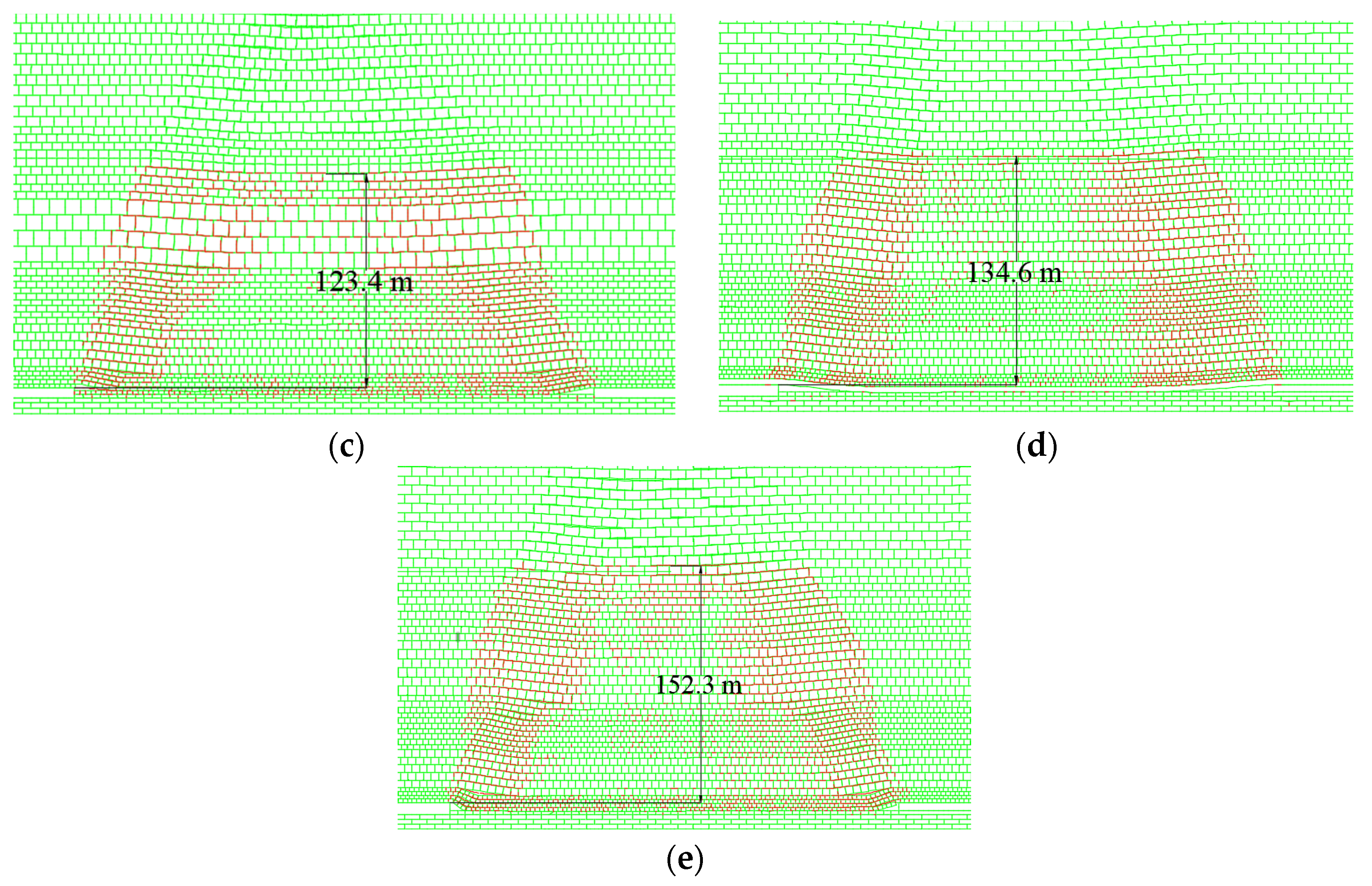
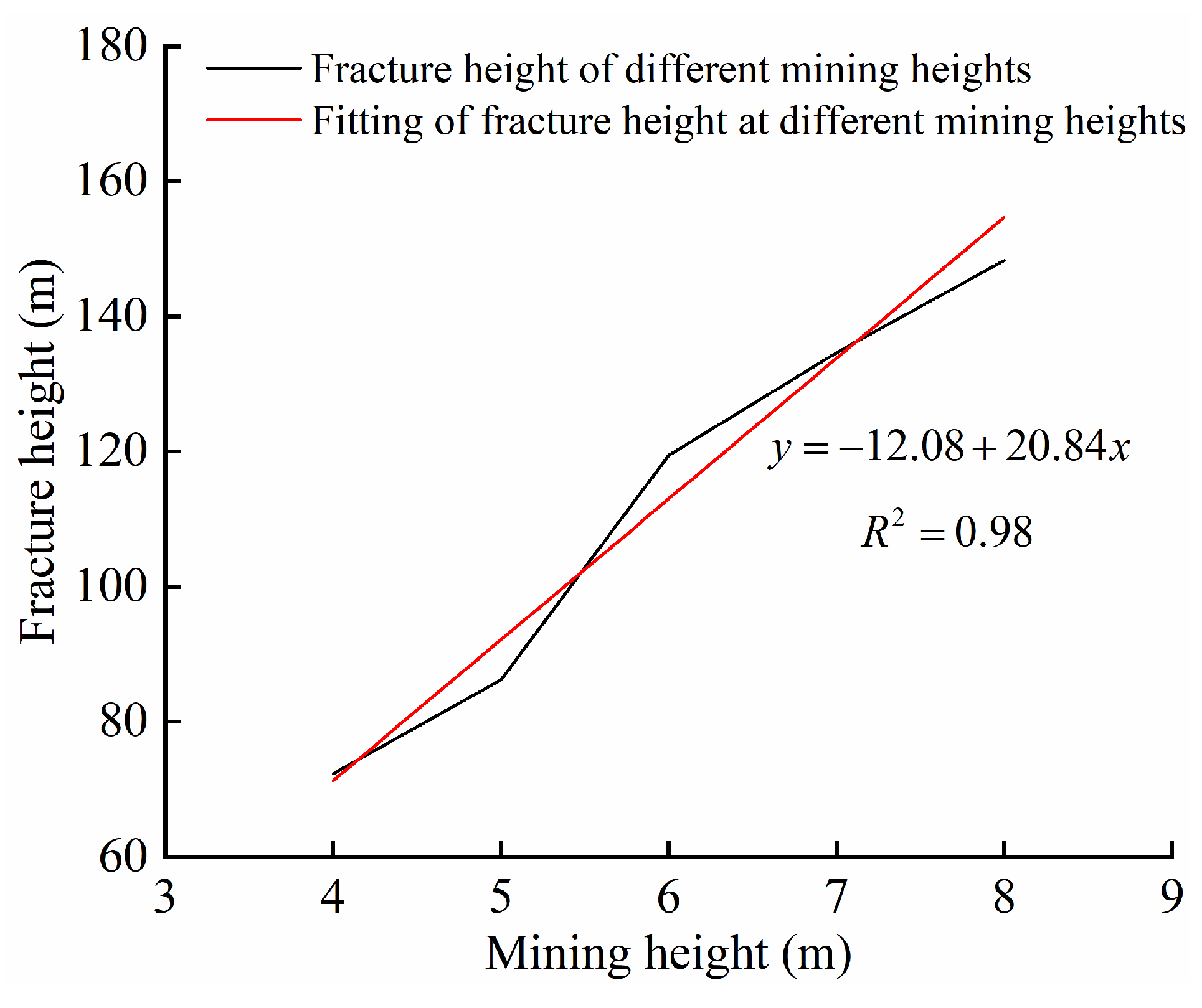
3.2.1. Development Characteristics of Overlying Strata Fractures under Different Mining Height Conditions
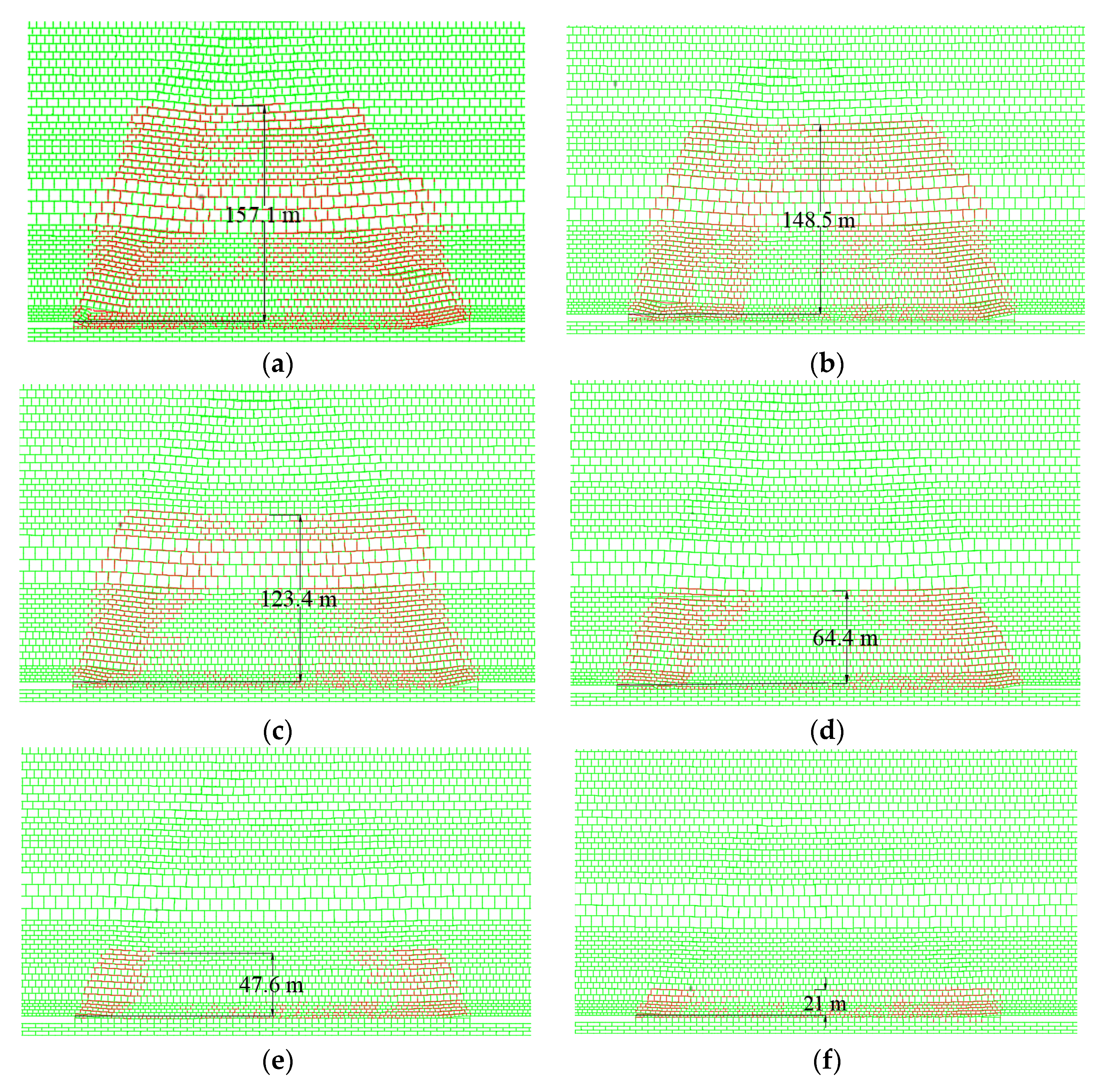
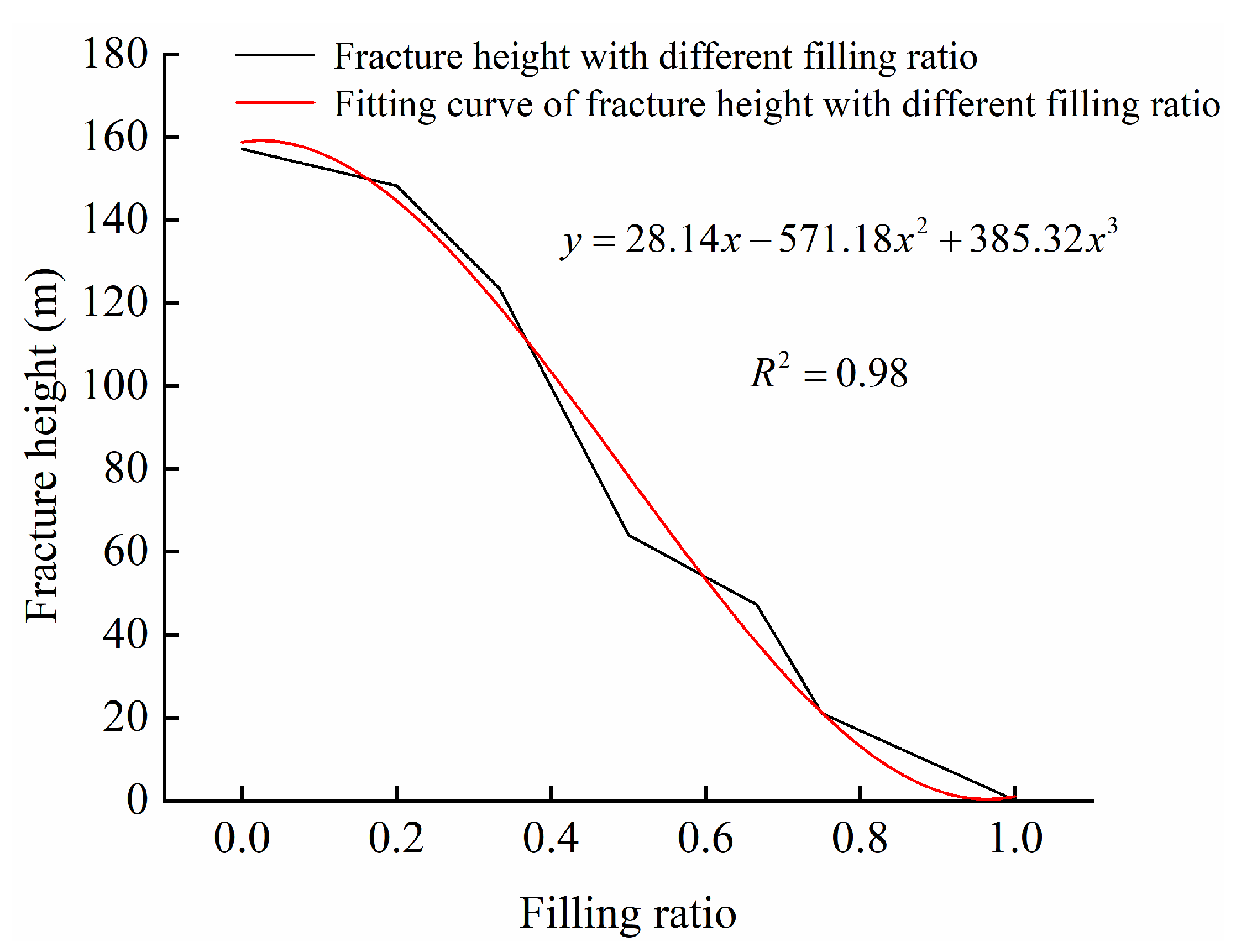
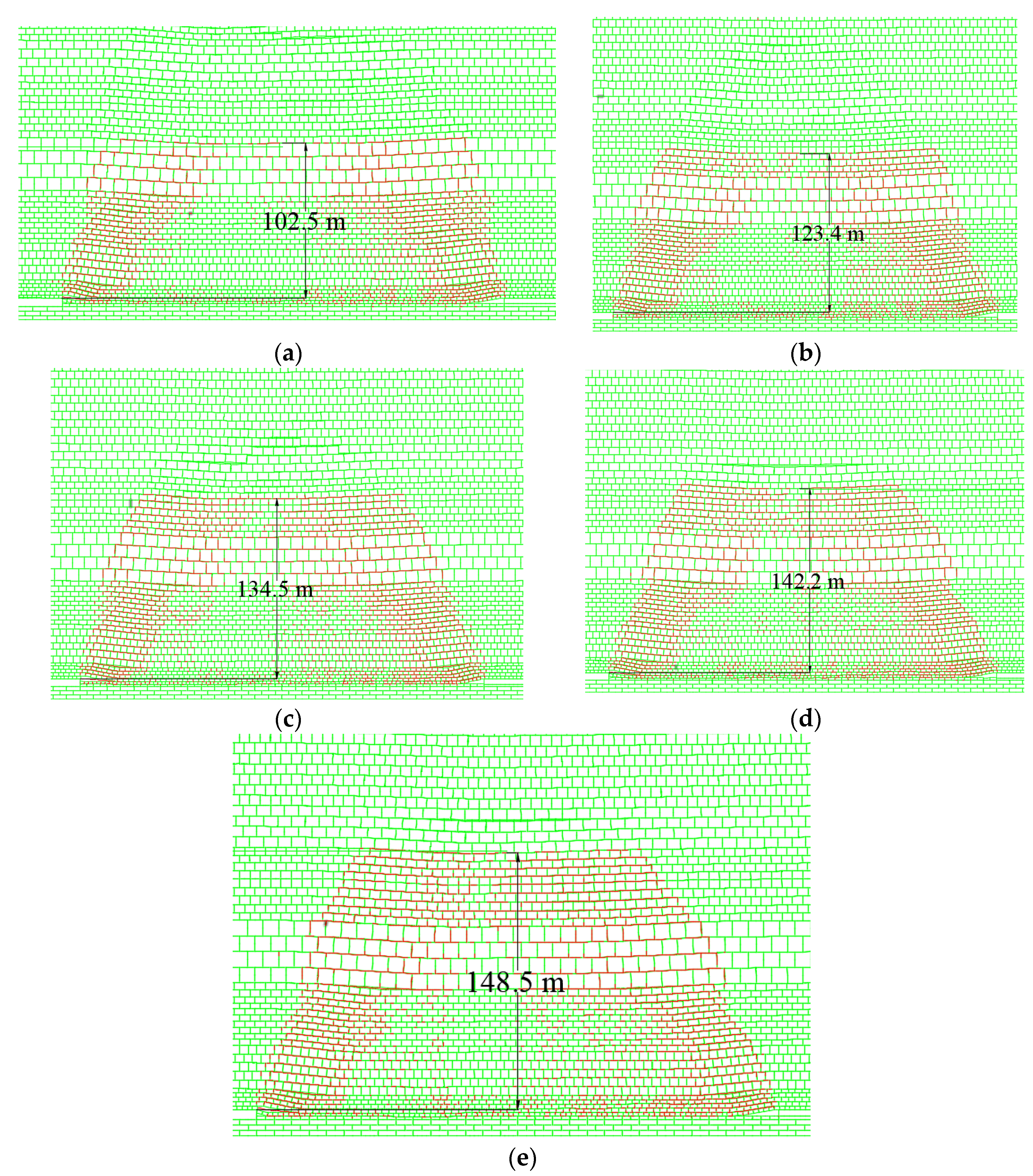
3.2.2. Development Characteristics of Overlying Strata Fractures under Different Filling Ratio Conditions
3.2.3. Development Characteristics of Overlying Strata Fractures under Different Burial Depth Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Q.X.; Du, J.W.; Chen, J.; He, Y.P. Coupling Study on strata control based on pillar stress concentration and surface cracks in shallow multi-seam mining. Int. J. Min. Sci. Technol. 2021, 31, 95–101. [Google Scholar] [CrossRef]
- Qian, M.G.; Xu, J.L.; Miao, X.X. Green mining technology in coal mine. J. China Univ. Min. Technol. 2003, 32, 343–348. [Google Scholar]
- Wang, S.M.; Sun, Q.; Qiao, J.W.; Wang, S.Q. Geological guarantee of coal green mining. J. China Coal Soc. 2020, 45, 8–15. [Google Scholar]
- Wang, S.M. Coal Accumulating and Coal Resource Evaluation of ORDOS Basin; China Coal Industry Publishing House: Beijing, China, 1996. [Google Scholar]
- Wen, P.; Guo, W.; Tan, Y.; Bai, E.; Ma, Z.; Wu, D.; Yang, W. Paste backfilling longwall mining technology for thick coal seam extraction under buildings and above confined aquifers: A case study. Minerals 2022, 12, 470. [Google Scholar] [CrossRef]
- Qiu, H.F.; Zhang, F.S.; Liu, L. Experimental study on acoustic emission characteristics of cemented rock-tailings backfill. Constr. Build. Mater. 2022, 315, 125278. [Google Scholar] [CrossRef]
- Kostecki, T.; Spearing, A.J.S. Influence of backfill on coal pillar strength and floor bearing capacity in weak floor conditions in the Illinois Basin. Int. J. Rock Mech. Min. 2015, 76, 55–67. [Google Scholar] [CrossRef]
- Khaldoun, A.; Ouadif, L.; Baba, K.; Bahi, L. Valorization of mining waste and tailings through paste backfilling solution, Imiter operation, Morocco. Int. J. Min. Sci. Technol. 2016, 26, 146–151. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Taheri, A.; Deng, J.; Ke, B. Effects of superplasticizer on the hydration, consistency, and strength development of cemented paste backfill. Minerals 2018, 8, 381. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.L.; Xuan, D.Y.; Zhu, W.B.; Wang, X.Z. Partial backfilling coal mining technology based on key strata control. J. Min. Strata Control Eng. 2019, 1, 013504. [Google Scholar]
- Zhang, P.F.; Zhao, T.B.; Ma, X.Y.; Fu, Z.Y.; Tian, X.G.; Li, Z.H. Analysis on crack distribution and evolution characteristics of gangue backfilled working face roof. Chin. J. Rock. Mech. Eng. 2022, 41, 969–978. [Google Scholar] [CrossRef]
- Chen, S.J.; Guo, W.J.; Zhou, H.; Wen, G.H. Structure model and movement law of overburden during strip pillar mining backfill with cream-body. J. China Coal Soc. 2011, 36, 1081–1086. [Google Scholar]
- Guo, G.L.; Guo, K.K.; Zhang, G.J.; Li, H.Z. Research on deformation characteristics of coupled coal-backfills bearing in deep strip backfilling mining. J. Min. Saf. Eng. 2020, 37, 101–108. [Google Scholar]
- Li, J. Evolution Mechanical and Control of Water-Flowing Fracture with Gangue Backfill under Aquifer in Coal Mines. Ph.D. Thesis, China University of Mining & Technology, Xuzhou, China, 2013. [Google Scholar]
- Yang, G.; Hang, Y.; Zhang, J.C.; Zhao, Q.J. Study on overburden failure numerical simulation in paste—Like material backfill mining. Coal Geol. China 2021, 33, 56–60. [Google Scholar]
- Lv, W.Y.; Wu, Y.P.; Liu, M.; Yin, J.H. Migration Law of the Roof of a Composited Backfilling Longwall Face in a Steeply Dipping Coal Seam. Minerals 2019, 9, 188. [Google Scholar] [CrossRef] [Green Version]
- Helinski, M.; Fahey, M.; Fourie, A. Behavior of cemented paste backfill in two mine stopes: Measurements and modeling. J. Geotech. Geoenviron. 2010, 137, 171–182. [Google Scholar] [CrossRef]
- Ivannikov, A.L.; Kongar-Syuryun, C.; Rybak, J.; Tyulyaeva, Y. The reuse of mining and construction waste for backfill as one of the sustainable activities. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012130. [Google Scholar] [CrossRef]
- Kongar-Syuryun, C.; Tyulyaeva, Y.; Khairutdinov, A.M.; Kowalik, T. Industrial waste in concrete mixtures for construction of underground structures and minerals extraction. IOP Conf. Ser. Mat. Sci. Eng. 2020, 869, 032004. [Google Scholar] [CrossRef]
- Khairutdinov, A.; Ubysz, A.; Adigamov, A. The concept of geotechnology with a backfill is the path of integrated development of the subsoil. IOP Conf. Ser. Earth Environ. Sci. 2021, 684, 012007. [Google Scholar]
- Kongar-Syuryun, C.; Ubysz, A.; Faradzhov, V. Models and algorithms of choice of development technology of deposits when selecting the composition of the backfilling mixture. IOP Conf. Ser. Earth Environ. Sci. 2021, 684, 012008. [Google Scholar] [CrossRef]
- Hefni, M.; Hassani, F. Effect of air entrainment on cemented mine backfill properties: Analysis based on response surface methodology. Minerals 2021, 11, 81. [Google Scholar] [CrossRef]
- Hefni, M.; Ali, M.A. The Potential to Replace Cement with Nano-Calcium Carbonate and Natural Pozzolans in Cemented Mine Backfill. Adv. Civ. Eng. 2021, 2021, 5574761. [Google Scholar] [CrossRef]
- Al-Moselly, Z.; Fall, M.; Haruna, S. Further insight into the strength development of cemented paste backfill materials containing polycarboxylate ether-based superplasticizer. J. Build. Eng. 2022, 47, 103859. [Google Scholar] [CrossRef]
- Ali, G.; Fall, M.; Alainachi, I. Time- and Temperature-Dependence of Rheological Properties of Cemented Tailings Backfill with Sodium Silicate. J. Mater. Civ. Eng. 2021, 33, 04020498. [Google Scholar] [CrossRef]
- Yilmaz, T.; Ercikdi, B.; Deveci, H. Utilisation of construction and demolition waste as cemented paste backfill material for underground mine openings. Environ. Manag. 2018, 222, 250–259. [Google Scholar] [CrossRef]
- Yılmaz, T.; Ercikdi, B. Effect of construction and demolition waste on the long-term geo-environmental behaviour of cemented paste backfill. Int. J. Environ. Sci. Technol. 2021, 19, 3701–3714. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Benzaazoua, M. Effects of curing and stress conditions on hydromechanical, geotechnical and geochemical properties of cemented paste backfill. Eng. Geol. 2014, 168, 23–37. [Google Scholar] [CrossRef]
- Bai, E.H.; Guo, W.B.; Tan, Y.; Huang, G.S.; Guo, M.J.; Ma, Z.B. Roadway backfill mining with super-high-water material to protect surface buildings: A case study. Appl. Sci. 2020, 10, 107. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Cao, W.; Brandenberg, S.; Zhang, J.M. Method for calculating axial force and settlement of pile foundation in consolidating and reconsolidating ground. Chin. J. Geotech. Eng. 2015, 37, 512–518. [Google Scholar]
- Yu, H.T.; Cai, J.; Zhang, Z.W. Analytical solutions for long tunnels under arbitrary dynamic loading. J. Tongji Univ. Nat. Sci. Ed. 2018, 46, 1–6. [Google Scholar]
- Sui, W.; Zhang, D.; Cui, Z.C.; Wu, Z.; Zhao, Q. Environmental implications of mitigating overburden failure and subsidences using paste-like backfill mining: A case study. Int. J. Min. Reclam. Environ. 2015, 29, 521–543. [Google Scholar] [CrossRef]
- Sheshpari, M. A review of underground mine backfilling methods with emphasis on cemented paste backfill. Electron. J. Geotech. Eng. 2015, 20, 5183–5208. [Google Scholar]
- Xie, P.S.; Wu, Y.P.; Luo, S.H.; Wang, H.W.; Lang, D. Evolution and stability analysis of inclined bench structure in large dip and high mining height stope. Chin. J. Rock Mech. Eng. 2018, 35, 953–959. [Google Scholar]
- Yao, Q.; Feng, T.; Liao, Z. Instability mechanism and reasonable size of sharply inclined segmented filling column. J. Min. Saf. Eng. 2018, 35, 49–57. [Google Scholar]
- Wu, Y.P. Basic Research on Dynamic Control of “R-S-F” System in Large Dip Seam Mining; Shaanxi Science and Technology Press: Xi’an, China, 2003. [Google Scholar]
- Lu, L.J.; Li, T.B.; Wang, G.; Wu, X.Z.; Jiang, Y.J.; Han, Z.Z. Crack expansion judgment method in overlying strata and its application for coal mining under aquifers. J. China Coal Soc. 2014, 39, 301–307. [Google Scholar]
- Jafari, M.; Shahsavari, M.; Grabinsky, M. Experimental study of the behavior of cemented paste backfill under high isotropic compression. J. Geotech. Geoenviron. Eng. 2020, 146, 06020019. [Google Scholar] [CrossRef]
- Ke, X.; Zhou, X.; Wang, X.S.; Wang, T.; Hou, H.B.; Zhou, M. Effect of tailings fineness on the pore structure development of cemented paste backfill. Constr. Build. Mater. 2016, 126, 345–350. [Google Scholar] [CrossRef]
- Chang, Q.; Chen, J.; Zhou, H.; Bai, J. Implementation of paste backfill mining technology in Chinese coal mines. Sci. World J. 2014, 2014, 821025. [Google Scholar] [CrossRef]




| Name | Bulk Density (kg/m3) | Modulus of Elasticity (GPa) | Shear Modulus (GPa) | Poisson’s Ratio | Compression Strength (MPa) | Cohesive Force (MPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|
| Sand | 1860 | 0.05 | 0.0176 | 0.31 | 0.21 | 0.126 | 35 |
| Laterite | 1920 | 0.02 | 0.0176 | 0.31 | 0.29 | 0.019 | 26 |
| Mudstone | 2430 | 8.73 | 7.41 | 0.21 | 20 | 1.2 | 20 |
| Fine sandstone | 2530 | 4.52 | 2.62 | 0.27 | 42.1 | 2.0 | 32 |
| Siltstone | 2630 | 8.36 | 9.1 | 0.32 | 36.0 | 2.5 | 38 |
| Fine sandstone | 2520 | 4.52 | 2.63 | 0.27 | 32 | 2.0 | 32 |
| Siltstone | 2630 | 8.36 | 9.12 | 0.32 | 36.0 | 2.5 | 38 |
| Medium grained sandstone | 2510 | 4.2 | 3.10 | 0.29 | 35.0 | 2.2 | 20 |
| Siltstone | 2630 | 8.36 | 3.72 | 0.32 | 36.0 | 2.5 | 38 |
| Fine sandstone | 2520 | 4.52 | 2.63 | 0.27 | 42.1 | 2.0 | 32 |
| Siltstone | 2630 | 8.36 | 7.68 | 0.32 | 36.0 | 2.5 | 38 |
| Medium grained sandstone | 2510 | 6.9 | 7.31 | 0.29 | 35.3 | 2.2 | 35 |
| Fine sandstone | 2520 | 4.52 | 2.62 | 0.27 | 42.1 | 2.0 | 32 |
| Siltstone | 2630 | 8.36 | 10.81 | 0.32 | 36.0 | 2.5 | 38 |
| 2−2 coal | 1420 | 1.52 | 0.38 | 0.15 | 12.2 | 1.0 | 37 |
| Geometric Similarity Constant | 150 |
|---|---|
| Model size | 3000 mm × 200 mm × 1800 mm |
| Bulk density similarity constant | 1.6 |
| Stress similarity constant | 240 |
| Time similarity constant |
| Name | Formation Thickness (m) | Model Thickness (cm) | Matching Number | Consumption of Each Material (kg/cm) | |||
|---|---|---|---|---|---|---|---|
| River Sand | Plaster | Big White Powder | Fly Ash | ||||
| Laterite | 20 | 13.3 | 673 | 8.23 | 0.96 | 0.41 | |
| Mudstone | 22 | 14.7 | 928 | 8.53 | 0.32 | 0.75 | |
| Fine sandstone | 9 | 6 | 746 | 8.40 | 0.48 | 0.72 | |
| Siltstone | 9 | 6 | 728 | 8.40 | 0.24 | 0.96 | |
| Fine sandstone | 16 | 10.7 | 746 | 8.40 | 0.48 | 0.72 | |
| Siltstone | 9 | 6 | 728 | 8.40 | 0.24 | 0.96 | |
| Medium grained sandstone | 36 | 24 | 737 | 8.40 | 0.36 | 0.84 | |
| Siltstone | 8 | 5.3 | 728 | 8.40 | 0.24 | 0.96 | |
| Fine sandstone | 10 | 6.7 | 746 | 8.40 | 0.48 | 0.72 | |
| Siltstone | 15 | 10 | 728 | 8.40 | 0.24 | 0.96 | |
| Medium grained sandstone | 25 | 16.7 | 737 | 8.40 | 0.36 | 0.84 | |
| Fine sandstone | 10 | 6.7 | 746 | 8.40 | 0.48 | 0.72 | |
| Siltstone | 2 | 1.3 | 728 | 8.40 | 0.24 | 0.96 | |
| 2-2 coal | 6 | 4 | 20:1:5:20 (Fly ash) | 6.78 | 0.34 | 1.7 | 6.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Guo, K.; Wang, H.; Feng, K.; Jia, D. Evolution Characteristics of Overlying Strata Fractures in Paste Composite Filling Stope. Minerals 2022, 12, 654. https://doi.org/10.3390/min12050654
Lv W, Guo K, Wang H, Feng K, Jia D. Evolution Characteristics of Overlying Strata Fractures in Paste Composite Filling Stope. Minerals. 2022; 12(5):654. https://doi.org/10.3390/min12050654
Chicago/Turabian StyleLv, Wenyu, Kai Guo, Haijin Wang, Kun Feng, and Dongdong Jia. 2022. "Evolution Characteristics of Overlying Strata Fractures in Paste Composite Filling Stope" Minerals 12, no. 5: 654. https://doi.org/10.3390/min12050654
APA StyleLv, W., Guo, K., Wang, H., Feng, K., & Jia, D. (2022). Evolution Characteristics of Overlying Strata Fractures in Paste Composite Filling Stope. Minerals, 12(5), 654. https://doi.org/10.3390/min12050654





