Uranium Retardation Capacity of Lithologies from the Negev Desert, Israel—Rock Characterization and Sorption Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rock Sample Collection and Characterization
2.2. Uranium Batch Sorption Experiments
2.3. Surface Complexation Modeling
2.4. Non-Mechanistic Sorption Isotherm Modeling
3. Results
3.1. Rock Sample Characterization
3.2. Uranium Batch Sorption Results
3.2.1. Equilibration Results
3.2.2. Batch Sorption and Desorption Experiments
3.3. Surface Complexation and Non-Mechanistic Sorption Modeling
4. Discussion
4.1. Component Additive Surface Complexation Modeling
4.2. Empirical Contributions from Adsorbing Phases Determined from Linear Combinations
4.3. Examination of Discrepancies Caused by Organic Carbon
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
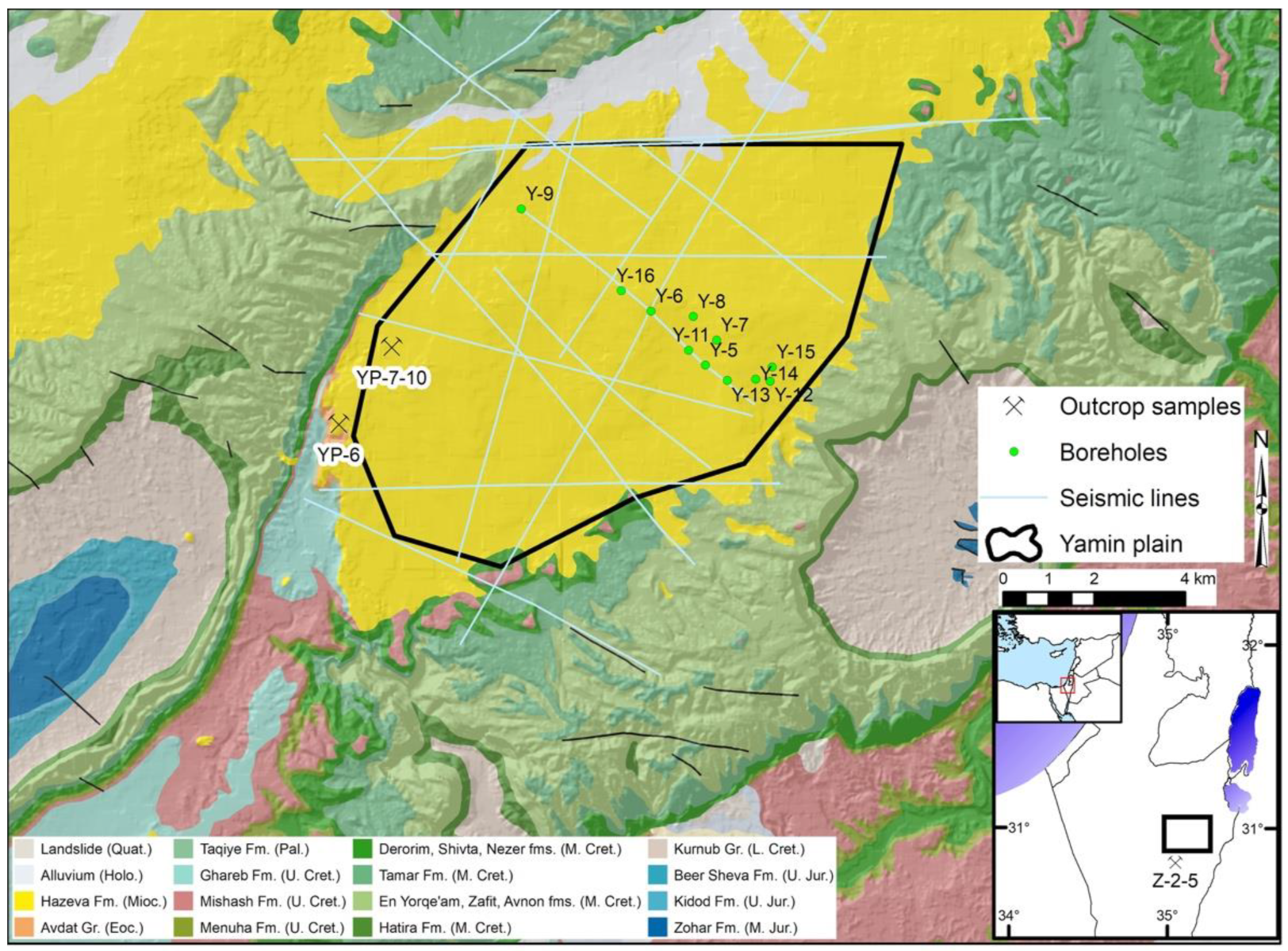


Appendix B
Sample Preparation and Methodology for XRF, qXRD, BET, and TOC
Appendix C
Appendix C.1. Methodology for Equilibration Batch Experiments
Appendix C.2. Methodology for Kinetic Batch Sorption Studies
Appendix D
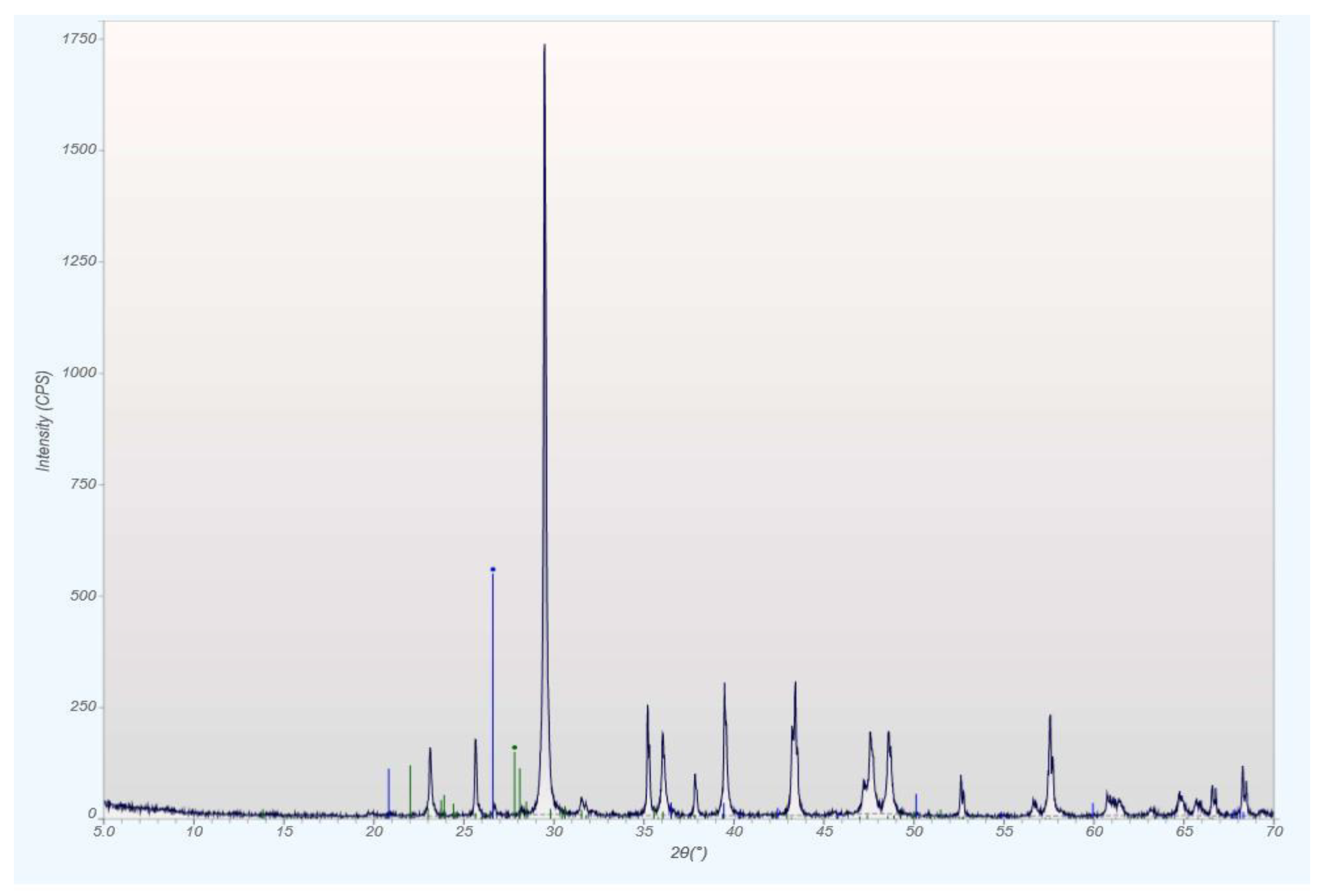
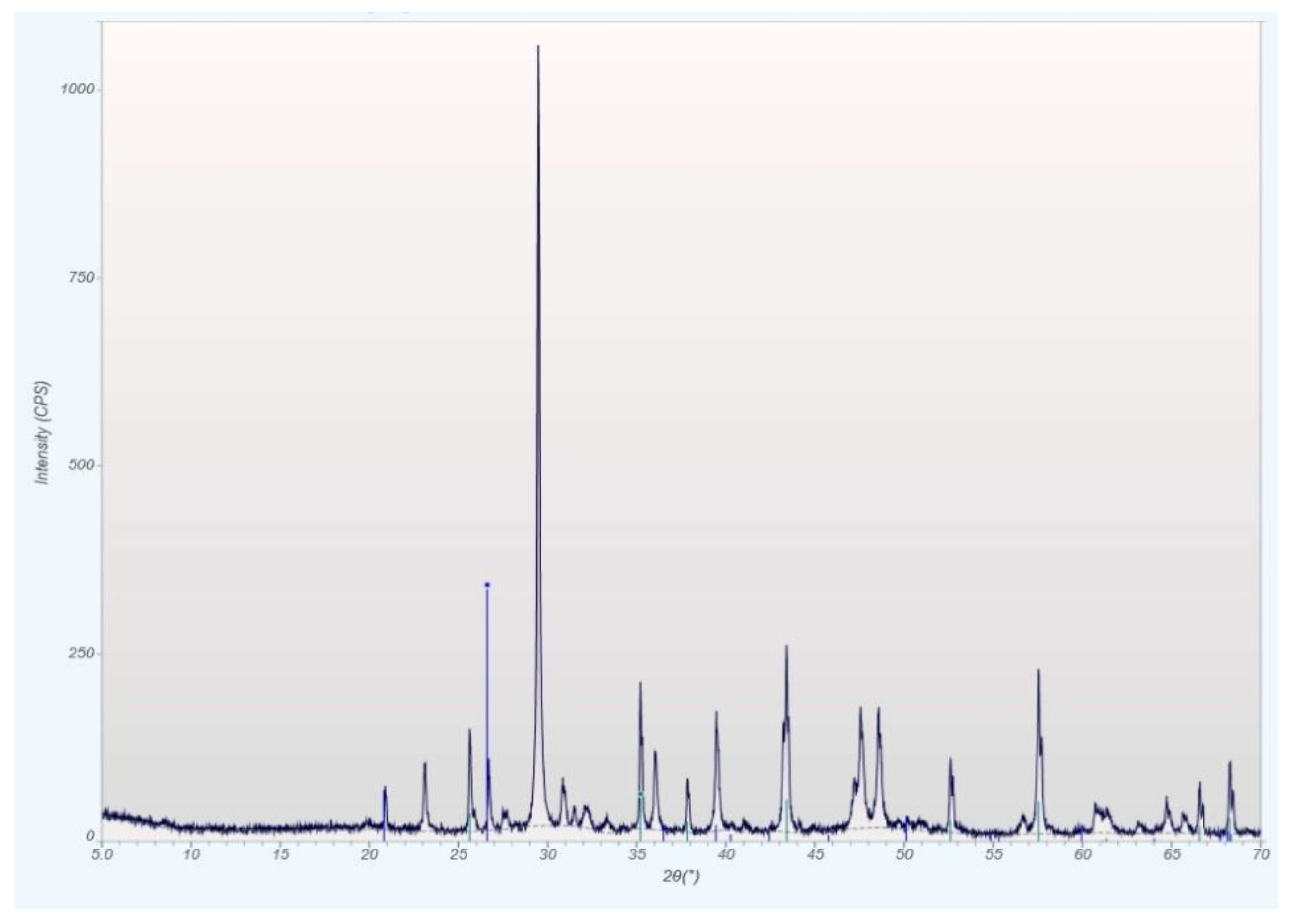
qXRD Diffractograms of the Four Different Rock Types


Appendix E
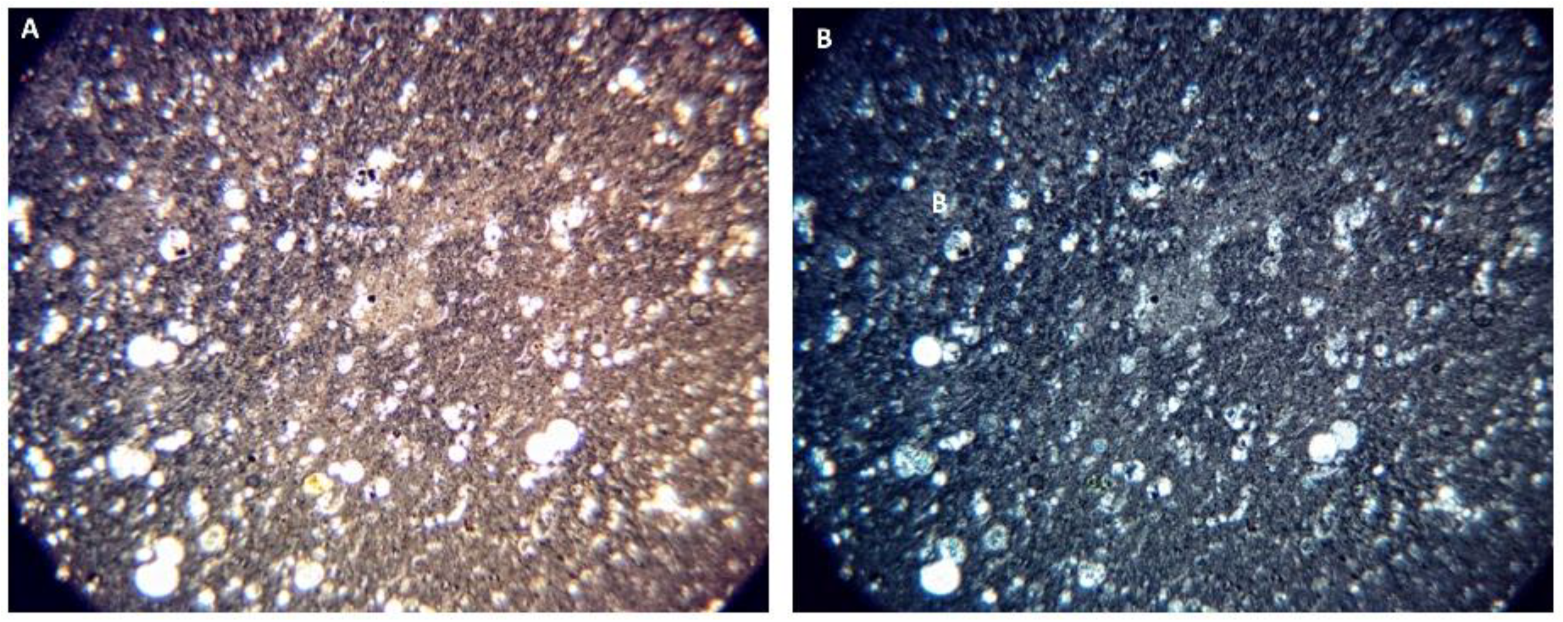
Petrographic Images and SEM-EDS Analysis of the Four Rock Specimens





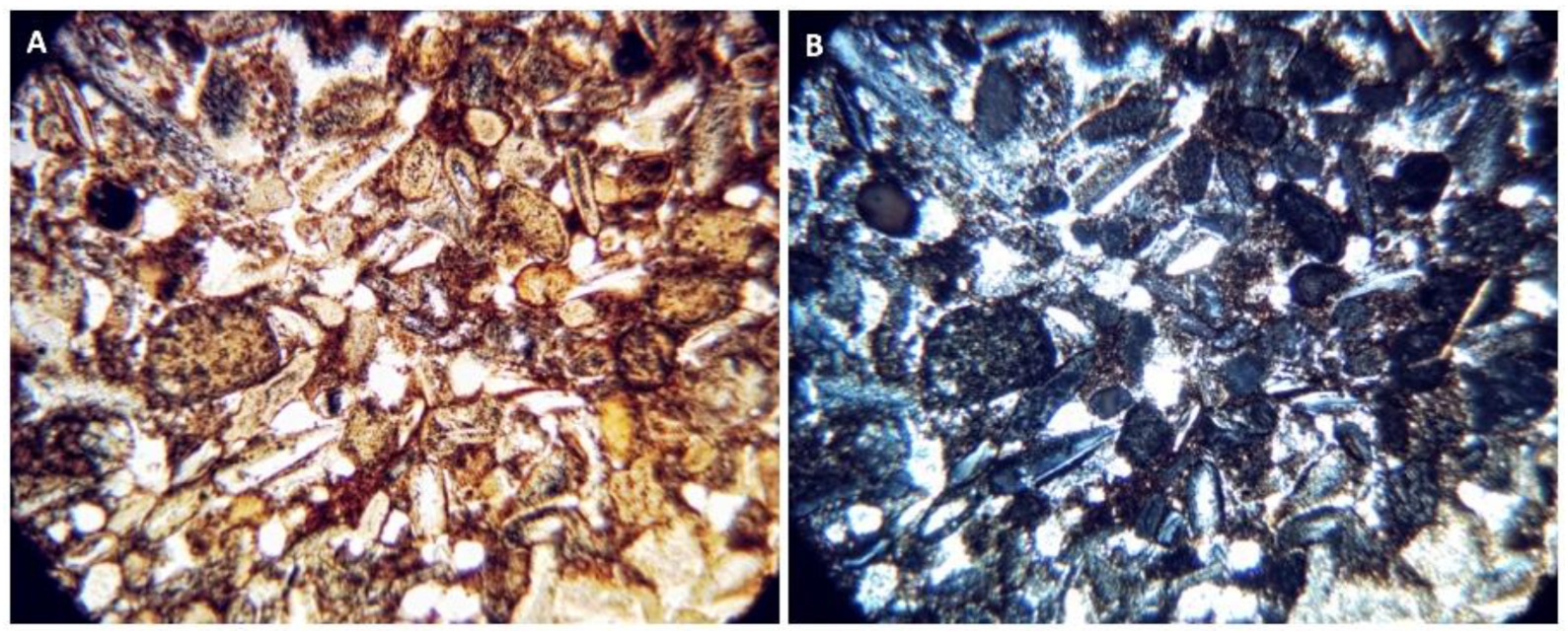

Appendix F
SEM-EDS Analyses of Select OS-3 and HOP-5 Sections
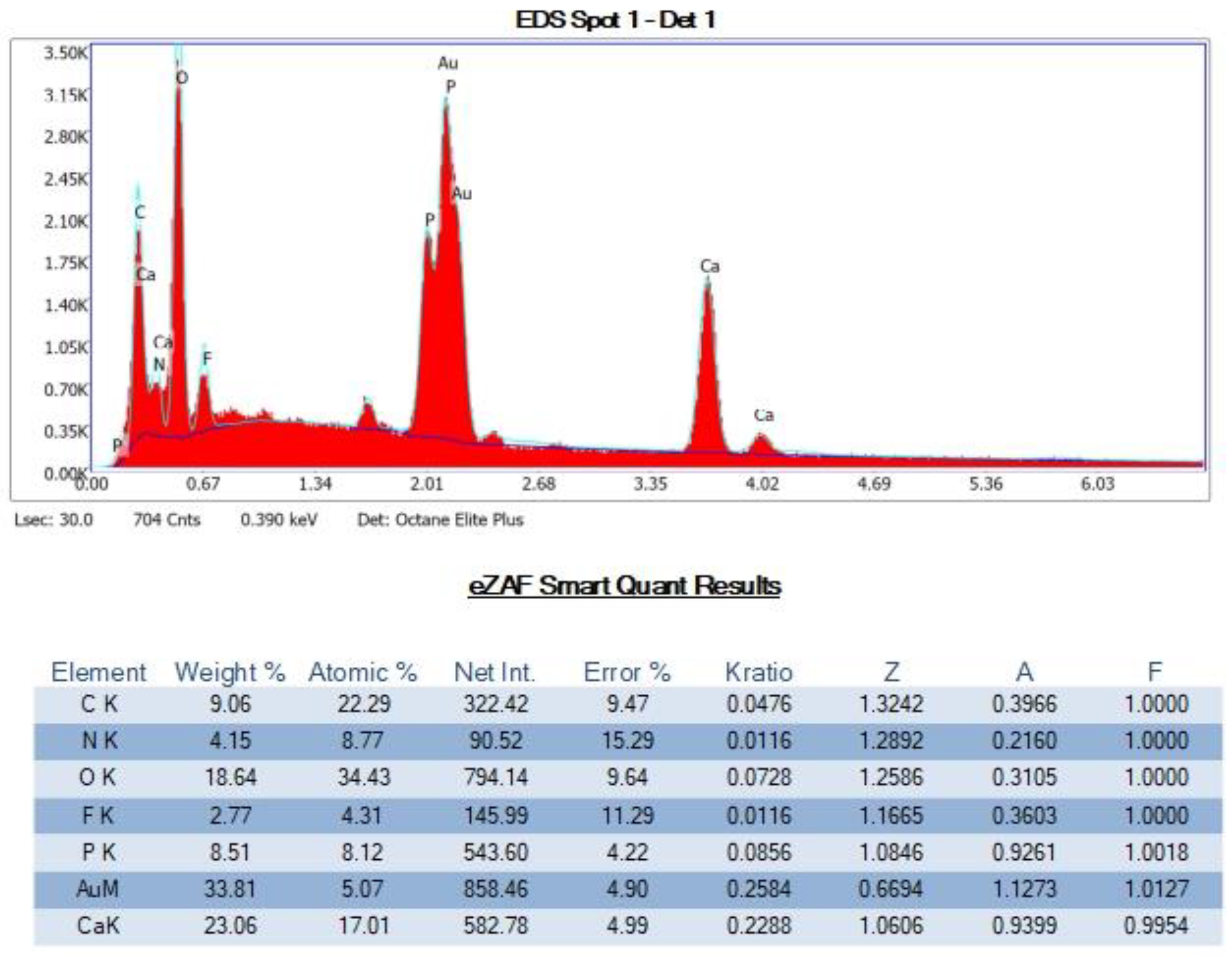
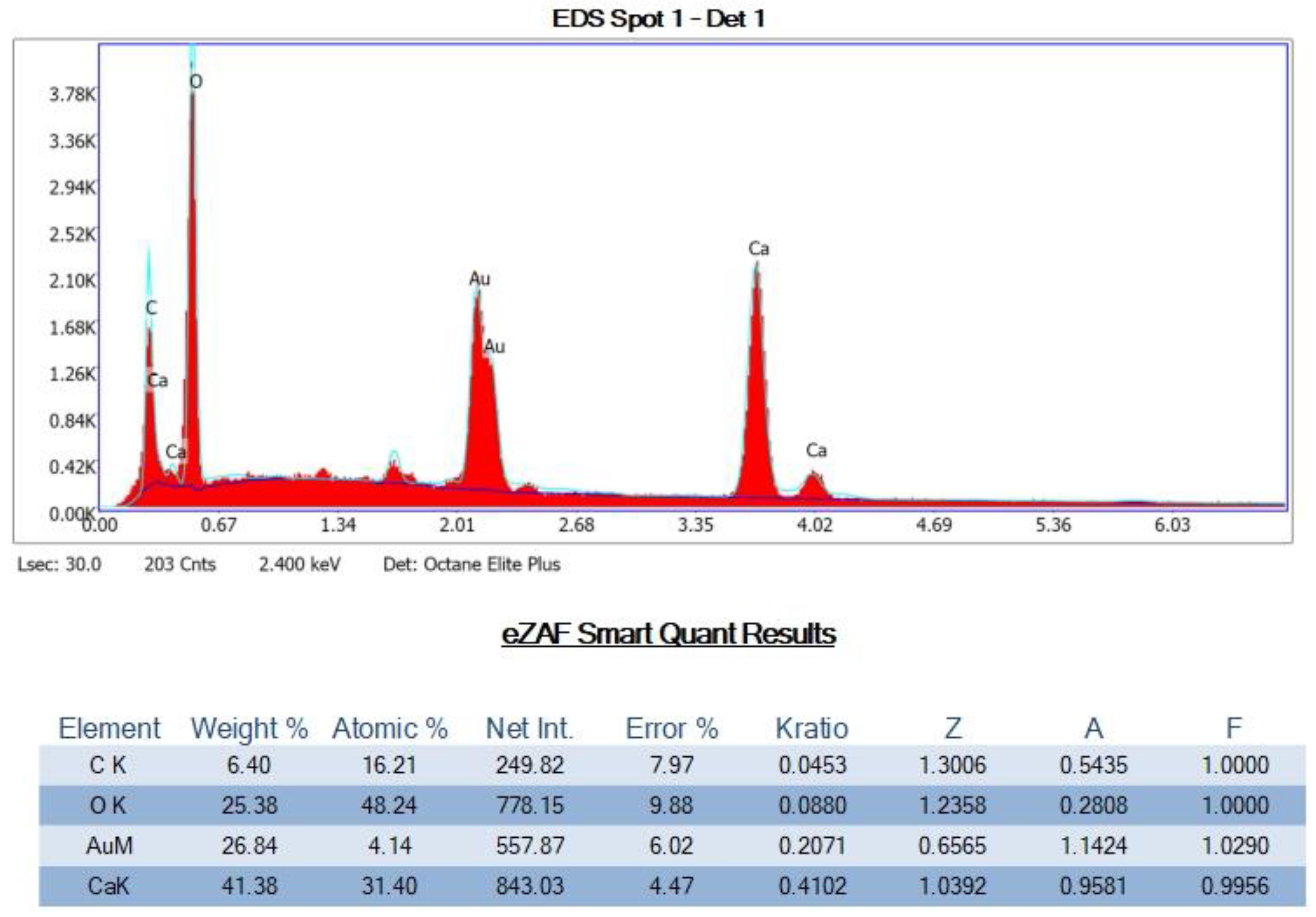
Appendix G
Long-Term Sorption Experiment
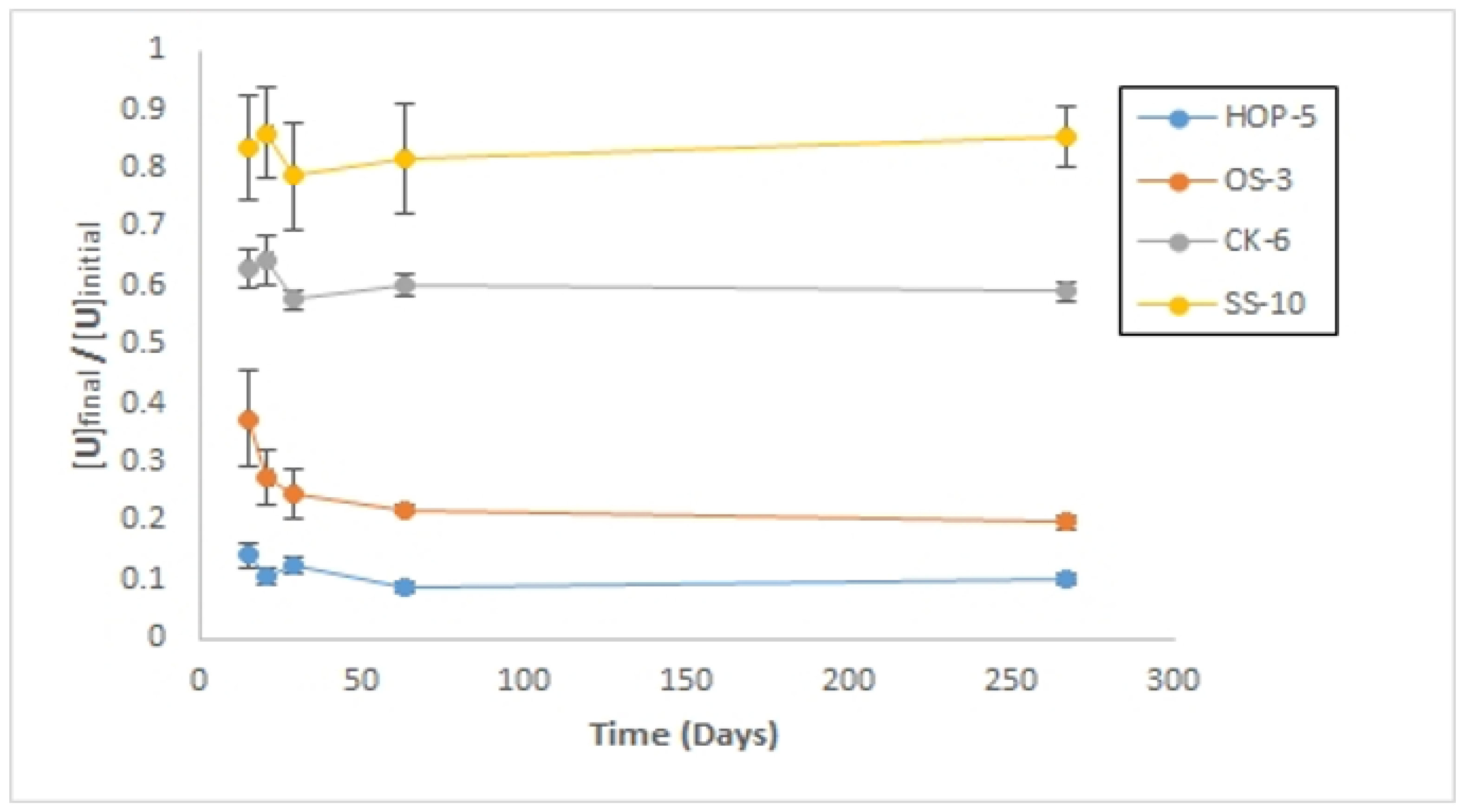
References
- Bussod, G.Y.; Rosenzweig, R.; Reimus, P.W.; Stauffer, P.H.; Dangelmayr, M.A.; Calvo, R.; Hayes-Rich, N.G.; Klein-BenDavid, O.; Dody, A.; Balaban, N. Subsurface Radionuclide Transport: Northeastern Negev Desert Vadose Zone Model Development. In Scientific, Strategic and Conceptual Contributions to Deep Geological Repository Siting Process, Proceedings of the 45th Waste Management Conference, Phoenix, AZ, USA, 3–7 March 2019; WM Symposia: Phoenix, AZ, USA, 2020; pp. 1–14. [Google Scholar]
- Calvo, R.; Bartov, Y. Hazeva Group, southern Israel: New observations, and their implications for its stratigraphy, paleogeography, and tectono-sedimentary regime. Isr. J. Earth Sci. 2001, 50, 71–99. [Google Scholar] [CrossRef]
- Fabryka-Martin, J.T.; Flint, A.; Meijer, A.; Bussod, G.Y. Water and Radionuclide Transport in the Unsaturated Zone. In Uncertainties Underground: Yucca Mountain and the Nation’s Hugh-Level Nuclear Waste; MacFarlane, A., Ewing, R., Eds.; The MIT Press: Cambridge, MA, USA, 2006; pp. 179–197. [Google Scholar]
- Robinson, B.A.; Bussod, G.Y. Radionuclide Transport in the Unsaturated Zone at Yucca Mountain: Numerical Model and Preliminary Field Observations. In Dynamics of Fluids in Fractured Rocks, Witherspoon Volume; Geophysical Monograph Series 122; Faybishenko, B., Ed.; American Geophysical Union: Washington, DC, USA, 2000; pp. 323–336. [Google Scholar]
- Eckhardt, R.C.; Bish, D.L.; Bussod, G.Y.; Fabryka-Martin, J.T.; Levy, S.S.; Reimus, P.W.; Robinson, B.A.; Runde, W.H.; Triay, I.; Vaniman, D.T. Yucca Mountain: Looking ten thousand years into the future. In Challenges in Plutonium Science; Los Alamos Science: Los Alamos, NM, USA, 2000; Volume II, pp. 464–488. [Google Scholar]
- Bethke, C.M.; Brady, P.V. How the Kd approach undermines ground water cleanup. Groundwater 2000, 38, 435–443. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C. A case against Kd-based transport models: Natural attenuation at a mill tailings site. Comput. Geosci. 2003, 29, 351–359. [Google Scholar] [CrossRef]
- Stoliker, D.L.; Kent, D.B.; Zachara, J.M. Quantifying Differences in the Impact of Variable Chemistry on Equilibrium Uranium (VI) Adsorption Properties of Aquifer Sediments. Environ. Sci. Technol. 2011, 45, 8733–8740. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Meece, D.E.; Kohler, M.; Curtis, G.P. Approaches to surface complexation modeling of Uranium (VI) adsorption on aquifer sediments. Geochim. Cosmochim. Acta 2004, 68, 3621–3641. [Google Scholar] [CrossRef]
- Waite, T.D.; Davis, J.A.; Payne, T.E.; Waychunas, G.A.; Xu, N. Uranium (VI) adsorption to ferrihydrite: Application of a surface complexation model. Geochim. Cosmochim. Acta 1994, 58, 5465–5478. [Google Scholar] [CrossRef]
- Bernhard, G.; Geipel, G.; Reich, T.; Brendler, V.; Amayri, S.; Nitsche, H. Uranyl (VI) carbonate complex formation: Validation of the Ca2UO2 (CO3)3 (aq.) species. Radiochim. Acta 2001, 89, 511–518. [Google Scholar] [CrossRef]
- Davis, J.A.; Curtis, G.P.; Wilkins, M.J.; Kohler, M.; Fox, P.; Naftz, D.L.; Lloyd, J.R. Processes affecting transport of uranium in a suboxic aquifer. Phys. Chem. Earth Parts A/B/C 2006, 31, 548–555. [Google Scholar] [CrossRef]
- Kohler, M.; Curtis, G.P.; Meece, D.E.; Davis, J.A. Methods for Estimating Adadsorbed Uranium (VI) and Distribution Coefficients of Contaminated Sediments. Environ. Sci. Technol. 2004, 38, 240–247. [Google Scholar] [CrossRef]
- Stewart, B.D.; Mayes, M.A.; Fendorf, S. Impact of uranyl− calcium− carbonato complexes on uranium (VI) adsorption to synthetic and natural sediments. Environ. Sci. Technol. 2010, 44, 928–934. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Brooks, S.C. Determination of the formation constants of ternary complexes of uranyl and carbonate with alkaline earth metals (Mg2+, Ca2+, Sr2+, and Ba2+) using anion exchange method. Environ. Sci. Technol. 2006, 40, 4689–4695. [Google Scholar] [CrossRef] [PubMed]
- Curtis, G.P.; Fox, P.; Kohler, M.; Davis, J.A. Comparison of in situ uranium KD values with a laboratory determined surface complexation model. Appl. Geochem. 2004, 19, 1643–1653. [Google Scholar] [CrossRef]
- Davis, J.A.; Ochs, M.; Olin, M.; Payne, T.E.; Tweed, C.J. Interpretation and Prediction of Radionuclide Sorption onto Substrates Relevant for Radioactive Waste Disposal Using Thermodynamic Sorption, Models; NEA Sorption Project, Phase II, NEA Report 5992; OECD: Paris, France, 2005. [Google Scholar]
- Johnson, R.H.; Tutu, H. Predictive Reactive Transport Modeling at a Proposed Uranium In Situ Recovery Site with a General Data Collection Guide. Mine Water Environ. 2016, 35, 369–380. [Google Scholar] [CrossRef]
- Dangelmayr, M.A.; Reimus, P.W.; Wasserman, N.L.; Punsal, J.J.; Johnson, R.H.; Clay, J.T.; Stone, J.J. Laboratory column experiments and transport modeling to evaluate retardation of uranium in an aquifer downgradient of a uranium in-situ recovery site. Appl. Geochem. 2017, 80, 1–13. [Google Scholar] [CrossRef]
- Reimus, P.W.; Dangelmayr, M.A.; Clay, J.T.; Chamberlain, K.R. Uranium Natural Attenuation Downgradient of an In-situ Recovery Mine Inferred from a Cross-Hole Field Test. Environ. Sci. Technol. 2019, 53, 7483–7493. [Google Scholar] [CrossRef]
- Dzombak, D.D.; Morel, F.M.M. Surface Complex Modeling: Hydrous Ferric Oxide; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Payne, T.E.; Brendler, V.; Ochs, M.; Baeyens, B.; Brown, P.L.; Davis, J.A.; Ekberg, C.; Kulik, D.A.; Lutzenkirchen, J.; Missana, T. Guidelines for thermodynamic sorption modelling in the context of radioactive waste disposal. Environ. Model. Softw. 2013, 42, 143–156. [Google Scholar] [CrossRef]
- Stockdale, A.; Bryan, N.D.; Lofts, S.; Tipping, E. Investigating humic substances interactions with Th4+, UO22+, and NpO2+ at high pH: Relevance to cementitious disposal of radioactive wastes. Geochim. Cosmochim. Acta 2013, 121, 214–228. [Google Scholar] [CrossRef]
- Dong, W.; Wan, J. Additive surface complexation modeling of uranium (VI) adsorption onto quartz-sand dominated sediments. Environ. Sci. Technol. 2014, 48, 6569–6577. [Google Scholar] [CrossRef]
- Klein-BenDavid, O.; Harlavan, Y.; Levkov, I.; Teutsch, N.; Brown, K.G.; Gruber, C.; Ganor, J. Interaction between spent fuel components and carbonate rocks. Sci. Total Environ. 2019, 689, 469–480. [Google Scholar] [CrossRef] [PubMed]
- Payne, T.E.; Davis, J.A.; Ochs, M.; Olin, M.; Tweed, C.J. Uranium adsorption on weathered schist–intercomparison of modelling approaches. Radiochim. Acta 2004, 92, 651–661. [Google Scholar] [CrossRef]
- Payne, T.E.; Davis, J.A.; Ochs, M.; Olin, M.; Tweed, C.J.; Altmann, S.; Askarieh, M.M. Comparative evaluation of surface complexation models for radionuclide sorption by diverse geologic materials. Interface Sci. Technol. 2006, 11, 605–633. [Google Scholar]
- Davis, J.A. Application of Surface Complexation Modeling to Selected Radionuclides and Aquifer Sediments. US Nuclear Regulatory Commission, Office of Nuclear Regulatory Research: Rockville, MD, USA, 2008. [Google Scholar]
- Loganathan, V.A.; Barnett, M.O.; Clement, T.P.; Kanel, S.R. Scaling of adsorption reactions: U (VI) experiments and modeling. Appl. Geochem. 2009, 24, 2051–2060. [Google Scholar] [CrossRef]
- Johnson, R.H.; Tutu, H. Reactive transport modelling at uranium in situ recovery sites: Uncertainties in uranium sorption on iron hydroxides. In “Reliable Mine Water Technology”, Proceedings of the International Mine Water Association Conference, Golden, CO, USA, 6–9 August 2013; Brown, A., Ed.; International Mine Water Association: Wendelstein, Germany, 2013; Volume I. [Google Scholar]
- Beckingham, L.E.; Steefel, C.I.; Swift, A.M.; Voltolini, M.; Yang, L.; Anovitz, L.M.; Xue, Z. Evaluation of accessible mineral surface areas for improved prediction of mineral reaction rates in porous media. Geochim. Cosmochim. Acta 2017, 205, 31–49. [Google Scholar] [CrossRef] [Green Version]
- Dangelmayr, M.A.; Reimus, P.W.; Johnson, R.H.; Clay, J.T.; Stone, J.J. Uncertainty and variability in laboratory derived sorption parameters of sediments from a uranium in situ recovery site. J. Contam. Hydrol. 2018, 213, 28–39. [Google Scholar] [CrossRef] [PubMed]
- Dody, A.; Nahlieli, A.; Avni, Y.; Cohen, H.; Weiner, D.; Porat, N. Late Quaternary deposition and erosion processes along the margins of the Yamin Plain, northeast Negev, Israel. Isr. J. Earth Sci. 2008, 57, 199–211. [Google Scholar] [CrossRef]
- Weinberger, G.; Rosenthal, E.; Flexer, A. The subsurface geology of Central and Northern Negev with possible implications on the regional ground water flow pattern. J. Afr. Earth Sci. 1992, 14, 155–172. [Google Scholar] [CrossRef]
- Dody, A.; Weiner, D. Recharge processes of the Neogene aquifer at Yamin–Rotem Plateau, northeast Negev, Israel. Isr. J. Earth Sci. 2005, 54, 29–34. [Google Scholar] [CrossRef]
- Matmon, A.; Dody, A.; Finkel, R. A 300-ky history of sand erosion in the Yamin Plain, Negev Desert, Israel. Isr. J. Earth Sci. 2009, 58, 29–39. [Google Scholar] [CrossRef]
- Riley, R.G.; Zachara, J.M.; Wobber, F.J. Chemical Contaminants on DOE Lands and Selection of Contaminant Mixtures for Subsurface Science Research; DOE/ER-0547T; U.S. Department of Energy: Washington, DC, USA, 1992.
- Hedaya, M.A.; Birkenfeld, H.P.; Kathren, R.L. A sensitive method for the determination of uranium in biological samples utilizing kinetic phosphorescence analysis (KPA). J. Pharm. Biomed. Anal. 1997, 15, 1157–1165. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey: Denver, CO, USA, 2013; pp. 2328–7055.
- Guillaumont, R.; Mompean, F.J. Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technetium; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Gorman-Lewis, D.; Burns, P.C.; Fein, J.B. Review of uranyl mineral solubility measurements. J. Chem. Thermodyn. 2008, 40, 335–352. [Google Scholar] [CrossRef]
- Gorman-Lewis, D.; Shvareva, T.; Kubatko, K.A.; Burns, P.C.; Wellman, D.M.; McNamara, B.; Szymanowski, J.E.S.; Navrotsky, A.; Fein, J.B. Thermodynamic Properties of Autunite, Uranyl Hydrogen Phosphate, and Uranyl Orthophosphate from Solubility and Calorimetric Measurements. Environ. Sci. Technol. 2009, 43, 7416–7422. [Google Scholar] [CrossRef]
- Dong, W.; Brooks, S.C. Formation of aqueous MgUO2 (CO3)32− complex and uranium anion exchange mechanism onto an exchange resin. Environ. Sci. Technol. 2008, 42, 1979–1983. [Google Scholar] [CrossRef]
- Davis, J.A.; Coston, J.A.; Kent, D.B.; Fuller, C.C. Application of the Surface Complexation Concept to Complex Mineral Assemblages. Environ. Sci. Technol. 1998, 32, 2820–2828. [Google Scholar] [CrossRef]
- Arai, Y.; McBeath, M.; Bargar, J.R.; Joye, J.; Davis, J.A. Uranyl adsorption and surface speciation at the imogolite–water interface: Self-consistent spectroscopic and surface complexation models. Geochim. Cosmochim. Acta 2006, 70, 2492–2509. [Google Scholar] [CrossRef]
- Bargar, J.R.; Reitmeyer, R.; Lenhart, J.J.; Davis, J.A. Characterization of U (VI)-carbonato ternary complexes on hematite: EXAFS and electrophoretic mobility measurements. Geochim. Cosmochim. Acta 2000, 64, 2737–2749. [Google Scholar] [CrossRef]
- Chisholm-Brause, C.J.; Berg, J.M.; Matzner, R.A.; Morris, D.E. Uranium (VI) sorption complexes on montmorillonite as a function of solution chemistry. J. Colloid Interface Sci. 2001, 233, 38–49. [Google Scholar] [CrossRef] [Green Version]
- Doherty, J.E.; Hunt, R.J. Approaches to Highly Parameterized Inversion—A Guide to Using Pest for Groundwater-Model Calibration; U.S. Geological Survey: Denver, CO, USA, 2010; pp. 1–58.
- Langmuir, D.L. Aqueous Environmental Geochemistry. Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Liu, J.; Zhao, C.; Zhang, Z.; Liao, J.; Liu, Y.; Cao, X.; Yang, J.; Yang, Y.; Liu, N. Fluorine effects on U(VI) sorption by hydroxyapatite. Chem. Eng. J. 2016, 288, 505–515. [Google Scholar] [CrossRef]
- Ohnuki, T.; Kozai, N.; Samadfam, M.; Yasuda, R.; Yamamoto, S.; Narumi, K.; Naramoto, H.; Murakami, T. The formation of autunite (Ca(UO2)2(PO4)2 nH2O) within the leached layer of dissolving apatite: Incorporation mechanism of uranium by apatite. Chem. Geol. 2004, 211, 1–14. [Google Scholar] [CrossRef]
- Fuller, C.C.; Bargar, J.R.; Davis, J.A.; Piana, M.J. Mechanisms of Uranium Interactions with Hydroxyapatite: Implications for Groundwater Remediation. Environ. Sci. Technol. 2002, 36, 158–165. [Google Scholar] [CrossRef]
- Krestou, A.; Xenidis, A.; Panias, D. Mechanism of aqueous uranium (VI) uptake by hydroxyapatite. Miner. Eng. 2004, 17, 373–381. [Google Scholar] [CrossRef]
- Brendler, V.; Fuchs, L.; Baumann, N. Uranium (VI) Interactions with Hydroxylapatite; Forschungszentrum Rossendorf Annual Report 2005; Institute of Radiochemistry: Dresden, Germany, 2006; pp. 14–15. [Google Scholar]
- Abd El-Naby, H.H.; Dawood, Y.H. Natural attenuation of uranium and formation of autunite at the expense of apatite within an oxidizing environment, southeastern Desert of Egypt. Appl. Geochem. 2008, 23, 3741–3755. [Google Scholar] [CrossRef]
- Lammers, L.N.; Rasmussen, H.; Adilman, D.; deLemos, J.L.; Zeeb, P.; Larson, D.G.; Quicksall, A.N. Groundwater uranium stabilization by a metastable hydroxyapatite. Appl. Geochem. 2017, 84, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Mehta, V.S.; Maillot, F.; Wang, Z.; Catalano, J.G.; Giammar, D.E. Effect of reaction pathway on the extent and mechanism of uranium (VI) immobilization with calcium and phosphate. Environ. Sci. Technol. 2016, 50, 3128–3136. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, Q.; Zhang, G.; Liu, D.; Liu, R. Effect of sodium pyrophosphate on the reverse flotation of dolomite from apatite. Minerals 2018, 8, 278. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Pan, Z.; Giammar, D.; Li, L. Enhanced Uranium Immobilization by Phosphate Amendment under Variable Geochemical and Flow Conditions: Insights from Reactive Transport Modeling. Environ. Sci. Technol. 2018, 52, 5841–5850. [Google Scholar] [CrossRef] [PubMed]
- Borovec, Z.; Kribek, B.; Tolar, V. Sorption of uranyl by humic acids. Chem. Geol. 1979, 27, 39–46. [Google Scholar] [CrossRef]
- Lenhart, J.J.; Cabaniss, S.E.; MacCarthy, P.; Honeyman, B.D. Uranium (VI) complexation with citric, humic and fulvic acids. Radiochim. Acta 2000, 88, 345–354. [Google Scholar] [CrossRef]
- Pompe, S.; Schmeide, K.; Bubner, M.; Geipel, G.; Heise, K.H.; Bernhard, G.; Nitsche, H. Investigation of humic acid complexation behavior with uranyl ions using modified synthetic and natural humic acids. Radiochim. Acta 2000, 88, 553–558. [Google Scholar] [CrossRef]
- Saito, T.; Nagasaki, S.; Tanaka, S. Evaluation of the complexation behavior between humic acid and UO22+ with fluorescence spectroscopy and its mixture analysis. Radiochim. Acta 2002, 90, 27–33. [Google Scholar] [CrossRef]
- Sachs, S.; Brendler, V.; Geipel, G. Uranium (VI) complexation by humic acid under neutral pH conditions studied by laser-induced fluorescence spectroscopy. Radiochim. Acta 2007, 95, 103–110. [Google Scholar] [CrossRef]
- Pompe, S.; Brachmann, A.; Bubner, Μ.; Geipel, G.; Heise, Κ.H.; Bernhard, G.; Nitsche, H. Determination and Comparison of Uranyl Complexation Constants with Natural and Model Humic Acids. Radiochim. Acta 1998, 89–96. [Google Scholar] [CrossRef]
- Tran, E.L.; Teutsch, N.; Klein-BenDavid, O.; Kersting, A.B.; Zavrin, M.; Weisbrod, N. Radionuclide transport in brackish water through chalk fractures. Water Res. 2019, 163, 114886. [Google Scholar] [CrossRef]
- Schmeide, K.; Fritsch, K.; Lippold, H. Retention of Radionuclides Relevant for Final Disposal in Natural Clay Rock and Saline Systems; Subproject 2. Geochemical Behavior and Transport of Radionuclides in Saline Systems in the Presence of Repository-Relevant Organics, Final Report; Institut für Kernchemie, Johannes Gutenberg-Universität Mainz: Mainz, Germany, 2016; pp. 1–169. [Google Scholar]
- Poulton, S.W.; Canfield, D.E. Development of a sequential extraction procedure for iron: Implications for iron partitioning in continentally derived particulates. Chem. Geol. 2005, 214, 209–221. [Google Scholar] [CrossRef]
- Roshan, H.; Al-Yaseri, A.Z.; Sarmadivaleh, M.; Iglauer, S. On Wettability of Shale Rocks. J. Colloid Interf. Sci. 2016, 475, 104–111. [Google Scholar] [CrossRef]
- Larson, T.E.; Heikoop, J.M.; Perkins, G.; Chipera, S.J.; Hess, M.A. Pretreatment technique for siderite removal for organic carbon isotope and C:N ratio analysis in geological samples. Rapid Commun. Mass Spectrom 2008, 22, 865–872. [Google Scholar] [CrossRef] [PubMed]
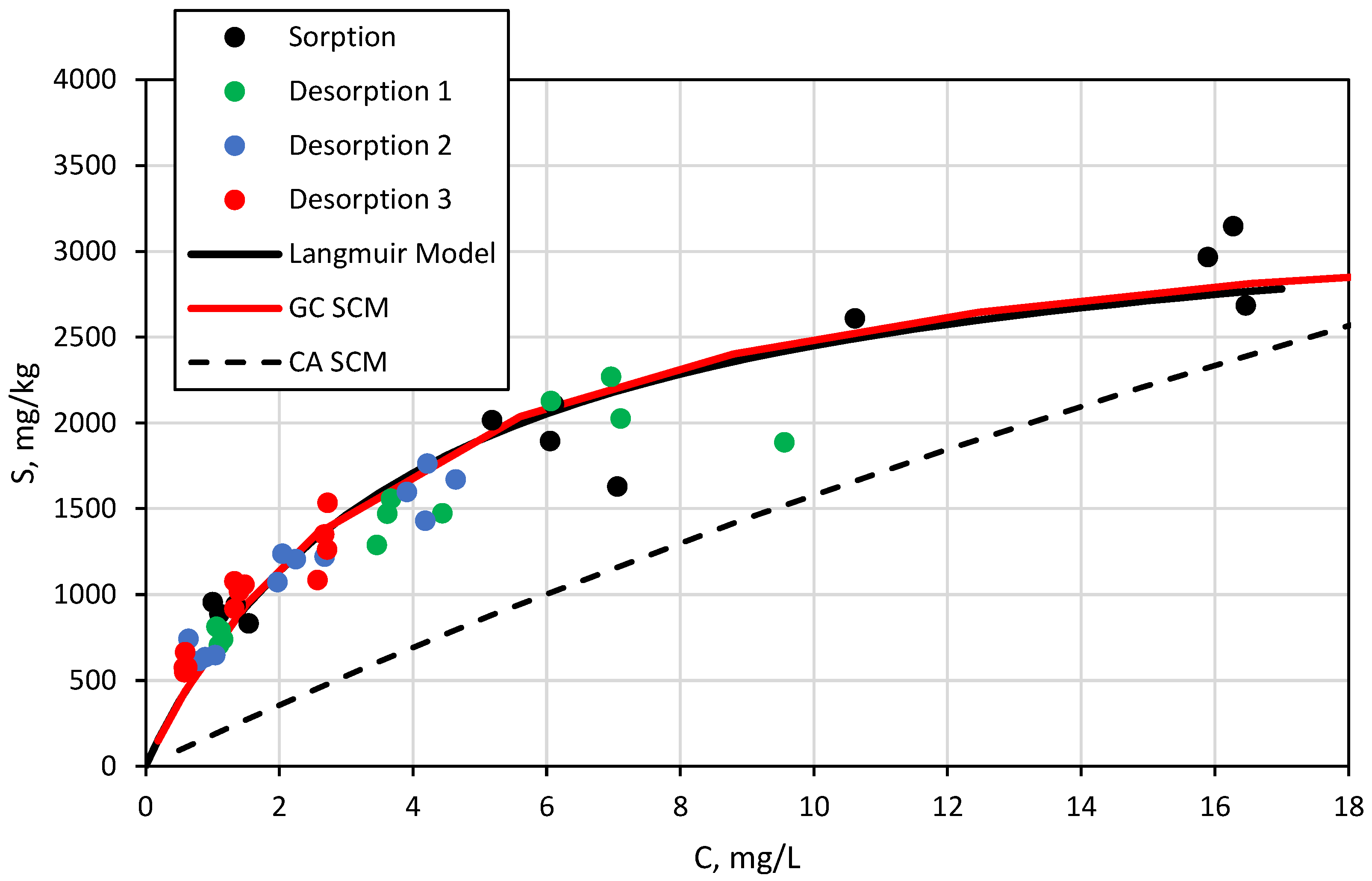
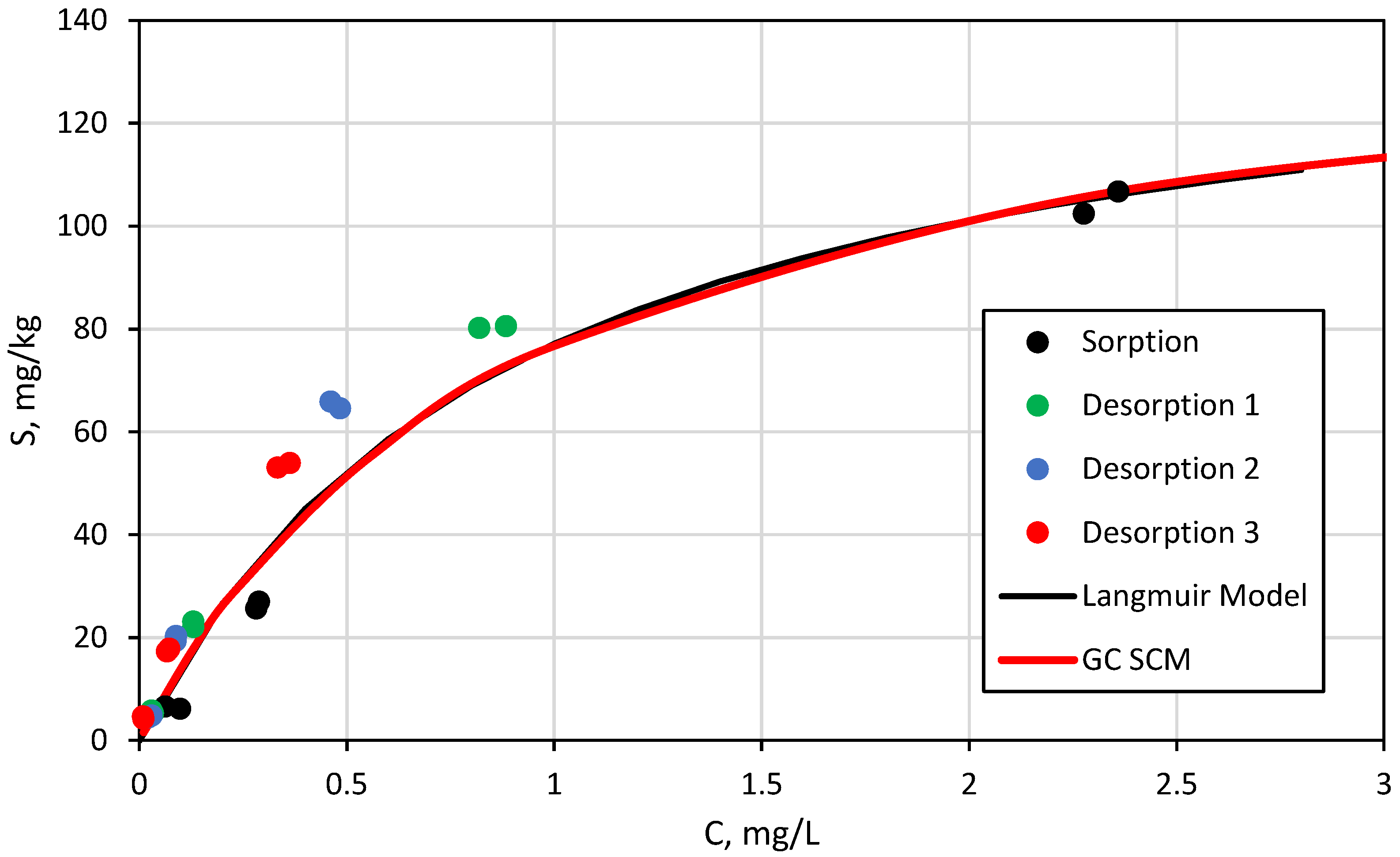

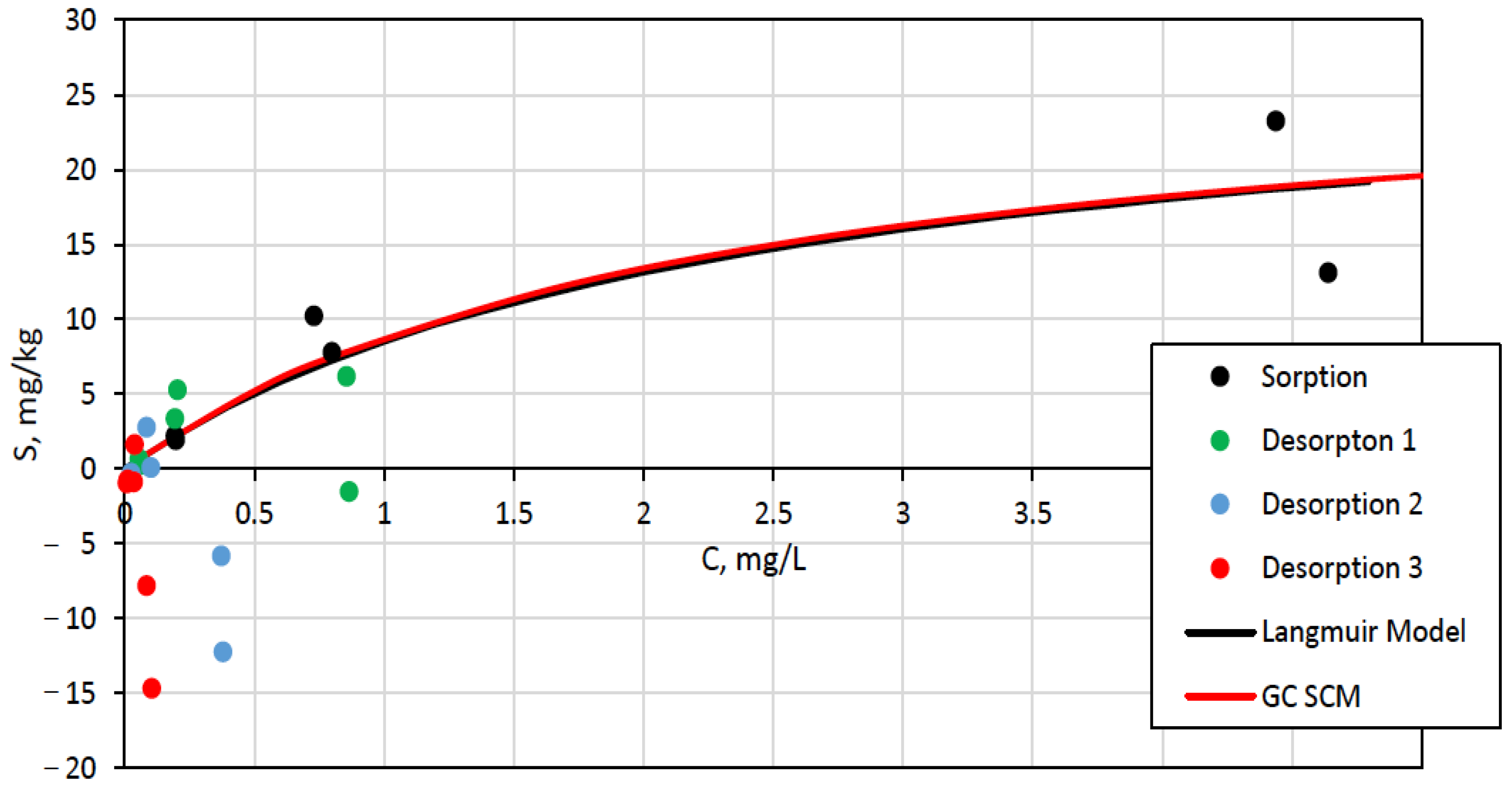

| Ionic Species | SSW | Post Equilibration | |||
|---|---|---|---|---|---|
| (mg/L) | Composition | HOP-5 | OS-3 | SS-10 | CK-6 |
| Ba | 0.01 | 0.12 | 0.029 | 0.23 | 0.08 |
| Ca | 36.0 | 35.1 | 59.0 | 34.1 | 26.5 |
| Cr | ND | 0.002 | 0.003 | 0.003 | 0.003 |
| Fe | 0.013 | ND | ND | ND | ND |
| K | 9.1 | 10.7 | 9.5 | 8.6 | 8.9 |
| Mg | 12.0 | 12.4 | 17.2 | 11.0 | 12.2 |
| Mn | ND | ND | ND | ND | ND |
| Na | 73.0 | 90.7 | 90.2 | 91.5 | 110.3 |
| Si | 20.8 | 25.0 | 28.2 | 20.5 | 20.1 |
| Sr | 0.0 | 1.23 | 0.88 | 2.69 | 0.24 |
| Zn | ND | 0.032 | 0.036 | 0.036 | 0.034 |
| Br | 0.0 | 0.013 | 0.020 | 0.015 | 0.011 |
| Cl | 117.6 | 172.5 | 154.4 | 141.5 | 157.0 |
| F | ND | 0.28 | 0.32 | 0.76 | 0.50 |
| NO3 | 32.9 | 37.8 | 32.8 | 34.1 | 32.5 |
| PO4 | ND | ND | ND | ND | ND |
| SO42− | 52.8 | 114.0 | 164.9 | 75.0 | 89.9 |
| Alkalinity | 149 | 126–138 | 136 | 135 | 131 |
| pH | 7.6–8.1 | 7.7–7.9 | 7.6 | 7.9 | 7.7 |
| Uranium Species% | HOP-5 | OS-3 | SS-10 | CK-6 |
|---|---|---|---|---|
| CaUO2(CO3)3−2 | 60.1 | 50.0 | 59.0 | 62.9 |
| Ca2UO2(CO3)3 | 35.2 | 47.6 | 37.9 | 32.3 |
| MgUO2(CO3)3−2 | 2.4 | 1.2 | 1.7 | 2.5 |
| UO2(CO3)3−4 | 1.2 | 0.5 | 0.9 | 1.3 |
| UO2(CO3)2−2 | 1.0 | 0.3 | 0.6 | 0.9 |
| Sum | 99.9 | 99.6 | 100.1 | 99.9 |
| Schoepite (S.I.) | −2.44 | −4.15 | −3.90 | −3.68 |
| UO3 (S.I.) | −4.20 | −5.91 | −5.70 | −5.44 |
| Modal Mineralogy qXRD, wt.% | Phosphorite HOP-5 | Bit. Marl OS-3 | Sandstone SS-10 | Chalk CK-6 |
|---|---|---|---|---|
| Quartz | 3.0 | 2.7 | 74.7 | 0.7 |
| K-Feldspar | -- | 10.5 | 5.8 | -- |
| Plagioclase | -- | 13.7 | 2.6 | -- |
| Apatite | 76.8 | 7.6 | -- | -- |
| Pyrite | -- | -- | 0.2 | -- |
| Calcite | 13.9 | 44.6 | 16.2 | 83.2 |
| Dolomite | 6.3 | 3.3 | -- | 0.6 |
| Clay Fraction | -- | 17.1 | -- | 14.7 |
| LOI | 1.61 | 11.2 | 0.07 | 0.11 |
| TOC (wt.%) | 2.0 | 11.0 | tr | tr |
| BET (m2/g) | 18.9 | 9.83 | 4.13 | 5.49 |
| Select XRF Data | ||||
| Fe2O3 % | 0.16 | 0.68 | 1.82 | 0.67 |
| P2O5 % | 29.22 | 2.67 | 0.22 | 0.41 |
| CaO % | 52.7 | 36.1 | 15.7 | 50.3 |
| SiO2 % | 5.11 | 11.8 | 63.8 | 4.3 |
| Rock Type | GC SCM | Langmuir Isotherm | ||
|---|---|---|---|---|
| Log (β) | [XOH] mg/kg Rock | KL L/kg | Smax mg/kg Rock | |
| HOP-5 | 5.85 | 3332 | 0.183 | 3610 |
| OS-3 | 6.40 | 145.5 | 1.106 | 146.8 |
| CK-6 | 6.34 | 59.1 | 0.589 | 62.9 |
| SS-10 | 6.21 | 28.5 | 0.421 | 28.7 |
| Adsorbing Phase | GC SCM [XOH] mg/kg/Mass Frac | GC SCM log (β) Mass Fraction | Langmuir Smax mg/kg/Mass Frac | Langmuir KL L/kg/Mass Frac |
|---|---|---|---|---|
| Apatite | 4335 | 5.85 | 4697 | 0.183 |
| Fe2O3 | 1566 | 6.21 | 1574 | 0.421 |
| Clay | 331 | 6.35 | 356 | 0.597 |
| Org. Carbon | 1467 | 6.40 | 1480 | 1.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dangelmayr, M.A.; Bussod, G.Y.; Reimus, P.W.; WoldeGabriel, G.; Calvo, R.; Harris, R.J.; Stauffer, P.H.; Boukhalfa, H.; Klein-BenDavid, O.; Balaban, N.; et al. Uranium Retardation Capacity of Lithologies from the Negev Desert, Israel—Rock Characterization and Sorption Experiments. Minerals 2022, 12, 728. https://doi.org/10.3390/min12060728
Dangelmayr MA, Bussod GY, Reimus PW, WoldeGabriel G, Calvo R, Harris RJ, Stauffer PH, Boukhalfa H, Klein-BenDavid O, Balaban N, et al. Uranium Retardation Capacity of Lithologies from the Negev Desert, Israel—Rock Characterization and Sorption Experiments. Minerals. 2022; 12(6):728. https://doi.org/10.3390/min12060728
Chicago/Turabian StyleDangelmayr, Martin A., Gilles Y. Bussod, Paul W. Reimus, Giday WoldeGabriel, Ran Calvo, Rose J. Harris, Philip H. Stauffer, Hakim Boukhalfa, Ofra Klein-BenDavid, Noa Balaban, and et al. 2022. "Uranium Retardation Capacity of Lithologies from the Negev Desert, Israel—Rock Characterization and Sorption Experiments" Minerals 12, no. 6: 728. https://doi.org/10.3390/min12060728
APA StyleDangelmayr, M. A., Bussod, G. Y., Reimus, P. W., WoldeGabriel, G., Calvo, R., Harris, R. J., Stauffer, P. H., Boukhalfa, H., Klein-BenDavid, O., Balaban, N., & Rosenzweig, R. (2022). Uranium Retardation Capacity of Lithologies from the Negev Desert, Israel—Rock Characterization and Sorption Experiments. Minerals, 12(6), 728. https://doi.org/10.3390/min12060728







