Three-Dimensional Magnetotelluric Inversion for Triaxial Anisotropic Medium in Data Space
Abstract
:1. Introduction
2. Basic Theory
2.1. 3-D Magnetotelluric Forward Modeling with a Secondary Field Formulation
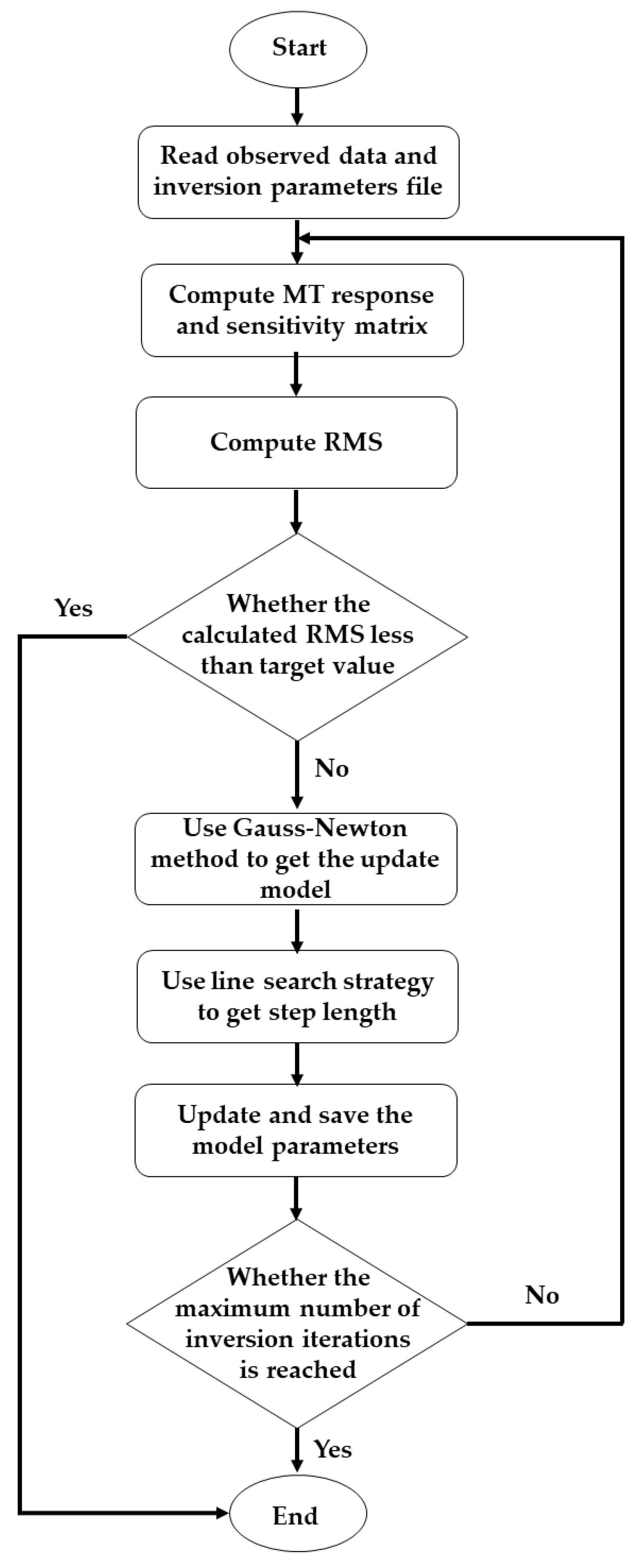
2.2. Data-Space Inversion Theory for Triaxial Anisotropic Medium
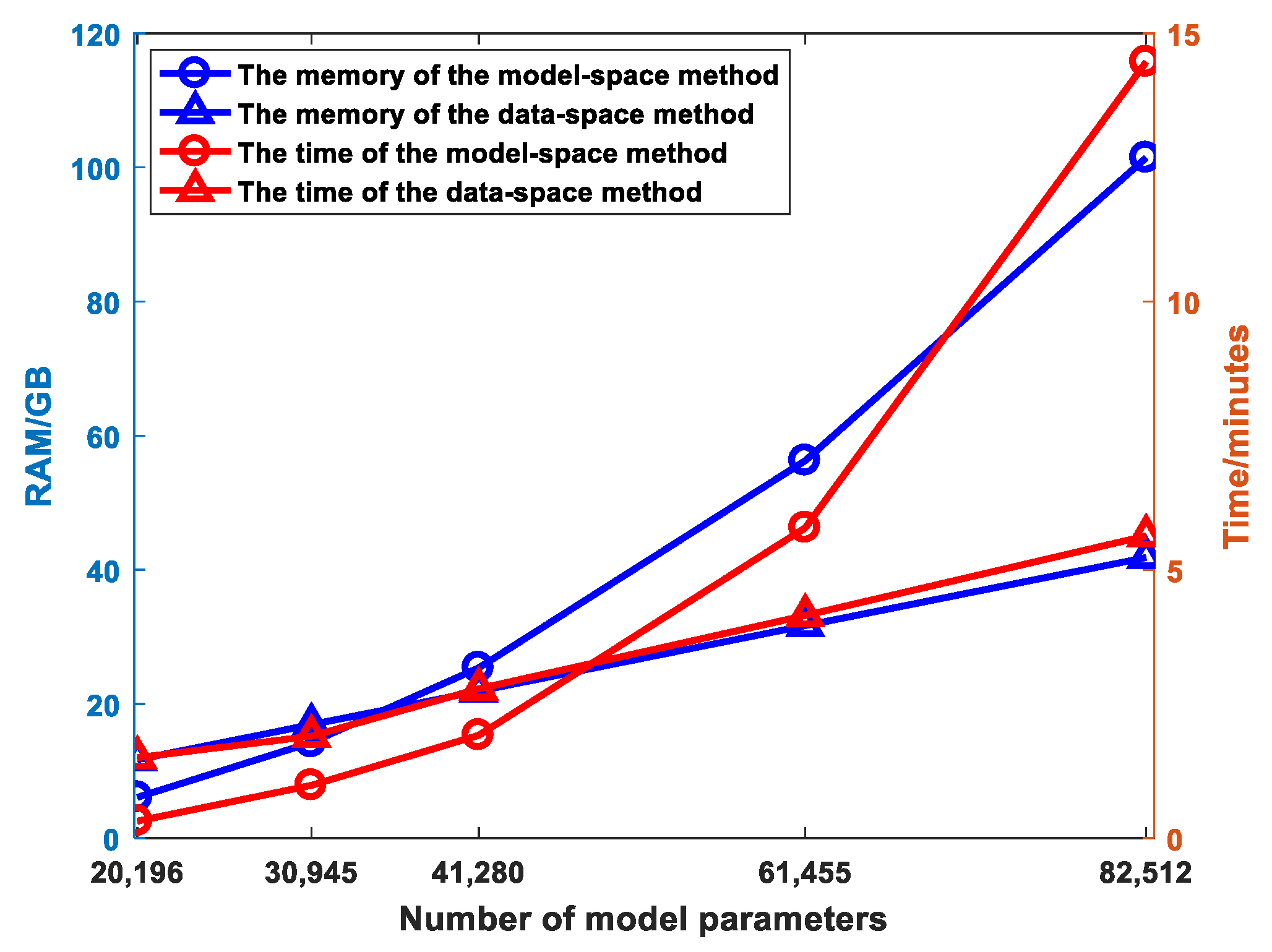
3. Synthetic Model Studies
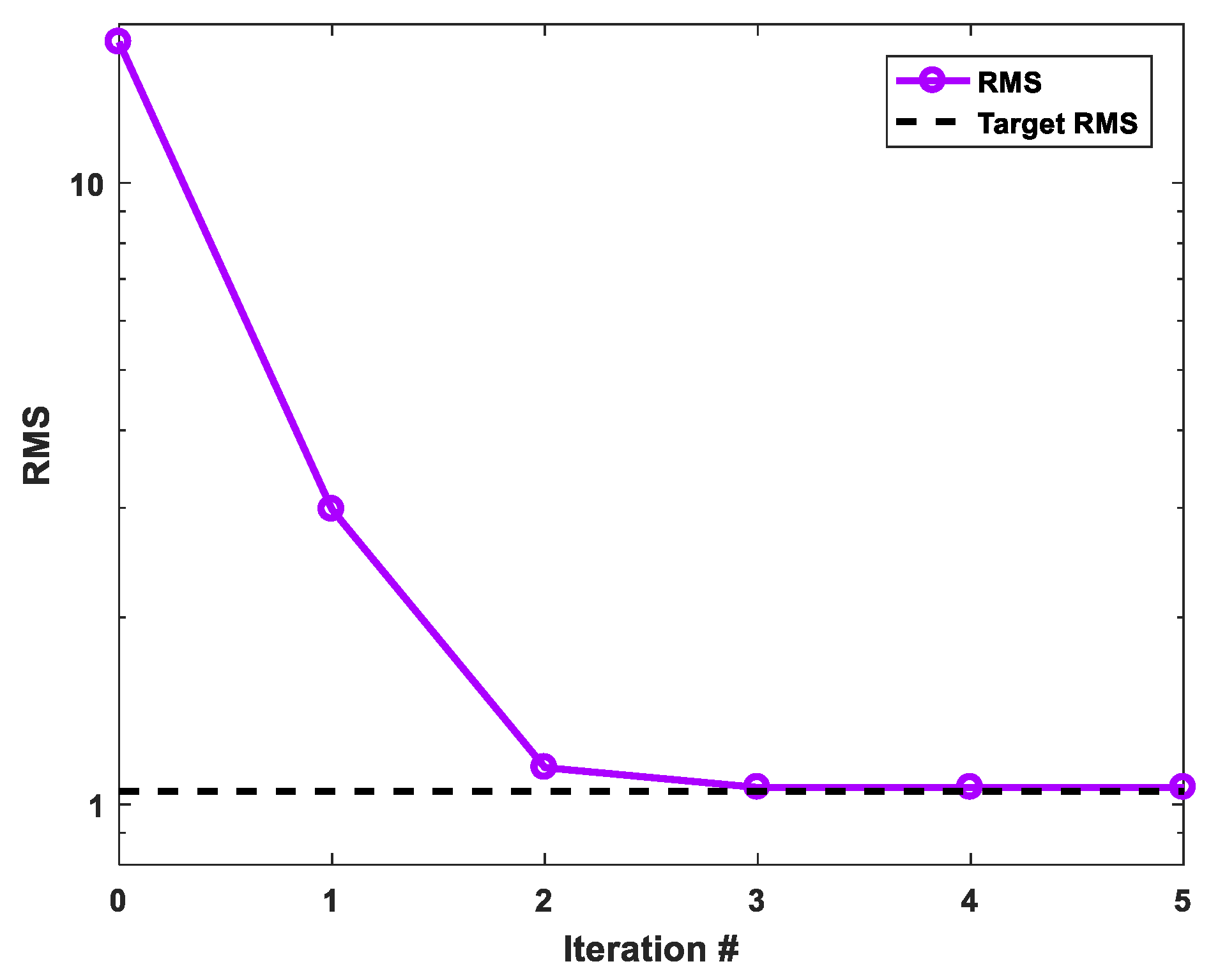
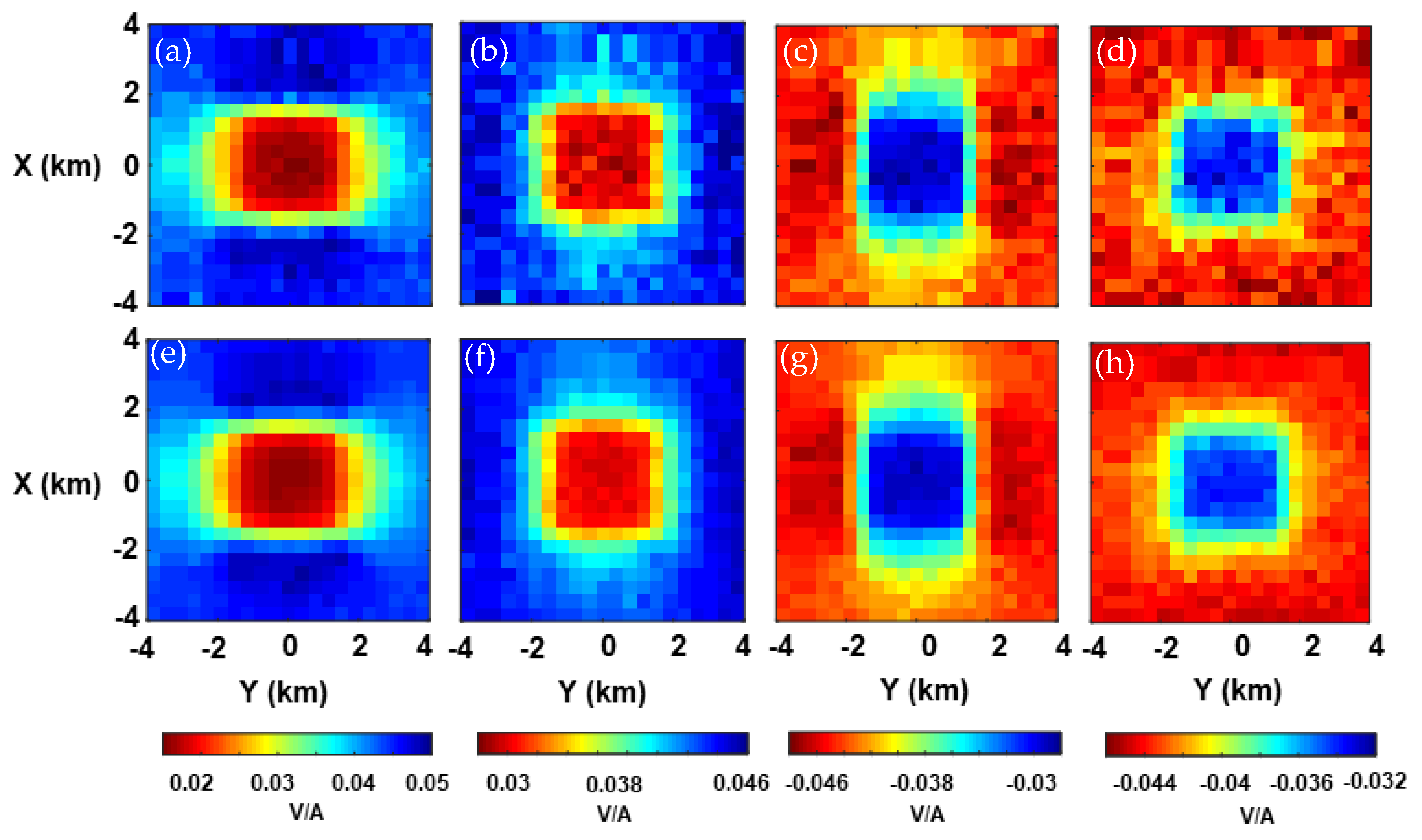
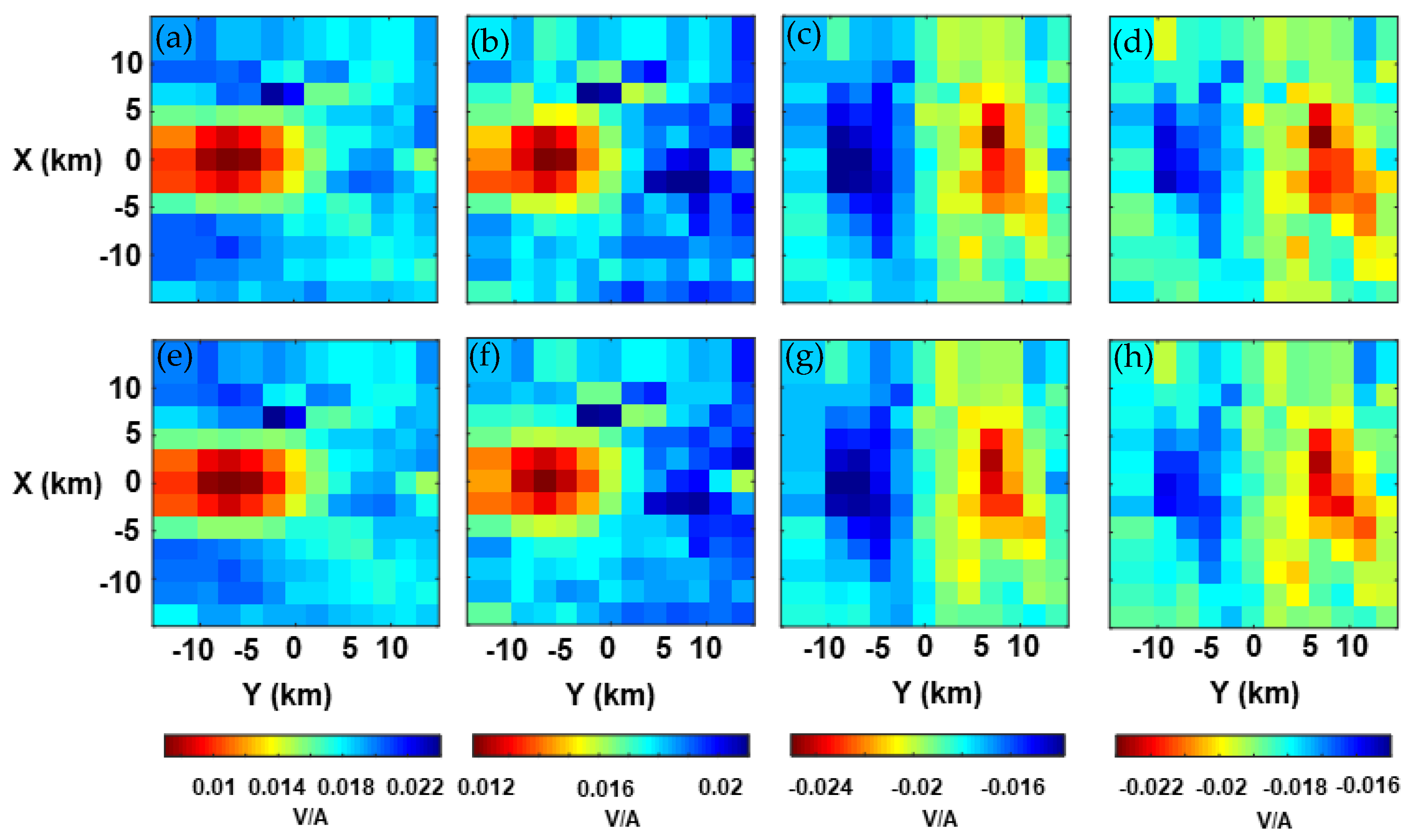
3.1. Algorithm Validation
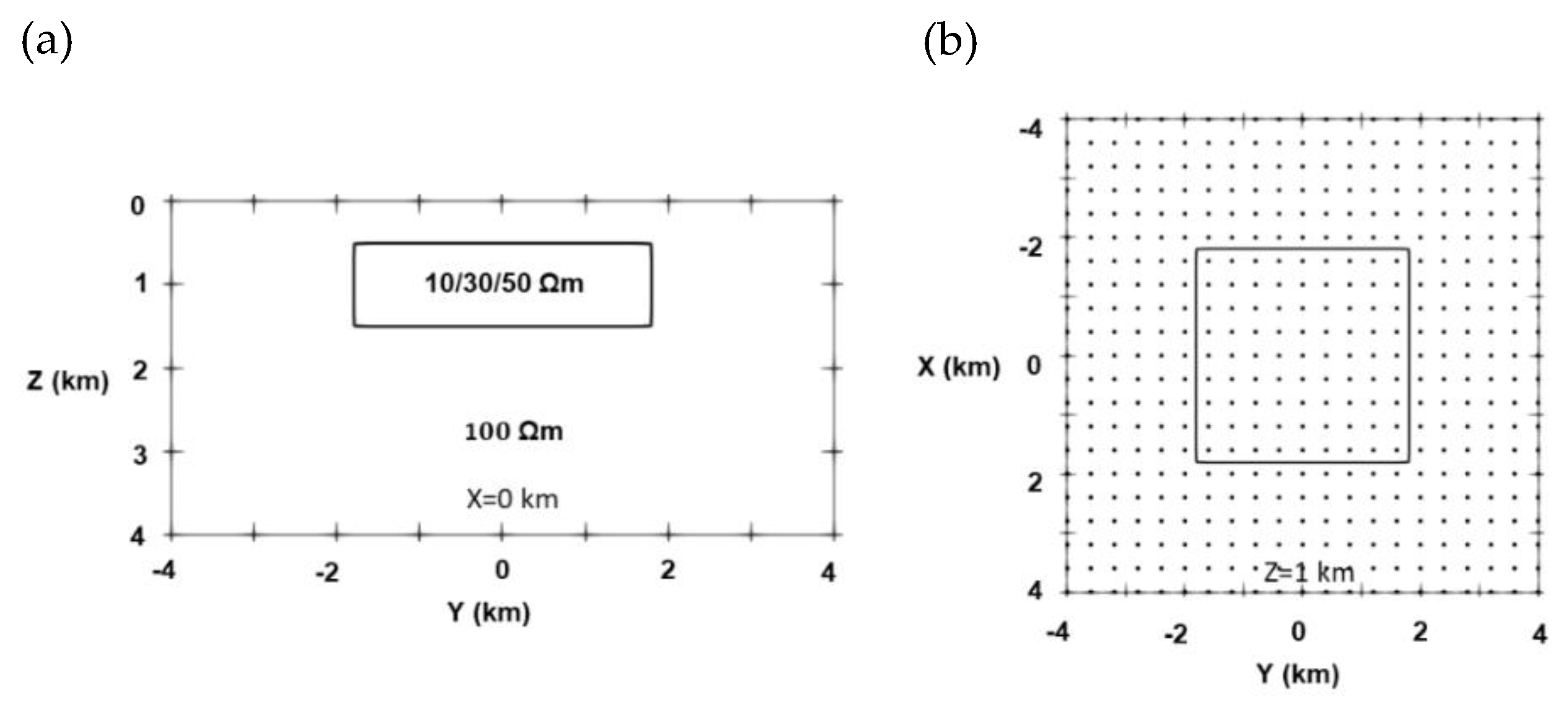
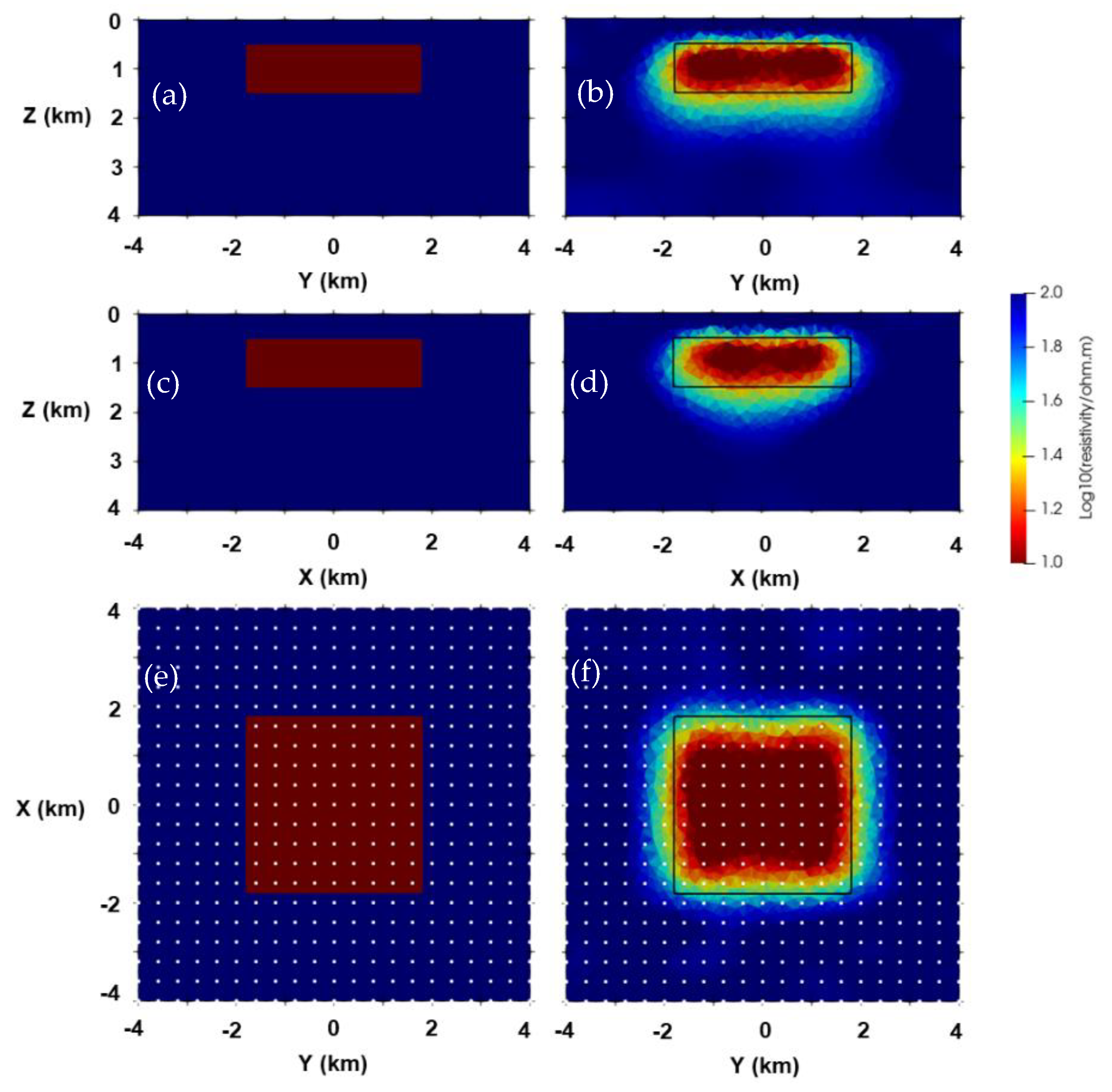
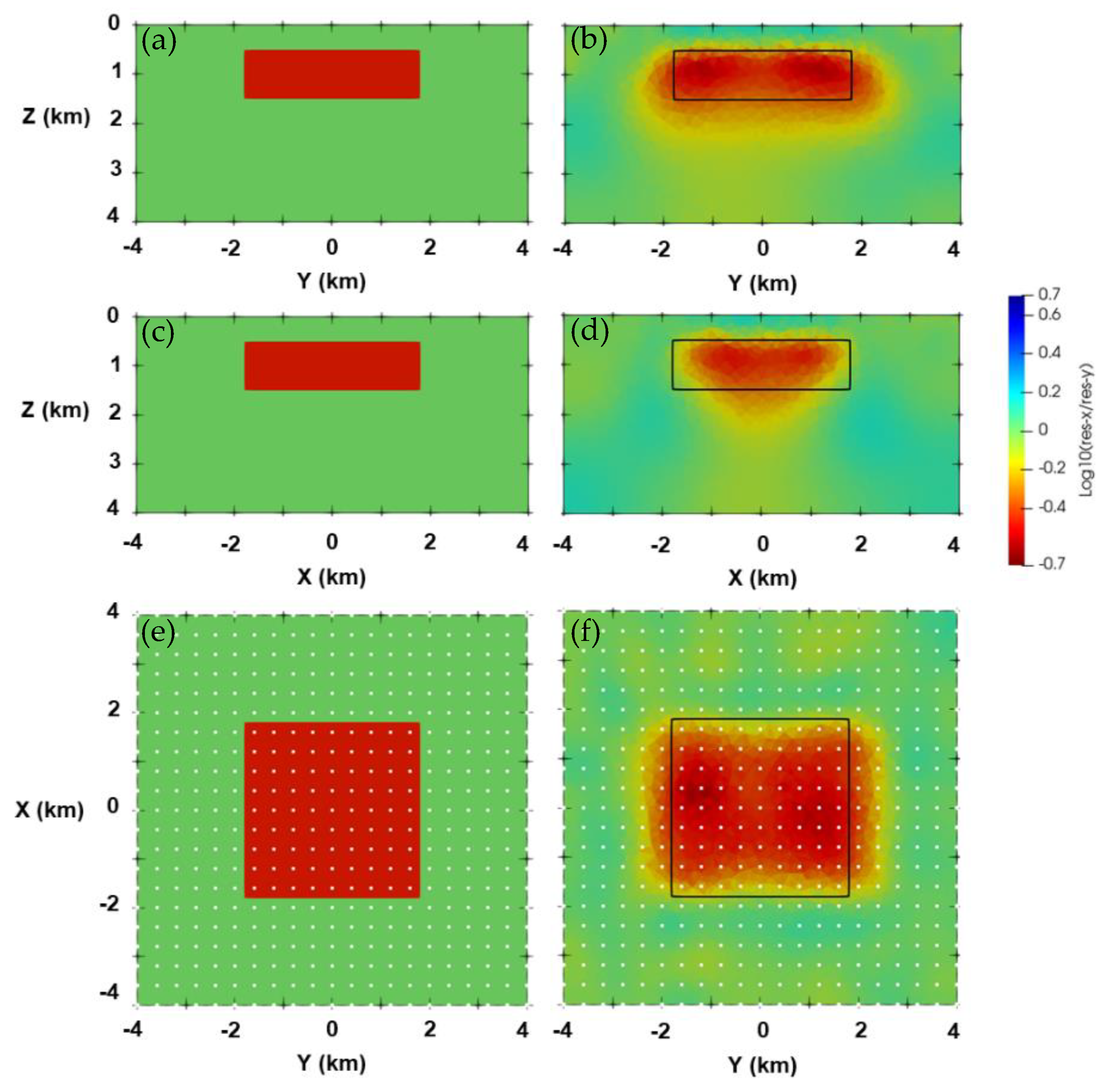
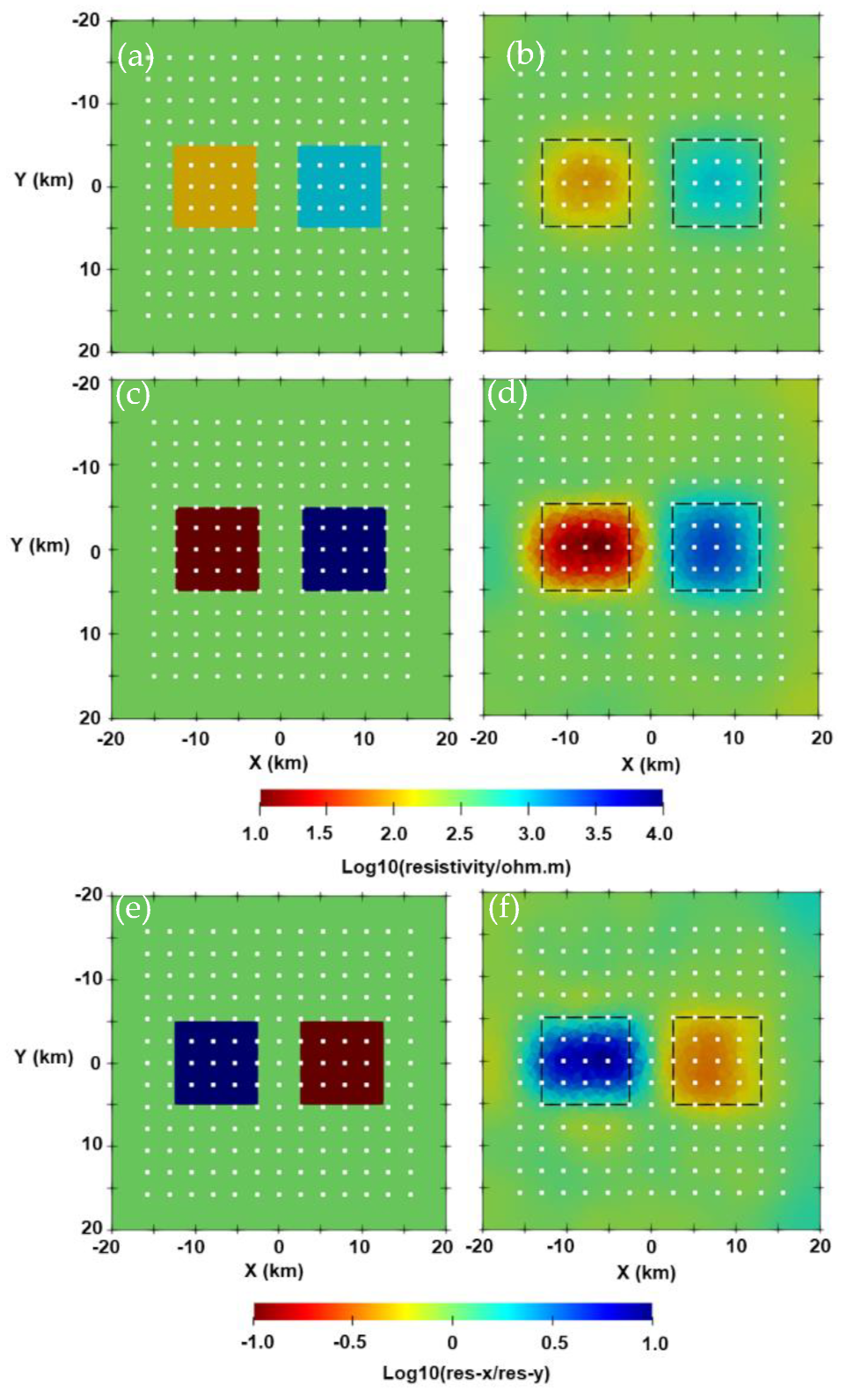
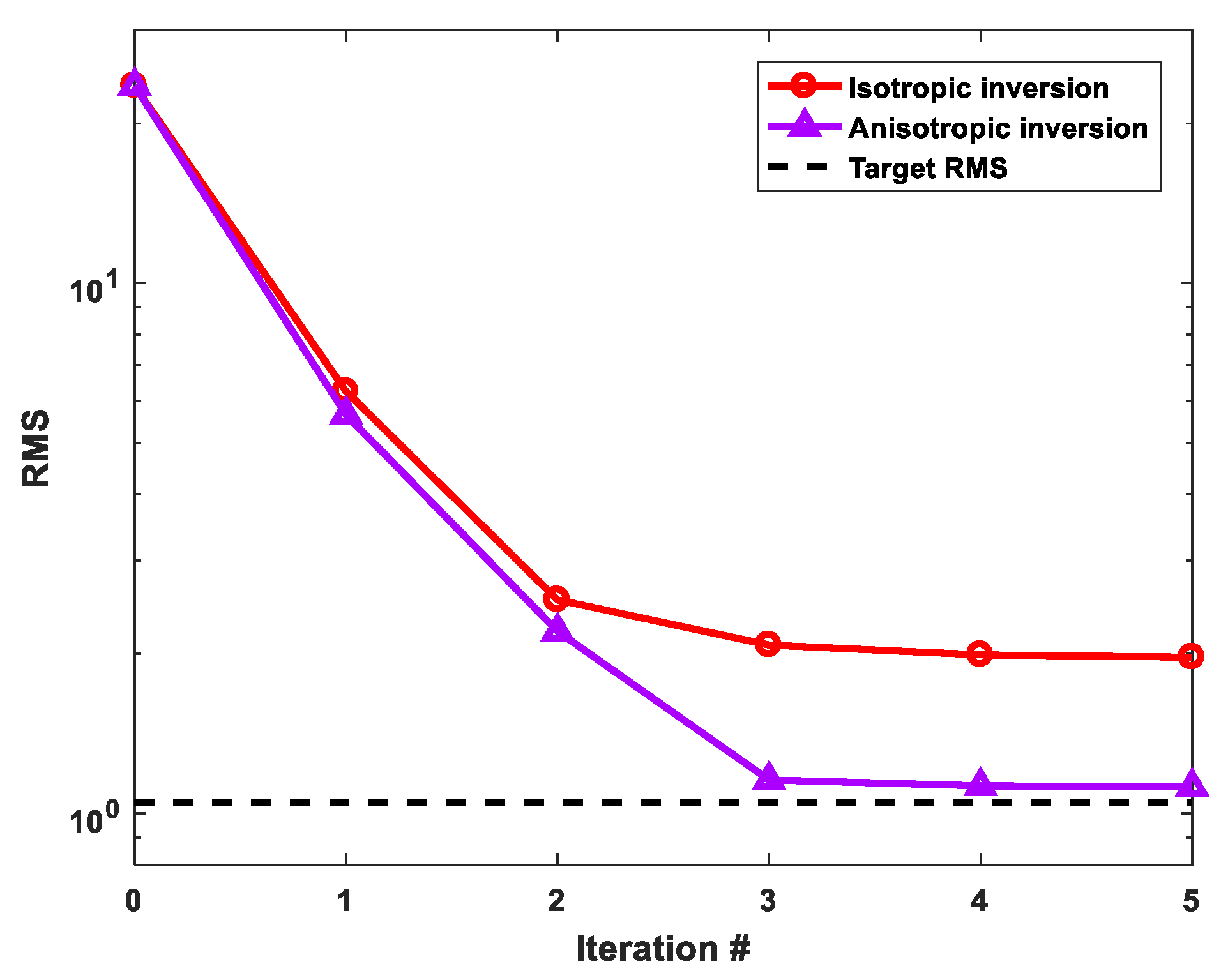
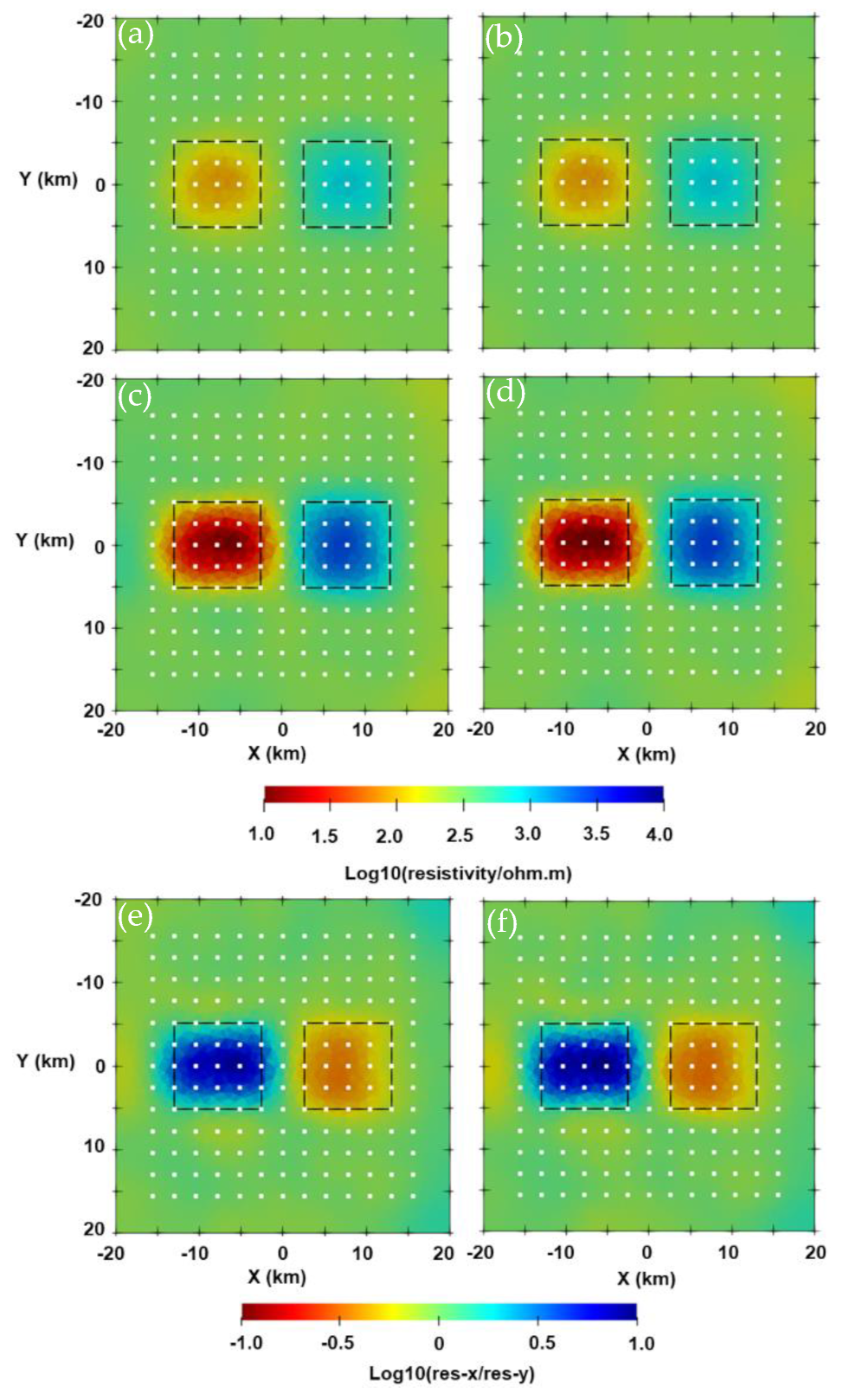
3.2. Two-Blocks Model
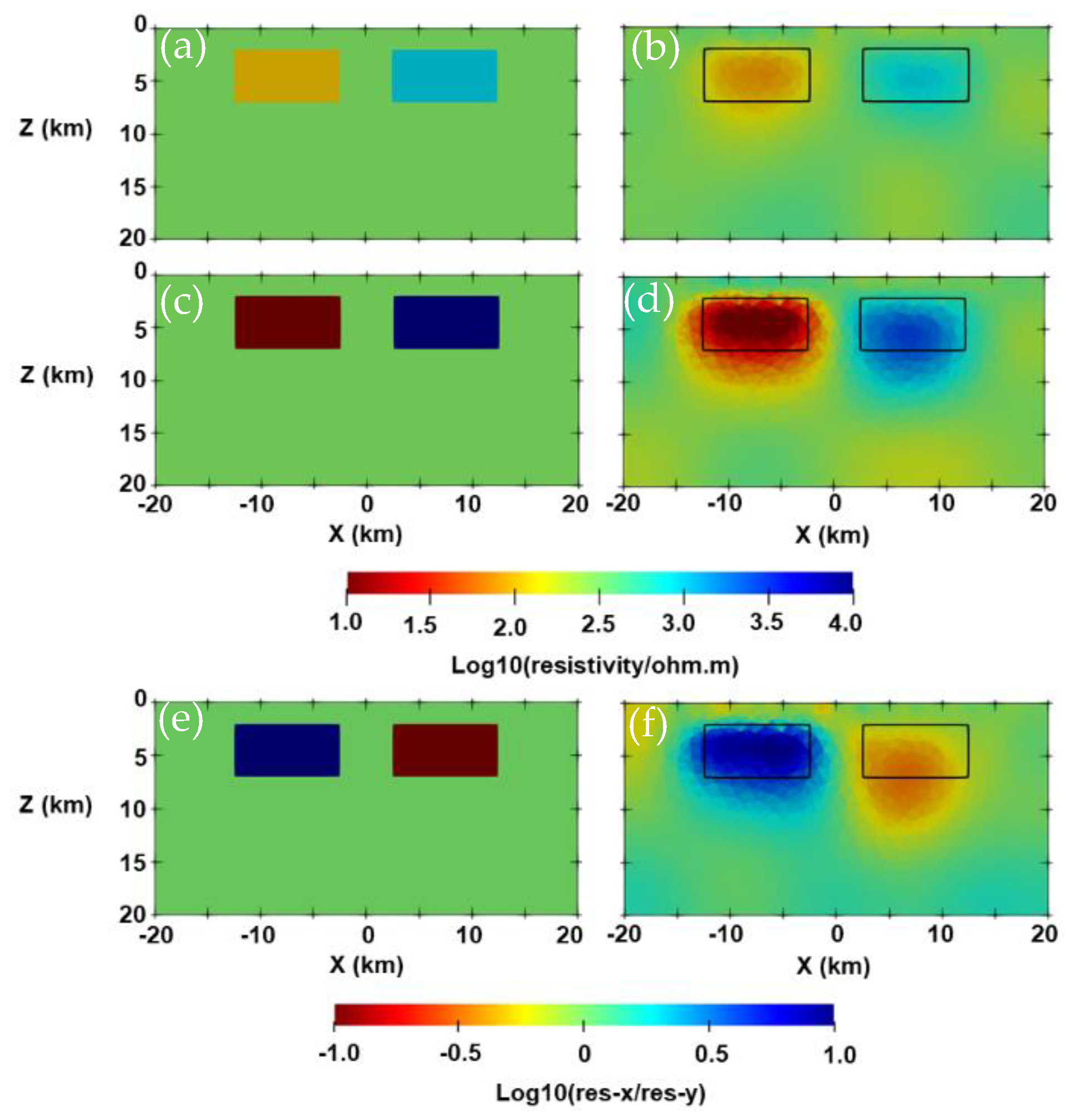
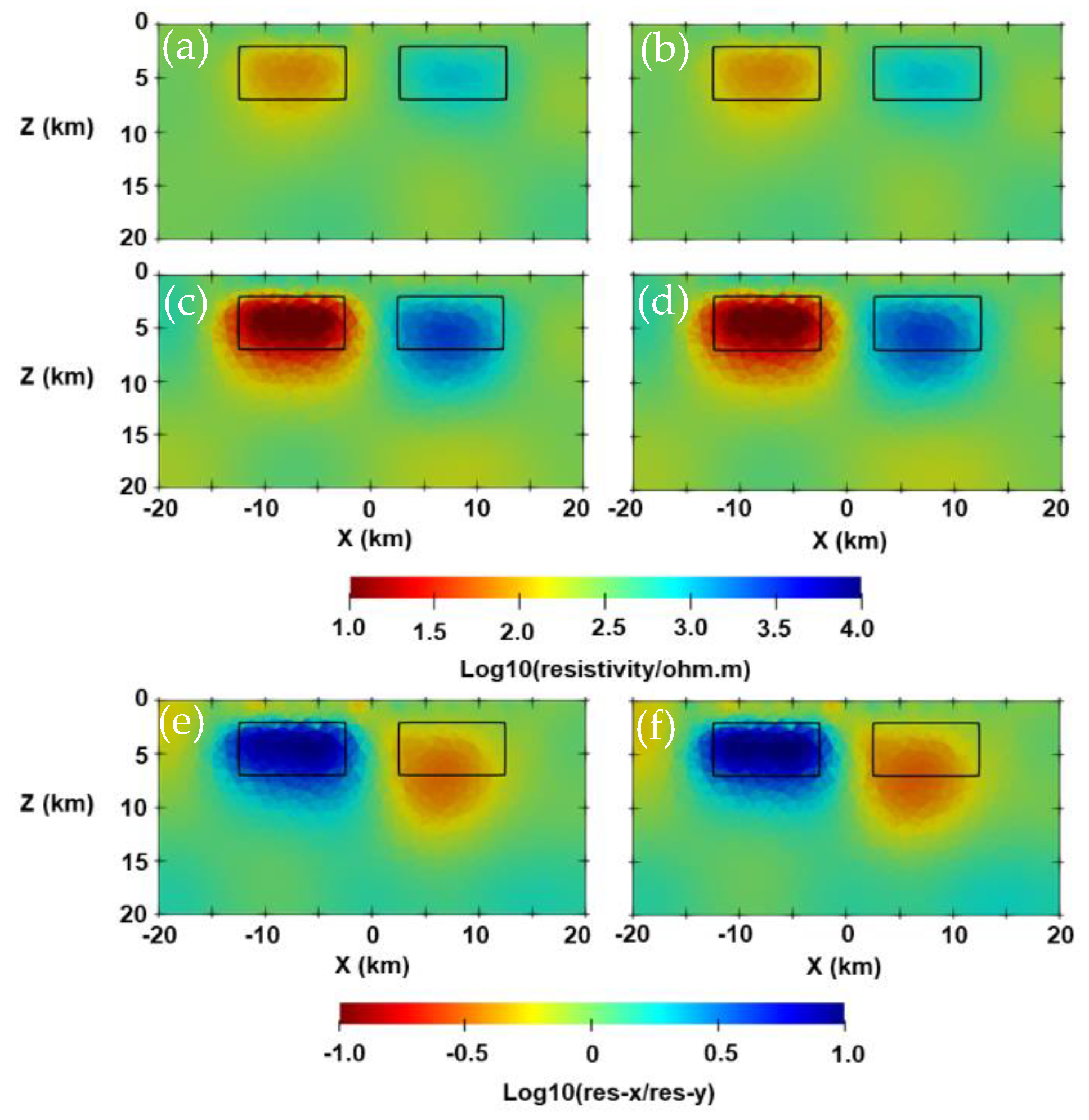
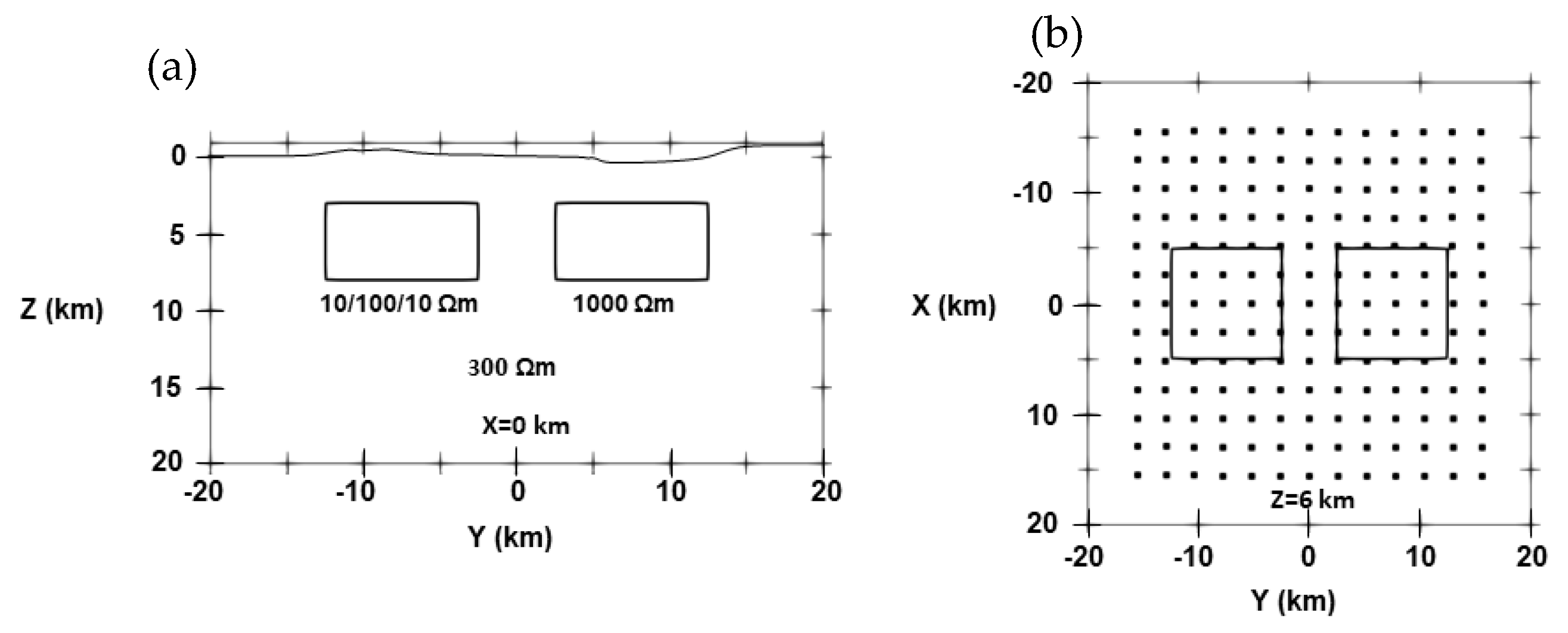
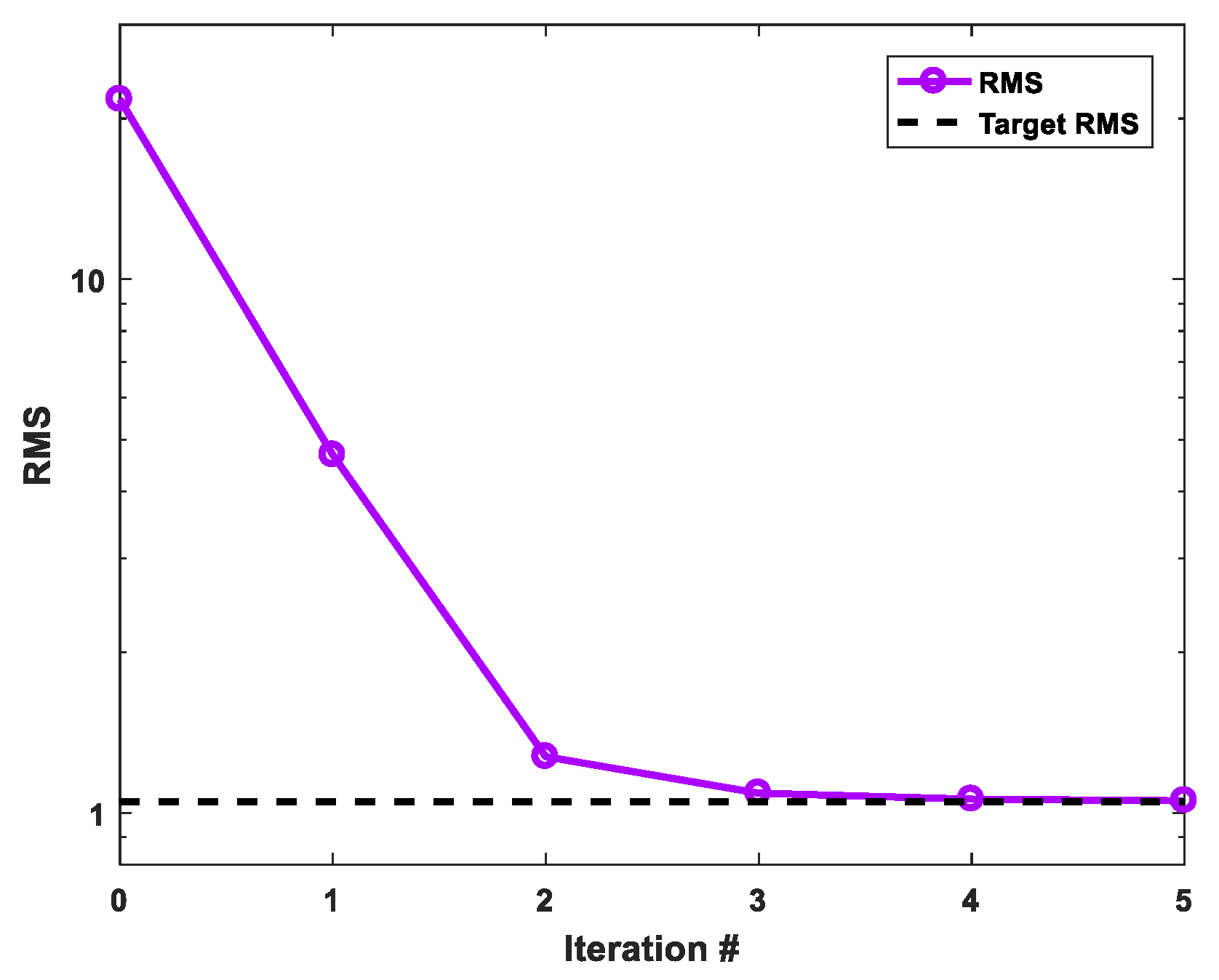
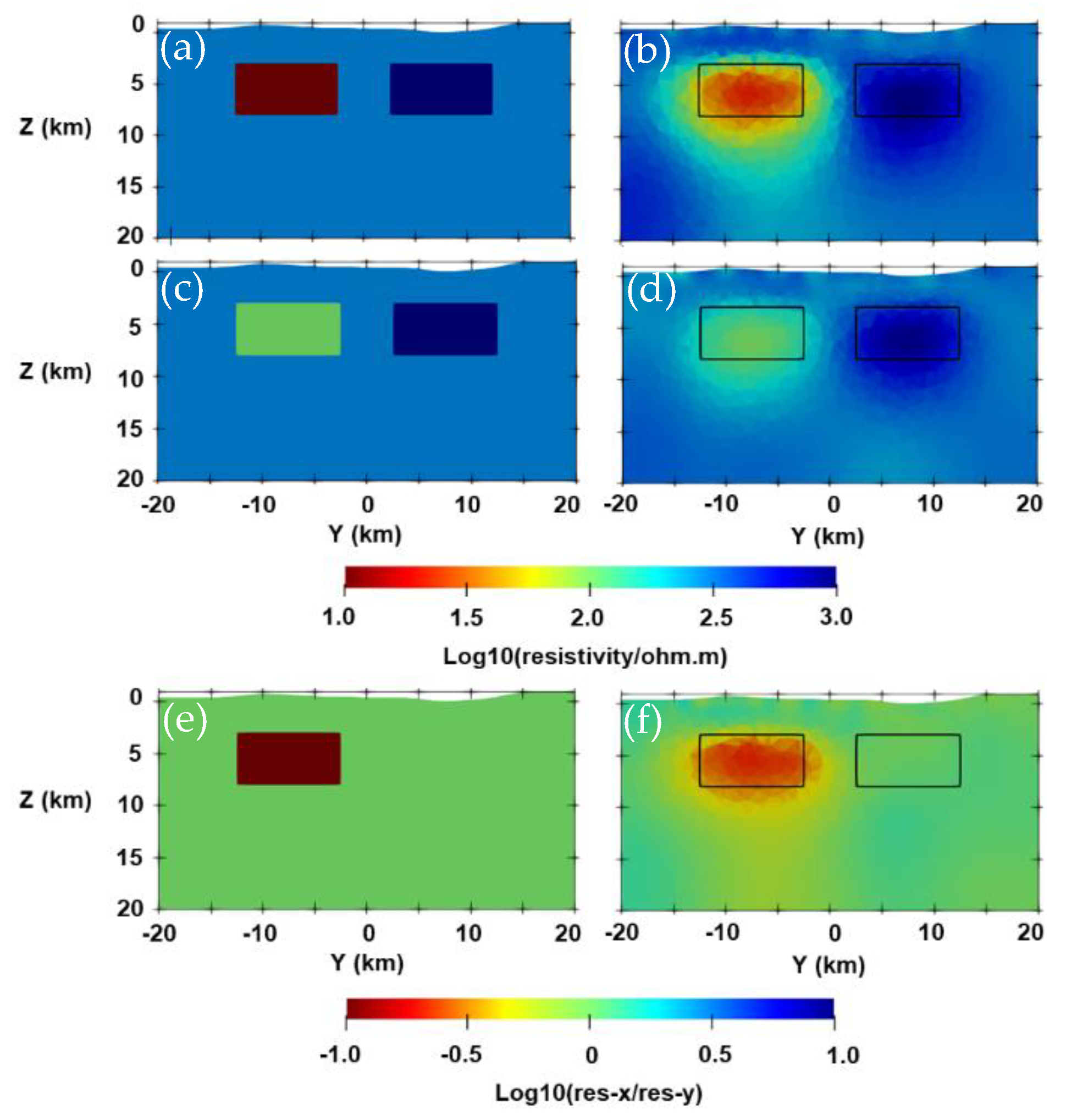
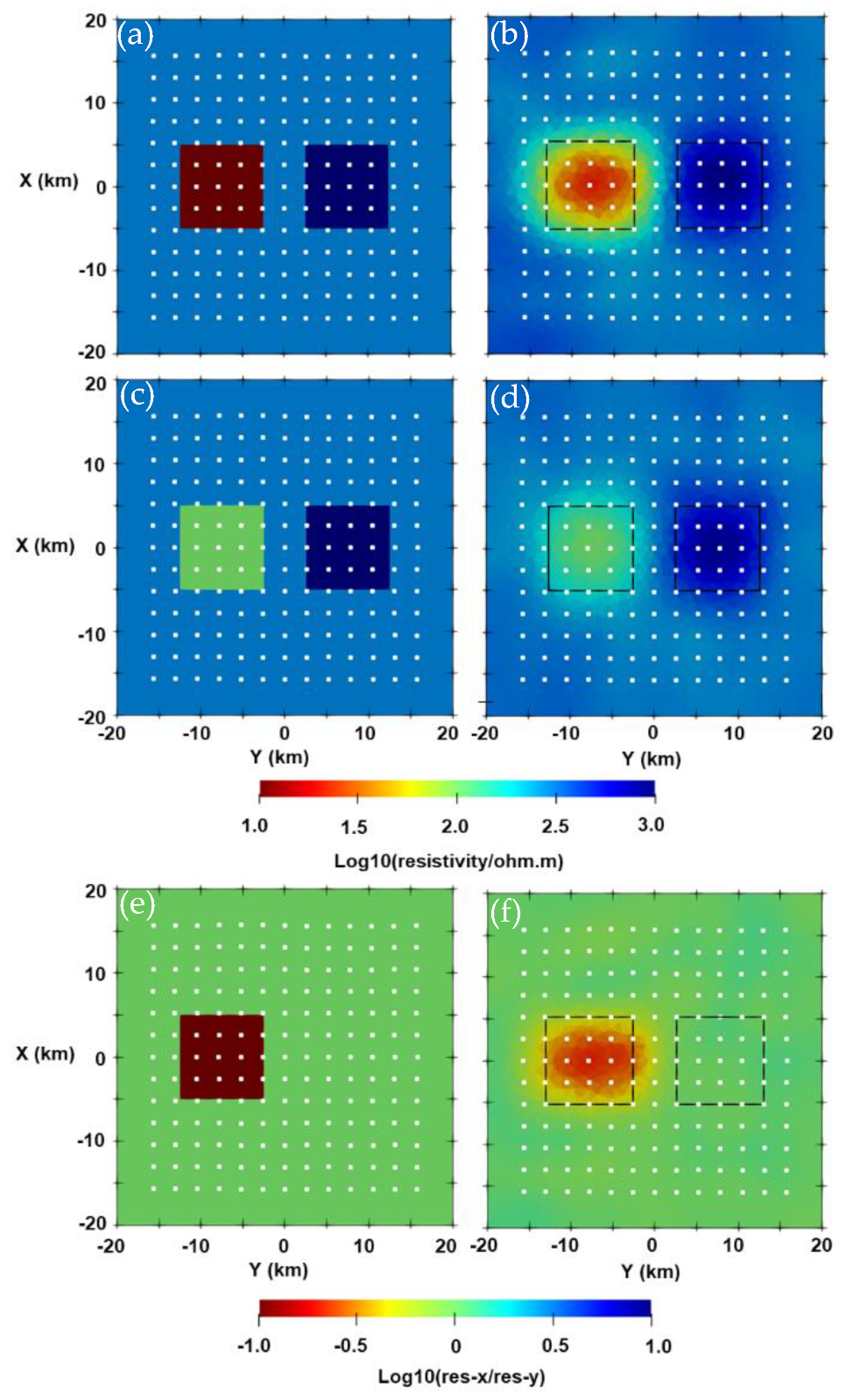
3.3. Isotropic and Anisotropic Blocks Model with Topography
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
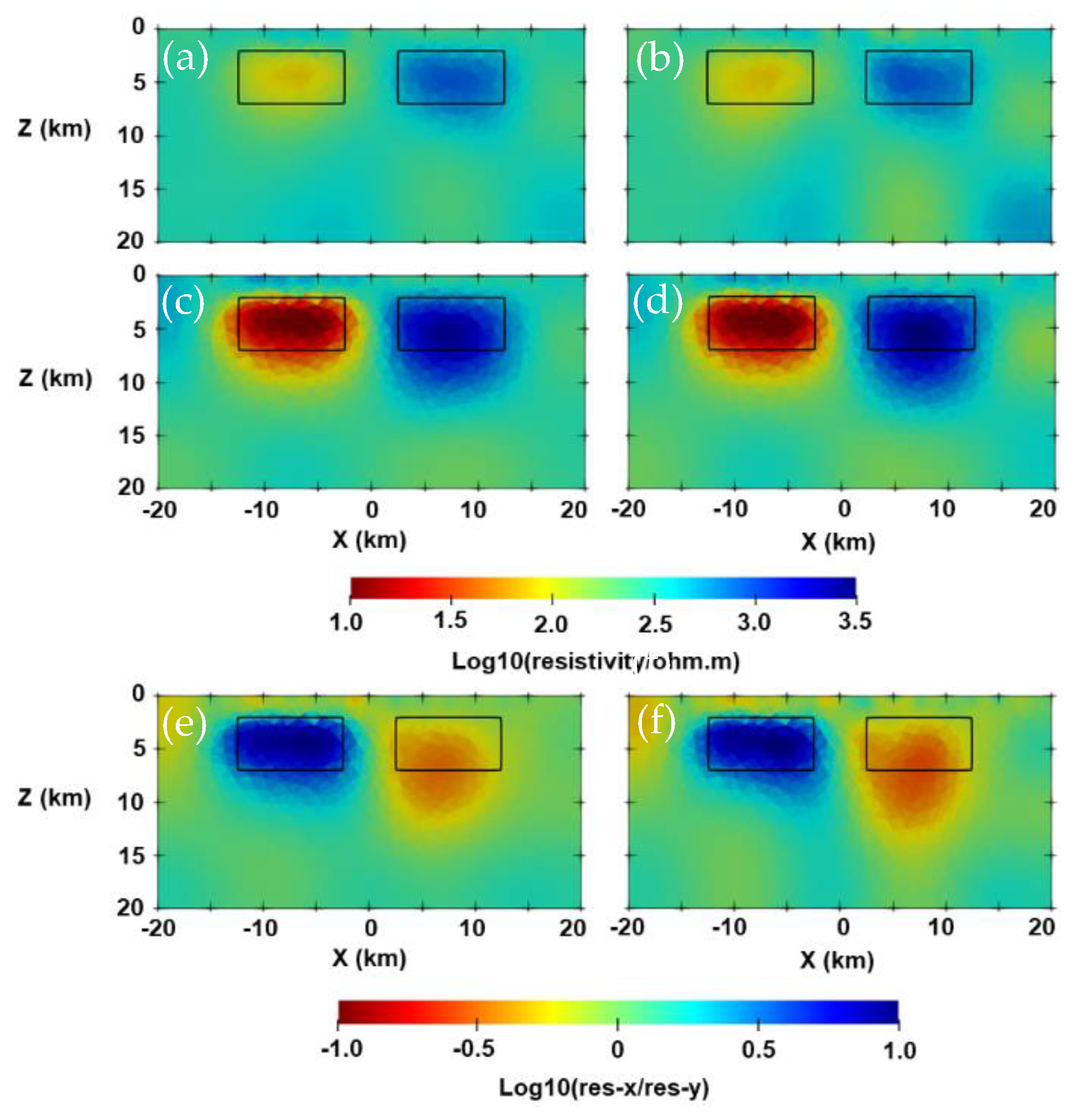
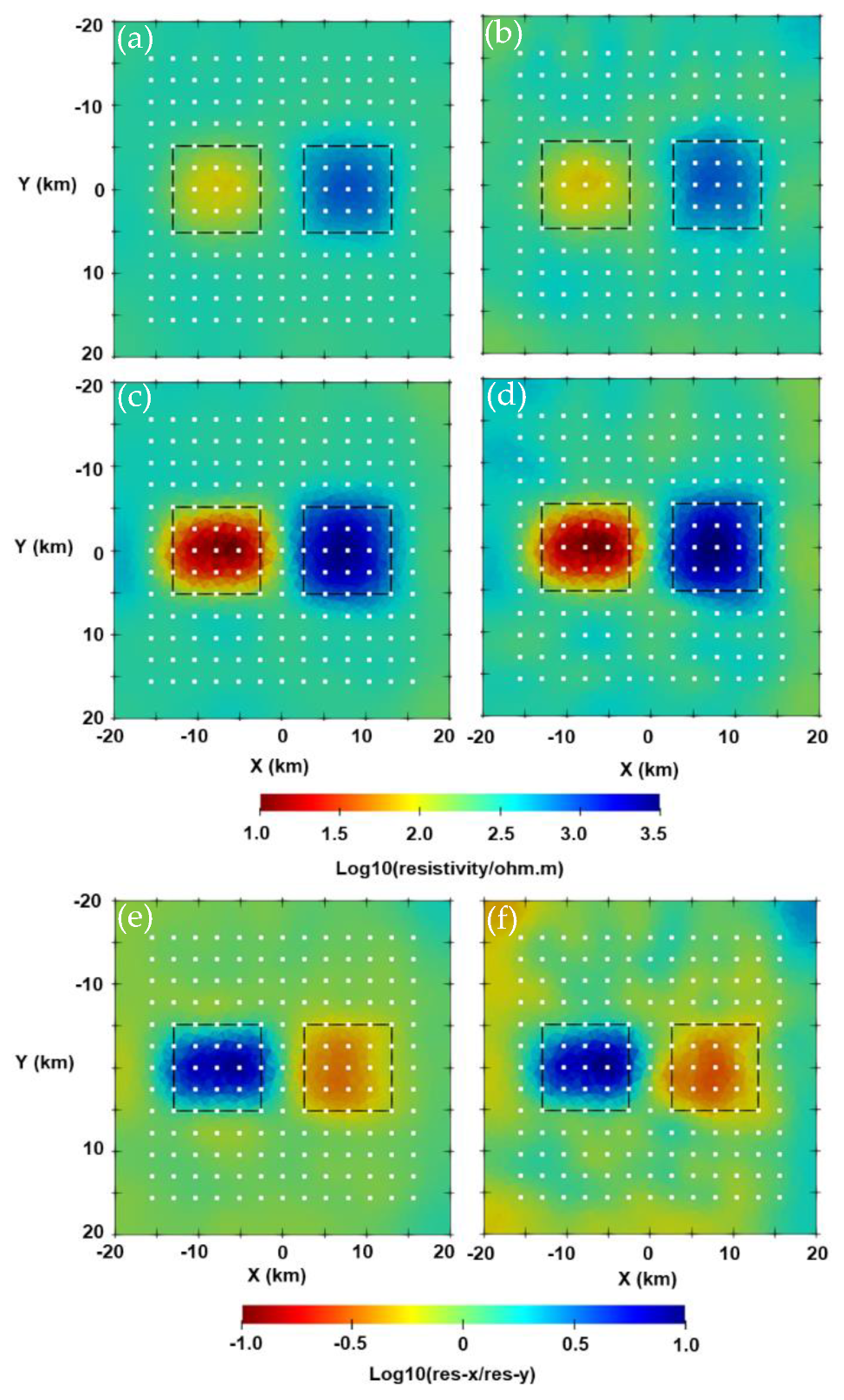
Appendix B
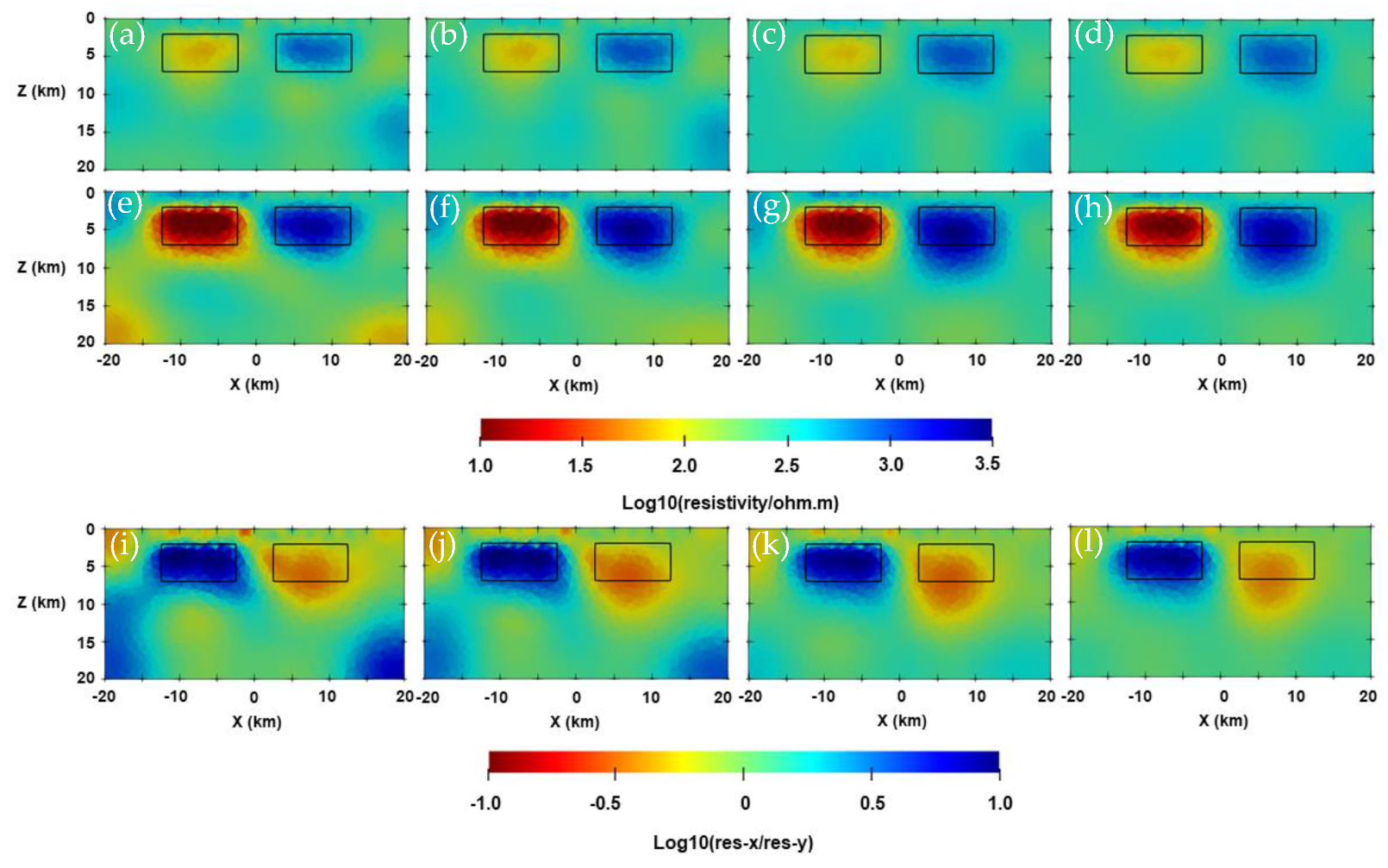
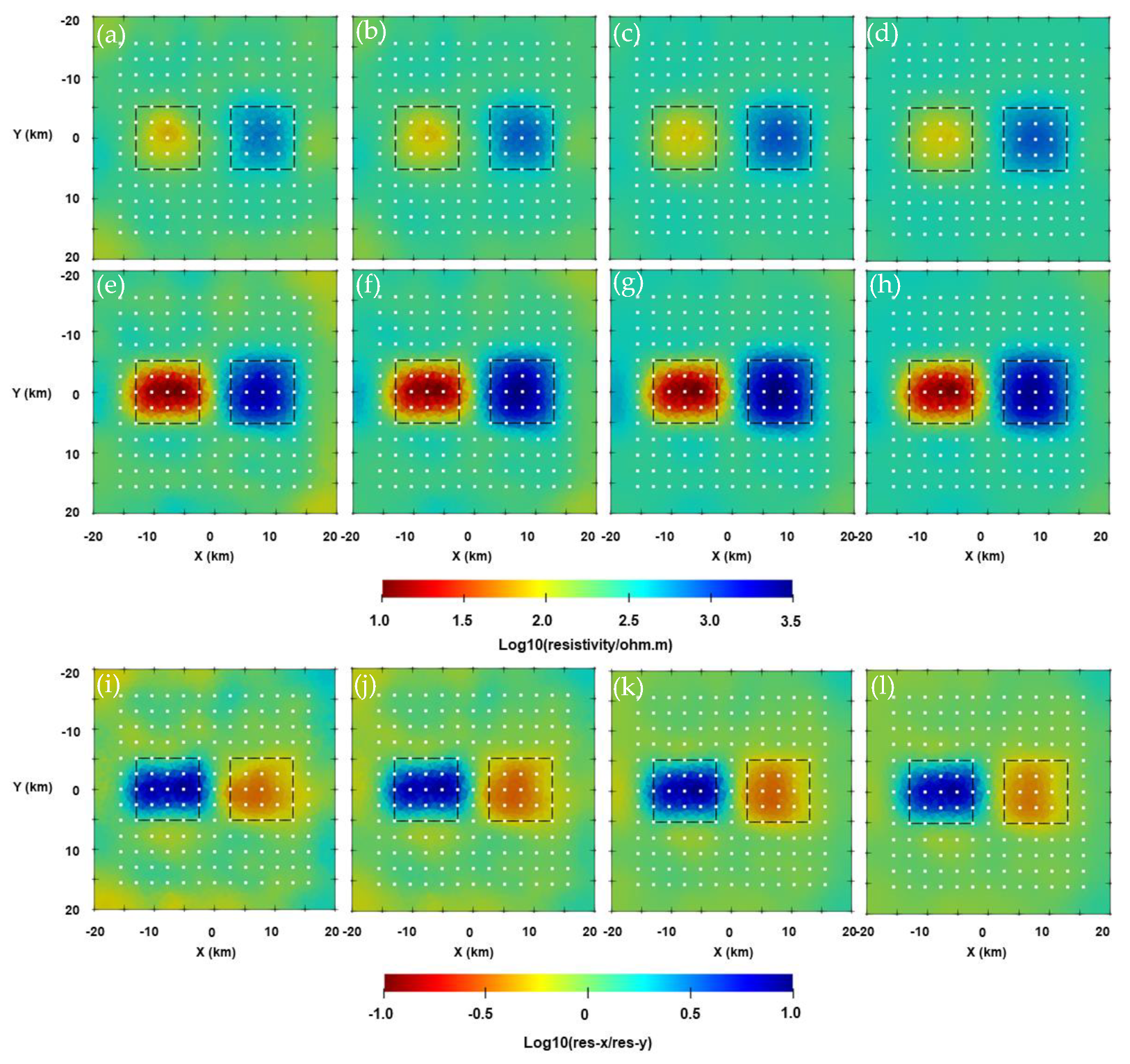
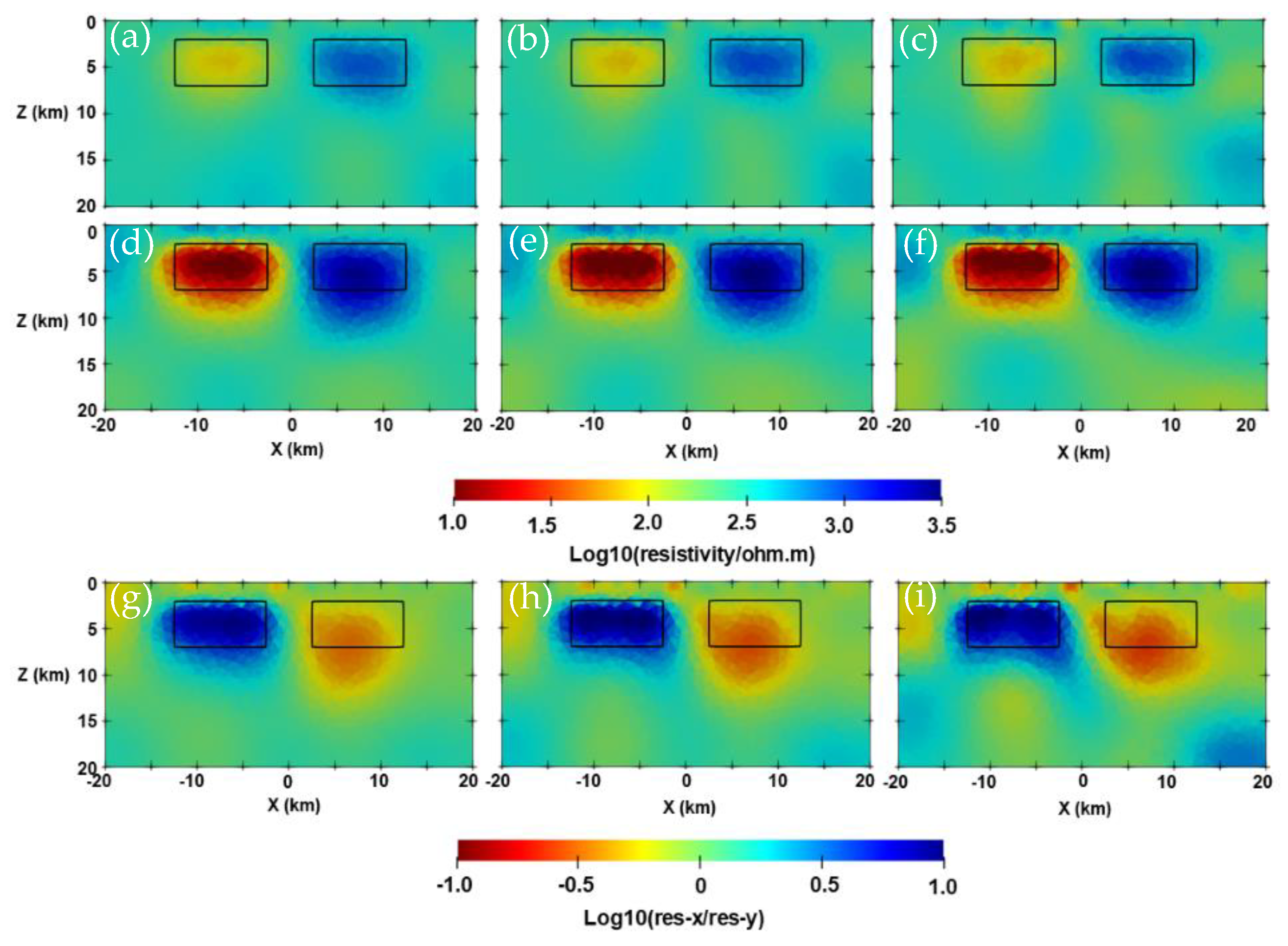
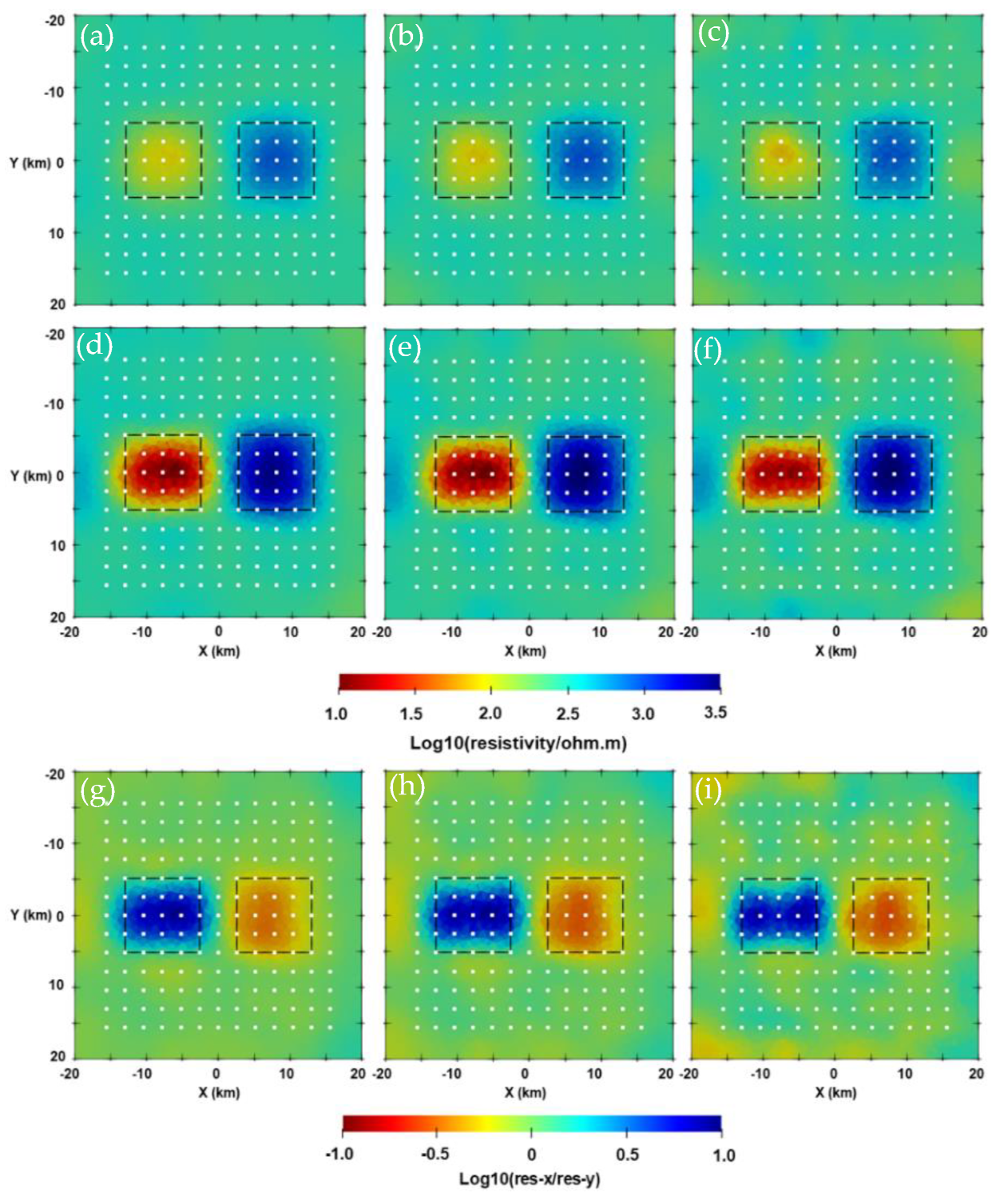
Appendix C
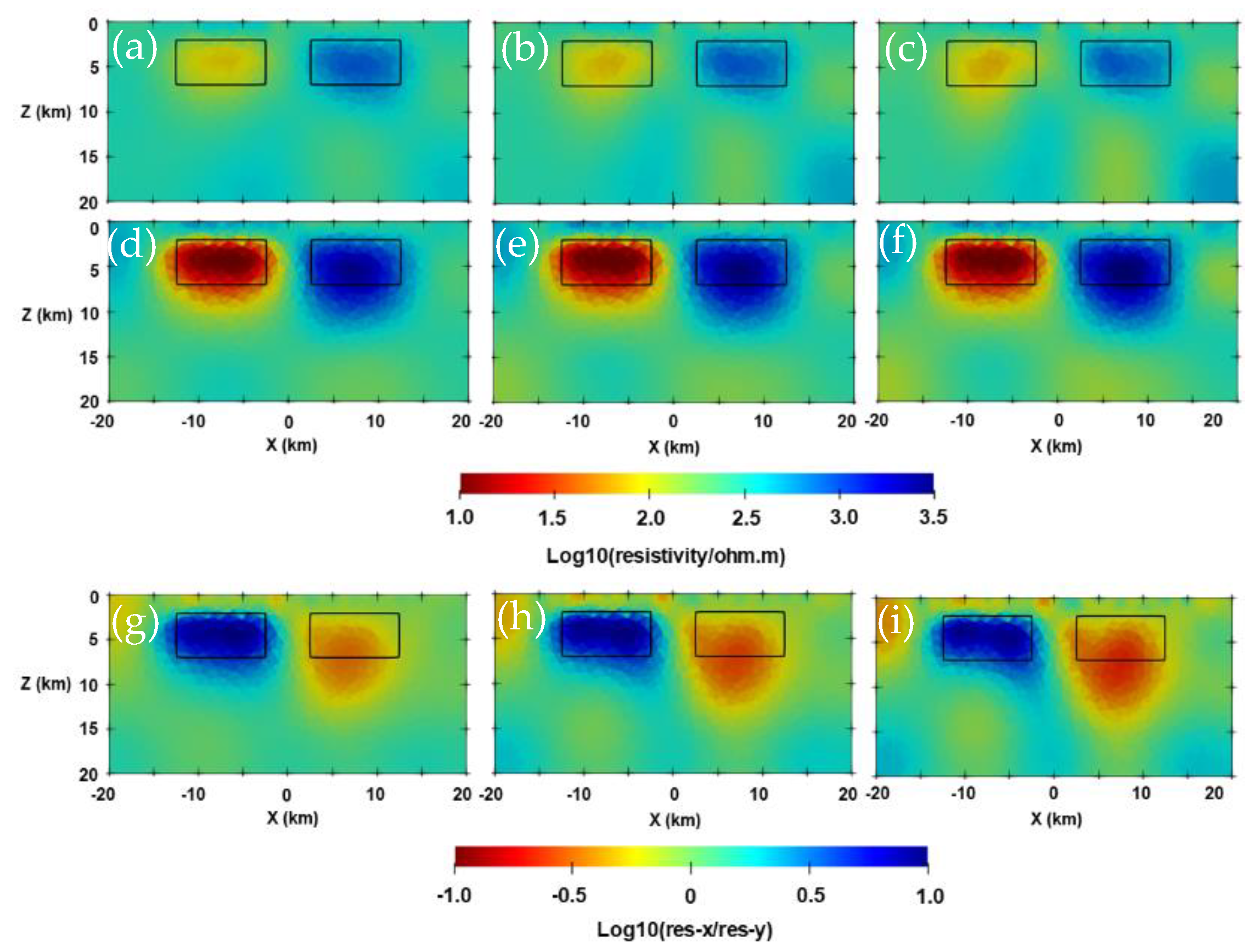
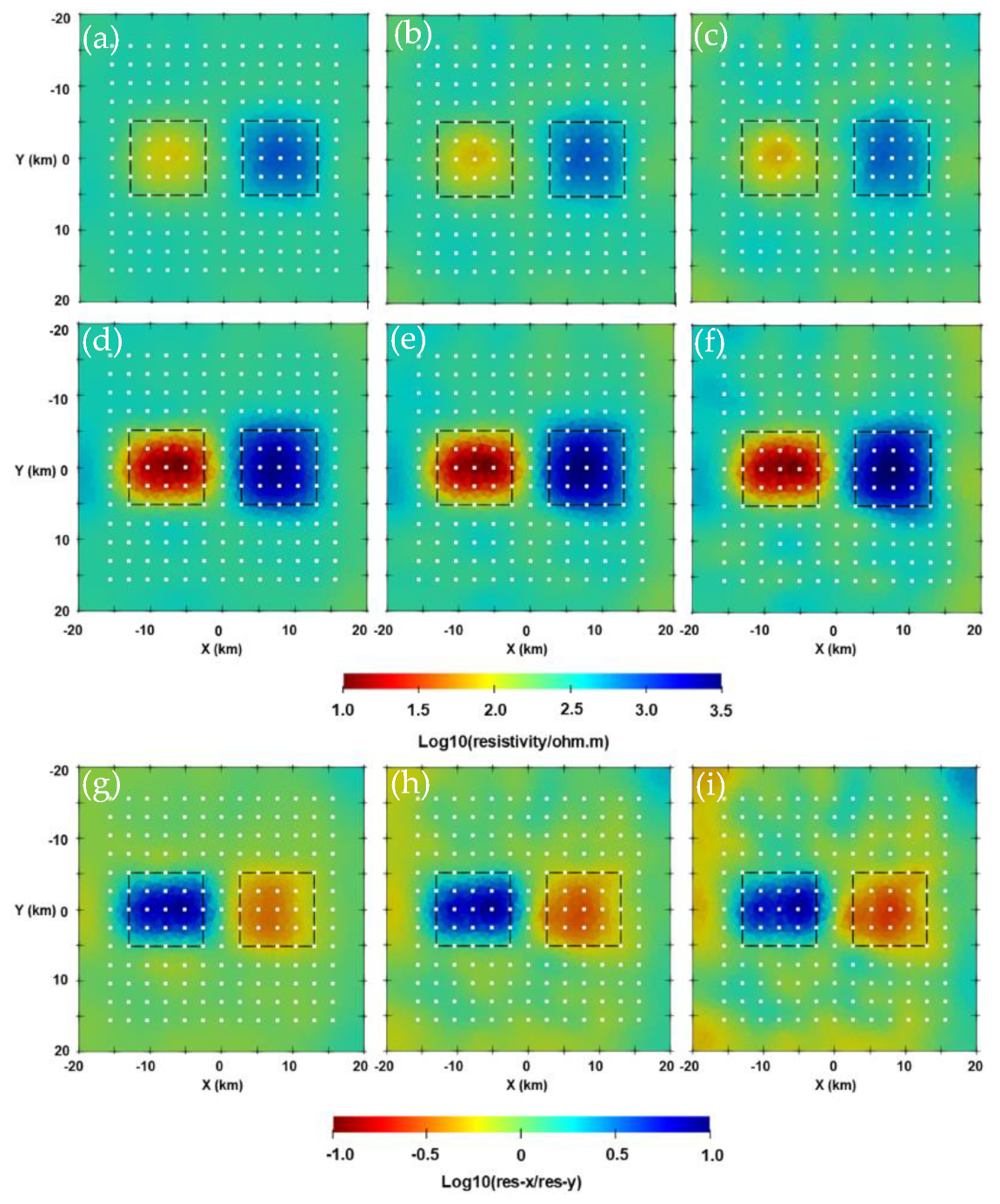
References
- Hübert, J.; Lee, B.M.; Liu, L.; Unsworth, M.J.; Richards, J.P.; Abbassi, B.; Cheng, L.; Oldenburg, D.W.; Legault, J.M.; Rebagliati, M. Three-dimensional imaging of a Ag-Au-rich epithermal system in British Columbia, Canada, using airborne z-axis tipper electromagnetic and ground-based magnetotelluric data. Geophysics 2016, 81, B1–B12. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Han, J.; Liu, Y.; Liu, L.; Guo, L.; Guang, Y.; Zhang, Y.; Li, S. Three-dimensional electrical structures and mineralization significance in the Shuangjianzishan ore-concentrated area, Inner Mongolia. Chin. J. Geophys. 2021, 64, 1291–1304. (In Chinese) [Google Scholar]
- Bai, D.; Unsworth, M.J.; Meju, M.A.; Ma, X.; Teng, J.; Kong, X.; Sun, Y.; Sun, J.; Wang, L.; Jiang, C.; et al. Crustal deformation of the eastern Tibetan plateau revealed by magnetotelluric imaging. Nat. Geosci. 2010, 3, 358–362. [Google Scholar] [CrossRef]
- Ogawa, Y.; Ichiki, M.; Kanda, W.; Mishina, M.; Asamori, K. Three-dimensional magnetotelluric imaging of crustal fluids and seismicity around Naruko volcano, NE Japan. Earth Planets Space 2014, 66, 158. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Jin, S.; Zhang, L.; Qu, C.; Hu, X.; Wei, W.; Yu, C.; Yu, P. The three-dimensional resistivity structures of the lithosphere beneath the Qinghai-Tibet Plateau. Chin. J. Geophys. 2020, 63, 817–827. (In Chinese) [Google Scholar]
- Piña-Varas, P.; Ledo, J.; Queralt, P.; Marcuello, A.; Bellmunt, F.; Hidalgo, R.; Messeiller, M. 3-D magnetotelluric exploration of Tenerife geothermal system (Canary Islands, Spain). Surv. Geophys. 2014, 35, 1045–1064. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, S.; Song, R.; Zuo, Y.; Jiang, G.; Lei, Y.; Zhang, S.; Wang, Z. Genesis of the hot dry rock geothermal resources in the Gonghe basin: Constraints from the radiogenic heat production rate of rocks. Chin. J. Geophys. 2020, 63, 2697–2709. (In Chinese) [Google Scholar]
- Christensen, N.B. Difficulties in determining electrical anisotropy in subsurface investigations. Geophys. Prospect. 2000, 48, 1–19. [Google Scholar] [CrossRef]
- Wannamaker, P.E. Anisotropy versus heterogeneity in continental solid Earth electromagnetic studies: Fundamental response characteristics and implications for physicochemical state. Surv. Geophys. 2005, 26, 733–765. [Google Scholar] [CrossRef]
- Newman, G.A.; Commer, M.; Carazzone, J.J. Imaging CSEM data in the presence of electrical anisotropy. Geophysics 2010, 75, F51–F61. [Google Scholar] [CrossRef]
- Guo, Z.; Wei, W.; Ye, G.; Jin, S.; Jing, J. Canonical decomposition of magnetotelluric responses: Experiment on 1D anisotropic structures. J. Appl. Geophys. 2015, 119, 79–88. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Z.; Li, Y. Adaptive finite element modelling of three-dimensional magnetotelluric fields in general anisotropic media. J. Appl. Geophys. 2018, 151, 113–124. [Google Scholar] [CrossRef]
- Weidelt, P. 3-D conductivity models: Implications of electrical anisotropy. In Three-Dimensional Electromagnetics; Society of Exploration Geophysicists: Houston, TX, USA, 1999. [Google Scholar]
- Miensopust, M.P.; Jones, A.G. Artefacts of isotropic inversion applied to magnetotelluric data from an anisotropic Earth. Geophys. J. Int. 2011, 187, 677–689. [Google Scholar] [CrossRef]
- Cao, H.; Wang, K.; Wang, T.; Hua, B. Three-dimensional magnetotelluric axial anisotropic forward modeling and inversion. J. Appl. Geophys. 2018, 153, 75–89. [Google Scholar] [CrossRef]
- Li, Y.; Berlin, F.U.; Prag, J.P.; Brasse, H. Magnetotelluric inversion for 2D anisotropic conductivity structures Inversion methodology. In Kolloquium Elektromagnetische Tiefenforschung; Burg Ludwigstein; Deutsche Geophysikalische Gesellschaft e.V.: Königstein, Germany, 2003. [Google Scholar]
- Pek, J.; Santos, F.; Li, Y. Non-linear conjugate gradient magnetotelluric inversion for 2-D anisotropic conductivities. In Proceedings of the 24 SchmuckerWeidelt-Colloquium, Neustadt an der Weinstraße, Germany, 19–23 September 2011. [Google Scholar]
- Yu, G.; Farquharson, C.G.; Xiao, Q.; Li, M. Two-dimensional anisotropic magnetotelluric inversion using a limited-memory quasi-Newton method. Geophysics 2021, 87, E13–E34. [Google Scholar] [CrossRef]
- Wang, K.; Wang, X.; Cao, H.; Lan, X.; Duan, C.; Luo, W.; Yuan, J. Magnetotelluric axial anisotropic parallelized 3D inversion based on cross gradient structural constraint. Chin. J. Geophys. 2021, 64, 1305–1319. (In Chinese) [Google Scholar]
- Kong, W.; Tan, H.; Lin, C.; Unsworth, M.; Lee, B.; Peng, M.; Wang, M.; Tong, T. Three-dimensional inversion of magnetotelluric data for a resistivity model with arbitrary anisotropy. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020562. [Google Scholar] [CrossRef]
- Hauserer, M.; Junge, A. Electrical mantle anisotropy and crustal conductor: A 3-D conductivity model of the Rwenzori Region in western Uganda. Geophys. J. Int. 2011, 185, 1235–1242. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Junge, A.; Yang, B.; Lower, A.; Cembrowski, M.; Xu, Y. Electrically anisotropic crust from three-dimensional magnetotelluric modeling in the western Junggar, NW China. J. Geophys. Res. Solid Earth 2019, 124, 9474–9494. [Google Scholar] [CrossRef] [Green Version]
- Siripunvaraporn, W.; Egbert, G.; Lenbury, Y.; Uyeshima, M. Three-dimensional magnetotelluric inversion: Data-space method. Phys. Earth Planet. Inter. 2005, 150, 3–14. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Yang, W.; Wei, W.; Guo, R.; Han, B.; Peng, R. Three-dimensional magnetotelluric parallel inversion algorithm using the data-space method. Chin. J. Geophys. 2013, 56, 484–493. (In Chinese) [Google Scholar]
- Usui, Y.; Ogawa, Y.; Aizawa, K.; Kanda, W.; Hashimoto, T.; Koyama, T.; Yamaya, Y.; Kagiyama, T. Three-dimensional resistivity structure of Asama Volcano revealed by data-space magnetotelluric inversion using unstructured tetrahedral elements. Geophys. J. Int. 2016, 208, 1359–1372. [Google Scholar] [CrossRef]
- Kordy, M.; Wannamaker, P.; Maris, V.; Cherkaev, E.; Hill, G. 3-dimensional magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on symmetric multiprocessor computers—Part II: Direct data-space inverse solution. Geophys. J. Int. 2016, 204, 94–110. [Google Scholar] [CrossRef] [Green Version]
- Pek, J.; Santos, F.A.M. Magnetotelluric inversion for anisotropic conductivities in layered media. Phys. Earth Planet. Inter. 2006, 158, 139–158. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Key, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar] [CrossRef]
- Cai, H.; Long, Z.; Lin, W.; Li, J.; Lin, P.; Hu, X. 3D multinary inversion of controlled-source electromagnetic data based on the finite-element method with unstructured mesh. Geophysics 2021, 86, E77–E92. [Google Scholar] [CrossRef]
- Wang, F.; Morten, J.P.; Spitzer, K. Anisotropic three-dimensional inversion of CSEM data using finite-element techniques on unstructured grids. Geophys. J. Int. 2018, 213, 1056–1072. [Google Scholar] [CrossRef]
- Golob, G.H.; Loan, C.F.V. Matrix Computations, 4th ed.; Johns Hopkins University: Baltimore, MD, USA, 2013. [Google Scholar]
- Pacheco, P.S. An Introduction to Parallel Programming; Morgan Kaufmann: Burlington, VT, USA, 2013. [Google Scholar]
- Grayver, A.V.; Streich, R.; Ritter, O. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver. Geophys. J. Int. 2013, 193, 1432–1446. [Google Scholar] [CrossRef] [Green Version]
- Usui, Y. 3-D inversion of magnetotelluric data using unstructured tetrahedral elements: Applicability to data affected by topography. Geophys. J. Int. 2015, 202, 828–849. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Yu, P.; Zhang, L.; Feng, S.; Utada, H. Regularized magnetotelluric inversion based on a minimum support gradient stabilizing functional. Earth Planets Space 2017, 69, 158. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Huang, X.; Yin, C.; Yan, L.; Zhang, B. 3D MT anisotropic inversion based on unstructured finite-element method. J. Environ. Eng. Geoph. 2021, 26, 49–60. [Google Scholar] [CrossRef]
- Zhang, L.; Koyama, T.; Utada, H.; Yu, P.; Wang, J. A regularized three-dimensional magnetotelluric inversion with a minimum gradient support constraint. Geophys. J. Int. 2012, 189, 296–316. [Google Scholar] [CrossRef] [Green Version]
- Menke, W.; Creel, R. Gaussian process regression reviewed in the context of inverse theory. Surv. Geophys. 2021, 42, 473–503. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Cai, H.; Hu, X.; Han, S.; Liu, M. Three-Dimensional Magnetotelluric Inversion for Triaxial Anisotropic Medium in Data Space. Minerals 2022, 12, 734. https://doi.org/10.3390/min12060734
Xie J, Cai H, Hu X, Han S, Liu M. Three-Dimensional Magnetotelluric Inversion for Triaxial Anisotropic Medium in Data Space. Minerals. 2022; 12(6):734. https://doi.org/10.3390/min12060734
Chicago/Turabian StyleXie, Jingtao, Hongzhu Cai, Xiangyun Hu, Shixin Han, and Minghong Liu. 2022. "Three-Dimensional Magnetotelluric Inversion for Triaxial Anisotropic Medium in Data Space" Minerals 12, no. 6: 734. https://doi.org/10.3390/min12060734
APA StyleXie, J., Cai, H., Hu, X., Han, S., & Liu, M. (2022). Three-Dimensional Magnetotelluric Inversion for Triaxial Anisotropic Medium in Data Space. Minerals, 12(6), 734. https://doi.org/10.3390/min12060734





