Effects of Accumulated Damage on the Dynamic Properties of Coal Measures Sandstone
Abstract
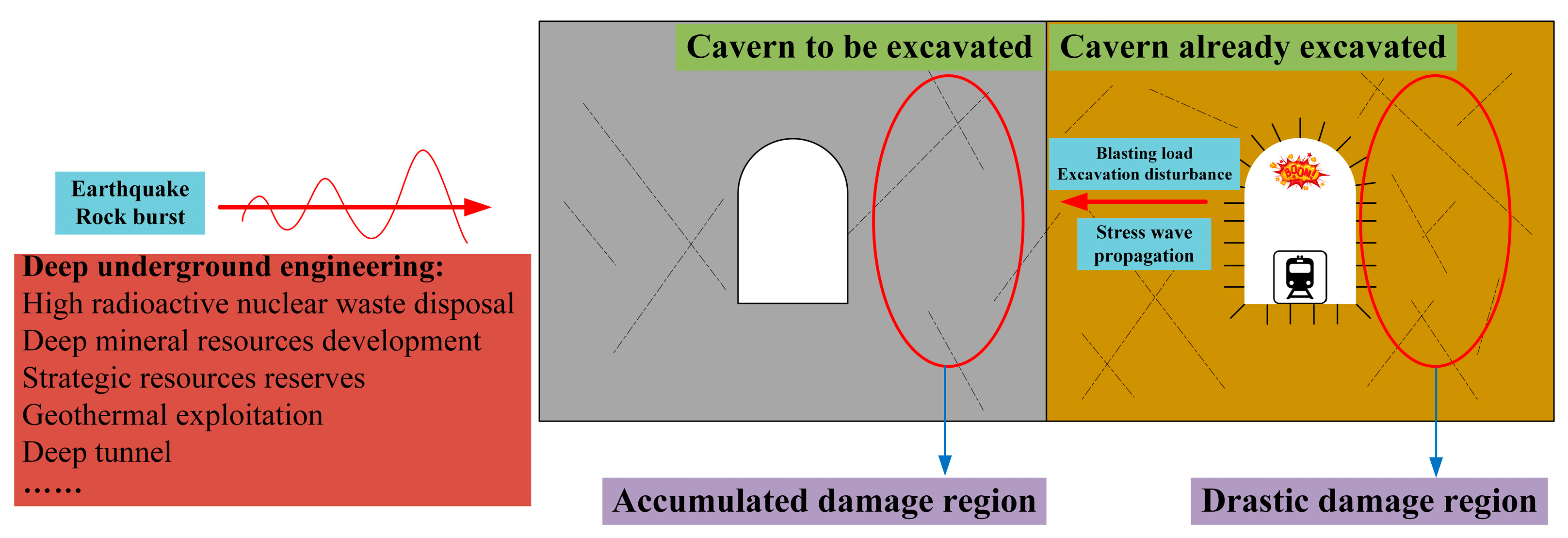
:1. Introduction
2. Material and Methods
2.1. Material Characterization
2.2. Physical and Quasi-Static Tests
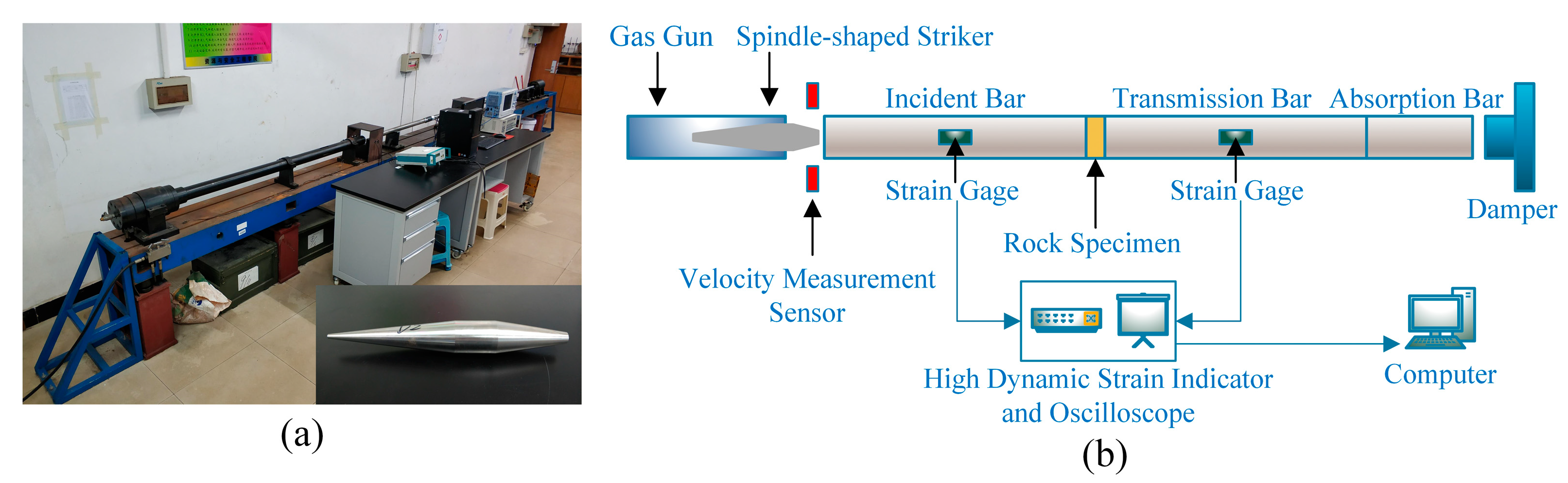
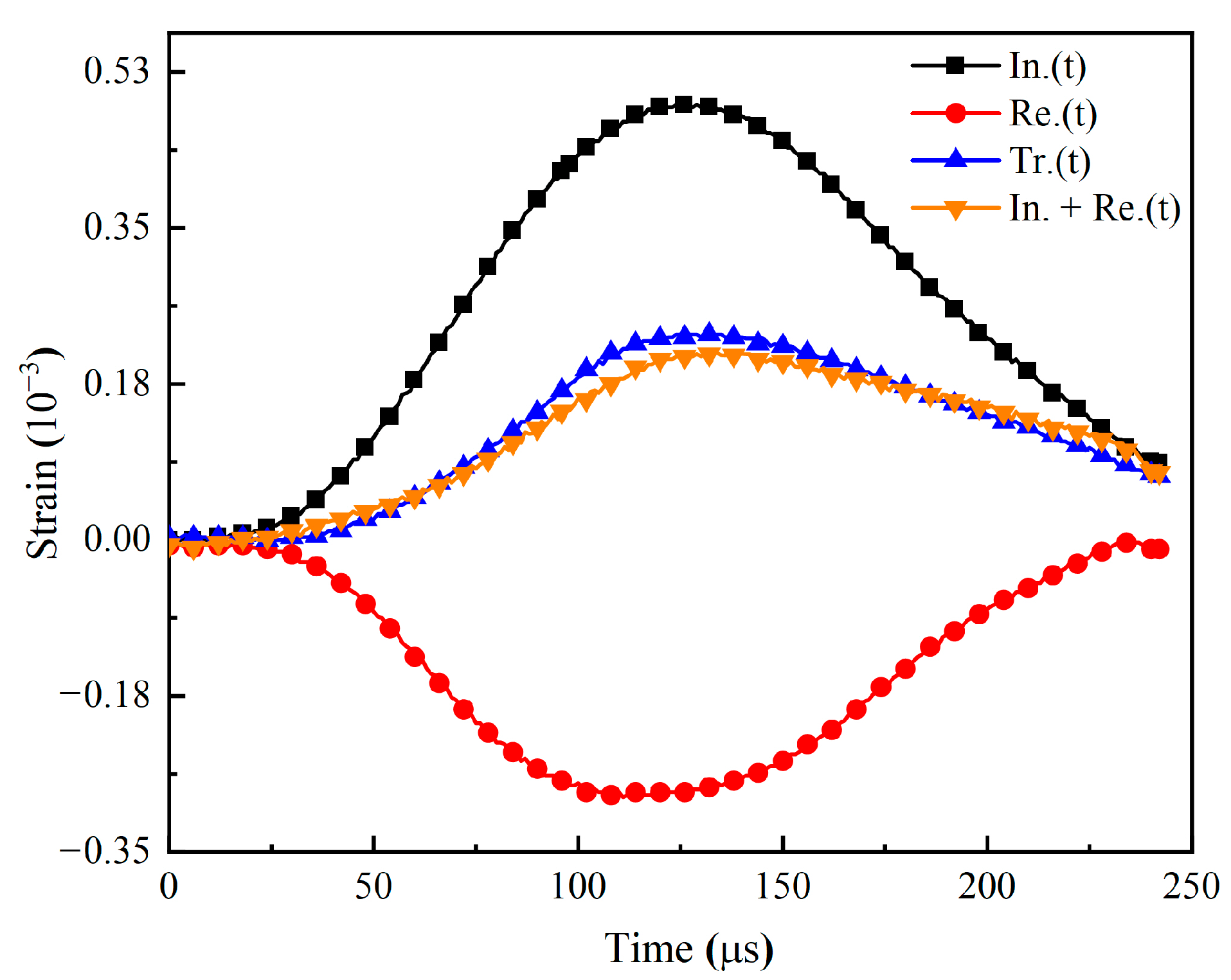
2.3. Dynamic Testing Facilities
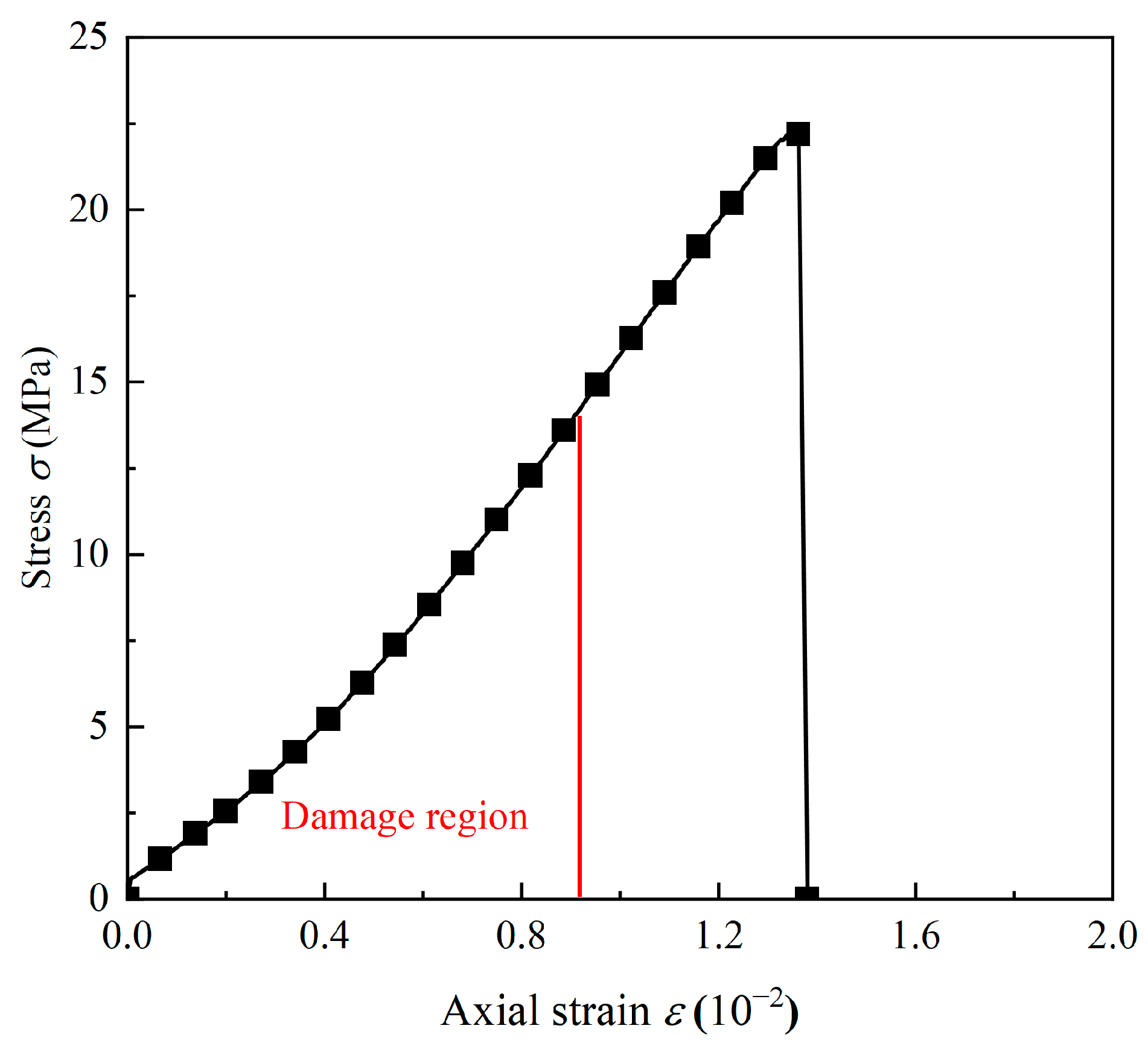
2.4. Definition of Accumulated Damage
2.5. Dynamic Testing Scheme
- Initial accumulated damage tests. The MTS816 is used to apply various levels of accumulated damage to selected coal measures sandstone specimens. The accumulated damage factor is calculated to measure the extent of the sandstone damage.
- Dynamic tests of sandstone. The SHPB test equipment is used to perform impact tests on sandstone to investigate the coupling effect of a high strain rate and the accumulated damage. There are five different strain rates and seven different accumulated damage conditions in this study. In each condition, only one test is conducted. In the event of a significant irregularity in the test results, a second test under the identical settings is required to ensure reliability.
- Observation of sandstone failure modes. An SEM device is used to observe sandstone’s microstructure after failure and compare it with the macroscopic failure morphology. Finally, the effects of high strain rates and accumulated damages on the sandstone failure mode are explored.
2.6. Dynamic Testing Facilities
3. Results and Discussion
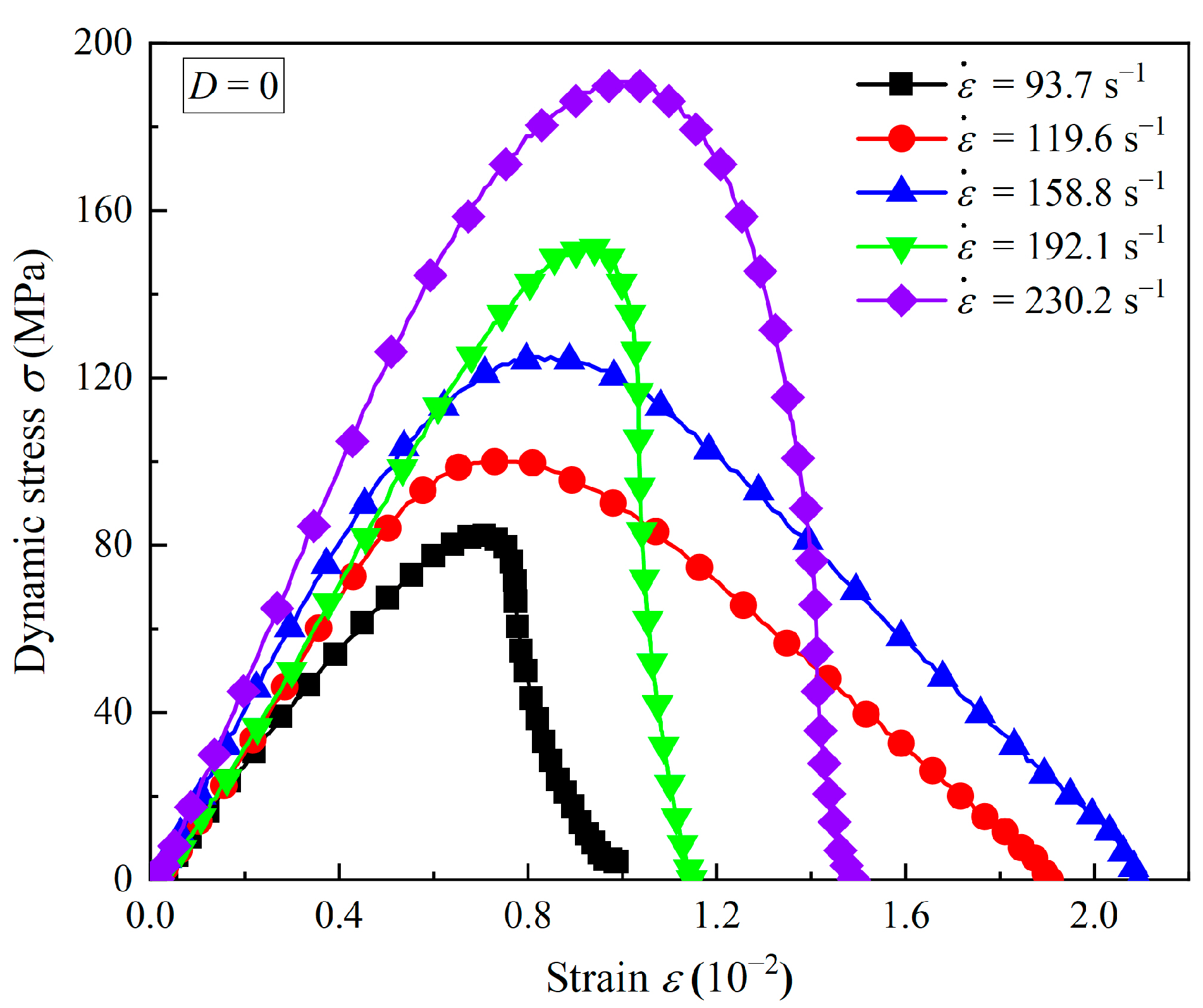
3.1. Dynamic Properties of Coal Measures Sandstone
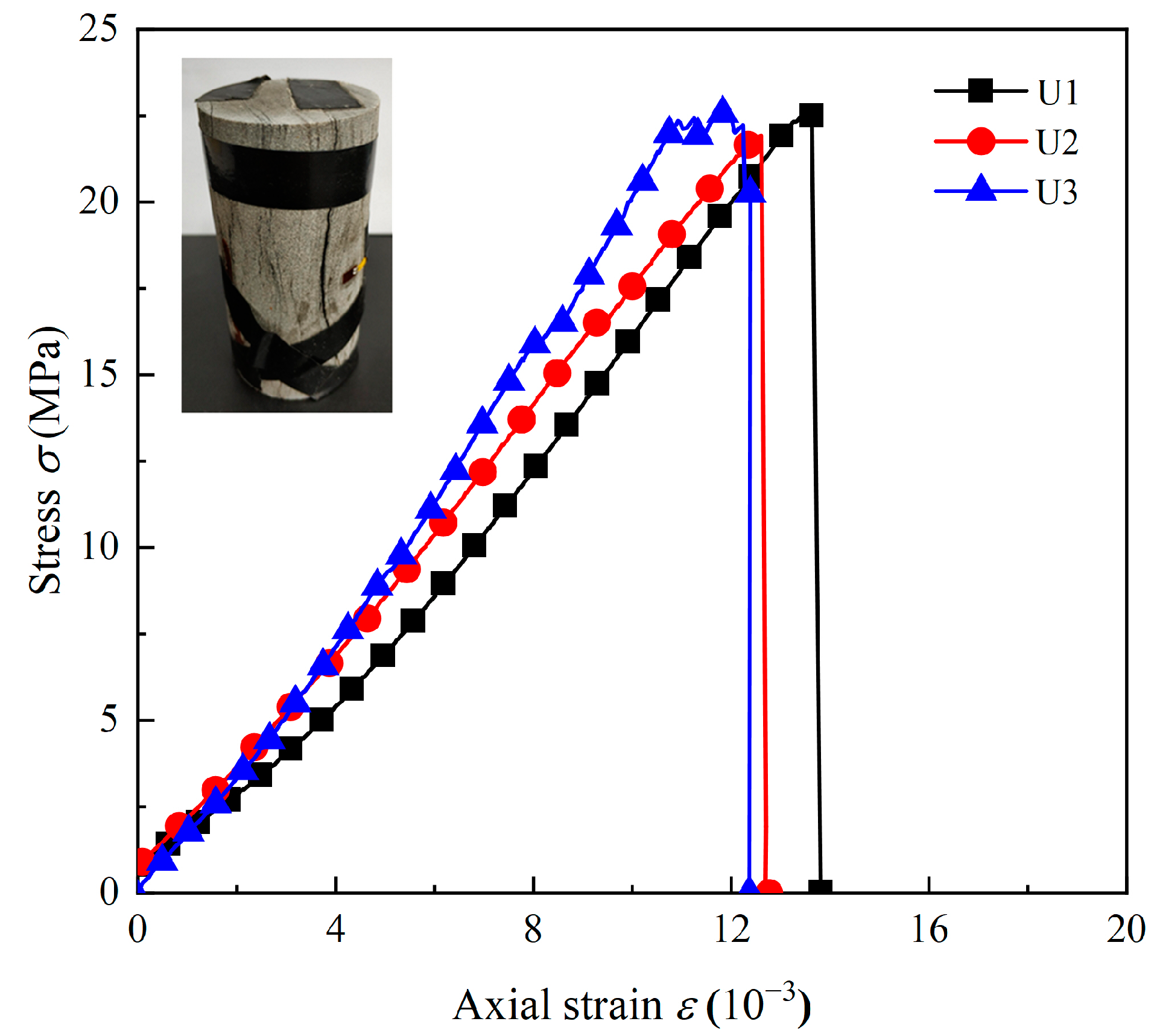
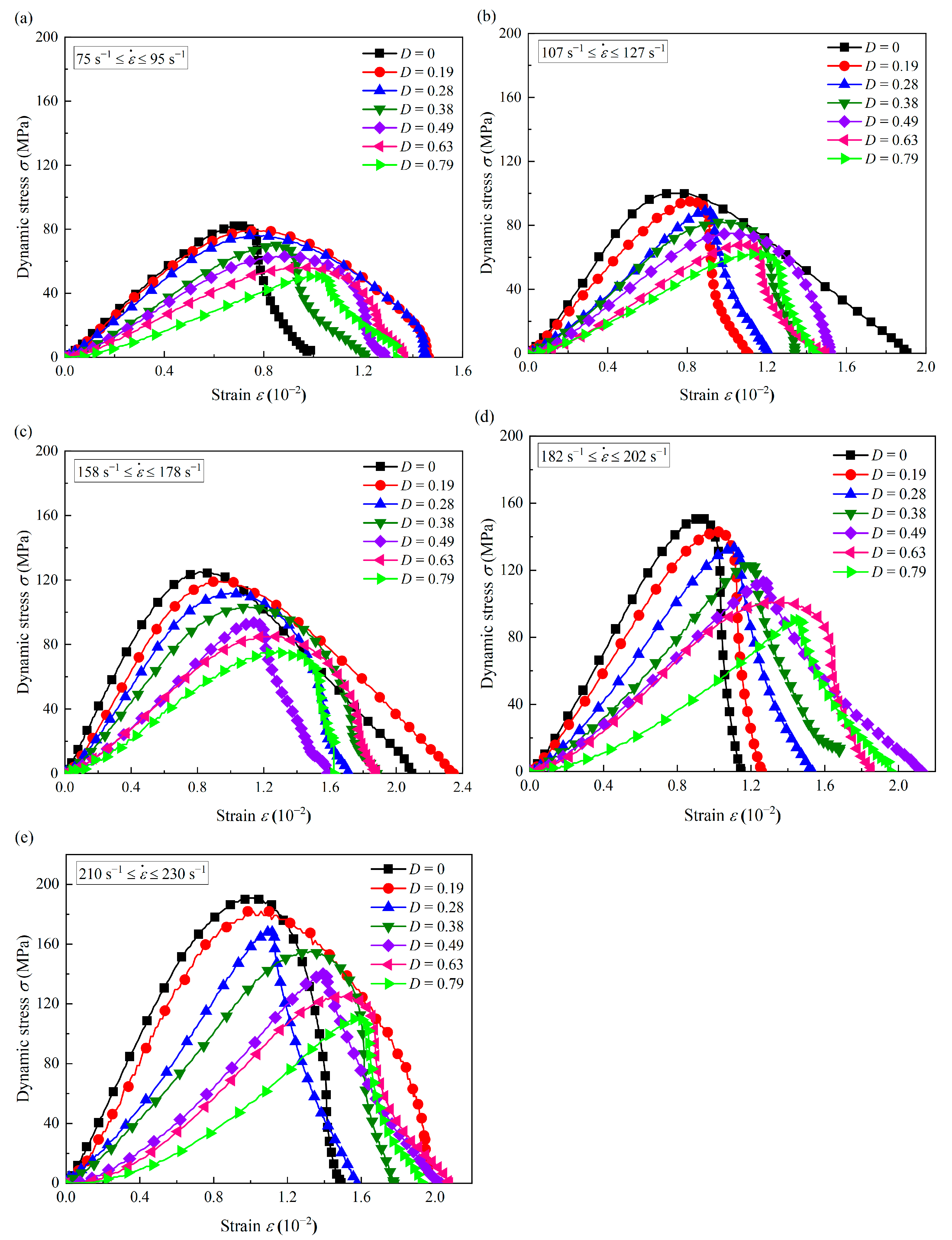
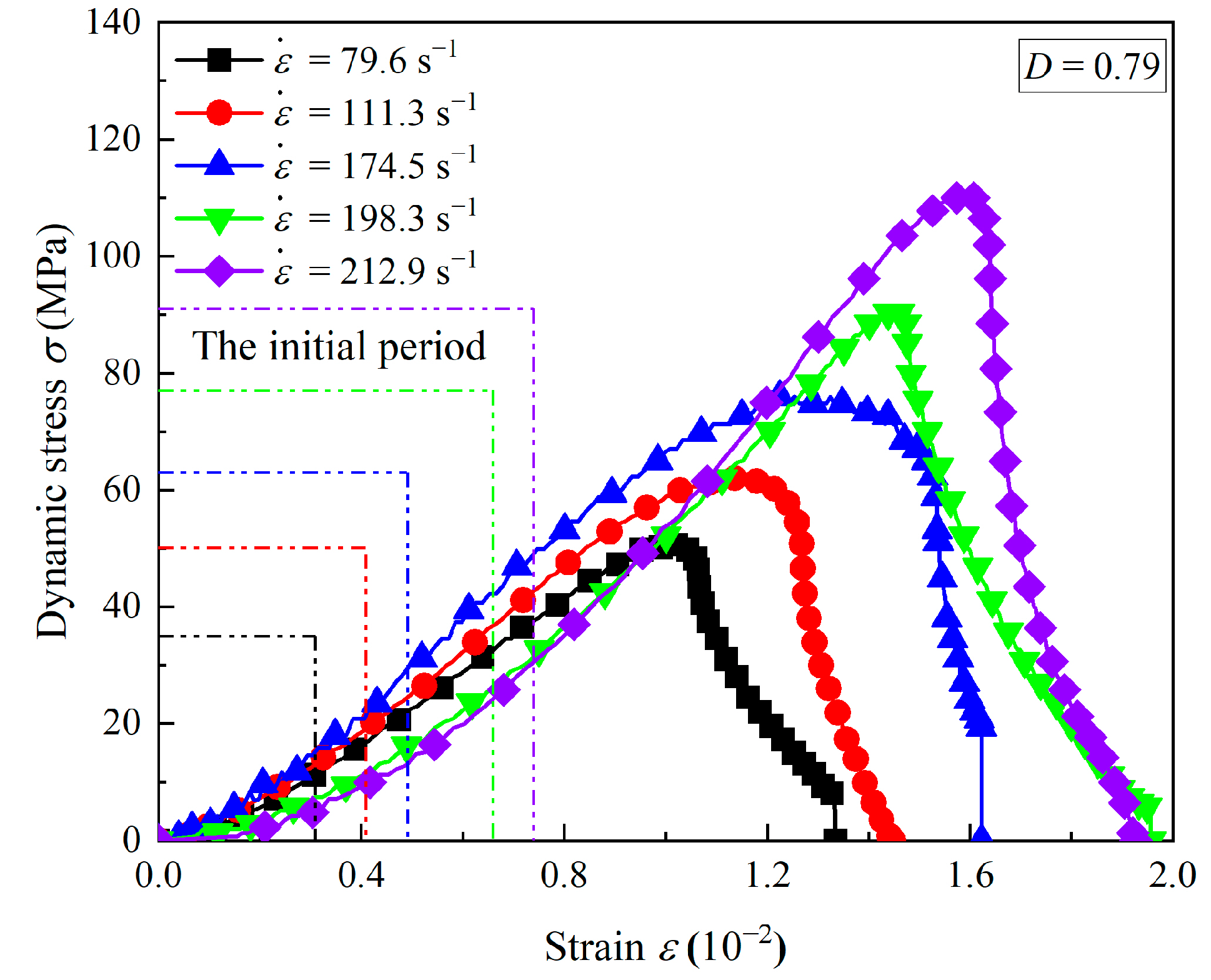
3.2. Effects of Accumulated Damage on the Stress–Strain Curves
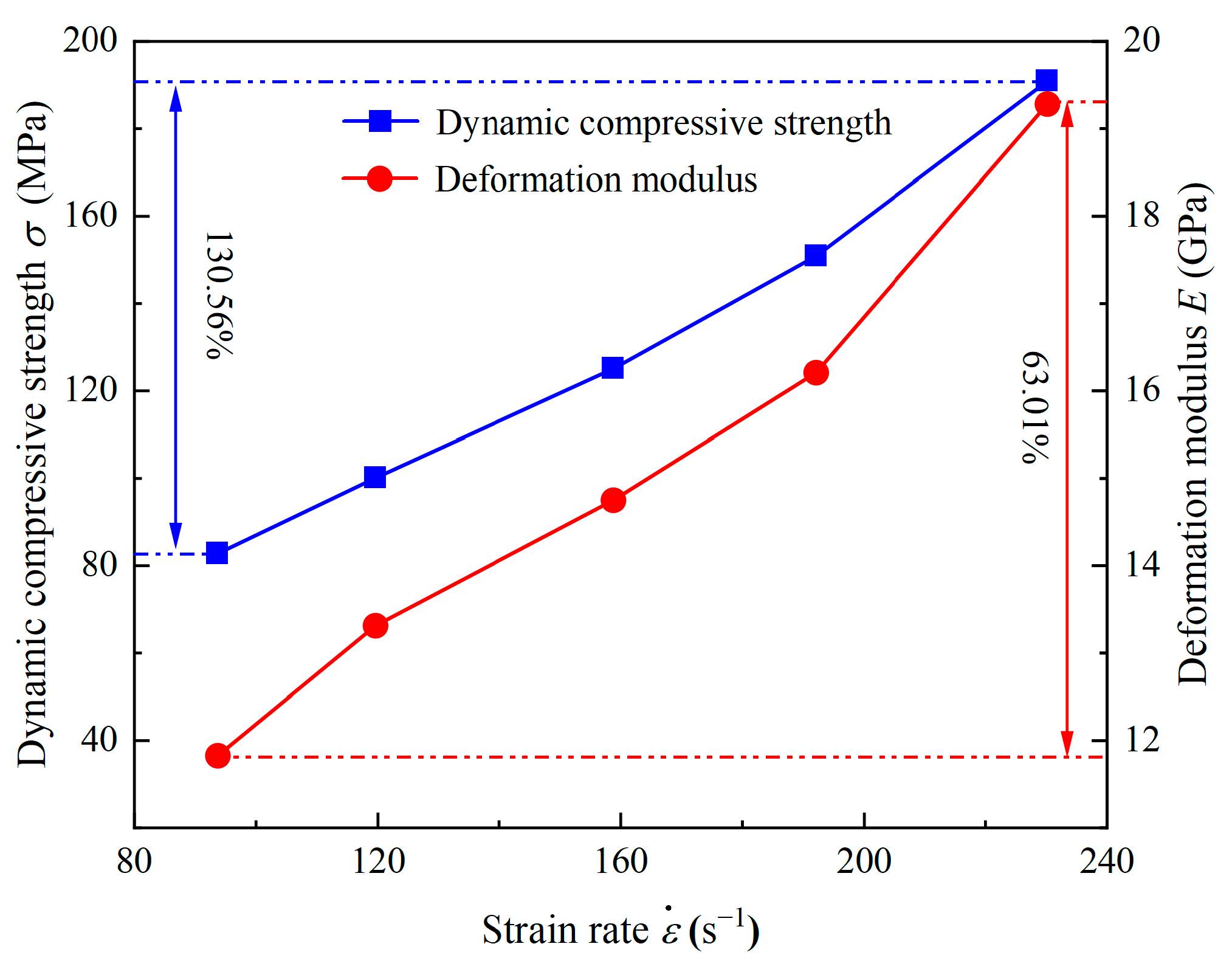
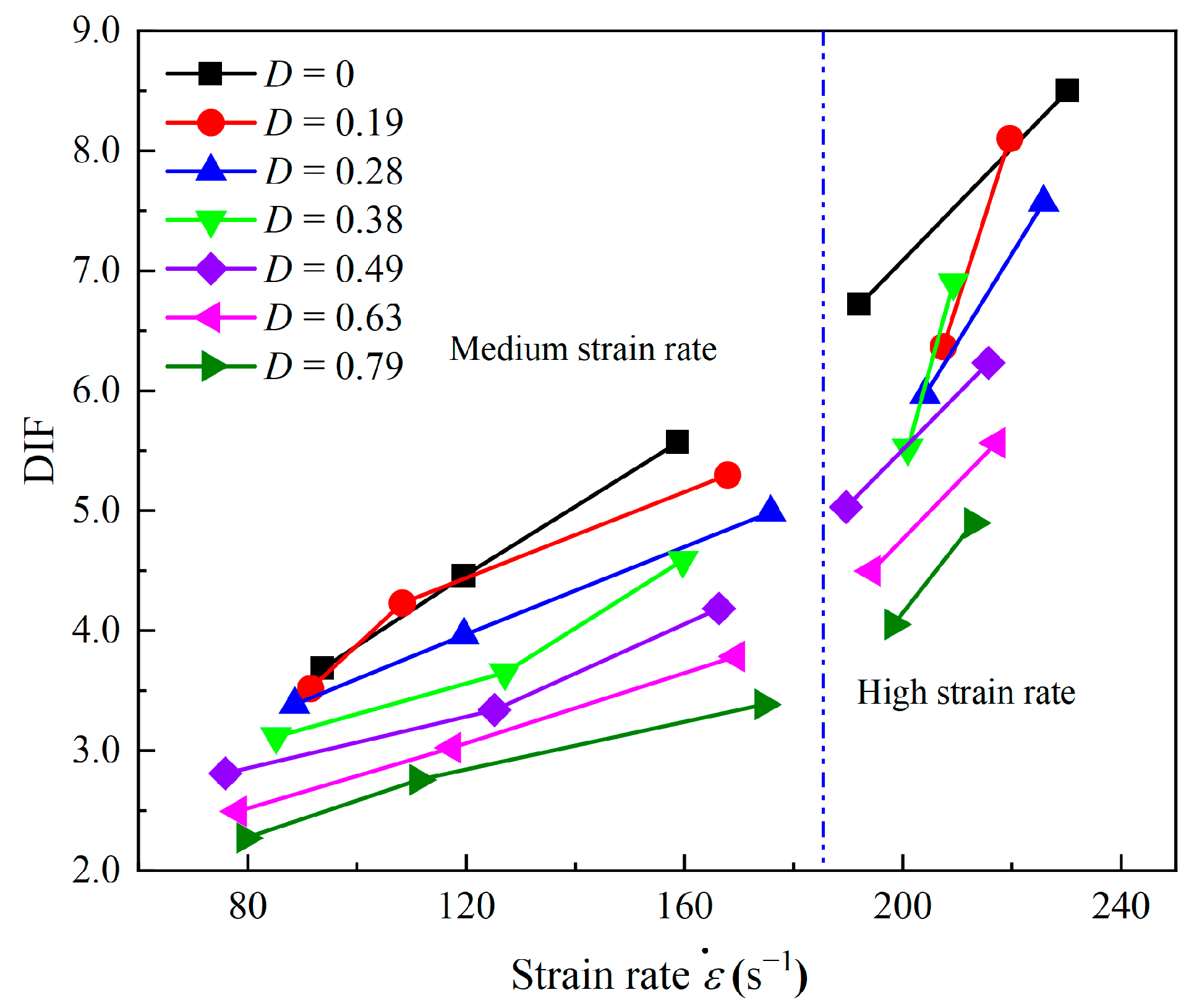
3.3. Effects of Accumulated Damage on the Compressive Strength
3.4. Effects of Accumulated Damage on the Deformation Modulus
4. Deformation and Failure Modes of Coal Measures Sandstone
4.1. Macroscopic Failure Modes
4.2. Microscopic Failure Modes
4.3. Energy Absorption Law
5. Statistical Damage Constitutive Model Considering the Strain Rate Effect and the Accumulated Damage
5.1. Statistical Damage Constitutive Model
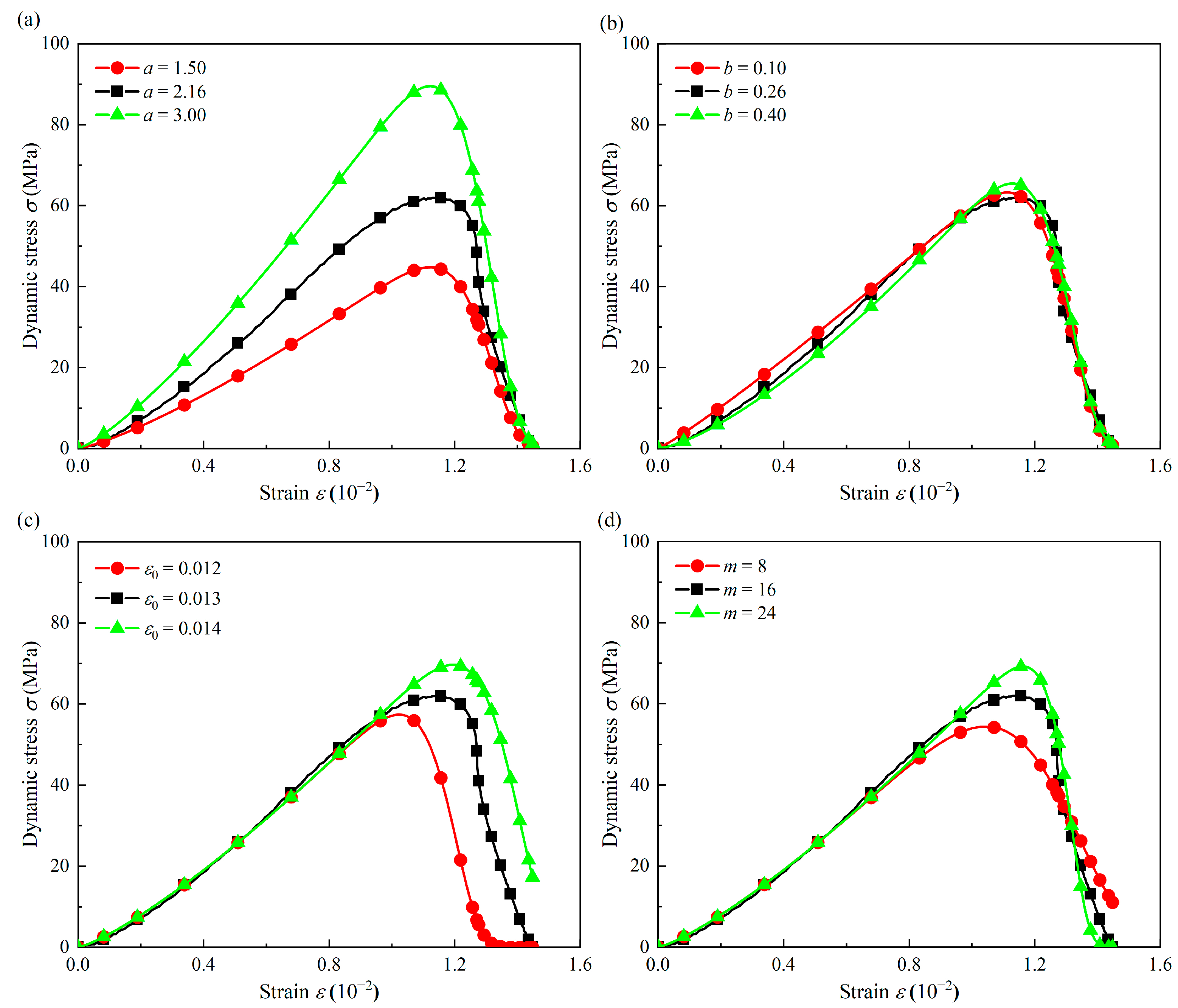
5.2. Sensitivity Analysis of Parameters
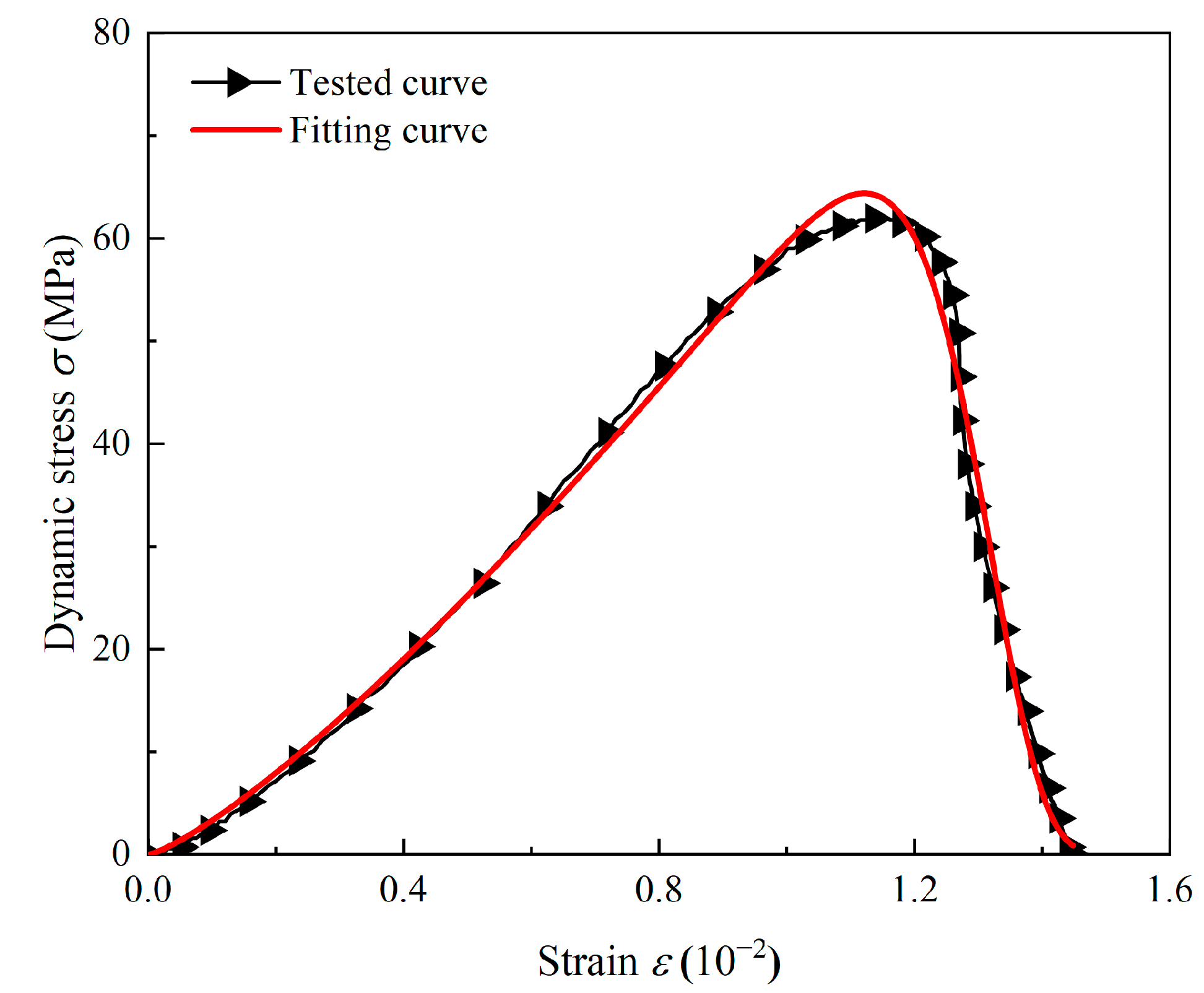
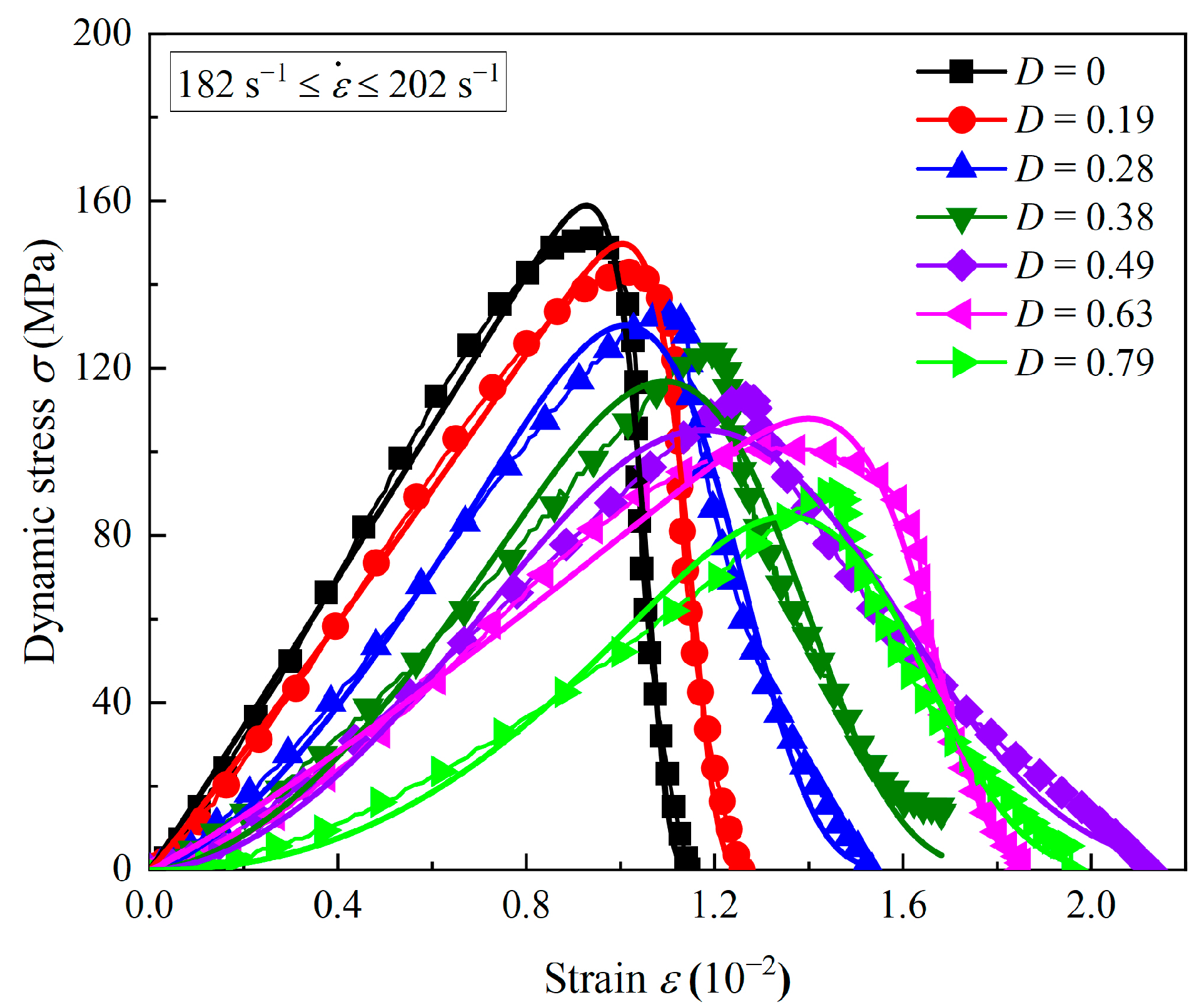
5.3. Validation and Discussion of the Model
6. Conclusions
- The stress–strain curves of the intact coal measures sandstone are classified into three phases: the linear elastic phase, the plastic deformation phase, and the strain-softening phase. The accumulated damages result in the crack closure phases in the dynamic curves of sandstone, and the greater the accumulated damage, the longer the crack closure phase.
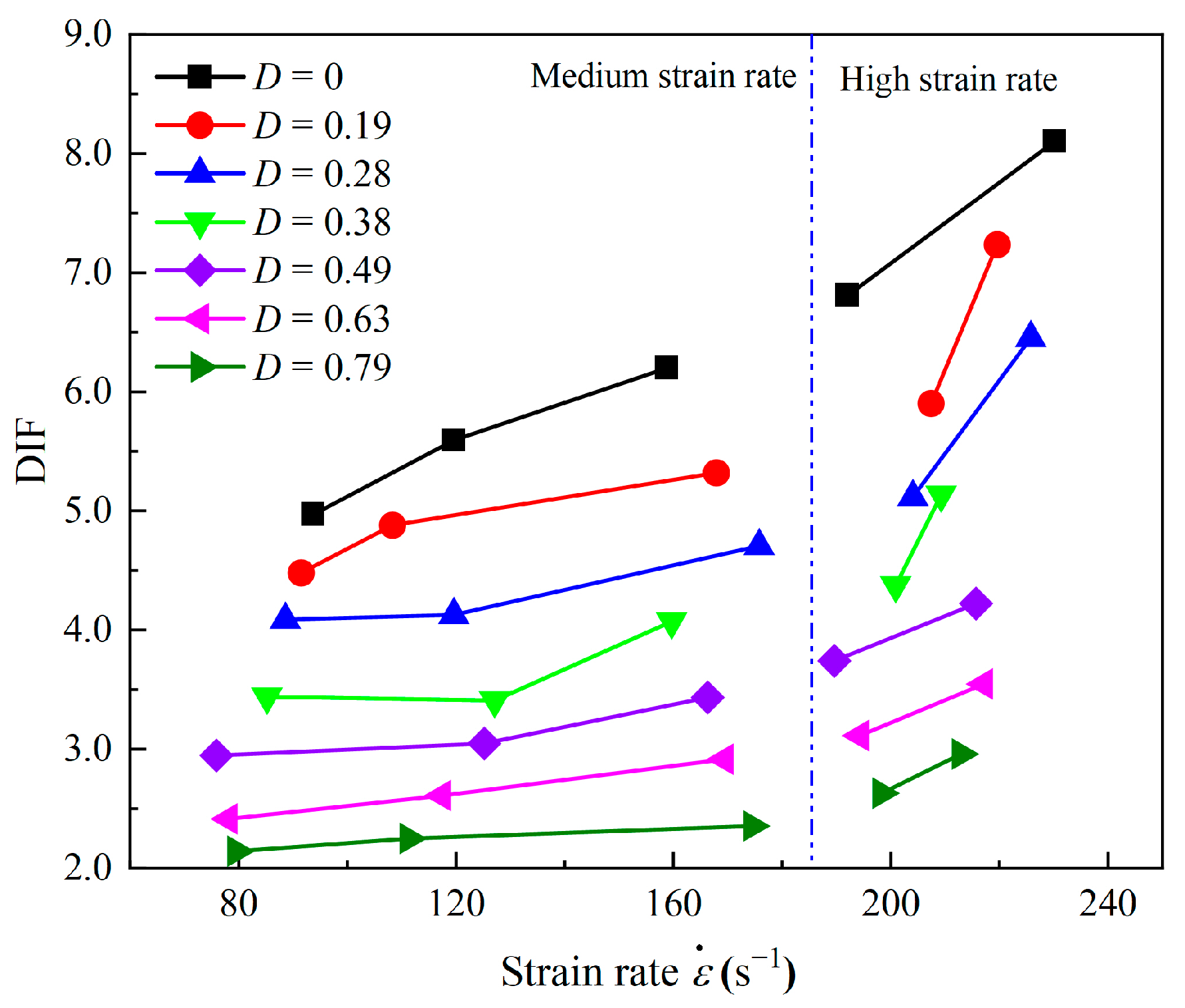
- The accumulated damage results in a significant reduction in the dynamic strength and the deformation modulus of the sandstone specimens. Compared with the compressive strength, the deformation modulus of sandstone is more susceptible to accumulated damage. The DIFs of strength and the deformation modulus are divided into two stages. The high-strain-rate phase has a faster change rate than the low- and medium-strain-rate phases.
- Accumulated damage reduces the internal friction angle of sandstone, leading to tensile fracture and shear fracture in the macroscopic failure mode. From a microscopic perspective, accumulated damage leads to intergranular fracture between mineral particles, whereas a high strain rate induces transgranular fracture in mineral particles. The energy absorption law corresponds to the failure modes of sandstone specimens.
- A statistical damage constitutive model of sandstone is established, which can well reflect the effect of the strain rate and accumulated damage on the dynamic response. Parameter a mainly affects the peak stress, while parameter b mainly affects the crack closure phase. The parameters and m have certain effects on the peak stress and the deformation modulus, but parameter m also affects the strain-softening phase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on Rock Mechanics in Deep Mining Engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Huang, L.X. Development and New Achievements of Rock Dynamics in China. Rock Soil Mech. 2011, 32, 2889–2900. [Google Scholar]
- Qian, Q.H. Challenges Faced by Underground Projects Construction Safety and Countermeasures. Chin. J. Rock Mech. Eng. 2012, 31, 1945–1956. [Google Scholar]
- Xie, H.P. Research Review of the State Key Research Development Program of China: Deep Rock Mechanics and Mining Theory. J. China Coal Soc. 2019, 44, 1283–1305. [Google Scholar]
- Xia, K.W.; Wang, S.; Xu, Y.; Chen, R.; Wu, B.B. Advances in Experimental Studies for Deep Rock Dynamics. Chin. J. Rock Mech. Eng. 2021, 40, 448–475. [Google Scholar]
- Rong, T.L.; Zhou, H.W.; Wang, L.J.; Ren, W.G.; Guo, Y.B. A Damage-Based Permeability Models of Deep Coal under Mining Disturbance. Rock Soil Mech. 2018, 39, 3983–3992. [Google Scholar]
- Bauer, S.J.; Song, B.; Sanborn, B. Dynamic Compressive Strength of Rock Salts. Int. J. Rock Mech. Min. Sci. 2019, 113, 112–120. [Google Scholar] [CrossRef]
- Duan, K.; Li, Y.C.; Wang, L.; Zhao, G.F.; Wu, W. Dynamic Responses and Failure Modes of Stratified Sedimentary Rocks. Int. J. Rock Mech. Min. Sci. 2019, 122, 104060. [Google Scholar] [CrossRef]
- Mishra, S.; Khetwal, A.; Chakraborty, T. Dynamic Characterisation of Gneiss. Rock Mech. Rock Eng. 2019, 52, 61–81. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhao, G.F. Dynamic Indirect Tensile Strength of Sandstone under Different Loading Rates. Rock Mech. Rock Eng. 2013, 47, 2271–2278. [Google Scholar] [CrossRef]
- Jiang, W.; Lu, Y.B.; Jiang, X.Q.; Duan, J.Z. Experimental Study on Dynamic Direct Tensile Mechanical Properties of Mortar-Granite ITZ. Chin. J. Rock Mech. Eng. 2018, 37, 1905–1915. [Google Scholar]
- Li, M.; Mao, X.B.; Cao, L.L.; Pu, H.; Mao, R.R.; Lu, A.H. Effects of Thermal Treatment on the Dynamic Mechanical Properties of Coal Measures Sandstone. Rock Mech. Rock Eng. 2016, 49, 3525–3539. [Google Scholar] [CrossRef]
- Yin, T.B.; Li, X.B.; Yin, Z.Q.; Zhou, Z.L.; Liu, X.L. Study and Comparison of Mechanical Properties of Sandstone under Static and Dynamic Loadings after High Temperature. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2012, 31, 273–279. [Google Scholar]
- Gong, F.Q.; Li, X.B.; Liu, X.L.; Zhao, J. Experimental Study of Dynamic Characteristics of Sandstone under One-Dimensional Coupled Static and Dynamic Loads. Chin. J. Rock Mech. Eng. 2010, 29, 2076–2085. [Google Scholar]
- Zhu, W.C.; Bai, Y.; Li, X.B.; Niu, L.L. Numerical Simulation on Rock Failure under Combined Static and Dynamic Loading during SHPB Tests. Int. J. Impact Eng. 2012, 49, 142–157. [Google Scholar] [CrossRef]
- Han, T.L.; Shi, J.P.; Cao, X.S. Fracturing and Damage to Sandstone under Coupling Effects of Chemical Corrosion and Freeze–Thaw Cycles. Rock Mech. Rock Eng. 2016, 49, 4245–4255. [Google Scholar] [CrossRef]
- Xu, J.C.; Pu, H.; Sha, Z.H. Mechanical Behavior and Decay Model of the Sandstone in Urumqi under Coupling of Freeze–Thaw and Dynamic Loading. Bull. Eng. Geol. Environ. 2021, 80, 2963–2978. [Google Scholar] [CrossRef]
- Zhou, T.; Dong, S.L.; Zhao, G.F.; Zhang, R.; Wu, S.Y.; Zhu, J.B. An Experimental Study of Fatigue Behavior of Granite under Low-Cycle Repetitive Compressive Impacts. Rock Mech. Rock Eng. 2018, 51, 3157–3166. [Google Scholar] [CrossRef]
- Tong, L.H.; Yu, Y.; Lai, S.K.; Lim, C.W. Dynamic Weakening of Sandstone Subjected to Repetitive Impact Loading. Rock Mech. Rock Eng. 2019, 52, 2197–2206. [Google Scholar] [CrossRef]
- Peng, K.; Liu, Z.P.; Zou, Q.L.; Zhang, Z.Y.; Zhou, J.Q. Static and Dynamic Mechanical Properties of Granite from Various Burial Depths. Rock Mech. Rock Eng. 2019, 52, 3545–3566. [Google Scholar]
- Li, X.; Wang, S.; Xu, Y.; Yao, W.; Xia, K.W.; Lu, G.M. Effect of Microwave Irradiation on Dynamic Mode-Ι Fracture Parameters of Barre Granite. Eng. Fract. Mech. 2020, 224, 106748. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Y.; Xia, K.W.; Tong, T.Y. Dynamic Fragmentation Of Microwave Irradiated Rock. J. Rock Mech. Geotech. Eng. 2021, 13, 300–310. [Google Scholar] [CrossRef]
- Yan, Z.L.; Dai, F.; Liu, Y.; Du, H.B.; Luo, J. Dynamic Strength and Cracking Behaviors of Single Flawed Rock Subjected to Coupled Static-Dynamic Compression. Rock Mech. Rock Eng. 2020, 53, 4289–4298. [Google Scholar] [CrossRef]
- Yan, Z.L.; Dai, F.; Zhu, J.B.; Xu, Y. Dynamic Cracking Behaviors and Energy Evolution of Multi-Flawed Rocks under Static Pre-Compression. Rock Mech. Rock Eng. 2021, 54, 5117–5139. [Google Scholar] [CrossRef]
- Liu, K.; Xu, P.X.; Wang, F.; Jin, C.; Liu, Q.T.; Pang, H.P.; Xie, H.Z. The Accumulated Stress Damage and Residual Life Prediction of Unreinforced Concrete Pavement with Electric Heating Pipes. Constr. Build. Mater. 2021, 278, 122258. [Google Scholar] [CrossRef]
- Ni, H.Y.; Liu, J.F.; Chen, T.; Chen, S.J.; Meng, Q. Bin Coal Permeability Prediction Method Based on the Microscopic Pore-Fracture Dual-Porosity Structure. J. Pet. Sci. Eng. 2022, 211, 110107. [Google Scholar] [CrossRef]
- Jia, B.; Chen, Z.L.; Xian, C.G. Investigations of CO2 Storage Capacity and Flow Behavior in Shale Formation. J. Pet. Sci. Eng. 2022, 208, 109659. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C.G. Permeability Measurement of the Fracture-Matrix System with 3D Embedded Discrete Fracture Model. Pet. Sci. 2022. [Google Scholar] [CrossRef]
- Kim, T.; Jeon, S. Experimental Study on Shear Behavior of a Rock Discontinuity under Various Thermal, Hydraulic and Mechanical Conditions. Rock Mech. Rock Eng. 2019, 52, 2207–2226. [Google Scholar] [CrossRef]
- Ai, H.A.; Ahrens, T.J. Simulation of Dynamic Response of Granite: A Numerical Approach of Shock-Induced Damage beneath Impact Craters. Int. J. Impact Eng. 2006, 33, 1–10. [Google Scholar] [CrossRef]
- Taylor, L.M.; Chen, E.P.; Kuszmaul, J.S. Microcrack-Induced Damage Accumulation in Brittle Rock under Dynamic Loading. Comput. Methods Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Liu, H.Y.; Lv, S.R.; Zhang, L.M.; Yuan, X.P. A Dynamic Damage Constitutive Model for a Rock Mass with Persistent Joints. Int. J. Rock Mech. Min. Sci. 2015, 75, 132–139. [Google Scholar] [CrossRef]
- Grady, D.E.; Kipp, M.E. The Micromechanics of Impact Fracture of Rock. Int. J. Rock Mech. Min. Sci. 1979, 16, 293–302. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Li, X.B.; Ye, Z.Y.; Liu, K.W. Obtaining Constitutive Relationship for Rate-Dependent Rock in SHPB Tests. Rock Mech. Rock Eng. 2010, 43, 697–706. [Google Scholar] [CrossRef]
- Li, H.Y.; Shi, G.Y. A Dynamic Material Model for Rock Materials under Conditions of High Confining Pressures and High Strain Rates. Int. J. Impact Eng. 2016, 89, 38–48. [Google Scholar] [CrossRef]
- Wu, A.J.; Deng, J.H.; Gu, X.; Hong, Y. Research on Mechanical Properties and Damage Evolution Law of Argillaceous Dolomite under Freeze-Thaw Cycles. Rock Soil Mech. 2014, 35, 3065–3072. [Google Scholar]
- Dai, F.; Huang, S.; Xia, K.W.; Tan, Z.Y. Some Fundamental Issues in Dynamic Compression and Tension Tests of Rocks Using Split Hopkinson Pressure Bar. Rock Mech. Rock Eng. 2010, 43, 657–666. [Google Scholar] [CrossRef]
- Cai, M.F.; He, M.C.; Liu, D.Y. Rock Mechanics and Engineering; Science Press: Beijing, China, 2013. [Google Scholar]
- Li, X.B.; Zhou, T.; Li, D.Y.; Wang, Z.W. Experimental and Numerical Investigations on Feasibility and Validity of Prismatic Rock Specimen in SHPB. Shock Vib. 2016, 2016, 7198980. [Google Scholar] [CrossRef] [Green Version]
- Qiu, J.D.; Li, D.Y.; Li, X.B.; Zhou, Z.L. Dynamic Fracturing Behavior of Layered Rock with Different Inclination Angles in SHPB Tests. Shock Vib. 2017, 2017, 7687802. [Google Scholar] [CrossRef] [Green Version]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic Characteristics of Granite Subjected to Intermediate Loading Rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Gong, F.Q.; Si, X.F.; Li, X.B.; Wang, S.Y. Dynamic Triaxial Compression Tests on Sandstone at High Strain Rates and Low Confining Pressures with Split Hopkinson Pressure Bar. Int. J. Rock Mech. Min. Sci. 2019, 113, 211–219. [Google Scholar] [CrossRef]
- Su, C.D. Testing Study on the Effect of Crystal Size and Specimen Length on the Rockburst Tendency. Chin. J. Rock Mech. Eng. 2004, 23, 3750–3753. [Google Scholar]
- Zhang, Q.B.; Zhao, J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Li, S.C.; Feng, X.D.; Li, W.T.; Yuan, C. Study of Numerical Simulation Method of Rock Fracture Based on Strain Energy Density Theory. Rock Soil Mech. 2011, 32, 1575–1582. [Google Scholar]
- Wen, Z.J.; Tian, L.; Jiang, Y.J.; Zuo, Y.J.; Meng, F.B.; Dong, Y.; Lin, G.; Yang, T.; Lv, D.W. Research on Damage Constitutive Model of Inhomogeneous Rocks Based on Strain Energy Density. Chin. J. Rock Mech. Eng. 2019, 38, 1332–1343. [Google Scholar]
- Xie, H.P.; Ju, Y.; Li, L. Yun Criteria for Strength and Structural Failure of Rocks Based on Energy Dissipation and Energy Release Principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Li, L.Y.; Xu, Z.Q.; Xie, H.P.; Ju, Y.; Ma, X.; Han, Z.C. Failure Experimental Study on Energy Laws of Rock under Differential Dynamic Impact Velocities. J. China Coal Soc. 2011, 36, 2007–2011. [Google Scholar]
- Millon, O.; Ruiz-Ripoll, M.L.; Hoerth, T. Analysis of the Behavior of Sedimentary Rocks under Impact Loading. Rock Mech. Rock Eng. 2016, 49, 4257–4272. [Google Scholar] [CrossRef]
- Wang, Z.L.; Shi, H.; Wang, J.G. Mechanical Behavior and Damage Constitutive Model of Granite under Coupling of Temperature and Dynamic Loading. Rock Mech. Rock Eng. 2018, 51, 3045–3059. [Google Scholar] [CrossRef]
- Wang, Z.L.; Li, Y.C.; Wang, J.G. A Damage-Softening Statistical Constitutive Model Considering Rock Residual Strength. Comput. Geosci. 2007, 33, 1–9. [Google Scholar] [CrossRef]
- Tang, C.A. Numerical Simulation of Progressive Rock Failure and Associated Seismicity. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Li, Y.W.; Jia, D.; Rui, Z.H.; Peng, J.Y.; Fu, C.K.; Zhang, J. Evaluation Method of Rock Brittleness Based on Statistical Constitutive Relations for Rock Damage. J. Pet. Sci. Eng. 2017, 153, 123–132. [Google Scholar] [CrossRef]
- Lemaitre, J. Coupled Elasto-Plasticity and Damage Constitutive Equations. Comput. Methods Appl. Mech. Eng. 1985, 51, 31–49. [Google Scholar] [CrossRef]
- Xie, H.P.; Ju, Y.; Dong, Y.L. Discussion on the “Elastic Modulus Method” in the Classical Damage Definition. Mech. Eng. 1997, 19, 1–5. [Google Scholar]
- Xie, L.X.; Zhao, G.M.; Meng, X.R. Research on Damage Viscoelastic Dynamic Constitutive Model of Soft Rock and Concrete Materials. Chin. J. Rock Mech. Eng. 2013, 32, 857–864. [Google Scholar]
- Zhu, J.J.; Li, X.B.; Gong, F.Q.; Wang, S.M. Dynamic Characteristics and Damage Model for Rock under Uniaxial Cyclic Impact Compressive Loads. Chin. J. Geotech. Eng. 2013, 35, 531–539. [Google Scholar]
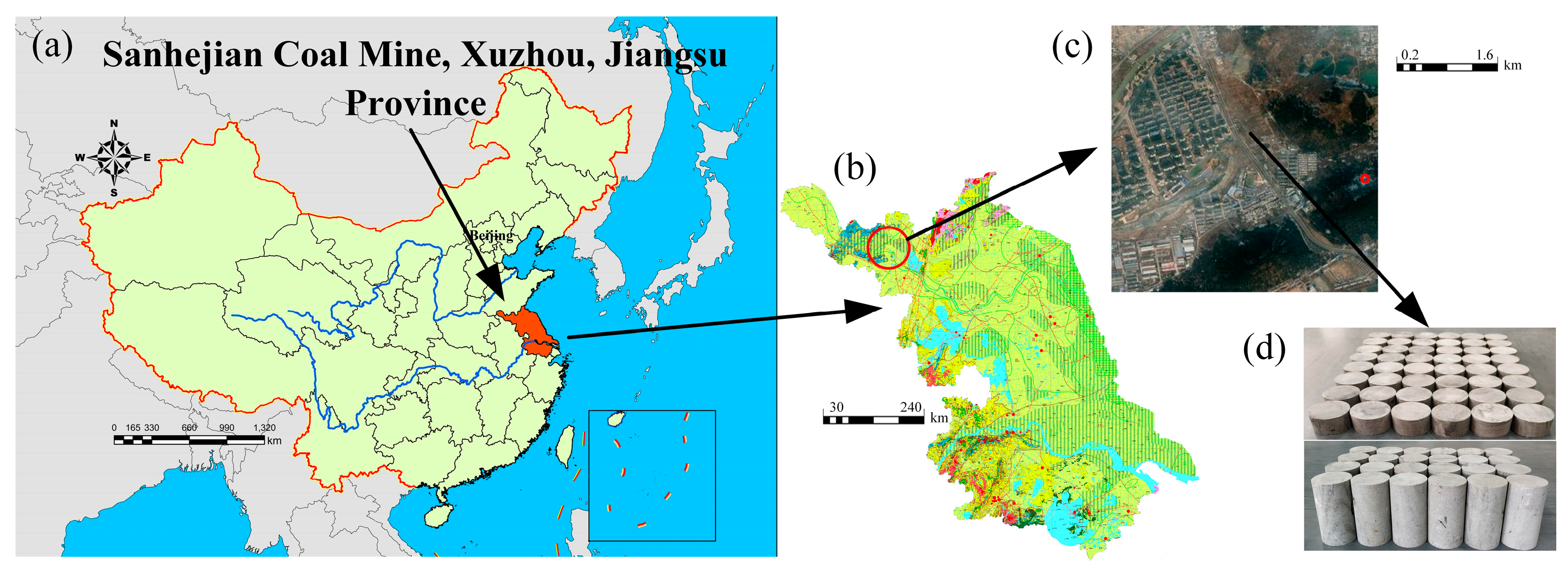

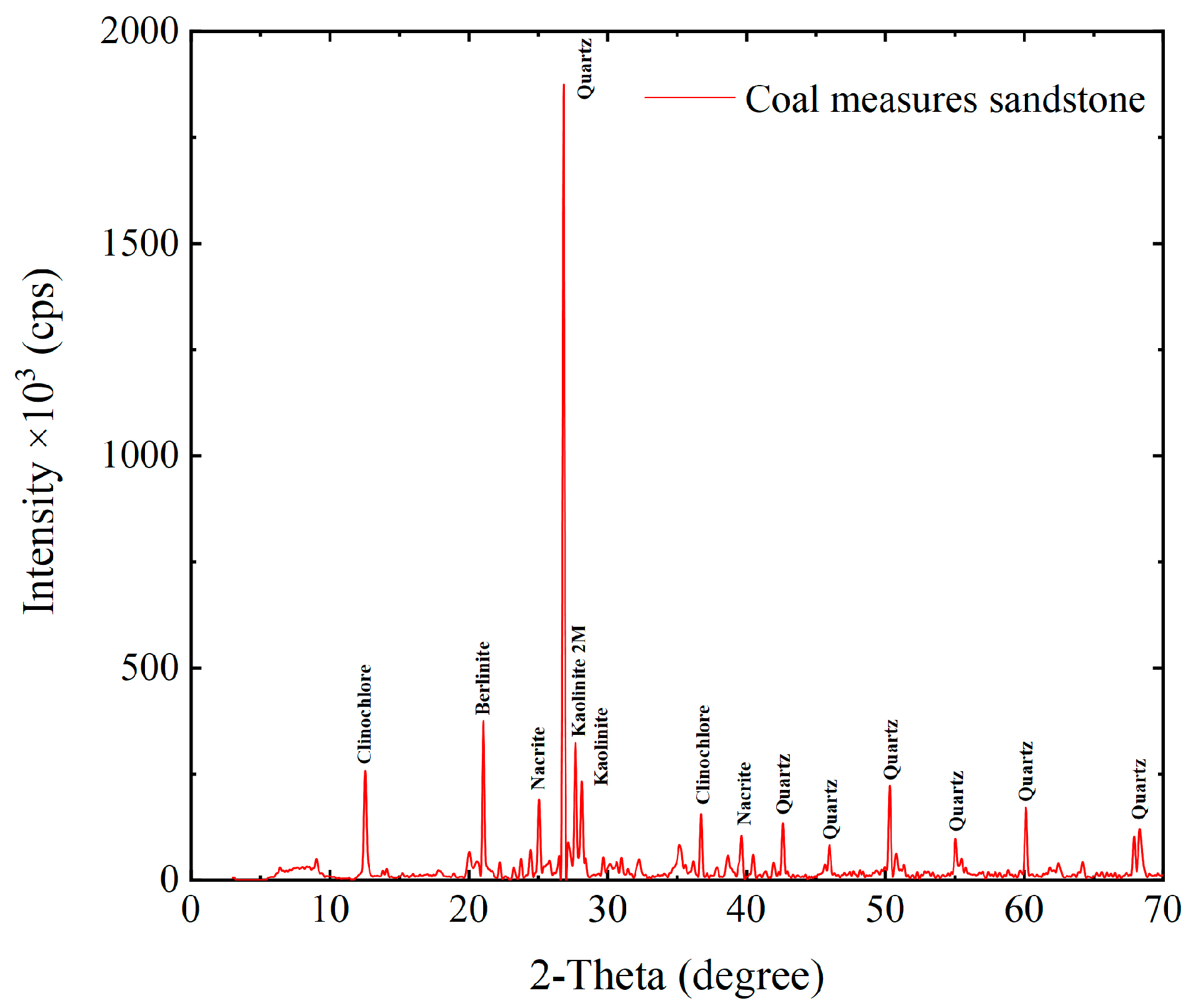










| ρ/(kg·m−3) | VP/(m·s−1) | ω/% | E/GPa | σu/MPa | σT/MPa | μ |
|---|---|---|---|---|---|---|
| 2589 | 3682 | 1.13 | 1.91 | 22.46 | 2.38 | 0.14 |
| σ/MPa | 8.99 | 11.23 | 13.48 | 15.73 | 17.97 | 20.22 |
| D | 0.1893 | 0.2764 | 0.3789 | 0.4939 | 0.6283 | 0.7891 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, Z.; Pu, H.; Xu, J.; Ni, H.; Guo, S. Effects of Accumulated Damage on the Dynamic Properties of Coal Measures Sandstone. Minerals 2022, 12, 810. https://doi.org/10.3390/min12070810
Sha Z, Pu H, Xu J, Ni H, Guo S. Effects of Accumulated Damage on the Dynamic Properties of Coal Measures Sandstone. Minerals. 2022; 12(7):810. https://doi.org/10.3390/min12070810
Chicago/Turabian StyleSha, Ziheng, Hai Pu, Junce Xu, Hongyang Ni, and Shiru Guo. 2022. "Effects of Accumulated Damage on the Dynamic Properties of Coal Measures Sandstone" Minerals 12, no. 7: 810. https://doi.org/10.3390/min12070810
APA StyleSha, Z., Pu, H., Xu, J., Ni, H., & Guo, S. (2022). Effects of Accumulated Damage on the Dynamic Properties of Coal Measures Sandstone. Minerals, 12(7), 810. https://doi.org/10.3390/min12070810







