Quantification of Small-Scale Heterogeneity at the Core–Mantle Boundary Using Sample Entropy of SKS and SPdKS Synthetic Waveforms
Abstract
:1. Introduction
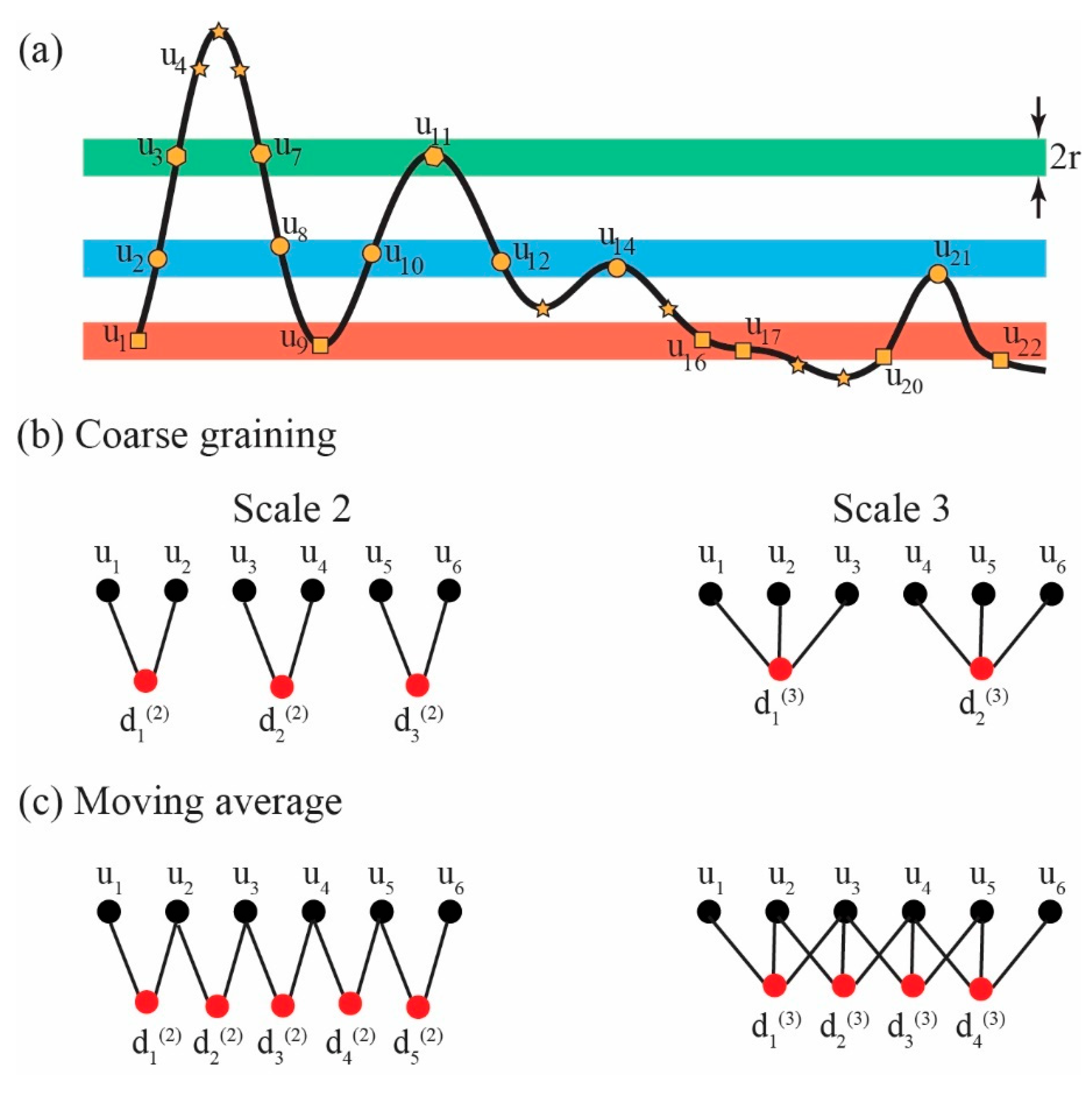
2. The Sample Entropy Method
2.1. Sample Entropy
2.2. Multi-Scale Sample Entropy
3. Synthetic Analysis of Sample Entropy
3.1. Sample Entropy of 1-D Models
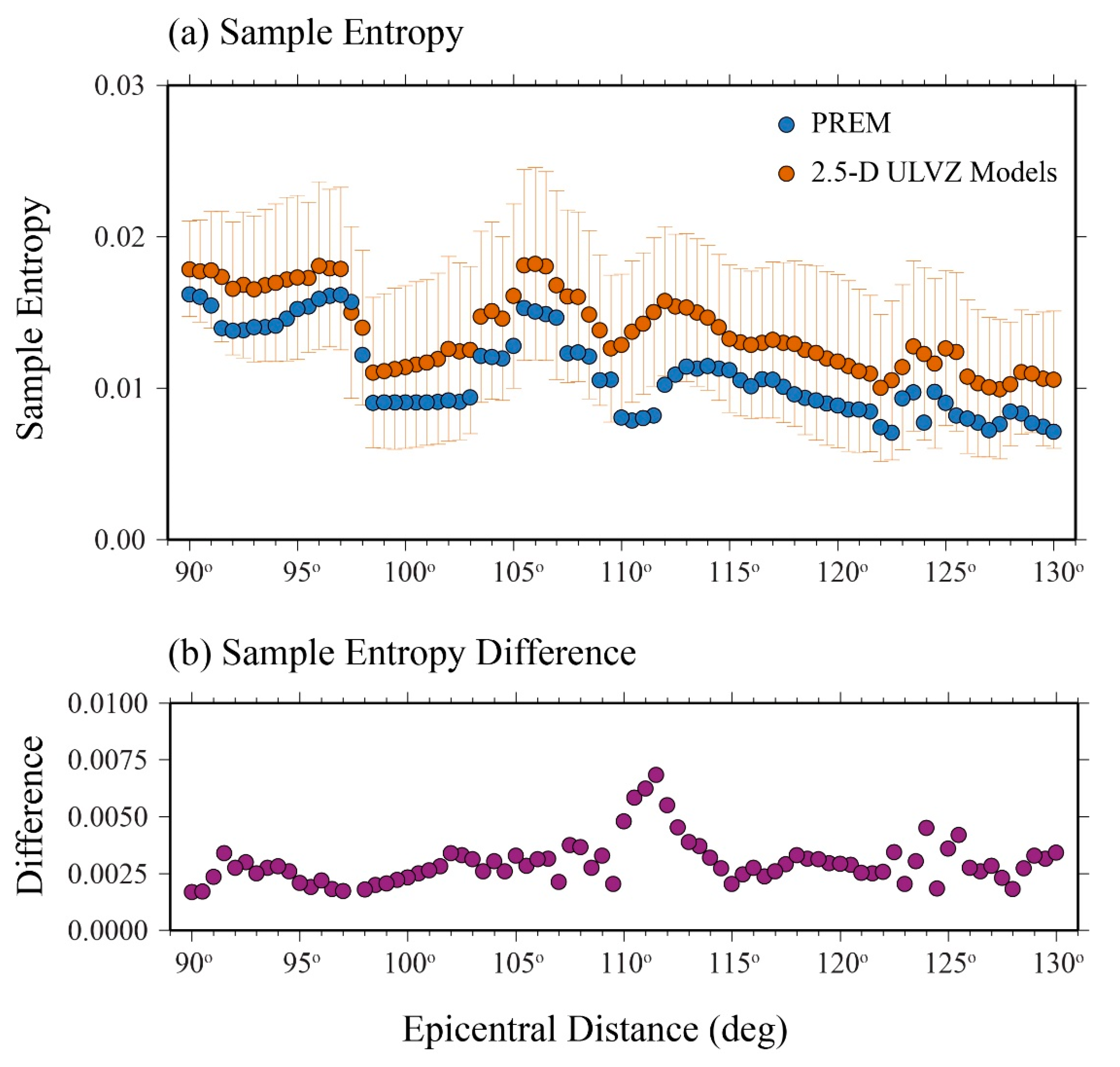
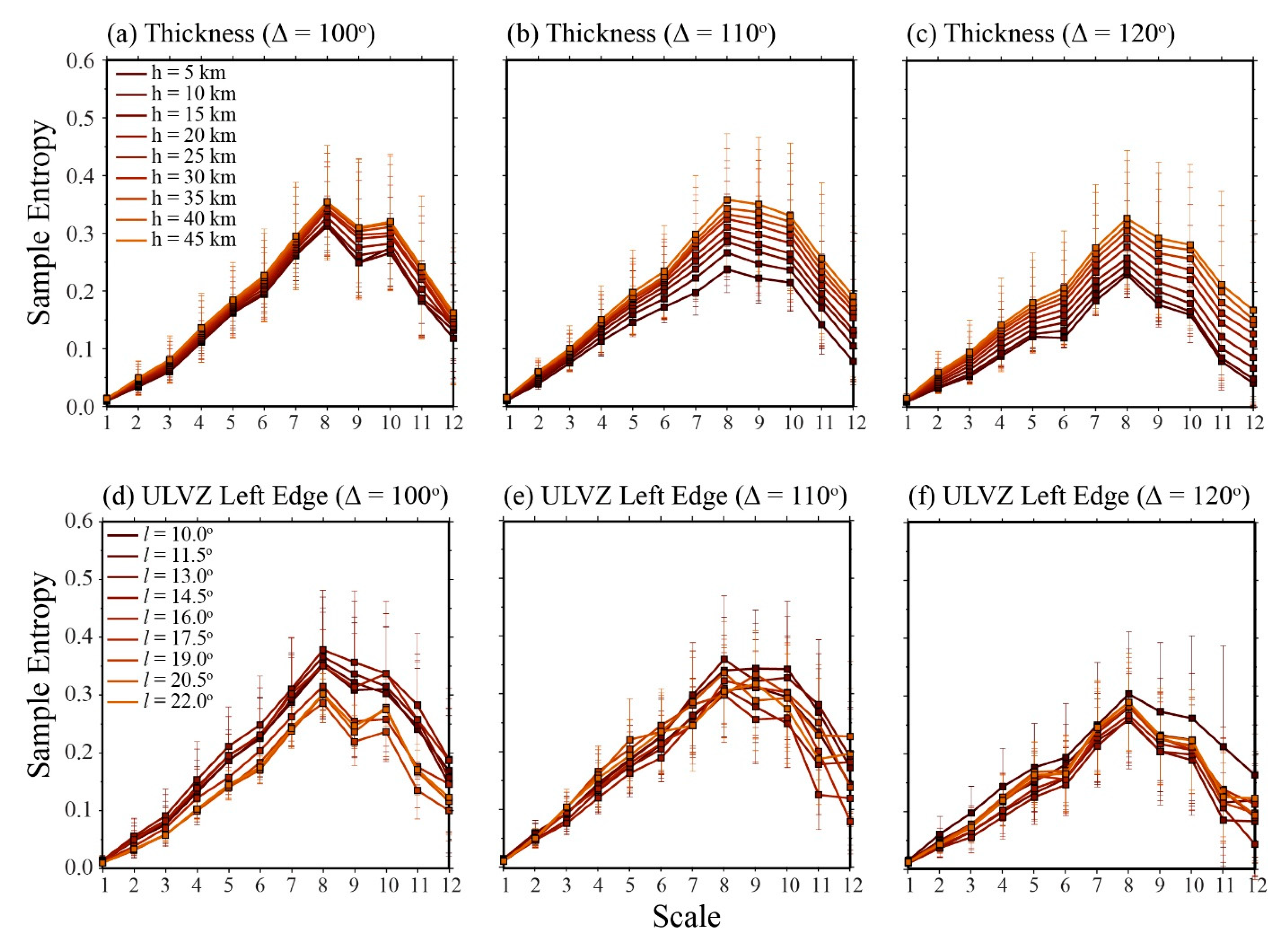
3.2. Sample Entropy of 2.5-D Models
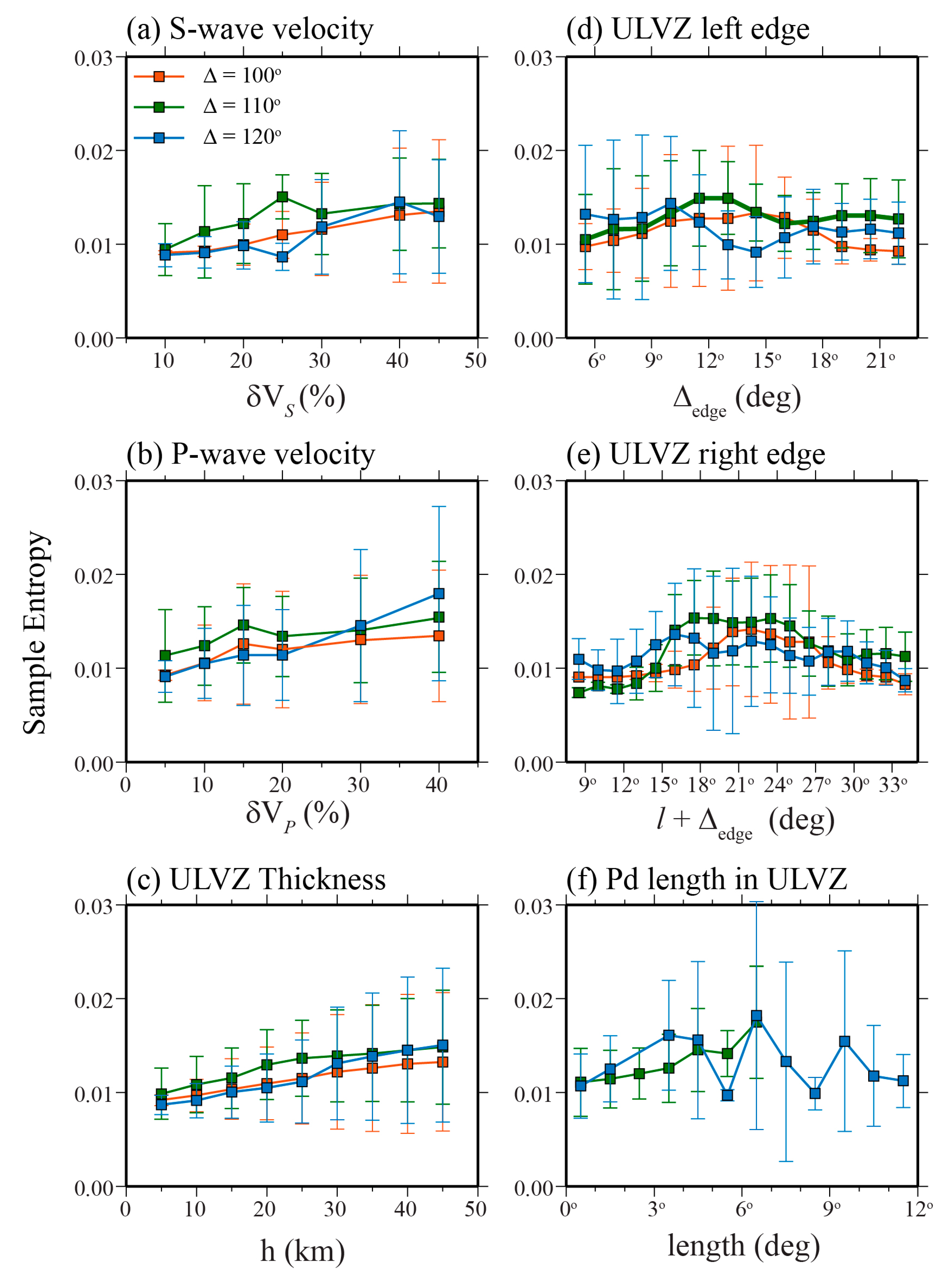
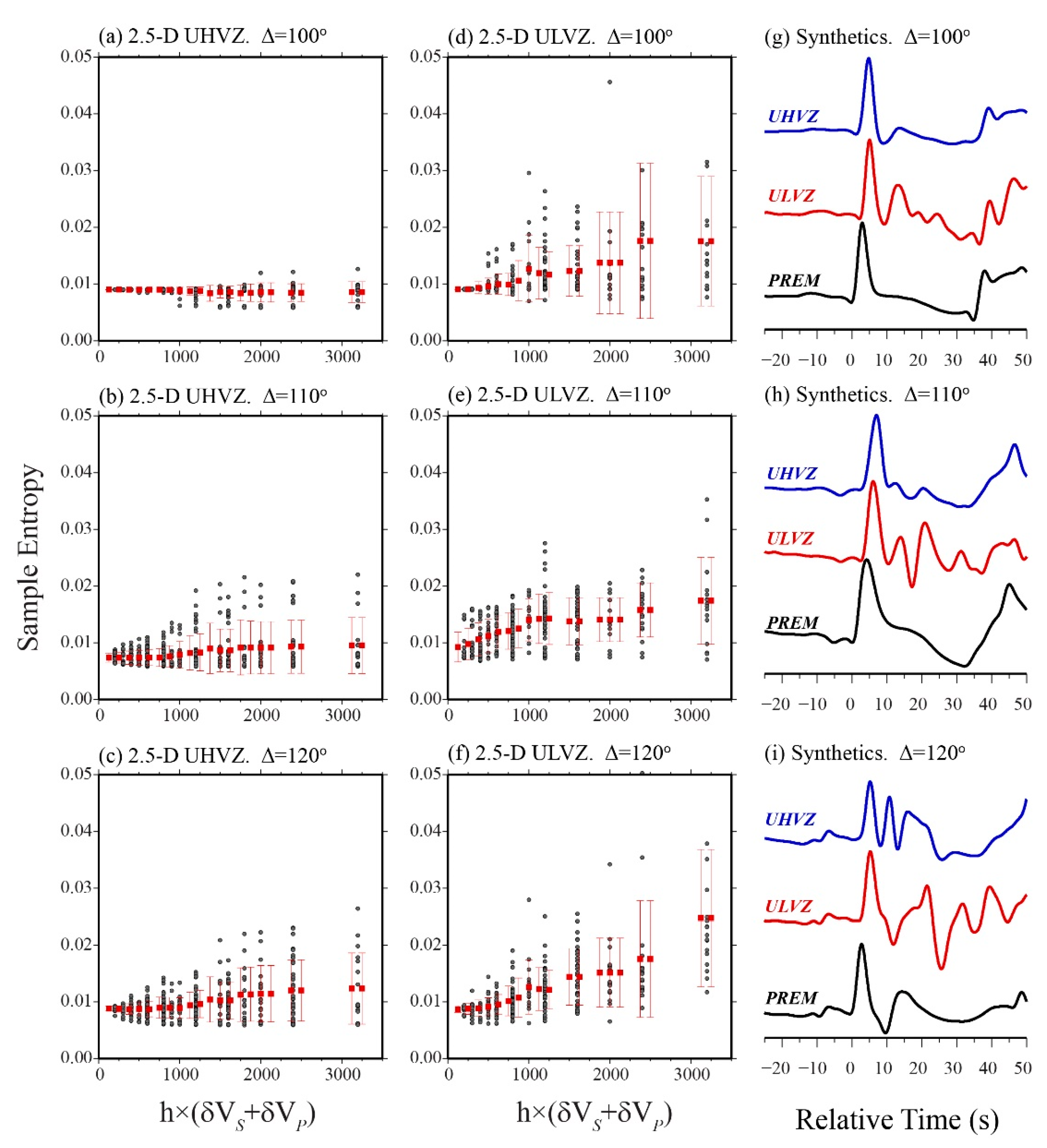
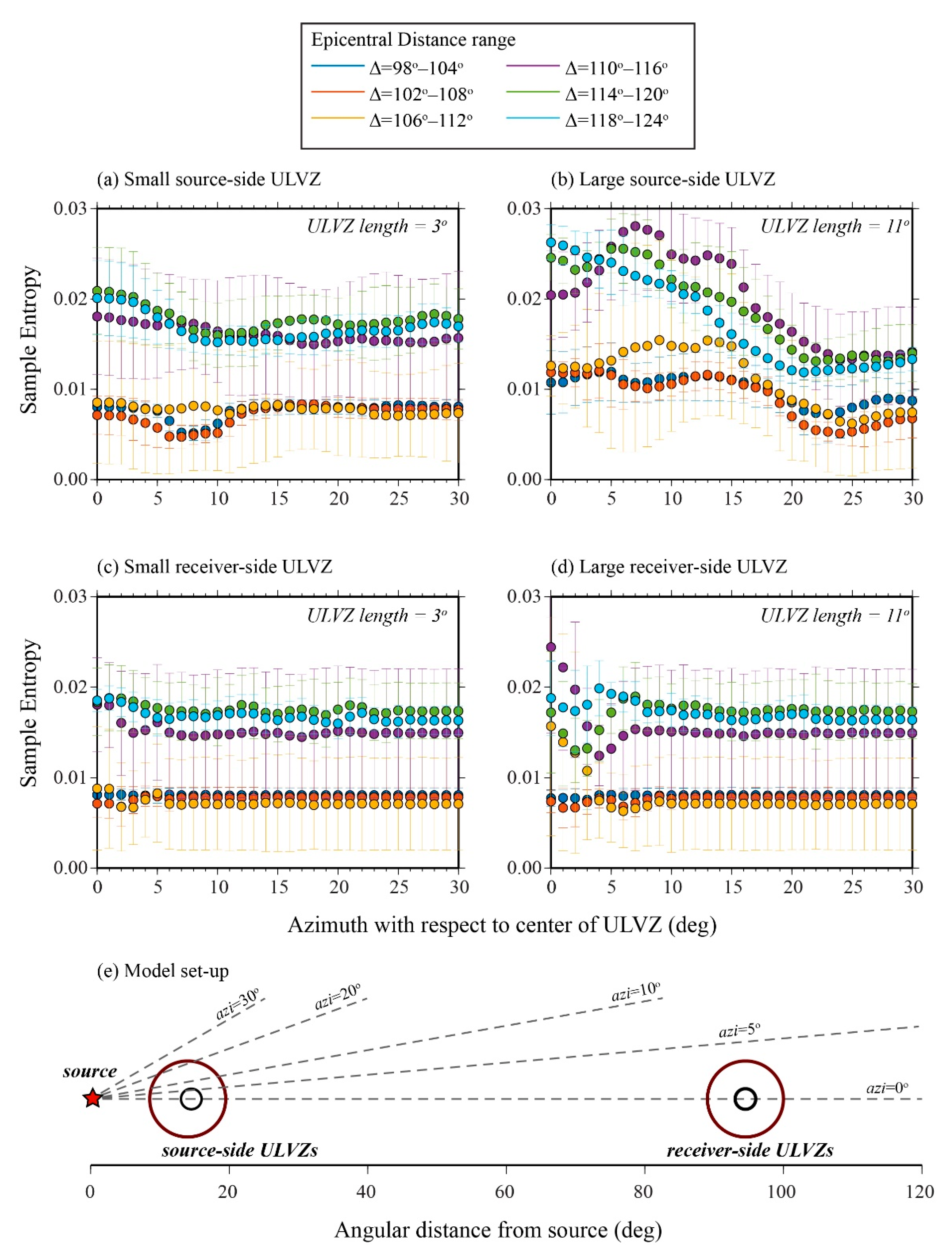
3.2.1. Sample Entropy of ULVZ Models in 2.5-D
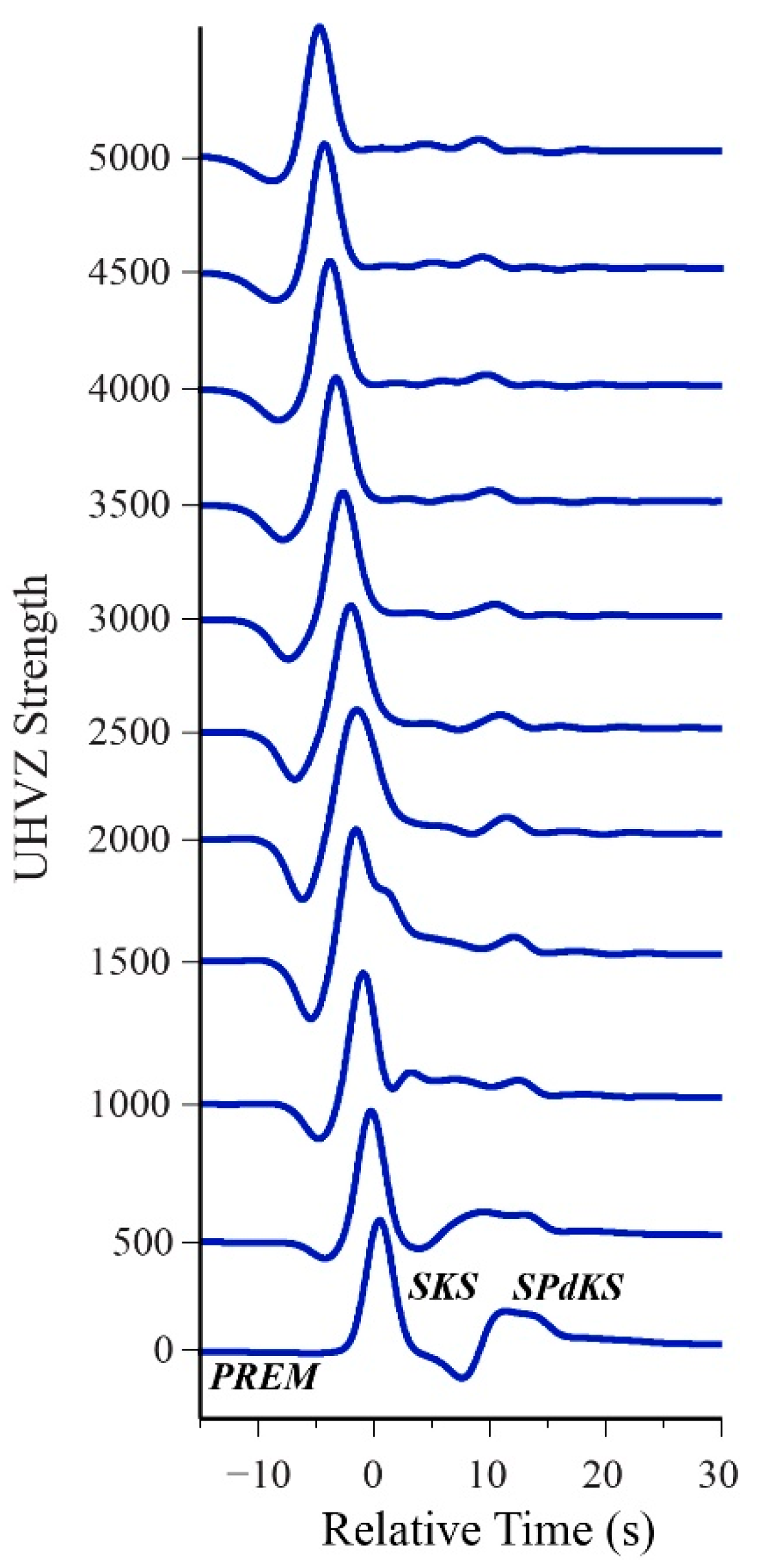
3.2.2. Sample Entropy of UHVZ Models in 2.5-D
3.3. Sample Entropy of 3-D ULVZ Models
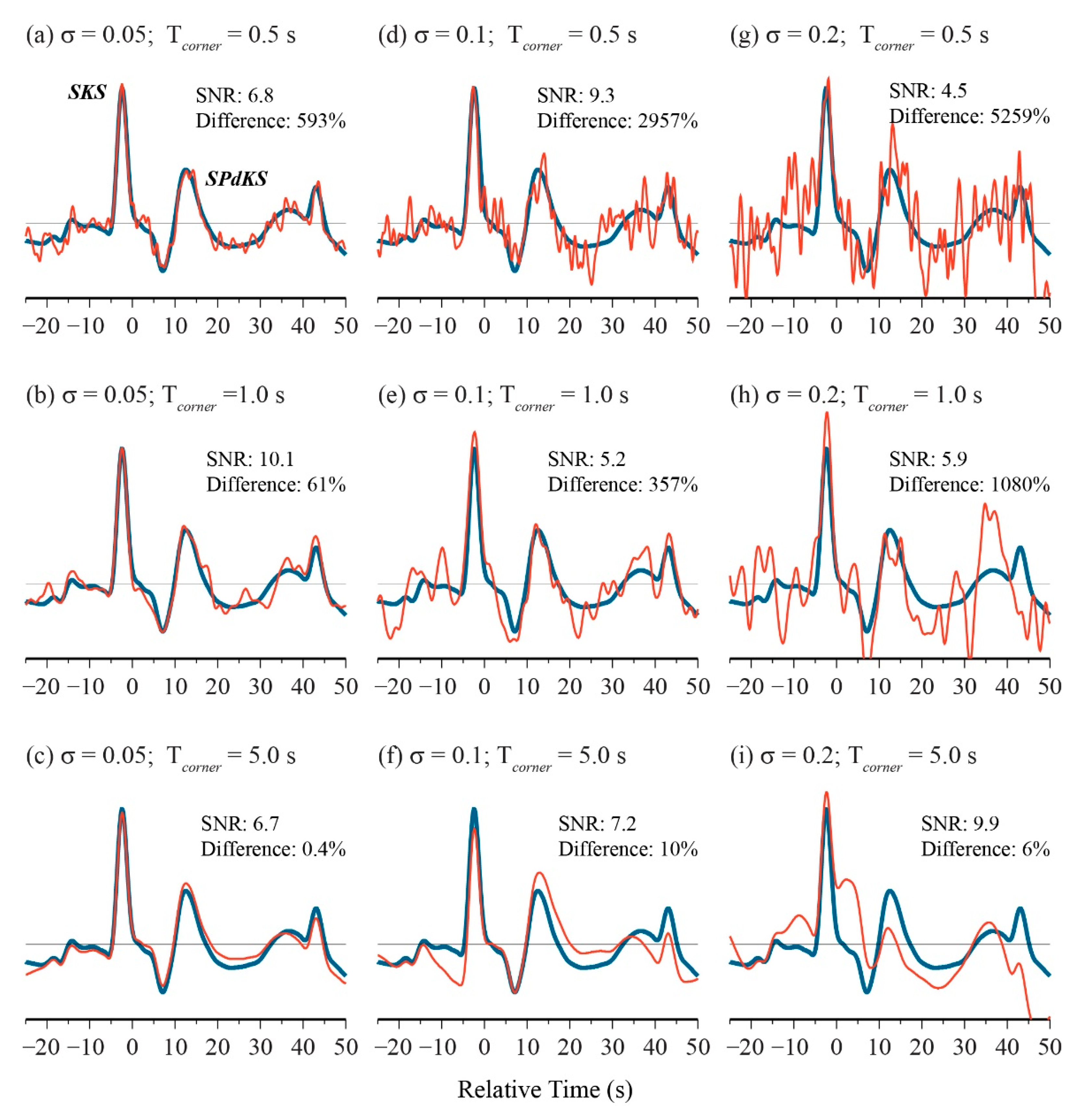
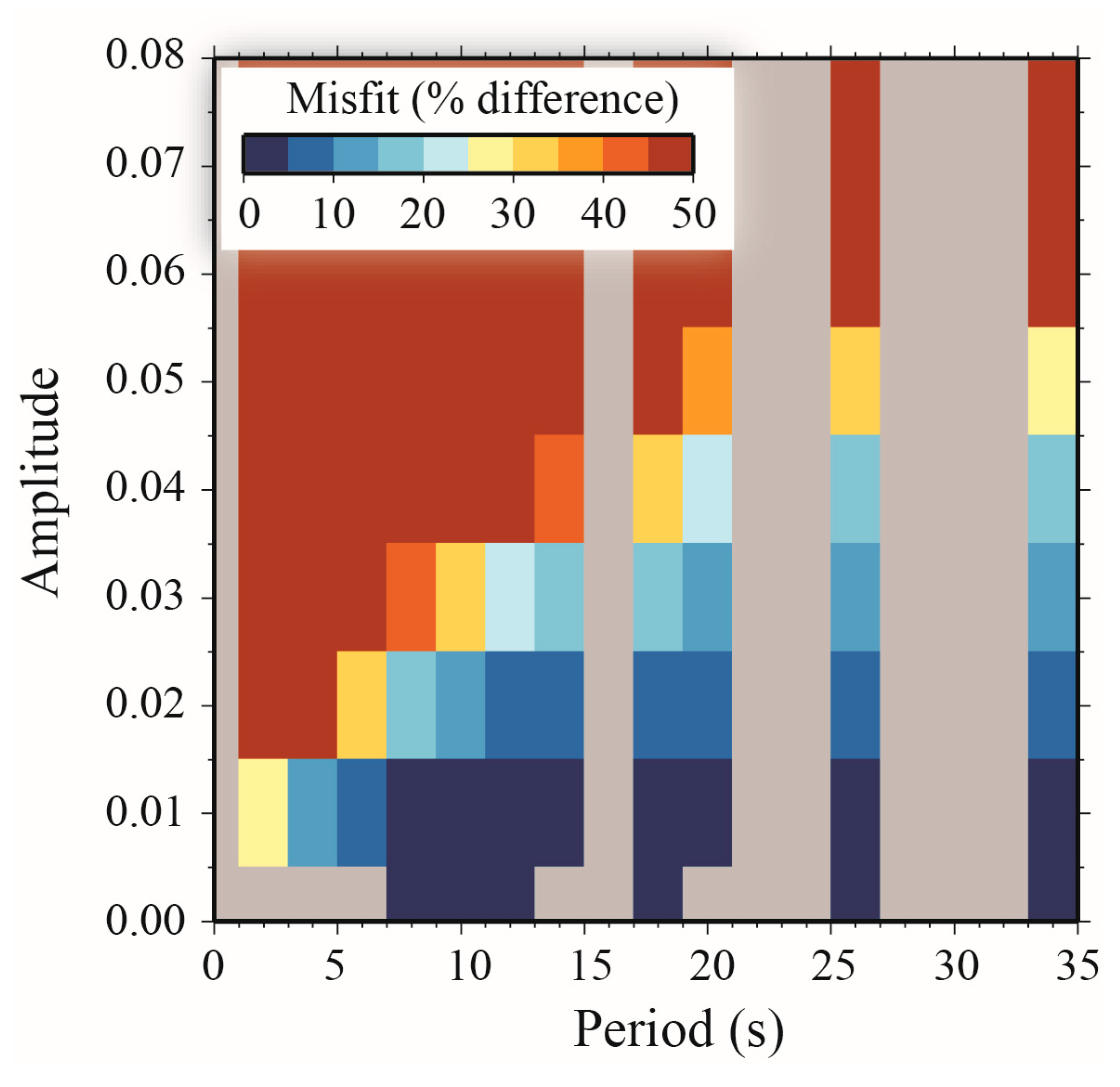
3.4. Effect of Noise
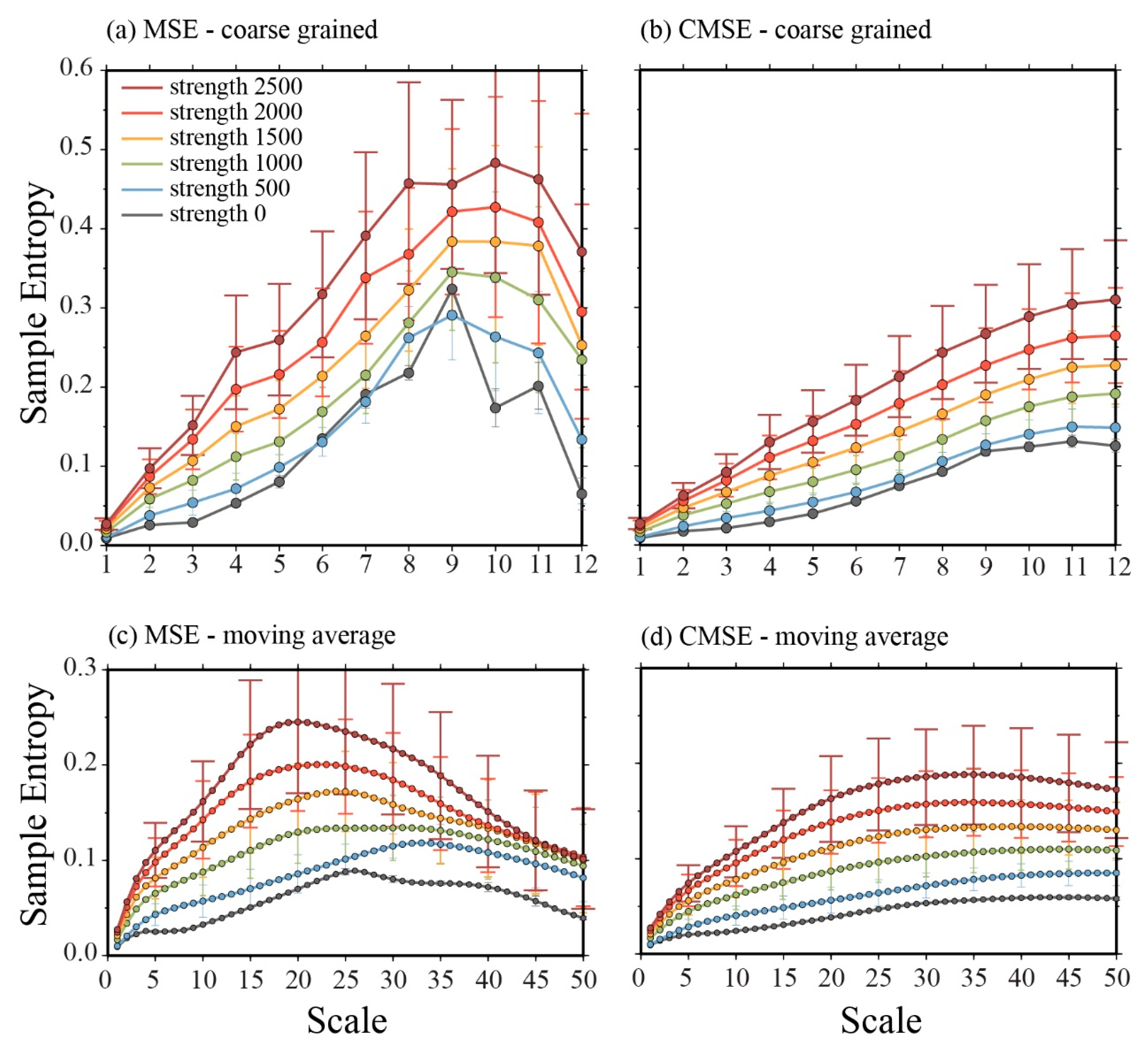
4. Synthetic Analysis of Multi-Scale and Composite Multi-Scale Sample Entropy
4.1. MSE and CMSE of 1-D ULVZ Models
4.2. MSE and CMSE of 2.5-D ULVZ Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Boehler, R. Melting of the FeFeO and the FeFeS Systems at high pressure: Constraints on core temperatures. Earth Planet. Sci. Lett. 1992, 111, 217–227. [Google Scholar] [CrossRef]
- Lay, T.; Hernlund, J.; Buffett, B.A. Core-mantle boundary heat flow. Nat. Geosci. 2008, 1, 25–32. [Google Scholar] [CrossRef]
- Garnero, E.J. Heterogeneity of the lowermost mantle. Annu. Rev. Earth Planet. Sci. 2000, 28, 509–537. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Forte, A.M.; Su, W.; Woodward, R.L. Seismic tomography and geodynamics. In Relating Geophysical Structures and Processes: The Jeffreys Volume; Aki, K., Dmowska, R., Eds.; Washington DC American Geophysical Union Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 1993; Volume 76, pp. 67–105. [Google Scholar]
- Simmons, N.A.; Forte, A.M.; Boschi, L.; Grand, S.P. GyPSuM: A joint tomographic model of mantle density and seismic wave speeds. J. Geophys. Res. Solid Earth 2010, 115, B12310. [Google Scholar] [CrossRef]
- Ritsema, J.; Deuss, A.; van Heijst, H.-J.; Woodhouse, J.H. S40RTS: A degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 2011, 184, 1223–1236. [Google Scholar] [CrossRef] [Green Version]
- Koelemeijer, P.; Ritsema, J.; Deuss, A.; Van Heijst, H.-J. SP12RTS: A degree-12 model of shear- and compressional-wave velocity for Earth’s mantle. Geophys. J. Int. 2016, 204, 1024–1039. [Google Scholar] [CrossRef] [Green Version]
- French, S.W.; Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 2015, 525, 95–99. [Google Scholar] [CrossRef]
- Houser, C.; Masters, G.; Shearer, P.; Laske, G. Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms. Geophys. J. Int. 2008, 174, 195–212. [Google Scholar] [CrossRef] [Green Version]
- Rao, B.P.; Kumar, M.R. Seismic evidence for slab graveyards atop the Core Mantle Boundary beneath the Indian Ocean Geoid Low. Phys. Earth Planet. Inter. 2014, 236, 52–59. [Google Scholar]
- Cobden, L.; Thomas, C.; Trampert, J. Seismic detection of post-perovskite inside the Earth. In The Earth’s Heterogeneous Mantle; Deschamps, F., Khan, A., Eds.; Springer Geophysics: Berlin/Heidelberg, Germany, 2015; pp. 391–440. [Google Scholar]
- Whittaker, S.; Thorne, M.S.; Schmerr, N.C.; Miyagi, L. Seismic array constraints on the D″ discontinuity beneath Central America. J. Geophys. Res. Solid Earth 2016, 121, 152–169. [Google Scholar] [CrossRef] [Green Version]
- Borgeaud, A.F.; Kawai, K.; Konishi, K.; Geller, R.J. Imaging paleoslabs in the D ′′ layer beneath Central America and the Caribbean using seismic waveform inversion. Sci. Adv. 2017, 3, e1602700. [Google Scholar] [CrossRef] [Green Version]
- Garnero, E.J.; McNamara, A.K.; Shim, S.-H. Continent-sized anomalous zones with low seismic velocity at the base of Earth’s mantle. Nat. Geosci. 2016, 9, 481–489. [Google Scholar] [CrossRef]
- Hosseini, K.; Sigloch, K.; Tsekhmistrenko, M.; Zaheri, A.; Nissen-Meyer, T.; Igel, H. Global mantle structure from multifrequency tomography using P, PP and P-diffracted waves. Geophys. J. Int. 2020, 220, 96–141. [Google Scholar] [CrossRef]
- Lay, T. Deep earth structure: Lower mantle and D″. In Seismology and the Structure of the Earth. Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 1. [Google Scholar]
- Rost, S.; Thorne, M.S.; Garnero, E.J. Imaging Global Seismic Phase Arrivals by Stacking Array Processed Short-Period Data. Seismol. Res. Lett. 2006, 77, 697–707. [Google Scholar] [CrossRef]
- Mancinelli, N.J.; Shearer, P.; Thomas, C. On the frequency dependence and spatial coherence of PKP precursor amplitudes. J. Geophys. Res. Solid Earth 2016, 121, 1873–1889. [Google Scholar] [CrossRef]
- Waszek, L.; Thomas, C.; Deuss, A. PKP precursors: Implications for global scatterers. Geophys. Res. Lett. 2015, 42, 3829–3838. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Garnero, E.J. Ultralow velocity zone locations: A global assessment. Geochem. Geophys. Geosyst. 2018, 19, 396–414. [Google Scholar] [CrossRef]
- Wen, L. Intense seismic scattering near the Earth’s core-mantle boundary beneath the Comores hotspot. Geophys. Res. Lett. 2000, 27, 3627–3630. [Google Scholar] [CrossRef]
- Idehara, K.; Yamada, A.; Zhao, D. Seismological constraints on the ultralow velocity zones in the lowermost mantle from core-reflected waves. Phys. Earth Planet. Inter. 2007, 165, 25–46. [Google Scholar] [CrossRef]
- Pachhai, S.; Dettmer, J.; Tkalčić, H. Ultra-low velocity zones beneath the Philippine and Tasman Seas revealed by a trans-dimensional Bayesian waveform inversion. Geophys. J. Int. 2015, 203, 1302–1318. [Google Scholar] [CrossRef]
- Cottaar, S.; Romanowicz, B. An unsually large ULVZ at the base of the mantle near Hawaii. Earth Planet. Sci. Lett. 2012, 355, 213–222. [Google Scholar] [CrossRef]
- Krier, J.; Thorne, M.S.; Leng, K.; Nissen-Meyer, T. A compositional component to the Samoa ultralow-velocity zone revealed through 2- and 3-D waveform modeling of SKS and SKKS differential travel-times and amplitudes. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021897. [Google Scholar] [CrossRef]
- Jenkins, J.; Mousavi, S.; Li, Z.; Cottaar, S. A high-resolution map of Hawaiian ULVZ morphology from ScS phases. Earth Planet. Sci. Lett. 2021, 563, 116885. [Google Scholar] [CrossRef]
- McNamara, A.K. A review of large low shear velocity provinces and ultra low velocity zones. Tectonophysics 2019, 760, 199–220. [Google Scholar] [CrossRef]
- Ma, X.; Sun, X.; Thomas, C. Localized ultra-low velocity zones at the eastern boundary of Pacific LLSVP. Earth Planet. Sci. Lett. 2019, 507, 40–49. [Google Scholar] [CrossRef]
- Garnero, E.J.; Helmberger, D.V. A very slow basal layer underlying large-scale low-velocity anomalies in the lower mantle beneath the Pacific: Evidence from core phases. Phys. Earth Planet. Inter. 1995, 91, 161–176. [Google Scholar] [CrossRef]
- Choy, G.L. Theoretical seismograms of core phases calculated by frequency-dependent full wave theory, and their interpretation. Geophys. J. Roy. Astron. Soc. 1977, 51, 275–311. [Google Scholar] [CrossRef] [Green Version]
- Kohler, M.D.; Vidale, J.E.; Davis, P.M. Complex scattering within D” observed on the very dense Los Angeles Region Seismic Experiment passive array. Geophys. Res. Lett. 1997, 24, 1855–1858. [Google Scholar] [CrossRef] [Green Version]
- Hutko, A.R.; Lay, T.; Revenaugh, J. Localized double-array stacking analysis of PcP: D” and ULVZ structure beneath the Cocos plate, Mexico, central Pacific, and north Pacific. Phys. Earth Planet. Inter. 2009, 173, 60–74. [Google Scholar] [CrossRef]
- Garnero, E.J.; Vidale, J.E. ScP; a probe of ultralow velocity zones at the base of the mantle. Geophys. Res. Lett. 1999, 26, 377–380. [Google Scholar] [CrossRef] [Green Version]
- Hansen, S.E.; Carson, S.E.; Garnero, E.J.; Rost, S.; Yu, S. Investigating ultra-low velocity zones in the southern hemisphere using an Antarctic dataset. Earth Planet. Sci. Lett. 2020, 536, 116142. [Google Scholar] [CrossRef]
- Ni, S.; Helmberger, D.V. Horizontal transition from fast to slow structures at the core-mantle boundary; South Atlantic. Earth Planet. Sci. Lett. 2001, 187, 301–310. [Google Scholar] [CrossRef]
- Thomas, C.; Weber, M.; Wicks, C.W.; Scherbaum, F. Small scatterers in the lower mantle observed at German broadband arrays. J. Geophys. Res. 1999, 104, 15073–15088. [Google Scholar] [CrossRef]
- Thomas, C.; Kendall, J.-M.; Helffrich, G. Probing two low-velocity regions with PKP b-caustic amplitudes and scattering. Geophys. J. Int. 2009, 178, 503–512. [Google Scholar] [CrossRef] [Green Version]
- Rondenay, S.; Fischer, K.M. Constraints on localized core-mantle boundary structure from multichannel, broadband SKS coda analysis. J. Geophys. Res. 2003, 108, 2537. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Lekic, V.; Menard, B.; Baron, D.; Taghizadeh-Popp, M. Sequencing seismograms: A panoptic view of scattering in the core-mantle boundary region. Science 2020, 368, 1223–1228. [Google Scholar] [CrossRef]
- Yuan, K.; Romanowicz, B. Seismic evidence for partial melting at the root of major hot spot plumes. Science 2017, 357, 393–397. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Koper, K.D. Detection of a ULVZ at the base of the mantle beneath the northwest Pacific. Geophys. Res. Lett. 2009, 36, L17301. [Google Scholar] [CrossRef] [Green Version]
- Rost, S.; Garnero, E.J. Detection of an ultralow velocity zone at the core-mantle boundary using diffracted PKKPab waves. J. Geophys. Res. 2006, 111, B07309. [Google Scholar] [CrossRef] [Green Version]
- Thorne, M.S.; Garnero, E.J. Inferences on ultralow-velocity zone structure from a global analysis of SPdKS waves. J. Geophys. Res. 2004, 109, B08301. [Google Scholar] [CrossRef]
- Luo, S.-N.; Ni, S.; Helmberger, D.V. Evidence for a sharp lateral variation of velocity at the core–mantle boundary from multipathed PKPab. Earth Planet. Sci. Lett. 2001, 189, 155–164. [Google Scholar] [CrossRef]
- Vidale, J.E.; Hedlin, M.A. Evidence for partial melt at the core–mantle boundary north of Tonga from the strong scattering of seismic waves. Nature 1998, 391, 682–685. [Google Scholar] [CrossRef]
- Garnero, E.J.; Revenaugh, J.; Williams, Q.; Lay, T.; Kellogg, L.H. Ultralow velocity zone at the core-mantle boundary. In The Core-Mantle Boundary Region; American Geophysical Union: Washington, DC, USA, 1998; Volume 28, pp. 319–334. [Google Scholar]
- Pachhai, S.; Tkalčić, H.; Dettmer, J. Bayesian inference for ultralow velocity zones in the Earth’s lowermost mantle: Complex ULVZ beneath the east of the Philippines. J. Geophys. Res. Solid Earth 2014, 119, 8346–8365. [Google Scholar] [CrossRef]
- Wen, L.; Helmberger, D.V. Ultra-low velocity zones near the core-mantle boundary from broadband PKP precursors. Science 1998, 279, 1701–1703. [Google Scholar] [CrossRef] [Green Version]
- Rondenay, S.; Cormier, V.F.; Van Ark, E.M. SKS and SPdKS sensitivity to two-dimensional ultralow-velocity zones. J. Geophys. Res. Solid Earth 2010, 115, B04311. [Google Scholar] [CrossRef]
- Thorne, M.S.; Garnero, E.J.; Jahnke, G.; Igel, H.; McNamara, A.K. Mega ultra low velocity zone and mantle flow. Earth Planet. Sci. Lett. 2013, 364, 59–67. [Google Scholar] [CrossRef]
- Thorne, M.S.; Takeuchi, N.; Shiomi, K. Melting at the edge of a slab in the deepest mantle. Geophys. Res. Lett. 2019, 46, 8000–8008. [Google Scholar] [CrossRef]
- Pachhai, S.; Li, M.; Thorne, M.S.; Dettmer, J.; Tkalčić, H. Internal structure of ultralow-velocity zones consistent with origin from a basal magma ocean. Nat. Geosci. 2022, 15, 79–84. [Google Scholar] [CrossRef]
- Williams, Q.; Garnero, E.J. Seismic evidence for partial melt at the base of Earth’s mantle. Science 1996, 273, 1528–1530. [Google Scholar] [CrossRef] [Green Version]
- Berryman, J.G. Seismic velocity decrement ratios for regions of partial melt in the lower mantle. Geophys. Res. Lett. 2000, 27, 421–424. [Google Scholar] [CrossRef]
- Williams, Q.; Revenaugh, J.; Garnero, E. A correlation between ultra-low basal velocities in the mantle and hot spots. Science 1998, 281, 546–549. [Google Scholar] [CrossRef] [PubMed]
- Niu, F.; Wen, L. Strong seismic scatterers near the core-mantle boundary west of Mexico. Geophys. Res. Lett. 2001, 28, 3557–3560. [Google Scholar] [CrossRef] [Green Version]
- Thorne, M.S.; Pachhai, S.; Leng, K.; Wicks, J.K.; Nissen-Meyer, T. New candidate ultralow-velocity zone locations from highly anomalous SPdKS waveforms. Minerals 2020, 10, 211. [Google Scholar] [CrossRef] [Green Version]
- Thorne, M.S.; Leng, K.; Pachhai, S.; Rost, S.; Wicks, C.W.; Nissen-Meyer, T. The most parsimonious ultralow-velocity zone distribution from highly anomalous SPdKS waveforms. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009467. [Google Scholar] [CrossRef]
- Andrault, D.; Pesce, G.; Bouhifd, M.A.; Bolfan-Casanova, N.; Hénot, J.-M.; Mezouar, M. Melting of subducted basalt at the core-mantle boundary. Science 2014, 344, 892–895. [Google Scholar] [CrossRef]
- Wicks, J.; Jackson, J.; Sturhahn, W. Very low sound velocities in iron-rich (Mg, Fe) O: Implications for the core-mantle boundary region. Geophys. Res. Lett. 2010, 37, L15304. [Google Scholar] [CrossRef] [Green Version]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhang, D. Sound velocity and density of magnesiowüstites: Implications for ultralow-velocity zone topography. Geophys. Res. Lett. 2017, 44, 2148–2158. [Google Scholar] [CrossRef]
- Finkelstein, G.J.; Jackson, J.M.; Said, A.; Alatas, A.; Leu, B.M.; Sturhahn, W.; Toellner, T.S. Strongly anisotropic magnesiowüstite in Earth’s lower mantle. J. Geophys. Res. Solid Earth 2018, 123, 4740–4750. [Google Scholar] [CrossRef]
- Jackson, J.M.; Thomas, C. Seismic and mineral physics constraints on the D″ layer. In Mantle Convection and Surface Expressions; Marquardt, H., Ballmer, M., Cottaar, S., Konter, J., Eds.; American Geophysical Union: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Mao, W.L.; Mao, H.-k.; Sturhahn, W.; Zhao, J.; Prakapenka, V.B.; Meng, Y.; Shu, J.; Fei, Y.; Hemley, R.J. Iron-rich post-perovskite and the origin of ultralow-velocity zones. Science 2006, 312, 564–565. [Google Scholar] [CrossRef] [Green Version]
- Buffett, B.A.; Garnero, E.J.; Jeanloz, R. Sediments at the Top of Earth’s Core. Science 2000, 290, 1338–1342. [Google Scholar] [CrossRef]
- Otsuka, K.; Karato, S.-i. Deep penetration of molten iron into the mantle caused by a morphological instability. Nature 2012, 492, 243–246. [Google Scholar] [CrossRef]
- Garnero, E.J.; Jeanloz, R. Fuzzy Patches on the Earth’s Core-Mantle Boundary? Geophys. Res. Lett. 2000, 27, 2777–2780. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Kim, D.Y.; Yang, W.; Yang, L.; Meng, Y.; Zhang, L.; Mao, H.-K. FeO2 and FeOOH under deep lower-mantle conditions and Earth’s oxygen–hydrogen cycles. Nature 2016, 534, 241–244. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Hrubiak, R.; Smith, J.S. Origins of ultralow velocity zones through slab-derived metallic melt. Proc. Natl. Acad. Sci. USA 2016, 113, 5547–5551. [Google Scholar] [CrossRef] [Green Version]
- Labrosse, S.; Hernlund, J.W.; Coltice, N. A crystallizing dense magma ocean at the base of the Earth’s mantle. Nature 2007, 450, 866–869. [Google Scholar] [CrossRef]
- Rost, S.; Revenaugh, J. Seismic Detection of Rigid Zones at the Top of the Core. Science 2001, 294, 1911–1914. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Healey, J. Multiscale entropy analysis of complex heart rate dynamics: Discrimination of age and heart failure effects. In Proceedings of the Computers in Cardiology, Thessaloniki, Greece, 21–24 September 2003; pp. 705–708. [Google Scholar]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef] [Green Version]
- Balzter, H.; Tate, N.J.; Kaduk, J.; Harper, D.; Page, S.; Morrison, R.; Muskulus, M.; Jones, P. Multi-scale entropy analysis as a method for time-series analysis of climate data. Climate 2015, 3, 227–240. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.-K.; Lee, D.-Y. Composite multiscale cross-sample entropy analysis for long-term structural health monitoring of residential buildings. Entropy 2021, 23, 60. [Google Scholar] [CrossRef]
- Yu, S.; Garnero, E.J.; Shim, S.-H.; Li, M. Ultra-High Velocity Zones (UHVZs) at Earth’s core mantle boundary. In Fall Meeting 2018; American Geophysical Union: Washington, DC, USA, 2018. [Google Scholar]
- Wu, S.-D.; Wu, C.-W.; Lee, K.-Y.; Lin, S.-G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Its Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Li, W.; Shen, X.; Li, Y. A comparative study of multiscale sample entropy and hierarchical entropy and its application in feature extraction for ship-radiated noise. Entropy 2019, 21, 793. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, K.; Müller, G. Computation of Synthetic Seismograms with the Reflectivity Method and Comparison with Observations. Geophys. J. R. Astron. Soc. 1971, 23, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Kind, R.; Müller, G. Computations of SV Waves in Realistic Earth Models. J. Geophys. 1975, 41, 149–172. [Google Scholar]
- Ko, B.; Chariton, S.; Prakapenka, V.B.; Chen, B.; Yu, S.; Garnero, E.; Li, M.; Shim, S.-H. Water-induced diamond formation at the Earth’s core-mantle boundary. In Fall Meeting 2020; American Geophysical Union: Washington, DC, USA, 2020. [Google Scholar]
- Sun, D.; Helmberger, D.V.; Lai, V.H.; Gurnis, M.; Jackson, J.M.; Yang, H.-Y. Slab control on the northeastern edge of the mid-Pacific LLSVP near Hawaii. Geophys. Res. Lett. 2019, 46, 3142–3152. [Google Scholar] [CrossRef]
- Li, J.; Sun, D.; Bower, D.J. Slab control on the mega-sized North Pacific ultra-low velocity zone. Nat. Commun. 2022, 13, 1042. [Google Scholar] [CrossRef]
- Rost, S.; Garnero, E.J.; Stefan, W. Thin and intermittent ultralow-velocity zones. J. Geophys. Res. 2010, 115, B06312. [Google Scholar] [CrossRef] [Green Version]
- Rost, S.; Garnero, E.J.; Thorne, M.S.; Hutko, A.R. On the absence of an ultralow-velocity zone in the North Pacific. J. Geophys. Res. 2010, 115, B04312. [Google Scholar] [CrossRef]
- Jensen, K.J.; Thorne, M.S.; Rost, S. SPdKS analysis of ultralow-velocity zones beneath the western Pacific. Geophys. Res. Lett. 2013, 40, 4574–4578. [Google Scholar] [CrossRef] [Green Version]
- Jahnke, G. Methods for Seismic Wave Propagation on Local and Global Scales with Finite Differences. Ph.D. Thesis, Faculty of Geosciences, LMU, Munich, Germany, 2009. [Google Scholar]
- Zhang, Y.; Ritsema, J.; Thorne, M.S. Modeling the ratios of SKKS and SKS amplitudes with ultra-low velocity zones at the core-mantle boundary. Geophys. Res. Lett. 2009, 36, L19303. [Google Scholar] [CrossRef] [Green Version]
- Jahnke, G.; Thorne, M.S.; Cochard, A.; Igel, H. Global SH-wave propagation using a parallel axisymmetric spherical finite-difference scheme: Application to whole mantle scattering. Geophys. J. Int. 2008, 173, 815–826. [Google Scholar] [CrossRef] [Green Version]
- Bower, D.J.; Wicks, J.K.; Gurnis, M.; Jackson, J.M. A geodynamic and mineral physics model of a solid-state ultralow-velocity zone. Earth Planet. Sci. Lett. 2011, 303, 193–202. [Google Scholar] [CrossRef] [Green Version]
- Hier-Majumdar, S.; Revenaugh, J. Relationship between the viscosity and topography of the ultralow-velocity zone near the core–mantle boundary. Earth Planet. Sci. Lett. 2010, 299, 382–386. [Google Scholar] [CrossRef]
- Vanacore, E.A.; Rost, S.; Thorne, M.S. Ultralow-velocity zone geometries resolved by multidimensional waveform modeling. Geophys. J. Int. 2016, 206, 659–674. [Google Scholar] [CrossRef] [Green Version]
- Koper, K.D.; Burlacu, R. The fine structure of double-frequency microseisms recorded by seismometers in North America. J. Geophys. Res. Solid Earth 2015, 120, 1677–1691. [Google Scholar] [CrossRef]
- McNamara, D.E.; Buland, R.P. Ambient noise levels in the continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Ikelle, L.T.; Yung, S.K.; Daube, F. 2-D random media with ellipsoidal autocorrelation functions. Geophysics 1993, 58, 1359–1372. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, C.; Wan, J.; Zhang, W.; Guan, B.; Xiong, N. Measuring complexity and predictability of time series with flexible multiscale entropy for sensor networks. Sensors 2017, 17, 787. [Google Scholar] [CrossRef] [Green Version]
- Humeau-Heurtier, A. Multiscale entropy approaches and their applications. Entropy 2020, 22, 644. [Google Scholar] [CrossRef]
- Leng, K.; Korenaga, J.; Nissen-Meyer, T. 3-D scattering of elastic waves by small-scale heterogeneities in the Earth’s mantle. Geophys. J. Int. 2020, 223, 502–525. [Google Scholar] [CrossRef]
- Leng, K.; Nissen-Meyer, T.; van Driel, M.; Hosseini, K.; Al-Attar, D. AxiSEM3D: Broad-band seismic wavefields in 3-D global earth models with undulating discontinuities. Geophys. J. Int. 2019, 217, 2125–2146. [Google Scholar] [CrossRef] [Green Version]
- Thorne, M.S.; Zhang, Y.; Ritsema, J. Evaluation of 1D and 3D seismic models of the Pacific lower mantle with S, SKS, and SKKS traveltimes and amplitudes. J. Geophys. Res. 2013, 118, 985–995. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Wen, L. Geographic boundary of the “Pacific Anomaly” and its geometry and transitional structure in the north. J. Geophys. Res. Solid Earth 2012, 117, B09308. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Helmberger, D.V.; Ni, S.; Bower, D. Direct measures of lateral velocity variation in the deep Earth. J. Geophys. Res. 2009, 114, B05303. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wen, L. Geometry and P and S velocity structure of the “African Anomaly”. J. Geophys. Res. 2007, 112, B05313. [Google Scholar] [CrossRef]
- Sun, X.; Song, X.; Zheng, S.; Helmberger, D.V. Evidence for a chemical-thermal structure at base of mantle from sharp lateral P-wave variations beneath Central America. Proc. Natl. Acad. Sci. USA 2007, 104, 26–30. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Whittaker, S.; Thorne, M.S. D” discontinuity structure beneath the North Atlantic from Scd observations. Geophys. Res. Lett. 2015, 42, 3793–3801. [Google Scholar] [CrossRef]
- Takeuchi, N.; Obara, K. Fine-scale topography of the D” discontinuity and its correlation to volumetric velocity fluctuations. Phys. Earth Planet. Inter. 2010, 183, 126–135. [Google Scholar] [CrossRef]
- Ward, J.; Nowacki, A.; Rost, S. Lateral velocity gradients in the African lower mantle inferred from slowness space observations of multipathing. Geochem. Geophys. Geosyst. 2020, 21, e2020GC009025. [Google Scholar] [CrossRef]
- Shearer, P.M. Deep Earth Structure—Seismic Scattering in the Deep Earth. Treatise Geophys. 2007, 1, 695–729. [Google Scholar]
- Eaton, W. Investigating the Parameters Controlling the Ballistic-to-Diffusive Scattering Transition in Seismic Waves through Novel Analytical Techniques. Master’s Thesis, University of Oxford, Oxford, UK, 2021. [Google Scholar]
- Frost, D.A.; Rost, S.; Garnero, E.J.; Li, M. Seismic evidence for Earth’s crusty deep mantle. Earth Planet. Sci. Lett. 2017, 470, 54–63. [Google Scholar] [CrossRef] [Green Version]
- Haugland, S.M.; Ritsema, J.; van Keken, P.E.; Nissen-Meyer, T. Analysis of PKP scattering using mantle mixing simulations and axisymmetric 3D waveforms. Phys. Earth Planet. Inter. 2018, 276, 226–233. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pachhai, S.; Thorne, M.S.; Nissen-Meyer, T. Quantification of Small-Scale Heterogeneity at the Core–Mantle Boundary Using Sample Entropy of SKS and SPdKS Synthetic Waveforms. Minerals 2022, 12, 813. https://doi.org/10.3390/min12070813
Pachhai S, Thorne MS, Nissen-Meyer T. Quantification of Small-Scale Heterogeneity at the Core–Mantle Boundary Using Sample Entropy of SKS and SPdKS Synthetic Waveforms. Minerals. 2022; 12(7):813. https://doi.org/10.3390/min12070813
Chicago/Turabian StylePachhai, Surya, Michael S. Thorne, and Tarje Nissen-Meyer. 2022. "Quantification of Small-Scale Heterogeneity at the Core–Mantle Boundary Using Sample Entropy of SKS and SPdKS Synthetic Waveforms" Minerals 12, no. 7: 813. https://doi.org/10.3390/min12070813
APA StylePachhai, S., Thorne, M. S., & Nissen-Meyer, T. (2022). Quantification of Small-Scale Heterogeneity at the Core–Mantle Boundary Using Sample Entropy of SKS and SPdKS Synthetic Waveforms. Minerals, 12(7), 813. https://doi.org/10.3390/min12070813





