Magnetotelluric Responses of an Anisotropic 1-D Earth with a Layer of Exponentially Varying Conductivity
Abstract
:1. Introduction
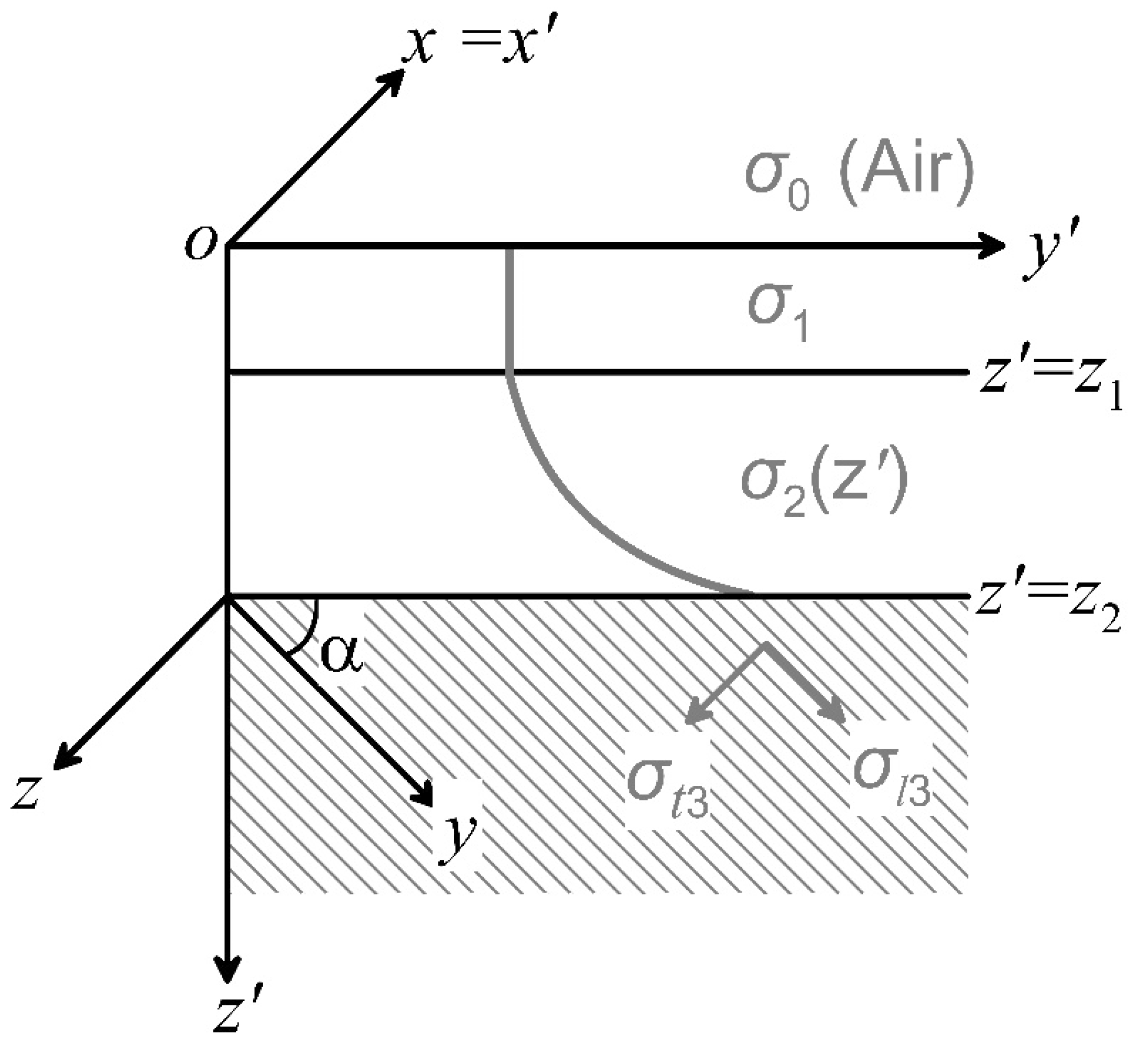
2. Model and Formulations
2.1. The Vertical Inhomogeneous and Anisotropic Model
2.2. The EM Fields in the Top Layer
2.3. The EM Fields in the Middle Layer
2.4. The EM Fields in the Bottom Layer
2.5. Evaluation of Undetermined Coefficients
2.6. Apparent Resistivity and Impedance Phase
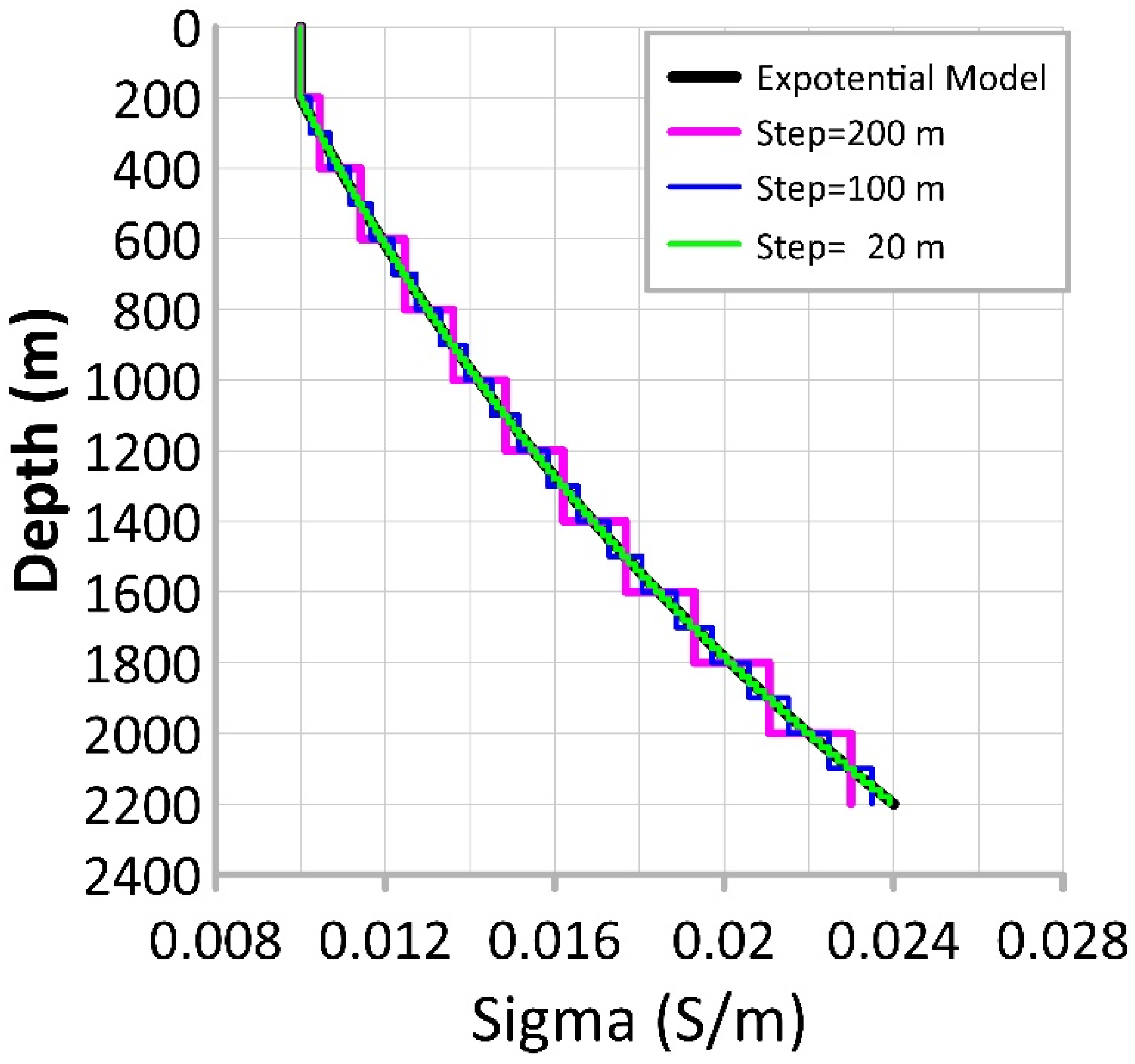
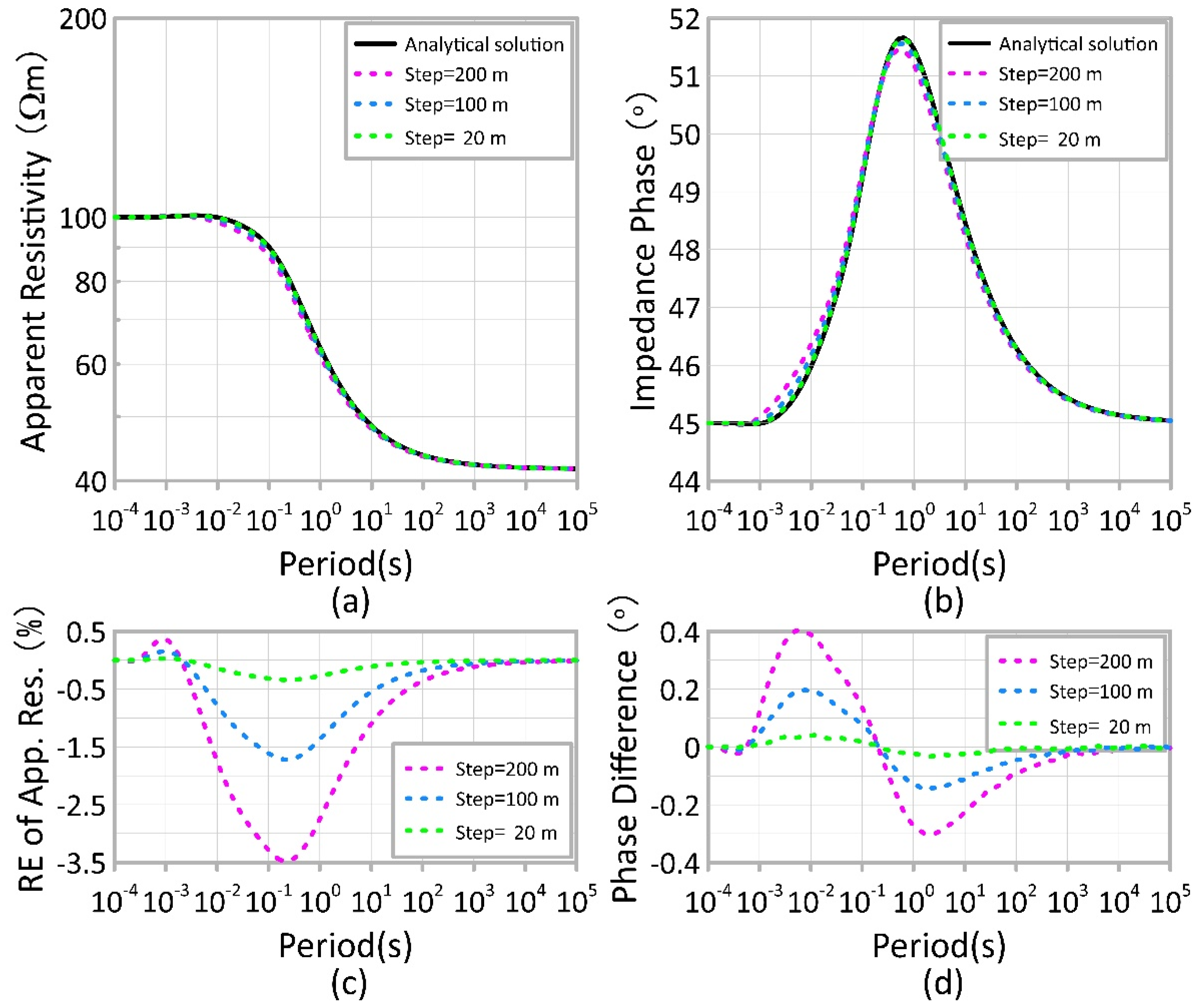
3. Validation of the Method
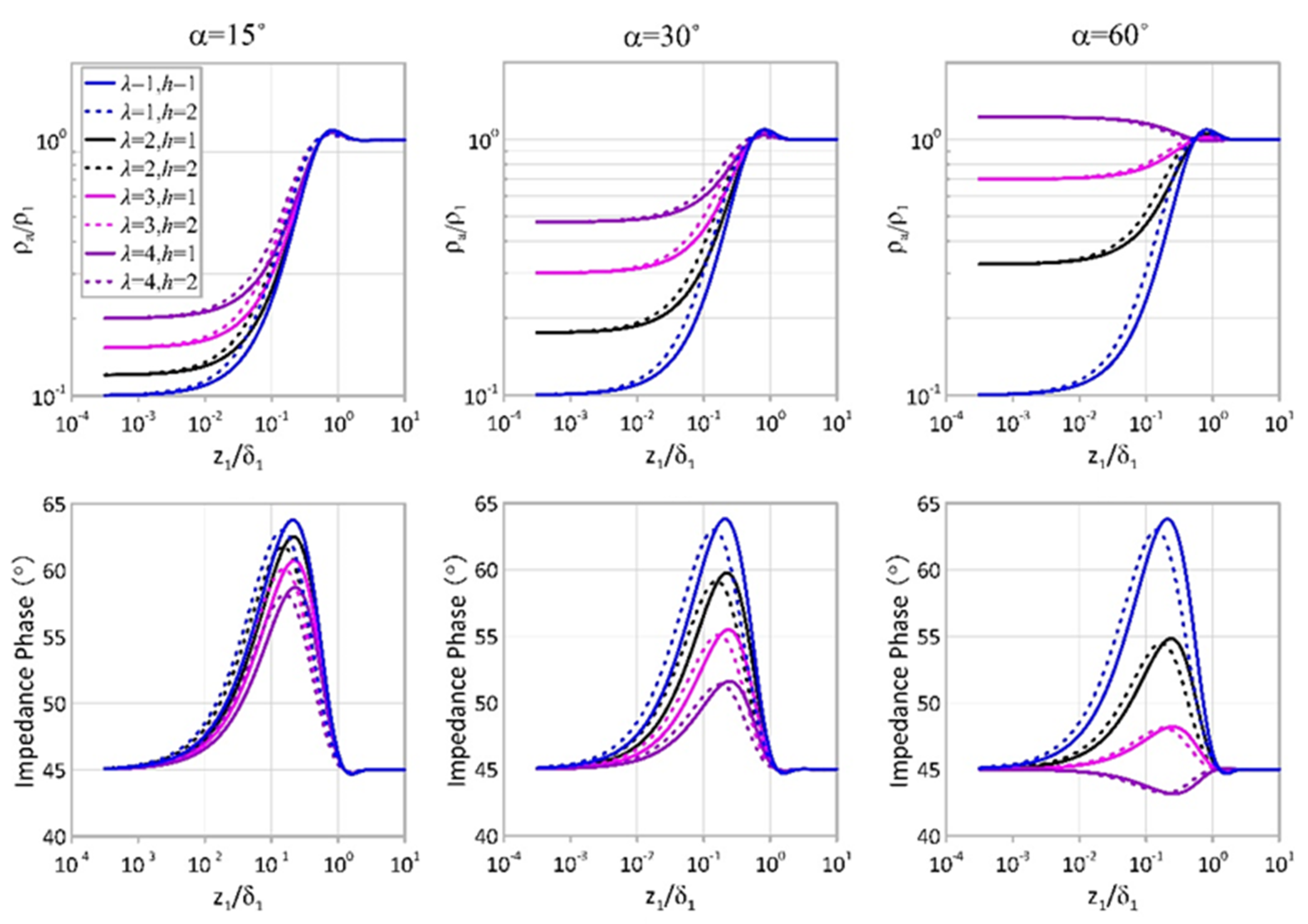
4. Dependence of the Apparent Resistivity and Impedance Phase on the Model Parameters
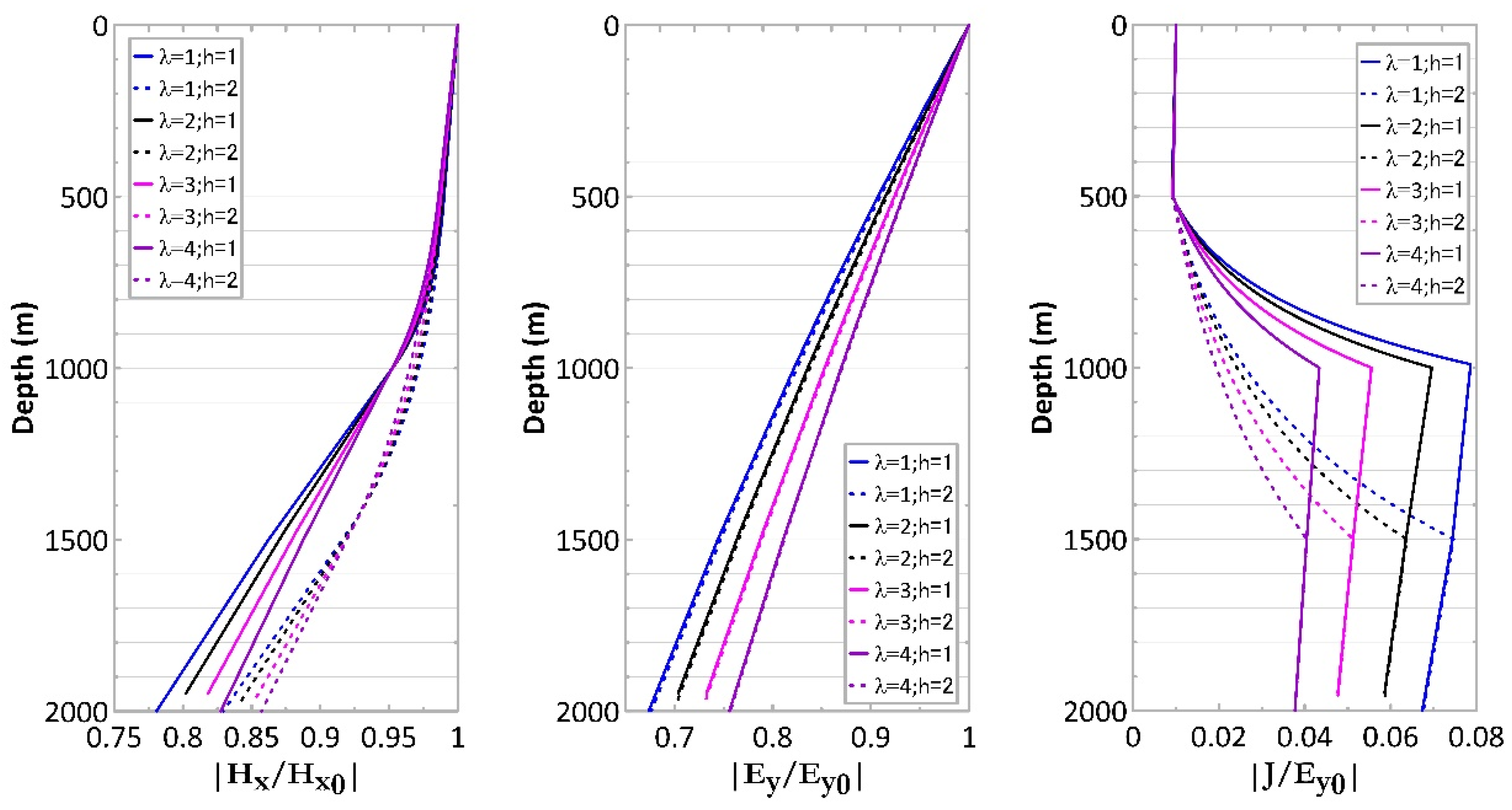
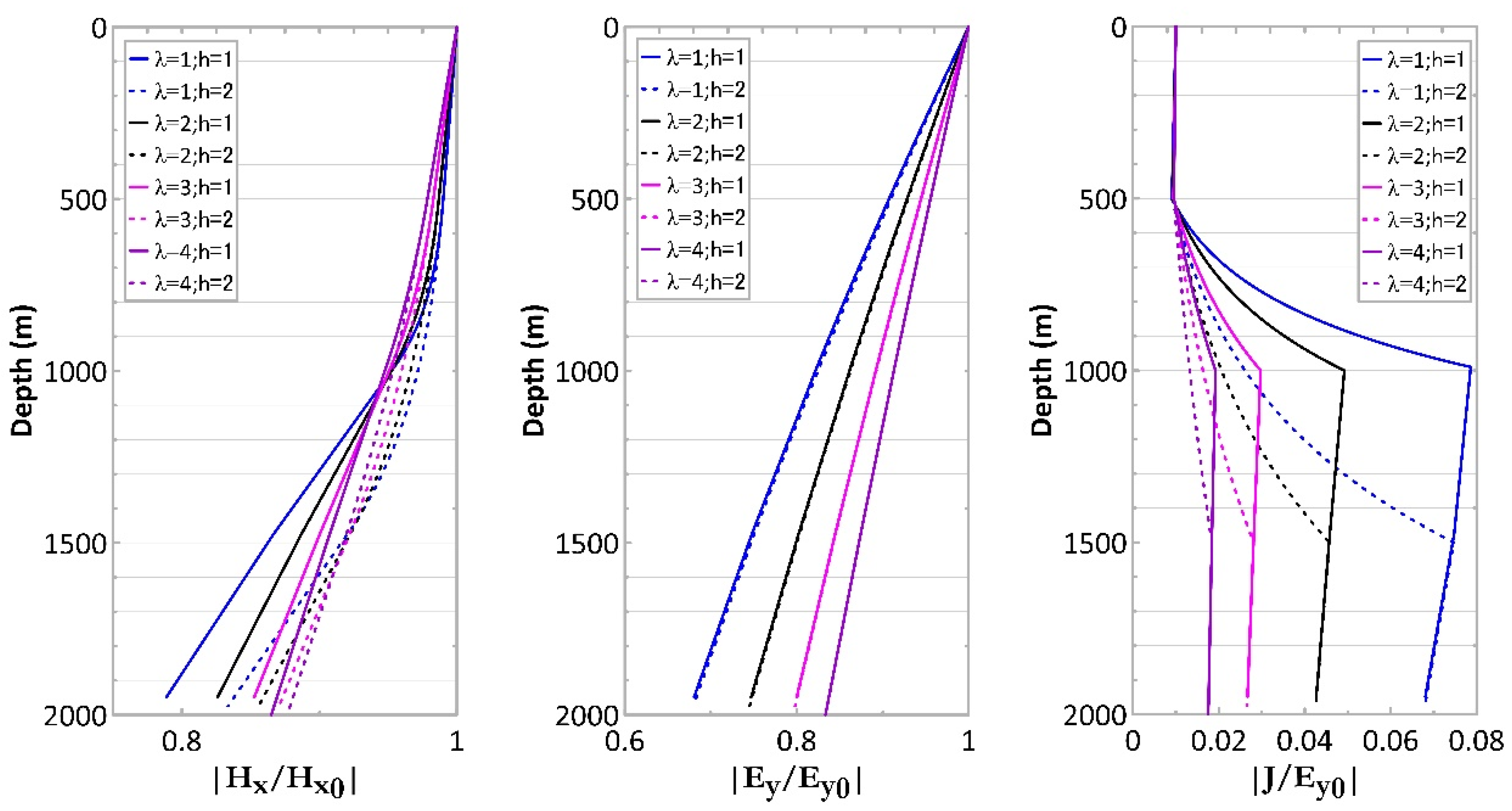
5. Discussion: Variations in the EM Fields with Model Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determination of the Unknown Coefficients in Equation (19)
Appendix B. Instructions for the Code Z1ANIS
References
- Cagniard, L. Basic Theory of the MT methods of Geophysical Propecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Tikhonov, A.N. The determination of the electrical properties of the deep layers of the earth’s crust. Dokl. Acad. Nauk. SSR 1950, 73, 295–297. (In Russian) [Google Scholar]
- Tikhonov, A.N. On determining electrical characteristics of the deep layers of the earth’s crust. In Magnetotelluric Methods; Vozoff, K., Ed.; Society of Exploration Geophysicists: Tulsa, Oklahoma, 1986; pp. 2–3. [Google Scholar]
- Wannamaker, P.E.; Stodt, J.A.; Rijo, L. PW2D—Finite Element Program for Solution of Magnetotelluric Responses of Two-Dimensional Earth Resistivity Structure; User Documentation; Earth Sciences Lab-158; Utah University Research Institute: Salt Lake City, UT, USA, 1985. [Google Scholar]
- Wannamaker, P.E.; Stodt, J.A.; Rijo, L. A stable finite-element solution for two-dimensional magnetotelluric modeling. Geophys. J. R. Astron. Soc. 1987, 88, 277–296. [Google Scholar] [CrossRef] [Green Version]
- Mackie, R.L.; Madden, T.R.; Wannamaker, P.E. Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions. Geophysics 1993, 58, 215–226. [Google Scholar] [CrossRef] [Green Version]
- Pek, J.; Verner, T. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Int. 1997, 128, 505–521. [Google Scholar] [CrossRef]
- Li, Y.G. A finite-element algorithm for electromagnetic induction in two-dimensional anisotropic conductivity structures. Geophys. J. Int. 2002, 148, 389–401. [Google Scholar] [CrossRef] [Green Version]
- Yang, C. MT numerical simulation of symmetrically 2D anisotropic media based on the finite element method. Northwest. Seismol. J. 1997, 19, 27–33. (In Chinese) [Google Scholar]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int. 2000, 140, 410–424. [Google Scholar] [CrossRef] [Green Version]
- Avdeev, D.; Avdeeva, A. 3D magnetotelluric inversion using a limited-memory quasi-Newton optimization. Geophysics 2009, 74, F45–F57. [Google Scholar] [CrossRef] [Green Version]
- Siripunvaraporn, W.; Egbert, G. WSINV3DMT: Vertical magnetic field transfer function inversion and parallel implementation. Phys. Earth Planet. Inter. 2009, 173, 317–329. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef] [Green Version]
- Čuma, M.; Gribenko, A.; Zhdanov, M.S. Inversion of magnetotelluric data using integral equation approach with variable sensitivity domain: Application to EarthScope MT data. Phys. Earth Planet. Inter. 2017, 270, 113–127. [Google Scholar] [CrossRef]
- Singh, A.; Dehiya, R.; Gupta, P.K.; Israil, M. A MATLAB based 3D modeling and inversion code for MT data. Comput. Geosci. 2017, 104, 1–11. [Google Scholar] [CrossRef]
- Grayver, A.V. Parallel three-dimensional magnetotelluric inversion using adaptive finite-element method. Part I: Theory and synthetic study. Geophys. J. Int. 2015, 202, 584–603. [Google Scholar] [CrossRef] [Green Version]
- Kordy, M.; Wannamaker, P.; Maris, V.; Cherkaev, E.; Hill, G. 3-D magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on SMP computers–Part I: Forward problem and parameter Jacobians. Geophys. J. Int. 2016, 204, 74–93. [Google Scholar] [CrossRef]
- Kruglyakov, M.; Kuvshinov, A. 3-D inversion of MT impedances and inter-site tensors, individually and jointly. New lessons learnt. Earth Planets Space 2019, 71, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Kruglyakov, M.; Geraskin, A.; Kuvshinov, A. Novel accurate and scalable 3-D MT forward solver based on a contracting integral equation method. Comput. Geosci. 2016, 96, 208–217. [Google Scholar] [CrossRef] [Green Version]
- Seama, N.; Baba, K.; Utada, H.; Toh, H.; Tada, N.; Ichiki, M.; Matsuno, T. 1-D electrical conductivity structure beneath the Philippine Sea: Results from an ocean bottom magnetotelluric survey. Phys. Earth Planet. Inter. 2007, 162, 2–12. [Google Scholar] [CrossRef]
- Ádám, A.; Novák, A.; Szarka, L. Basement depths of 3D basins, estimated from 1D magnetotelluric inversion. Acta Geod. Geophys. Hung. 2007, 42, 59–67. [Google Scholar] [CrossRef]
- Oskooi, B. 1D interpretation of the Magnetotelluric data from Travale Geothermal Field in Italy. J. Earth Space Phys. 2006, 32, 1–16. [Google Scholar]
- Ariani, E.; Srigutomo, W. 1D and 2D occam’s inversion of magnetotelluric data applied in Volcano-Geothermal area in Central Java, Indonesia. J. Phys. Conf. Ser. 2016, 739, 012039. [Google Scholar] [CrossRef]
- Lichoro, C.M.; Árnason, K.; Cumming, W. Resistivity imaging of geothermal resources in northern Kenya rift by joint 1D inversion of MT and TEM data. Geothermics 2017, 68, 20–32. [Google Scholar] [CrossRef]
- Marsenić, A. Understanding 1D magnetotelluric apparent resistivity and phase. J. Electromagn. Waves Appl. 2020, 34, 246–258. [Google Scholar] [CrossRef]
- Reddy, I.K.; Rankin, D. Magnetotelluric effect of dipping anisotropies. Geophys. Prospect. 1971, 19, 84–97. [Google Scholar] [CrossRef]
- Loewenth, D.; Landisma, M. Theory for magnetotelluric observations on surface of a layered anisotropic half space. Geophys. J. R. Astron. Soc. 1973, 35, 195–214. [Google Scholar] [CrossRef]
- Shoham, Y.; Loewenthal, D. Magnetotelluric impedance tensor computational for an anisotropic 1-Dimensional layered media. Geophysics 1975, 40, 155. [Google Scholar]
- Kaufman, A.A.; Keller, G.V. The Magnetotelluric Sounding Method. Methods in Geochemistry and Geophysics; Elsevier Scientific: Amsterdam, The Netherlands, 1981; Volume 15, p. 596. [Google Scholar]
- Yungul, S.H. Magnetotelluric sounding three-layer interpretation curves. Geophysics 1961, 26, 465–473. [Google Scholar] [CrossRef]
- Patella, D. Interpretation of magnetotelluric resistivity and phase soundings over horizontal layers. Geophysics 1976, 41, 96–105. [Google Scholar] [CrossRef]
- Mallick, K. Magnetotelluric sounding on a layered earth with transitional boundary. Geophys. Prospect. 1970, 18, 738–757. [Google Scholar] [CrossRef]
- Srivastav, J.; Niwas, S. Magnetotellurics sounding over models of continuously varying conductivity. Proc. Natl. Acad. Sci. USA India Sect. A 1976, 42, 320–327. [Google Scholar]
- Kao, D.; Rankin, D. Magnetotelluric response on inhomogeneous layered earth. Geophysics 1980, 45, 1793–1802. [Google Scholar] [CrossRef]
- Kao, D. Magnetotelluric Response on Vertically Inhomogeneous Earth. J. Geophys. Res. 1981, 86, 3027–3038. [Google Scholar] [CrossRef]
- Kao, D. Magnetotelluric response on vertically inhomogeneous earth having conductivity varying exponentially with depth. Geophysics 1982, 47, 89–99. [Google Scholar] [CrossRef]
- Banerjee, B.; Sengupta, B.J.; Pal, B.P. Apparent resistivity of a multilayered earth with a layer having exponential variation of conductivity. Geophys. Prospect. 1980, 28, 430–452. [Google Scholar] [CrossRef]
- Peterson, F.L.; Lao, C. Electric well logging of Hawaiian basaltic aquifers. Groundwater 1970, 8, 11–18. [Google Scholar] [CrossRef]
- Spichak, V.V.; Zakharova, O.K. Porosity estimation at depths below the borehole bottom from resistivity logs and electromagnetic resistivity. Near Surf. Geophys. 2016, 14, 299–306. [Google Scholar] [CrossRef]
- Asfahani, J. Porosity and hydraulic conductivity estimation of the basaltic aquifer in Southern Syria by using nuclear and electrical well logging techniques. Acta Geophys. 2017, 65, 765–775. [Google Scholar] [CrossRef]
- Berdichevsky, M.; Dmitriyev, V.; Mershchikova, N. Investigation of gradient media in deep electromagnetic sounding. 1ZV Akad. Nauk SSSR Series Fiz. Zemli 1974, 10, 61–72. [Google Scholar]
- Kim, H.-S.; Lee, K. Response of a multilayered earth with layers having exponentially varying resistivities. Geophysics 1996, 61, 180–191. [Google Scholar] [CrossRef]
- Pal, B.P. Magnetotelluric response on a layered earth with non-monotonic resistivity distribution. In Deep Electromagnetic Exploration; Narosa Publishing House: New Delhi, India, 1998; pp. 425–431. [Google Scholar]
- Berdichevsky, M.N.; Dmitriev, V.I. Magnetotellurics in the Context of the Theory of Ill-Posed Problems; Society of Exploration Geophysicists: Tulsa, OK, USA, 2002. [Google Scholar]
- Yoshio, K.; Takehiko, K. On the Phase Difference of Earth Current Induced by the Changes of the Earth’s Magnetic Field. Sci. Rep. Tohoku Univ. 1950, 2, 138–141. [Google Scholar]
- Qin, L.; Yang, C. Magnetotelluric Soundings on a Stratified Earth with Two Transitional Layers. Pure Appl. Geophys. 2020, 177, 5263–5274. [Google Scholar] [CrossRef]
- Negi, J.G.; Saraf, P.D. Inductive sounding of a stratified earth with transition layer resting on dipping anisotropic beds. Geophys. Prospect. 1973, 21, 635–647. [Google Scholar] [CrossRef]
- Kovacikova, S.; Pek, J. Generalized Riccati equations for 1-D magnetotelluric impedances over anisotropic conductors Part I: Plane wave field model. Earth Planets Space 2002, 54, 473–482. [Google Scholar] [CrossRef] [Green Version]
- Qin, L.; Yang, C.; Ding, W. Magnetotelluric responses of a vertical inhomogeneous and anisotropic resistivity structure with a transitional layer. Acta Geod. Geophys. 2022, 57, 157–176. [Google Scholar] [CrossRef]
- Chlamtac, M.; Abramovici, F. The electromagnetic fields of a horizontal dipole over a vertically inhomogeneous and anisotropic earth. Geophysics 1981, 46, 904–915. [Google Scholar] [CrossRef]
- Zima, L. The Interpretation of Resistivity Sounding over Weathered Rocks. Geophys. Trans. 1987, 32, 319–332. [Google Scholar]
- Sinha, A.K. The magnetotelluric effect in an inhomogeneous and anisotropic earth. Geoexploration 1969, 7, 9–28. [Google Scholar] [CrossRef]
- Cavaliere, T.; Jones, A.G. On the identification of a transition zone in electrical conductivity between the lithosphere and asthenosphere: A plea for more precise phase data. J. Geophys. 1984, 55, 23–30. [Google Scholar]
- Simpson, F.; Bahr, K. Practical Magnetotellurics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Chave, A.D.; Jones, A.G. The Magnetotelluric Method: Theory and Practice; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Boas, M.L. Mathematical Methods in the Physical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Persidis, S. Mathematical Handbook; ESPI Publishing: Athens, Greece, 2007. [Google Scholar]
- Negi, J.; Saraf, P. Impedance of a Plane Electromagnetic Wave at the Surface of a Layered Conducting Earth with Dipping Anisotropy. Geophys. Prospect. 1972, 20, 785–799. [Google Scholar] [CrossRef]
- Pek, J.; Santos, F.A.M. Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media. Comput. Geosci. 2002, 28, 939–950. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Ding, W.; Yang, C. Magnetotelluric Responses of an Anisotropic 1-D Earth with a Layer of Exponentially Varying Conductivity. Minerals 2022, 12, 915. https://doi.org/10.3390/min12070915
Qin L, Ding W, Yang C. Magnetotelluric Responses of an Anisotropic 1-D Earth with a Layer of Exponentially Varying Conductivity. Minerals. 2022; 12(7):915. https://doi.org/10.3390/min12070915
Chicago/Turabian StyleQin, Linjiang, Weifeng Ding, and Changfu Yang. 2022. "Magnetotelluric Responses of an Anisotropic 1-D Earth with a Layer of Exponentially Varying Conductivity" Minerals 12, no. 7: 915. https://doi.org/10.3390/min12070915
APA StyleQin, L., Ding, W., & Yang, C. (2022). Magnetotelluric Responses of an Anisotropic 1-D Earth with a Layer of Exponentially Varying Conductivity. Minerals, 12(7), 915. https://doi.org/10.3390/min12070915




