Quantitative Evaluation of Faults by Combined Channel Wave Seismic Transmission-Reflection Detection Method
Abstract
:1. Introduction
2. Method
2.1. Dispersion Analysis and the Elliptical Tangent Method
2.2. Logistic Regression Model
2.3. Neural Network Model
2.4. Calculation of the Fractional Dimension
3. Experimental Test
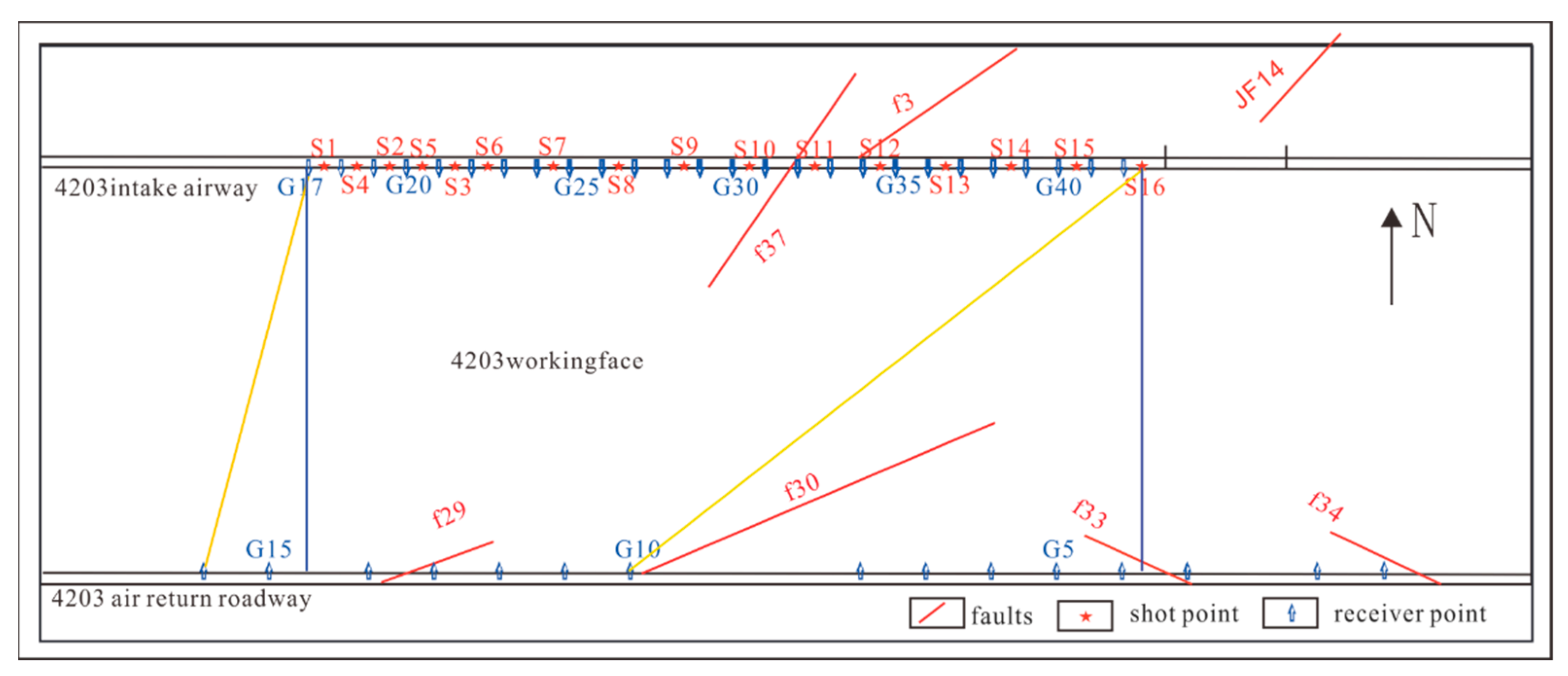
3.1. Test Site Layout and the Actual Measurement System
3.2. Geophones and Source Installation
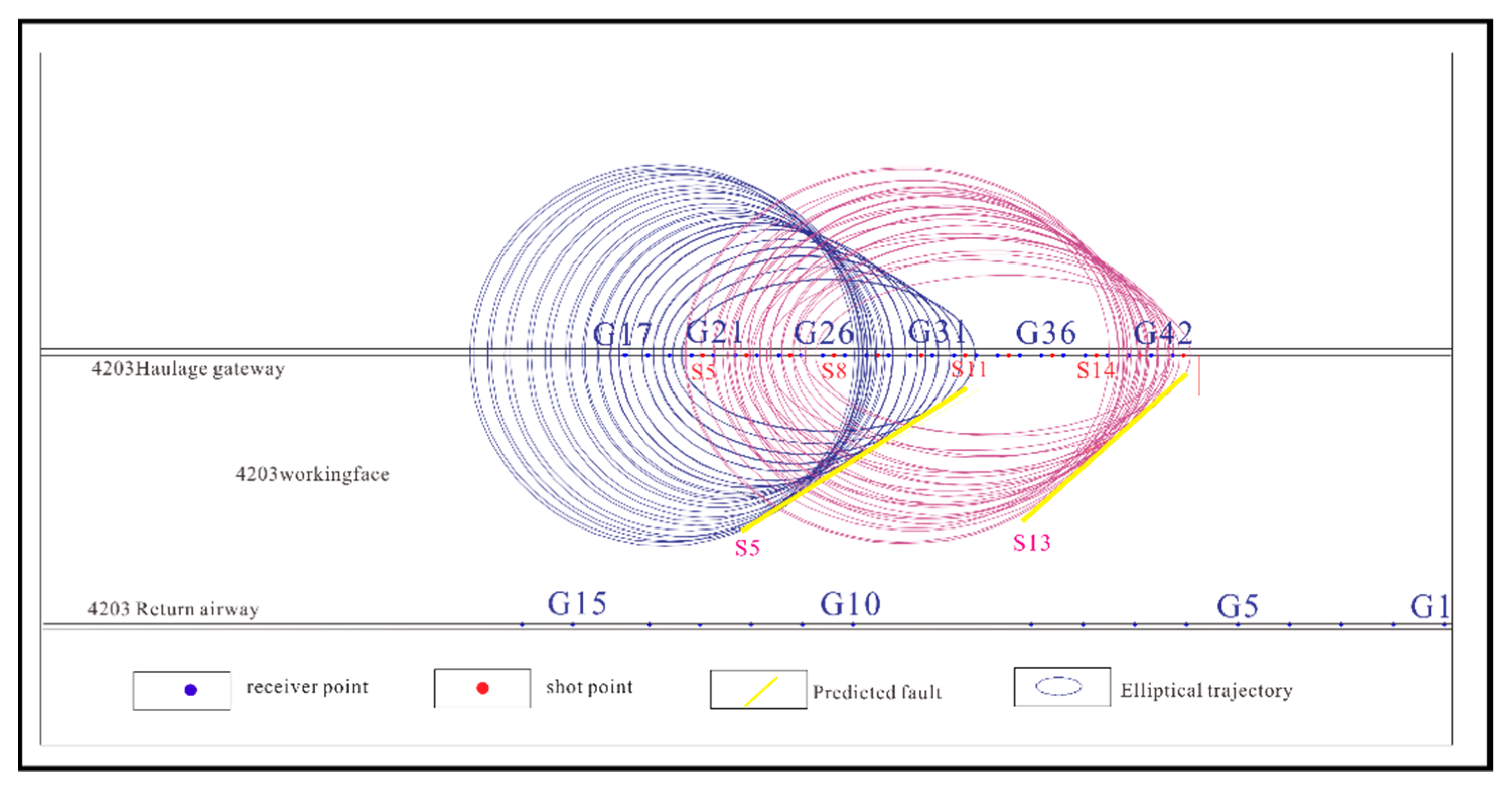
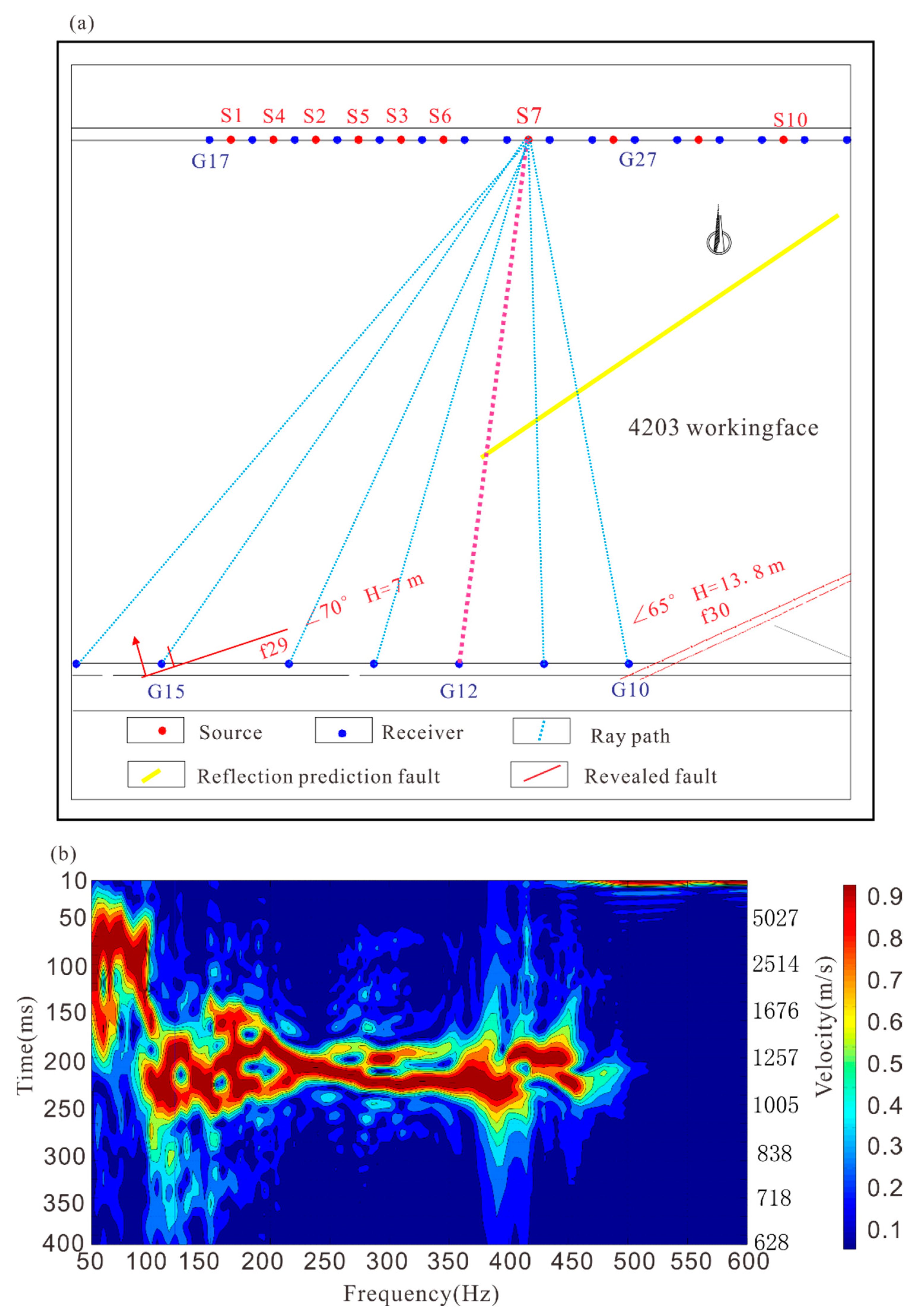
3.3. Velocity Analysis and Elliptic Tangent Offset
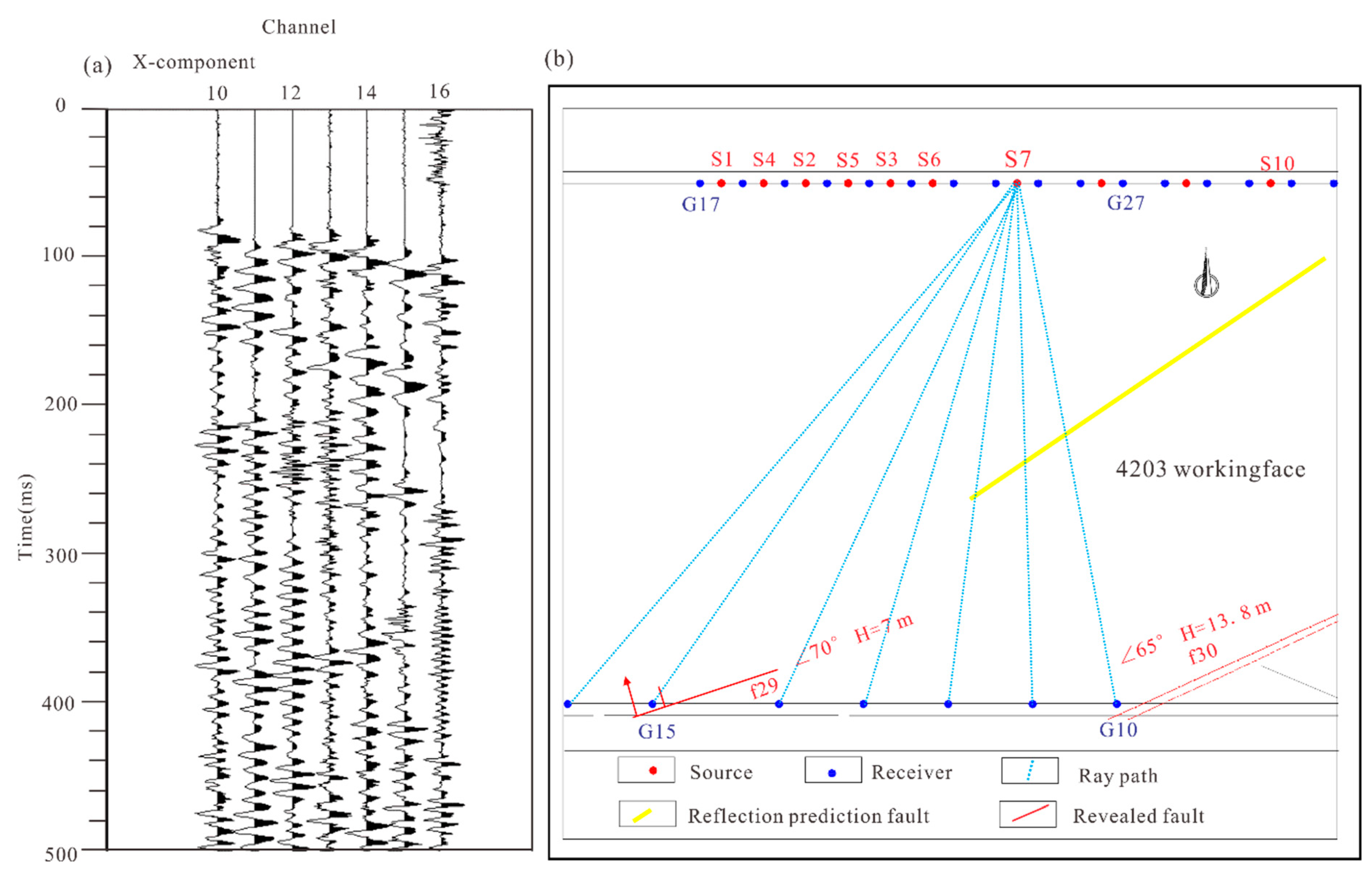
3.4. Classification Feature Extraction and Fault Location Extension
3.5. Fault Throw Prediction
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Q.S.; Wu, Q.L.; Yuan, A.Y.; Wu, Y. Analysis of Mining Effect and Fault Stability Under the Influence of Normal Faults. Geotech. Geol. Eng. 2021, 39, 49–63. [Google Scholar] [CrossRef]
- Hu, Y.; Mcmechan, G.A. Imaging mining hazards within coalbeds using prestack wave equation migration of in-seam seismic survey data: A feasibility study with synthetic data. J. Appl. Geophys. 2007, 63, 24–34. [Google Scholar] [CrossRef]
- Liu, H.H.; Cao, Y.Q. Technologies of Preventing Coal Mine Water Hazards for Sustainable Developmentin North China. Geotech. Geol. Eng. 2011, 29, 1–5. [Google Scholar]
- Pei, X. Signal acquisition method for 3D seismic exploration in high density coal mining area. Arab. J. Geosci. 2020, 13, 712. [Google Scholar] [CrossRef]
- Xiao, Y.L.; Wu, R.X.; Yan, J.P.; Zhang, P.S. Field strength propagation law of radio wave penetration and effective perspective width for coal face. J. China Coal Soc. 2017, 42, 712–718. [Google Scholar]
- Qi, S.W.; Sun, J.Z.; He, H. Review of Rayleigh Wave Exploration. Prog. Geophys. 2002, 17, 630–635. (In Chinese) [Google Scholar]
- Wang, B.; Liu, S.D.; Zhou, F.B.; Zheng, J. Diffraction characteristics of small fault ahead of tunnel face in coal roadway. Earth Sci. Res. J. 2017, 21, 95–99. [Google Scholar] [CrossRef]
- Peng, S.P.; Yang, F. Fine geological radar processing and interpretation. Appl. Geophys. 2004, 1, 89–94. [Google Scholar] [CrossRef]
- Hu, G.Z.; Teng, J.W.; Pi, J.L.; Wang, W.; Qiao, Y.H. In-seam seismic exploration techniques—A geophsical method predictting coal-Mine disaster. Prog. Geophys. 2013, 28, 439–451. (In Chinese) [Google Scholar]
- Evison, F.F. A coal seam as a guide for seismic energy. Nature 1955, 176, 1224–1225. [Google Scholar] [CrossRef]
- Krey, T.C. Channel waves as a tool of applied geophysics in coal mining. Geophysics 1963, 28, 701–714. [Google Scholar] [CrossRef]
- Edward, S.A.; Asten, M.W.; Drake, L.A. P-SV wave scattering by coal seam inhomogeinities. Geophysics 1985, 50, 214–223. [Google Scholar] [CrossRef]
- Buchanan, D.J. The scattering of SH-channel waves by a fault in a coal seam. Geophys. Prospect. 1986, 34, 343–365. [Google Scholar] [CrossRef]
- Cheng, J.Y.; Ji, G.Z.; Zhu, P.M. Love channel-waves dispersion characteristic analysis of typical coal models. J. China Coal Soc. 2012, 37, 67–72. (In Chinese) [Google Scholar]
- Buchanan, D.J. The propagation of attenuated SH channel waves. Geophys. Prospect. 1978, 26, 16–28. [Google Scholar] [CrossRef]
- Mason, I.M.; Buchanan, D.J.; Booer, A.K. Channel wave mapping of coal seams in the United Kingdom. Geophysics 1980, 45, 1131–1143. [Google Scholar] [CrossRef]
- Wang, W.; Gao, X.; Li, S.Y.; Yue, Y.; Hu, G.Z.; Li, Y.Y. Channel wave tomography method and its application in coal mine exploration: An example from Henan Yima Mining Area. Chin. J. Geophys. 2012, 55, 1054–1062. (In Chinese) [Google Scholar]
- Schneider, W.A. The common depth point stack. Proc. IEEE 1984, 72, 1238–1254. [Google Scholar] [CrossRef]
- Hua, B.; Mcmechan, G.A. Parsimonious 3D post-stack Kirchhoff depth migration. Geophys. Prospect. 2005, 53, 507–522. [Google Scholar] [CrossRef]
- Teng, J.W.; Li, S.Y.; Jia, M.; Lian, J.; Liu, G.D.; Wang, W.; Volker, S.; Feng, L.; Yao, X.S.; Wang, K.; et al. Research and application of in-seam seismic survey technology for disaster-causing potential geology anomalous body in coal seam. Acta Geol. Sin. 2019, 94, 10–26. (In English) [Google Scholar] [CrossRef]
- Buchanan, D.J.; Jackson, P.; Davis, D. Attenuation and anisotropy of channel waves in coal seams. Geophysics 1983, 48, 133–147. [Google Scholar] [CrossRef]
- Krey, T.; Arnetzb, H.; Knecht, M. Theoretical and practical aspect of absorption the application of in-seamse is miccoal exploration. Geophysics 1982, 47, 1645–1656. [Google Scholar] [CrossRef]
- Rader, D.; Schott, W.; Dresen, L.; Ruter, H. Calculation of dispersion curves and amplitude-depth distributions of Love channel waves in horizontally-layered media. Geophys. Prospect. 2010, 33, 800–816. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Y. Dispersion calculation method based on S-transform and coordinate rotation for Love channel waves with two components. Acta Geophys. 2017, 65, 757–764. [Google Scholar] [CrossRef]
- Wang, B.; Liu, S.D.; Zhou, F.B.; Hu, Z.A.; Huang, L.Y.; Jiang, Y.H. Dispersion characteristics of SH transmitted channel waves and comparative study of dispersion analysis methods. J. Comput. Theor. Nanosci. 2016, 13, 1468–1474. [Google Scholar] [CrossRef]
- Ji, G.Z.; Li, H.; Wei, J.C.; Yang, S.T. Preliminary study on wave field and dispersion characteristics of channel waves in VTI coal seam media. Acta Geophys. 2019, 67, 1379–1390. [Google Scholar] [CrossRef]
- Ge, M.; Wang, H.; Hardy, H.R.; Ramani, R. Void detection at an anthracite mine using an in-seam seismic method. Int. J. Coal Geol. 2008, 73, 201–212. [Google Scholar] [CrossRef]
- Arnold, B.; Robertson, C. Autoregressive logistic processes. J. Appl. Probab. 1989, 26, 524–531. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S.; Mansor, S.; Buchroithner, M.; Jamaluddin, N.; Khujaimah, Z. Utilization of optical remote sensing data and geographic information system tools for regional landslide hazard analysis by using binomial logistic regression model. J. Appl. Remote Sens. 2008, 2, 023542. [Google Scholar]
- Wu, Y.H.; Wang, W.; Zhu, G.W.; Wang, P. Application of seismic multiattribute machine learning to determine coal strata thickness. J. Geophys. Eng. 2021, 18, 834–844. [Google Scholar] [CrossRef]
- Ke, B.; Pan, R.; Zhang, J.; Wang, W.; Hu, Y.; Lei, G.; Chi, X.; Ren, G.; You, Y. Parameter Optimization and Fragmentation Prediction of Fan-Shaped Deep Hole Blasting in Sanxin Gold and Copper Mine. Minerals 2022, 12, 788. [Google Scholar] [CrossRef]
- Wu, J.R. On a linearity between fractal dimension and order of fractional calculus in Hölder space. Appl. Math. Comput. 2020, 385, 1–11. [Google Scholar] [CrossRef]
- Wang, P.X.; Shi, H.; Yang, X.B.; Mi, J. Three-way k-means: Integrating k-means and three-way decision. Int. J. Mach. Learn. Cybern. 2019, 10, 2767–2777. [Google Scholar] [CrossRef]




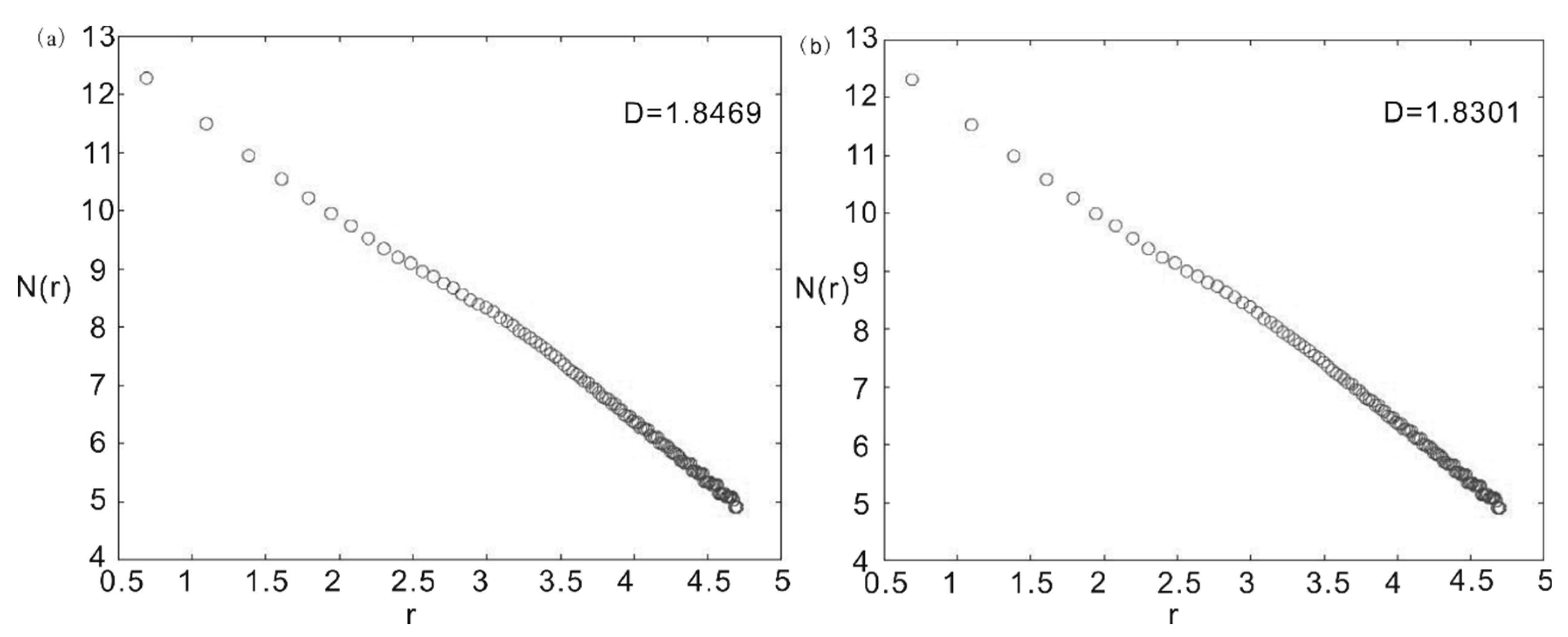
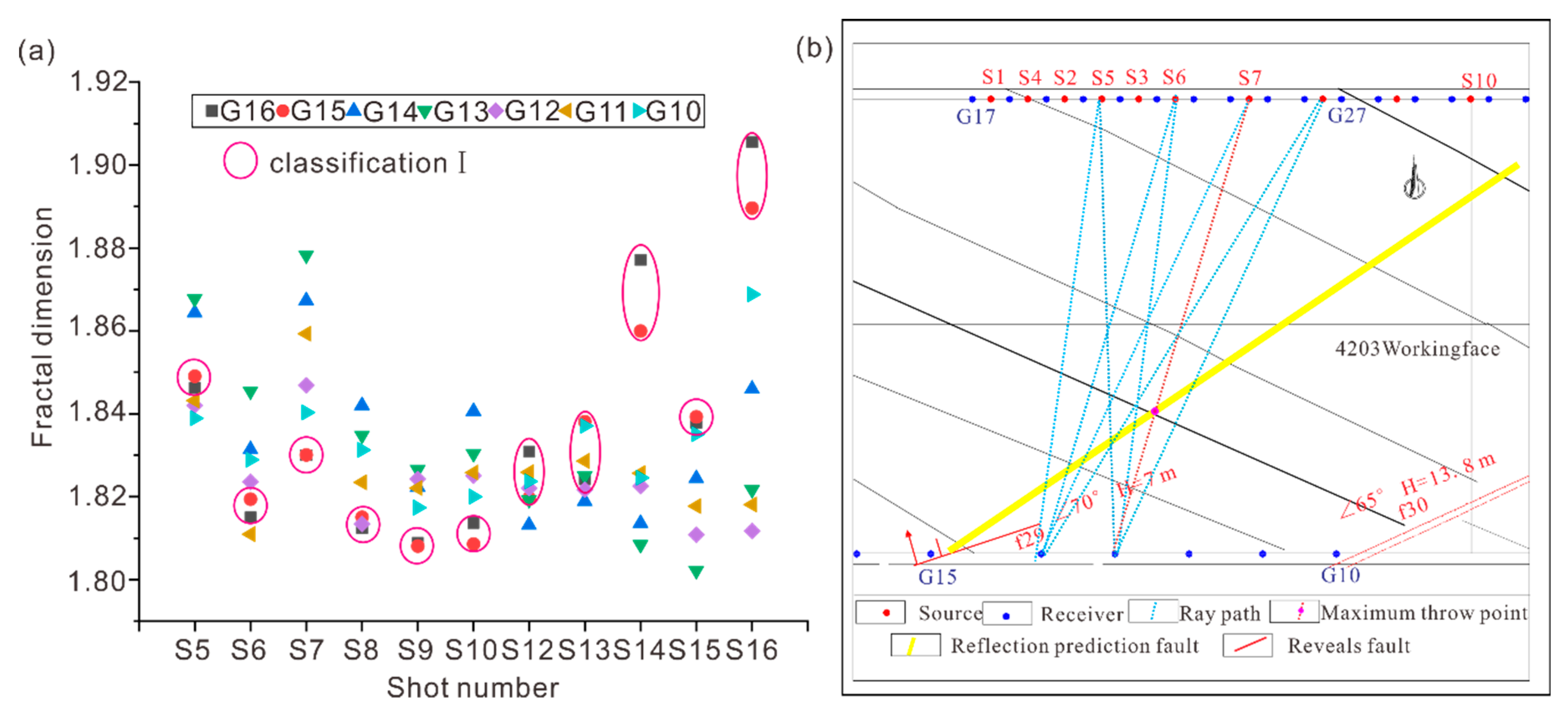
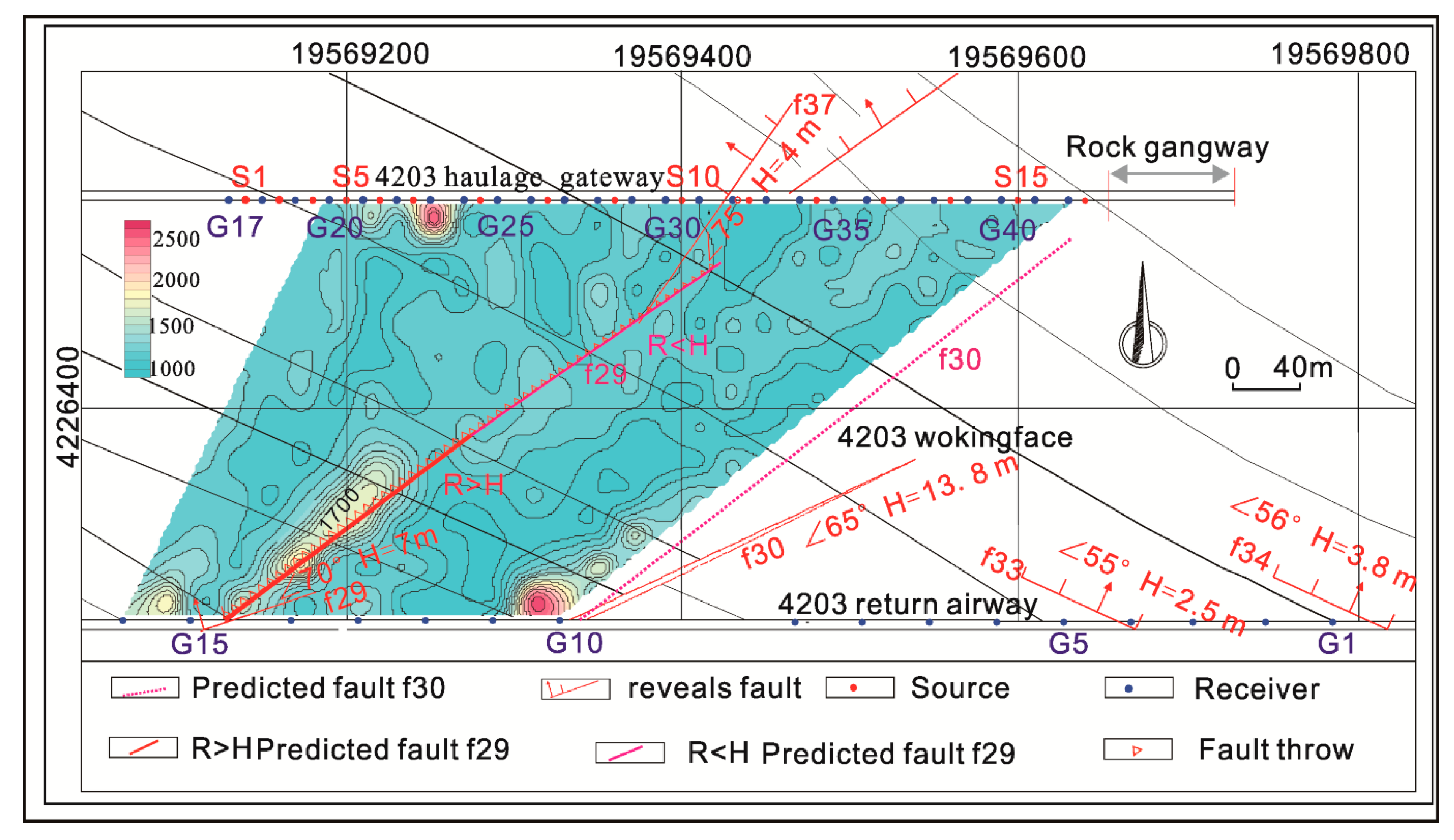
| Ray Path | vmin | vmax | fmin | fmax | Real Value | Logistic Regression Predicted Value | Neural Network Predicted Value |
|---|---|---|---|---|---|---|---|
| S5-11 | 920 | 2600 | 72.6 | 82.8 | 1 | 1 | 1 |
| S5-12 | 1100 | 2600 | 63 | 120 | 1 | 1 | 1 |
| S5-13 | 1600 | 2700 | 59 | 69 | 1 | 1 | 1 |
| S5-14 | 2500 | 4000 | 57 | 95 | 1 | 1 | 1 |
| S6-12 | 1200 | 2500 | 76 | 96 | 1 | 1 | 1 |
| S6-13 | 1000 | 2500 | 50 | 112 | 1 | 1 | 1 |
| S6-14 | 1100 | 2600 | 55 | 113 | 1 | 1 | 1 |
| S7-13 | 1100 | 2600 | 78 | 98 | 1 | 1 | 1 |
| S7-14 | 1100 | 2300 | 97 | 104 | 1 | 1 | 1 |
| S8-13 | 1100 | 1600 | 53 | 171 | 1 | 0 | 0 |
| S8-14 | 1100 | 2500 | 48 | 168 | 1 | 1 | 1 |
| S9-14 | 1100 | 2200 | 68 | 83 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhu, G.; Wang, W.; Zhang, M.; Gao, Z. Quantitative Evaluation of Faults by Combined Channel Wave Seismic Transmission-Reflection Detection Method. Minerals 2022, 12, 1022. https://doi.org/10.3390/min12081022
Wu Y, Zhu G, Wang W, Zhang M, Gao Z. Quantitative Evaluation of Faults by Combined Channel Wave Seismic Transmission-Reflection Detection Method. Minerals. 2022; 12(8):1022. https://doi.org/10.3390/min12081022
Chicago/Turabian StyleWu, Yanhui, Guowei Zhu, Wei Wang, Mengbo Zhang, and Zhen Gao. 2022. "Quantitative Evaluation of Faults by Combined Channel Wave Seismic Transmission-Reflection Detection Method" Minerals 12, no. 8: 1022. https://doi.org/10.3390/min12081022
APA StyleWu, Y., Zhu, G., Wang, W., Zhang, M., & Gao, Z. (2022). Quantitative Evaluation of Faults by Combined Channel Wave Seismic Transmission-Reflection Detection Method. Minerals, 12(8), 1022. https://doi.org/10.3390/min12081022






