Experimental Study on the Thermal Conductivity of Compacted SPV200 Bentonite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
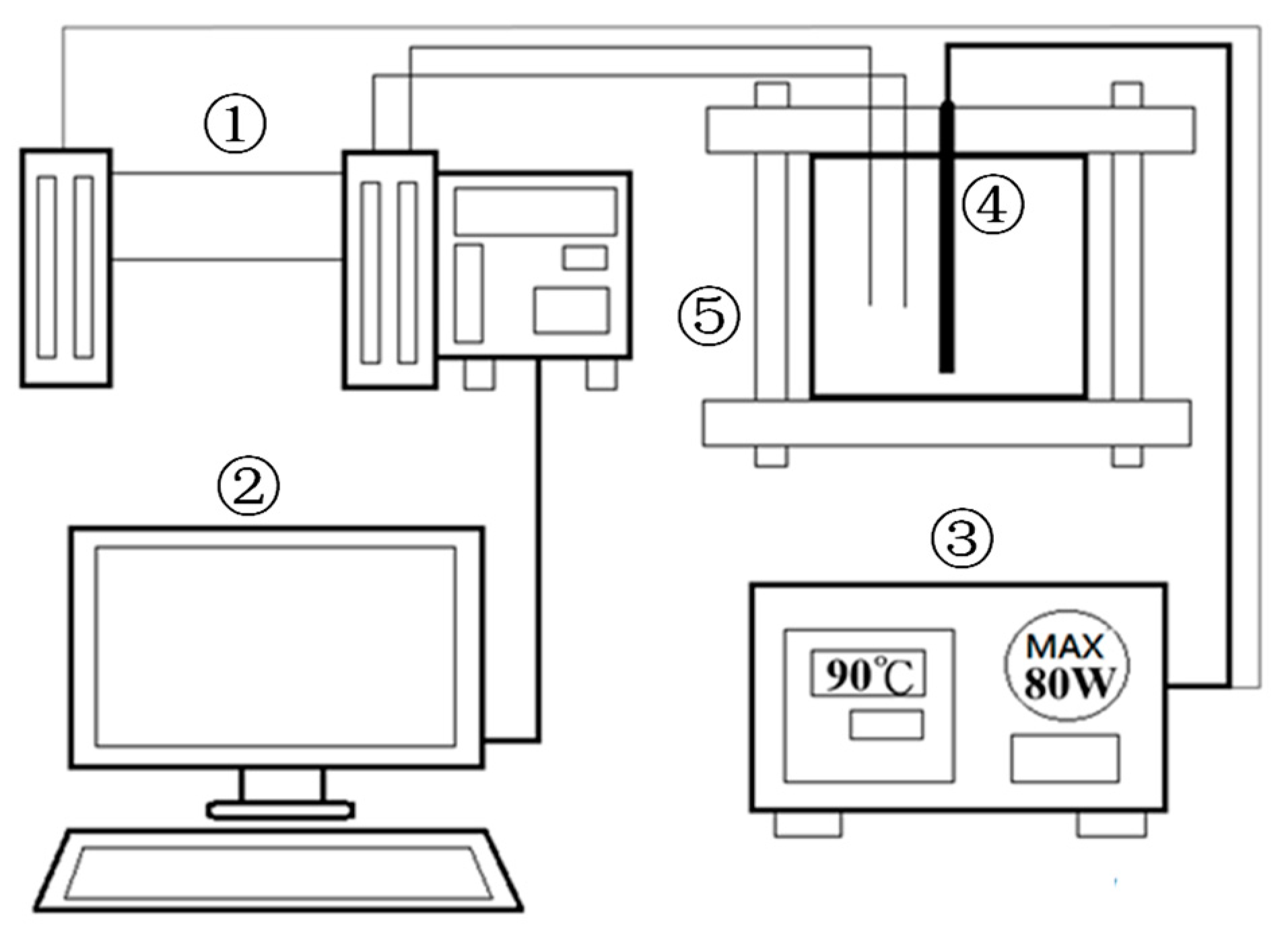
2.2. Experiment Methodology
3. Experimental Results and Discussion
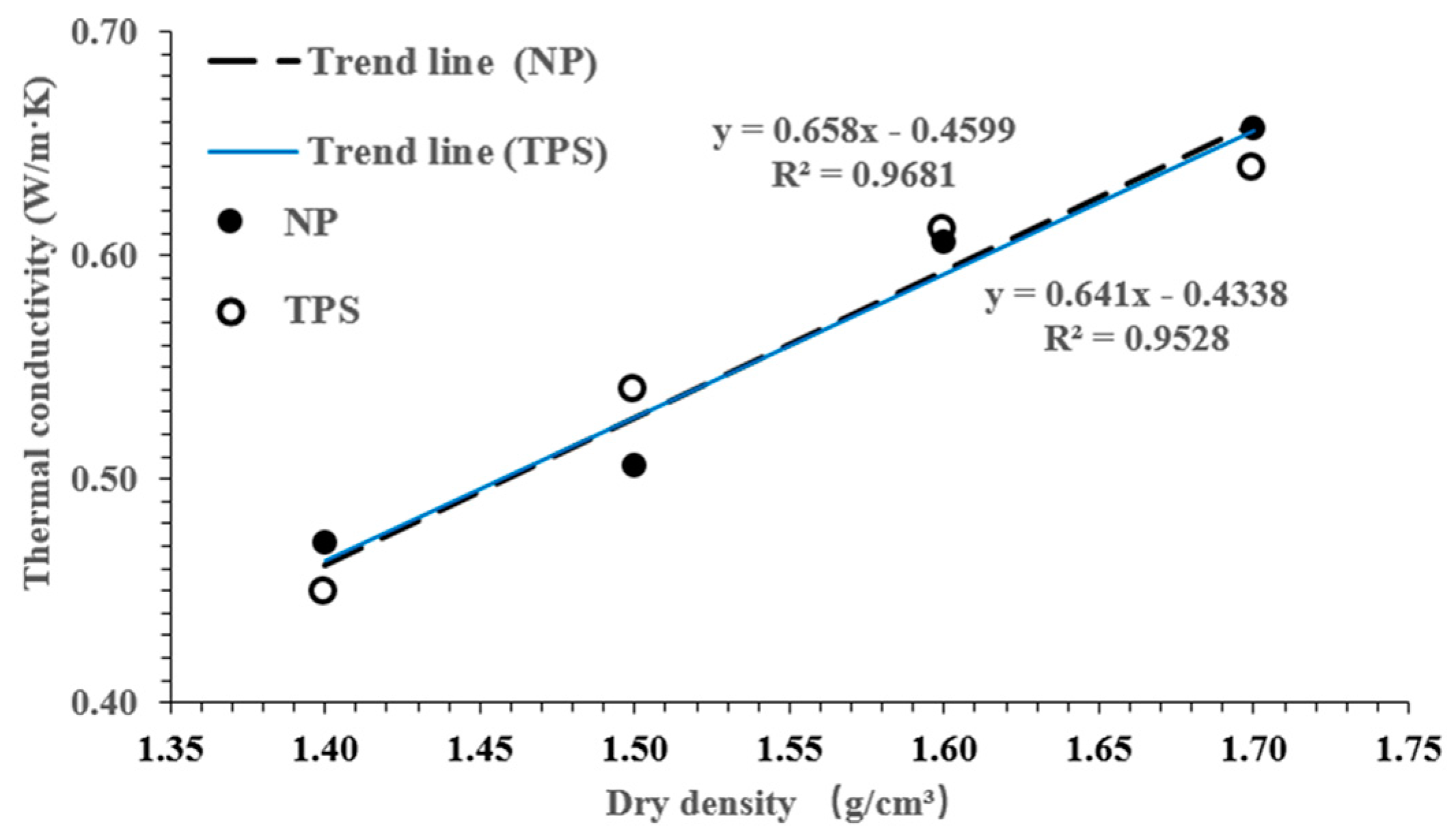
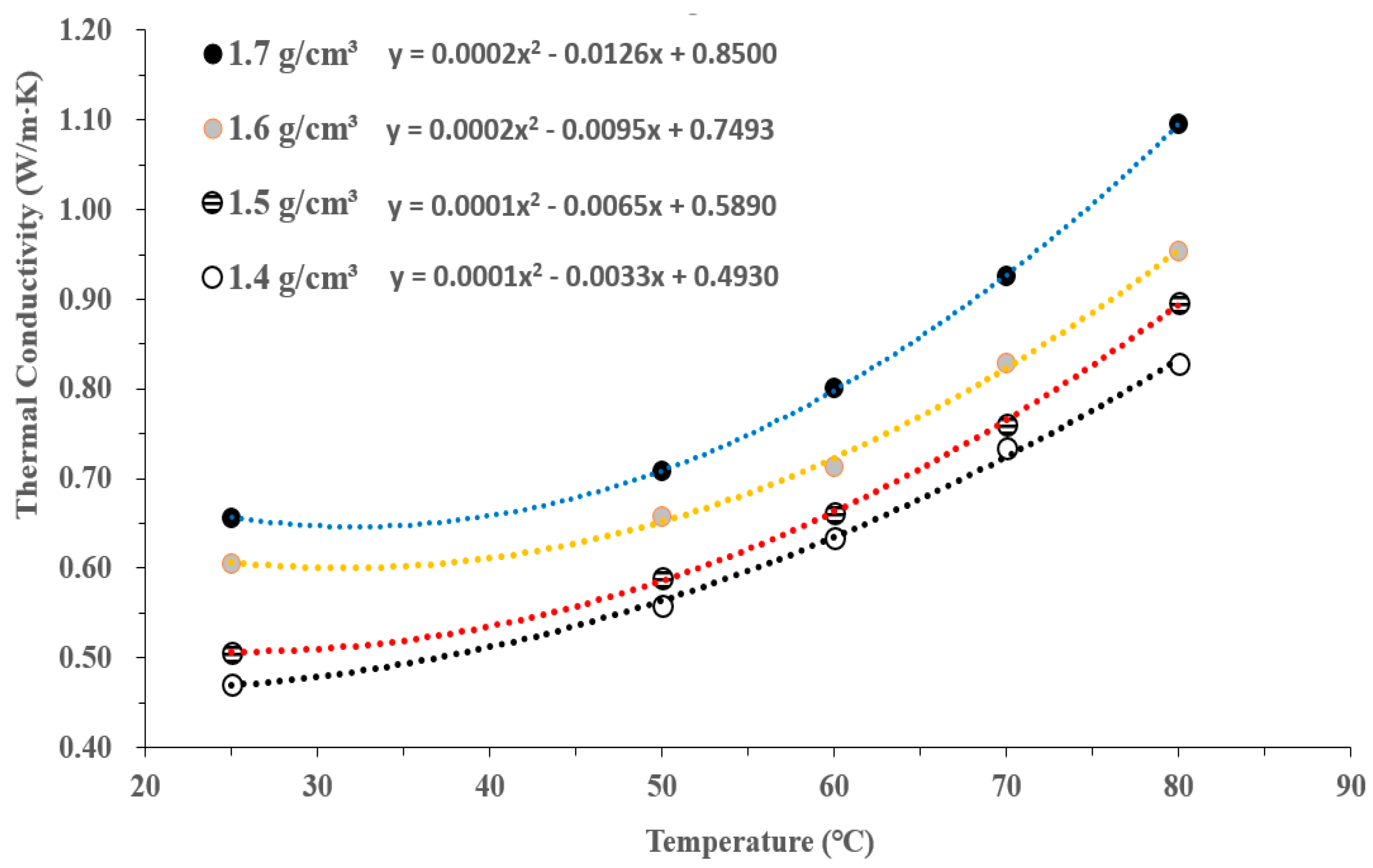
3.1. Thermal Conductivity of SPV200 Bentonite Based on the NP and TPS Methods
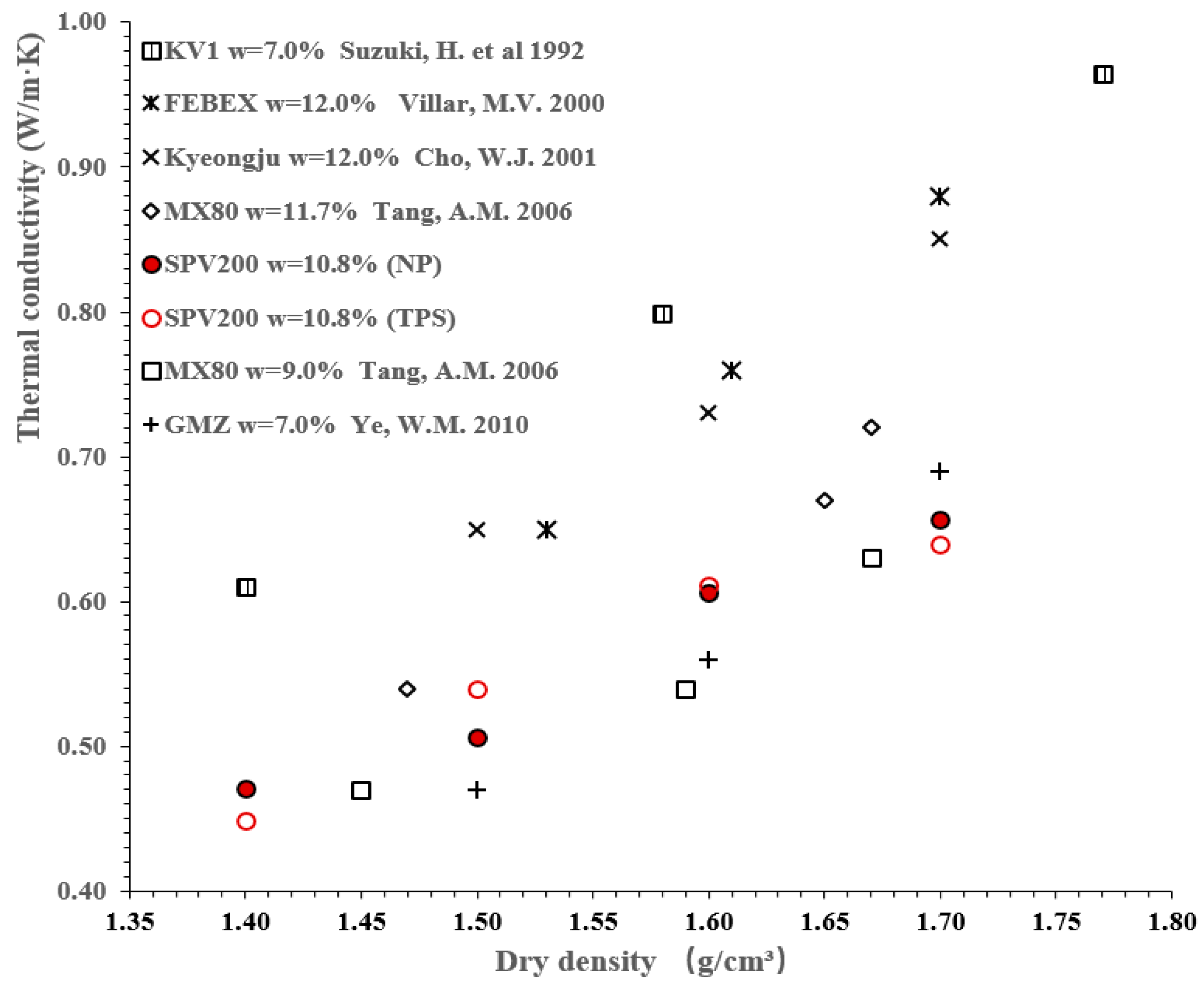
3.2. Comparison of Thermal Conductivity of SPV200 Bentonite with Other Bentonites
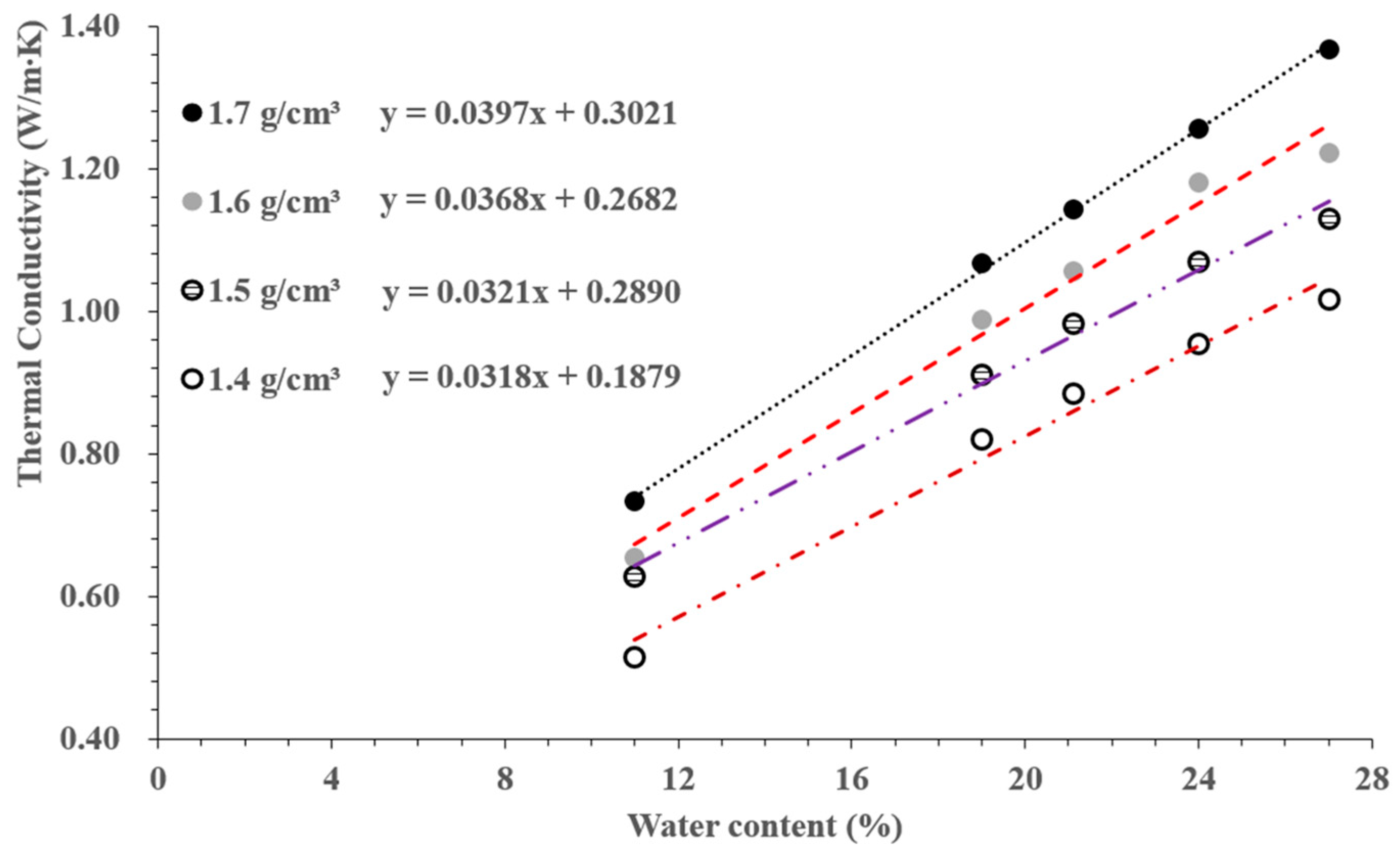
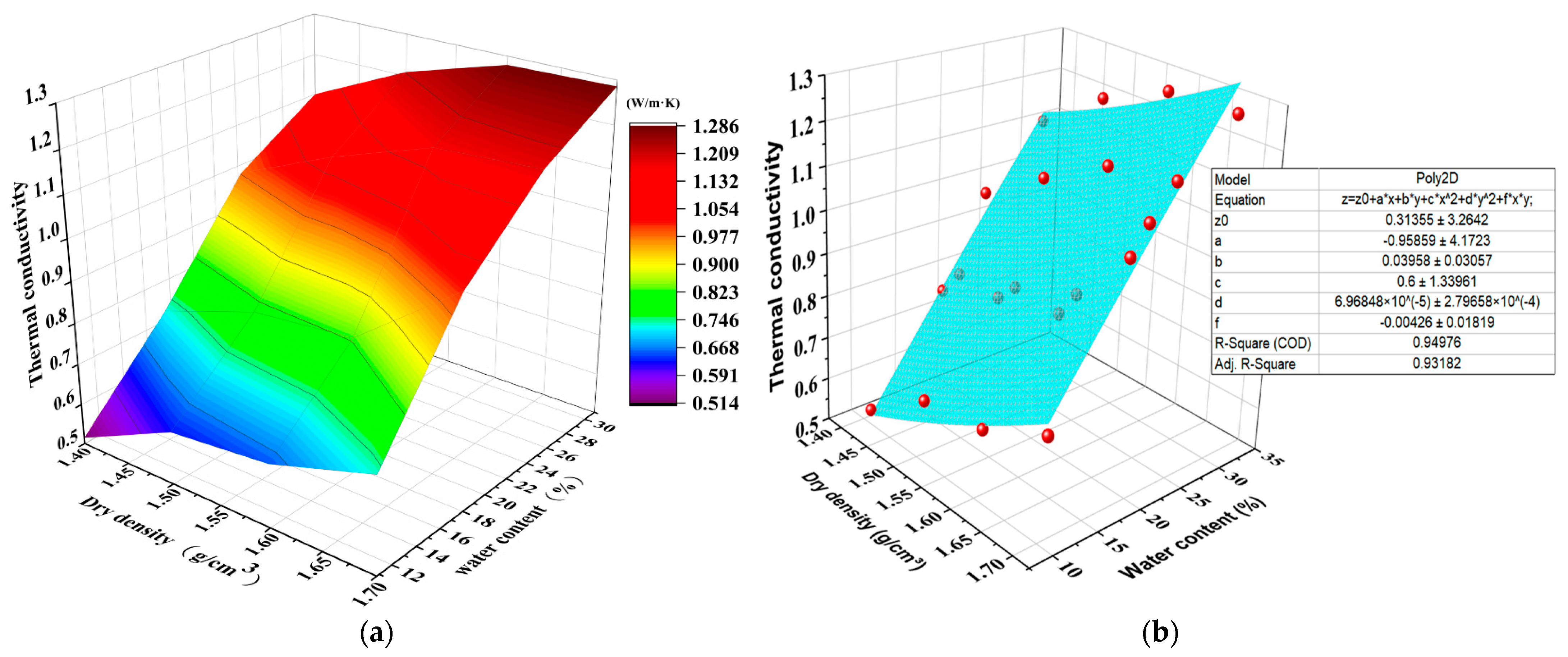
3.3. Three-Dimensional Representation of Thermal Conductivity with Water Content and Dry Density
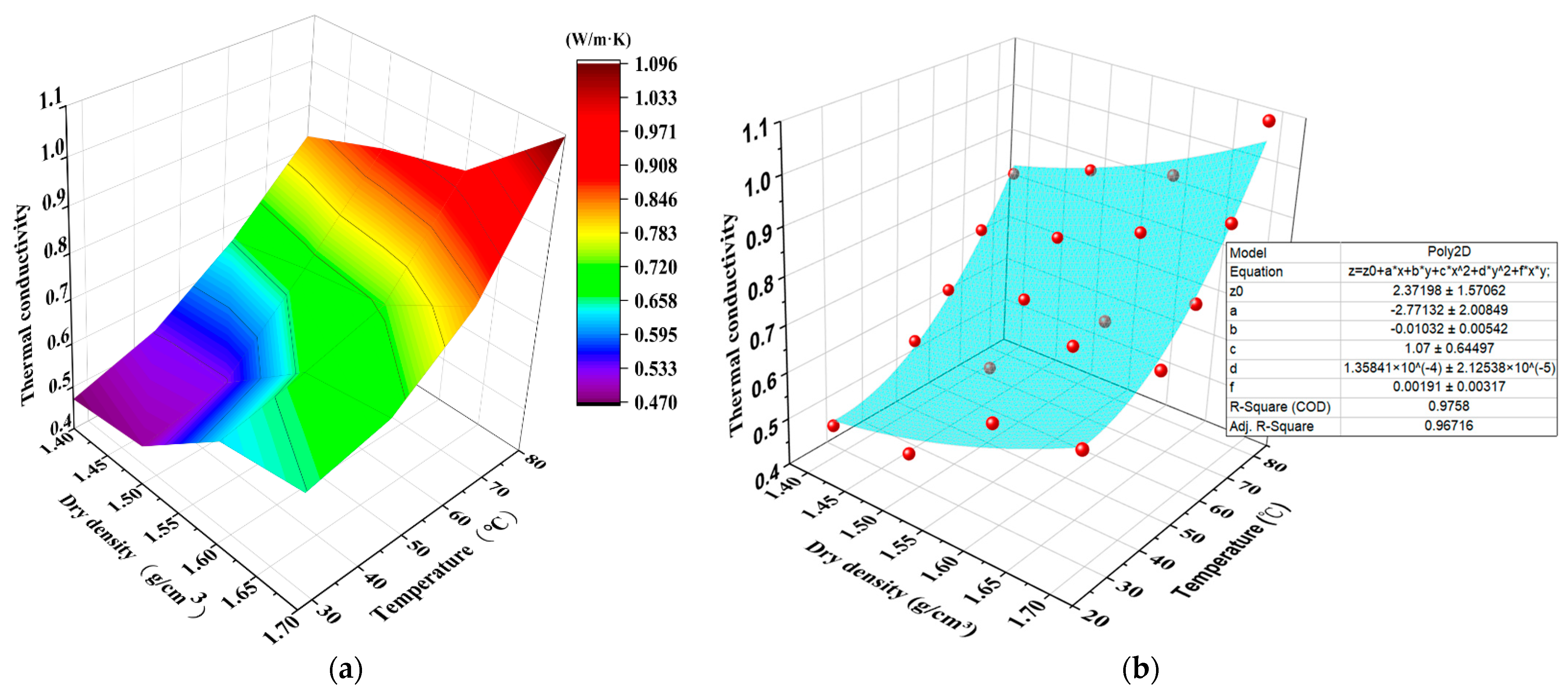
3.4. D Representation of Thermal Conductivity with Dry Density and Temperature
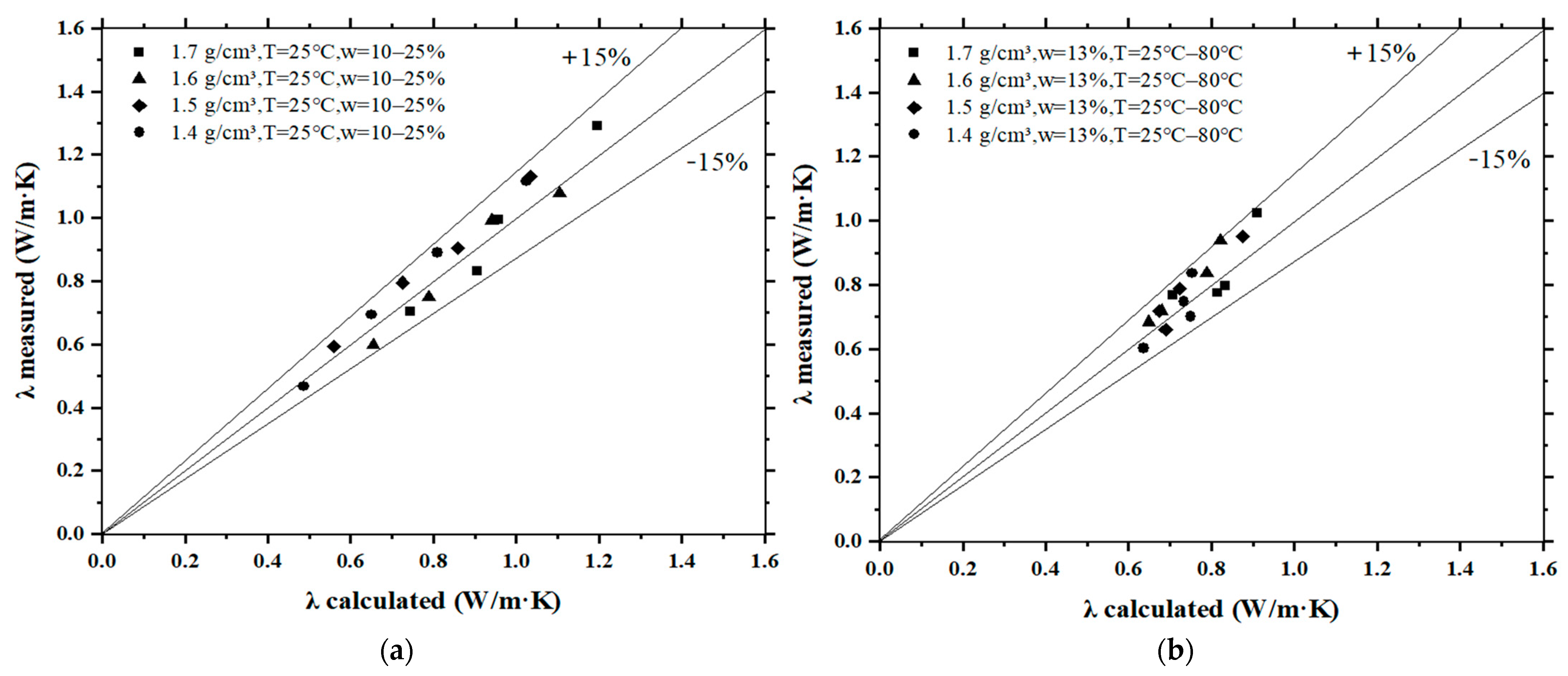
3.5. Comparison between the Calculated and Measured Thermal Conductivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pusch, R. The Microstructure of MX-80 Clay with Respect to Its Bulk Physical Properties under Different Environmental Conditions; Technical Report TR-01-08; SvenskKärnbränslehantering AB (SKB): Stockholm, Sweden, 2001. [Google Scholar]
- Pintado, X.; Hassan, M.d.M.; Martikainen, J. Thermo-Hydro-Mechanical Tests of Buffer Material; Report 2012-49; POSIVA: Eurajoki, Finland, 2013. [Google Scholar]
- Abarca, E.; Sampietro, D.; Sanglas, J.; Molinero, J. Modelling of the Near-Field Hydrogeology; Report for the safety assessment SR-PSU.; Technical Report R-19-20; SvenskKärnbränslehantering AB (SKB): Stockholm, Sweden, 2020. [Google Scholar]
- Hoek, J.; Hartley, L.; Baxter, S. Hydrogeological Modelling for the KBS-3H Safety Case; Report 2016-21; POSIVA: Eurajoki, Finland, 2018. [Google Scholar]
- Karvonen, T. Safety Case for the Operating Licence Application: Surface and Near Surface Hydrological Modelling; Report 2020-23; POSIVA: Eurajoki, Finland, 2021. [Google Scholar]
- Liu, Y.M.; Chen, Z.R. Bentonite from GaoMiaozi, inner mongolia as an ideal buffer/backfilling material in handling highly radioactive wastes—A feasibility study. Acta Mineral. Sin. 2001, 21, 541–543. [Google Scholar] [CrossRef]
- Alberdi, J.; Barcala, J.M.; Campos, R.; Cuevas, A.M.; Fernandez, E. FEBEX Project: Full-Scale Engineered Barriers Experiment for a Deep Geological Repository for High Level Radioactive Waste in Crystalline Host Rock Final Report (ENRESA–1/2000); Office for Official Publications of the European Communities: Madrid, Spain, 2000. [Google Scholar]
- Komine, H. Design flow for specifications of bentonite-based buffer from the viewpoint of self-sealing capability using theoretical equations for swelling characteristics. In Proceedings of the 15th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Fukuoka, Japan, 9–13 November 2015; Japanese Geotechnical Society Special Publication: Tokyo, Japan, 2015. [Google Scholar] [CrossRef] [Green Version]
- Madsen, F.T. Clay mineralogical invest igations related to nuclear waste disposal. Clay Miner 1998, 33, 109–129. [Google Scholar] [CrossRef]
- Dixon, D.A. Review of the T-H-M-C Properties of MX-80 Bentonite; NWMO-TR-2019-07; NWMO: Toronto, ON, Canada, 2019. [Google Scholar]
- Villar, M.V. Caracterización termo-hidro-mecánica de una bentonitade Cabo de Gata. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2000. [Google Scholar]
- Rutqvist, J. Thermal management associated with geologic disposal of large spent nuclear fuel canisters in tunnels with thermally engineered backfill. Tunn. Undergr. Space Technol. 2020, 102, 4–11. [Google Scholar] [CrossRef]
- Ould-Lahoucine, C.; Sakashita, H.; Kumada, T. Measurement of thermal conductivity of buffer materials and evaluation of existing correlations predicting it. Nucl. Eng. Des. 2002, 216, 1–11. [Google Scholar] [CrossRef]
- Huang, W.H. Experimental study on the thermo- and hydro-properties of two bentonites as buffer materials. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. EGU2020-19178. [Google Scholar] [CrossRef]
- Huang, W.H.; Chen, W.C. Swelling behavior of a potential material under simulated near field environment. J. Nucl. Sci. Technol. 2004, 41, 1271–1279. [Google Scholar] [CrossRef]
- Ye, W.M.; Chen, Y.G.; Chen, B.; Wang, Q.; Wang, J. Advances on the knowledge of the buffer/backfill properties of heavily-compacted GMZ bentonite. Eng. Geol. 2010, 116, 12–20. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, X.; Sun, D.; Zeng, Z.T. Thermal properties of GMZ bentonite pellet mixtures subjected to different temperatures for high-level radioactive waste repository. Acta Geotech. 2022, 17, 981–992. [Google Scholar] [CrossRef]
- Cho, W.J.; Lee, J.O.; Kwon, S.K. Thermal Conductivity of Compacted Bentonite and Bentonite-Sand Mixture. J. Nucl. Fuel Cycle Waste Technol. 2008, 6, 101–109. [Google Scholar]
- Yoon, S.; Jeon, J.S.; Kim, G.Y.; Seong, J.H.; Baik, M.H. Specific heat capacity model for compacted bentonite buffer materials. Ann. Nucl. Energy 2019, 125, 18–25. [Google Scholar] [CrossRef]
- DeVries, D.A. Thermal Properties of Soils. In Physics of Plant Environment; van Wijk, W.R., Ed.; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1963; pp. 210–235. [Google Scholar]
- Nikolaev, I.V.; Leong, W.H.; Rosen, M.A. Experimental investigation of soil thermal conductivity over a wide temperature range. Int. J. Thermophys. 2013, 34, 1110–1129. [Google Scholar] [CrossRef]
- Johansen, O. Thermal conductivity of soils. Ph.D. Dissertation, Norwegian University of Science and Technology, Trondheim, Norway, 1975. [Google Scholar]
- Cho, W.J.; Lee, J.O.; Kwon, S. An empirical model for the thermal conductivity of compacted bentonite and a bentonite-sand mixture. Heat Mass Transf. 2011, 47, 1385–1393. [Google Scholar] [CrossRef]
- Chen, Y.G.; Liu, X.M.; Mu, X.; Ye, W.M.; Cui, Y.J.; Chen, B.; Wu, D.B. Thermal Conductivity of Compacted GO-GMZ Bentonite Used as Buffer Material for a High-Level Radioactive Waste Repository. Adv. Civil. Eng. 2018, 4, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Bang, H.T.; Yoon, S.; Jeon, H. Application of machine learning methods to predict a thermal conductivity model for compacted bentonite. Ann. Nucl. Energy. 2020, 142, 1–11. [Google Scholar] [CrossRef]
- Kim, M.J.; Lee, G.J.; Yoon, S. Numerical Study on the Effect of Enhanced Buffer Materials in a High-Level Radioactive Waste Repository. Appl. Sci. 2021, 11, 8733. [Google Scholar] [CrossRef]
- Vieira, A.; Alberdi-Pagola, M.; Christodoulides, P.; Javed, S.; Loveridge, F.; Nguyen, F.; Cecinato, F.; Maranha, J.; Florides, G.; Prodan, I.; et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies 2017, 10, 2044. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.S.; Podlech, C.; Grathoff, G.; Warr, L.N.; Svensson, D. Thermally Induced, Bentonite Alterations in the SKB ABM5 Hot Bentonite Experiment. Minerals 2021, 11, 1017. [Google Scholar] [CrossRef]
- Holmboe, M.; Wold, S.; Jonsson, M. Porosity investigation of compacted bentonite using XRD profile modeling. J. Contam. Hydrol. 2012, 128, 19–32. [Google Scholar] [CrossRef]
- Sakashita, H.; Kumada, T. Heat transfer model for predicting thermal conductivity of highly compacted bentonite. J. Jpn. At. Soc. 1998, 40, 235–240. [Google Scholar]
- Tang, A.M.; Cui, Y.J.; Le, T.T. A study on the thermal conductivity of compacted bentonites. Appl. Clay Sci. 2008, 41, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.S.; Zeng, Z.T.; Lv, H.B. Temperature dependence of apparent thermal conductivity of compacted bentonites as buffer material for high-level radioactive waste repository. Appl. Clay Sci. 2019, 174, 10–14. [Google Scholar] [CrossRef]
- Ortiz de Zárate, J.M.; Hita, J.L.; Khayet, M.; Legido, J.L. Measurement of the thermal conductivity of clays used in pelotherapy by the multi-current hot-wire technique. Appl. Clay Sci. 2010, 50, 423–426. [Google Scholar] [CrossRef]
- Alrtimi, A.; Rouainia, M.; Manning, D.A.C. An improved steady-state apparatus for measuring thermal conductivity of soils. Int. J. Heat Mass Transf. 2014, 72, 630–636. [Google Scholar] [CrossRef]
- ASTM D 5334-14; Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure. ASTM, 100 Barr Harbor Dr.: West Conshocken, PA, USA, 2014. Available online: https://www.en-standard.eu/d5334-14-standard-test-method-for-determination-of-thermal-conductivity-of-soil-and-soft-rock-by-thermal-needle-probe-procedure/ (accessed on 25 June 2022).
- ISO 22007-2; Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (Hot Disc) Method. ISO Copyright Office: Geneva, Switzerland, 2015.
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–798. [Google Scholar] [CrossRef]
- Tang, A.M.; Cui, Y. Determining the Thermal Conductivity of Compacted MX80 Clay. Geotechnical Special Publication. In Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2 April 2006; pp. 1695–1706. [Google Scholar] [CrossRef]
- Cho, W.J.; Lee, J.W.; Kang, C.H. A Compilation and Evaluation of Thermal and Mechanical Properties of Compacted Bentonite for the Performance Assessment of Engineered Barriers in the High-Level Waste Repository; KAERI Report, KAERI/TR−1826/2001. KR0100897; Korea Atomic Energy Research Institute, Taejon: Daejeon, Korea, 2001. (In Korean) [Google Scholar]
- Shen, Z.Y.; Li, G.D.; Li, S.K. Thermal property of highly compacted bentonite, Embankment. Obs. Soil Test. 2001, 22, 39–40. (In Chinese) [Google Scholar]
- Lee, J.O.; Choi, H.; Lee, J.Y. Thermal conductivity of compacted bentonite as a buffer material for a high-level radioactive waste repository. Ann. Nucl. Energy 2016, 94, 848–855. [Google Scholar] [CrossRef]
- Suzuki, H.; Shibata, M.; Yamagata, J.; Hirose, I.; Terakado, K. Physical and Mechanical Properties of Bentonite (I). PNC TN1410 1992, 92-052. (In Japanese) [Google Scholar]
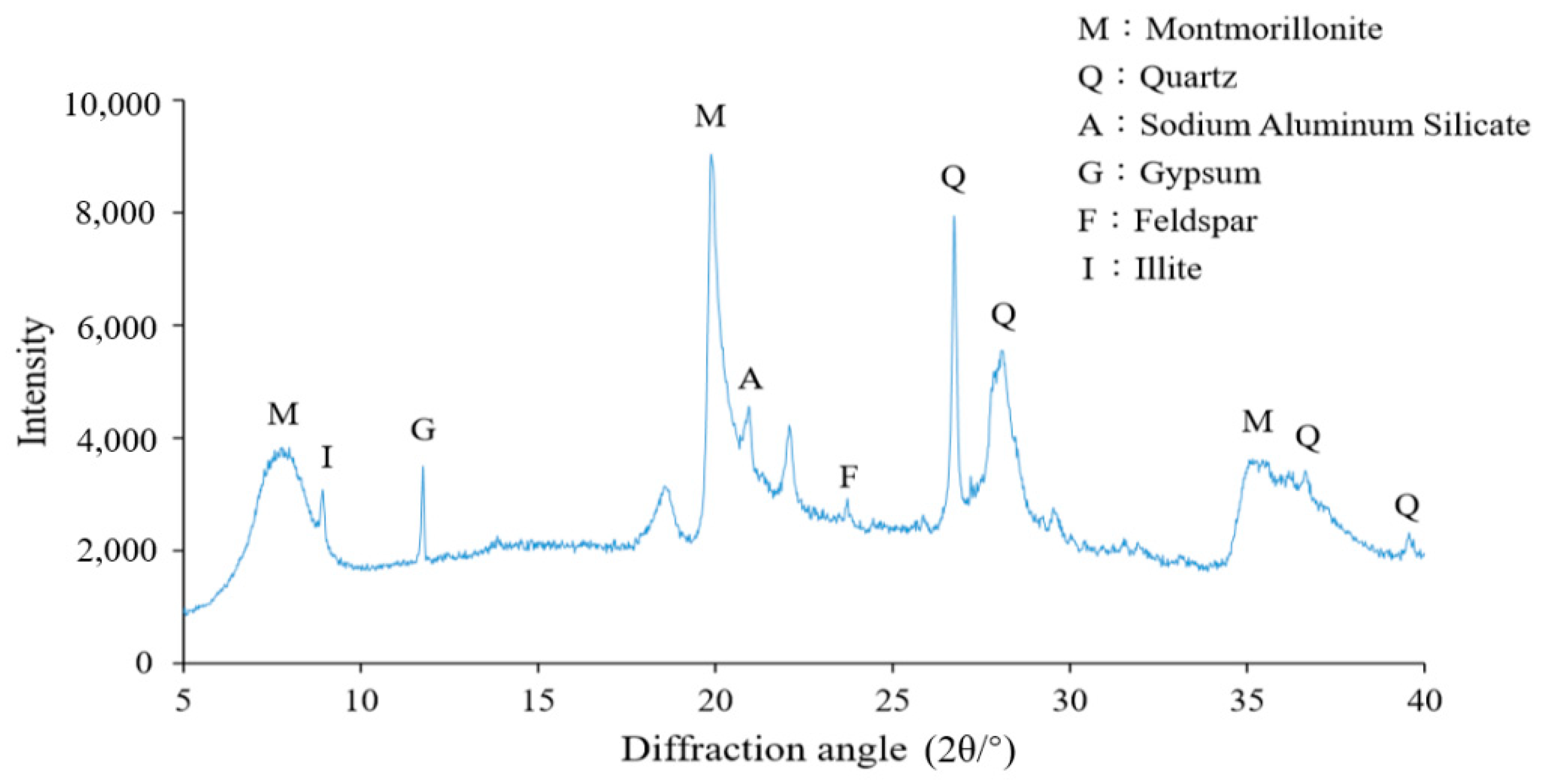






| Basic Properties | ||||||||
|---|---|---|---|---|---|---|---|---|
| Water Content w (%) | Specific Gravity Gs | Liquid Limit LL(%) | Plastic Limit PL(%) | Plastic Index PI | ||||
| 10.8 | 2.67 | 421 | 43 | 378 | ||||
| Chemical Composition (%) | ||||||||
| SiO2 | Fe2O3 | MgO | CaO | Al2O3 | FeO | Na2O | Trace | LOI |
| 63.02 | 3.25 | 2.67 | 0.65 | 21.08 | 0.35 | 2.57 | 0.72 | 5.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, G.-L.; Chung, C.-C.; Tsai, C.-E.; Cuo, C.-J.; Huang, W.-H. Experimental Study on the Thermal Conductivity of Compacted SPV200 Bentonite. Minerals 2022, 12, 932. https://doi.org/10.3390/min12080932
Ren G-L, Chung C-C, Tsai C-E, Cuo C-J, Huang W-H. Experimental Study on the Thermal Conductivity of Compacted SPV200 Bentonite. Minerals. 2022; 12(8):932. https://doi.org/10.3390/min12080932
Chicago/Turabian StyleRen, Guo-Liang, Chih-Chung Chung, Chia-En Tsai, Che-Jui Cuo, and Wei-Hsing Huang. 2022. "Experimental Study on the Thermal Conductivity of Compacted SPV200 Bentonite" Minerals 12, no. 8: 932. https://doi.org/10.3390/min12080932
APA StyleRen, G.-L., Chung, C.-C., Tsai, C.-E., Cuo, C.-J., & Huang, W.-H. (2022). Experimental Study on the Thermal Conductivity of Compacted SPV200 Bentonite. Minerals, 12(8), 932. https://doi.org/10.3390/min12080932






