Effect of Al2O3 on Sound Velocity of MgSiO3 Glass at High Pressure
Abstract
:1. Introduction
2. Experiments
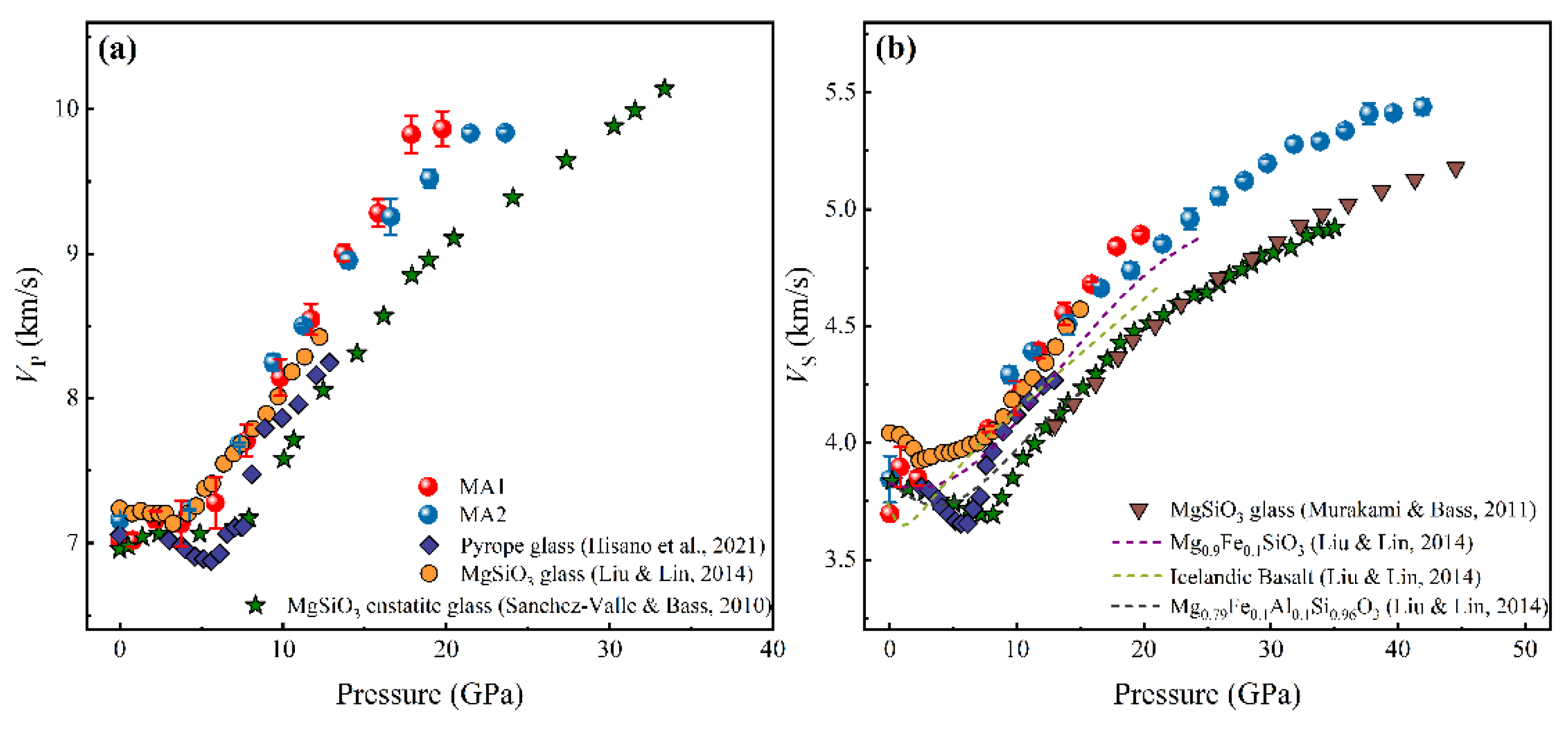
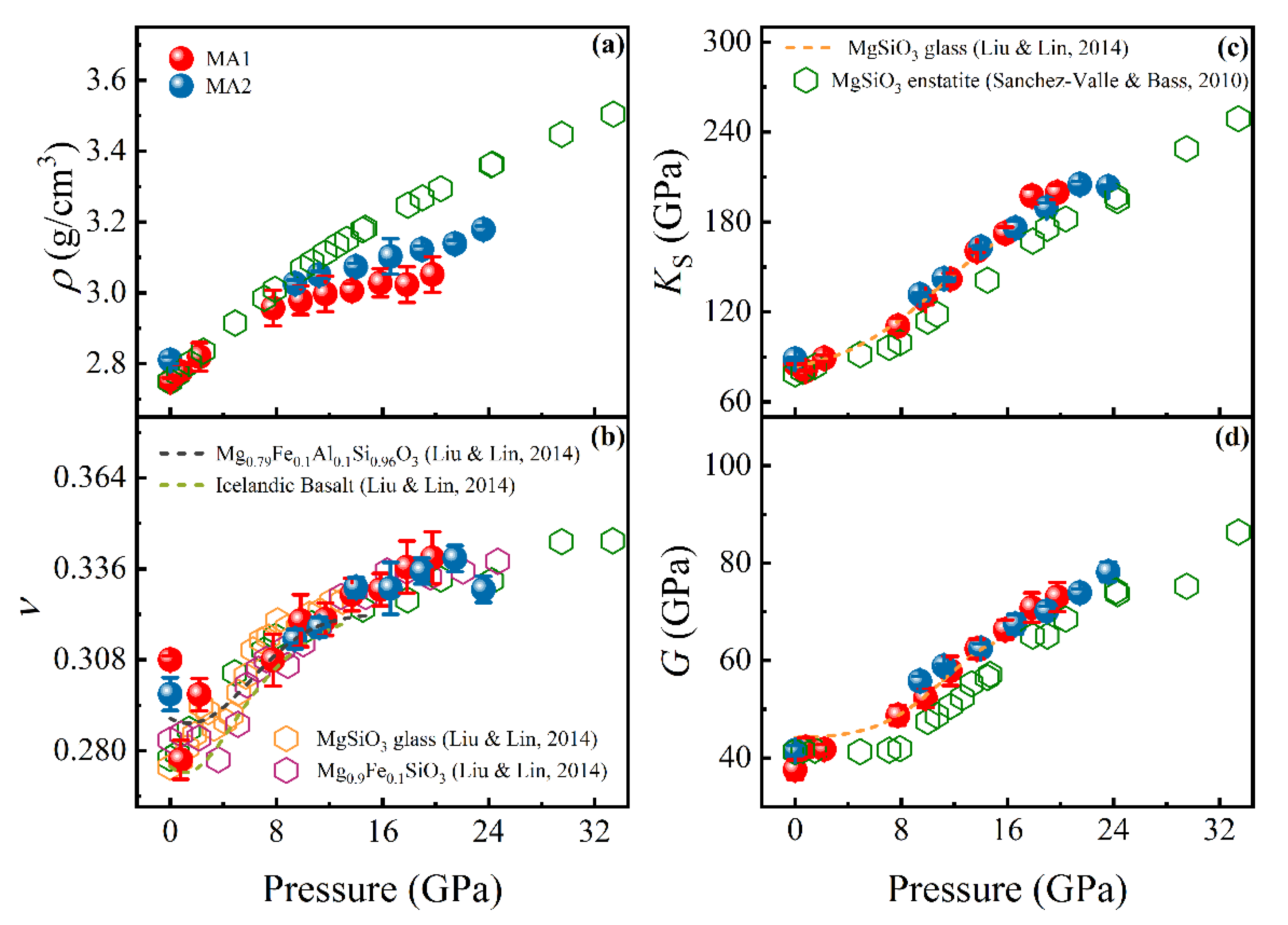
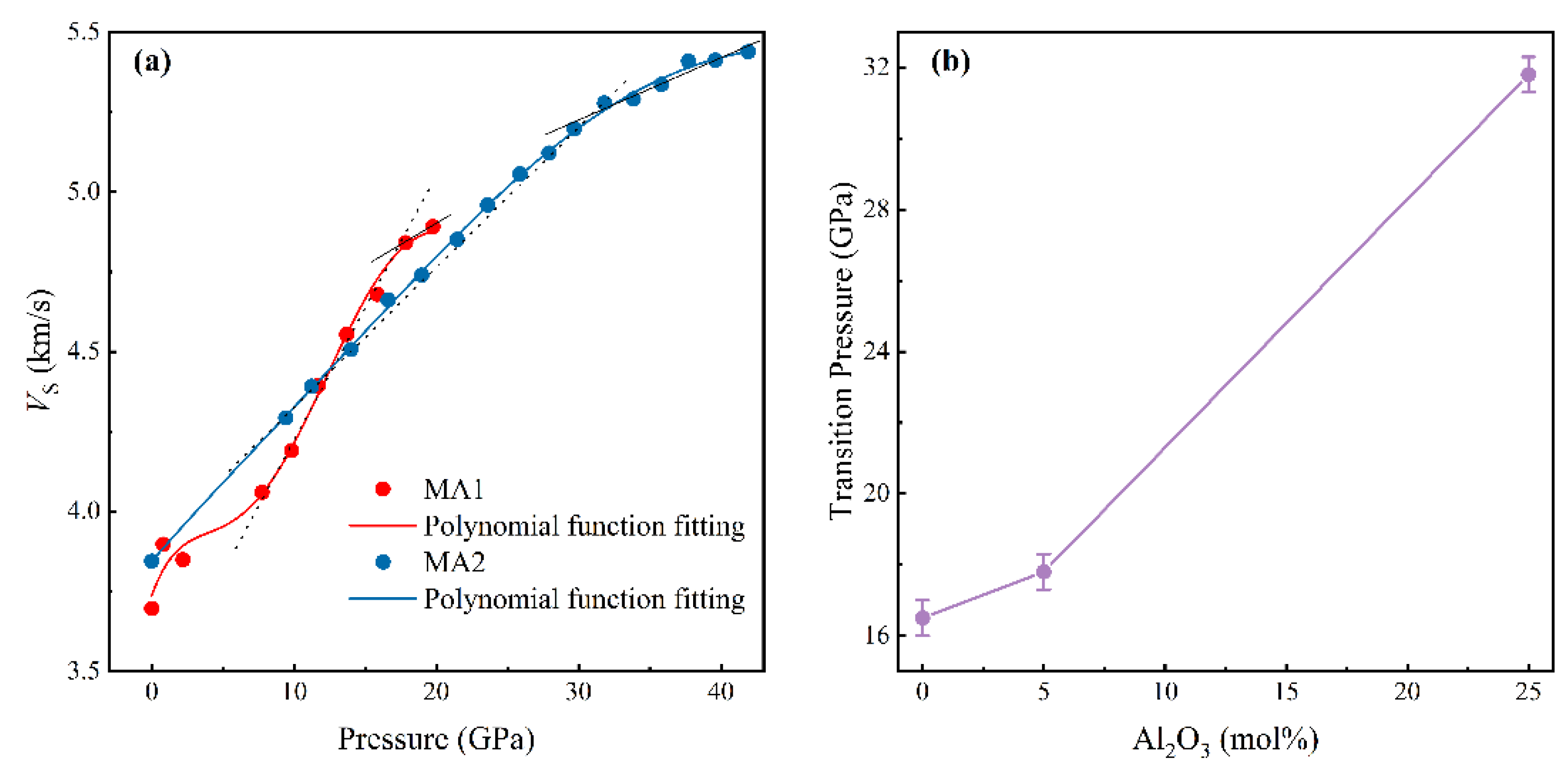
3. Results and Discussion
4. Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Debayle, E.; Bodin, T.; Durand, S.; Ricard, Y. Seismic evidence for partial melt below tectonic plates. Nature 2020, 586, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Song, T.-R.; Helmberger, D.V.; Grand, S.P. Low-velocity zone atop the 410-km seismic discontinuity in the northwestern United States. Nature 2004, 427, 530–533. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.; Romanowicz, B. Seismic evidence for partial melting at the root of major hot spot plumes. Science 2017, 357, 393–397. [Google Scholar] [CrossRef] [Green Version]
- Agee, C.B. Static compression of hydrous silicate melt and the effect of water on planetary differentiation. Earth Planet. Sci. Lett. 2008, 265, 641–654. [Google Scholar] [CrossRef]
- Huisman, J.; Pham Thi, N.N.; Karl, D.M.; Sommeijer, B. Reduced mixing generates oscillations and chaos in the oceanic deep chlorophyll maximum. Nature 2006, 439, 322–325. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Jing, Z.; Yu, T.; Alp, E.E.; Lavina, B.; Van Orman, J.A.; Wang, Y. Sound velocity and compressibility of melts along the hedenbergite (CaFeSi2O6)-diopside (CaMgSi2O6) join at high pressure: Implications for stability and seismic signature of Fe-rich melts in the mantle. Earth Planet. Sci. Lett. 2022, 577, 117250. [Google Scholar] [CrossRef]
- Jing, Z.; Yu, T.; Xu, M.; Chantel, J.; Wang, Y. High-Pressure Sound Velocity Measurements of Liquids Using In Situ Ultrasonic Techniques in a Multianvil Apparatus. Minerals 2020, 10, 126. [Google Scholar] [CrossRef] [Green Version]
- Solomatova, N.V.; Caracas, R. Pressure-Induced Coordination Changes in a Pyrolitic Silicate Melt From Ab Initio Molecular Dynamics Simulations. J. Geophys. Res. Solid Earth 2019, 124, 11232–11250. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, D.B.; Karki, B.B. Transport properties of carbonated silicate melt at high pressure. Sci. Adv. 2017, 3, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wan, J.T.K.; Duffy, T.S.; Scandolo, S.; Car, R. First-principles study of density, viscosity, and diffusion coefficients of liquid MgSiO3 at conditions of the Earth’s deep mantle. J. Geophys. Res. Solid Earth 2007, 112, B03208. [Google Scholar] [CrossRef] [Green Version]
- Murakami, M.; Bass, J.D. Spectroscopic Evidence for Ultrahigh-Pressure Polymorphism in SiO2 Glass. Phys. Rev. Lett. 2010, 104, 025504. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lin, J.-F. Abnormal acoustic wave velocities in basaltic and (Fe,Al)-bearing silicate glasses at high pressures. Geophys. Res. Lett. 2014, 41, 8832–8839. [Google Scholar] [CrossRef] [Green Version]
- Murakami, M.; Bass, J.D. Evidence of denser MgSiO3 glass above 133 gigapascal (GPa) and implications for remnants of ultradense silicate melt from a deep magma ocean. Proc. Natl. Acad. Sci. USA 2011, 108, 17286–17289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanchez-Valle, C.; Bass, J.D. Elasticity and pressure-induced structural changes in vitreous MgSiO3-enstatite to lower mantle pressures. Earth Planet. Sci. Lett. 2010, 295, 523–530. [Google Scholar] [CrossRef]
- Fukui, H.; Hiraoka, N. Electronic and local atomistic structure of MgSiO3 glass under pressure: A study of X-ray Raman scattering at the silicon and magnesium L-edges. Phys. Chem. Miner. 2018, 45, 211–218. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Hemley, R.J.; Hofmeister, A.M. Raman and infrared study of pressure-induced structural changes in MgSiO3, CaMgSi2O6, and CaSiO3 glasses. Am. Mineral. 1992, 77, 258–269. [Google Scholar]
- Lee, S.K.; Lin, J.-F.; Cai Yong, Q.; Hiraoka, N.; Eng Peter, J.; Okuchi, T.; Mao, H.-k.; Meng, Y.; Hu Michael, Y.; Chow, P.; et al. X-ray Raman scattering study of MgSiO3 glass at high pressure: Implication for triclustered MgSiO3 melt in Earth’s mantle. Proc. Natl. Acad. Sci. USA 2008, 105, 7925–7929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stolper, E. A phase diagram for mid-ocean ridge basalts: Preliminary results and implications for petrogenesis. Contrib. Mineral. Petrol. 1980, 74, 13–27. [Google Scholar] [CrossRef]
- Sun, S.-S. Chemical composition and origin of the earth’s primitive mantle. Geochim. Cosmochim. Acta 1982, 46, 179–192. [Google Scholar] [CrossRef]
- Liu, Z.; Irifune, T.; Nishi, M.; Tange, Y.; Arimoto, T.; Shinmei, T. Phase relations in the system MgSiO3–Al2O3 up to 52 GPa and 2000 K. Phys. Earth Planet. Int. 2016, 257, 18–27. [Google Scholar] [CrossRef]
- Hisano, N.; Sakamaki, T.; Ohashi, T.; Funakoshi, K.; Higo, Y.; Shibazaki, Y.; Suzuki, A. Elastic properties and structures of pyrope glass under high pressures. Am. Mineral. 2021, 106, 7–14. [Google Scholar] [CrossRef]
- Hughes, S.W. Archimedes revisited: A faster, better, cheaper method of accurately measuring the volume of small objects. Phys. Educ. 2005, 40, 468–474. [Google Scholar] [CrossRef] [Green Version]
- Kantor, I.; Prakapenka, V.; Kantor, A.; Dera, P.; Kurnosov, A.; Sinogeikin, S.; Dubrovinskaia, N.; Dubrovinsky, L. BX90: A new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 2012, 83, 125102. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, C.H.; Brody, E.M.; Bassett, W.A. Elastic moduli of NaCl by Brillouin scattering at high pressure in a diamond anvil cell. Rev. Sci. Instrum. 1976, 47, 942–947. [Google Scholar] [CrossRef]
- Yang, H.; Gleason, A.E.; Tkachev, S.N.; Chen, B.; Jeanloz, R.; Mao, W.L. Noble gas incorporation into silicate glasses: Implications for planetary volatile storage. Geochem. Perspect. Lett. 2021, 17, 1–5. [Google Scholar] [CrossRef]
- Weigel, C.; Polian, A.; Kint, M.; Rufflé, B.; Foret, M.; Vacher, R. Vitreous Silica Distends in Helium Gas: Acoustic Versus Static Compressibilities. Phys. Rev. Lett. 2012, 109, 245504. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. Solid Earth 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Liang, Y.; Wei, X.-F.; Gu, C.; Liu, J.-X.; Li, F.; Yan, M.; Zheng, X.; Han, Z.; Zhao, Y.; Wang, S.; et al. Enhanced Hardness in Transition-Metal Monocarbides via Optimal Occupancy of Bonding Orbitals. ACS Appl. Mater. Interfaces 2021, 13, 14365–14376. [Google Scholar] [CrossRef]
- Mohammadi, R.; Turner, C.L.; Xie, M.; Yeung, M.T.; Lech, A.T.; Tolbert, S.H.; Kaner, R.B. Enhancing the Hardness of Superhard Transition-Metal Borides: Molybdenum-Doped Tungsten Tetraboride. Chem. Mater. 2016, 28, 632–637. [Google Scholar] [CrossRef]
- Akopov, G.; Yeung, M.T.; Turner, C.L.; Mohammadi, R.; Kaner, R.B. Extrinsic Hardening of Superhard Tungsten Tetraboride Alloys with Group 4 Transition Metals. J. Am. Chem. Soc. 2016, 138, 5714–5721. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Z. Elasticity of Corundum at High Pressures and Temperatures: Implications for Pyrope Decomposition and Al-Content Effect on Elastic Properties of Bridgmanite. J. Geophys. Res. Solid Earth 2018, 123, 1201–1216. [Google Scholar] [CrossRef]




| Sample | MgSiO3∙5 mol%Al2O3 (Mg0.95Al0.1Si0.95O3) | MgSiO3∙24.5 mol%Al2O3 (Mg0.76Al0.49Si0.76O3) | |
|---|---|---|---|
| Element | |||
| MgO | 38.1(1) | 30.3(1) | |
| Al2O3 | 5.1(1) | 24.7(1) | |
| SiO2 | 56.8(1) | 45.2(1) | |
| Mg | 0.95(2) | 0.76(2) | |
| Al | 0.101(3) | 0.49(1) | |
| Si | 0.95(2) | 0.76(1) | |
| O | 3.00(6) | 3.00(6) | |
| Mg/Si | 1 | 1 | |
| MA1 | ||||||
| Pressure (GPa) | (g/cm3) | VP (km/s) | VS (km/s) | KS (GPa) | G (GPa) | |
| 0 | 2.75(1) | 7.02(1) | 3.70(1) | 85.4(3) | 37.5(3) | 0.308(1) |
| 0.80 | 2.78(2) | 7.02(5) | 3.90(8) | 80.6(2) | 42(2) | 0.277(6) |
| 2.20 | 2.82(4) | 7.17(5) | 3.85(3) | 89(2) | 42(1) | 0.298(5) |
| 3.75 | - | 7.1(2) | - | - | - | - |
| 5.85 | - | 7.3(2) | - | - | - | - |
| 7.75 | 2.95(5) | 7.7(1) | 4.06(1) | 111(5) | 49(2) | 0.308(8) |
| 9.83 | 2.98(4) | 8.2(1) | 4.19(7) | 128(3) | 52(3) | 0.320(8) |
| 11.70 | 3.00(5) | 8.6(1) | 4.39(3) | 142(4) | 58(3) | 0.321(5) |
| 13.70 | 3.01(2) | 9.01(5) | 4.56(5) | 160.6(9) | 62(2) | 0.328(5) |
| 15.85 | 3.03(4) | 9.28(9) | 4.68(1) | 173(4) | 66(2) | 0.330(5) |
| 17.85 | 3.02(5) | 9.8(1) | 4.84(3) | 197(5) | 71(3) | 0.337(8) |
| 19.76 | 3.05(5) | 9.8(1) | 4.89(2) | 200(5) | 73(3) | 0.340(8) |
| MA2 | ||||||
| Pressure (GPa) | (g/cm3) | VP (km/s) | VS (km/s) | KS (GPa) | G (GPa) | |
| 0 | 2.81(1) | 7.16(3) | 3.8(1) | 89(1) | 42(1) | 0.298(5) |
| 4.25 | - | 7.23(1) | - | - | - | - |
| 7.30 | - | 7.68(1) | - | - | - | - |
| 9.41 | 3.03(1) | 8.25(5) | 4.29(4) | 131(1) | 56(1) | 0.314(3) |
| 11.23 | 3.05(1) | 8.50(1) | 4.391(4) | 142(1) | 58.9(4) | 0.318(3) |
| 14 | 3.07(1) | 8.95(5) | 4.51(4) | 163(1) | 63(1) | 0.330(3) |
| 16.60 | 3.10(5) | 9.3(1) | 4.662(5) | 176(5) | 68(2) | 0.330(8) |
| 18.97 | 3.12(1) | 9.52(6) | 4.74(4) | 189(3) | 70(1) | 0.335(4) |
| 21.47 | 3.14(1) | 9.83(3) | 4.85(2) | 205(2) | 73.9(8) | 0.339(4) |
| 23.61 | 3.18(1) | 9.84(3) | 4.96(5) | 203(1) | 78(2) | 0.330(4) |
| 25.89 | - | - | 5.06(3) | - | - | - |
| 27.92 | - | - | 5.12(2) | - | - | - |
| 29.70 | - | - | 5.20(2) | - | - | - |
| 31.83 | - | - | 5.28(3) | - | - | - |
| 33.96 | - | - | 5.29(2) | - | - | - |
| 35.84 | - | - | 5.34(2) | - | - | - |
| 37.72 | - | - | 5.41(4) | - | - | - |
| 39.62 | - | - | 5.411(1) | - | - | - |
| 41.92 | - | - | 5.44(3) | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Dong, L.; Li, F.; Zhou, Q.; Zhang, C.; Guo, M.; Wei, Y.; Zhang, X.; Li, L.; Li, X.; et al. Effect of Al2O3 on Sound Velocity of MgSiO3 Glass at High Pressure. Minerals 2022, 12, 1069. https://doi.org/10.3390/min12091069
Wei X, Dong L, Li F, Zhou Q, Zhang C, Guo M, Wei Y, Zhang X, Li L, Li X, et al. Effect of Al2O3 on Sound Velocity of MgSiO3 Glass at High Pressure. Minerals. 2022; 12(9):1069. https://doi.org/10.3390/min12091069
Chicago/Turabian StyleWei, Xinmiao, Lingling Dong, Fangfei Li, Qiang Zhou, Caizi Zhang, Mengqi Guo, Yingzhan Wei, Xue Zhang, Liang Li, Xinyang Li, and et al. 2022. "Effect of Al2O3 on Sound Velocity of MgSiO3 Glass at High Pressure" Minerals 12, no. 9: 1069. https://doi.org/10.3390/min12091069
APA StyleWei, X., Dong, L., Li, F., Zhou, Q., Zhang, C., Guo, M., Wei, Y., Zhang, X., Li, L., Li, X., & Liu, Z. (2022). Effect of Al2O3 on Sound Velocity of MgSiO3 Glass at High Pressure. Minerals, 12(9), 1069. https://doi.org/10.3390/min12091069







