Macro-Microscopic Deterioration Behavior of Gypsum Rock after Wetting and Its Constitutive Model Based on Acoustic Emission
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation and Micro-Damage Characterization
2.2. The Mechanical Test Scheme and Acoustic Emission Monitoring
2.3. The Damage Constitutive Model Based on AE
3. Results and Discussion
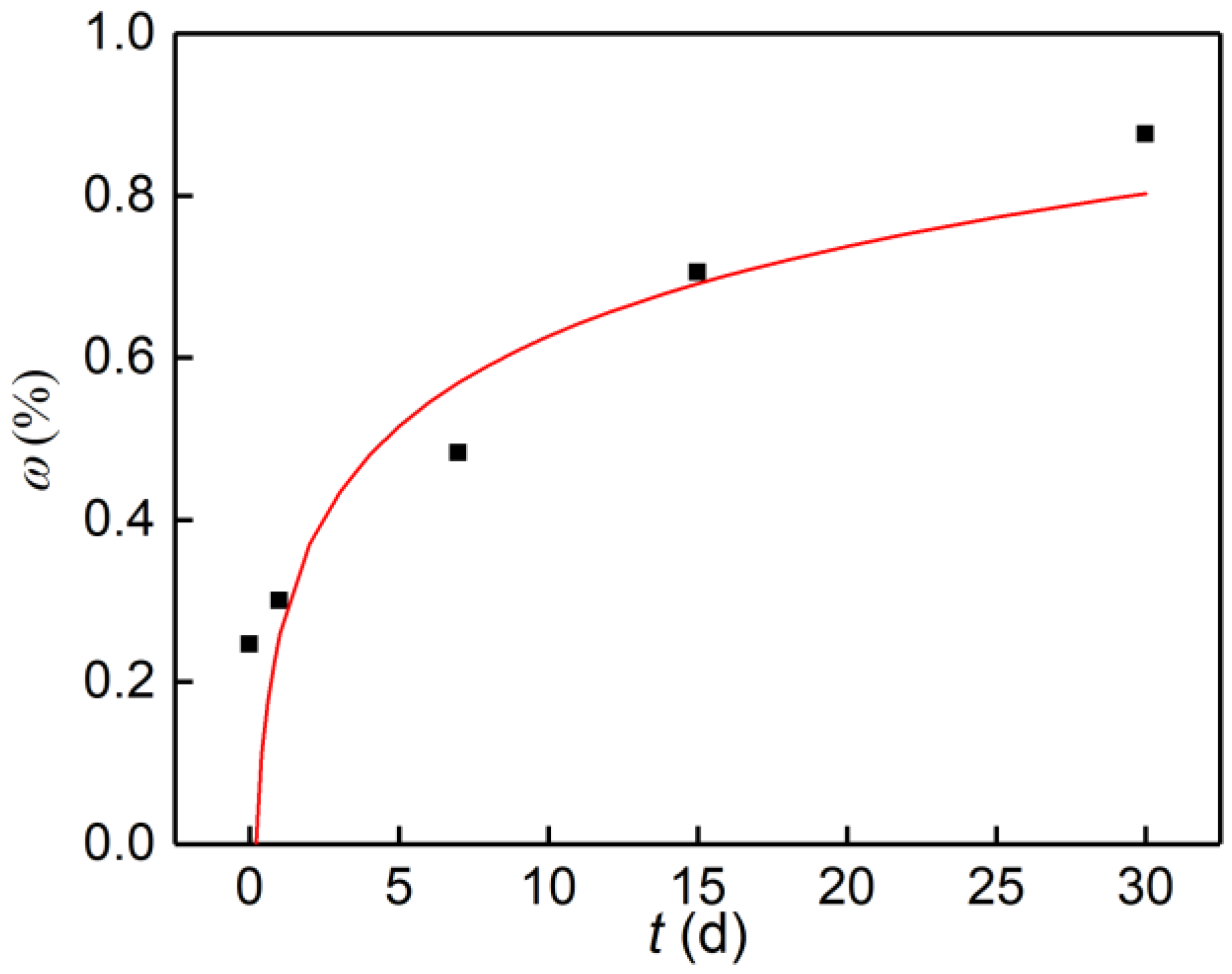
3.1. Water Content
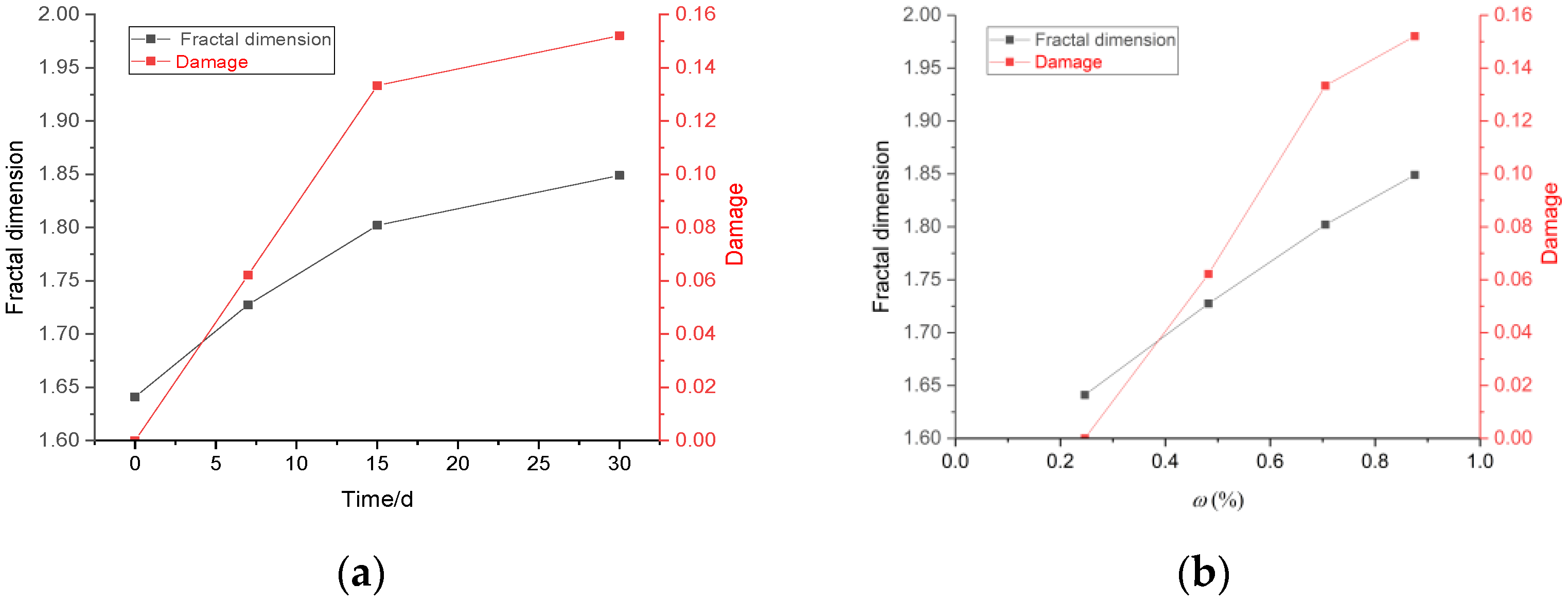
3.2. Fractal Damage Analysis of Gypsum Rock after Wetting
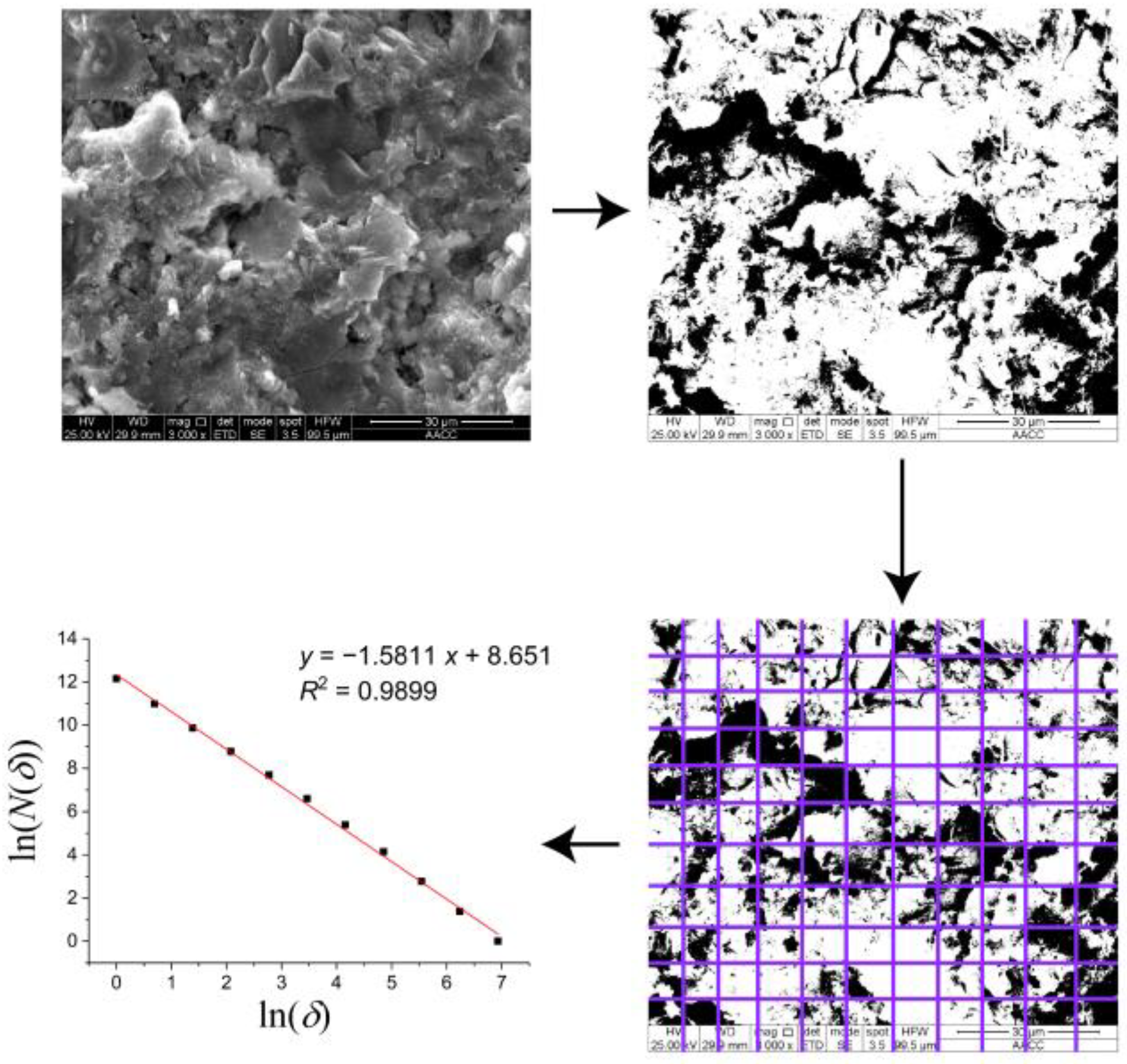
3.2.1. SEM Image Analysis
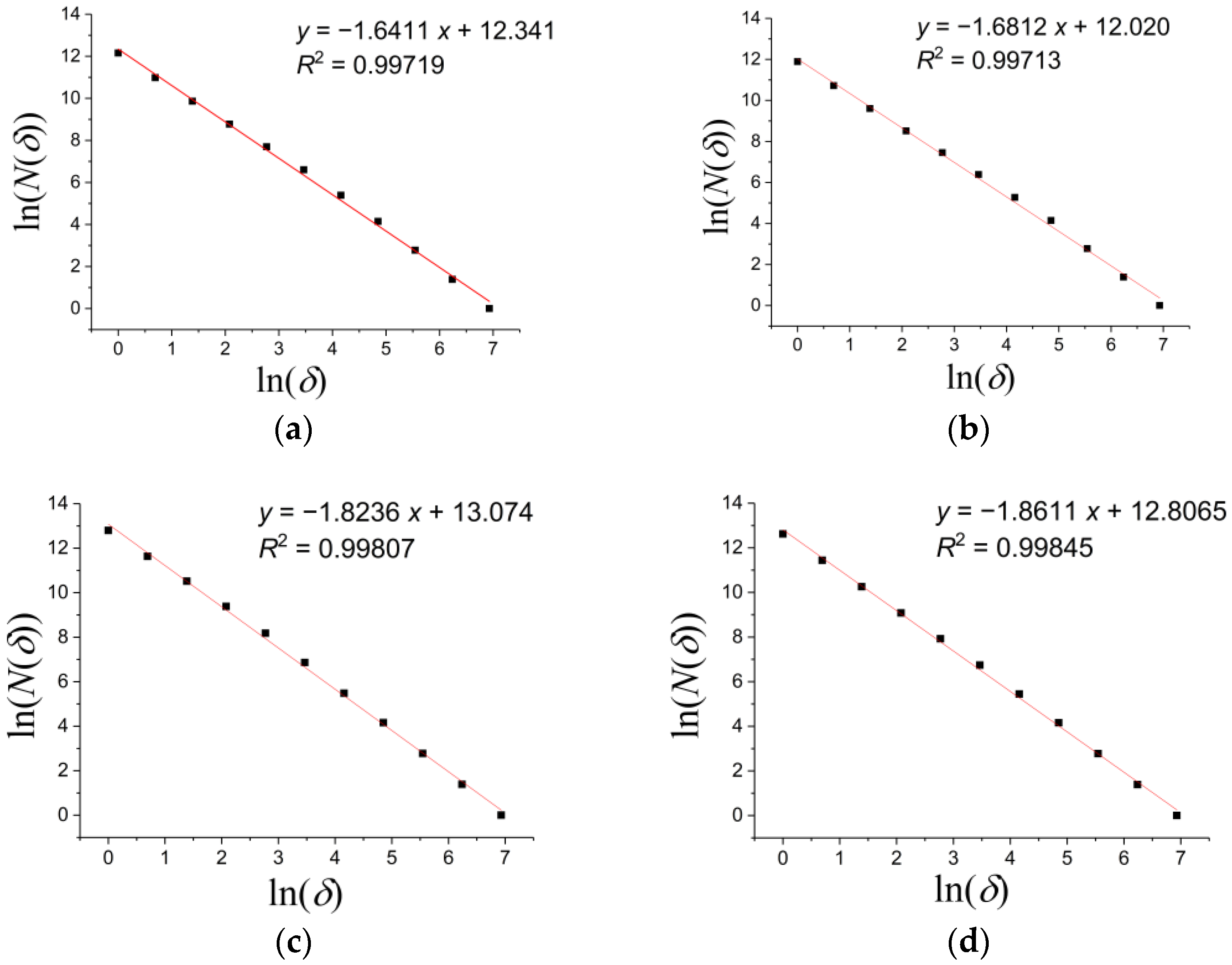
3.2.2. The Fractal Dimension and The Degree of Damage
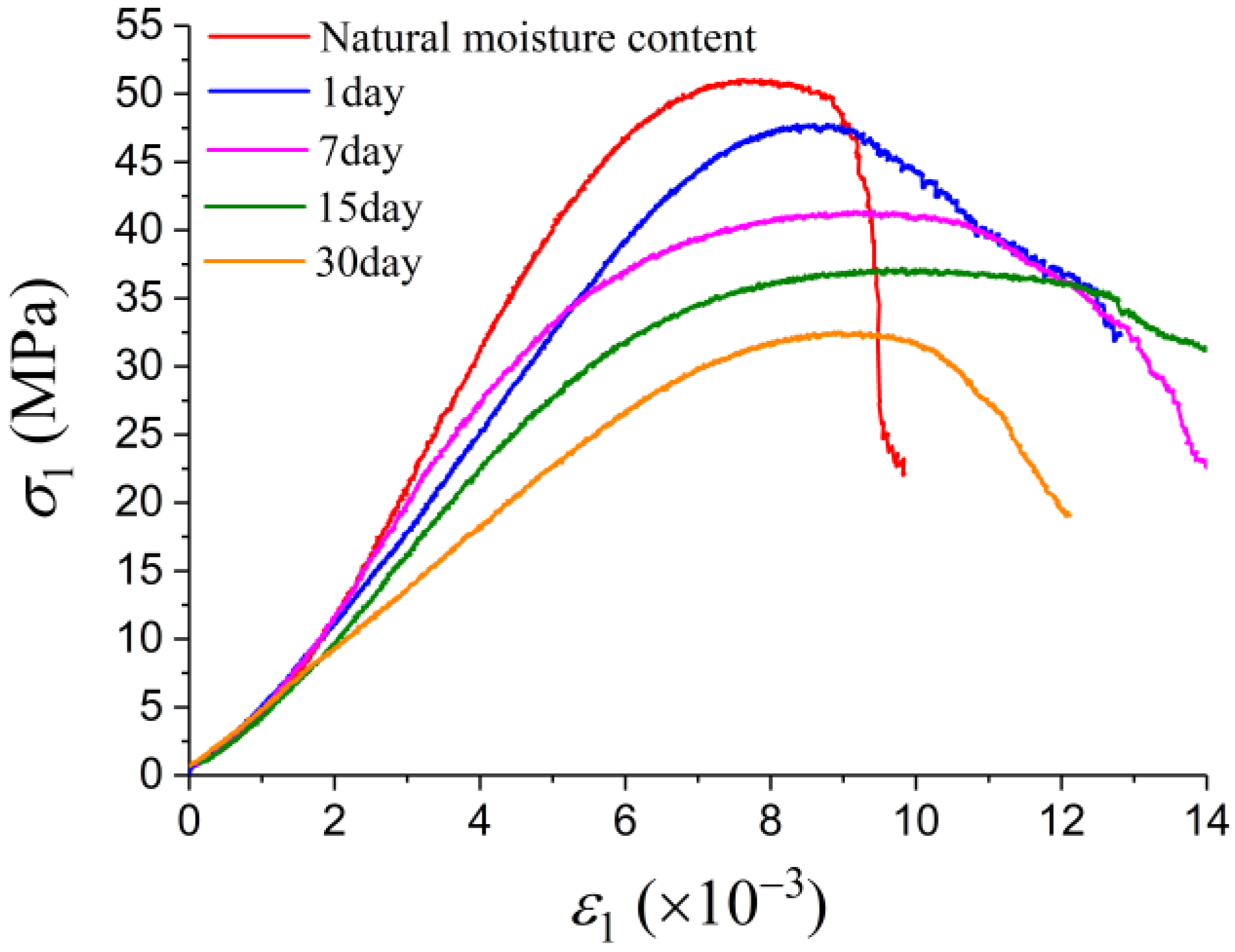
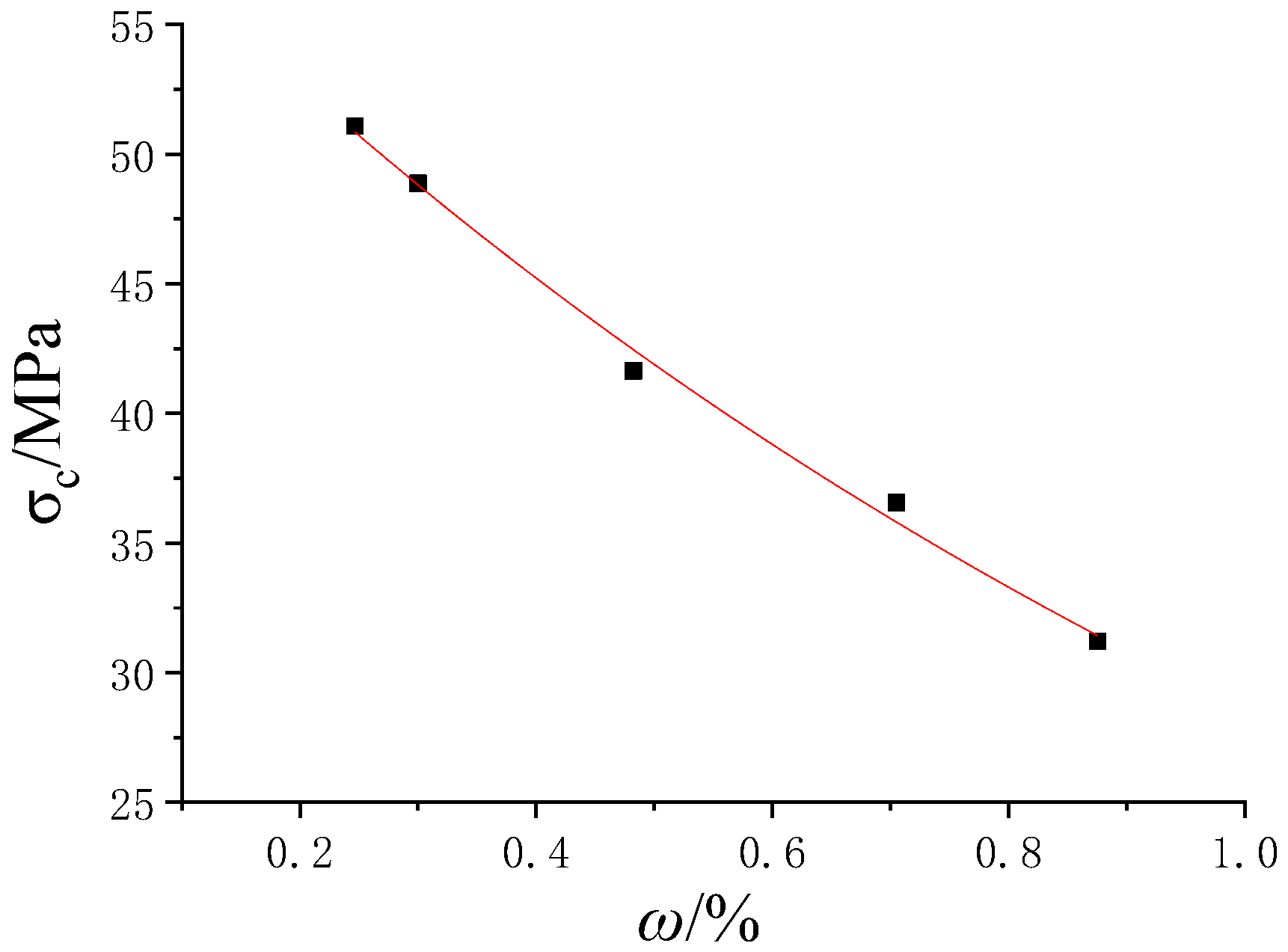
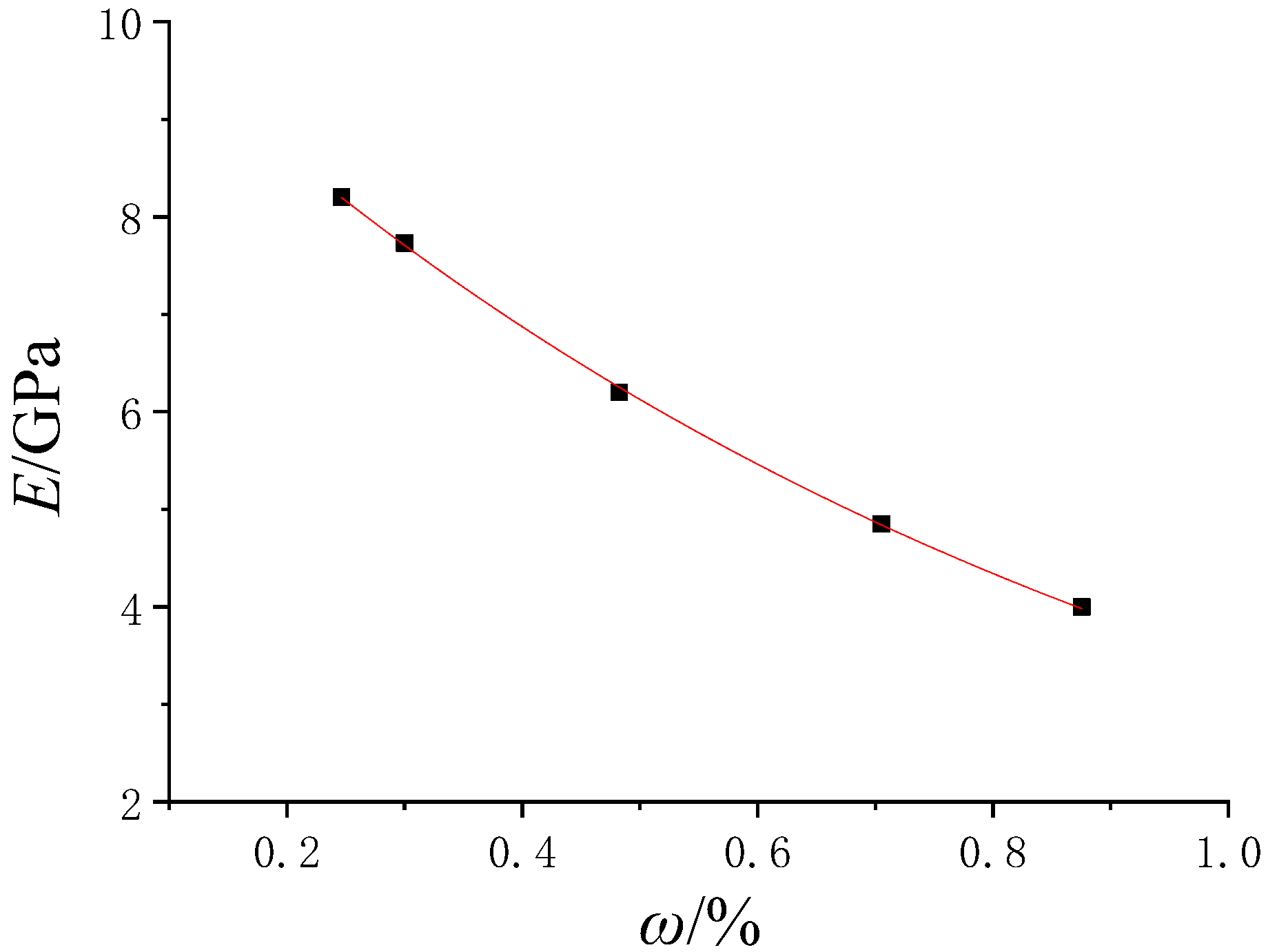
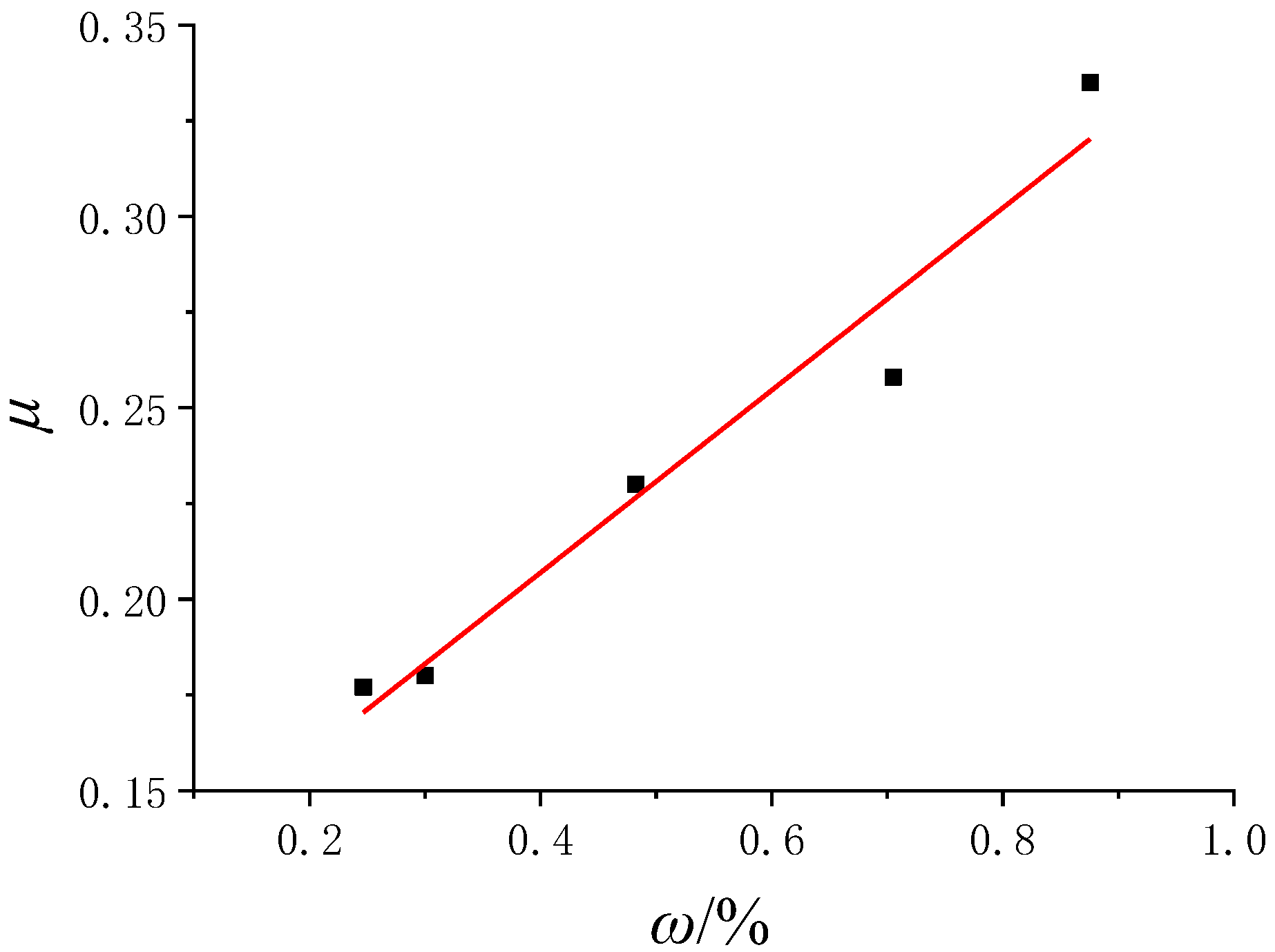
3.3. The Analysis of Strength and Deformability
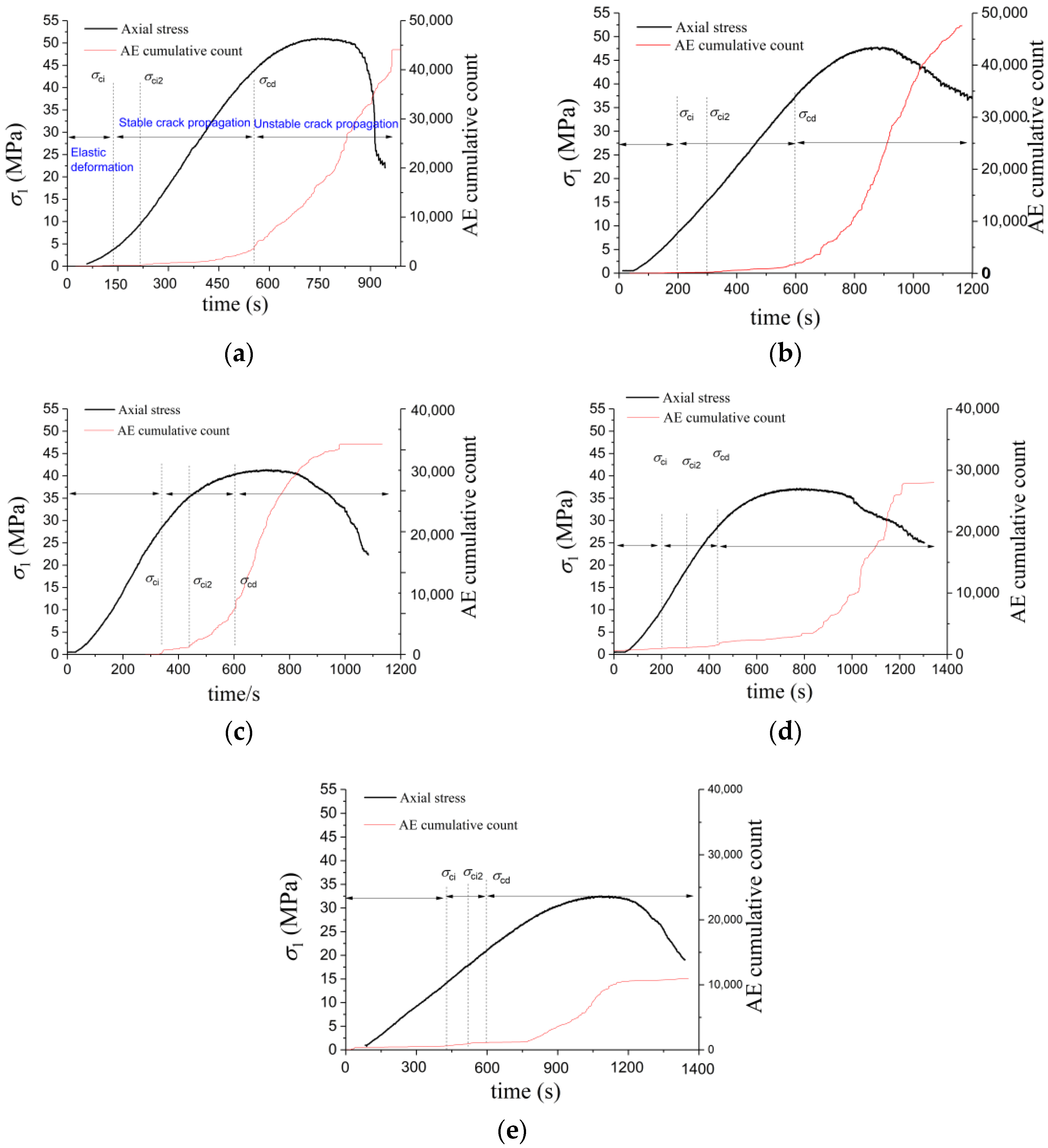
3.4. The Analysis of Acoustic Emission Characteristics
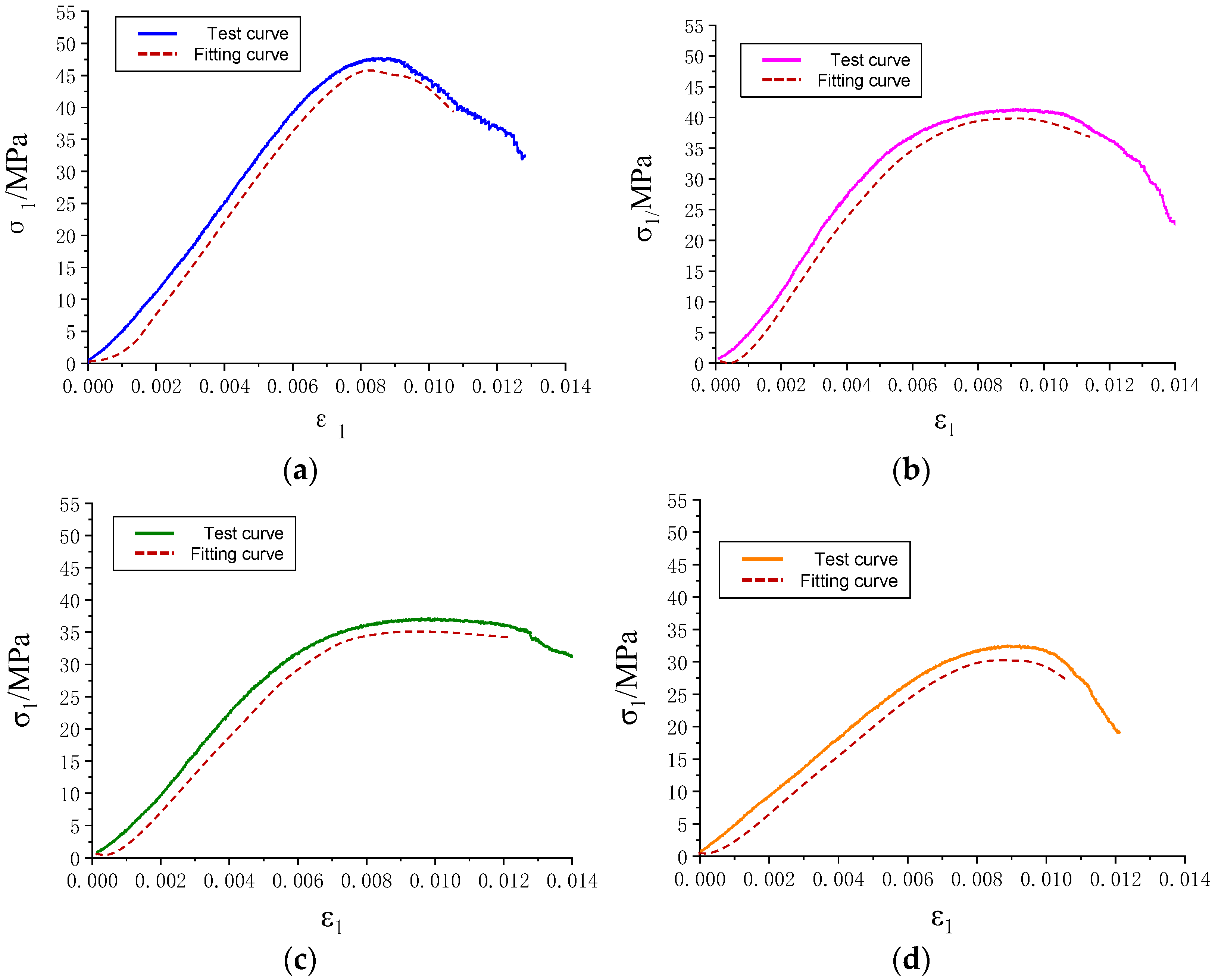
3.5. Validation of the Damage Constitutive Model
4. Conclusions
- Gypsum rock’s water content after water immersion was evaluated, and SEM scanning and fractal damage analysis were carried out. Our results indicate that gypsum rock is highly hydrophilic and that the rock water content grows with the increase of immersion time; however, the rate of increase declines as the immersion time increases. The SEM image analysis qualitatively showed that as the water immersion time increased, the complexity of the micropore structure and the porosity of the gypsum rock increased. The further fractal damage calculation quantitatively showed that the fractal dimension and the degree of damage to the rock microstructure increased with the increase in water immersion time; and this increase was quick in the early stage and slow in the later stage of the water immersion.
- The effect of the water content on the AE characteristics of the gypsum rock during the triaxial compression was significant, especially in the failure stage. With the increase in immersion time, the AE count intensified, due to the dissolving and softening effect of the water on the interior of the gypsum rock, leading to an accelerated failure rate in the failure stage. The AE cumulative count declined with the increase in the immersion time because a longer immersion time increased the degree of damage to the rock microstructure. Hence, the amount of fracture and energy required for rock failure decreased. Our observations on the threshold stress indicated that the wetting induced a shortened stable crack propagation stage during the loading process.
- A damage constitutive model of gypsum rock after wetting has been developed, where the damage degree is defined based on the AE characteristics during the triaxial compression tests. The model can effectively reproduce the experimental mechanical responses of gypsum rock after different water immersion times.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, C.; Xu, X.; Liu, W.; Xiong, F.; Lin, Y.; Cao, C.; Liu, X. Softening damage analysis of gypsum rock with water immersion time based on laboratory experiment. IEEE Access 2019, 7, 125575–125585. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, M.; Wu, X.; Chen, Z.; Zhang, K. Deterioration behavior of gypsum breccia in surrounding rock under the combined action of cyclic wetting-drying and flow rates. Bull. Eng. Geol. Environ. 2021, 80, 4985–5001. [Google Scholar] [CrossRef]
- Jeschke, A.A.; Vosbeck, K.; Dreybrodt, W. Surface controlled dissolution rates of gypsum in aqueous solutions exhibit nonlinear dissolution kinetics. Geochim. Cosmochim. Acta 2001, 65, 27–34. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.-C.; Li, L.-P.; Lin, P.; Xu, Z.-H.; Gao, C.-L. Attribute recognition model for risk assessment of water inrush. Bull. Eng. Geol. Environ. 2019, 78, 1057–1071. [Google Scholar] [CrossRef]
- Torabi-Kaveh, M.; Heidari, M.; Miri, M. Karstic features in gypsum of Gachsaran Formation (case study; Chamshir Dam reservoir, Iran). Carbonates Evaporites 2012, 27, 291–297. [Google Scholar] [CrossRef]
- Auvray, C.; Homand, F.; Sorgi, C. The aging of gypsum in underground mines. Eng. Geol. 2004, 74, 183–196. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, X.; Guo, J.; Xiao, F.; Zhao, F. Experimental study of fatigue characteristics of gypsum rock under cyclic loading. Chin. J. Rock Mech. Eng. 2017, 36, 940. [Google Scholar] [CrossRef]
- Sadeghiamirshahidi, M.; Vitton, S.J. Laboratory Study of Gypsum Dissolution Rates for an Abandoned Underground Mine. Rock Mech. Rock Eng. 2019, 52, 2053–2066. [Google Scholar] [CrossRef]
- Meng, T.; Xiangxi, M.; Donghua, Z.; Hu, Y. Using micro-computed tomography and scanning electron microscopy to assess the morphological evolution and fractal dimension of a salt-gypsum rock subjected to a coupled thermal-hydrological-chemical environment. Mar. Pet. Geol. 2018, 98, 316–334. [Google Scholar] [CrossRef]
- Auvray, C.; Homand, F.; Hoxha, D. The influence of relative humidity on the rate of convergence in an underground gypsum mine. Int. J. Rock Mech. Min. Sci. 2008, 45, 1454–1468. [Google Scholar] [CrossRef]
- Yilmaz, I. Influence of water content on the strength and deformability of gypsum. Int. J. Rock Mech. Min. Sci. 2010, 47, 342–347. [Google Scholar] [CrossRef]
- Li, W.; Einstein, H.H. Theoretical and numerical investigation of the cavity evolution in gypsum rock. Water Resour. Res. 2017, 53, 9988–10001. [Google Scholar] [CrossRef]
- Yu, W.D.; Liang, W.G.; Li, Y.R.; Yu, Y.M. The meso-mechanism study of gypsum rock weakening in brine solutions. Bull. Eng. Geol. Environ. 2016, 75, 359–367. [Google Scholar] [CrossRef]
- Ouyang, Y.; Chen, S.; Chen, W.; Zhang, L.; Matthai, S.; Duan, W. Toward the Understanding of Stress-Induced Mineral Dissolution via Molecular Scale Simulations. J. Phys. Chem. C 2020, 124, 19166–19173. [Google Scholar] [CrossRef]
- Chen, W.Q.; Sedighi, M.; Jivkov, A.P. Thermo-osmosis in hydrophilic nanochannels: Mechanism and size effect. Nanoscale 2021, 13, 1696–1716. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, W.Q.; Ouyang, Y.; Matthai, S.; Zhang, L. Transitions between nanomechanical and continuum mechanical contacts: New insights from liquid structure. Nanoscale 2019, 11, 22954–22963. [Google Scholar] [CrossRef]
- Du, M.R.; Chen, S.J.; Duan, W.H.; Chen, W.Q.; Jing, H.W. Role of multiwalled carbon nanotubes as shear reinforcing nanopins in quasi-brittle matrices. ACS Appl. Nano Mater. 2018, 1, 1731–1740. [Google Scholar] [CrossRef]
- Chen, W.; Sedighi, M.; Jivkov, A.P. Thermo-osmosis in silica nanochannels. Jpn. Geotech. Soc. Spec. Publ. 2021, 9, 210–214. [Google Scholar] [CrossRef]
- Kovari, K.; Tisa, A.; Einstein, H.; Franklin, J. Suggested methods for determining the strength of rock materials in triaxial compression: Revised version. Intl. J. Rock Mech. Min. Sci. Geomech. Abs. 1983, 20, 285–290. [Google Scholar] [CrossRef]
- Franklin, J.A. Suggest methods for determining water content, porosity, density, absorption and related properties and swelling and slake-durability index properties. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 141–156. [Google Scholar] [CrossRef]
- Shi, X.; Jing, H.; Chen, W.; Gao, Y.; Zhao, Z. Investigation on the Creep Failure Mechanism of Sandy Mudstone Based on Micromesoscopic Mechanics. Geofluids 2021, 2021, 5550733. [Google Scholar] [CrossRef]
- Jing, H.; Yin, Q.; Yang, S.; Chen, W. Micro-mesoscopic creep damage evolution and failure mechanism of sandy mudstone. Int. J. Geomech. 2021, 21, 04021010. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 2009, 18, 315–340. [Google Scholar] [CrossRef]
- Feng, Z.; Sun, X. Box-counting dimensions of fractal interpolation surfaces derived from fractal interpolation functions. J. Math. Anal. Appl. 2014, 412, 416–425. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, R.; Zhou, H.W.; Pei, J.L. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Peng, R.; Yang, Y.; Ju, Y.; Mao, L.; Yang, Y. Computation of fractal dimension of rock pores based on gray CT images. Chin. Sci. Bull. 2011, 56, 3346. [Google Scholar] [CrossRef]
- Xu, X.; He, M.; Zhu, C.; Lin, Y.; Cao, C. A new calculation model of blasting damage degree—Based on fractal and tie rod damage theory. Eng. Fract. Mech. 2019, 220, 106619. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Jasinge, D.; Song, J.; Choi, S. A study of the effect of displacement rate and moisture content on the mechanical properties of concrete: Use of acoustic emission. Mech. Mater. 2008, 40, 453–469. [Google Scholar] [CrossRef]
- Chun, Z.; Yun, L.; Gan, F. Influence of temperature on quantification of mesocracks: Implications for physical properties of fine-grained granite. Lithosphere 2021, 2021, 7824057. [Google Scholar] [CrossRef]
- Yin, Q.; Jing, H.; Ma, G. Experimental study on mechanical properties of sandstone specimens containing a single hole after high-temperature exposure. Geotech. Lett. 2015, 5, 43–48. [Google Scholar] [CrossRef]
- Ren, F.; Zhu, C.; He, M. Moment tensor analysis of acoustic emissions for cracking mechanisms during schist strain burst. Rock Mech. Rock Eng. 2020, 53, 153–170. [Google Scholar] [CrossRef]

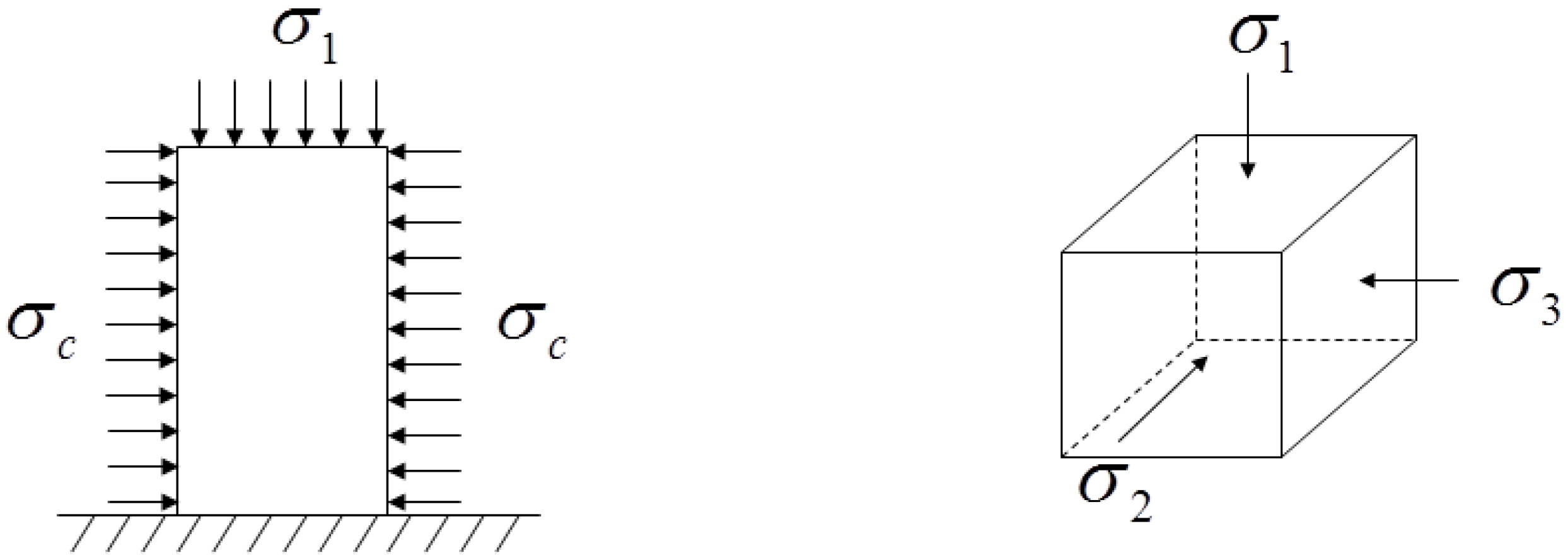


| Sample | ||||||
|---|---|---|---|---|---|---|
| dz0-1 | Natural | 441.91 | 441.15 | 0.76 | 0.1723 | 0.2467 |
| dz0-2 | 444.01 | 442.71 | 1.30 | 0.2936 | ||
| dz0-3 | 442.58 | 441.37 | 1.21 | 0.2741 | ||
| dz1-1 | 1 | 447.37 | 446.11 | 1.26 | 0.2824 | 0.3001 |
| dz1-2 | 445.35 | 443.85 | 1.50 | 0.3379 | ||
| dz1-3 | 451.22 | 449.96 | 1.26 | 0.2800 | ||
| dz7-1 | 7 | 444.28 | 442.12 | 2.16 | 0.4886 | 0.4824 |
| dz7-2 | 448.60 | 446.32 | 2.28 | 0.5108 | ||
| dz7-3 | 449.62 | 447.48 | 2.14 | 0.4479 | ||
| dz15-1 | 15 | 447.84 | 444.68 | 3.16 | 0.7106 | 0.7051 |
| dz15-2 | 449.35 | 446.00 | 3.35 | 0.7511 | ||
| dz15-3 | 451.18 | 448.25 | 2.93 | 0.6537 | ||
| dz30-1 | 30 | 446.01 | 441.35 | 4.66 | 1.1056 | 0.8755 |
| dz30-2 | 444.35 | 440.88 | 3.47 | 0.7870 | ||
| dz30-3 | 446.17 | 442.92 | 3.25 | 0.7338 |
| Image Number | Magnification | Fractal Dimension | R2 |
|---|---|---|---|
| a | 1000 | 1.6411 | 0.99719 |
| b | 1000 | 1.6812 | 0.99713 |
| c | 1000 | 1.8236 | 0.99807 |
| d | 1000 | 1.8611 | 0.99845 |
| Sample Number | (MPa) | (GPa) | Poisson’s Ratio | ||||
|---|---|---|---|---|---|---|---|
| Test Value | Average Value | Test Value | Average Value | Test Value | Average Value | ||
| sz0-1 | 0 | 51.02 | 51.08 | 8.45 | 8.20 | 0.176 | 0.177 |
| sz0-2 | 52.54 | 8.28 | 0.171 | ||||
| sz0-3 | 49.68 | 7.87 | 0.183 | ||||
| sz1-1 | 1 | 47.74 | 48.87 | 7.61 | 7.73 | 0.179 | 0.180 |
| sz1-2 | 48.66 | 7.56 | 0.187 | ||||
| sz1-3 | 50.21 | 8.01 | 0.175 | ||||
| sz7-1 | 7 | 41.38 | 41.64 | 6.22 | 6.20 | 0.231 | 0.230 |
| sz7-2 | 44.27 | 6.41 | 0.216 | ||||
| sz7-3 | 39.28 | 5.96 | 0.243 | ||||
| sz15-1 | 15 | 36.98 | 36.56 | 4.98 | 4.85 | 0.271 | 0.258 |
| sz15-2 | 35.84 | 4.76 | 0.256 | ||||
| sz15-3 | 37.18 | 4.81 | 0.247 | ||||
| sz30-1 | 30 | 32.41 | 31.21 | 4.08 | 4.00 | 0.352 | 0.335 |
| sz30-2 | 29.68 | 3.91 | 0.311 | ||||
| sz30-3 | 31.54 | 4.01 | 0.343 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhou, Y.; Chen, W.; Gao, Y.; Fu, Q.; Liu, X.; Feng, C. Macro-Microscopic Deterioration Behavior of Gypsum Rock after Wetting and Its Constitutive Model Based on Acoustic Emission. Minerals 2022, 12, 1168. https://doi.org/10.3390/min12091168
Xu X, Zhou Y, Chen W, Gao Y, Fu Q, Liu X, Feng C. Macro-Microscopic Deterioration Behavior of Gypsum Rock after Wetting and Its Constitutive Model Based on Acoustic Emission. Minerals. 2022; 12(9):1168. https://doi.org/10.3390/min12091168
Chicago/Turabian StyleXu, Xiaoding, Yuejin Zhou, Weiqiang Chen, Yubing Gao, Qiang Fu, Xue Liu, and Chundi Feng. 2022. "Macro-Microscopic Deterioration Behavior of Gypsum Rock after Wetting and Its Constitutive Model Based on Acoustic Emission" Minerals 12, no. 9: 1168. https://doi.org/10.3390/min12091168
APA StyleXu, X., Zhou, Y., Chen, W., Gao, Y., Fu, Q., Liu, X., & Feng, C. (2022). Macro-Microscopic Deterioration Behavior of Gypsum Rock after Wetting and Its Constitutive Model Based on Acoustic Emission. Minerals, 12(9), 1168. https://doi.org/10.3390/min12091168







