Abstract
Remote sensing data provide significant information about surface geological features, but they have not been fully investigated as a tool for delineating mineral prospective targets using the latest advancements in machine learning predictive modeling. In this study, besides available geological data (lithology, structure, lineaments), Landsat-8, Sentinel-2, and ASTER multispectral remote sensing data were processed to produce various predictor maps, which then formed four distinct datasets (namely Landsat-8, Sentinel-2, ASTER, and Data-integration). Remote sensing enhancement techniques, including band ratio (BR), principal component analysis (PCA), and minimum noise fraction (MNF), were applied to produce predictor maps related to hydrothermal alteration zones in Hamissana area, while geological-based predictor maps were derived from applying spatial analysis methods. These four datasets were used independently to train a random forest algorithm (RF), which was then employed to conduct data-driven gold mineral prospectivity modeling (MPM) of the study area and compare the capability of different datasets. The modeling results revealed that ASTER and Sentinel-2 datasets achieved very similar accuracy and outperformed Landsat-8 dataset. Based on the area under the ROC curve (AUC), both datasets had the same prediction accuracy of 0.875. However, ASTER dataset yielded the highest overall classification accuracy of 73%, which is 6% higher than Sentinel-2 and 13% higher than Landsat-8. By using the data-integration concept, the prediction accuracy increased by about 6% (AUC: 0.938) compared with the ASTER dataset. Hence, these results suggest that the framework of exploiting remote sensing data is promising and should be used as an alternative technique for MPM in case of data availability issues.
1. Introduction
The prediction of mineral prospectivity is one of the substantial practices in mineral exploration, which is used to fulfill the growing demand for mineral resources in industrial development countries [1,2]. Mineral prospectivity mapping (MPM), also known as mineral prospectivity modeling, is a multivariable decision-making tool that aims to delimit and prioritize high-potential zones for exploring a particular type of mineral in unexplored regions [2,3,4]. Model-based MPM is a vital but challenging process that essentially attempts to establish a function for integrating a collection of geological features (input variables) with the presence of the targeted mineral (output variables) [5]. Establishing this integration function is carried out by analyzing the spatial relationships between input variable features and known mineral occurrences through different numerical algorithms [6]. Hence, it is essential to select a convenient algorithm that is capable to learn the complex relationships between variables (input/output) to obtain an accurate prediction [7]. In practice, the most critical procedure in prospectivity modeling is the selection of evidential features that represent the spatial representatives of ore-controlling factors, which can be extended to combine available multi-source exploration datasets such as geological, geophysical, geochemical, and remote sensing data [8,9]. Based on the ease of implementation and the availability of data and software tools, prospectivity modeling can be categorized into two types: (i) knowledge-driven models that depend on expert knowledge to heuristically estimate the parameters of the models using the given information of mineral deposits in the given geological setting [10,11]; (ii) data-driven models that depend on the quantitative measures of the spatial associations between evidential features and targeted deposit locations to empirically estimate the parameters [6,12,13,14].
Remote sensing data have been successfully and extensively employed in mineral exploration since they can detect and delineate geological and structural features that aid in identifying new areas of mineralization [15,16,17,18]. Remotely-sensed images with the proper spatial and spectral resolution, including multispectral and hyperspectral satellite imagery allow to identify rocks and minerals based on their spectral signatures in the visible-near-infrared (VNIR) and the shortwave infrared (SWIR) regions [19,20,21,22]. In specific, multispectral satellite imagery with a high spatial resolution (10–30 m) and coarse spectral resolution such as Landsat-8, Sentinel-2, and ASTER, have been widely utilized to map and remotely sense fault/fracture zones and/or hydrothermal alteration zones associated with ore mineralization [23,24,25,26,27,28]. Nevertheless, the remote-sensing approach in mineral exploration applications has often been exclusive to classification models and knowledge-driven regression models. Whereas classification models aim to classify different hydrothermal alteration zones (argillic, phyllic, and propylitic) or minerals associated with alteration (e.g., iron-bearing and hydroxyl-bearing minerals) [29,30,31]. On the other hand, in the GIS-based knowledge-driven method, each remote sensing predictor layer is assigned a weight reflecting its importance in the modeling process. Subsequently, producing a map with a continuous prospectivity score indicates the likelihood of the targeted mineral [15,32].
In recent years, the development of machine learning (ML) and deep learning (DL) methods have boosted the regression models of mineral prospectivivty, which achieve better predictive performance than traditional statistical techniques and empirical explorative models [2,3,33]. Some of the most commonly used supervised learning models include Random Forest (RF) [4,34], Support Vector Machine (SVM) [35], and Artificial Neural Network (ANN) [36], which have been efficiently applied for MPM. RF is well known to be the first choice for data-driven predictive modeling of MPM, considering its accuracy in the delineation of prospective areas and sensitivity of parameter configuration [7]. Furthermore, RF performance is very stable in the case of: (i) the sufficiency of the number of known locations of mineral occurrences [34]; (ii) and the sensitivity of using different training sets of non-occurrence locations [4]. Another advantage that makes RF a great objective tool for data assessment is its capability to measure and rank the importance of evidential features to the training process [37].
Although remote sensing data were utilized in several studies for mapping mineral potential using supervised learning models, they have not been used as the main core for the derivation of the evidential features to train ML data-driven predictive models (e.g., RF, SVM, and ANN). For instance, Mansouri et al. [38] processed ASTER data with a multivariate regression analysis method to map iron mineral resources in the Sarvian area, Iran. Moreover, three multispectral data, namely Landsat-7 ETM+, Landsat-8, and ASTER were utilized by Bolouki et al., [39], to produce several predictor maps (evidential features), then were fused together to train Naïve Bayes (NB) classifier for producing a map showing the probability of gold occurrence in Ahar-Arasbaran area, NW Iran. On the other hand, remote sensing imagery was integrated with other sources of data to train various ML predictive models. As an example of that, two band ratios (BR) images of Landsat TM (5/7 and 3/1) were integrated with other predictor variables such as three geochemical survey maps and a couple of geophysical maps. Rodriguez-Galiano et al., used these two BRs as an indication for ore-related hydroxyl and iron oxide alteration to train RF model for gold MPM in Rodalquilar area, Southern Spain [40].
Considering the global development in GIS and ML fields, data availability is still an issue for conducting a comprehensive MPM study in third-world countries. Carranza [33] reported that from 2006 to 2016 about 116 MPM studies were exclusive only to 25 countries such as Iran, Australia, China, Canada, etc. Whereas countries such as Sudan have almost no research about ML applications in the mineral exploration field, even though Sudan is the third largest gold-producing country in Africa and among the 20 countries in the world gold mine production in 2019 [41]. Therefore, it is worth noting that since the data of several multispectral satellite sensors are free, a comprehensive study of the capability of various remote sensing data for training multiple predictive models is needed.
In this study, mineral prospectivity modeling was performed for delineating gold prospective regions in west Hamissana, northeast Sudan. The present research aims at investigating the potential of Landsat-8, Sentinel-2, and ASTER for mapping mineral potential. Specifically, (i) remote sensing datasets were utilized to identify geological features and hydrothermal alteration zones associated with gold mineralization in the study area; (ii) spatial analysis methods and remote sensing enhancement techniques were applied to produce different thematic layers, which were afterward assessed based on their contribution to the prediction process; (iii) all datasets were also combined into another dataset to investigate the synergy of various data for developing a comprehensive scheme of MPM in the study area; and (iv) random forest algorithm was used as a tool of comprehensive comparison to obtaining the optimal dataset for accurate prediction.
2. Study Area
The study area comprises approximately 1379 km2, which is situated between latitudes (20°22′ N and 20°50′ N) and longitudes (34°00′ E and 34°45′ E). It is located in Wadi Edom to the west of Hamissana, Red Sea State, Sudan (Figure 1). Topographically, the area studied is in the northern part of the Red Sea hills, which rises almost 2000 m (≈6561 ft) above sea level. The area is characterized by a dry climate, with very poor vegetation cover. The highest temperature reaches 46 °C in the summer (October–march). The Winter season is relatively short, from November to February, with an average temperature of around 25 °C in the daytime [42].
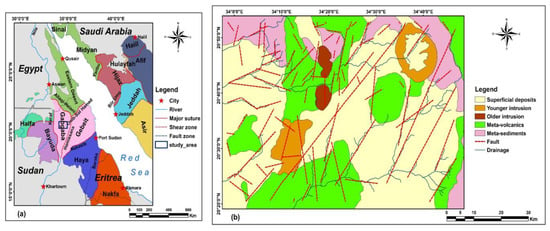
Figure 1.
Location of the study area. (a) Sketch map of the main terranes, major suture, and shear zones of the Arabian-Nubian shield in the Red Sea Hills Region of Sudan (modified after Bierlein et al. [43]); (b) geological map of the study area (modified after Mohamed et al. [42]).
The geological setting of the Hamissana area forms a part of the Arabian Nubian Shield (ANS) (Figure 1a). ANS covers the eastern part of Sudan and broad areas of other countries such as Saudi Arabia, Ethiopia, Eritrea, Yemen, and Egypt [15]. During the Pan-African tectonic event, the collision and the accretion of Neoproterozoic island arcs to the Nile craton formed ANS [44]. The evolution of the shield including the complete orogenic cycle between 900 and 550 Ma is documented, where the island arcs characterized by basic to acid metavolcanics, and metasediments of the Proterozoic age are exposed [44,45]. Different arc assemblages are separated by ophiolitic-decorated suture zone forming five terranes in Sudan, while subduction-related calc-alkaline I-type granodiorites (older granites) intruded these assemblages [45,46]. The entire sequence is intruded by post-orogenic alkali A-type granitoid (younger granites) [44,47]. A NE-SW suture zone named after the study area forms a transition terrane between Bayuda craton terrane and Gebiet island arc terrane, called Gabgaba terrane. The main exposed lithological units in the study area are predominant with metavolcanic, syn-orogenic (older intrusion), and post-orogenic (younger intrusion) rocks [42]. The metasediments represent the oldest rock unit in the study area, which has E-W linear trending and is composed of quartzite and marble. Metavolcanics are generally composed of gray meta-acid volcanic and dark metatrachyte. Granite and coarse to medium-grained granodiorite, form the older intrusions. Younger intrusions are non-foliated and consist of porphyritic microgranite, highly sheared and dark granodiorite, and quartz feldspar porphyry. Several low outcrops of sediments and superficial deposits are scattered in the region. Structural trends of faults and dykes are NW-SE, NE-SW, and E-W, while most faults are in the form of strike-slip faults [42].
3. Materials and Methods
3.1. Data and Data-Preprocessing
Mohamed et al. [42] integrated important geological information about the study area. They established a comprehensive geodatabase containing the updated geological map, primary faults/fractures map, and locations of gold occurrences. All these geological datasets were digitized from paper maps of the published study [42]. Intrusion rock units were extracted separately as shapefile of polygons, while faults with different azimuth directions were saved as line shapefiles. 25 locations of gold occurrence were carefully selected from the overall 34 locations that constituted the database, where the minimum distance between each location corresponds to the grid size of 30m. The preparation of these geological datasets was carried out using ArcGIS 10.6.1 software.
The satellite remote sensing data employed in this study are Landsat-8, Sentinel-2A, and ASTER. All three types of multispectral imagery were freely downloaded from the U.S. Geological Survey’s Earth Resources Observation and Science (EROS) Centre, using the USGS earth explorer website (https://earthexploere.usgs.gov). In addition, the user must also register on the National Aeronautics and Space Administration website (NASA) to obtain ASTER data (https://earthdata.nasa.gov). In this study, one scene of Landsat-8, two scenes of Sentinel-2, and four scenes of ASTER were obtained on different dates to cover the study area. All scenes have (0%–2%) cloud coverage and (>0.05) maximum Normalized Different Vegetation Index (NDVI), which suit the basic requirements for geological investigation. Table 1 shows the technical properties of different sensors and the characteristics of various scenes used in this investigation.

Table 1.
Technical characteristics and dataset attributes of different remote sensing data.
In this study, the spatial resolution of various multispectral data was resampled to 30m using nearest neighbor technique. Since ASTER scenes were obtained on different dates, the Thermal Infrared (TIR) bands of ASTER and Landsat-8 were excluded to avoid unfavorable changes in surface thermal emission. Moreover, the coastal and cirrus bands of Landsat-8 and Sentinel-2 were designed for atmospheric correction. Therefore, they were not used in the analysis, as well as the panchromatic band (band 8) of Landsat-8 and water-vapor band (band 9) of Sentinel-2. Landsat-8 level 1 terrain corrected (L1T) data and ASTER level 1 Precision Terrain Corrected Registered At-Sensor Radiance (AST_L1A) data are radiometrically calibrated and geometrically corrected [27]. Both datasets were atmospherically corrected using the FLASH (Fast Line of Sight Atmospherics Analysis of Hypercubes) algorithm provided by ENVI 5.2 software. The FLASH algorithm was applied to ASTER data after implementing a cross-track illumination correction to the short waves infrared (SWIR) bands. Dark Object Subtraction (DOS) method in the semi-automatic classification plugin provided by QGIS 3.16.7 software, was employed to automatically atmospherically correct Sentinel-2 data. All atmospherically corrected datasets were georeferenced to the Universal Transverse Mercator (UTM) coordinate system in zone 36 N.
3.2. Random Forest (RF)
RF is an ensemble learning algorithm that is developed based on the concept of Decision Trees (DTs) [48]. The accumulation of multiple classification or regression DTs is employed to obtain repeated predictions of the target phenomenon represented by the training dataset [40]. These trees are grown based on random selection from the original training datasets using a procedure known as “bootstrap bagging” [49]. This sampling method increases the diversity of the trees by generating training subsets (bag samples) using about two-thirds of the training features for prediction, whereby the left out of the training samples (out-of-bag (OOB) samples) are used to validate the prediction accuracy [34].
To overcome the overfitting issue of the DT, RF attempts to grow trees in a way that maximizes the reduction in purity by searching through the optimal feature/split node, which varies from pruning trees according to discriminative conditions in the standard DT [50]. In other words, RF generates a tree using the best variable within bag samples, which reduces the correlation between the trees and minimizes the generalization error [48]. RF uses the Gini index to ensure the best split selection based on the comparison of the information purity of the leaf nodes with that of their root nodes. The Gini index used in this study is shown in the following equation [50]:
where is the probability of class n, which can be calculated by dividing the number of samples belonging to class j, by (m) the total number of samples in a specific node. The ultimate decision of RF is made by combining the votes of every DT, then averaging the results as shown in Equation (2) [7]:
where T(x) represents the result of DTs using x input vector, while K denotes the number of DTs that are grown to obtain RF results () [2].
It is important to mention that RF has another essential advantage besides the unbiased estimation of the generalization error, which is the ability to measure and sort the importance of different predictor variables [51,52]. This is achieved internally by using the OOB samples, which originally are used to calculate the number of classified trees. Variables’ importance is measured by randomly permutating each variable including OOB samples and then sending down these permuted OOB cases to the trees again. Calculating the correctly classified cases and subtracting them from the original correctly classified cases derived from non-permuted data, allows measuring the importance of that variable [53]. In other words, RF measures the marginal effect of a specific variable by holding all other predictor variables constant [4]. This asset is vital for multi-source data that are characterized by high dimensionality, where it is significant to grasp the influence of each predictor on the prediction performance [7,37,54].
3.3. Induction of RF Predictive Model
The process of inducting data-driven predictive machine learning modeling consists of three main steps, which directly affect the model’s outcome. These three steps are: (i) the preparation of the input training dataset, which is considered the most important and critical step in the MPM field; (ii) specifying the suitable configuration of parameters in each model, also known as “hyperparameters tuning”; (iii) assessing predictive model performance [7,37]. Figure 2 shows the technical flowchart of this study’s overall methodology and different stages to completely train RF predictive model. As shown in the figure, the preparation of input data includes generating predictor variables (also called feature predictors) and target variables. Predictor variables are thematic maps derived from integrating muti-source data and guided by a deep understanding of the gold mineral system. These predictor maps represent the critical stipulations for generating a desirable prediction of mineral potential [3]. On the other hand, target variables are the ground truth data of the studied phenomena. Unlike classification tasks where the target is defined by categorical data that are presented as labeled classes, predictive models (regression tasks) use continuous data as target variables to predict a continuous quantity of specific phenomena. In the case of MPM, mineral occurrence and non-occurrence are given as binary values (1 and 0, respectively) to predict continuous output representing the likelihood of gold value. In this study, the generation of different input datasets was accomplished by using ENVI and ArcGIS software. Meanwhile, Python 3 was implemented to train different RF by using “Scikit-Learn” library.
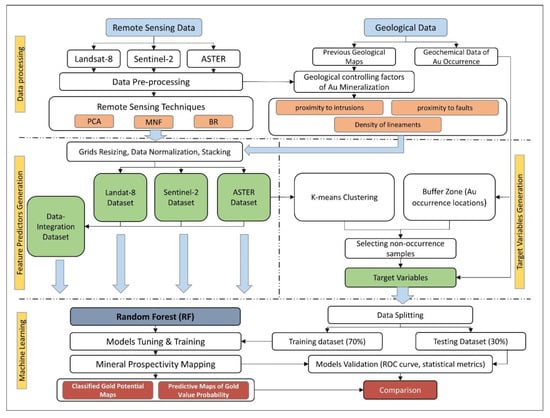
Figure 2.
A technical flowchart shows the study’s overall methodology to delineate MPM.
In common practice, leave-out and cross-validation methods are utilized to assess model performance [55]. The leave-out approach is achieved by randomly splitting the target variables into training and testing subsets. Data split usually takes different portions according to the user’s definition when it typically is carried out at 75:25 or 80:20. On the other hand, the cross-validation approach, namely K-Fold cross-validation method, employs all the target data in the training and testing process simultaneously. This is achieved by splitting the data into k subsets, where each subset serves once as a testing set while the remaining sets are used to train the model. This process is repeated k times until all of the target data appear in the training and testing set. This method, thereafter, averages the scores of the prespecified accuracy metric from each k fold performance. Since the study focuses on regression task, the mean square error (MSE) was utilized to measure the average squared difference between the trained model predicted result () and the true value of each sample (). This can be formalized as follow:
where N is the number of samples in the test dataset.
This study uses both approaches for assessing performance and reducing overfitting. The train-test split method was utilized to introduce possible bias since there is limited target data. Moreover, this method aids in comparing the performance of various outputs of RF by measuring accuracy metrics from the testing dataset. On the other hand, the purpose of employing five K-Fold cross-validations is to reduce overfitting and obtain optimal parameters for training each dataset. The possibility to find an optimal combination of parameters varies with different input datasets. Therefore, an objective grid search method known as “GridSearchCV” was used for hyperparameter tuning. This method is provided by the Scikit-Learn library (https://scikit-learn.org). As shown in Figure 3, this method searches through all possible combinations of parameters using k iteration for each combination. The user defines a dictionary of the possible set of values for each parameter whether they are categorical or numerical (e.g., number of trees). Although this process has a high computational cost, it is vital to measure the influence of model configuration on prediction performance. In the present study the range of the number of trees was set between 50 and 500 at intervals of 50, and the number of features between 2 and 12 at 2 intervals [3,7,8,40].
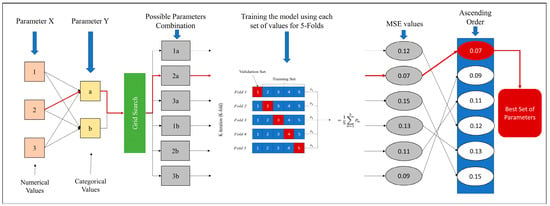
Figure 3.
A plot demonstrates the GridSearchCV method: in this case using two parameters (numerical/categorical) and 5-folds cross-validation.
3.4. Predictor Variables
As mentioned before, the input datasets (input-feature vectors) of MLA are the set of information derived from combining different thematic layers at each grid location. In this regard, different layers combination represents a unique input dataset. Four different datasets are employed in this study from integrating geological data with various multispectral remote sensing data. In addition to the geological predictor maps in each dataset, predictor maps processed from data of a specific sensor are appended. Therefore, dataset-1, dataset-2, and dataset-3 are formed by Landsat-8, Sentinel-2, and ASTER data, respectively, while the fourth dataset is composed of synergy from the three datasets.
3.4.1. Geological-Based Predictor Maps
According to the primer understanding of gold mineralization controlling factors, and geological data availability as well, we produced four geological-based predictor maps by using GIS spatial analysis methods. Identifying permissive lithologies, structures, and hydrothermal alteration zones is the main criterion of exploration. From prior literature about the Red Sea Hills, it is well known that mineralization zones have the same linear structures and exist in the acid meta-volcanic rocks [42,44,56]. Faults/fractures are favored channels for fluid migration, which represent the main ore-controlling factor in shear zone-related gold deposits. Therefore, two maps of distance to NE- and NW- faults were generated by using the Euclidean distance method (Figure 4a,b). The contact zone of the intrusive rocks (older and younger) lies in meta-sediments and metavolcanics, which may indicate the spatial agreement with gold mineralization in Hamissana area. Moreover, younger intrusions in the study area are highly sheared and contain several dykes. Hence, the proximity to outcropped intrusions was employed as a predictor map (Figure 4c).
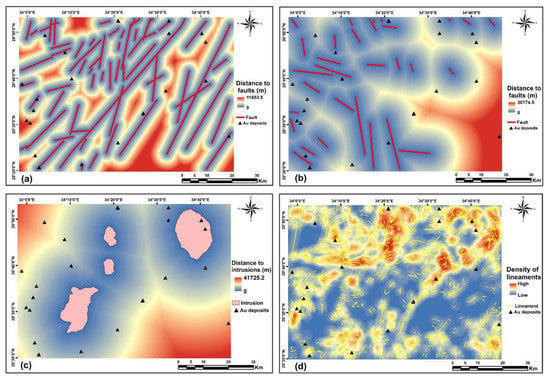
Figure 4.
Geological evidential features of the study area used as predictor variables: (a) Proximity to NE-SW faults; (b) proximity to NW-SE faults; (c) proximity to intrusions; (d) density of lineaments.
Since the valleys and drainage in the study area are structurally controlled by the shear zone, we automatically extracted lineaments as an indication of structural weakness, faults, fractures, or lines that separate different formations [57,58]. In mineral exploration, excessive lineaments are often localized close to mineralogical deposits, which may correspond to the main conduits for carrying hydrothermal solutions [15,25,58,59]. Therefore, these lineaments are adequate to be an indirect indicator of mining potential. Sentinel-2 has a higher spatial resolution than Landsat-8 and ASTER, which makes it more suitable for lineament extraction. Prior literature reported that Principal Component Analysis (PCA) has a better capability for automated lineament extraction compared with the original remote sensing data and other enhancement techniques [58,60]. Using PCI Geomatica software, lineaments were automatically extracted from PC5 of Sentinel-2. (Figure 4d) shows the concentration of lineaments distribution as a density map, which was employed as the fourth geological-based predictor map.
3.4.2. Remote Sensing-Based Predictor Maps
Remote sensing data provides significant information about different geological objects, such as mineral assemblages, lithological units, and hydrothermal alteration zones. Studying the existence of different alteration zones was another exploration key criterion since economic mineralization is often associated with these alteration zones. Multispectral data such as Landsat-8, Sentinel-2, and ASTER can be utilized to detect surface alteration zones using various remote sensing enhancement techniques. The main objective of these processing techniques is to interpret the remote sensing spectral signature of different alteration zones (Argillic, Phyllic, Propylitic) or minerals that are associated with hydrothermal alteration (iron oxides, clay, and hydroxyl bearing minerals). To generate different thematic layers of different alteration zones, this study employs different enhancement technique methods, such as Band Ratio (BR), PCA, and Minimum Noise Fraction (MNF).
BR is one of the most applicable techniques which aims to reduce the shadow effects of topography [15,61,62]. This method improves the spectral characteristic of specific alteration minerals (e.g., iron oxide, alunite, kaolinite, or chlorite) or alteration zones by dividing the digital number (DN) value of one band by the DN of another band [27,39,63]. On the other hand, Relative Absorption Band Depth (RBD) is another method that attempts to detect the typical absorption of targeted minerals, but it uses three bands to formalize the ratio (the sum of two bands is divided by the absorption band) instead of two bands [39]. Since ASTER sensor was developed particularly for geological investigations, several mineralogical indices were developed using bands in SWIR and TIR regions [64,65,66]. Table 2 lists all selected BR, RBD, and mineralogical indices, which were suggested by previous studies [15,39,61,66,67,68,69,70] to map targeted alteration minerals and zones. It is important to point out that the BR image for mapping ferric oxide was excluded in the case of Landsat-8 and ASTER datasets because the range of the data values (histogram width) of the generated imagery is very low, which may affect the output of the MLA models.

Table 2.
Selected BR, RBD, and mineralogical indices of each sensor to map targeted minerals.
PCA and MNF are transformation methods, which have been successfully utilized to enhance remote sensing imagery. Both statistical methods are employed for spectral data reduction by transforming the information in the original remote sensing data into a new set of data. In the PCA procedure, the new dataset (PC components) has less variance, since each component is extracted based on uncorrelated linear combinations of values (also called eigenvector loadings). These eigenvectors are calculated in a matrix called covariance matrix (Eigen matrix), which comes across the statistical relation between all the PCs. On the other hand, MNF method also uses the covariance matrix to rescale and segregate noise in the data. In the new dataset, the noise is reduced and whitened in a descending way based on the eigenvalue of each MNF component.
Since the eigenvector loadings (sign and magnitude) are linked to the spectral feature (absorption and reflectance) of objects, they can be utilized to detect the existence of a specific alteration mineral. For this purpose, the selective PCA technique (also known as Crosta technique) was developed to extract features of the specific object as bright or dark pixels in the PCs. This method is applied to VNIR+SWIR bands, where bands are selected (mostly 3 or 4 bands) based on the prior knowledge of the spectral behavior of an alteration mineral. One of the PCs will have two strong loadings with opposite signs that indicate the reflection and absorption bands of that alteration mineral. If the loading has a positive sign in the reflection band, the PC enhances the targeted mineral in bright pixels. In the meantime, this PC could also enhance that mineral in dark pixels, if the sign is negative in the reflectance band [29,39,46,71]. In this study, all selected bands from different sensor data to map different hydrothermal alteration zones and minerals, are illustrated in Table 3.

Table 3.
Selected bands of each sensor’s data to perform PCA transformation for mapping defined targets.
Unlike PCA method, MNF technique is less interpretable and very subjective. MNF results are only statistics and do not indicate specific mineral occurrences. However, separating and rescaling the noise process helps MNF to identify differences inside the image in the first few bands, while the latest few bands subsequently convey more noise [24,72]. Therefore, we visually assessed all MNF bands in each dataset, then for each dataset (Landsat-8, Sentinel-2, ASTER), we carefully selected three MNF that have a spatial agreement with different hydrothermal alteration minerals.
3.4.3. Data Preparation
At this stage, different predictor maps are generated from multisource data, so the numeric range of each input data is different. This variance in the range gives a chance for more domination to those inputs with a greater range than those with a smaller one. This issue directly affects the outputs of RF and brings numerical obstacles during the models’ execution [73]. In this regard, each input was normalized in the range of [0, 1] using the following equation:
where x is the input data, xmax and xmin donate to the maximum and minimum values of the original data respectively. After normalizing each predictor map, they were stacked to form four distinct datasets as shown in Table 4.

Table 4.
Input layers of each dataset to conduct data-driven MPM.
3.5. Target Variable
The target binary variables, corresponding to the gold occurrence and non-occurrence location, are used to train and validate the performance of supervised predictive models. A set of 25 occurrence locations are given a score of 1. In the meantime, the non-occurrence locations corresponding to the score of 0, were selected based on prespecified criteria. The selection of non-occurrence samples was achieved according to (i) a clustering procedure similar to the one proposed by Torppa [74]; (ii) several other criteria that were defined in previous literature [2,3,6,35]. Unsupervised classification (clustering) is utilized to describe the spatial distribution of gold occurrence using several clusters. By classifying these clusters using known occurrences, we can delineate geologically similar areas of occurrence and non-occurrence. In this study, we employed k-means as a clustering method to generate some clusters that do not exceed the number of known occurrences. Hence, 20 clusters were produced by applying this method to ASTER dataset, since ASTER dataset has more input layers than those in Landsat-8 and Sentinel-2. Thereafter, we divided those clusters into six prsopectivity classes (very high, high, moderate, low, very low, non-occurrence), by visually counting the frequency of known occurrence in each cluster. Non-occurrence samples were then selected from low, very low, or non-occurrence classes according to the following criteria:
- The number of non-occurrence samples must be equal to the number of mineral occurrences.
- Non-occurrence samples should be spatially distributed randomly.
- The selection of non-occurrence locations should be distal from any known gold occurrences. Here, we applied a 10 km buffer zone around known occurrences.
By following these requirements, we generated a full set of target variables, which contains 50 points of samples. Furthermore, we randomly split these variables into training and testing datasets. 70% of target variables were assigned to the training dataset (35 points), and the remaining 30% were employed as the testing dataset.
3.6. Model Assessment
The performance of the trained RF predictive model was comprehensively assessed by various statistical measurements, including the prediction and classification performance. Classification, here, means labeling the floating value (0, 1) at each cell as prospective or non-prospective (barren region) by using a 0.5 threshold value. A confusion matrix can be successfully utilized to evaluate and explain the classification performance of predictive models using the following categories: (i) true-positive “TP”, when there is an agreement between the model and the reality about mineral occurrence; (ii) true-negative “TN”, when there is an agreement between the model and reality about mineral non-occurrence; (iii) false-positive “FP” when the model incorrectly classified a non-occurrence sample into mineral occurrence; and (iv) false-negative “FN”, when the model mistakenly classified a mineral occurrence as non-occurrence [2,37,75]. These four situations are used to calculate six statistical metrics, namely overall accuracy (OA), sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and Kappa [76,77]. These statistical matrics can be formalized as follow [3,78]:
Furthermore, the overall predictive performances of different datasets were compared using the success-rate curve and receiver operating characteristic (ROC) curve [4,7]. The success-rate curve was created by plotting the percentage of correctly classified gold (true positive rate “TPR”) against the area percentage of prospective regions that are generated by reclassifying MPM using moving threshold values [79]. Subsequently, the optimal goal of the model is to capture as many mineral occurrences as possible in the smallest possible prospective area. This method is very useful in delineating or classifying different prospective regions (high, moderate, low), by identifying the change in curve slope. Since the success-rate curve only depends on the TPR, the ROC curve was created to also consider the false positive rate (FPR). In the ROC curve, TPR and FPR are plotted against each other on the y-axis and x-axis, respectively. In addition, the predictive performance can be measured by calculating the area under ROC curve (AUC), where the better model performance is indicated by how closer the curve can be to the upper left corner [7,80,81].
4. Results
4.1. Generating Remote Sensing-Based Predictor Maps
Figure 5a–c illustrate hydroxyl-bearing minerals derived from BR 6/7 of Landsat-8, BR 11/12 of Sentinel-2, and BR 4/6 of ASTER, respectively. The distribution of these minerals (Al-OH and Fe, Mg-OH) is shown as cyan pixels. As seen in the figure, the spatial distribution of hydroxyl-bearing minerals is similar in all three images. However, Landsat-8 and Sentinel-2 ratio images show these minerals in association with drainage channels. On the other hand, ASTER BR image extensively mapped these minerals in the southeastern part. Another method employed to map hydroxyl-bearing minerals is OH bearing altered minerals index (OHI = 6/7 * 4/6). As displayed in Figure 6a, the spatial distribution of these minerals is relatively similar to ASTER BR image. OH-bearing altered minerals are concentrated in the metavolcanic rocks and have a spatial agreement with known gold occurrence.
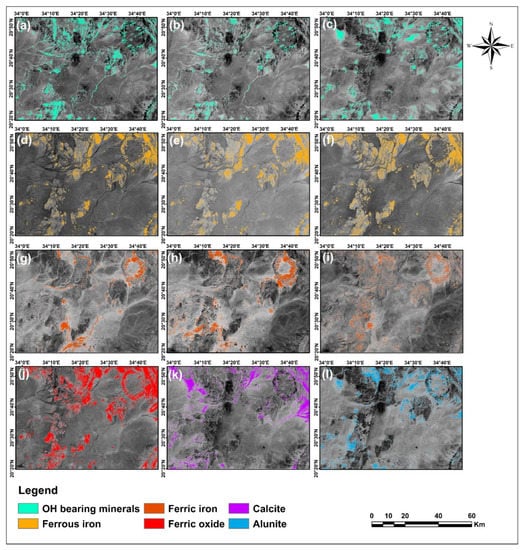
Figure 5.
BR images derived from different sensors showing various targeted minerals in colored pixels (a–c) Hydroxyl-bearing minerals derived from Landsat-8 (6/7), Sentinel-2 (11/12), and ASTER (4/6), respectively; (d–f) Ferrous iron minerals derived from Landsat-8 (7/5 + 3/4), Sentinel-2 (12/8a + 3/4), and ASTER (5/3 + 1/2), respectively; (g–i) Ferric iron minerals derived from Landsat-8 (4/2), Sentinel-2 (4/3), and ASTER (2/1), respectively; (j) Ferric oxide minerals derived from Sentinel-2 (11/8a); (k,l) Calcite and Alunite minerals derived from ASTER BR 4/7 and 4/5, respectively.
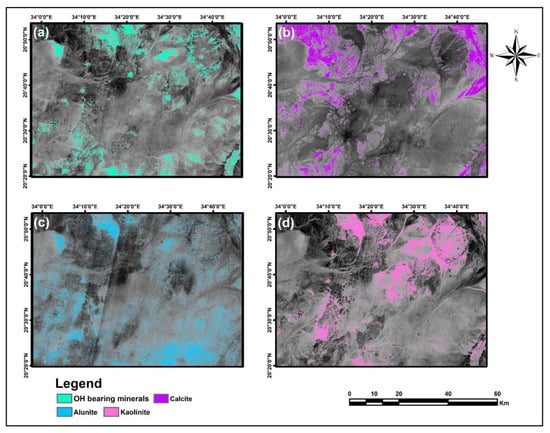
Figure 6.
The mineralogical indices images derived from ASTER SWIR bands show the spatial distribution of targeted minerals in colored pixels: (a) OHI; (b) CLI; (c) ALI; (d) KLI.
Iron minerals, including ferrous iron Fe+2 and ferric iron Fe+3, are shown in Figure 5d-i. The light orange color in Figure 5d–f depicts ferrous iron minerals, which were produced by using BRs (7/5) + (3/4) of Landsat-8, BRs (12/8a) + (3/4) of Sentinel-2, and BRs (5/3) + (1/2) of ASTER. The distribution of ferrous iron minerals in the three images is concentrated in the northeastern part. However, it can be seen in other parts of ASTER image, while it almost disappeared in the western part of Landsat-8 image. On the other hand, Figure 5g–i show ferric iron minerals as dark orange pixels, derived from BR 4/2 of Landsat-8, BR 4/3 of Sentinel-2, and BR 2/1 of ASTER, respectively. Unlike the spatial distribution of ferrous minerals, ferric iron minerals are significantly detected in the drainage areas around younger intrusion in the northeast and the lower middle parts of the three BR images. This distribution of these minerals has less association with documented gold occurrences compared with ferrous iron minerals. Moreover, another BR using Sentinel-2 data was used to map ferric oxide minerals, which is 11/8a. In this imagery, iron oxide minerals are illustrated by red pixels in Figure 5j. By using this ratio image, ferric oxide minerals were mapped in a very extensive way that cover most of the outcrops, including younger and older intrusions, metasediments, and metavolcanics rock units. This distribution relatively matches the density of lineaments features.
In order to delineate minerals that indicate the existence of specific alteration zone, further BR and mineralogical indices were employed in the present study using ASTER data. Calcite, indicating propylitic alteration, was derived from BR 4/7 (Figure 5k) and cal-cite mineral index (CLI = 6/8 * 9/8) (Figure 6b). The prominent areas of calcite were marked as purple color in both images. The distribution of calcite is almost similar in both produced images, but it is more outspread in the northeastern part of the CLI image than the BR image. Argillic or advanced argillic alteration zone is characterized by the existence of kaolinite and alunite minerals. BR 4/5 and alunite mineral index (ALI = 7/5 * 7/8) were utilized to detect alunite altered mineral, while kaolinite mineral index (KLI = 4/5 * 8/6) was utilized to detect kaolinite. The identification of the alunite mineral in the BR image (Figure 5l) exhibits mineral distribution pattern different from the ALI image (Figure 6c). As shown in the images, the BR image mapped alunite similarly to the 4/6 ratio image (OH-bearing minerals), but it has a lower surface abundance. On the other hand, areas of alunite in the ALI image are highlighted in sky-blue tone in the drainage area and superficial deposits. Kaolinite mineral also coincides with drainage areas, but it is more concentrated in the northern part.
Three ASTER RBD images were specifically used for the detailed mapping of alteration zones (Figure 7). RBD1 (4+6/5), RBD2 (5+7/6), and RBD3 (6+9/7 + 8) were used to obtain argillic, phyllic, and propylitic alteration zone, respectively. The argillic alteration zone is illustrated by red pixels, which is more concentrated in the northern part around younger and older intrusions, meanwhile, it can also be seen in the southwestern part between younger intrusions and metavolcanics. The phyllic alteration zone is typically concentrated in the metavolcanic rock unit and partially scattered in the younger intrusion unit. The output of the third RBD, indicating the propylitic alteration zone, is similar to the image derived from CLI index (see Figure 6b).

Figure 7.
The RBD images derived from ASTER SWIR bands show the spatial distribution of different alteration zones in colored pixels: (a) RBD1; (b) RBD2; (c) RBD3.
Figure 8a–c show hydroxyl-bearing minerals derived from PCA using selective bands of Landsat-8, Sentinel-2, and ASTER, respectively. The eigenvector loadings corresponding to bands 2,5,6 and 7 of Landsat-8, bands 2,8a,11, and 12 of Sentinel-2, and bands 1,3,4, and 6 of ASTER, are listed in Table 5. After careful scanning of the eigenvectors, PCA derived from the selected bands of Landsat-8 shows a unique contribution of OH-bearing minerals, which corresponds to reflection in band 6 and absorption in band 7. This PCA has strong negative loading in the reflectance band (−0.7) followed by a strong positive loading in the absorption band (0.633). Hence, PCA 4 mapped OH-bearing minerals as dark pixels, due to the negative loading in the reflectance band. Thereafter, we inverted the dark pixels to bright ones by multiplying the image by −1. Similarly, PCA results using Sentinel-2 and ASTER data exhibit similar patterns for mapping OH-bearing minerals, since PCA4 in both datasets contains unique eigenvectors that correspond to the spectral feature. PCA4 of Sentinel-2 has strong loading in band 11 (−0.675) and band 12 (0.609), while the strong loadings in ASTER data correspond to band 4 (−0.595) and band 6 (0.692). both PCA 4 images of Sentinel-2 and ASTER were negated to display hydroxyl-bearing in bright pixels.
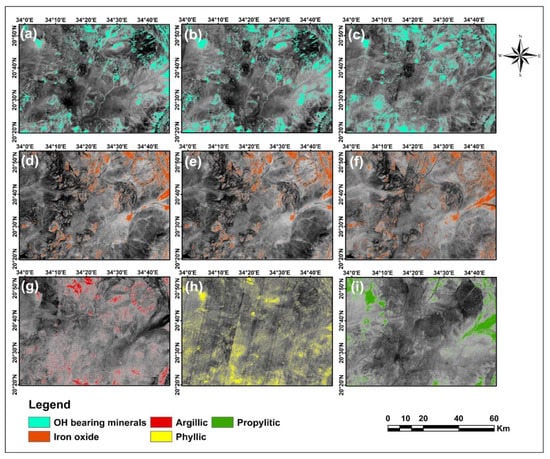
Figure 8.
The PCA images derived from different sensors based on band selection in (Table 2). (a–c) PCA4 of Landsat-8, Sentinel-2, and ASTER, respectively, for mapping hydroxyl-bearing minerals. (d–f) PCA of Landsat-8, Sentinel-2 and ASTER, respectively, for mapping iron oxide minerals. (g–i) ASTER PCA for mapping argillic (PCA4), phyllic (PCA4), and propylitic (PCA3), respectively.

Table 5.
The eigenvector matrixes of PCA results for mapping hydroxyl-bearing minerals using different remote sensing data; Bold text represents the selected PCA and the unique eigenvalues.
Moreover, PCA was applied on Landsat-8 bands 2,4,5, and 6, Sentinel-2 bands 2,4,8a, and 11, and ASTER bands 1,2,3, and 4, for mapping iron oxide minerals. Exploring eigenvector loadings displayed in Table 6 reveals that PCA2 in all three datasets has unique loadings corresponding to the spectral feature of iron oxide minerals. these PCAs showed moderate loadings with a positive sign in absorption bands (Landsat-8 B2 and B5, Sentinel-2 B2 and B8a, and ASTER B1 and B3), and strong loadings with a negative sign in the reflectance band (Landsat-8 B6, Sentinel-2 B11, and ASTER B4). The three PCA2 images were transferred to ArcGIS software and negated. Then, the pixels representing the iron oxide minerals were changed to orange color (Figure 8d–f). It is quite noticeable that the surface abundance of these minerals is lower compared to images derived from BR. Nevertheless, these minerals in PCA images are more distributed in northeast parts and have spatial agreement with hydroxyl-bearing minerals (see Figure 8a–f).

Table 6.
The eigenvector matrixes of PCA results for mapping iron oxide minerals using different remote sensing data; Bold text represents the selected PCA and the unique eigenvalues.
For more details about argillic, phyllic, and propylitic alteration zones, PCA method was also applied specifically to ASTER data. Table 7 shows the eigenvector loadings for argillic using bands 1, 4, 6, and 7, phyllic using bands 1, 3, 5, and 6, and propylitic using bands 1, 3, 5, and 8. The argillic zone has reflectance spectral features in bands 1 and 6, and absorption ones in bands 4 and 7 [29]. Subsequently, most loadings that correspond to this typical spectral feature are found in PCA 4, although the loadings are weaker in band 1 (−0.025) and band 4 (0.133) compared with band 6 (−0.767) and band 7 (0.631). PCA4 is selected to map phyllic alteration zone since it shows loadings with opposite signs in band 5 (−0.694) and band 6 (0.707). Thus, this loadings pattern corresponds to the assumption that band 5 could be considered as a reflection band since the absorption of muscovite mineral (typical mineral reveals phyllic alteration) is lower in band 5 than in band 6 [39]. Then PCA4 image of phyllic alteration was negated because band 5 has negative loading. PCA3 loadings in the eigenvector matrix of propylitic alteration, correspond to the calcite spectral properties. This PCA shows strong negative loading in band 5 (−0.722) and strong positive loading in band 8 (0.563). In this case band 5 was treated as a reflectance band because Fe, Mg-oh group has a lower absorption feature in band 5 compared with the strong absorption in band 8. Therefore, this PCA imagery was also negated. As seen in Figure 8g–i, PCA images are significantly different from those derived by RBD method. The surface abundance of the PCA images is much lower and the spatial distribution is almost different than RBD images.

Table 7.
The eigenvector matrixes of applying PCA to ASTER selected bands for detailed mapping of argillic, phyllic, and propylitic alteration zones; Bold text represents the selected PCA and the unique eigenvalues.
MNF method was employed to extract further information about alteration minerals and zones in the study area. After careful screening of the features presented in dark and bright colors in each MNF band. Three bands were selected and displayed in RGB colors. MNF 3, 4, and 5 of Landsat-8, and MNF 2, 3, and 4 of Sentinel-2 were selected. It can be seen in Figure 9a,b that altered rocks are presented as white to sky-blue tones. The white color demonstrates that there is important information in all three bands that were assigned to RGB colors. Combining negated MNF2, MNF3, and MNF4 clearly displays areas of alteration in white to yellow color (Figure 9).

Figure 9.
MNF results: (a) Landsat-8 MNF3, MNF4, and MNF5 in RGB.; (b) Sentinel-2 MNF2, MNF3, and MNF4 in RGB.; (c) ASTER MNF2 (negated), MNF3, and MNF 4 in RGB.
4.2. Generating Target Variable Using K-Means Clustering
All evidence layers of ASTER dataset that were mentioned earlier, including geological predictor maps, were utilized to classify the study area using k-means clustering. The purpose of this unsupervised method is to delineate non-prospective tracts, which then aids the process of selecting non-occurrence samples. Defining the proper number of clusters is the most critical step because these clusters will be assigned to different classes based on their spatial agreement with known gold occurrences. Each class prospectivity score is defined according to the percentage of captured deposits in the clusters. For instance, if each of the n clusters captured x deposits, then these n clusters will be classified as one class and the class prospectivity score is determined by the percentage of x deposits from the total known deposits. Therefore, increasing cluster numbers increases the number of clusters with no occurrence’s association, which subsequently increases the area of non-prospective. Herein, we proposed that the number of clusters must be equal to or less than the number of known occurrences (k ≤ Au samples). In this case, the worst scenario will be if the frequency of occurrence in each cluster is one, which indicates that the k-means calculation process failed to find a connection between occurrences distribution and evidential layers.
Figure 10a shows the twenty clusters derived from applying k-means on ASTER dataset. As displayed in Figure 10b, the highest frequency is found to be 5 samples per cluster, which takes place in clusters 11 and 12. These two clusters were then classified as the very high prospective class. Clusters 14 and 8 captured four and three Au occurrence samples, respectively, so they were labeled as high and moderate classes. Each one of clusters 7,13, and 15 captured 2 occurrences, which were afterward combined to form the low prospective class. In the meantime, the pattern of one occurrence per cluster is found in clusters 16 and 20, which were defined as the very low prospective class. Finally, the rest of the clusters were classified as the non-prospective class, since none of the Au occurrences is spatially associated with these clusters. Figure 10c illustrates the selection of 25 non-occurrence points following the results of classifying k-means outputs, as well as the criteria described earlier in the methodology section.
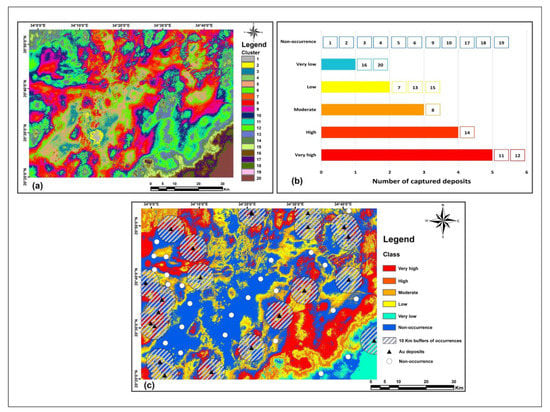
Figure 10.
(a) K-means 20 clusters derived from ASTER and geological evidential layers.; (b) the number of Au occurrences spatially associated with different clusters.; (c) classified prospectivity clusters based on the frequency of the occurrences in each cluster obtained from (b).
4.3. Sensitivity of RF Predictive Model to Parameter Tuning
The success key for training data-driven models with higher accuracy prediction is the configuration of parameters (also called parametrization). Thus, due to its great impact on the robustness and generalization capacity of ML predictive models. The parameterization process was achieved using the GridSearchCV method based on 5-fold cross-validation. Figure 11 shows significant variations in MSE values of four RF models obtained from different parameter combinations and different datasets. Generally, RF is a very stable model since the higher MSE values are lower than 0.138 in all four datasets. Although there are complex variations of parameter selection using different datasets, the minimum score of MSE is very promising in the case of ASTER and data-integration datasets. The minimum score of MSE obtained by training ASTER and data-integration datasets were 0.096 and 0.093, respectively. Meanwhile, RF model had less accuracy in the case of using Sentinel-2 and Landsat-8, reaching minimum MSE values of 0.102 and 0.12, respectively. The results of MSE indicate that the complex architecture of RF does not lead to an accurate performance in different cases. For instance, the grid searching method selected only two features to be used in individual trees in both Landsat-8 and Sentinel-2 datasets. It is also suggested that the number of trees in the forest was set to 50 in training Sentinel-2 and data-integration datasets. The highest number of trees grown in the forest was 300 trees in the case of Landsat-8, while the highest number of features was 8 in the case of data-integration dataset.
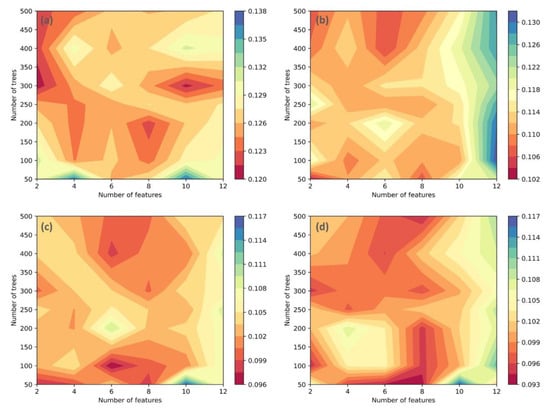
Figure 11.
Contour maps showing the sensitivity of RF model based on MSE results obtained by training different datasets; the number of trees and number of features employed for training RF models based on: (a) Landsat-8; (b) Sentinel-2; (c) ASTER; (d) data integration.
4.4. Comparison of Various Datasets Performance
Different RF regression models were trained by the optimal parameter configurations to produce gold potential maps, where the prediction at each cell denotes the likelihood of gold occurrence by floating probability value (0–1) (Figure 12). The accuracy report of the classification performance is produced by labeling each cell into binary classes (prospective areas and barren areas), and thus by using a threshold value of 0.5 to define those areas. Table 8 lists all statistical metrics for measuring the classification performance of RF using four various datasets. In general, both ASTER and Data-integration datasets achieved an overall classification accuracy of 73.3%, which outperformed the classification of Sentinel-2 and Landsat-8 datasets. OA of Landsat-8 and Sentinel-2 were 60% and 66.7%, respectively. Although the OA of ASTER and data-integration datasets are the same, ASTER is more sensitive to correctly identifying 73.2 of the occurrence locations, while data-integration dataset has higher predictive values whether it is PPV or NPV. However, the highest predictive values (PPV and NPV) are found in Sentinel-2 dataset. RF models trained by Landsat-8 and Sentinel-2 have the worst specificity scores (28.6).
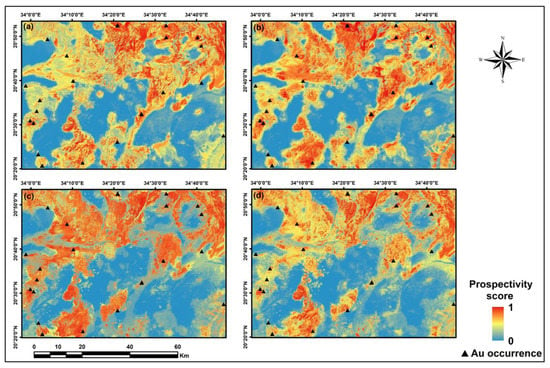
Figure 12.
Predictive maps of likelihood score of gold propsectivity obtained from RF predictive modeling using: (a) Landsat-8; (b) Sentinel-2; (c) ASTER; and (d) Data-integration.

Table 8.
Classification report of RF performance using different datasets.
Taking the cost of mineral exploration in the real world into counts, it is impractical to make a decision based on prospective tract delineation from the classification scenario (i.e., probability > 0.5) [3]. Therefore, it is essential to assess the predictive performance of high-probability zones using ROC curve. Figure 13 shows ROC curves and AUC values of various MLAs trained by four different input datasets. The closest ROC curve to the top left corner belongs to the data-integration dataset, whereby the AUC value is 0.938. Both ASTER and Sentinel-2 have AUC values of 0.875, which clarifies that both datasets have comparable prediction performance. Landsat-8 performs the weakest predictive capability with AUC value of 0.625.
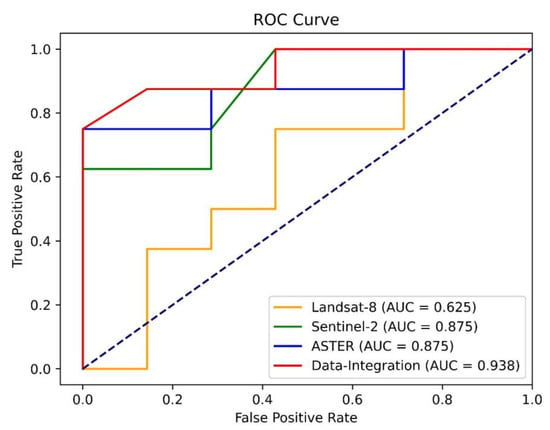
Figure 13.
ROC curves showing AUC value of each RF model trained by Landsat-8, Sentinel-2, ASTER, and data integration datasets.
For a better understanding of the spatial distribution of Au deposits, and delineating exploration target areas, it is important to reclassify the MPM probability score into different levels (very high, high, moderate, and low). This can be achieved by classifying the success-rate curve based on the variations in the curve slope using four regression lines. The higher predictive region is defined by the steeper slope. Figure 14 shows the success-rate curves of four RF MPMs derived from different datasets, while the classified maps are displayed in Figure 15. The steepest curve is achieved by data-integration dataset, which indicates that this data predictive performance has the ability to define a smaller prospective area compared with datasets. The very high potential class of the data-integration identifies about 70.6% of the deposits in 11.5% of the total area. However, ASTER dataset was able to identify all of the occurrence locations in 33.3% of the total area, which is 4.5% lower than the total area that captured all occurrences in the MPM of data-integration. The total area of capturing all deposits is larger in the case of Landsat-8 and Sentinel-2, which are 47.2 and 42.1, respectively. As it is displayed in Figure 14a, the curves of ASTER and Landsat started similarly with a high angle, but they quickly become less steep by increasing the percentage of cumulative area. Hence, about 35% of the occurrence are captured in approximately 3.5% of the study area.
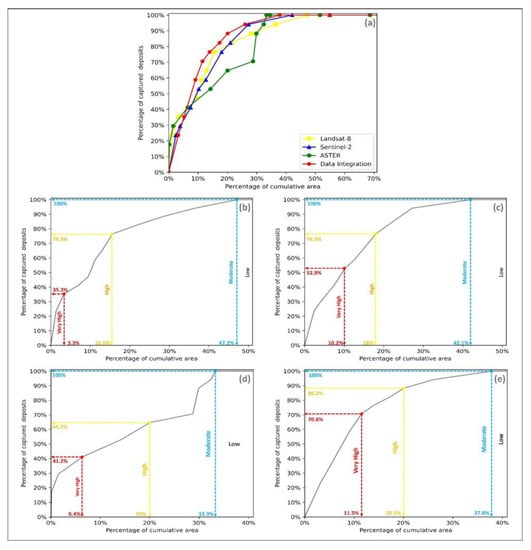
Figure 14.
Success-rate curves of RF predictive maps trained using various datasets: (a) all success-rate curves; (b–e) curve of Landsat-8, Sentinel-2, ASTER, and data integration, respectively.
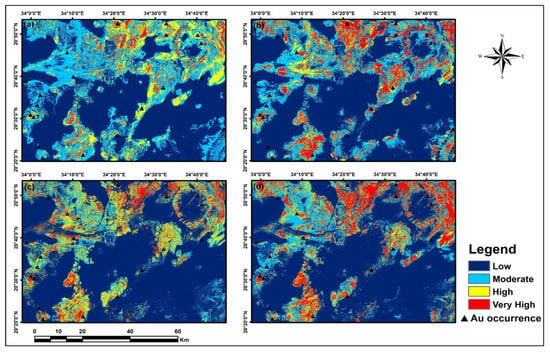
Figure 15.
Reclassified gold prospectivity maps based on threshold values derived from success-rate curves: (a) Landsat-8; (b) Sentinel-2; (c) ASTER; (d) data-integration.
5. Discussion
The discovery of new prospective areas is deliberated as the most significant issue in mineral exploration. MPM has been successfully used to integrate geological features derived from multisource data to outline new undiscovered mineral deposits. Although remote sensing data represent a great source for recognizing surface alteration and other geological features (e.g., lineament and lithology), they have not yet been fully investigated as the main core of the input data for training mineral prospectivity predictive modeling. The comparison of Landsat-8, Sentinel-2, ASTER, as well as data fusion, for training 714 RF data-driven predictive model is successfully illustrated in the present study. The main findings are discussed below.
Several remote sensing enhancement techniques including BR, MNF, and PCA, have been employed in this study for generating predictor maps. MNF imagery is the only data used to produce color composite images, where the detection of altered rocks is specified by color tones. The selection of three MNF bands to composite images in RGB is the only subjective procedure in the study, which mainly depends on visual judgment and prior knowledge of hydrothermal alteration. Other methods are employed to produce grey-scale predictor maps, where the alteration zones or minerals are presented by the bright regions (higher value) of that image. These methods were extensively and successfully used in prior literature for mapping alteration zones associated with mineral deposits, which mainly depend on the spectral signatures of hydrothermal alteration minerals [29,31,39,68,69,70,82]. In this regard, all three multispectral sensors data have the capability to detect hydroxyl-bearing and iron-oxide minerals in general. Clay and carbonate minerals including kaolinite, alunite, muscovite, calcite, and dolomite, have high reflectance near 1.6 µm and absorption near 2.2 µm [15,61]. This reflectance signature relatively coincides with band 6 of Landsat-8, band 11 of Sentinel-2, and band 4 of ASTER, meanwhile, the absorption signature coincides with band 7 of Landsat-8, band 12 of Sentinel-2 and band 6 of ASTER. Therefore, these were employed to map OH-bearing minerals using BR method (Landsat-8: 6/7; Sentinel-2: 11/12; and ASTER: 4/6) and selective PCA method as well (Landsat-8: 2,5,6,7; Sentinel-2: 2,8a,11,12; and ASTER: 1,3,4,6). Likewise, iron (ferric and ferrous)/iron-oxide minerals, such as hematite, jarosite, and goethite, display significant absorption features in the VNIR region (from 0.4 µm to 1.3 µm) [61,83]. Specifically, iron-bearing minerals have two absorption features near 0.5 µm and 0.87 µm, which perfectly corresponds to bands 2 and 5 of Landsat-8, and bands 2 and 8a of Sentinel-2 [69,84]. Unfortunately, ASTER can only detect one diagnostic absorption feature near to 0.5 µm (band 2), due to its course spectral resolution in the VNIR region. Due to its higher spectral resolution in the VNIR than ASTER data, and its higher bandpass than Landsat-8, Sentinel-2 data have potential for MPM similar to ASTER data and greater than Landsat-8 data.
Unlike the limited capability of Landsat-8 and Sentinel-2 to map alteration minerals (mapping OH-bearing minerals in general), the higher resolution of ASTER data in the SWIR region allows it for detailed mapping of the hydrothermal alteration zones. Diagnosing Al-OH and Mg-OH groups of minerals helps define different alteration zones. The argillic alteration zone which is characterized by kaolinite and alunite minerals has a double absorption signature at 2.16 µm and 2.2 µm, which coincide with bands 5 and 6, respectively [15]. These bands, therefore, are used to enhance argillic to advance-argillic zone using 4/5 BR, (4 + 6)/5 RBD, and PCA (using bands 1, 4, 6, and 7). Identifying kaolinite and alunite minerals can be achieved using KLI and ALI mineral indices, respectively. The phyllic alteration can be recognized by the muscovite mineral, which shows double absorption features at 2.17 µm and 2.2 µm. The absorption at 2.2 µm (coinciding band 6) is stronger than that at 2.17 µm (coinciding band 5) [39]. This spectral feature is employed to map phyllic alteration using only two methods, which are (5 + 7)/6 RBD, and PCA using bands 1,3,5, and 6. For the optimum discovery of Mg-OH group minerals (e.g., chlorite, epidote, and calcite), band 8 is employed to detect such minerals. These minerals represent the propylitic alteration zone, which has a spectral absorption feature near 2.33 µm (coinciding with band 8). This high absorption property is used to detect propylitic zone using different methods, including propylitic RBD (6 + 9/7 + 8), calcite mineral index (CLI = (6/8) * (9/8)), and PCA (using bands 1,3,5, and 8). Although thermal bands of ASTER are not used in this study, they can be utilized to extend the number of predictor maps. TIR region helps identify minerals at the surface with specific emissivity and absorption features [37,65]. For example, silicate and carbonate can be mapped using BRs 13/12 and 13/14, respectively [24,66]. Moreover, Quartz Index (QI = 11 * 11/10 * 12) can be used as a predictor in the case of gold associated with Quartz dykes/veins [66]. It can be concluded that the possible number of predictor maps that are produced using ASTER data, is about 11 higher than those derived from other remote sensing data. Subsequently, this could be the main reason why ASTER dataset outperforms Landsat-8 and Sentinel-2 datasets in the classification performance of the MPM in the study area.
Since RF is trained using different input variable data, it is essential to assess the spatial association between these predictor variables and the gold occurrence (target variables). In the present study, predictor variables are produced from (i) different sources including geological and remote sensing data; (ii) different multispectral sensors including Landsat-8, Sentinel-, and ASTER; (iii) different processing methods including spatial analysis methods and remote sensing enhancement techniques. Hence, it is critical to measure the influence of each predictor variable on the prediction performance. As mentioned earlier, RF algorithm ranks the importance of the feature variables according to their marginal effect on the target variables [34]. Graphs in Figure 16 illustrate the importance of input feature variables in each dataset. Through all datasets, the most important geological-based predictor variable turns out to be lineaments. In both Landsat-8 and Sentinel-2 datasets, the lineaments density map yields the first rank of importance, while it comes second after propylitic RBD in ASTER and data-integration datasets. The second prominent pattern of the geological predictors through all datasets is that the distance from NW- faults is more important than the NE- faults, which indicates that the spatial association of known gold occurrences is much closer to NW-SE trending faults. RF did not vote for a specific enhancement technique method to be highly distinct from other methods. However, it can be noticed from data-integration dataset that four out of the first five important predictors are produced by the rationing technique. Predictor maps indicating iron-bearing minerals are much more important than those corresponding to hydroxyl-bearing minerals in Landsat-8 and Sentinel-2 datasets. In ASTER dataset, predictors of propylitic alteration zone are significantly more important than other alteration zones, since the propylitic RBD and calcite BR (4/7) are ranked as the first and the fourth important features. It can be noticed that mineralogical indices are relatively less important than other enhancement techniques. It is important to mention that predictors from different remote sensing sensors are highly representative in data-integration dataset. In other words, the rating of features’ importance is roughly distributed between different remote sensing data.
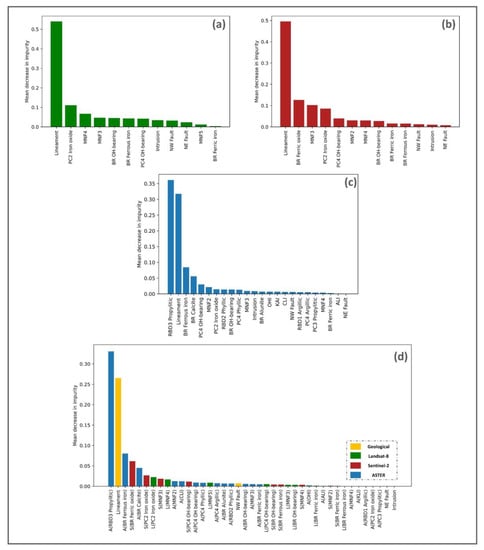
Figure 16.
RF model important feature analysis results: (a) Landsat-8; (b) Sentinel-2; (c) ASTER; (d) data integration (Symbol ‘L’ represents Landsat-8; ‘S’ represents Sentinel-2; ‘A’ represents ASTER).
6. Conclusions
The investigation of various multispectral remote sensing data capabilities was carried out to produce mineral prospectivity map for gold mineralization in the Hamissana area, NE Sudan. Based on the combination of geological-based predictor maps (proximity to intrusion and faults, and density of lineaments) with remote sensing-based predictor maps (BR, PCA, and MNF), four input datasets including Landsat-8, Sentinel-2, ASTER, and data-integration datasets were prepared. The random forest algorithm was used as an objective tool for comparing the capabilities of various datasets.
As it is demonstrated by the comparison results and discussion, we conclude that Sentinel-2 and ASTER multispectral data have greater potential for mineral prospectivity modeling than Landsat-8. Both datasets achieved 0.875 AUC, while the overall classification accuracy of ASTER dataset (73.3%) is higher than Sentinel-2 (66.7%). Data-integration dataset boosts the prediction performance of RF up to (AUC: 0.938). The density of the lineaments plays a significant role in the prediction performance in all datasets.
Modeling results using different datasets suggest several prospecting regions. Nevertheless, considering the uncertainty of remote sensing data and MPM results, further geological investigation and exploration should be taken into account. Specifically, drilling, geophysical and geochemical surveys, and 3D modeling techniques are essential for future work and further accurate targeting.
In our future research, we plan to compare current multispectral remote sensing data with other data from multiple sources (e.g., comprehensive geochemical survey, gravity, and magnetic geophysical survey), which are not available at present. Moreover, we would like to conduct a comprehensive comparison using other machine learning algorithms such as a support vector machine and an artificial neural network. Finally, other deep learning techniques are preferable to be applied also in MPM, since deep learning is still a hot research topic in several geoscience fields.
Author Contributions
“Conceptualization, A.M.M.T. and Y.X.; methodology, A.M.M.T. and Q.H.; software, A.M.M.T., S.W. and X.L.; validation, A.M.M.T., Q.H. and A.H.; formal analysis, A.M.M.T. and Y.X.; data curation, A.M.M.T.; writing—original draft preparation, A.M.M.T.; writing—review and editing, A.M.M.T. and Y.X.; supervision, Y.X.; funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Data Availability Statement
All remote sensing data used in this paper are freely available online on the websites mentioned in Section 3.1—Data. Python codes are available online on the first author’s GitHub webpage (https://github.com/Abdallah-M-Ali).
Acknowledgments
We would like to express our respect and gratitude to the anonymous reviewers and editors for their professional comments and suggestions on improving the quality of this paper. The research was undertaken thanks to funding from the Priority Academic Program Development of Jiangsu Higher Education Institutions [PAPD].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arndt, N.T.; Fontboté, L.; Hedenquist, J.W.; Kesler, S.E.; Thompson, J.F.; Wood, D.G. Future global mineral resources. Geochem. Perspect. 2017, 6, 1–171. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, X.; Wang, G.; Liu, D.; Cui, N. A Multi-Model Ensemble Approach for Gold Mineral Prospectivity Mapping: A Case Study on the Beishan Region, Western China. Minerals 2020, 10, 1126. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-Driven Predictive Modelling of Mineral Prospectivity Using Machine Learning and Deep Learning Methods: A Case Study from Southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of Random Forests algorithm. Ore Geol. Rev. 2015, 71, 777–787. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M. Introduction to the Special Issue: GIS-based mineral potential modelling and geological data analyses for mineral exploration. Ore Geol. Rev. 2015, 71, 477–483. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Hale, M.; Faassen, C. Selection of coherent deposit-type locations and their application in data-driven mineral prospectivity mapping. Ore Geol. Rev. 2008, 33, 536–558. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.; Liu, W.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Introduction to the special issue: GIS-based mineral potential targeting. J. Afr. Earth Sci. 2017, 128, 1–4. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Agterberg, F.P. Fuzzy weights of evidence method and its application in mineral potential mapping. Nat. Resour. Res. 1999, 8, 27–35. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.-H.; Fathianpour, N. Fuzzy outranking approach: A knowledge-driven method for mineral prospectivity mapping. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 556–567. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Bigdeli, A.; Carranza, E.J.M. Regional-Scale Mineral Prospectivity Mapping: Support Vector Machines and an Improved Data-Driven Multi-criteria Decision-Making Technique. Nat. Resour. Res. 2021, 30, 1977–2005. [Google Scholar] [CrossRef]
- Harris, J.R.; Grunsky, E.; Behnia, P.; Corrigan, D. Data- and knowledge-driven mineral prospectivity maps for Canada’s North. Ore Geol. Rev. 2015, 71, 788–803. [Google Scholar] [CrossRef]
- Abdelkareem, M.; Al-Arifi, N. Synergy of Remote Sensing Data for Exploring Hydrothermal Mineral Resources Using GIS-Based Fuzzy Logic Approach. Remote Sens. 2021, 13, 4492. [Google Scholar] [CrossRef]
- Rowan, L.C.; Mars, J.C. Lithologic mapping in the Mountain Pass, California area using advanced spaceborne thermal emission and reflection radiometer (ASTER) data. Remote Sens. Environ. 2003, 84, 350–366. [Google Scholar] [CrossRef]
- Pazand, K.; Pazand, K. Identification of hydrothermal alteration minerals for exploring porphyry copper deposit using ASTER data: A case study of Varzaghan area, NW Iran. Geol. Ecol. Landsc. 2020, 6, 217–223. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. Identification of hydrothermal alteration minerals for exploring of porphyry copper deposit using ASTER data, SE Iran. J. Asian Earth Sci. 2011, 42, 1309–1323. [Google Scholar] [CrossRef]
- Guha, A.; Mondal, S.; Chatterjee, S.; Kumar, K.V. Airborne imaging spectroscopy of igneous layered complex and their mapping using different spectral enhancement conjugated support vector machine models. Geocarto Int. 2020, 37, 349–365. [Google Scholar] [CrossRef]
- Rao, D.A.; Guha, A. Potential Utility of Spectral Angle Mapper and Spectral Information Divergence Methods for mapping lower Vindhyan Rocks and Their Accuracy Assessment with Respect to Conventional Lithological Map in Jharkhand, India. J. Indian Soc. Remote 2018, 46, 737–747. [Google Scholar] [CrossRef]
- Rani, N.; Mandla, V.R.; Singh, T. Spatial distribution of altered minerals in the Gadag Schist Belt (GSB) of Karnataka, Southern India using hyperspectral remote sensing data. Geocarto Int. 2016, 32, 225–237. [Google Scholar] [CrossRef]
- Rani, N.; Mandla, V.R.; Singh, T. Evaluation of atmospheric corrections on hyperspectral data with special reference to mineral mapping. Geosci. Front. 2017, 8, 797–808. [Google Scholar] [CrossRef]
- Noori, L.; Pour, A.; Askari, G.; Taghipour, N.; Pradhan, B.; Lee, C.-W.; Honarmand, M. Comparison of Different Algorithms to Map Hydrothermal Alteration Zones Using ASTER Remote Sensing Data for Polymetallic Vein-Type Ore Exploration: Toroud–Chahshirin Magmatic Belt (TCMB), North Iran. Remote Sens. 2019, 11, 495. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. Identifying areas of high economic-potential copper mineralization using ASTER data in the Urumieh–Dokhtar Volcanic Belt, Iran. Adv. Space Res. 2012, 49, 753–769. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M.; Makoundi, C.; Zaw, K. Structural Mapping of the Bentong-Raub Suture Zone Using PALSAR Remote Sensing Data, Peninsular Malaysia: Implications for Sediment-hosted/Orogenic Gold Mineral Systems Exploration. Resour. Geol. 2016, 66, 368–385. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M.; Park, Y. Application of ASTER SWIR bands in mapping anomaly pixels for Antarctic geological mapping. J. Phys. Conf. Ser. 2017, 852, 012025. [Google Scholar] [CrossRef]
- Pour, A.B.; Park, Y.; Park, T.-Y.S.; Hong, J.K.; Hashim, M.; Woo, J.; Ayoobi, I. Regional geology mapping using satellite-based remote sensing approach in Northern Victoria Land, Antarctica. Polar Sci. 2018, 16, 23–46. [Google Scholar] [CrossRef]
- Son, Y.-S.; Lee, G.; Lee, B.H.; Kim, N.; Koh, S.-M.; Kim, K.-E.; Cho, S.-J. Application of ASTER Data for Differentiating Carbonate Minerals and Evaluating MgO Content of Magnesite in the Jiao-Liao-Ji Belt, North China Craton. Remote Sens. 2022, 14, 181. [Google Scholar] [CrossRef]
- Bahrami, Y.; Hassani, H.; Maghsoudi, A. Investigating the capabilities of multispectral remote sensors data to map alteration zones in the Abhar area, NW Iran. Geosyst. Eng. 2018, 24, 18–30. [Google Scholar] [CrossRef]
- Fereydooni, H.; Mojeddifar, S. A directed matched filtering algorithm (DMF) for discriminating hydrothermal alteration zones using the ASTER remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 1–13. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, Z.-F.; Xia, J.-S.; Zhao, X.; Yang, H.-Y.; Zhang, X.-L. Improving the accuracy of hydrothermal alteration mapping based on image fusion of ASTER and Sentinel-2A data: A case study of Pulang Cu deposit, Southwest China. Geocarto Int. 2022, 1–26. [Google Scholar] [CrossRef]
- Joly, A.; Porwal, A.; McCuaig, T.C.; Chudasama, B.; Dentith, M.C.; Aitken, A.R.A. Mineral systems approach applied to GIS-based 2D-prospectivity modelling of geological regions: Insights from Western Australia. Ore Geol. Rev. 2015, 71, 673–702. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Natural Resources Research Publications on Geochemical Anomaly and Mineral Potential Mapping, and Introduction to the Special Issue of Papers in These Fields. Nat. Resour. Res. 2017, 26, 379–410. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Brown, W.M.; Gedeon, T.D.; Groves, D.I.; Barnes, R.G. Artifcial neural network: A new method for mineral prospectivity mapping. Aust. J. Earth Sci. 2000, 47, 757–770. [Google Scholar] [CrossRef]
- Xi, Y.; Mohamed Taha, A.M.; Hu, A.; Liu, X. Accuracy comparison of various remote sensing data in lithological classification based on random forest algorithm. Geocarto Int. 2022, 1–29. [Google Scholar] [CrossRef]
- Mansouri, E.; Feizi, F.; Jafari Rad, A.; Arian, M. Remote-sensing data processing with the multivariate regression analysis method for iron mineral resource potential mapping: A case study in the Sarvian area, central Iran. Solid Earth 2018, 9, 373–384. [Google Scholar] [CrossRef]
- Bolouki, S.M.; Ramazi, H.R.; Maghsoudi, A.; Beiranvand Pour, A.; Sohrabi, G. A Remote Sensing-Based Application of Bayesian Networks for Epithermal Gold Potential Mapping in Ahar-Arasbaran Area, NW Iran. Remote Sens. 2019, 12, 105. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Chica-Rivas, M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar] [CrossRef]
- Gaboury, D.; Nabil, H.; Ennaciri, A.; Maacha, L. Structural setting and fluid composition of gold mineralization along the central segment of the Keraf suture, Neoproterozoic Nubian Shield, Sudan: Implications for the source of gold. Int. Geol. Rev. 2020, 64, 45–71. [Google Scholar] [CrossRef]
- Mohamed, M.T.A.; Al-Naimi, L.S.; Mgbeojedo, T.I.; Agoha, C.C. Geological mapping and mineral prospectivity using remote sensing and GIS in parts of Hamissana, Northeast Sudan. J. Pet. Explor. Prod. 2021, 11, 1123–1138. [Google Scholar] [CrossRef]
- Bierlein, F.; Reynolds, N.; Arne, D.; Bargmann, C.; McKeag, S.; Bullen, W.; Al-Athbah, H.; McKnight, S.; Maas, R. Petrogenesis of a Neoproterozoic magmatic arc hosting porphyry Cu-Au mineralization at Jebel Ohier in the Gebeit Terrane, NE Sudan. Ore Geol. Rev. 2016, 79, 133–154. [Google Scholar] [CrossRef]
- Zeinelabdein, K.A.E.; Nadi, A.H.H.E. The use of Landsat 8 OLI image for the delineation of gossanic ridges in the Red Sea Hills of NE Sudan. Am. J. Earth Sci. 2014, 1, 62–67. [Google Scholar]
- Sasmaz, A. The Atbara porphyry gold–copper systems in the Red Sea Hills, Neoproterozoic Arabian–Nubian Shield, NE Sudan. J. Geochem. Explor. 2020, 214, 106539. [Google Scholar] [CrossRef]
- El Khidir, S.O.; Babikir, I.A. Digital image processing and geospatial analysis of landsat 7 ETM+ for mineral exploration, Abidiya area, North Sudan. Int. J. Geomat. Geosci. 2013, 3, 645–658. [Google Scholar]
- Ali, A.; Pour, A. Lithological mapping and hydrothermal alteration using Landsat 8 data: A case study in ariab mining district, red sea hills, Sudan. Int. J. Basic Appl. Sci. 2014, 3, 199–208. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth & Brooks; Cole Statistics/Probability Series; Chapman & Hall: London, UK, 1984. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Kulkarni, A.D.; Lowe, B. Random forest algorithm for land cover classification. Int. J. Recent Innov. Trends Comput. Commun. 2016, 4, 58–63. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Maepa, F.; Smith, R.S.; Tessema, A. Support vector machine and artificial neural network modelling of orogenic gold prospectivity mapping in the Swayze greenstone belt, Ontario, Canada. Ore Geol. Rev. 2021, 130, 103968. [Google Scholar] [CrossRef]
- Zeinelabdein, K.E.; Albiely, A. Ratio image processing techniques: A prospecting tool for mineral deposits, Red Sea Hills, NE Sudan. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1295–1298. [Google Scholar]
- Abdullah, A.; Nassr, S.; Ghaleeb, A. Remote Sensing and Geographic Information System for Fault Segments Mapping a Study from Taiz Area, Yemen. J. Geol. Res. 2013, 2013, 201757. [Google Scholar] [CrossRef]
- Adiria, Z.; Hartia, A.E.; Jelloulia, A.; Lhissoua, R.; Maachab, L.; Azmib, M.; Zouhairb, M.; Bachaouia, E.M. Comparison of Landsat-8, ASTER and Sentinel 1 satellite remote sensing data in automatic lineaments extraction: A case study of Sidi Flah Bouskour inlier, Moroccan Anti Atlas. Adv. Space Res. 2017, 60, 2355–2367. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. ASTER, ALI and Hyperion sensors data for lithological mapping and ore minerals exploration. SpringerPlus 2014, 3, 130. [Google Scholar] [CrossRef]
- Li, N. Textural and Rule-Based Lithological Classification of Remote Sensing Data, and Geological Mapping in Southwestern Prieska Sub-Basin, Transvaal Supergroup, South Africa. Ph.D. Thesis, LMU, München, Germany, 2010. [Google Scholar]
- Zhang, T.; Yi, G.; Li, H.; Wang, Z.; Tang, J.; Zhong, K.; Li, Y.; Wang, Q.; Bie, X. Integrating Data of ASTER and Landsat-8 OLI (AO) for Hydrothermal Alteration Mineral Mapping in Duolong Porphyry Cu-Au Deposit, Tibetan Plateau, China. Remote Sens. 2016, 8, 890. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
- Inzana, J.; Kusky, T.; Higgs, G.; Tucker, R. Supervised classifications of Landsat TM band ratio images and Landsat TM band ratio image with radar for geological interpretations of central Madagascar. J. Afr. Earth Sci. 2003, 37, 59–72. [Google Scholar] [CrossRef]
- Ninomiya, Y. Lithologic Mapping with Multispectral ASTER TIR and SWIR Data; SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Ninomiya, Y.; Fu, B.; Cudahy, T.J. Detecting lithology with Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) multispectral thermal infrared “radiance-at-sensor” data. Remote Sens. Environ. 2005, 99, 127–139. [Google Scholar] [CrossRef]
- Rajan Girija, R.; Mayappan, S. Mapping of mineral resources and lithological units: A review of remote sensing techniques. Int. J. Image Data Fusion 2019, 10, 79–106. [Google Scholar] [CrossRef]
- Ninomiya, Y. A stabilized vegetation index and several mineralogic indices defined for ASTER VNIR and SWIR data. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium, Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; pp. 1552–1554. [Google Scholar]
- van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A. Potential of ESA’s Sentinel-2 for geological applications. Remote Sens. Environ. 2014, 148, 124–133. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Jing, L.; Wang, F.; Zhao, M.; Ding, H. Assessment of the Capability of Sentinel-2 Imagery for Iron-Bearing Minerals Mapping: A Case Study in the Cuprite Area, Nevada. Remote Sens. 2020, 12, 3028. [Google Scholar] [CrossRef]
- Timkin, T.; Abedini, M.; Ziaii, M.; Ghasemi, M.R. Geochemical and Hydrothermal Alteration Patterns of the Abrisham-Rud Porphyry Copper District, Semnan Province, Iran. Minerals 2022, 12, 103. [Google Scholar] [CrossRef]
- Crosta, A.; De Souza Filho, C.; Azevedo, F.; Brodie, C. Targeting key alteration minerals in epithermal deposits in Patagonia, Argentina, using ASTER imagery and principal component analysis. Int. J. Remote Sens. 2003, 24, 4233–4240. [Google Scholar] [CrossRef]
- Ourhzif, Z.; Algouti, A.; Algouti, A.; Hadach, F. Lithological Mapping Using Landsat 8 Oli and Aster Multispectral Data in Imini-Ounilla District South High Atlas of Marrakech. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 1255–1262. [Google Scholar] [CrossRef]
- Saljoughi, B.S.; Hezarkhani, A. A comparative analysis of artificial neural network (ANN), wavelet neural network (WNN), and support vector machine (SVM) data-driven models to mineral potential mapping for copper mineralizations in the Shahr-e-Babak region, Kerman, Iran. Appl. Geomat. 2018, 10, 229–256. [Google Scholar] [CrossRef]
- Torppa, J.; Nykänen, V.; Molnár, F. Unsupervised clustering and empirical fuzzy memberships for mineral prospectivity modelling. Ore Geol. Rev. 2019, 107, 58–71. [Google Scholar] [CrossRef]
- Bachri, I.; Hakdaoui, M.; Raji, M.; Teodoro, A.C.; Benbouziane, A. Machine Learning Algorithms for Automatic Lithological Mapping Using Remote Sensing Data: A Case Study from Souk Arbaa Sahel, Sidi Ifni Inlier, Western Anti-Atlas, Morocco. ISPRS Int. J. Geo-Inf. 2019, 8, 248. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Heydari, S.S.; Mountrakis, G. Effect of classifier selection, reference sample size, reference class distribution and scene heterogeneity in per-pixel classification accuracy using 26 Landsat sites. Remote Sens. Environ. 2018, 204, 648–658. [Google Scholar] [CrossRef]
- Barsi, Á.; Kugler, Z.; László, I.; Szabó, G.; Abdulmutalib, H.M. Accuracy Dimensions in Remote Sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3, 61–67. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Bonham-Carter, G.F. Measuring the Performance of Mineral-Potential Maps. Nat. Resour. Res. 2005, 14, 1–17. [Google Scholar] [CrossRef]
- Landgrebe, T.C.W.; Paclik, P. The ROC skeleton for multiclass ROC estimation. Pattern Recognit. Lett. 2010, 31, 949–958. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Hua, B.; Xua, Y.; Wana, B.; Wua, X.; Yi, G. Hydrothermally altered mineral mapping using synthetic application of Sentinel-2A MSI, ASTER and Hyperion data in the Duolong area, Tibetan Plateau, China. Ore Geol. Rev. 2018, 101, 384–397. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Jing, L.; Armenakis, C.; Ding, H. Lithological discrimination using ASTER and Sentinel-2A in the Shibanjing ophiolite complex of Beishan orogenic in Inner Mongolia, China. Adv. Space Res. 2018, 62, 1702–1716. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Tang, Y.; Jing, L.; Gao, C. Lithological Classification Using Sentinel-2A Data in the Shibanjing Ophiolite Complex in Inner Mongolia, China. Remote Sens. 2018, 10, 638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).