Controls on Mg/Ca Ratios in Recent Stromatolites: Insights from Fluvial Systems in the Iberian Range (Spain)

Abstract

The utility of the Mg/Ca elemental ratio of calcite ((Mg/Ca)_calcite) as a temperature indicator in continental carbonate deposits is a matter of debate due to the different results obtained by diverse authors. In this study, we aimed to test the reliability of the (Mg/Ca)_calcite in fluvial carbonates. We selected the recent tufa stromatolite records of four rivers on the Iberian Peninsula for the trace element analysis based on six-monthly sampling. Previous sedimentary and hydrological studies on these fluvial basins provided the information for this work. The water temperature estimates for the stromatolite (Mg/Ca)_calcite substantially differed from the measured water temperatures in most of the studied cases. We thus assessed other factors that participate in the control of the Mg partitioning between water and calcite. The correction of the detrital Mg content yielded water temperatures that matched the measured ones in one of the rivers. The (Mg/Ca)_water, water discharge and calcite precipitation rates may also occasionally influence the (Mg/Ca)_calcite. The six-month behaviour of some of these parameters could interfere with the relationship between the (Mg/Ca)_calcite and water temperature. According to these results, and their comparison with other non-marine carbonates, the wide variety of parameters that are involved in the (Mg/Ca)_calcite limit it as a geochemical thermometer in continental sedimentary environments.

1. Introduction

The use of trace elements in carbonate deposits as climate proxies has been a matter of debate for a long time. In the case of the Mg/Ca ratio in sedimentary nonmarine carbonates, we lack a consensus on its application to the geological record to obtain temperature data because of the varied and usually negative or inconclusive results that researchers have obtained in several studies [1,2,3,4,5,6,7,8]. One important problem is the presence of Mg-bearing clay minerals and other detrital particles (e.g., carbonates) that can be present in small amounts in the carbonate deposits, which is added, in the sample analysis, to the Mg incorporated in the calcite lattice (e.g., [6]) and produce misleading temperature results for the calcite precipitation. The estimation of the contribution of allochthonous Mg to the total amount of Mg in the rock is not straightforward and requires meticulous mineralogical analysis [1]. Moreover, the influence of the biological activity on the Mg partitioning [4,7,8], or the changes in the Mg/Ca ratios of the water that are not related to temperature [2,3], could affect the Mg/Ca ratios in fluvial carbonate deposits. These inconsistencies could be the result of the complex hydrology in carbonate aquifers, the seasonal patterns of the water recharge in some karst systems (e.g., [5]), prior calcite precipitation within the aquifer (e.g., [9]) or the anthropogenic contamination of the water (e.g., [3]). In some cases, the causes of the Mg/Ca variations in water and minerals over time cannot be depicted (e.g., [2]). The use of the isotope compositions of trace metals that coprecipitate with calcite (Mg, U) as a prospective method for estimating the sources of Mg in authigenic carbonates ([10,11,12] and the references therein) might be an additional way to clarify the sometimes-puzzling Mg/Ca variations in some tufa-precipitating systems.

In this work, we compared the recent fluvial stromatolite records from four river basins in the Iberian Range, Spain. The four basins have similar Mediterranean continental climate conditions. However, the deposition rates, stable isotope composition of the water and carbonate deposits formed in each case are noticeably different. The available data on the depositional rates and isotopic, hydrochemical and climatic parameters for each basin taken every six months, over a period from 3 to 13 years, as well as the corresponding recent stromatolite records, offer an excellent opportunity to decipher whether—or under which conditions—geochemical proxies, such as the Mg/Ca ratio, are reliable indicators of the climatic conditions in sedimentary carbonates.

Therefore, in this work, we aimed to test the reliability of the Mg/Ca ratio in fluvial tufa calcite as the depositional (detrital sediment input), hydrological (discharge, in-aquifer residence time of water) and climate (temperature, precipitation, evaporation) indicators of past environments. For this purpose, we analysed the Mg/Ca ratios of the recent six-month fluvial stromatolite records and their water counterparts obtained from 1999 to 2012 for four river valleys in the Iberian Range, Spain. We compared the calculated temperature values with the corresponding measured water temperatures and the water temperatures calculated from the tufa δ¹⁸O_calcite in the same records by the authors of [13]. We analysed the influence of the different parameters on the tufa Mg content, and we compared the results with similar outcomes for other fluvial systems. According to our findings, the use of the Mg content in calcite as a temperature proxy is difficult because of the complex interplay of the other acting parameters (e.g., the water discharge and calcite precipitation rates). Specifically, the influence of the Mg derived from detrital minerals may be responsible for the generally higher temperatures yielded by this proxy.

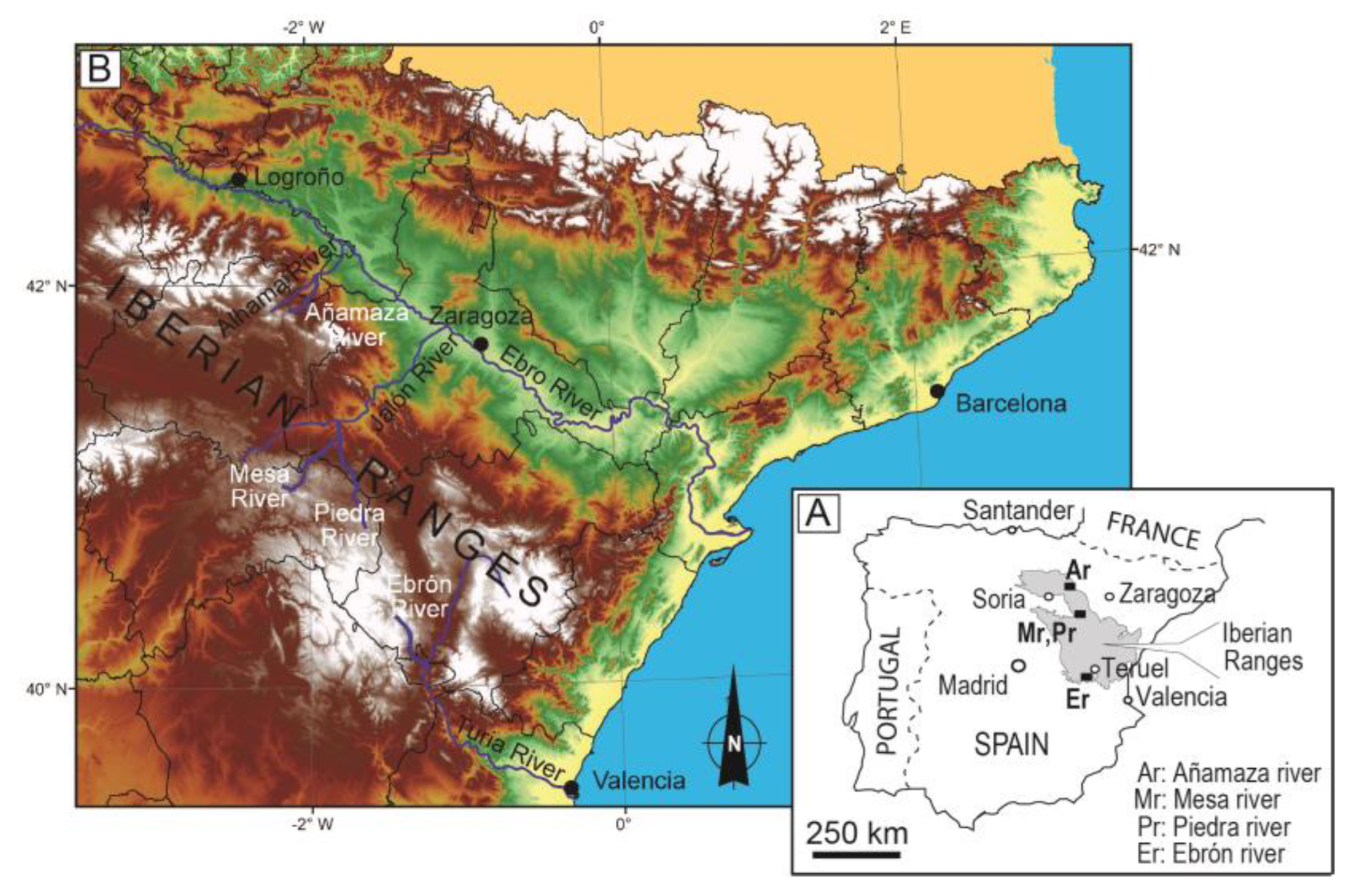
2. Location, Geological Context, Climate and Hydrology

The Añamaza, Piedra, Mesa and Ebrón Rivers are located along a 210 km long, nearly N–S transect across the Iberian Range (Figure 1). The Iberian Range is an Alpine intraplate mountain range that was formed as the result of the convergence of the Eurasian and Iberian plates [14]. The Paleozoic-to-Cenozoic succession is formed mainly of siliciclastic and carbonate sedimentary rocks. The Mesozoic sequence includes thick and extensive successions of carbonate rocks that make up most of the aquifers in the region. This sequence is overlain by Cenozoic fluvial and lacustrine detrital and carbonate rocks [14]. A number of valleys include Pleistocene and Holocene conspicuous tufa buildups [15,16,17,18,19]. In many of these valleys, the present-day rivers continue to form tufa deposits via a long stretch downstream of the headwater springs [19,20,21,22].

The river sections studied by the authors of [19,21,22,23] in the four fluvial basins (Añamaza, Piedra, Mesa and Ebrón) have similar lengths, elevations and topographies, and they share the general Mediterranean continental climate conditions. The four rivers are mainly sourced from Jurassic carbonate rock aquifers (plus Upper Cretaceous carbonate rock aquifers in the case of the Piedra and Mesa Rivers), which supply water of the HCO₃–Ca (Piedra, Ebrón and Mesa) and SO₄–HCO₃–Ca (Añamaza) types. Most of the water is not only provided by the springs that are located in the uppermost reaches of each fluvial valley, but also by the variable contributions from the springs along the river paths, which are greater along the Ebrón River.

The Ebrón and Mesa Rivers have similar mean water discharge values (1.49 and 1.5 m³/s, respectively), which are slightly higher than that of the Piedra River (1.26 m³/s). The Añamaza River has a much smaller discharge value (0.21 m³/s). The longitudinal profile of the Añamaza River has the highest gradient (mean slope of 1.9%), those of the Ebrón and Piedra Rivers have more moderate gradients (1.4% and 1.3%, respectively) and that of the Mesa River has the lowest gradient (1%).

3. Characteristics of Stromatolite Formation in the Studied Rivers

The authors of [19,21,22,23] performed sedimentary and hydrochemical studies on the calcite-depositing rivers: Añamaza, Ebrón, Mesa and Piedra Rivers (hereafter referred to as RA, RE, RM and RP, respectively), and they indicated that the deposition rates were strongly controlled by the mechanical CO₂ outgassing in the four cases, with minor contribution from the biological parameters, such as the photosynthetic CO₂ uptake. The highest deposition rates corresponded to the fast flow conditions along the gently to highly inclined river sites in which the stromatolite deposits were formed (mean measured deposition rates: RM: 4.0 mm/y; RE: 4.4 mm/y; RP: 13.7 mm/y; RA: 18.3 mm/y). The researchers measured from moderate to high deposition rates in the varied-sized waterfalls with continuous and turbulent flows, in which crudely laminated deposits of moss, macroscopic algae and minor stromatolites had formed (mean measured deposition rates: RM: 2.4 mm/y; in RE: 7.4 mm/y; RP: 8.2 mm/y; RA: 8.4 mm/y). The lower rates were those of the slow flowing water areas, in which the sediment consisted of loose lime mud, small phytoclasts and oncoids, as well as uneven and thin stromatolites. Other contexts, such as spray areas or caves, yielded much smaller deposition rates. In all cases, the deposition rates were much higher in the warm periods (i.e., spring and summer months) than in the cool periods (i.e., autumn and winter months). The six-month difference was explained by the differential effects of the temperature and temperature-related parameters on the calcite solubility in the water and on the biota activity, the latter either through plants or prokaryotes that act as substrates for calcite precipitation, or even through the photosynthesis process [24,25]. However, despite these similarities, there are large variations in the deposition rates between the four rivers due to differences in the discharges, water chemical compositions, riverbed slopes and water temperatures [21]. Among the studied facies, the most continuous records were for the stromatolite deposits, which allowed for the identification of the successive six-month period intervals that were monitored on site and in the laboratory (Figure 2). Therefore, we selected a number of stromatolite deposits formed on tablets for this study. These stromatolite deposits consist of thicker and denser composite laminae that alternate with thinner and more porous composite laminae. The former includes up to six simple laminae, and the latter includes up to four [26]. The laminae primarily consist of cyanobacterial calcite tubes that form palisades, fan-shaped calcite bodies and/or intertwined-calcite-tube mats (Figure 3). According to the RNA determinations from the same sites as the tablets, most of the studied samples coincided with Phormidium incrustatum [27,28]. In addition, diatoms, insect cavities and extracellular polymeric substances (EPSs) were variably present between the tubes (Figure 3).

We selected the stromatolite records that were suitable for this study as follows: For the RE and RA rivers, the highest deposition rates were measured in Tablets RE-8 and RA-6 (8.44 mm/y over 3.5 years, and 18.3 mm/y over 3 years, respectively). For RP, Tablet R-14 provided the longest and most continuous record (12 years, with a mean rate of 16.02 mm/y). For the RM, Tablet M-4 had a continuous record that was suitable for this study (3.5 years, with a mean rate of 5.45 mm/y).

4. Methods

4.1. Sediment Sampling and Analyses

The researchers obtained the sediment samples from tufa stromatolites developed on limestone tablets. The authors of [13,19,21,22,23,25] gathered the sediment records and the related water parameters in a multidisciplinary study performed between 1999 and 2012. They installed the tablets (25 × 15 × 2 cm) on the riverbeds at several places that represented different environmental conditions. They set the tablets at the end of the winter, and they removed them at the end of the summer to measure their thickness in the laboratory. After a week, they returned the same tablets back to the same places until the next semester. The authors of [25] explain the procedure in detail. Once they definitively removed the tablets, they cut them perpendicular to the depositional surfaces, and they identified the six-month intervals (hereafter, we refer to spring and summer as the warm period, and we refer to autumn and winter as the cool period) by plotting the corresponding measurements on the raw cuts (see [29] for details).

From these sections, they took from one to two sediment samples from each six-month interval with a punch and a microdrill (Navfram model N120 Micromotor 25.000 rpm with electronic speed regulator, AB SHOT TECNICS SL, Cervello, Barcelona, Spain). They ground the powdered matter and sieved it through a 50 µm size mesh, and they then separated it for different uses.

For the Ca and Mg analyses, they homogenised each stromatolite sample. They digested the subsamples of approximately 0.2 g using a mixture of concentrated Suprapur nitric acid (2.5 mL) and hydrochloric acid (7.5 mL) (all Merck), in closed Teflon crucibles (V = 35 cm³) on a hotplate at a temperature of 170 °C, and then in open Teflon crucibles (V = 35 cm³) at a temperature of 220 °C.

The researchers used a high-resolution inductively coupled plasma mass spectrometer (HR ICP-MS) (Element 2, Thermo Finnigan, Bremen, Germany) for the determination of the Ca and Mg concentrations. We present the results for all the six-month sediment intervals recorded on the tablets of the four rivers in Table S1 (Supplementary Material).

The stable isotope composition values of the sediment and water (δ¹³C and δ¹⁸O ‰VPDB) of the RA, RE and RP used in this paper are those published in [13]. The stable isotope composition values of the sediment and water of the RM presented in this contribution were obtained with the same technique described by [13].

The researchers determined the bulk mineralogical composition of the sediment by powder X-ray diffraction using a Phillips PW 1729 diffractometer (Crystallography and Mineralogy Division of the University of Zaragoza, Spain). According to the X-ray diffraction, all the stromatolite samples were composed of low-Mg calcite with minor amounts of detrital particles such as quartz, clay minerals and, occasionally, dolomite [19,21,22,23]). To assess the possible contribution of these detrital minerals to the chemical composition of the analysed samples, the researchers studied the clay mineral content using the RP as an example. For this purpose, they took five sediment samples (stromatolites) along the river in July 2011. They ground and sieved the samples, and they separated the < 2 μm sediment fraction by centrifugation, and they then analysed it for both the mineral (by means of oriented aggregates) and chemical (with the same methodology indicated above for the stromatolite samples) compositions. They performed a semi-quantitative determination of the clay minerals with the reference intensity ratio (RIR) method, and by using the RIR values of [30] taken from [31].

4.2. Water Sampling and Analysis

The researchers obtained the water samples for the chemical analysis at the sites in the four rivers that coincided with the tablet sites. They conducted biannual sampling (approximately in the middle of the warm and cool periods, i.e., at the end of June and in January, respectively) from June 2004 to December 2009 at the RP, from June 2004 to June 2006 at the RM, from December 2007 to December 2009 at the RA and from June 2007 to December 2009 at the RE.

They measured the water temperature (Tw) and pH on site using a portable pH meter (Jenway 4200; Bibby Scientific Limited, Stone, UK). They filtered the samples using a 0.45 μm Millipore cellulose filter, and they acidified them with ultra-pure HNO₃ to a pH of < 2 for the cation analyses. They determined the alkalinity, SO₄, Cl, Ca, Mg, Na and K with the same protocols and analytical methods (as is detailed, for instance, in [19]) for the four rivers. The charge imbalance percentage for the analytical data used in this study was always below 10% as calculated with the PHREEQC code (see below). We present the analytical results for the study sites on the four rivers in Table S2 (Supplementary Material).

4.3. Geochemical Modelling Calculations

The researchers performed the speciation–solubility calculations to obtain the values of the calcite saturation index (SIc), total dissolved inorganic carbon (TDIC) and partial pressure of CO₂ (pCO₂) values for the water samples with the PHREEQC code [32], and with the WATEQ4F thermodynamic database distributed with the code.

They calculated the inorganic precipitation rate for the calcite (mmol/cm²/s) using the rate law in [33], which is commonly referred to as the PWP (Plummer, Wigley, Parkhurst) rate equation:

R = −κ₁ aH⁺ − κ₂ aH₂ CO₃^* − κ₃ aH₂O + κ₄ aCa²⁺ aHCO₃⁻

(1)

where H₂CO₃^* = H₂CO₃⁰ + CO_2(aq), and κ₁, κ₂, κ₃ and κ₄ are the empirically determined rate constants. They used the temperature functions proposed by Plummer et al. (1978) for the κ₁, κ₂ and κ₃ rate constants [33]. The rate constant κ₄ depends on the temperature and pCO₂. The researchers used the equation proposed in [34] by fitting it to the empirical data of Plummer et al. (1978) [34].

The empirical rate (Equation (1)) was originally provided for calcite dissolution; however, it is also applicable to precipitation [33,35]. In the form presented in Equation (1), the negative values correspond to the dissolution rates and the positive values to the precipitation rates. Researchers frequently use this equation for tufa-depositing streams [2,19,21,23,36,37,38,39,40,41,42] because it provides the maximum rate of the inorganic precipitation in turbulent water [43]. The rate is usually larger than the actual precipitation rate; however, we can achieve a reasonable estimation by reducing the calculated PWP rate with Equation (1) by a factor of 10 [37,38,44]. The PWP values calculated in this study were transformed in this manner when they were assessed with the precipitation rates obtained in the literature by other methods.

We estimated the magnesium distribution coefficient between calcite and water from:

$${\mathrm{D}}_{\mathrm{Mg}}=\frac{{\left(\mathrm{Mg}/\mathrm{Ca}\right)}_{\mathrm{calcite}}}{{\left(\mathrm{Mg}/\mathrm{Ca}\right)}_{\mathrm{water}}}$$

(2)

where (Mg/Ca)_calcite denotes the molar ratio of the Mg and Ca concentrations in the stromatolites and (Mg/Ca)_water denotes the molar ratio of the total dissolved Ca and Mg contents in the water. According to the results from the speciation–solubility calculations, there were no meaningful differences between the molar ratios calculated with the free Ca²⁺ and Mg²⁺ ion concentrations and those obtained with the total dissolved Ca and Mg contents; thus, we can neglect the effects of the Ca and Mg complexation in the estimation of the distribution coefficient.

4.4. Mg/Ca Thermometry

When using the Mg/Ca ratio in calcite as a water palaeothermometer, it is conventionally assumed that it is predominantly controlled by the Mg/Ca in the solution and a temperature-dependent partition coefficient. Although researchers have widely used Mg/Ca palaeothermometry in marine settings, to date, only a few researchers have utilized the Mg/Ca ratio for freshwater tufa deposits (e.g., [6], and the references therein). Moreover, the available experimental data for the Mg partitioning behaviour under karst/speleothem-specific conditions (e.g., for calcite precipitation from solutions of low ionic strength) are scarce, and to the best of our knowledge, only two experimental works are available in the literature: the Mg distribution coefficient D_Mg–temperature (D_Mg-T) relationships obtained by [45] and by [46].

The D_Mg-T relationships obtained by these authors have important differences. The equation in [46] always provides higher temperatures than that in [45], and in our case, it provided exceedingly higher temperatures with respect to the measured ones (see Figure S2, Supplementary Material). Furthermore, researchers have only used the D_Mg-T relationships in [45] to calculate the water temperatures from the Mg concentrations of tufa samples (e.g., [1,3,6]).

Therefore, in this work, we only used the D_Mg-T relationship from [45], as adjusted by [3]:

$$\mathrm{T} (℃)=\frac{{\mathrm{D}}_{\mathrm{Mg}}-0.001}{0.0012}$$

(3)

where D_Mg is the Mg distribution coefficient (see Equation (2)), which is used to calculate the river Tw from the measured Mg/Ca ratios of the waters. Despite the adjustment-derived uncertainties of this equation, researchers have repeatedly used it to estimate the Tw in fluvial environments [1,3,6].

We compared the Mg-derived Tw values with the water temperatures measured in the sampling moment, as well as with the Tw values estimated from the δ¹⁸O of both the stromatolite calcite and river water, by means of the formula in [47]. Except for the RM river, researchers have reported these temperatures in previous works (RP: [20]; RA: [23]; RE: [21]).

As the researchers measured most of the parameters on a six-month basis, we calculated the moving averages of two periods for the examined parameters, to remove the seasonality and to obtain the corresponding season-free evolutions.

5. Results

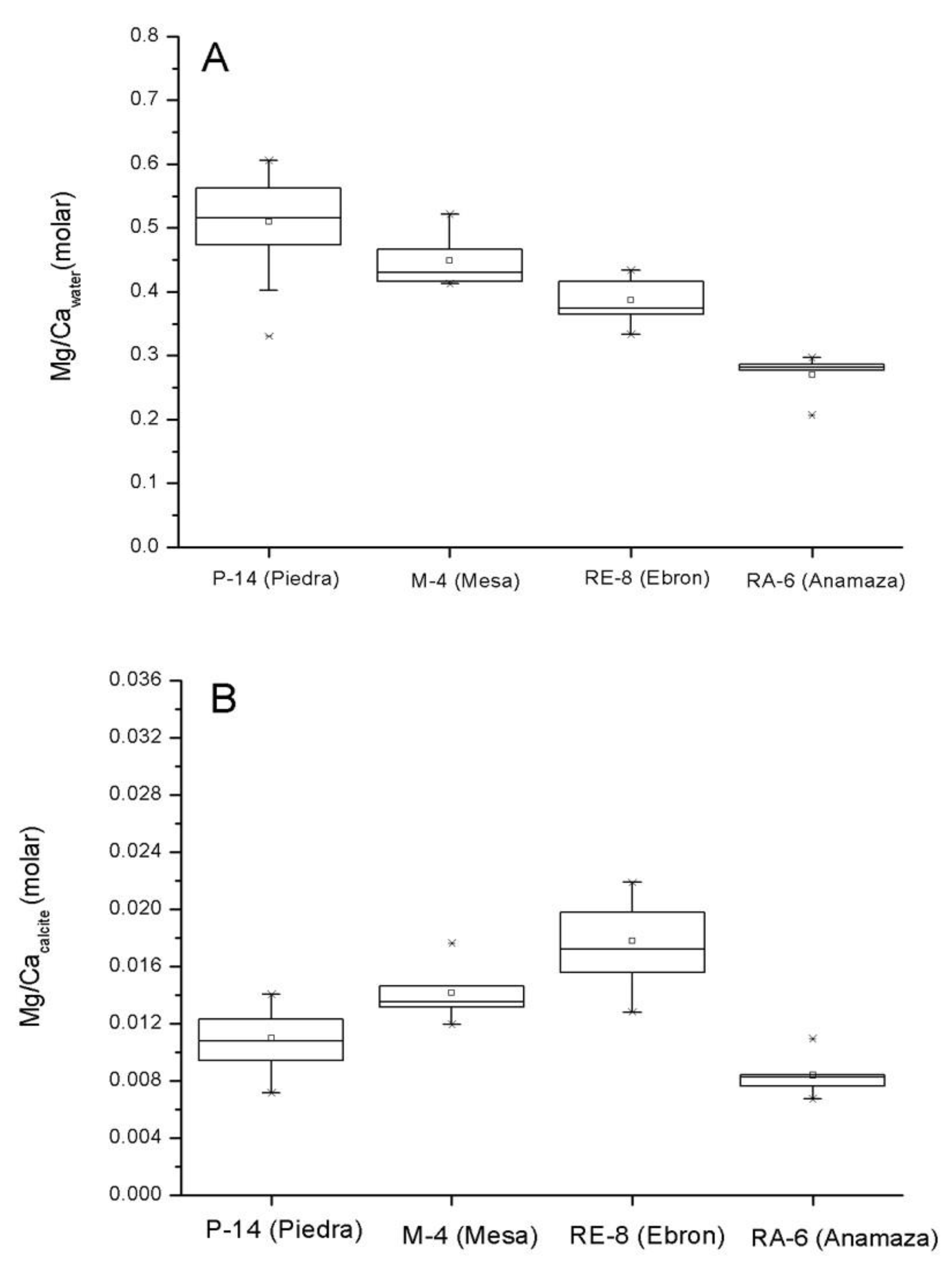
5.1. Hydrochemical Characteristics and Mg/Ca Ratios of the Waters

The hydrochemical characters of the waters at the studied sites are representative of the main compositional features of the four rivers. The water is of the HCO₃^–Ca type in the cases of the RE, RM and RP. In the case of the RA, the water is of the SO₄–HCO₃–Ca type (see Figure S1 Supplementary Material), which is the result of the intense interaction between the groundwater feeding the river and the bedrock evaporitic materials (gypsum/anhydrite) [23].

The Tw ranges measured in June and January at the studied sites (see Table S2, Supplementary Material) were similar in the four rivers: from 8 to 18 °C in the cases of the RA, RM and RP, and a bit narrower in the case of the RE (from 10.7 to 16 °C). The Tw values had a clear seasonal pattern (Figure 4). The differences between the mean temperatures for the warm and the cool periods were slightly higher in the RA and RP (6.3 and 5.2 °C, respectively) and lower in the RE and RM (2.6 and 2.7 °C, respectively) (Table S3, Supplementary Material).

The dissolved Mg concentrations were relatively similar in the four studied rivers (mean values between 0.8 and 1.04 mmol/L (

Table 1. Mean values (mean ± 1 σ) for dissolved Mg, Ca and Mg/Ca ratios in waters (Mg_water, Ca_water and Mg/Ca_water) and stromatolites (Mg_calcite, Ca_calcite and Mg/Ca_calcite), and for the distribution coefficients in the studied sites at Piedra, Mesa, Añamaza and Ebrón Rivers. We also include data for the Kaisinger Creek [8] and Krka River [6] for comparison.

Chemical Components	Piedra River	Mesa River	Añamaza River	Ebrón River	Kaisinger Creek	Krka (2) River
Mgwater (mmol/L)	1.04 ± 0.19	0.87 ± 0.034	0.87 ± 0.07	0.80 ± 0.054	0.32 ± 0.03	0.94 ± 0.15
Cawater (mmol/L)	2.04 ± 0.17	1.95 ± 0.22	3.24 ± 0.23	2.08 ± 0.17	3.16 ± 0.23	1.66 ± 0.1
Mg/Cawater (molar)	0.51 ± 0.08	0.449 ± 0.045	0.27 ± 0.036	0.386 ± 0.033	0.101 ± 0.01	0.56 ± 0.08
Cacalcite (wt%)	37.0 ±2.56	35.2 ± 0.97	34.05 ± 2.08	34.8 ±2.53	37.1 ± 0.99	34.02 ±1.04
Mgcalcite (g/kg)	2.46 ± 0.47	3.01 ± 0.38	1.73 ± 0.31	3.75 ± 0.8	0.58 ± 0.05	5.48 ± 0.71
Mg/Cacalcite (molar)	0.011 ± 0.002	0.014 ± 0.002	8.38 × 10−3 ± 1.6 × 10−3	0.018 ± 0.004	2.58 × 10−3 ± 0.27 × 10−3	0.027 ± 0.004
DMg	0.023 ± 0.008	0.032 ± 0.04	0.032 ± 0.012	0.046 ± 0.009	0.025 ± 0.003 (1)	0.044 ± 0.0068

⁽¹⁾ Averages from the tufas in three different sections of the Kaisinger Creek (from the data presented in [8]). ⁽²⁾ Data taken from [6] in Table 1 and Table S3. For Ca, Mg and Mg/Ca values in waters, we present values from the sampling site W3. For Ca, Mg and Mg/Ca ratios in tufa in Table S3, samples from T1 to T10 are considered.

)). The dissolved Ca contents had greater differences (mean values between 1.95 and 3.24 mmol/L (Table 1)). As a consequence, there were differences between the rivers for the Mg/Ca ratios of the waters (Mg/Ca_water) (Figure 5A and Table S2, Supplementary Material). The mean (Mg/Ca)_water values exhibited an overall decreasing evolution from the RP to the RM, RE and RA, from 0.51 ± 0.08 in the RP to 0.27 ± 0.036 in the RA (Figure 5A, Table 1).

The (Mg/Ca)_water values in the RE (RE-8) and RM (M-4) had a quasi-seasonal pattern, with higher values in the warm periods and lower values in the cool periods (Figure 4). This seasonal pattern was also present in the RP, from the beginning of the record until Cool 2007–2008; from this period onwards, the oscillations were wider than in the other rivers and did not present any regularity. Finally, the (Mg/Ca)_water values in the RA (site RA-6) were rather constant over the periods, except for the last recorded period (Cool 2009–2010), which had a lower value (Figure 4).

The waters were always oversaturated with respect to calcite, with the highest SIc values in the RA at the RA-6 site (mean value of 0.89 ± 0.23), and intermediate values in the RE at the RE-8 site (mean value of 0.73 ± 0.28), and in the RP at the RP-14 site (mean value of 0.67 ± 0.33). The lowest values were for the RM at the M-4 site (mean value of 0.57 ± 0.33). The calculated partial pressure of CO₂ (as log pCO₂) was always higher than the atmospheric values (mean values: RE: −2.79 ± 0.28; RA: −2.92 ± 0.25; RM: −2.62 ± 0.44; RP: −2.71 ± 0.35).

The mean values of the calcite precipitation rate ranged from 1.40 × 10⁻⁸ ± 1.13 × 10⁻⁸ mmol/cm²/s in the RM to 3.09 × 10⁻⁷ ± 1.44 × 10⁻⁷ mmol/cm²/s in the RA, with intermediate values in the RE and RP (1.91 × 10⁻⁸ ± 1.02 × 10⁻⁸ and 1.73 × 10⁻⁸ ± 1.16 × 10⁻⁸ mmol/cm²/s, respectively).

With some exceptions, the dissolved Ca, HCO₃ and TDIC concentrations at the studied sites had lower values in the warm periods due to the more intense calcite precipitation in these periods for most of the studied time intervals (which is in agreement with the overall trends previously detected in the studied rivers [19,20,21,22,23]). The PWP and SIc values are usually higher in the warm periods; however, in the case of Site M-4, the opposite trend was evident (Figure 4).

5.2. Geochemical Characteristics and Mg/Ca in Stromatolites

The calcium contents in the studied deposits ranged from 31.8 to 40 wt.% (Table S1, Supplementary Material), which corresponded to CaCO₃ percentages in the sediment from 80 to 100 wt.% (calculation based on Ca analytical data). Overall, these contents were consistent with those found in other modern (Krka River or Kaisenger Creek, Table 1) and older tufa deposits (e.g., [24,48,49,50]).

Although the analysed samples were primarily formed of calcite, there were some differences among the studied deposits, whereas the Ca contents in the deposits from the RA, RE, and RM were relatively similar, with mean values of 34–35 wt.% (85–87.5 wt.% as CaCO₃ (Table 1)), and the Ca concentrations in the stromatolite from the RP were higher, with a mean value of 37 wt.% (92.5 wt.% as CaCO₃).

The magnesium concentrations ranged from 1.28 to 5.15 g/kg, with the highest values in the RE (3.75 ± 0.8 g/kg) and the lowest in the RA (1.73 ± 0.31) (Table 1). The MgCO₃ contents (calculated assuming that Ca and Mg were the only elements in the carbonate fraction) ranged from 0.65 to 2.07 mol%, which indicated that the calcite in the stromatolites was low-Mg calcite.

The Mg/Ca ratio of the studied stromatolites (herein (Mg/Ca)_calcite) also exhibited differences between the studied rivers (Figure 5B, Table S1, Supplementary Material). The highest mean (Mg/Ca)_calcite values were in the RE (0.018 ± 0.004), and the lowest were in the RA (8.38 × 10⁻³ ± 1.6 × 10⁻³) (Table 1). Overall, these values did not show a systematic evolution with respect to the corresponding (Mg/Ca)_water (compare Figure 5A,B). The RP had the highest (Mg/Ca)_water value and the second lowest (Mg/Ca)_calcite value.

The six-month (Mg/Ca)_calcite pattern over time was not the same for the four rivers (Figure 4). In the RE, and partially in the RP, there were six-month patterns with lower (Mg/Ca)_calcite values in the cool periods and with higher values in the warm periods. In RP, this pattern was more distinct from the Warm 2006 onwards, except for the last period (Cool 2009–2010). The (Mg/Ca)_calcite values in the RM did not show a cyclic pattern, and the values increased over time. The RA values had little variation, except for the last period (Cool 2009–2010). The overall (Mg/Ca)_calcite trends of the RM and RP were parallel (Figure 4).

The calculated D_Mg values for the studied stromatolites in the four rivers ranged from 0.012 to 0.053, with the lowest values in the RP (mean 0.023 ± 0.008) and the highest in the RE (mean 0.046 ± 0.009) (Table 1). Overall, these values were in the range of the D_Mg determined in the experimental studies (from 0.01 to 0.06, as reviewed in [8,45,51,52]) and in other natural fluvial tufa systems (from 0.011 to 0.058, as reviewed in [8]).

Most of the studied rivers had seasonal D_Mg patterns over time, except for the RA (Figure 4). Most of the examined record of RE revealed a six-month pattern with higher D_Mg values in the warm periods, and from Cool 2005–2006 to Warm 2009 in the RP. In the case of the RM, the D_Mg had a faint seasonal pattern, but with higher values in the cool periods.

We present the δ¹⁸O_calcite and δ¹³C_calcite of the stromatolite records in Table S4 (Supplementary Material) and Figure 4. The δ¹⁸O_calcite values in the four rivers were similar, although there were slightly higher in the RP. In the four rivers, the δ¹⁸O patterns were evident in the alternating higher values in the cool periods and lower values in the warm periods, which is consistent with the temperature dependence of the oxygen isotope fractionation in calcite precipitation. Therefore, the stromatolite δ¹⁸O values reflected the water temperature signature. The temperatures estimated from the δ¹⁸O_calcite and δ¹⁸O_water were close to the measured temperatures [13].

The δ¹³C_calcite values were also similar in the four rivers, and the ranges of variation were narrower than in the δ¹⁸O_calcite (Figure 4). The RM had the lowest values, and the RE and RA had the highest. In the RP, the δ¹³C had an oscillating pattern that was roughly parallel to the δ¹⁸O. In the RE, the δ¹⁸O and δ¹³C patterns were similar. In contrast, in the RM and RA, the δ¹⁸O and δ¹³C did not display any significant relationship.

The clay composition of the five analysed stromatolites were similar: only illite and chlorite were present. The average proportion of both minerals was 65% for the illite and 35% for the chlorite, and the mean Mg content in the clay fraction was about 10,000 mg/kg. Therefore, the stromatolite Mg/Ca analysis could have included Mg from chlorite. However, considering a maximum clay mineral content of 5%, the chlorite contribution to the stromatolite sample would be 500 ppm, which is significantly low with respect to the entire Mg content (Table S1, Supplementary Material).

6. Discussion

The (Mg/Ca)_water for the studied sites at the four rivers cover a relatively wide range of values (Table 1). If the (Mg/Ca)_calcite ratio primarily depends mainly on the Mg/Ca in the solution and on a temperature-dependent partition coefficient (Equation (2)), then the theoretical (Mg/Ca)_calcite values for the mean (Mg/Ca)_water for the rivers should parallel the decreasing (Mg/Ca)_water trends that can be observed in Figure 5A from the RP to RA rivers (given that the mean water temperatures were similar at the four sites, from 12.2 to 13.5 °C). However, this is far from reality, and there was even an increasing trend from the RP to the RE (Figure 5B). Thus, we need to consider other factors that participate in the control of the Mg partitioning in calcite when analysing the Tw derived from the Mg content in carbonates.

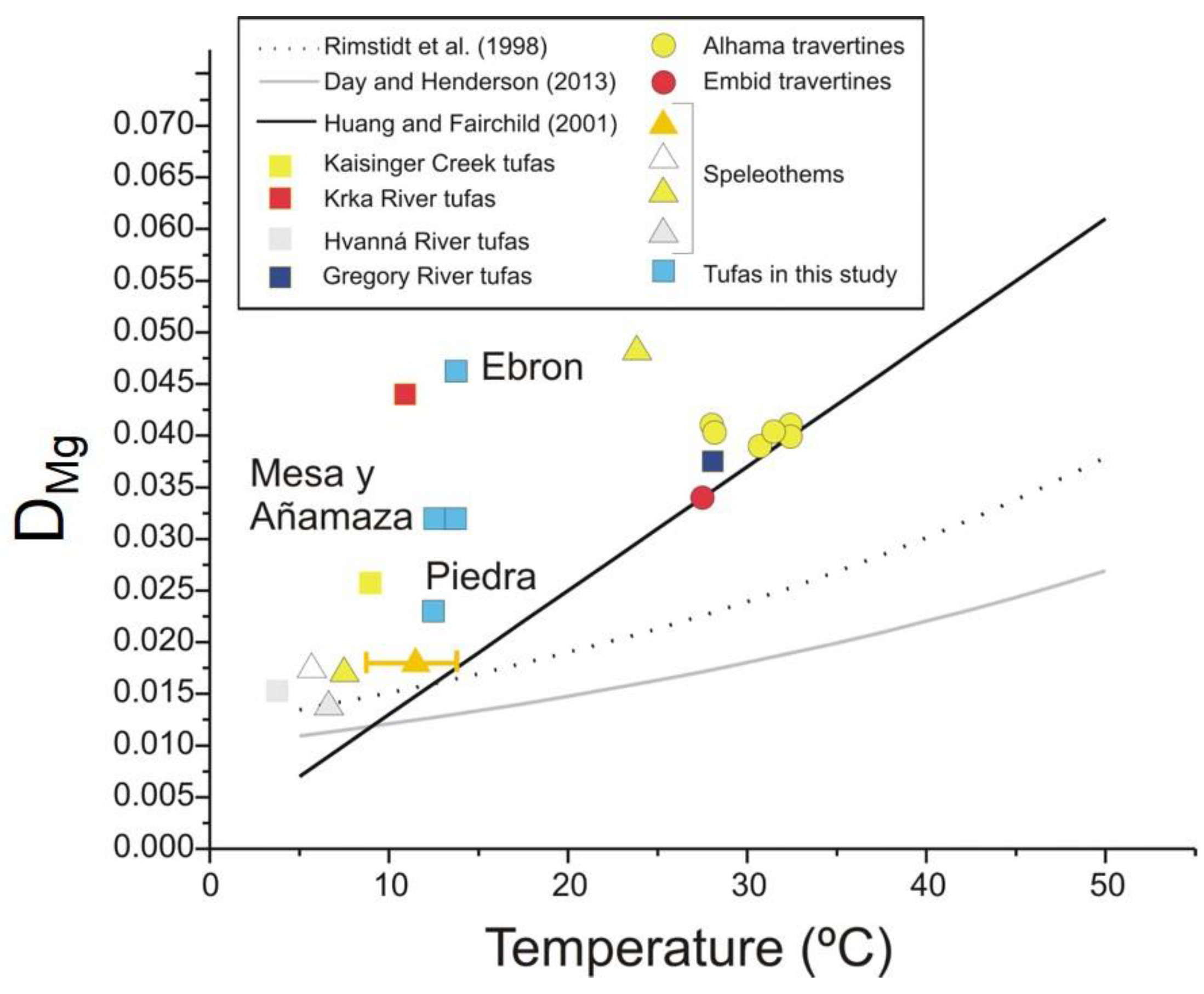
6.1. (Mg/Ca)_calcite and Temperature

The temperatures derived from the stromatolite Mg/Ca content substantially differ from both the Tw calculated from the stromatolite δ¹⁸O_calcite values and the measured Tw (Figure 4). Even in the RP, which had the best fitting between the Mg-derived Tw and measured Tw, the evolutions of the two temperatures were not parallel over time (Figure 6). Furthermore, in general, the Mg-derived Tw did not show the expected seasonality (e.g., higher values in the warm periods than in the cool periods), except partially in the RP. In the RE, the Mg-derived Tw had right oscillating behaviour in some periods. In the RA, there was no oscillation, and in the RM, the oscillation was reversed (Table S3, Supplementary Material, Figure 6).

The matching between the (Mg/Ca)_calcite and measured Tw was of a diverse degree (Figure 4;

Table 2. Correlations between some analytical parameters of studied tufa samples.

River (Number of Samples)	Mg/Cawater vs. T	Mg/Catufa vs. T	Mg/Catufa vs. Mg/Cawater	DMg vs. T	PWP vs. T	Tcalc-T measured Mean
Piedra (n = 12)	+0.15 (p = 0.627)	+0.391 (p = 0.208)	−0.577 (p = 0.049)	+0.064 (p = 0.845)	+0.863 (p = 0.0003)	4.89
Piedra Cool 06-07 to Cool 09-10 (n = 5)	−0.03 (p = 0.945)	0.576 (p = 0.176)	−0.787 (p = 0.036)	0.213 (p = 0.646)	+0.842 (p = 0.017)	+7.57
Piedra Warm 04 to Warm 06 (n = 7)	+0.346 (p = 0.568)	+ 0.379 (p = 0.529)	0.587 (p = 0.298)	0.27 (p = 0.66)	+0.967 (p = 0.007)	+1.15
Añamaza (n = 5)	+0.326 (p = 0.59)	−0.338 (p = 0.577)	−0.939 (p = 0.018)	−0.312 (p = 0.608)	+0.39 (p = 0.516)	13.9
Mesa (n = 56)	+0.479 (p = 0.414)	−0.023 (p = 0.971)	+0.61 (p = 0.273)	−0.48 (p = 0.40)	−0.663 (p = 0.222)	12.5
Ebrón (n = 6)	+0.892 (p = 0.017)	+0.691 (p = 0.128)	+0.551 (p = 0.256)	+0.269 (p = 0.28)	+0.103 (p = 0.845)	24.0

), and with respect to the season-free evolutions, the (Mg/Ca)_calcite and measured Tw exhibited a weaker similarity (Figure 6), even when there is a significant correlation between them (See Section A.1. in Appendix A for details). This inconsistency between the six-month pattern and the season-free evolution suggests that the correlation between the measured Tw and (Mg/Ca)_calcite is caused by the common seasonal changes of both parameters, and not necessarily by the temperature dependence of the Mg partitioning. According to these results, it is clear that there is a complex interplay of diverse factors other than the temperature that influences the (Mg/Ca)_calcite contents in the stromatolites and thus promotes different behaviours.

The abovementioned situation could explain the sparse results calculated with the D_Mg-T relation obtained by using the equation in [45]. The authors of [1] successfully used the D_Mg-T relationship to obtain the model temperatures from the Mg concentrations of tufa samples in Australia; however, there were discrepancies in the correlation between the tufa (Mg/Ca)_calcite ratios and water temperature [1,7]. The use of the relationship described by the authors of [45] in other modern tufas has provided higher temperatures than the ones measured in rivers with temperature-controlled (Mg/Ca)_water ratios (e.g., the Krka River in Croatia [3], and the Krka River in Slovenia [6]). The Mg/Ca paleothermometry in modern and ancient stream tufas is generally problematic due to the fact that the expected influence of the temperature on the (Mg/Ca)_calcite can be obscured by diverse factors, such as the hydrogeochemical conditions, the changes in the (Mg/Ca)_water and anthropogenic contamination [2,3,5,53], the influence of the microbial biofilm activity [4,7,8,54] and the presence of variable amounts of detrital limestone and dolomite in the tufa [12].

6.2. Other Factors That Influence (Mg/Ca)_calcite

6.2.1. Mg/Ca of Water

The (Mg/Ca)_calcite values not only depend on the temperature, but also on the (Mg/Ca)_water. Moreover, the empirical partitioning coefficient (D_Mg) depends on the (Mg/Ca)_water value (see Equation (2)). Accordingly, variations in the (Mg/Ca)_water may be involved in the systematic offset with respect to the measured temperatures. The authors of [2] found that the (Mg/Ca)_calcite ultimately relies on rainfall and aquifer processes, which determine the (Mg/Ca)_water content. The authors of [53] established that the seasonal variations in the (Mg/Ca)_calcite do not depend on the temperature, but on the seasonal (Mg/Ca)_water variations, which are induced by the preferential leaching of Mg from carbonates in dry periods [9]. Calcite precipitation can also modify the (Mg/Ca)_water along streams by removing Ca from the water [55].

Thus, the (Mg/Ca)_water variation may interfere with the temperature-dependent (Mg/Ca)_cacite content. In general, the (Mg/Ca)_water increases in warm and/or dry periods due to the greater Ca extraction by the calcite precipitation under these conditions, and in-aquifer effects produce the same result [53,55,56]. From a theoretical point of view, the increase in the (Mg/Ca)_water in warm periods emphasizes the increase in the derived (Mg/Ca)_calcite because the Mg content in calcite increases with increasing temperature. As the empirical D_Mg (Equation (2)) is the ratio between these coupled varying parameters, the simultaneous increases in both parameters cancel each other out, at least partially, which results in a smoothed D_Mg. This only occurred in the first interval of the RP (from Warm 2004 to Warm 2006), when oscillations in (Mg/Ca)_calcite flatten the expected seasonal oscillations of the Mg-derived Tw, although these values are close to the measured Tw. In the rest of the cases, the Mg-derived Tw are higher than the measured Tw due to the anomalously high (Mg/Ca)_calcite. (See Section A.2. in Appendix A for details).

6.2.2. Detrital Minerals

Given the type of chemical attack used for the trace element analysis of the sediments, some detrital matter may have been dissolved and then included in the analysed aliquot, which may have caused the total Mg content to be higher than the total Mg in the calcite lattice. Moreover, the Al content of the analysed samples was significantly correlated to the (Mg/Ca)_calcite in all the cases, except for the first time interval for the RP (RP from Warm 2004 to Warm 2006: r = 0.09; RP from Cool 2006–2007 to Cool 2009–2010: r = 0.62; RM: r = 0.88; RE: r = 0.96; RA: r = 0.87) (

Table 3. Trends and correlations for some analytical parameters of studied tufa samples.

River	Mg/Catufa	Al Contents in Tufas	Mg and Al Contents in Tufas	Correlation Coefficient (R, Pearson) for Al vs Mg/Ca (2) in Tufas
				All Periods	Warm 04 to Warm 06	Cool 2006–07 to Cool 2009–10
Piedra	Almost seasonal (1)	Not seasonal	Al > Mg	0.598	0.055	0.756
Ebron	Almost seasonal (1)	Almost seasonal (1)	Al > Mg	+0.88
Añamaza	Not seasonal	Seasonal (2)	Al > Mg	+0.965
Mesa	Not seasonal	Almost seasonal (2)	Mg ≈ Al	+0.93

⁽¹⁾ Higher values in the warm periods. ⁽²⁾ Higher values in the cool periods.

). Because of this, we cannot rule out the influence of Mg from a detrital source. The corresponding extra increase in the (Mg/Ca)_calcite value may have been responsible for the anomalously higher-than-real Tw values observed in most of the cases. Moreover, the amount of detrital sediment may regularly oscillate and consequently overemphasize the (Mg/Ca)_calcite values, and subsequently, the estimated Tw, while at least partially preserving the six-month oscillation, which may be the case for the RE, in which the (Mg/Ca)_calcite exhibited a six-month oscillating pattern; however, the values were much higher than the expected ones from the measured (Mg/Ca)_water.

Assuming that the Mg contents in the stromatolites included 500 ppm of clay-derived Mg (see Methods and Results), we can eliminate the corresponding contribution to the Tw calculation by subtracting this amount from the total measured Mg contents. Then, by recalculating the Tw with the corrected Mg values, the mean D_Mg decreases and, as a consequence, so does the estimated Tw. Inversely, we can estimate the Mg content that corresponds to the measured Tw from the measured (Mg/Ca)_water by using Equations (2) and (3), and we can then express the Mg excess (See Section A.3. in Appendix A for details).

The correction for the noncarbonate-derived Mg in the stromatolites was only able to cancel out the temperature offset in the RP, and likely in the RA, with small amounts of detrital Mg. In the first time interval of the RP (from Warm 2002 to Warm 2006), the detrital Mg fraction corresponded to probably less than the 5% of the clay minerals considered in the correction. In the second time interval of the RP (from Cool 2006–2007 to Cool 2009–2010) and in the RA, the detrital Mg fraction should have been higher, and it should have included not only clay minerals but also dolomite. In the other rivers (RE and RM), we have to invoke, most likely, additional factors to explain the high (Mg/Ca)_calcite.

6.2.3. Precipitation Rate

As stated above, in laboratory experiments, the (Mg/Ca)_calcite ratio is predominantly controlled by the Mg/Ca in the solution and Tw, without the meaningful influence of other factors, such as the mineral precipitation rate (e.g., [6,7,57] and the references therein). However, according to the results obtained in natural settings, the (Mg/Ca)_calcite values are dependent on additional factors, such as the mineral precipitation rate, crystal morphology and/or biological processes [7,8,57]. Furthermore, according to recent experimental results, the calcite precipitation rate may influence the (Mg/Ca)_calcite and D_Mg under both biotic and abiotic conditions (e.g., [7,51]).

We can theoretically estimate the calcite precipitation rates (see Methods) as the PWP rates from the hydrochemical characteristics of the waters, or from the six-monthly thicknesses recorded on the tablets [13]. The deposition recorded on the tablets and PWP values are not fully equivalent because the latter corresponds to single sampling moments in the six-month periods, whereas the deposition rates from the tablets represent the six-month-period net deposition and could have been affected by erosive processes [21,23]. However, we use them in a complementary manner for the discussion.

In most of the studied cases, the thicknesses were higher in the warm periods than in the cool periods due to the influence of the temperature on the calcite precipitation, except for the RM [22]. This produced a six-month rhythmic pattern for the thicknesses that paralleled the (Mg/Ca)_calcite in the cases in which the latter also exhibited a seasonal pattern (Figure 4). The PWP values, depending on the temperature and hydrochemical features, can also exhibit a six-month rhythmic pattern.

The calculated PWP values are in the upper range of the calculated precipitation rates in other tufa-depositing rivers (see the reviewed values in [8]). Overall, except for in the RM, there was a good correspondence between the PWP values and the thicknesses recorded on the tablets, with higher values in the warm periods (Figure 4) (See Section A.4. in Appendix A for details).

The best agreement between the measured thickness and PWP patterns occurred for the RP, for which both parameters exhibited six-month variations (Figure 4), especially for the first time interval (from Warm 2002 to Warm 2006). This differential behaviour of the RP with respect to the other rivers may be related to the lower partitioning coefficients (D_Mg) for this river. The inorganic precipitation rate influenced the Mg partitioning, at least in the RP, promoting a high (Mg/Ca)_calcite and D_Mg values in the second time interval. According to recent experimental results, this issue may be related to the influence of the precipitation rate on the D_Mg values in abiotic conditions [51]. In this study we demonstrate, for the first time, the increase in the D_Mg values in calcite at 25 °C, with calcite precipitation rates from 5 × 10⁻¹⁰ to 2.5 × 10⁻⁸ mmol/cm²/s; this range includes the values calculated for the studied rivers herein. Furthermore, according to the control experiments (abiotic experiments) performed by the authors of [7], there was a significant linear increment between the (Mg/Ca)_calcite and precipitation rates (at values from around 5 × 10⁻⁹ to 2.2 × 10⁻⁷ mmol/cm²/s). These results are also consistent with the theoretical fields [58] that predict an increase in the D_Mg values with the precipitation rate.

All these statements suggest a predominant inorganic precipitation rate control in the D_Mg values found in the RP, in which the abiotic parameters (e.g., temperature and CO₂ outgassing) importantly condition the tufa dynamics along the river [19].

6.2.4. Discharge

With respect to the discharge, the influence on the calcite composition is usually explained through changes in the (Mg/Ca)_water [55], due to the residence time of the water in the aquifer: a longer residence time permits the dissolution of higher proportions of Mg from carbonate rocks [53], and it yields higher (Mg/Ca)_water values. The studied rivers for this contribution are primarily fed by groundwater, for which the discharge oscillations are not high, except for the high discharge events linked to the punctual heavy rains (see mean discharge values for these rivers in “Location, geological context, climate and hydrology” section). The six-month accumulated discharge variation throughout the study time did not display any clear six-month oscillations, and it did not present any significant relationships with the (Mg/Ca)_water, except for some high discharge peaks (e.g., Ebrón: Cool 2009–2010, [21]; Añamaza: Cool 2008–2009; [23]) that coincided with decreases in the (Mg/Ca)_water (Figure 4).

6.2.5. Sulphate Content

The onset of the calcite precipitation and the precipitation rate are inhibited by the presence of sulphate [59,60,61,62,63], and this effect could be significant in the rivers with a high sulphate-to-bicarbonate ratio (e.g., from 0.56 to 0.63 in the RA; from 0.18 to 0.33 in the RP and RE; from 0.09 to 0.15 in the RM); however, the authors of [45] did not take this into consideration in their experiment, in which they studied Mg partitioning during the precipitation from sulphate-free solutions.

In this study, the sulphate content in the water had a significant positive correlation with the Mg/Ca ratio of the water (R² = 0.48), and it had a negative correlation with the D_Mg (R² = 0.63) in the RP. In the RM, there was a negative correlation (R² = 0.838) between the sulphate concentration and Mg/Ca ratio, while the sulphate and D_Mg did not show any correlation (R² = 0.008). According to the data for the two sections investigated in the RA, there was no correlation between the dissolved SO₄ and (Mg/Ca)_water (R² = 0.05) or D_Mg (R² = 0.015). In the other investigated streams, the sulphate did not seem to have any influence on any of the measured (or calculated) parameters. According to a study on the effect of dissolved sulphate on the deposition of tufa in the Trabaque River in Spain [63], the presence of sulphate can either limit or favour the precipitation of CaCO₃, depending on the occurrence of the incongruent dissolution of the bedrock dolomite, which subsequently either decreases or increases the D_Mg. However, the sulphate concentrations in our study were much lower than those discussed in [64] or [61], in which the authors found that the presence of sulphate decreased the calcite precipitation rate, which also affected the D_Mg.

Overall, the discussion on the effect of the sulphate ions on the Mg/Ca of the studied stromatolites requires more detailed hydrogeological study, which exceeds the scope of this paper.

6.2.6. Biogenic Influence on Stromatolite Mg/Ca

Biogenic processes, which arise from microbial metabolic activities and/or the presence of extracellular polymeric substances (EPSs), may also affect the D_Mg values through different mechanisms (e.g., the precipitation rate may be controlled by the biofilm growth rate [4,7] or by the presence of compositionally different EPSs [54]). Recently, the authors of [8] found that the spatial evolution of the D_Mg values along Kaisenger Creek (Germany) could be attributed to the changes in the relative proportions of the bioinfluenced and inorganically driven tufa formation processes, with a higher D_Mg when the bioinfluenced processes dominate.

Thus, we expected that the stromatolite formation would be enhanced, and higher D_Mg values would be favoured during the warm periods, whereas we expected lower D_Mg values in the cool periods, with reduced biological activity rates. If this is true, then the changes in the biological activity would move in the same direction as the observed seasonal effects of the inorganic precipitation rate and the decrease in the calcite solubility with higher temperatures.

6.3. Differential Behaviours of the Studied Rivers

6.3.1. Añamaza River

Neither the (Mg/Ca)_water nor the (Mg/Ca)_calcite exhibited seasonal evolution. Both had little variation, except in the last period (Cool 2009–2010), when they were inverse (Figure 4). The (Mg/Ca)_calcite did not follow the temperature oscillations despite the (Mg/Ca)_water stability. The sediment accumulation did not have any relationships with either the (Mg/Ca)_water or (Mg/Ca)_calcite (Figure 4). The Mg-derived Tw hardly showed seasonality (Table S3, Supplementary Material), and it was substantially higher than the measured Tw. Therefore, neither the temperature nor the (Mg/Ca)_water controlled the (Mg/Ca)_calcite. The water discharge in this river is relatively constant throughout the year (minimum ecological discharge), which may explain the lack of seasonal changes in the (Mg/Ca)_water.

6.3.2. Ebrón River

The (Mg/Ca)_calcite exhibited six-month oscillations that were parallel to the measured Tw, even in the season-free evolution (Figure 6). However, the Mg-derived Tw did not fully display the right seasonality, and the Tw values were systematically higher than the measured Tw, with differences of at least 17 °C (Table S3, Supplementary Material). Moreover, although the measured thickness data and (Mg/Ca)_water had six-month oscillating patterns (Figure 4), their season-free evolutions were not parallel to the (Mg/Ca)_calcite. The PWP values did not show an oscillating pattern (Figure 6).

These results indicate that the (Mg/Ca)_calcite is controlled by seasonal factors other than the temperature and (Mg/Ca)_water, which enhance the Mg content in the sediment. The six-month thickness evolution over time was opposite to the (Mg/Ca)_calcite, which researchers have interpreted as a sign of rapid calcite precipitation in other cases [7]. The higher-than-expected (Mg/Ca)_calcite values may reflect the input of the detrital material in the sediment, and likely with six-month variations.

6.3.3. Mesa River

The (Mg/Ca)_calcite did not display a rhythmic pattern; thus, it did not reflect either the (Mg/Ca)_water oscillating pattern or the measured Tw oscillations (Figure 4). The estimated D_Mg and, consequently, the Mg-derived Tw, had higher values in the cool periods and lower values in the warm periods, with substantially higher values than the measured Tw (Table S3, Supplementary Material). Moreover, the Mg-derived Tw displayed an increasing season-free evolution over time that paralleled the (Mg/Ca)_calc and PWP values, but not the measured Tw (Figure 6). Therefore, we can infer that the stromatolite (Mg/Ca)_calcite does not only directly depend on the water temperature but is also controlled by nonseasonal factors that are linked to calcite precipitation, such as changes in the water discharge. Due to the significant correlation between the Al and (Mg/Ca)_calcite, we cannot rule out the influence of a Mg detrital source.

6.3.4. Piedra River

The (Mg/Ca)_calcite follows a six-month pattern, which yielded the best agreement between the Mg-derived Tw and measured Tw (Figure 4), which occurred despite the fact that the (Mg/Ca)_water was not stable and was even inverse with respect to the (Mg/Ca)_calcite for many periods. In addition to the RA, this river had the lowest (Mg/Ca)_calcite values, the lowest D_Mg and the more realistic Mg-derived Tw values.

According to the relationships between the (Mg/Ca)_calcite and other parameters, we distinguished two different time intervals:

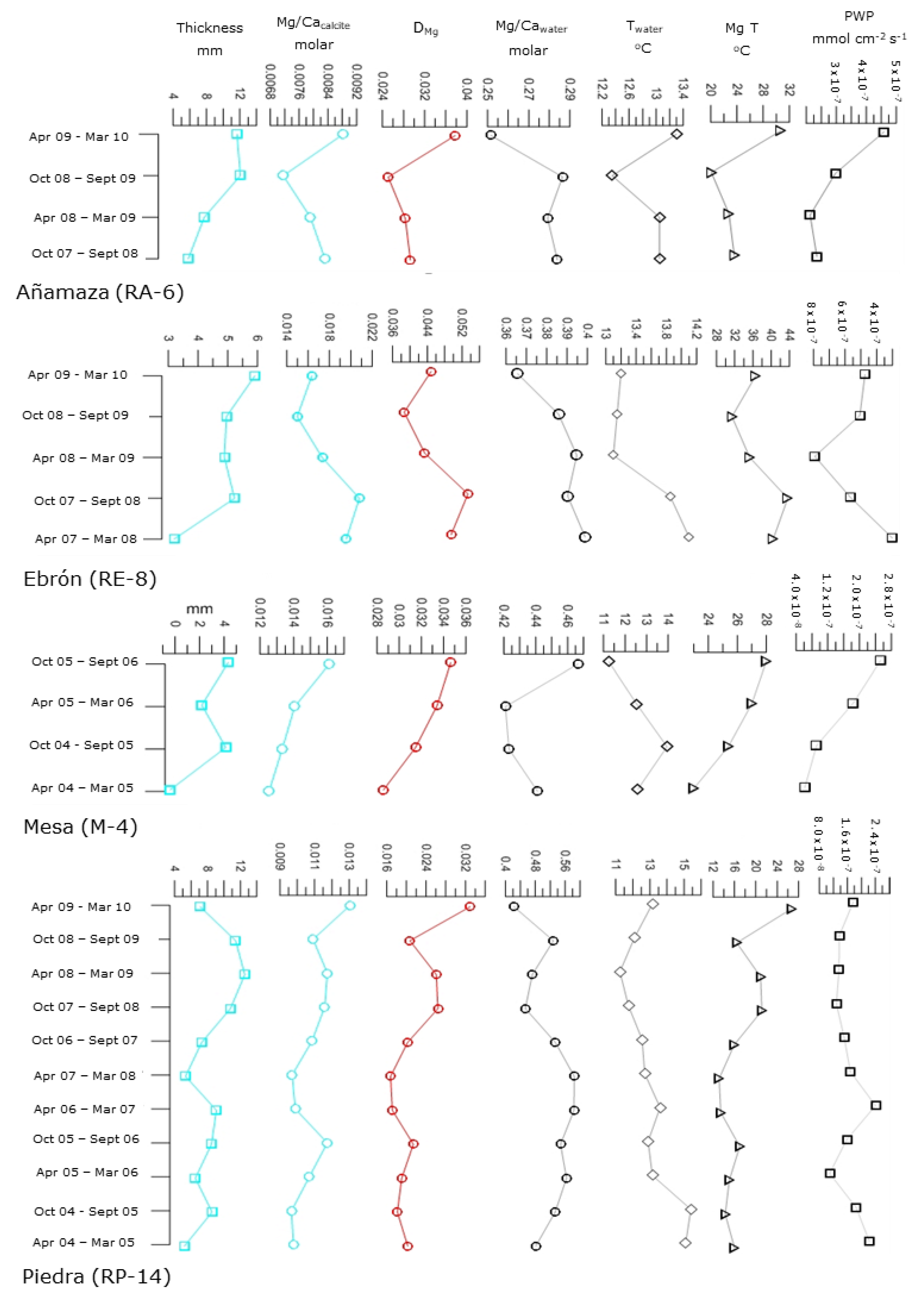
• In the first time interval (from Warm 2004 to Warm 2006), the (Mg/Ca)_water values were higher in the warm periods and had lower values in the cool periods (Figure 4), which highlight the temperature-partitioning effect (higher temperatures allow more Mg to enter into the calcite structure). However, the (Mg/Ca)_calcite oscillations were small, and thus, the empirical D_Mg was flattened (Figure 4), which determined that the Mg-derived Tw did not exhibit seasonal changes. Nevertheless, the corresponding Mg-derived Tw was the closest to the measured Tw as compared with the other rivers (Table S3, Supplementary Material). The PWP and sediment thickness values paralleled the Tw, with wide oscillations (Figure 4). Their season-free evolutions were also roughly parallel (Figure 6). Therefore, the (Mg/Ca)_calcite maintains the general Tw signature, although the parallel evolution of the (Mg/Ca)_water and (Mg/Ca)_calcite can erase the six-month changes in the estimated Tw. We found no evidence of detrital Mg in the corresponding sediment.
• In the second time interval (from Cool 2006–2007 to Cool 2009–2010), the (Mg/Ca)_water pattern did not match the (Mg/Ca)_calcite variation, and it was even opposite to both the calculated and measured Tw. Therefore, the empirical D_Mg oscillations were amplified by the high (Mg/Ca)_water values in the cool periods, when the (Mg/Ca)_calcite was lower. The Tw values obtained from this D_Mg, and from the formula in [45], exhibited the expected six-month oscillations; however, these were systematically higher (Table S3, Supplementary Material) not only in the warm periods, when the estimated D_Mg was too high, but also in the cool periods, which means that the stromatolite (Mg/Ca)_calcite was still higher than it should have been for the (Mg/Ca)_water and water temperature at which it was formed. Despite the six-month oscillation of the Mg-derived Tw, the corresponding season-free evolution was not parallel to the measured Tw (Figure 6). Therefore, another control over Mg entry into the calcite lattice has overprinted the influence of temperature on the (Mg/Ca)_calcite. The significant correlation between the contents in Al and (Mg/Ca)_calcite (Table 3) and the enhanced six-month oscillations of the (Mg/Ca)_calcite (with respect to the first time interval) point to the influence of a Mg detrital source.

In the RP, the six-month thickness and PWP values mimic the (Mg/Ca)_calcite pattern, except in the Cool 2009–2010 period, during which the (Mg/Ca)_calcite and Mg-derived Tw were also anomalous (Figure 4). However, the PWP season-free evolution matched the measured Tw evolution (Figure 6), while the six-month thickness evolution was not well marked in any of the periods of this second time-interval (from Cool 2006–2007 to Cool 2009–2010). During this time interval, the sediment thickness increased and had high values, even for the cool periods. The influence of the growth rate on the Mg content in the sediment through the Mg entry into the calcite in natural systems may be responsible for the increase in the stromatolite (Mg/Ca)_calcite [8], which would at least partially explain the anomalously high Mg-derived Tw. We cannot rule out the presence of a certain amount of Mg of detrital origin, as well as the biological influence.

In summary, the RP has the best adjustment between the Mg-derived and measured Tw. In addition, it also had the lowest estimated D_Mg, which was mostly below 0.025. According to the relationship between the Mg-derived and measured Tw, we distinguished two time intervals. In the first time interval (from Warm 2004 to Warm 2006), the Mg-derived Tw fit quite closely to the measured Tw, although neither of them exhibited seasonal oscillations. In the second time interval (from Cool 2006–2007 to Cool 2009–2010), the Mg-derived Tw displayed six-month changes; however, the values overpassed the measured Tw, and the season-free evolutions were very different. In the first interval, the (Mg/Ca)_calcite reflected the average Tw, although it did not show a seasonal pattern linked to the (Mg/Ca)_water six-month oscillations. In the second time interval, the different influences on the (Mg/Ca)_calcite emphasize the six-month oscillations and magnify the Mg entry into the sediment. The presence of Mg from detrital particles (dolomite and chlorite) could have also contributed to the increase in the (Mg/Ca)_calcite.

6.4. Comparison with Other Systems

Until now, only a few researchers have investigated tufas and water chemistry in enough detail to evaluate the behaviour of the trace elements, such as Mg, as proxies of tufa palaeothermometry through the calculation of the D_Mg (e.g., [6,8]).

We present the mean D_Mg and Tw values obtained in other tufa-depositing rivers and streams from the scarce data in the literature [1,6,8,65] in Figure 7, which we compared with the mean values from the tufa deposits and rivers in this study. In addition, we included the values obtained from travertine deposits in low-temperature thermal waters [66] and speleothems [9,45,67,68] for comparison.

As we can see in Figure 7, the D_Mg values of the stromatolites in the RE were the highest out of the four compared examples, although they were only slightly higher than those found in the Krka River (Slovenia) by the authors of [6]. The partition coefficients in other tufa-depositing rivers (Hvanná, Krka, Gregory and Kainsinger) had an even wider range than of the rivers studied herein. Moreover, the D_Mg values of the compared speleothems had an even a wider range than those in tufas and travertines, although most of them (excluding the data from the cave in Jamaica studied in [67]) are usually lower.

The distribution of the plotted D_Mg-T points in Figure 7 again suggests that the temperature is not the only/main factor that conditions the partition coefficient values for the compared tufas, which explains the unrealistically high temperatures that were obtained from the available D_Mg-T experimental relationships (also presented in Figure 7).

However, the results obtained from the recent travertine deposits at the Embid and Alhama thermal springs almost perfectly fit with the D_Mg-T relationship in [45], as adjusted by the authors of [3]. The low-temperature thermal waters at Embid and Alhama are also dilute waters of the SO₄–HCO₃–Ca type, with constant temperatures (between 27.2 and 32.4 °C at the studied springs) and chemical compositions over time (e.g., [66]). The values of the travertine samples plotted in Figure 7 correspond to the deposits that precipitate near the spring orifice, and in most cases, they are of inorganic origin (or with minor biological participation and without the contribution of detrital sediment). Thus, it appears that the constant temperature and chemical composition (e.g., (Mg/Ca)_water values (mostly around 0.7) [66]) of the waters during the precipitation process would favour the dominant role of the temperature over the Mg partitioning in the travertines, which additionally support the experimental D_Mg-T relationship in [45].

The travertine points in Figure 7 are also close to the Gregory River mean D_Mg and temperature values provided in [1]. This study is the only successful “thermometrical” application of the Mg partitioning in fluvial tufas from the literature. As in other tufa deposits, other factors besides the temperature may influence Mg partitioning (e.g., the biological influence through the effects of EPSs); however, the high deposition temperature in the Gregory River (with a mean value of 27.7 °C for the studied period, which was the highest among all of the compared rivers (Figure 7)) apparently dominates the partitioning process. Whether this high-temperature value is enough to dominate the process or whether the effects of other influencing processes must decrease at the same time should be further studied.

7. Conclusions

We analysed the Mg/Ca ratios of the recent stromatolite records of four rivers on the Iberian Peninsula and the different linked parameters, and we compared them to similar systems. We derived several conclusions from this work:

• We tested the equation in [45] in four different fluvial stromatolite records, and we found limited application. Except for the work of [1], this study is one of the few cases (i.e., Piedra River) in which the Mg-derived water temperatures match the measured ones, in the fluvial environment.
• The degree of the consistency between the Mg-derived water temperatures and measured water temperatures was variable, depending on the studied cases, which indicates that factors other than the temperature influence the (Mg/Ca)_calcite. This result is contrary to the high degree of agreement between the δ¹⁸O-derived and measured temperatures for the same samples.
• The Mg contents of detrital minerals were responsible for the offset of the Mg-derived water temperatures towards higher values than the measured water temperatures in at least one of the studied rivers (Piedra River), in which the correction of the detrital Mg content yielded water temperatures that matched the measured ones.
• In the three other studied cases, we need to consider the interference of several other factors, either seasonal or not, to explain the lack of agreement between the estimated and measured temperatures, such as the changes in the calcite precipitation rates and water discharges. The seasonal behaviour of the Mg_calcite, and its circumstantial correlation with the temperature, may be due to the influence of other seasonal parameters.
• The presence of noncarbonate Mg (and Ca) minerals, and the occurrence of nonequilibrium conditions in natural systems (e.g., variable flow rates, turbulent flows, the presence of biofilms or plant substrates), substantially limit the use of the (Mg/Ca)_cacite as a geochemical thermometer in continental sedimentary environments, except for well-defined systems (e.g., laminar flow, small seasonal variations, and in some hydrothermal systems).
• For the first time, we demonstrate the seasonal variation in the (Mg/Ca)_calcite and D_Mg in fluvial carbonates. Moreover, the seasonal variations in these two parameters are not necessarily associated with the temperature or temperature-dependent parameters, which researchers have recorded in the Piedra River and partially in the Ebrón River stromatolite records.