The Effect of Macroscopic Particle Features on Mineral Dissolution
Abstract
:1. Introduction
2. Materials and Methods
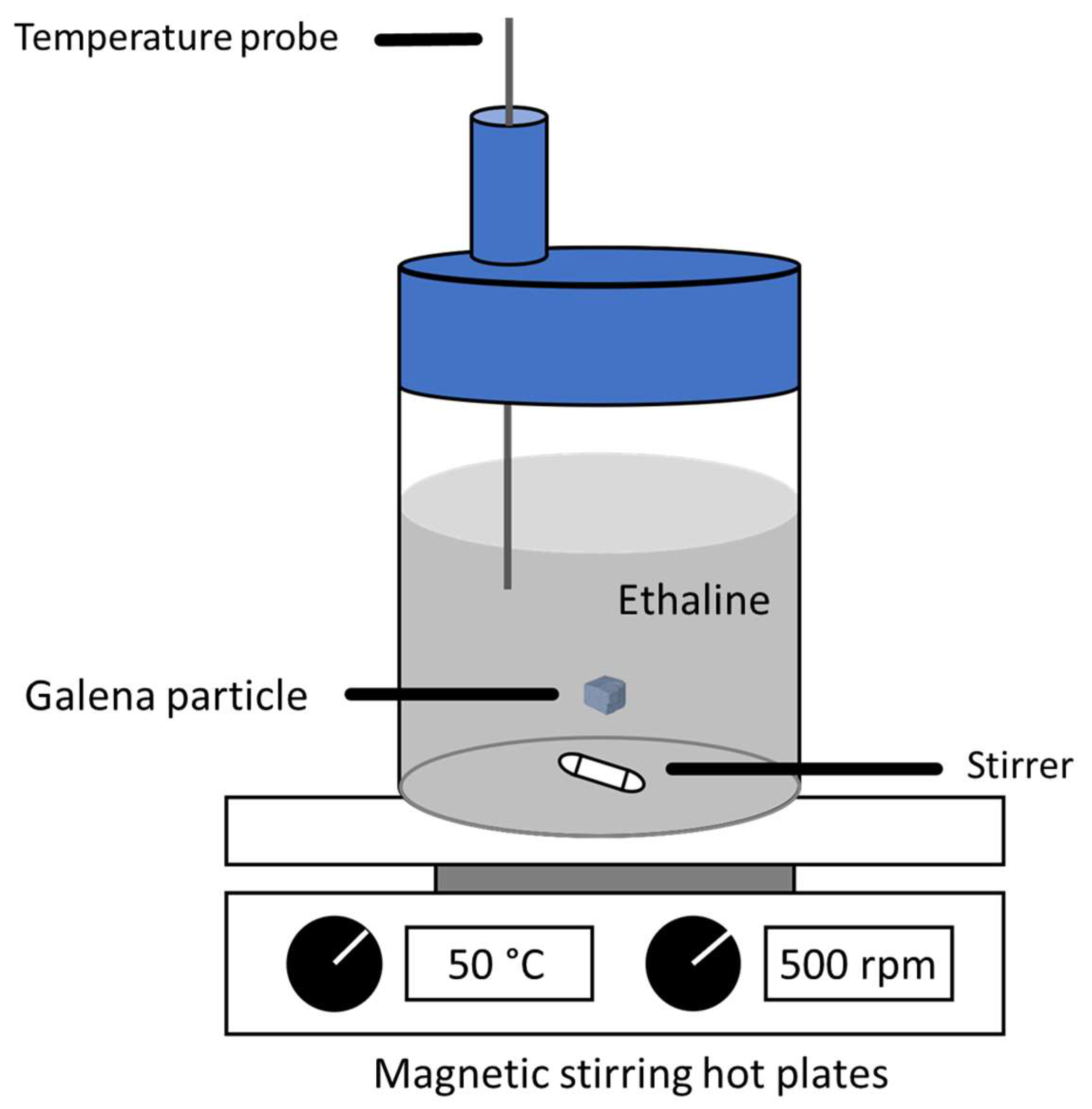
2.1. Materials and Sample Preparation
2.2. Dissolution Experiment
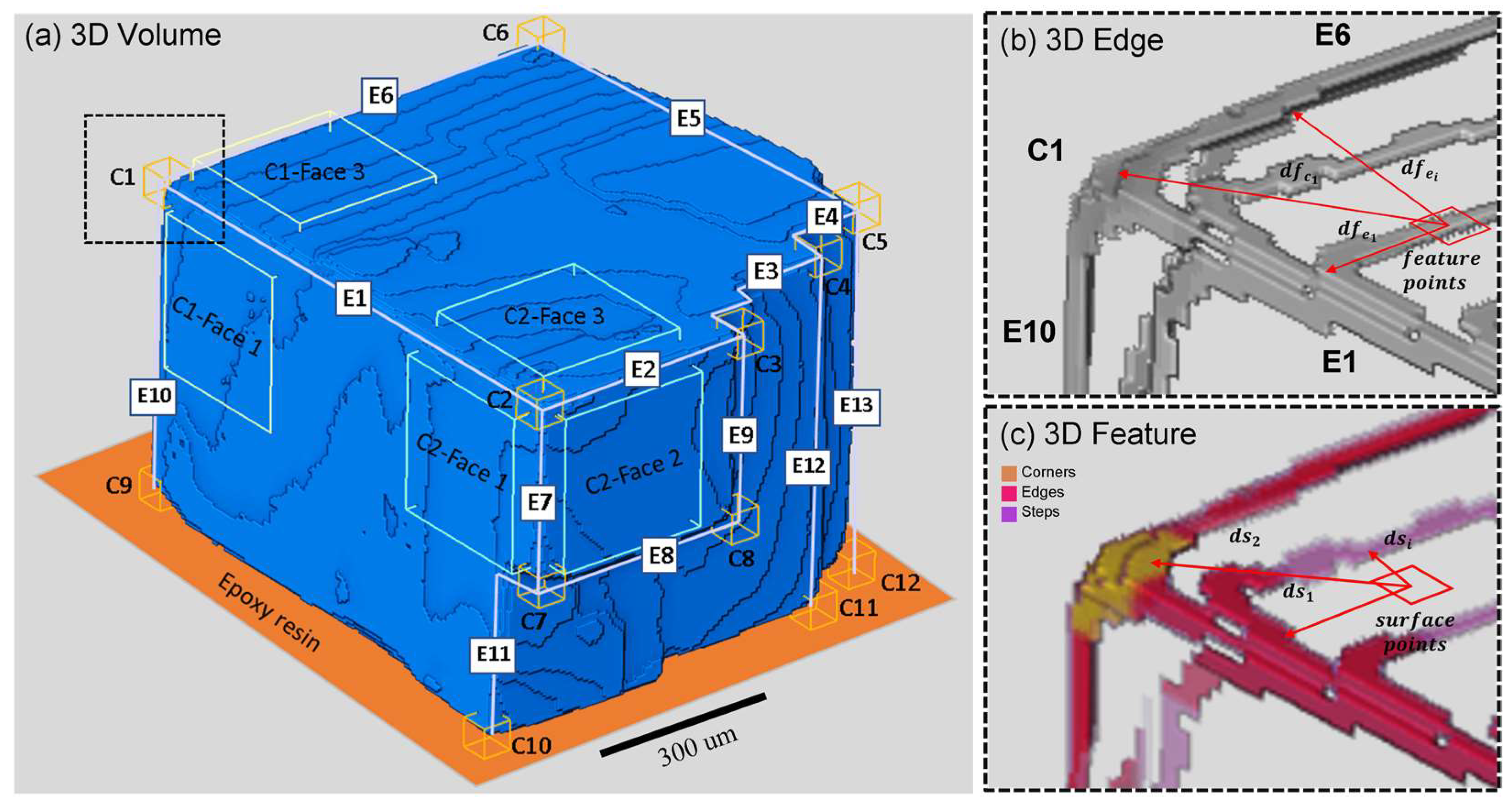
2.3. X-ray Micro-Computed Tomography (CT)
2.4. Reactivity Mapping
3. Results
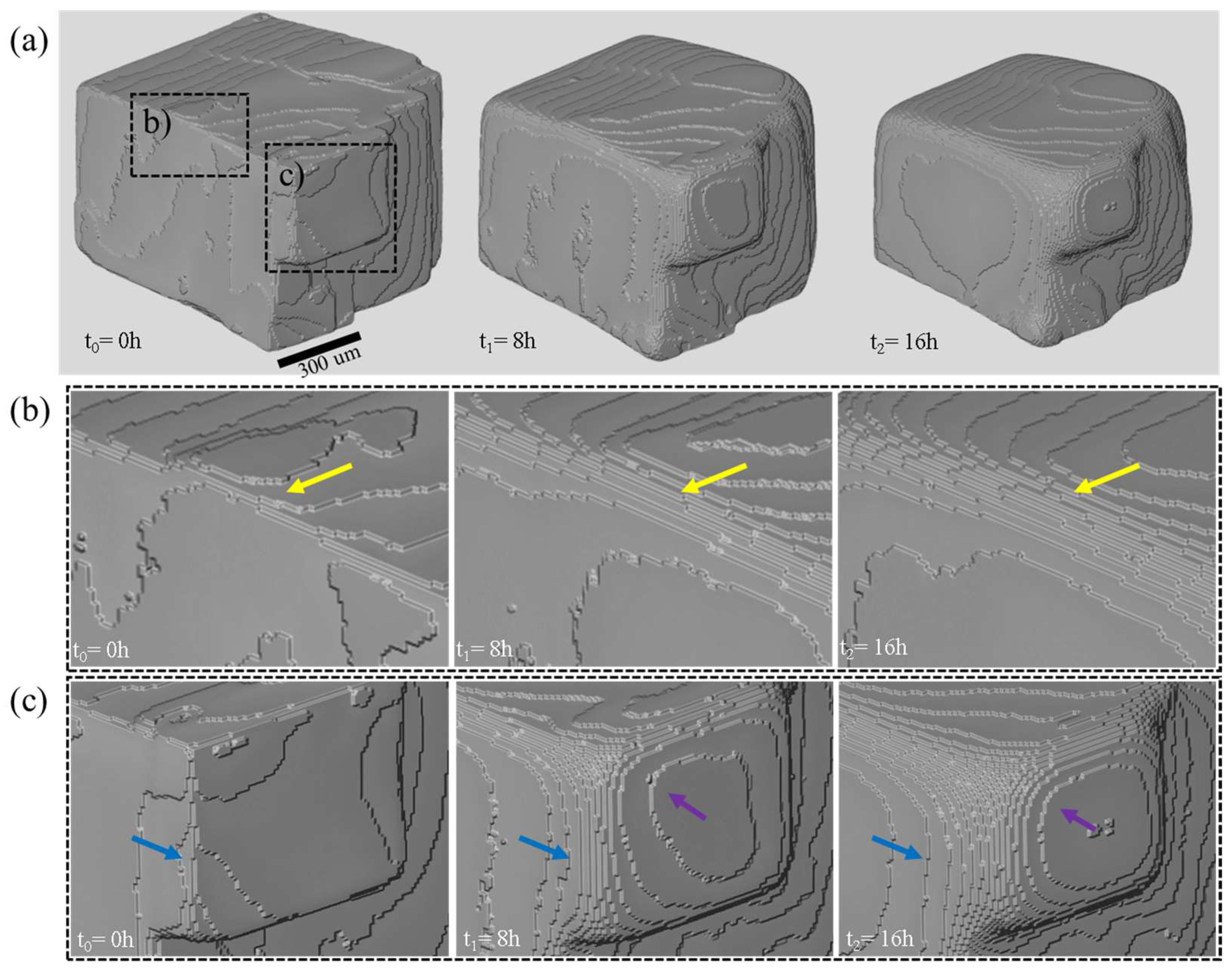
3.1. Dissolution Experiment
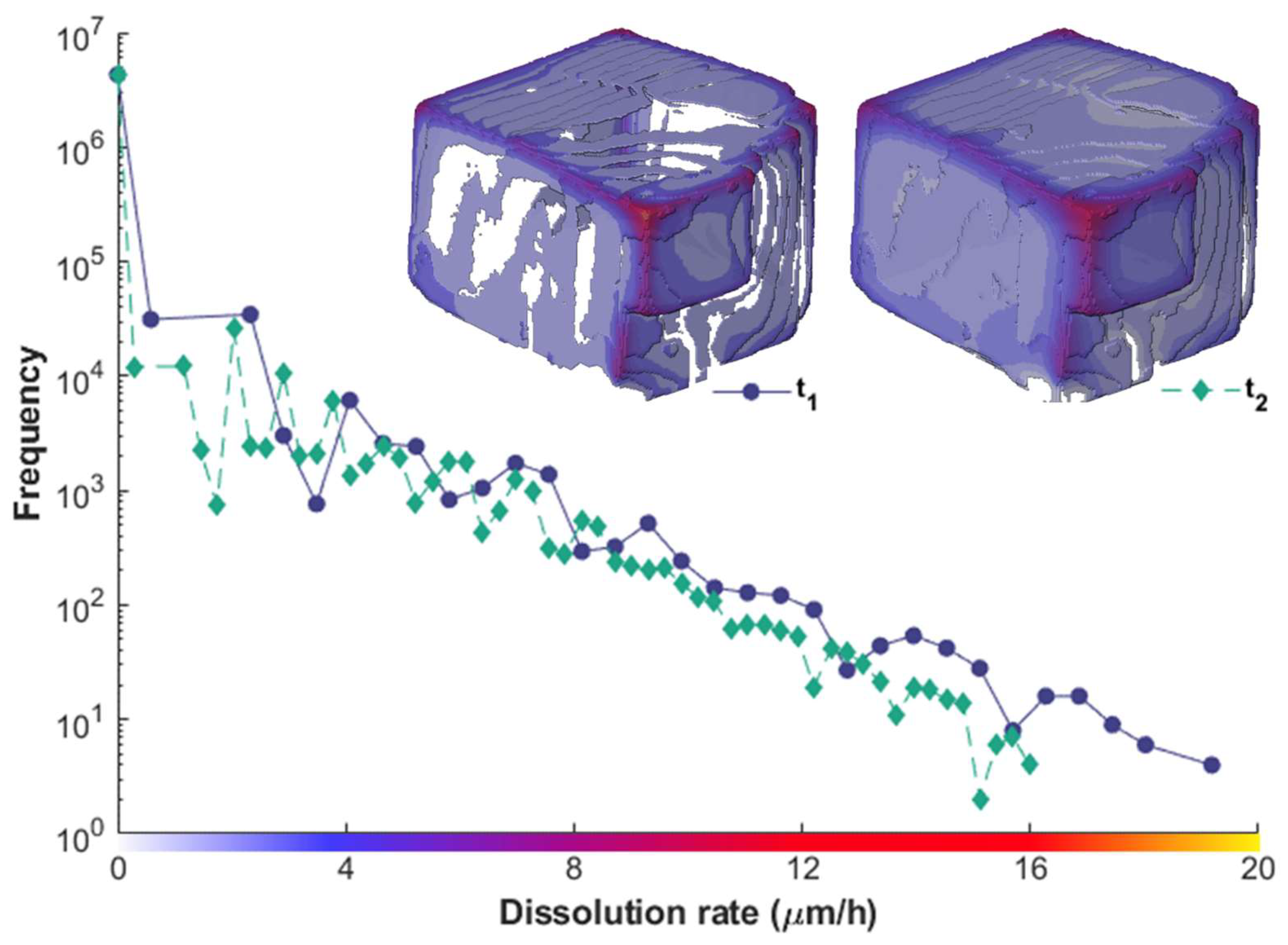
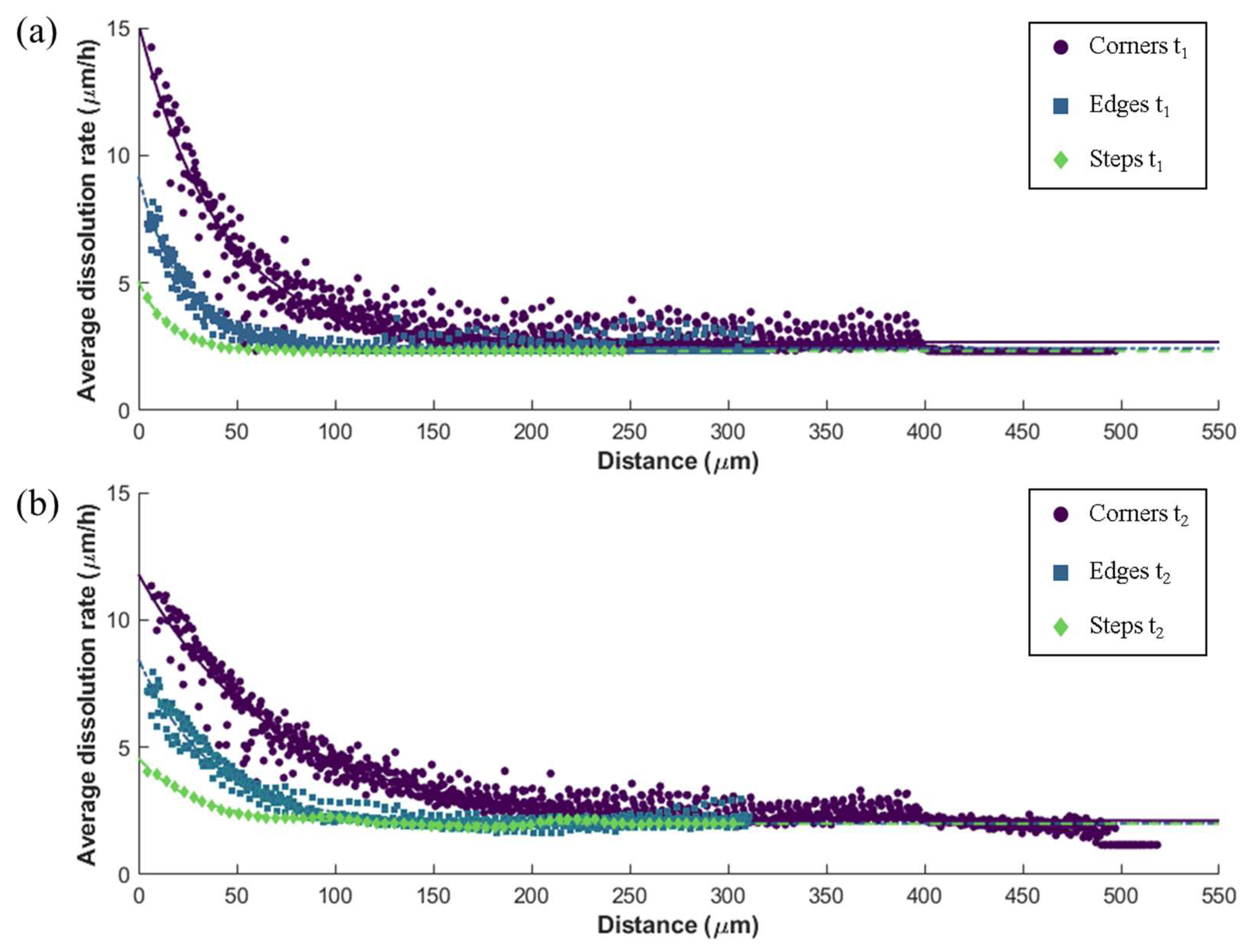
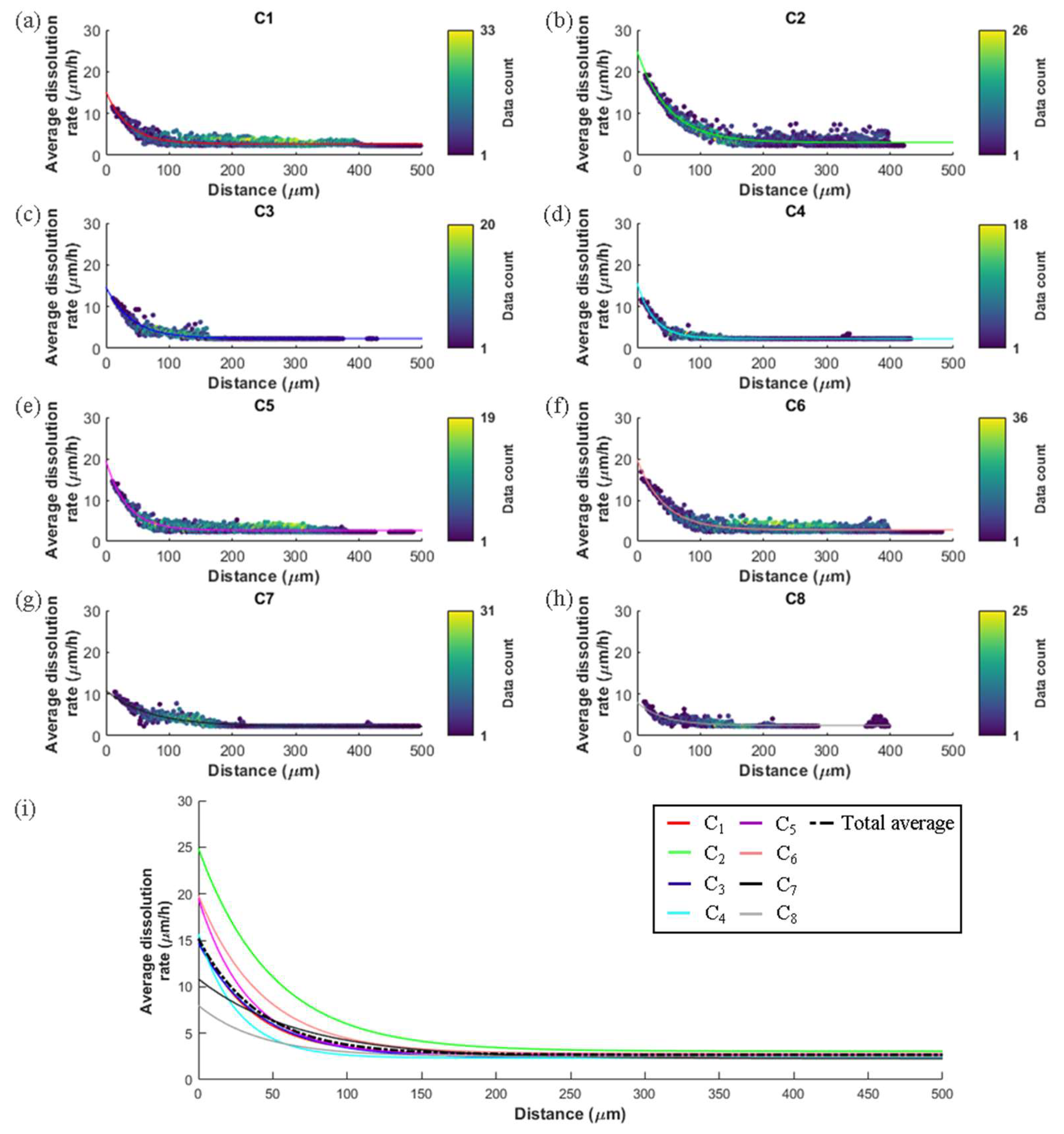
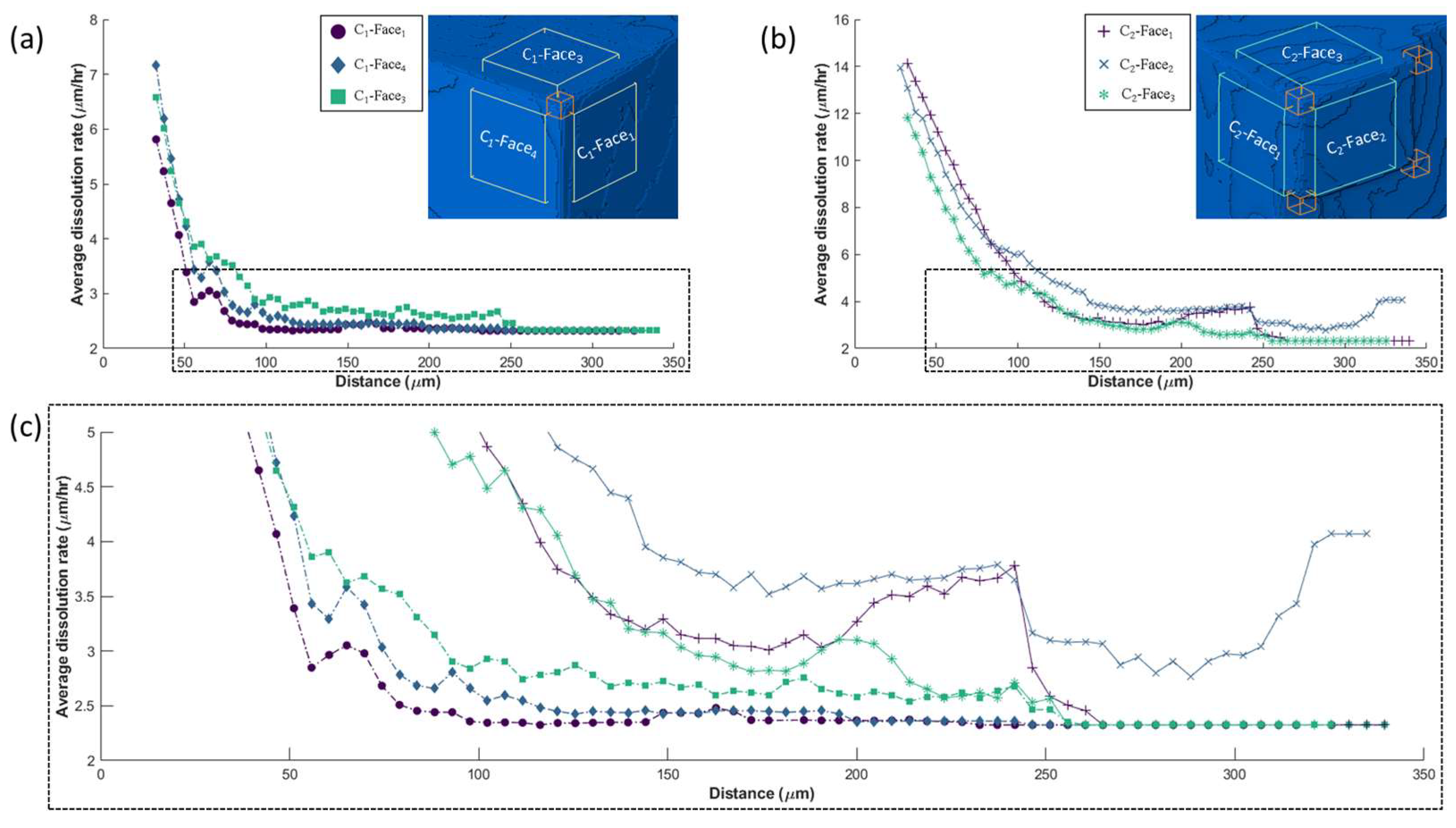
3.2. Relation of Macroscopic Scale Features and Dissolution Rate Spectra
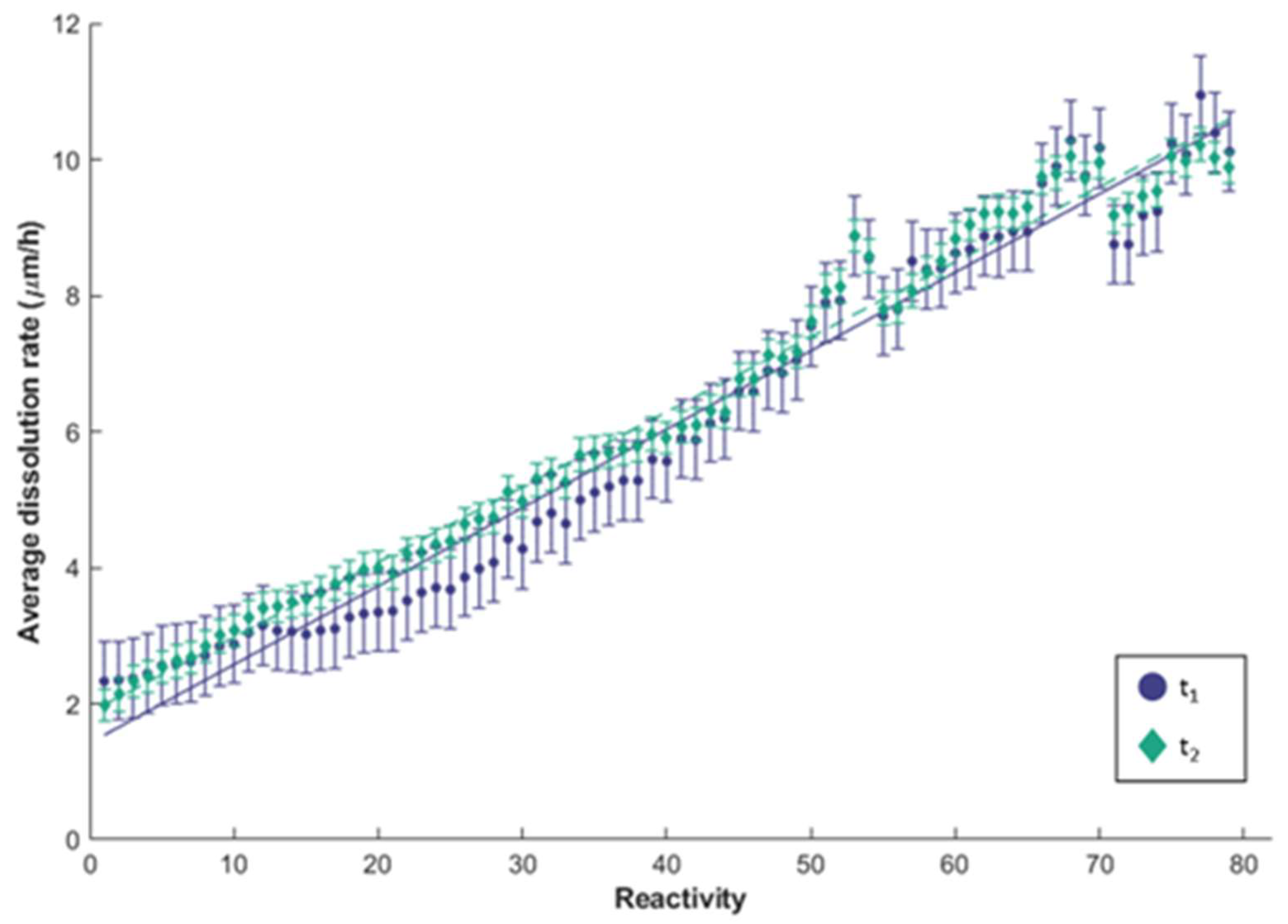
3.3. Reactivity Mapping
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yadav, S.K.; Chakrapani, G.J. Dissolution kinetics of rock–water interactions and its implications. Curr. Sci. 2006, 90, 932–937. [Google Scholar]
- Burton, M.; Bryant, S.L. Surface dissolution: Minimizing groundwater impact and leakage risk simultaneously. Energy Procedia 2009, 1, 3707–3714. [Google Scholar] [CrossRef]
- Iglauer, S.; Paluszny, A.; Pentland, C.H.; Blunt, M.J. Residual CO2 imaged with X-ray micro-tomography. Geophys. Res. Lett. 2011, 38, L21403. [Google Scholar] [CrossRef]
- Jenkin, G.R.; Al-Bassam, A.Z.; Harris, R.C.; Abbott, A.P.; Smith, D.J.; Holwell, D.A.; Chapman, R.J.; Stanley, C.J. The application of deep eutectic solvent ionic liquids for environmentally-friendly dissolution and recovery of precious metals. Miner. Eng. 2016, 87, 18–24. [Google Scholar] [CrossRef]
- Ilhan, S.; Akgün, D. Leaching Kinetics of Mo, Ni, and Al Oxides from Spent Nickel–Molybdenum Hydrodesulfurization Catalyst in H2SO4 Solution. J. Sustain. Metall. 2021, 7, 470–480. [Google Scholar] [CrossRef]
- Dávila-Pulido, G.I.; Salinas-Rodríguez, A.; Carrillo-Pedroza, F.R.; González-Ibarra, A.A.; Méndez-Nonell, J.; Garza-García, M. Leaching kinetics of electronic waste for the recovery of copper: Rate-controlling step and rate process in a multisize particle system. Int. J. Chem. Kinet. 2021, 53, 379–389. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Mees, F.; Jacobs, P.; Rodriguez-Navarro, C. The role of saline solution properties on porous limestone salt weathering by magnesium and sodium sulfates. Env. Geol 2007, 52, 269–281. [Google Scholar] [CrossRef]
- Yuan, K.; Starchenko, V.; Lee, S.S.; de Andrade, V.; Gursoy, D.; Sturchio, N.C.; Fenter, P. Mapping Three-dimensional Dissolution Rates of Calcite Microcrystals: Effects of Surface Curvature and Dissolved Metal Ions. ACS Earth Space Chem. 2019, 3, 833–843. [Google Scholar] [CrossRef]
- Agrawal, P.; Bollermann, T.; Raoof, A.; Iliev, O.; Fischer, C.; Wolthers, M. The contribution of hydrodynamic processes to calcite dissolution rates and rate spectra. Geochim. Et Cosmochim. Acta 2021, 307, 338–350. [Google Scholar] [CrossRef]
- Godinho, J.; Piazolo, S.; Evins, L.Z. Effect of surface orientation on dissolution rates and topography of CaF2. Geochim. Et Cosmochim. Acta 2012, 86, 392–403. [Google Scholar] [CrossRef]
- Arvidson, R.S.; Ertan, I.E.; Amonette, J.E.; Luttge, A. Variation in calcite dissolution rates. Geochim. Et Cosmochim. Acta 2003, 67, 1623–1634. [Google Scholar] [CrossRef]
- Fischer, C.; Kurganskaya, I.; Schäfer, T.; Lüttge, A. Variability of crystal surface reactivity: What do we know? Appl. Geochem. 2014, 43, 132–157. [Google Scholar] [CrossRef]
- Luttge, A.; Arvidson, R.S.; Fischer, C. A Stochastic Treatment of Crystal Dissolution Kinetics. Elements 2013, 9, 183–188. [Google Scholar] [CrossRef]
- Fischer, C.; Arvidson, R.S.; Lüttge, A. How predictable are dissolution rates of crystalline material? Geochim. Et Cosmochim. Acta 2012, 98, 177–185. [Google Scholar] [CrossRef]
- Saldi, G.D.; Voltolini, M.; Knauss, K.G. Effects of surface orientation, fluid chemistry and mechanical polishing on the variability of dolomite dissolution rates. Geochim. Et Cosmochim. Acta 2017, 206, 94–111. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Putnis, C.V.; Jiménez-López, C.; Rodriguez-Navarro, C. An atomic force microscopy study of calcite dissolution in saline solutions: The role of magnesium ions. Geochim. Et Cosmochim. Acta 2009, 73, 3201–3217. [Google Scholar] [CrossRef]
- Godinho, J.R.A.; Gerke, K.M.; Stack, A.G.; Lee, P.D. The dynamic nature of crystal growth in pores. Sci. Rep. 2016, 6, 33086. [Google Scholar] [CrossRef]
- Kurganskaya, I.; Trofimov, N.; Luttge, A. A Kinetic Monte Carlo Approach to Model Barite Dissolution: The Role of Reactive Site Geometry. Minerals 2022, 12, 639. [Google Scholar] [CrossRef]
- Bibi, I.; Arvidson, R.; Fischer, C.; Lüttge, A. Temporal Evolution of Calcite Surface Dissolution Kinetics. Minerals 2018, 8, 256. [Google Scholar] [CrossRef]
- Bollermann, T.; Fischer, C. Temporal evolution of dissolution kinetics of polycrystalline calcite. Am. J. Sci. 2020, 320, 53–71. [Google Scholar] [CrossRef]
- Kahl, W.-A.; Yuan, T.; Bollermann, T.; Bach, W.; Fischer, C. Crystal surface reactivity analysis using a combined approach of X-ray micro-computed tomography and vertical scanning interferometry. Am. J. Sci. 2020, 320, 27–52. [Google Scholar] [CrossRef]
- Noiriel, C.; Oursin, M.; Saldi, G.; Haberthür, D. Direct Determination of Dissolution Rates at Crystal Surfaces Using 3D X-ray Microtomography. ACS Earth Space Chem. 2019, 3, 100–108. [Google Scholar] [CrossRef]
- Noiriel, C.; Oursin, M.; Daval, D. Examination of crystal dissolution in 3D: A way to reconcile dissolution rates in the laboratory? Geochim. Et Cosmochim. Acta 2020, 273, 1–25. [Google Scholar] [CrossRef]
- Lin, Q.; Neethling, S.J.; Courtois, L.; Dobson, K.J.; Lee, P.D. Multi-scale quantification of leaching performance using X-ray tomography. Hydrometallurgy 2016, 164, 265–277. [Google Scholar] [CrossRef]
- Noiriel, C.; Luquot, L.; Madé, B.; Raimbault, L.; Gouze, P.; van der Lee, J. Changes in reactive surface area during limestone dissolution: An experimental and modelling study. Chem. Geol. 2009, 265, 160–170. [Google Scholar] [CrossRef]
- Winardhi, C.W.; Da Godinho, J.R.A.; Rachmawati, C.; Achin, I.D.; Iturbe, A.U.; Frisch, G.; Gutzmer, J. A particle-based approach to predict the success and selectivity of leaching processes using ethaline—Comparison of simulated and experimental results. Hydrometallurgy 2022, 211, 105869. [Google Scholar] [CrossRef]
- White, A.F.; Brantley, S.L. The effect of time on the weathering of silicate minerals: Why do weathering rates differ in the laboratory and field? Chem. Geol. 2003, 202, 479–506. [Google Scholar] [CrossRef]
- Lasaga, A.C.; Luttge, A. Variation of crystal dissolution rate based on a dissolution stepwave model. Science 2001, 291, 2400–2404. [Google Scholar] [CrossRef] [PubMed]
- Lasaga, A.C.; Lüttge, A. A model for crystal dissolution. Ejm 2003, 15, 603–615. [Google Scholar] [CrossRef]
- Spathariotis, S.; Peeters, N.; Ryder, K.S.; Abbott, A.P.; Binnemans, K.; Riaño, S. Separation of iron(iii), zinc(ii) and lead(ii) from a choline chloride-ethylene glycol deep eutectic solvent by solvent extraction. RSC Adv. 2020, 10, 33161–33170. [Google Scholar] [CrossRef] [PubMed]
- Godinho, J.R.A.; Stack, A.G. Growth Kinetics and Morphology of Barite Crystals Derived from Face-Specific Growth Rates. Cryst. Growth Des. 2015, 15, 2064–2071. [Google Scholar] [CrossRef]
- Rohlfs, R.; Fischer, C.; Kurganskaya, I.; Luttge, A. Crystal Dissolution Kinetics Studied by a Combination of Monte Carlo and Voronoi Methods. Minerals 2018, 8, 133. [Google Scholar] [CrossRef]
- Schulz, B.; Sandmann, D.; Gilbricht, S. SEM-Based Automated Mineralogy and Its Application in Geo- and Material Sciences. Minerals 2020, 10, 1004. [Google Scholar] [CrossRef]
- Godinho, J.R.A.; Grilo, B.L.D.; Hellmuth, F.; Siddique, A. Mounted Single Particle Characterization for 3D Mineralogical Analysis—MSPaCMAn. Minerals 2021, 11, 947. [Google Scholar] [CrossRef]


| Time Step | Time (h) | Surface Area (µm2) | Volume (µm3) | (mol·h−1) | (µm·h−1) |
|---|---|---|---|---|---|
| t0 | 0 | 2.09 × 106 | 2.25 × 108 | - | - |
| t1 | 8 | 1.93 × 106 | 2.10 × 108 | 6.16 × 10−4 | 0.97 |
| t2 | 16 | 1.81 × 106 | 1.94 × 108 | 6.23 × 10−4 | 0.99 |
| Time Steps | Macroscopic Feature | a (µm·h−1) | b (µm−1) | c (µm·h−1) | R2 | RMSE |
|---|---|---|---|---|---|---|
| t1 | Corners | 12.5 | −0.0245 | 2.68 | 0.9054 | 0.5493 |
| Edges | 6.75 | −0.0441 | 2.44 | 0.9167 | 0.2952 | |
| Steps | 2.74 | −0.0632 | 2.33 | 0.9982 | 0.0172 | |
| t2 | Corners | 9.68 | −0.0143 | 2.11 | 0.9353 | 0.4694 |
| Edges | 6.45 | −0.0268 | 2.00 | 0.9575 | 0.2597 | |
| Steps | 2.57 | −0.0336 | 1.99 | 0.9634 | 0.09255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winardhi, C.W.; Godinho, J.R.d.A.; Gutzmer, J. The Effect of Macroscopic Particle Features on Mineral Dissolution. Minerals 2023, 13, 253. https://doi.org/10.3390/min13020253
Winardhi CW, Godinho JRdA, Gutzmer J. The Effect of Macroscopic Particle Features on Mineral Dissolution. Minerals. 2023; 13(2):253. https://doi.org/10.3390/min13020253
Chicago/Turabian StyleWinardhi, Chandra Widyananda, Jose Ricardo da Assuncao Godinho, and Jens Gutzmer. 2023. "The Effect of Macroscopic Particle Features on Mineral Dissolution" Minerals 13, no. 2: 253. https://doi.org/10.3390/min13020253
APA StyleWinardhi, C. W., Godinho, J. R. d. A., & Gutzmer, J. (2023). The Effect of Macroscopic Particle Features on Mineral Dissolution. Minerals, 13(2), 253. https://doi.org/10.3390/min13020253






