On the Nature of Hydrophobic Organic Compound Adsorption to Smectite Minerals Using the Example of Hexachlorobenzene-Montmorillonite Interactions
Abstract
1. Introduction
2. Methodology
2.1. Structural Models
2.2. Computational Details
2.3. Processing of the Results
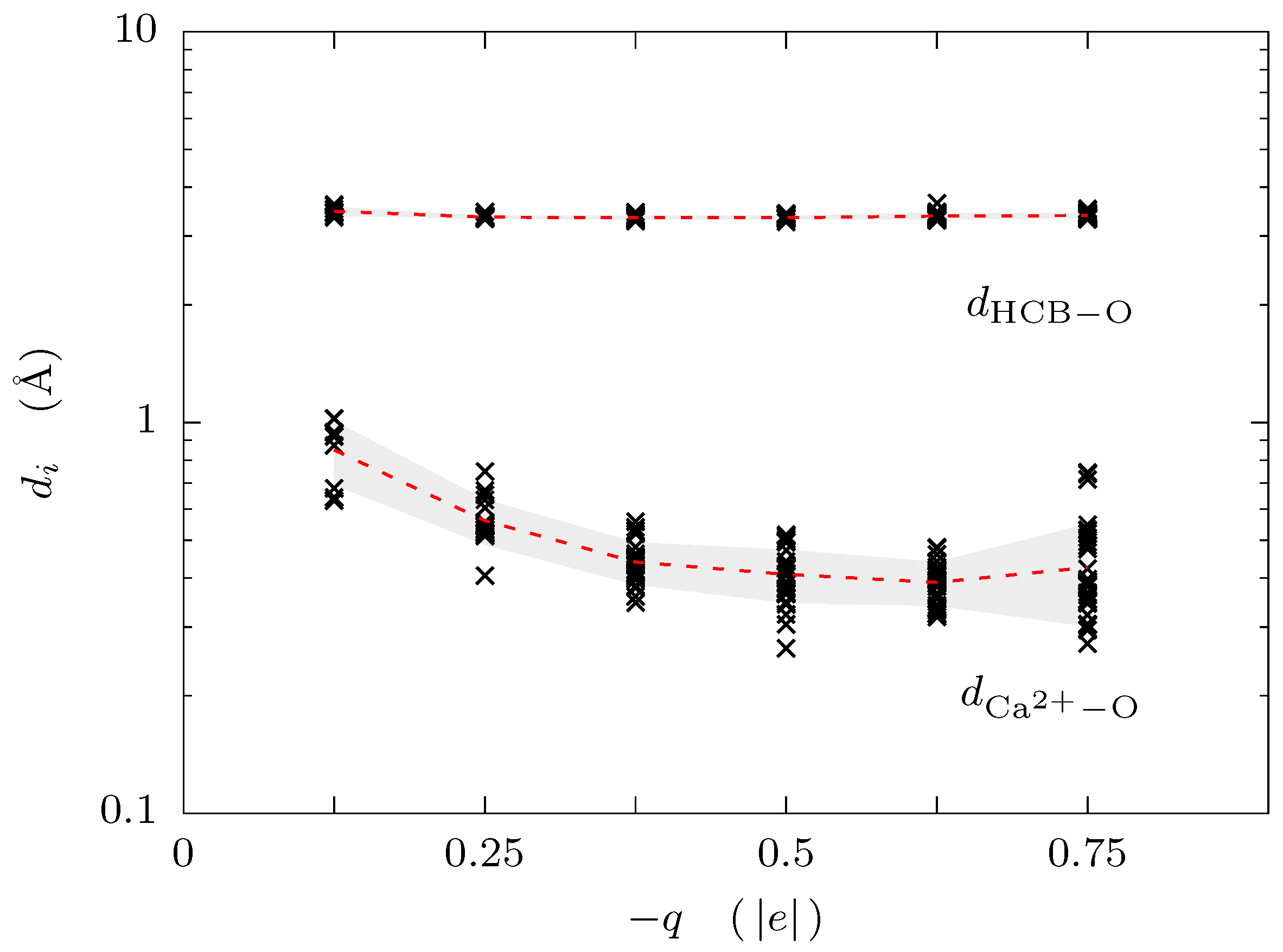
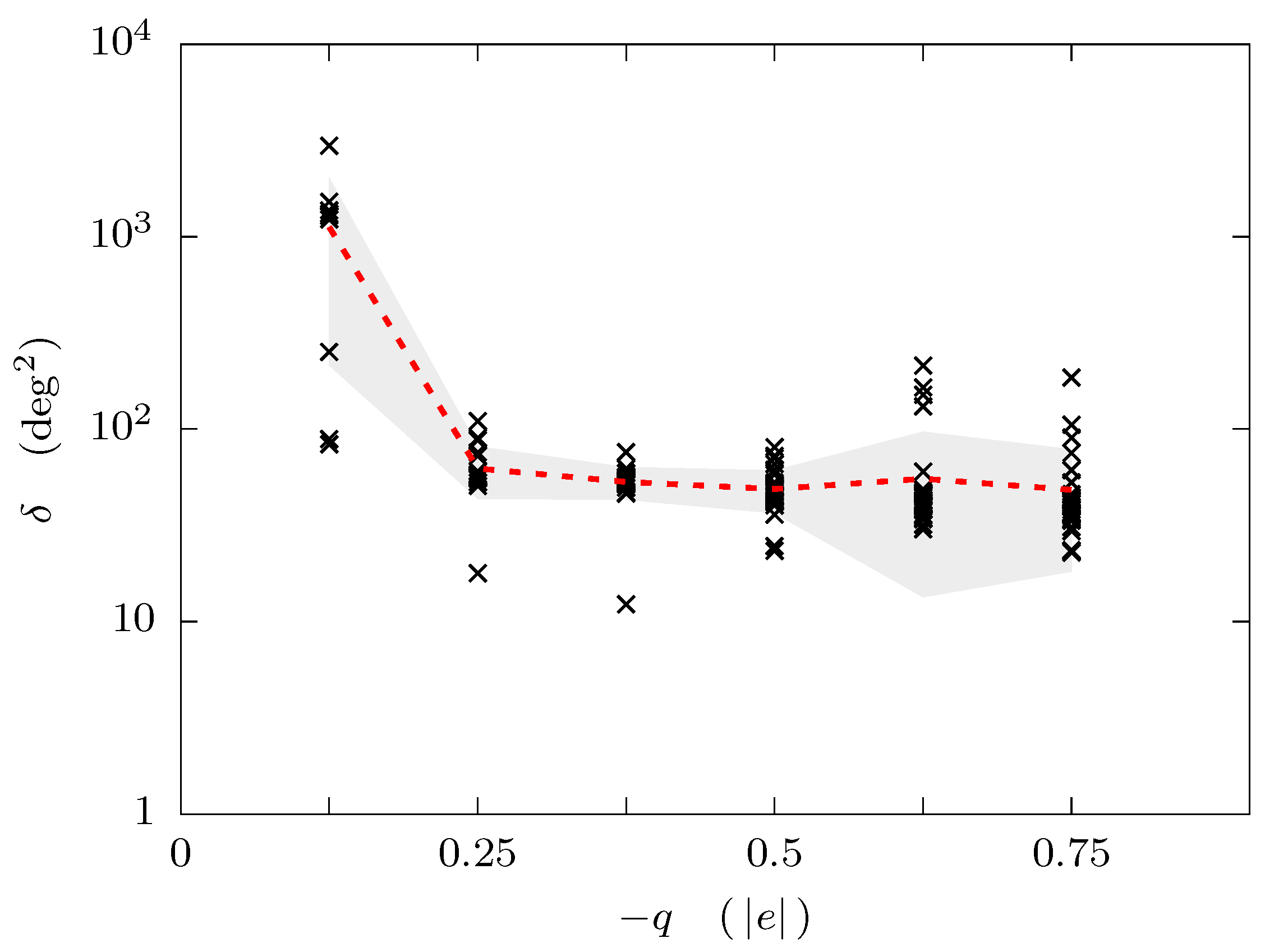
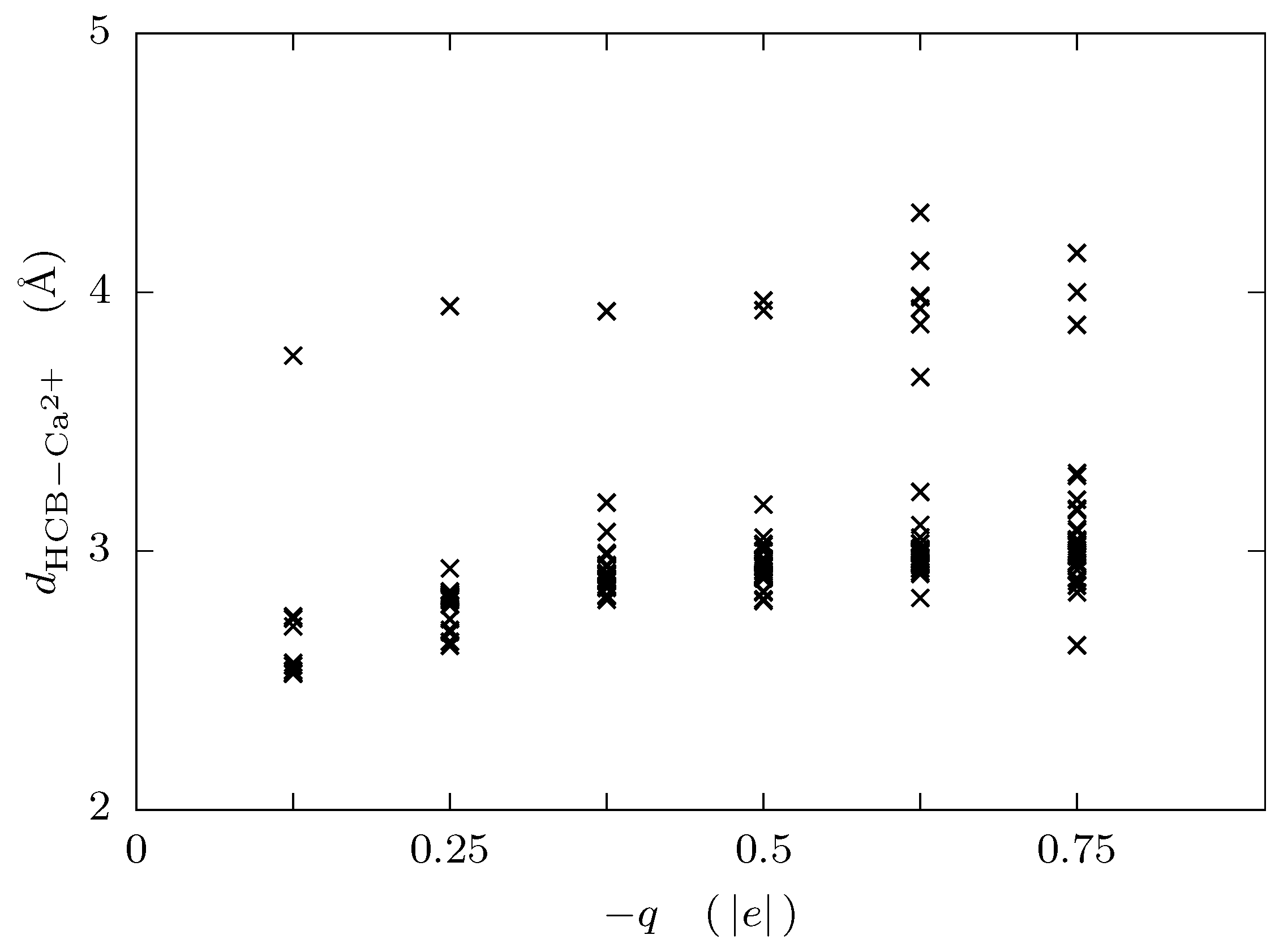
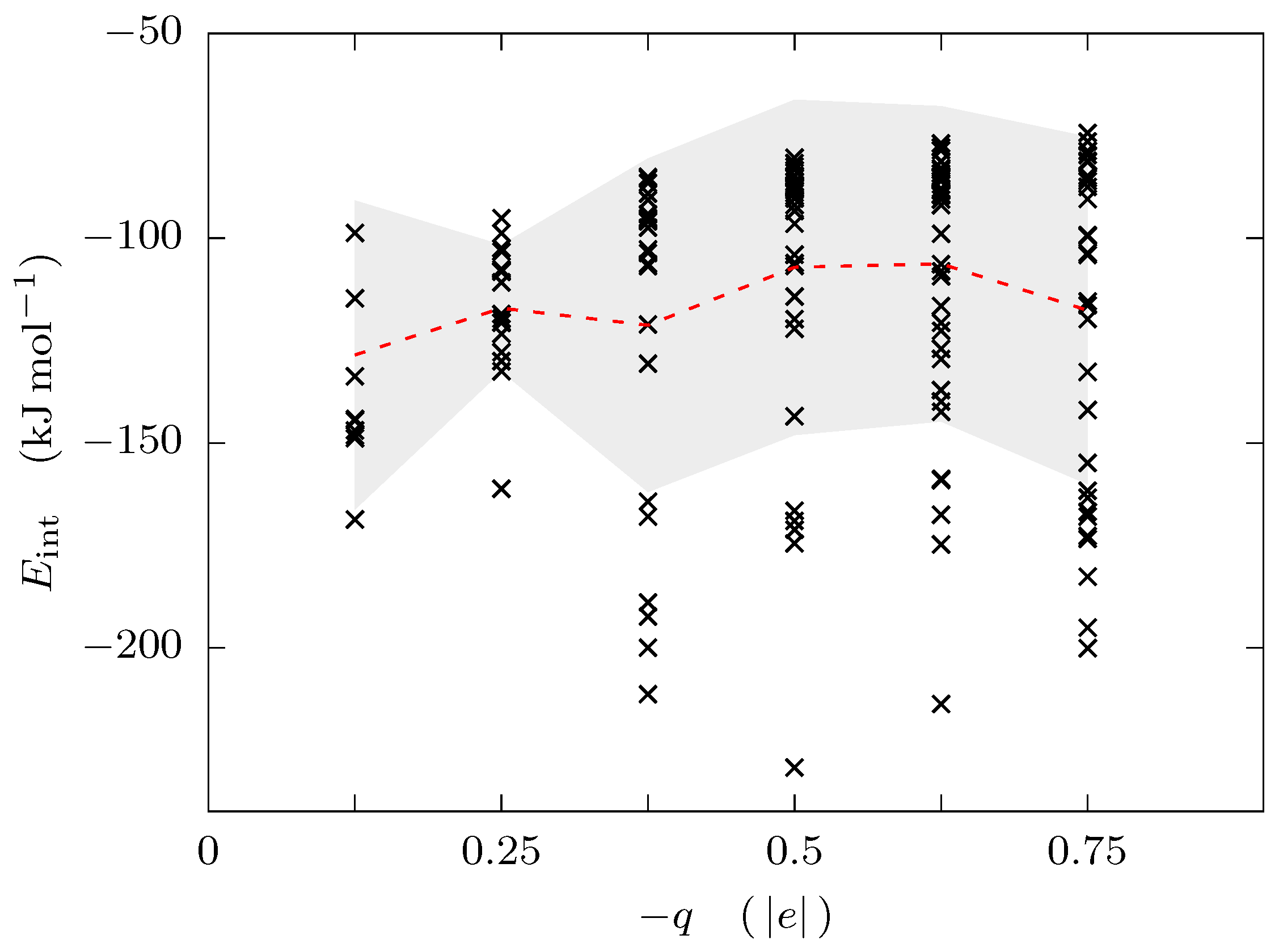
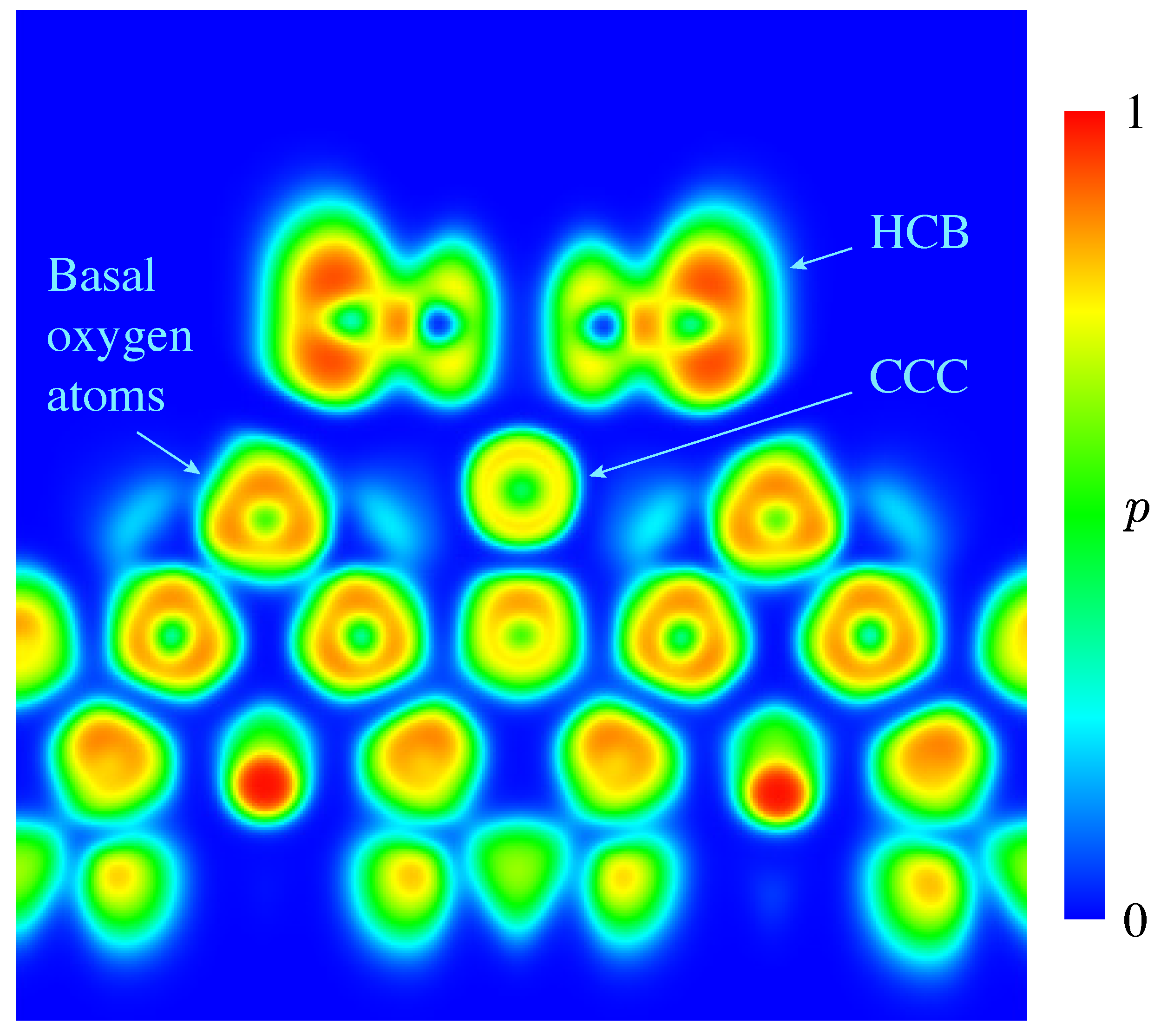
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barber, J.L.; Sweetman, A.J.; van Wijk, D.; Jones, K.C. Hexachlorobenzene in the global environment: Emissions, levels, distribution, trends and processes. Sci. Total Environ. 2005, 349, 1–44. [Google Scholar] [CrossRef]
- Brahushi, F.; Kengara, F.O.; Song, Y.; Jiang, X.; Munch, J.C.; Wang, F. Fate Processes of Chlorobenzenes in Soil and Potential Remediation Strategies: A Review. Pedosphere 2017, 27, 407–420. [Google Scholar] [CrossRef]
- Haynes, W.M.; Lide, D.R. Handbook of Chemistry and Physics, 95th ed.; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Meijer, S.N.; Ockenden, W.A.; Sweetman, A.; Breivik, K.; Grimalt, J.O.; Jones, K.C. Global distribution and budget of PCBs and HCB in background surface soils: Implications for sources and environmental processes. Environ. Sci. Technol. 2003, 37, 667–672. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Ning, P.; Xing, B. Part IV—Sorption of hydrophobic organic contaminants. Environ. Sci. Pollut. Res. 2008, 15, 554–564. [Google Scholar] [CrossRef]
- Karickhoff, S.W.; Brown, D.S.; Scott, T.A. Sorption of hydrophobic pollutants on natural sediments. Water Res. 1979, 13, 241–248. [Google Scholar] [CrossRef]
- Chiou, C.T.; Malcolm, R.L.; Brinton, T.I.; Kile, D.E. Water solubility enhancement of some organic pollutants and pesticides by dissolved humic and fulvic acids. Environ. Sci. Technol. 1986, 20, 502–508. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Thiele-Bruhn, S.; Aziz, S.G.; Hilal, R.H.; Elroby, S.A.; Al-Youbi, A.O.; Leinweber, P.; Kühn, O. Interaction of polar and nonpolar organic pollutants with soil organic matter: Sorption experiments and molecular dynamics simulation. Sci. Total Environ. 2015, 508, 276–287. [Google Scholar] [CrossRef]
- Böhm, L.; Düring, R.A.; Bruckert, H.J.; Schlechtriem, C. Can solid-phase microextraction replace solvent extraction for water analysis in fish bioconcentration studies with highly hydrophobic organic chemicals? Environ. Toxicol. Chem. 2017, 36, 2887–2894. [Google Scholar] [CrossRef]
- Böhm, L.; Schlechtriem, C.; Düring, R.A. Sorption of highly hydrophobic organic chemicals to organic matter relevant for fish bioconcentration studies. Environ. Sci. Technol. 2016, 50, 8316–8323. [Google Scholar] [CrossRef]
- Böhm, L.; Grančič, P.; Scholtzová, E.; Heyde, B.J.; Düring, R.A.; Siemens, J.; Gerzabek, M.H.; Tunega, D. Adsorption of the hydrophobic organic pollutant hexachlorobenzene to phyllosilicate minerals. Environ. Sci. Pollut. Res. Int. 2022. [Google Scholar] [CrossRef]
- Ferrage, E. Investigation of the Interlayer Organization of Water and Ions In Smectite from the Combined Use of Diffraction Experiments and Molecular Simulations. A Review of Methodology, Applications, And Perspectives. Clays Clay Miner. 2016, 64, 348–373. [Google Scholar] [CrossRef]
- Anthony, J.W.; Bideaux, R.A.; Bladh, K.W.; Nichols, M.C. Handbook of Mineralogy; Mineralogical Society of America: Chantilly, VA, USA, 2003. [Google Scholar]
- Bhattacharyya, K.G.; Gupta, S.S. Adsorption of a Few Heavy Metals on Natural and Modified Kaolinite and Montmorillonite: A Review. Adv. Colloid Interface Sci. 2008, 140, 114–131. [Google Scholar] [CrossRef] [PubMed]
- Meier, L.P.; Nüesch, R. The Lower Cation Exchange Capacity Limit of Montmorillonite. J. Colloid Interface Sci. 1999, 217, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Chang, J.; Liu, X.; Xue, Q.; Fu, J.; Zhang, A. Interfacial formation of environmentally persistent free radicals—A theoretical investigation on pentachlorophenol activation on montmorillonite in PM2.5. Ecotoxicol. Environ. Saf. 2019, 169, 623–630. [Google Scholar] [CrossRef]
- Jia, H.; Zhao, S.; Shi, Y.; Zhu, L.; Wang, C.; Sharma, V.K. Transformation of Polycyclic Aromatic Hydrocarbons and Formation of Environmentally Persistent Free Radicals on Modified Montmorillonite: The Role of Surface Metal Ions and Polycyclic Aromatic Hydrocarbon Molecular Properties. Environ. Sci. Technol. 2018, 52, 5725–5733. [Google Scholar] [CrossRef]
- Sainz-Díaz, C.I.; Francisco-Márquez, M.; Vivier-Bunge, A. Molecular structure and spectroscopic properties of polyaromatic heterocycles by first principle calculations: Spectroscopic shifts with the adsorption of thiophene on phyllosilicate surface. Theor. Chem. Acc. 2009, 125, 83–95. [Google Scholar] [CrossRef]
- Hu, E.; Zhao, X.; Pan, S.; Ye, Z.; He, F. Sorption of nonionic aromatic organics to mineral micropores: Interactive effect of cation hydration and mineral charge density. Environ. Sci. Technol. 2019, 53, 3067–3077. [Google Scholar] [CrossRef]
- Pašalić, H.; Aquino, A.J.A.; Tunega, D.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. Cation-π interactions in competition with cation microhydration: A theoretical study of alkali metal cation–pyrene complexes. J. Mol. Model. 2017, 23, 131. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, Y.; Li, H.; Zheng, S.; Zhu, D. Probing the Specific Sorption Sites on Montmorillonite Using Nitroaromatic Compounds and Hexafluorobenzene. Environ. Sci. Technol. 2011, 45, 2209–2216. [Google Scholar] [CrossRef]
- Viani, A.; Gualtieri, A.F.; Artioli, G. The Nature of Dsorder in Montmorillonite by Simulation of X-ray Powder Patterns. Am. Mineral. 2002, 87, 966–975. [Google Scholar] [CrossRef]
- Loewenstein, W. The Distribution of Aluminum in the Tetrahedra of Silicates and Aluminates. Am. Mineral. 1954, 39, 92–96. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Bučko, T.; Hafner, J.; Ángyán, J.G. Geometry optimization of periodic systems using internal coordinates. J. Chem. Phys. 2005, 122, 124508. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Bučko, T.; Lebègue, S.; Hafner, J.; Ángyán, J.G. Tkatchenko-Scheffler van der Waals correction method with and without self-consistent screening applied to solids. Phys. Rev. B 2013, 87, 064110. [Google Scholar] [CrossRef]
- Tunega, D.; Bučko, T.; Zaoui, A. Assessment of ten DFT methods in predicting structures of sheet silicates: Importance of dispersion corrections. J. Chem. Phys. 2012, 137, 114105. [Google Scholar] [CrossRef]
- Tunega, D.; Zaoui, A. Adsorption of polycyclic aromatic hydrocarbons on FeOOH polymorphs: A theoretical study. Surf. Sci. 2021, 706, 121795. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.R.; Becke, A.D. A post-Hartree–Fock model of intermolecular interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections. J. Chem. Phys. 2006, 124, 174104. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Chatterjee, A.; Iwasaki, T.; Ebina, T.; Miyamoto, A. A DFT study on clay–cation–water interaction in montmorillonite and beidellite. Comput. Mater. Sci. 1999, 14, 119–124. [Google Scholar] [CrossRef]
- Chatterjee, A.; Iwasaki, T.; Ebina, T. A Novel Method to Correlate Layer Charge and the Catalytic Activity of 2:1 Dioctahedral Smectite Clays in Terms of Binding the Interlayer Cation Surrounded by Monohydrate. J. Phys. Chem. A 2000, 104, 8216–8223. [Google Scholar] [CrossRef]
- Li, H.; Kang, T.; Zhang, B.; Zhang, J.; Ren, J. Influence of interlayer cations on structural properties of montmorillonites: A dispersion-corrected density functional theory study. Comput. Mater. Sci. 2016, 117, 33–39. [Google Scholar] [CrossRef]
- Seppälä, A.; Puhakka, E.; Olin, M. Effect of layer charge on the crystalline swelling of Na+, K+ and Ca2+ montmorillonites: DFT and molecular dynamics studies. Clay Miner. 2016, 51, 197–211. [Google Scholar] [CrossRef]
- Bowal, K.; Grančič, P.; Martin, J.W.; Kraft, M. Sphere Encapsulated Monte Carlo: Obtaining Minimum Energy Configurations of Large Aromatic Systems. J. Phys. Chem. A 2019, 123, 7303–7313. [Google Scholar] [CrossRef]
- Koumpouras, K.; Larsson, J.A. Distinguishing between chemical bonding and physical binding using electron localization function (ELF). J. Phys. Condens. Matter 2020, 32, 315502. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grančič, P.; Böhm, L.; Gerzabek, M.H.; Tunega, D. On the Nature of Hydrophobic Organic Compound Adsorption to Smectite Minerals Using the Example of Hexachlorobenzene-Montmorillonite Interactions. Minerals 2023, 13, 280. https://doi.org/10.3390/min13020280
Grančič P, Böhm L, Gerzabek MH, Tunega D. On the Nature of Hydrophobic Organic Compound Adsorption to Smectite Minerals Using the Example of Hexachlorobenzene-Montmorillonite Interactions. Minerals. 2023; 13(2):280. https://doi.org/10.3390/min13020280
Chicago/Turabian StyleGrančič, Peter, Leonard Böhm, Martin H. Gerzabek, and Daniel Tunega. 2023. "On the Nature of Hydrophobic Organic Compound Adsorption to Smectite Minerals Using the Example of Hexachlorobenzene-Montmorillonite Interactions" Minerals 13, no. 2: 280. https://doi.org/10.3390/min13020280
APA StyleGrančič, P., Böhm, L., Gerzabek, M. H., & Tunega, D. (2023). On the Nature of Hydrophobic Organic Compound Adsorption to Smectite Minerals Using the Example of Hexachlorobenzene-Montmorillonite Interactions. Minerals, 13(2), 280. https://doi.org/10.3390/min13020280





